1. Introduction
Balance is a basic human motor skill and is one of the most important functions involved in maintaining normal body posture and ensuring normal body movements. Balance is an important factor in the performance of both day-to-day activities and athletic skills, and people can typically improve their balance by means of regular exercises [
1]. The importance of balance to human beings can be demonstrated from two different perspectives, those of health and sports. From a health perspective, accidental falls, diseases associated with aging, and other problems can all affect balance. In the worst case, falling due to loss of balance can result in accidental death. Age-related diseases and other problems can cause deterioration in the sense of balance, limiting the mobility of the elderly; this narrows the space of possible activities in which they can partake, resulting in decreased involvement in social interactions and causing many other problems beyond physical disability [
2]. From an athletic perspective, athletes wishing to enhance their athletic performance must first consider establishing balance and stability in their movements before they can achieve their full potential [
3,
4,
5].
Many of the physiological signals collected empirically are non-linear, such as heartbeats [
6,
7], brain waves [
8], and the balancing state of the body [
9,
10]. The goal of non-linear analysis is to present non-linear data quantitatively. Complexity denotes a state of affairs that one can easily appreciate when confronted with it [
11]. Piasecki [
12] discussed the multi-scale complexity of binary and grey level pattern characteristics. Such an entropic descriptor can be also employed to reconstruct microstructure details [
13]. Complex systems are neither absolutely regular nor absolutely random [
14,
15]. Thus, multi-scale entropy (MSE) [
6,
16], a recent method of measuring the complexity of finite length time series, has been proposed. Entropy describes a measure of statistical or dynamical disorder, whereas complexity rather refers to the structural organization arising in the system. Both terms are obviously closely related, but can provide complementary information [
11]. This computational tool groups data points according to multiple different timescales to reveal repeated patterns, enabling the theoretical quantification of the complexity of the data using a variety of measures of entropy. MSE can be applied both to physical and physiological data sets; for example, this can be used to measure the complexity of physiological signals during the process of inhibitory control [
17]. Higher MSE values signify that the signal is less predictable and information-rich, whereas lower MSE values imply that the time series is more regular and less complex [
6,
16,
18]. In recent years, MSE analysis has become increasingly adopted to quantify the complexity of physiological signals. Many previous studies discuss the complexity differences between groups to demonstrate changes in balance ability [
19,
20,
21], while others explore the changes in complexity under different situations within a single group to elucidate the effect of different factors on balance ability [
2,
10]. Costa
et al. [
22] used MSE curves to show that diseased hearts have a significant decrease in sample entropy on multiple time scales, indicating a lower degree of complexity. Additionally, Cai
et al. [
23] used MSE to investigate the complexity of heart rate range. Such studies have demonstrated that MSE reveals valuable hidden information by measuring signal characteristics at various scales [
16].
It is a relatively new to use a method for analyzing complexity in physics to elucidate hidden information in physiological data. Entropy is a concept of complexity. Multiple entropy measures, such as approximate entropy, sample entropy and multi-scale entropy, can be used to investigate non-linear data. After a gradual evolution, MSE is now being used in clinical trials and human factor research to quantitatively analyze physiological data [
6,
16,
22,
24]. Gruber
et al. [
21] compared the time-to-contact (TtC), multi-scale entropy, and traditional center of presure (COP) indicator methods to analyze COP displacement data when standing still in order to rank disease severity amongst Adolescent Idiopathic Scoliosis patients and healthy controls. Compared to traditional measurements and time-to-contact (TtC), multi-scale entropy uses methods in dynamics to interpret changes in displacement data. Therefore, the multi-scale entropy method provides a better understanding of the hidden information. Busa
et al. [
20] indicated that compared to the COM or COP methods, multi-scale entropy, similar to sample entropy, enabled a deeper understanding of spacial and time-related parameter induced physiological changes in subjects in relation to sequences of times and posture control in an active sequence. Duarte
et al. [
25] believed that multi-scale entropy could be used to analyse the complexity of posture control during long-term standing as well as in the adapation of subjects to systemetic changes, whereas the Detrended Fluctuation Analysis (DFA) indicator cannot be used to reflect adaption.
Currently, balance training is available as part of various exercise classes and in fitness and sports training. However, these options are not appealing to all demographics; hence the demand for alternative forms of balance training, such as can be provided through exergames. To this end, Sun
et al. [
19] investigated how the parameters of a Kinect-based exergame can influence the balance control ability and intensity level tolerated by the player, by analyzing both objective metrics and gameplay-based player experience. Sun
et al., used traditional balance indicators to analyze postural stability, including Mean Distance-Anterior Posterior (MDISTAP), Mean Distance-Medial Lateral (MDISTML), Sway Area (AREA_SW), and Total Excursions (TOTEX). Please see the
Appendix for more details.
Traditional single-scale methods of analyzing time series ignore sequential properties that emerge across multiple time scales; as a result, they tend to confound low-complexity signals with signals whose order emerges across multiple different time series [
26]. Costa
et al. [
27] mention that, in the study of positional complexity, such hidden information can more effectively highlight the differences between two groups, in order to assess the risk and to predict the effectiveness of medical treatment. Busa
et al. [
20] also mention that, instead of using discrete data such as COP range, standard deviation, or path length to calculate statistical parameters, it is more important to define the mechanism of position control complexity. This investigation of the utility of multi-scale entropy complexity is motivated by these observations.
In our previous study analyzing traditional balance indicators, the parameters of a Kinect-based exergame were combined with balance training exercises, which influenced the balance control ability and intensity level that players could tolerate [
28]. The goal of the present study is to flexibly modify the exergame so that it can be tailored to the needs of various individuals using the same set of parameters. The exergame consists of virtual reality combined with the Kinect-based interactive equipment and collects movement data objectively using a force plate. The adaptability of the exergame will then be analyzed and explored using complexity analysis, in order to optimize the parameters of video game-based fitness training routines, and to inform future developments in personalized training. Thus, this study will achieve the following goals:
- (1)
Collect COP data using a force plate and assess the complexity of the displacement variable with multi-scale entropy analysis to determine the parameters affecting leg movement during a Kinect-based exergame.
- (2)
Characterize the responsiveness of the complexity index to the manipulation of various exergame parameters; for example, investigate how complexity varies under parameters corresponding to increasing levels of difficulty.
- (3)
Compare the results of traditional indicator analysis [
28] to those of multi-scale entropy analysis, to determine the viability of multi-scale entropy analysis as a tool for human-centered design, or as another assessment in the future.
3. Results and Discussion
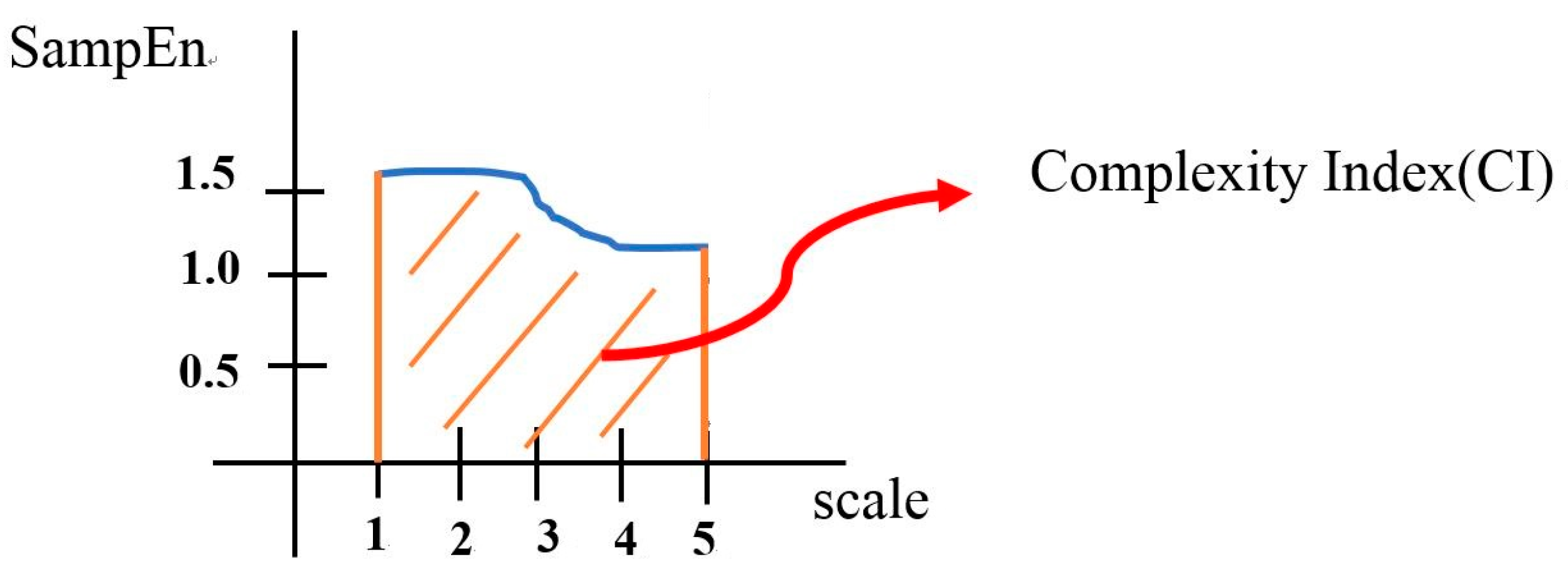
This study used multi-scale entropy analysis to compare the complexity indexes of subjects’ balancing movements under different parameter settings of both static and dynamic posture frames. The multi-scale entropy analysis parameters were set to values recommended by Costa
et al. [
21]: an embedding dimension (
m) of 2, a tolerance (
r) of 0.15. Also, the minimum number of data points required to apply the MSE method depends on the level of accepted uncertainty. Typically, in the previous study, a time series with 2 × 10
4 data points was used for analyses extending up to scale 20 [
27]. In this current study, as a sample rate of 100 Hz with a 10 min time series normally contains 5000–6000 COPs during the exergame, we used a scale of 5. All parameters were obtained from three experiments for each subject, following which descriptive statistics were used to calculate the average and standard deviation of the three tests.
Results for the static posture frame are shown in
Table 1. In both the ML and AP directions, complexity (indicating adaptability) is greatest with a wide posture frame and a 1-s posture frame travel time, while complexity is lowest with a narrow posture frame and a frame travel time of 2 s, indicating that subjects find the former parameter settings to be easier than the latter. In terms of parameter selection, the complexity of the frame travel time of 1 s is greater than that of the frame travel time of 2 s, indicating that travel time is an important factor to consider in adjusting the difficulty of the game. In terms of the direction of movement of the body’s center of mass, the complexity of anterior-posterior motion is higher than that of medio-lateral motion, indicating that for the static posture frame, maintaining medio-lateral balance is more difficult.
Table 1.
MSE results for different static posture frame parameter settings.
Table 1.
MSE results for different static posture frame parameter settings.
| | Smaller Frame Width with a Frame Travel Time of 1 s | Larger Frame Width with a Frame Travel Time of 1 s | Smaller Frame Width with a Frame Travel Time of 2 s | Larger Frame Width with a Frame Travel Time of 2 s |
|---|
| MSE-AP | 2.35 ± 1.04 | 2.36 ± 1.02 | 1.58 ± 0.82 | 1.92 ± 0.74 |
| MSE-ML | 1.63 ± 1.19 | 1.91 ± 1.33 | 0.95 ± 0.62 | 1.10 ± 0.74 |
Multiple measurements were taken to analyze the CI of the subjects under different static posture frame parameter settings (
i.e., different difficulty levels). The results are shown in
Table 2. It was found that for the static posture frame, MSE-AP and MSE-ML both demonstrated significant differences in complexity for different values of the posture frame travel time parameter. Of the static posture frame parameters, manipulation of posture frame travel time was found to cause significant variation in both MSE-AP and MSE-ML. These results are consistent with those obtained by Sun
et al. [
28] for mean distance-anterior posterior (MDIST-AP) COP measurements (see the
Appendix for more details).
Table 2.
P-values of MSE analysis for static posture frame parameters.
Table 2.
P-values of MSE analysis for static posture frame parameters.
| | Offset (Offset of the Frame) | Time (Travel Time of the Frame) | Off × Time |
|---|
| MSE-AP | 0.281 | 0.000 * | 0.300 |
| MSE-ML | 0.213 | 0.000 * | 0.566 |
Results for the dynamic posture frame are shown in
Table 3. In both ML and AP directions, complexity is greatest with a leg-raising rate of 1 s and a leg-raising angle of 45 degrees, indicating that subjects considered these parameter settings to be the easiest. In terms of parameter selection, the complexity of a leg-raising rate of 1 s is greater than 2 s, indicating that leg-raising rate is an important factor to consider in adjusting the difficulty of the game. In terms of the direction of movement of the body’s center of mass, the complexity of anterior-posterior motion is greater than that in the medio-lateral direction, indicating that for the dynamic posture frame, maintaining anterior-posterior balance is easier.
Table 3.
MSE results for different dynamic posture frame parameter settings.
Table 3.
MSE results for different dynamic posture frame parameter settings.
| | a Leg Raising Rate of 1 s with a Leg Raising Angle of 45 Degrees | a Leg Raising Rate of 1 s with a Leg Raising Angle of 90 Degrees | a Leg Raising Rate of 2 s with a Leg Raising Angle of 45 Degrees | a Leg Raising Rate of 2 s with a Leg Raising Angle of 90 Degrees |
|---|
| MSE-AP | 3.56 ± 2.37 | 2.93 ± 2.27 | 2.23 ± 1.06 | 2.28 ± 1.08 |
| MSE-ML | 1.93 ± 1.42 | 1.32 ± 0.99 | 1.46 ± 1.74 | 1.44 ± 1.26 |
Multiple measurements were taken to analyze the value of complexity index of the subjects under different dynamic posture frame parameter settings (
i.e., different difficulty levels). Results are shown in
Table 4. It was found that for the dynamic posture frame, MSE-AP varied significantly for different values of leg-raising rates. Of the dynamic posture frame parameters, manipulation of leg-raising angle and leg-raising rate was found to cause significant variation in MSE-AP, which is also consistent with the results of previous work on COP indicators by Sun
et al. [
28], in which mean distance-medial lateral (MDIST-ML) and total excursions (TOTEX) both manifested significant differences (see
Appendix).
Table 4.
P-values of MSE analysis for dynamic posture frame parameters.
Table 4.
P-values of MSE analysis for dynamic posture frame parameters.
| | Angle (Leg-Raising Angle) | Speed (Leg-Raising Rate) | Angle × Speed |
|---|
| MSE-AP | 0.412 | 0.019 * | 0.349 |
| MSE-ML | 0.254 | 0.443 | 0.151 |
With respect to parameter design and difficulty level, the results of the complexity analysis indicate that the posture frame travel time and leg-raising rate parameters affect the ability of the subjects to adapt. Regarding the different types of posture frames, the performance indicators calculated from the complexity analysis suggest that the dynamic posture frame facilitates balancing and accommodates greater adaptability compared to the static posture frame.
By comparing the traditional balance indicators to the complexity index through the collection of center of pressure signals to understand the use of complexity in human-centered design, we discovered that there was no significant difference between the traditional balance indicators and the complexity index obtained from multi-scale entropy analysis. Complexity is related to our ability to provide a short description of a phenomenon [
32]. Costa
et al. [
16] used the MSE method for quantifying the complexity expressed by physiological dynamics over multiple scales. Higher MSE values thus signify that the signal is less predictable and information-rich, whereas lower MSE values imply that the time series is more regular and less complex [
6,
16,
18]. Lower traditional COP indictors also represent a better balancing ability. Here, our results showed the same rule; for both static and dynamic posture frames, lower complexity was associated with higher values for the traditional balance indicators. Although the MSE-ML index seemed different from the traditional balance indicators for the dynamic posture frame, the p-value suggests that this difference is insignificant. No evidence was found to show inconsistency between the results of the MSE-ML index and those of the traditional balance indicators, indicating the appropriateness of using the complexity index as a means of distinguishing between different difficulty levels (or parameter settings).
When the complexity index was examined by comparing multi-scale entropy to the traditional indicators of self-balance control, including MDISTAP, MDISTML, TOTEX and AREA_SW, we found that even the traditional COP indicators were not consistent with one another. When balance ability was determined from different COP indicators, different results could be obtained from the evaluation. When considering the results of the dynamic posture frame parameters-speed, the traditional indicators TOTEX and AREA_SW could potentially allow different interpretations of the results. These divergent results inform dramatically different outcomes in terms of parameter design. Also, in comparing these traditional indicator results to those obtained from the MSE analysis, it was discovered that MDISTML caused a significant change in balance control (as measured by COP change), but MSE-ML did not. Although the complexity of MSE and COP indictors keep to the rule, the results obtained from using different indicators differed from one another and led to different conclusions.
MDISTAP and MDISTML had no significant effect on COP in terms of balance control. However, when these results were compared to those obtained from multi-scale entropy analysis, we discovered that both MDISTAP and MDISTML caused a significant change in balance control, as measured by COP change.
Each subject was tested randomly in either a dynamic or stastic posture frame experiment. The sequences of the four different tests were randomly generated, as it was discovered that the sequence of a test may affect the subjects’ performance. As shown in
Table 5 and
Table 6, subjects performed best in the first test that was randomly selected. This observation was true for both male and female subjects. A previous study published by Hung
et al. [
32] investigated the complexity of psychological and physiological changes in undergraduates and post-graduate research students after long-term internet surfing. They showed that there was higher complexity amongst undergraduate students. Hung
et al. [
32] suggested that this may have been because the undergraduate students were more entertained by internet surfing than the research students. This may be because the undergraduate students were still in the beginning of their university studies, where they had just begun to realize that a wide range of information exists online and were therefore more interested in surfing. Similarly, higher complexity was obtained from the first posture frame performed by our subjects. This may because our subjects were more interested in their first test since it was their first time performing in a balance exergame and their interest diminished as they were tested in the second posture frame.
Table 5.
Complexity of MSE performance of test subjects challenged to a dynamic posture four times. Test sequences were randomized.
Table 5.
Complexity of MSE performance of test subjects challenged to a dynamic posture four times. Test sequences were randomized.
| | Female Subjects | a Leg Raising Rate of 1 s with a Leg Raising Angle of 45 Degrees (PM0) | a Leg Raising Rate of 1 s with a Leg Raising Angle of 90 Degrees (PM1) | a Leg Raising Rate of 2 s with a Leg Raising Angle of 45 Degrees (PM2) | a Leg Raising Rate of 2 s with a Leg Raising Angle of 90 Degrees (PM3) | Test Sequence | The Best Performance Test |
| ML | a | 5.25869 | 2.811496 | 5.892542 | 2.16455 | PM(2013) | PM(2,0) |
| c | 0.868208 | 1.189067 | 1.130286 | 0.579494 | PM(1230) | PM(1,2) |
| e | 0.578581 | 0.227882 | 0.69477 | 0.582434 | PM(2301) | PM(2) |
| l | 0.874447 | 1.659434 | 0.61579 | 1.082984 | PM(1302) | PM(1) |
| m | 4.480645 | 0.787368 | 0.4631 | 0.565738 | PM(0132) | PM(0) |
| p | 3.159586 | 0.587987 | 0.860727 | 0.604589 | PM(0231) | PM(0) |
| AP | a | 7.66499 | 10.43948 | 3.533666 | 1.296804 | PM(1023) | PM(1) |
| c | 1.487664 | 1.323689 | 0.92777 | 2.903727 | PM(3012) | PM(3) |
| e | 1.370527 | 1.745869 | 1.226729 | 1.18286 | PM(1023) | PM(1) |
| l | 3.194118 | 6.86539 | 2.539416 | 2.363516 | PM(1023) | PM(1) |
| m | 11.33735 | 1.731955 | 1.773966 | 1.846398 | PM(0321) | PM(0) |
| p | 5.897371 | 2.781045 | 1.625832 | 1.291054 | PM(0123) | PM(0) |
| | Male Subjects | a Leg Raising Rate of 1 s with a Leg Raising Angle of 45 Degrees (PM0) | a Leg Raising Rate of 1 s with a Leg Raising Angle of 90 Degrees (PM1) | a Leg Raising Rate of 2 s with a Leg Raising Angle of 45 Degrees (PM2) | a Leg Raising Rate of 2 s with a Leg Raising Angle of 90 Degrees (PM3) | Test Sequence | The best Performance Test |
| ML | f | 0.674736 | 0.85155 | 0.299225 | 0.491154 | PM(1032) | PM(1) |
| i | 2.132251 | 1.128126 | 2.619524 | 1.387528 | PM(2031) | PM(2,0) |
| J | 1.589474 | 0.486658 | 1.209129 | 0.675377 | PM(0231) | PM(0,2) |
| l | 0.391238 | 0.335411 | 1.08763 | 0.359725 | PM(2031) | PM(2) |
| Q | 3.27169 | 2.210144 | 0.041206 | 1.180606 | PM(0132) | PM(0) |
| r | 1.136948 | 1.103727 | 1.343022 | 0.45476 | PM(2013) | PM(2,0) |
| AP | f | 2.126205 | 1.543292 | 1.608031 | 0.552859 | PM(2013) | PM(0) |
| i | 4.266938 | 0.536438 | 3.327552 | 2.117834 | PM(0231) | PM(0) |
| J | 2.100599 | 2.023573 | 1.560657 | 1.803152 | PM(0132) | PM(0,1) |
| l | 1.849903 | 3.633918 | 1.785388 | 1.511883 | PM(1023) | PM(1) |
| Q | 2.064002 | 3.529003 | 3.405516 | 2.145454 | PM(1230) | PM(1) |
| r | 1.627763 | 2.770163 | 2.04816 | 2.773686 | PM(3120) | PM(1,3) |
Table 6.
Complexity of MSE performance of test subjects challenged to a stastic posture four times. Test sequences were randomized.
Table 6.
Complexity of MSE performance of test subjects challenged to a stastic posture four times. Test sequences were randomized.
| | Female Subjects | Smaller Frame Width with a Frame Travel Time of 1 s (PM4) | Larger Frame Width with a Frame Travel Time of 1 s (PM5) | Smaller Frame Width with a Frame Travel Time of 2 s (PM6) | Larger Frame Width with a Frame Travel Time of 2 s (PM7) | Test Sequence | The Best Performance Test |
| ML | a | 2.807041 | 0.800131 | 0.49223 | 0.564508 | PM(4567) | PM(4) |
| c | 2.856832 | 3.223783 | 1.620555 | 1.179054 | PM(5467) | PM(5) |
| e | 3.066809 | 3.429541 | 1.39168 | 2.020441 | PM(5476) | PM(5) |
| l | 3.40571 | 3.581397 | 1.08021 | 1.444286 | PM(5476) | PM(5) |
| m | 3.717184 | 2.462208 | 0.905431 | 0.683047 | PM(4756) | PM(4) |
| p | 0.980827 | 3.499324 | 1.22245 | 0.973401 | PM(5674) | PM(5) |
| AP | a | 1.008593 | 1.712192 | 0.926326 | 0.922015 | PM(5467) | PM(5) |
| c | 1.419178 | 3.016837 | 1.584134 | 1.710214 | PM(5764) | PM(5) |
| e | 2.291959 | 5.224699 | 1.250506 | 1.269133 | PM(5476) | PM(5) |
| l | 3.957102 | 3.547704 | 2.31777 | 2.143899 | PM(4567) | PM(4) |
| m | 3.584933 | 1.80252 | 0.965174 | 2.234007 | PM(4756) | PM(4) |
| p | 2.912515 | 3.139438 | 1.672746 | 3.044492 | PM(5746) | PM(5) |
| | Male Subjects | Smaller Frame Width with a Frame Travel Time of 1 s (PM4) | Larger Frame Width with a Frame Travel Time of 1 s (PM5) | Smaller Frame Width with a Frame Travel Time of 2 s (PM6) | Larger Frame Width with a Frame Travel Time of 2 s (PM7) | Test Sequence | The Best Performance Test |
| ML | f | 1.598881 | 3.671485 | 1.50758 | 2.895301 | PM(5746) | PM(5) |
| i | 1.227865 | 2.995013 | 1.807266 | 2.487046 | PM(5764) | PM(5) |
| J | 0.361988 | 3.971029 | 0.641101 | 1.58386 | PM(5764) | PM(5) |
| l | 0.599678 | 1.389844 | 0.843141 | 0.968052 | PM(5674) | PM(5) |
| Q | 3.18901 | 2.069505 | 1.569167 | 0.963782 | PM(4567) | PM(4) |
| r | 3.262493 | 2.032848 | 1.020175 | 0.973401 | PM(4756) | PM(4) |
| AP | f | 2.126205 | 1.543292 | 1.608031 | 0.552859 | PM(5746) | PM(5) |
| i | 4.266938 | 0.536438 | 3.327552 | 2.117834 | PM(5764) | PM(5) |
| J | 2.100599 | 2.023573 | 1.560657 | 1.803152 | PM(5674) | PM(5) |
| l | 1.849903 | 3.633918 | 1.785388 | 1.511883 | PM(4567) | PM(4) |
| Q | 2.064002 | 3.529003 | 3.405516 | 2.145454 | PM(5476) | PM(5) |
| r | 1.627763 | 2.770163 | 2.04816 | 2.773686 | PM(5467) | PM(5) |
According to the dynamic postures in
Table 5, there was higher complexity for most subjects, regardless of gender, when tested in a ML direction “when raising the leg to an angle of 45 degrees at a rate of either one or two seconds”. This indicated that the subjects were better adapted to a leg raising angle of 45 degrees, and additionally suggests that raising a leg to 45 degrees was either than raising a leg to a 90 degree angle. When considering the AP direction, a higher complexity was observed, regardless of gender, in most subjects when the combination of “raising the leg to a 90 degree angle in one second” and “raising the leg to a 45 degree angle in one second” were performed. They could also adapt much better. This indicated that it was easier to adapt when performaing leg raise at a faster pace. According to the static postures in
Table 6, female subjects could adapt much better to different speeds regardless of whether they were tested in a AP or ML direction. This observation was more obvious in the one second tests. Male subjects were better at matching the posture of the frame regardless of whether they were tested in a AP or ML direction. This was more obvious in tests that used posture frames with larger widths.
The results of this study suggest that multi-scale entropy analysis reflects subjects’ adaptability during static and dynamic activities. Gruber
et al. [
21] considered that, in comparison to traditional balance indicators, multi-scale entropy explains changes in displacement using knowledge of dynamics and reveals more hidden information. In light of this, they suggest including two directions of postural control assessment in traditional balance indicators. The author inferred that this method seemed to be a rigorous tool for the analysis of dynamic activity, which is consistent with the conclusions of Busa
et al. [
20], in which multi-scale entropy was used to analyze position control during a static activity.
This study hoped to identify the parameters affecting activity performance in exergames using multi-scale entropy. We first investigated the parameters involved in Kinect-based exergame performance, then used the concept of complexity through MSE to define their control mechanisms, rather than simply arriving at an understanding of the statistical significance of discrete data [
20]. Not only is this method useful as an assessment criterion for future studies, it also opens up new avenues for exploration of the use of multi-scale entropy analysis as a tool in the design of virtual environments and in the selection of parameter settings by elucidating exergame performance mechanisms.