Projective Exponential Synchronization for a Class of Complex PDDE Networks with Multiple Time Delays
Abstract
:1. Introduction
1.1. Notations
2. Preliminaries and Problem Formulation
3. Distributed P-sD State Feedback Control Design for Projective Exponential Synchronization
4. Simulation Study
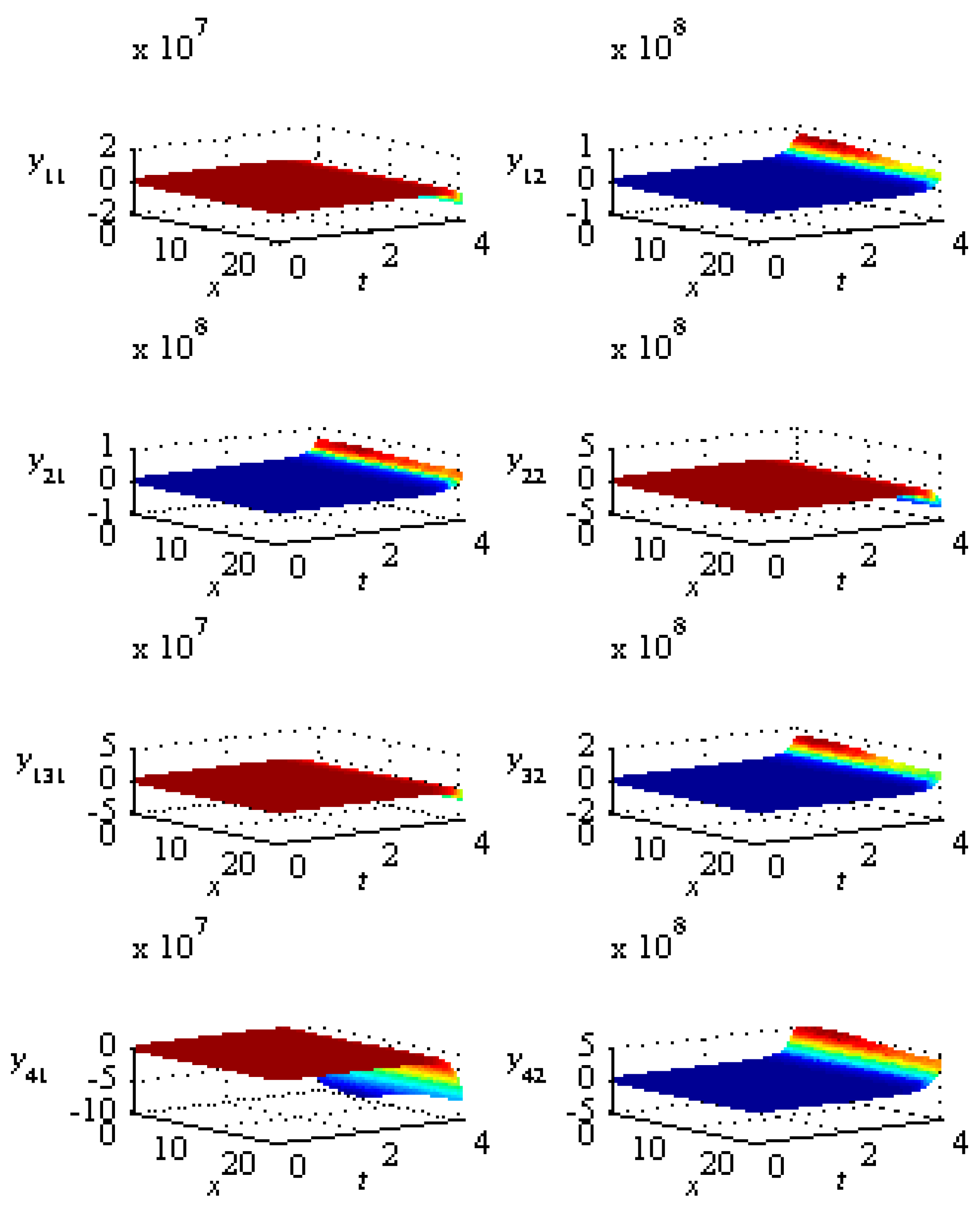

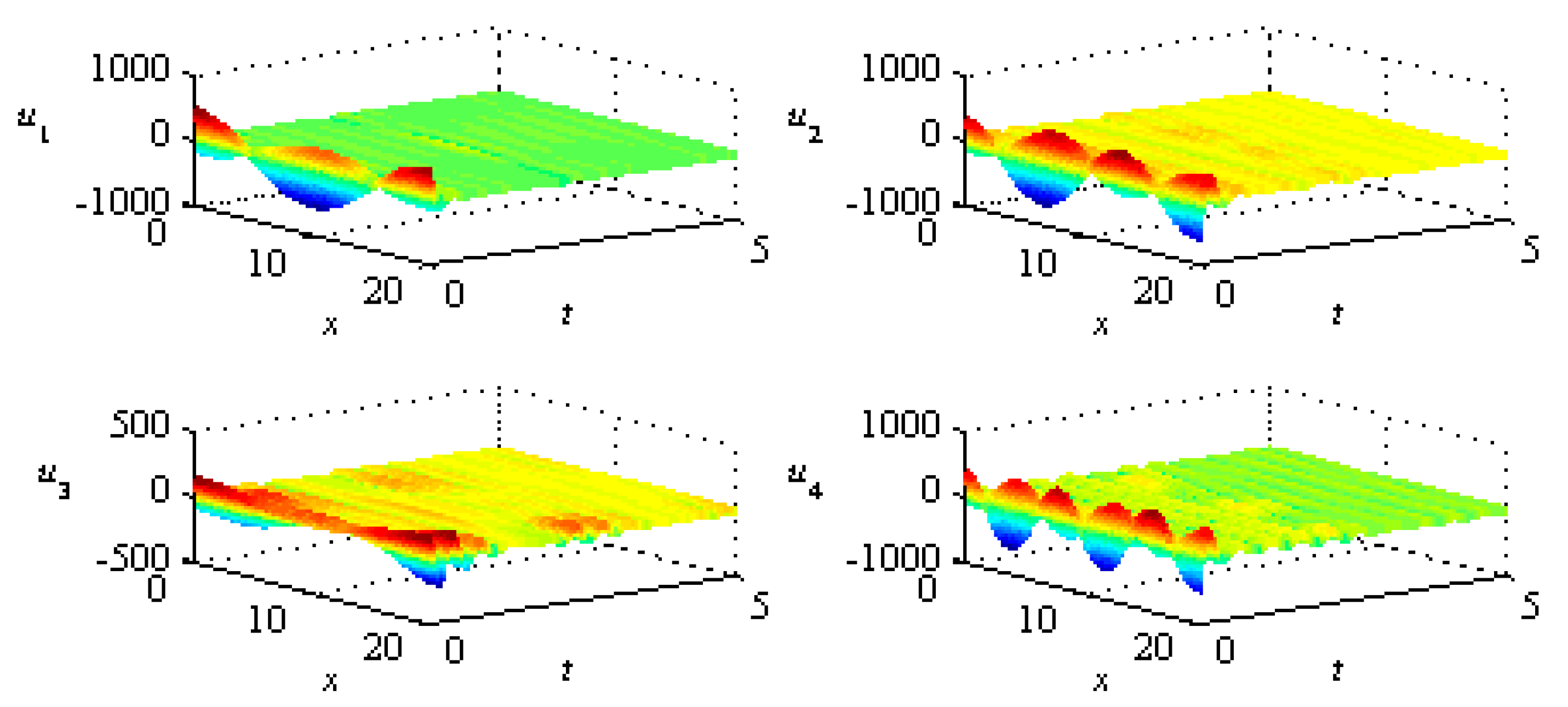
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cross, M.; Hohenberg, P. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851–1112. [Google Scholar] [CrossRef]
- Cohen, M.; Grossberg, S. Absolute stability and global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans. Syst. Man Cybern. 1983, 13, 815–826. [Google Scholar] [CrossRef]
- Marcus, C.; Westervelt, R. Stability of analog neural networks with delay. Phys. Rev. A 1989, 39, 347–359. [Google Scholar] [CrossRef] [PubMed]
- Cochocki, A.; Unbehauen, R. Neural Networks for Optimization and Signal Processing; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Bowong, S. Stability analysis for the synchronization of chaotic systems with different order: Application to secure communications. Phys. Lett. A 2004, 326, 102–113. [Google Scholar] [CrossRef]
- Cuomo, K.; Oppenheim, A.; Strogatz, S. Synchronization of Lorenz-based chaotic circuits with applications to communications. IEEE Trans. Circuits Syst. II 1993, 40, 626–633. [Google Scholar] [CrossRef]
- Yang, T.; Chua, L. Impulsive stabilization for control and synchronization of chaotic systems: Theory and application to secure communication. IEEE Trans. Circuits Syst. I 1997, 44, 976–988. [Google Scholar] [CrossRef]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.L.; Zhou, C.S. The synchronization of chaotic systems. Phys. Rep. 2006, 366, 1–101. [Google Scholar] [CrossRef]
- Arenas, A.; Díaz-Guilera, A.; Kurths, J.; Moreno, Y.; Zhou, C. Synchronization in complex networks. Phys. Rep. 2008, 469, 93–153. [Google Scholar] [CrossRef]
- Eisencraft, M.; Fanganiello, R.; Monteiro, L. Chaotic synchronization in discrete-time systems connected by bandlimited channels. IEEE Commun. Lett. 2011, 15, 671–673. [Google Scholar] [CrossRef]
- Nicosia, V.; Valencia, M.; Chavez, M.; Díaz-Guilera, A.; Latora, V. Remote synchronization reveals network symmetries and functional modules. Phys. Rev. Lett. 2013, 110, 174102. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Ho, D.; Yang, Y. Projective synchronization of a class of delayed chaotic systems via impulsive control. Phys. Lett. A 2009, 373, 3128–3133. [Google Scholar] [CrossRef]
- Zhou, P.; Bai, R.; Zheng, J. Projective synchronization for a class of fractional-order chaotic systems with fractional-order in the (1, 2) interval. Entropy 2015, 17, 1123–1134. [Google Scholar] [CrossRef]
- Xin, B.; Wu, Z. Projective synchronization of chaotic discrete dynamical systems via linear state error feedback control. Entropy 2015, 17, 2677–2687. [Google Scholar] [CrossRef]
- Baldi, P.; Atiya, A. How delays affect neural dynamics and learning. IEEE Trans. Neural Netw. 1994, 5, 612–621. [Google Scholar] [CrossRef] [PubMed]
- Chapeau-Blondeau, F.; Chauvet, G. Stable, oscillatory, and chaotic regimes in the dynamics of small neural networks with delay. Neural Netw. 1992, 5, 735–743. [Google Scholar] [CrossRef]
- Bélair, J.; Campbell, S.; Driessche, P. Frustration, stability, and delay-induced oscillations in a neural network model. SIAM J. Appl. Math. 1996, 56, 245–255. [Google Scholar] [CrossRef]
- Cao, J.; Lu, J. Adaptive synchronization of neural networks with or without time-varying delay. Chaos 2006, 16. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wang, Y.; Liu, Y. Global synchronization for discrete-time stochastic complex networks with randomly occurred nonlinearities and mixed time delays. IEEE Trans. Neural Netw. 2010, 21, 11–25. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Xiang, L.; Liu, Z. Synchronization in complex delayed dynamical networks with impulsive effects. Physica A 2007, 384, 684–692. [Google Scholar] [CrossRef]
- Yu, W.; Cao, J. Synchronization control of stochastic delayed neural networks. Physica A 2007, 373, 252–260. [Google Scholar] [CrossRef]
- Yang, X.; Yang, Z. Synchronization of TS fuzzy complex dynamical networks with time-varying impulsive delays and stochastic effects. Fuzzy Sets Syst. 2014, 235, 25–43. [Google Scholar] [CrossRef]
- He, P.; Jing, C.; Fan, T.; Chen, C.-Z. Robust decentralized adaptive synchronization of general complex networks with coupling delayed and uncertainties. Complexity 2014, 19, 10–26. [Google Scholar] [CrossRef]
- Murray, J. Mathematical Biology; Springer: Berlin, Germany, 1989. [Google Scholar]
- Grigoriev, R.; Cross, M.; Schuster, H. Pinning control of spatiotemporal chaos. Phys. Rev. Lett. 1997, 79, 2795–2798. [Google Scholar] [CrossRef]
- Parekh, N.; Parthasarathy, S.; Sinha, S. Global and local control of spatiotemporal chaos in coupled map lattices. Phys. Rev. Lett. 1998, 81, 1401–1404. [Google Scholar] [CrossRef]
- Wu, K.; Li, C.; Chen, B.; Yao, Y. Robust H∞ synchronization of coupled partial differential systems with spatial coupling delay. IEEE Trans. Circuits Syst. II 2013, 60, 451–455. [Google Scholar] [CrossRef]
- Wu, K.; Chen, B. Synchronization of partial differential systems via diffusion coupling. IEEE Trans. Circuits Syst. I 2012, 59, 2655–2668. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, H. Global asymptotic stability of reaction-diffusion Cohen-Grossberg neural networks with continuously distributed delays. IEEE Trans. Neural Netw. 2010, 21, 39–49. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wu, H.; Guo, L. Passivity and stability analysis of reaction-diffusion neural networks with Dirichlet boundary conditions. IEEE Trans. Neural Netw. 2011, 22, 2105–2116. [Google Scholar] [CrossRef] [PubMed]
- Codreanu, S. Synchronization of spatiotemporal nonlinear dynamical systems by an active control. Chaos Solitions Fractal 2003, 15, 507–510. [Google Scholar] [CrossRef]
- Yuan, K.; Alofi, A.; Cao, J.; Al-Mazrooei, A.; Elaiw, A. Synchronization of the coupled distributed parameter system with time delay via proportional-spatial derivative control. Discret. Dyn. Nat. Soc. 2014, 2014. [Google Scholar] [CrossRef]
- Wang, J.; Yang, C.; Sun, C. Exponential synchronization for a class of networked linear parabolic PDE systems via boundary control. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 3981–3986.
- Yang, C.; Qiu, J.; Yi, K.; Chen, X.; Zhang, A.; Chen, X.; Yang, L. Robust exponential synchronization for a class of master-slave distributed parameter systems with spatially variable coefficients and nonlinear perturbation. Math. Probl. Eng. 2015. [Google Scholar] [CrossRef]
- Yang, C.; Qiu, J.; He, H. Exponential synchronization for a class of complex spatio-temporal networks with space-varying coefficients. Neurocomputing 2015, 151, 401–407. [Google Scholar] [CrossRef]
- Mao, X.; Koroleva, N.; Rodkina, A. Robust stability of uncertain stochastic differential delay equations. Syst. Control Lett. 1998, 35, 325–336. [Google Scholar] [CrossRef]
- Wang, J.; Wu, H.; Li, H. Distributed proportional-spatial derivative control of nonlinear parabolic systems via fuzzy PDE modeling approach. IEEE Trans. Syst. Man Cybern. Part B 2012, 42, 927–938. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Qiu, J.; Wang, J. Robust H∞ control for a class of nonlinear distributed parameter systems via proportional-spatial derivative control approach. Abstr. Appl. Anal. 2014, 2014. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Qiu, J.; Li, T.; Zhang, A.; Chen, X. Projective Exponential Synchronization for a Class of Complex PDDE Networks with Multiple Time Delays. Entropy 2015, 17, 7298-7309. https://doi.org/10.3390/e17117298
Yang C, Qiu J, Li T, Zhang A, Chen X. Projective Exponential Synchronization for a Class of Complex PDDE Networks with Multiple Time Delays. Entropy. 2015; 17(11):7298-7309. https://doi.org/10.3390/e17117298
Chicago/Turabian StyleYang, Chengdong, Jianlong Qiu, Tongxing Li, Ancai Zhang, and Xiangyong Chen. 2015. "Projective Exponential Synchronization for a Class of Complex PDDE Networks with Multiple Time Delays" Entropy 17, no. 11: 7298-7309. https://doi.org/10.3390/e17117298
APA StyleYang, C., Qiu, J., Li, T., Zhang, A., & Chen, X. (2015). Projective Exponential Synchronization for a Class of Complex PDDE Networks with Multiple Time Delays. Entropy, 17(11), 7298-7309. https://doi.org/10.3390/e17117298





