Complexity-Regularized Regression for Serially-Correlated Residuals with Applications to Stock Market Data

Abstract

A popular approach in the investigation of the short-term behavior of a non-stationary time series is to assume that the time series decomposes additively into a long-term trend and short-term fluctuations. A first step towards investigating the short-term behavior requires estimation of the trend, typically via smoothing in the time domain. We propose a method for time-domain smoothing, called complexity-regularized regression (CRR). This method extends recent work, which infers a regression function that makes residuals from a model “look random”. Our approach operationalizes non-randomness in the residuals by applying ideas from computational mechanics, in particular the statistical complexity of the residual process. The method is compared to generalized cross-validation (GCV), a standard approach for inferring regression functions, and shown to outperform GCV when the error terms are serially correlated. Regression under serially-correlated residuals has applications to time series analysis, where the residuals may represent short timescale activity. We apply CRR to a time series drawn from the Dow Jones Industrial Average and examine how both the long-term and short-term behavior of the market have changed over time.

1. Introduction

When studying the short-term behavior of a time series, a common assumption is that the time series can be treated as a realization from a trend stationary stochastic process. That is, it is assumed that the time series can be modeled as the sum of a deterministic trend and a stationary stochastic process, where the deterministic trend is assumed to vary slowly compared to the stochastic process [1]. As an example, consider the closing price of the Dow Jones Industrial Average (DJIA) over time, shown in Figure 1. Over large enough timescales, the market exhibits clear trends. However, when considering short timescale (e.g., inter-day) behavior of the market, these long-term trends could mask the dynamics of day-to-day fluctuations. For example, because the value of the market tends to increase over time, nearby time points will tend to be positively correlated. However, this long-term correlation tells us nothing about the short-term dynamics of the market. A natural solution is to estimate the trend and remove it. The problem of estimating the long-term trend present in a time series can be cast as a time-domain regression problem, where we regress the observed values of the time series on the time index. Within this framework, nonparametric regression methods may be used to infer the underlying trend without making strong a priori assumptions on its form. The literature on nonparametric regression is rich and includes techniques, such as kernel-based methods, smoothing splines, wavelets and series expansions, in terms of orthogonal functions [1–3]. A complementary approach to non-parametric regression for more flexible modeling can be found in the tools from robust statistics, which offer statistical procedures that are flexible to deviations from an assumed model [4]. While the general issues related to robust statistics have received considerable attention in the literature, their application to time series analysis has largely been limited to robust tests for serial correlation [5,6] and linear trends [7]. To the best of our knowledge, little to no work has been done on robust statistics (in the formal sense) for trend estimation under correlated errors.

While nonparametric methods have the advantage that they can adapt to regularities in the data, they also come with tuning parameters that must be set by the investigator. These tuning parameters, also known as smoothing parameters, include the bandwidth for kernel-based methods, the effective degrees of freedom for smoothing splines and the number of basis functions for orthogonal expansions. The value for the smoothing parameter is often chosen via data-driven methods, such as cross-validation, where the data is split into a training set used to infer the model and a tuning set used to select the smoothing parameter [2]. However, many such procedures are designed for regression where the residuals are uncorrelated, as might be the case when performing regression on data in which each data point corresponds to a separate measurement from some underlying population. The assumption of uncorrelated residuals clearly does not hold for time-domain regression where we expect short-term serial correlations. For example, early work in econometrics found non-trivial serial correlations in stock prices [8]. Serial correlations in residuals greatly impact the performance of automated, data-dependent methods for choosing smoothing parameters. For instance, in [9], Hart shows that for kernel regression estimation, when the residuals are drawn from an order-one autoregressive (AR(1)) process [1] with coefficient φ, for φ ≳ 0.17 (with the exact value depending on the choice of kernel), in the limit of infinite data, cross-validation will choose an estimate that nearly interpolates the data. Thus, even for a very simple model of residuals with weak serial correlations, the standard method for choosing the smoothing parameter of a nonparametric regression method will result in a trend estimate that adapts to the correlations in the residuals, rather than reflecting the true trend. In this case, neither the trend nor the residuals are correctly estimated. This is especially problematic when the properties of the residuals are the object of study, as a near-interpolating trend estimate will cause the residuals to look like numerical noise. Many approaches have been proposed to generalize cross-validation for serially-correlated errors [10–13]. These methods typically involve block-wise versions of cross-validation, where appropriately chosen blocks of a time series are removed during each fold of the cross-validation procedure. See [14] for a review of other literature on regression with correlated errors.

A new class of nonparametric regression methods, first proposed in [15], considers the regression problem from a different perspective, where the focus shifts from the regression curve to the residuals. Instead of considering the estimator’s fidelity to the underlying curve, the method seeks to make the residuals look as random as possible while maintaining as simple a regression curve as possible. This method thus hinges on an often overlooked point from regression: under the assumption of most methods, residuals resulting from a smoothing method should look like white noise. However, because of this construction, the method from [15] does not immediately apply to time series with serially-correlated residuals.

In this paper, we develop a nonparametric regression technique that is model-agnostic with respect to both the long-term trend and the serial correlations in the residuals. This method relies on tools from the field of computational mechanics [16], a formalism for dissecting the structure and randomness present in a stationary stochastic process. Computational mechanics allows us to greatly expand the class of possible residuals considered in [15]. Any nonparametric smoother may be used to estimate the trend, and the residuals need not be white noise, though we do limit memory length. We then apply this technique to the Dow Jones Industrial Average, a time series where we expect serially-correlated residuals, and investigate how both the long-term and short-term behavior of the market has changed over time.

2. Methodology

2.1. Regression for Time Series

A typical model for time series is that the observed value Y_t can be treated as the sum of a “true” trend r_t plus some deviation from the trend η_t [1]. That is, we have the model:

$$Y_t=r_t+{\eta }_t,t=1,\dots ,T.$$

(1)

The residual process {η_t} is typically specified in terms of its first two moments. In particular, it is assumed to have zero mean:

$$E\left[{\eta }_t\right]=0,\text{for all}t$$

(2)

(if not, this non-zero value would be incorporated into r_t) and some autocorrelation structure dependent on the lag between two time points,

$$R(t,s)=R(|t-s|)=E\left[{\eta }_t{\eta }_s\right],$$

(3)

which specifies the form of the serial correlation. It should be noted that the form (1) for a time series addresses a very particular kind of non-stationarity. Other types of non-stationarity commonly occur in time series, including, but not limited to, heteroskedastic and heavy-tailed deviation processes. These types of non-stationarities are typically investigated using autoregressive conditional heteroskedastic (ARCH) models and their generalizations [1]. As we assume the trend stationary model, we do not address these types of non-stationarities with our method.

As stated and without careful interpretation, (1) can be problematic, both theoretically and practically [1]. One interpretation of this formulation is to consider {Y_t} as the discretization of a sample path from a continuous time stochastic process:

$$Y(t)=r(t)+\eta (t).$$

(4)

Such an interpretation frequently occurs with financial time series due to the prevalence of stochastic differential equation models, such as the famous Black–Scholes model [17] for options. This formulation also frequently occurs in longitudinal and functional data analysis, where the function r(t) is estimated using several independent realizations from (4) [18,19]. However, this model is inappropriate for time-domain smoothing, since it assumes that both r(t) and η(t) vary continuously in time. Thus, for small values of Δt, we expect Y (t ± Δt) to be nearly the same as Y (t), so nothing is gained from smoothing about the time index t. Moreover, under this formulation and without any additional assumptions, because of the smoothness in η(t), it is impossible to extract the trend with only a single realization. Because of this, a popular alternative formulation of (1) for time-domain smoothing is to consider the model:

$$Y_t=g(t/T)+{\eta }_t,t=1,2,\dots ,T,$$

(5)

which places the estimation problem within the framework of nonparametric estimation with equispaced design points [20–22]. This formulation explicitly assumes that the time trend r(t) = g(t/T) varies more slowly than the stochastic component {η_t}, thus motivating the use of smoothing about the time index and allowing for the recovery of the time trend from a single realization.

In nonparametric regression, we seek an estimator ${\widehat{r}}_t$ that should capture the true trend r_t without picking up too much of the false “trend” introduced by the residual term η_t. In the case of white noise, for example, this can be done by averaging over nearby time points. If the noise terms truly are uncorrelated, this averaging process reduces the pointwise variance in ${\widehat{r}}_t$, but also increases its pointwise bias, since, in general, r_t ≠ r_t′ for t ≠ t′. The amount of smoothing is decided by a smoothing parameter λ. Some standard smoothing methods for time series include kernel smoothing, smoothing splines and local polynomial smoothing, all of which have an associated smoothing parameter [1].

The choice of the smoothing parameter falls within the larger statistical framework of model selection [25]: from a certain class of models, how do we choose the model that best reflects the underlying process that generated the data? The model selection procedure depends on the operationalization of “best”: a model may be chosen to maximize a likelihood, minimize a certain error function, etc. In the case of estimating a regression function via smoothing, a standard approach is to choose the smoothing parameter λ by cross-validation on the estimated mean-squared prediction error between the observation Y_t and regression function ${\widehat{r}}_t$ [2]. Let the T data points be indexed by I = {1, 2,…, T}. To perform cross-validation, we partition the indices into K disjoint subsets $P_1,P_2,\dots ,P_K$. For each subset of indices, we use the data indexed by $I\backslash P_k$ to estimate ${\widehat{r}}_t^{(-k)}(\lambda )$, i.e., ${\widehat{r}}_t^{(-k)}(\lambda )$ is estimated using all of the data except the data indexed by the subset $P_k$. The mean-squared error is then computed on the held out data for each subset:

$$\widehat{\mathrm{MSE}}({\widehat{r}}^{(-k)};\lambda )=\frac{1}{|P_k|}{\displaystyle \sum _{t\in P_k}{(Y_t-{\widehat{r}}_t^{(-k)}(\lambda ))}^2},k=1,\dots ,K.$$

(6)

The estimate for the mean-squared error is then determined by averaging the mean-squared error over the held-out subsets, giving:

$$\widehat{\mathrm{MSE}}(\lambda )=\frac{1}{K}{\displaystyle \sum _{k=1}^K\widehat{\mathrm{MSE}}({\widehat{r}}^{(-k)};\lambda )}.$$

(7)

Finally, the smoothing parameter is taken to minimize this estimate of the mean-squared error, giving:

$$\widehat{\lambda }=\underset{\lambda }{\arg min}\widehat{\mathrm{MSE}}(\lambda ).$$

(8)

This approach to choosing the smoothing parameter can be problematic when the residuals are serially correlated [13], as we have discussed in the introduction.

2.2. Model-Free Regression

As we have stated, regression models of the form (1) typically require the specification of a probability model for the stochastic component {η_t}. Recent work by P. L. Davies and co-authors has proposed methods for nonparametric regression without such models [15,26]. We recast their problem, which is stated for general regression, in terms of time-domain regression. The basic idea, as summarized in [27], is to choose the simplest regression function that makes the residuals “look random”. The fact that the residuals should look random is a natural consequence of the statistical model for the regression function. The problem of deciding whether the residuals look sufficiently random is well developed and typically involves simple diagnostic plots and tests on the residuals [23,24]. As a simple example, consider the case where the observed time series is a sinusoid over a single period corrupted by a small amount of white noise. Using a linear trend will induce both short- and long-range correlation in the residuals: residuals near the peaks/troughs of the sinusoid will be positively correlated with residuals near the peaks/troughs and negatively correlated with residuals near the troughs/peaks. At the opposite extreme, a near-interpolating trend would result in uncorrelated residuals, but the estimated trend will also have many degrees of freedom. Davies et al.’s approach seeks to balance between these two extremes.

The setup for Davies et al.’s approach is as follows. We observe T observations of a time series Y₁,…, Y_T, and we seek the regression function r, such that we will model Y_t = r_t. For a given choice of r, we may compute the residuals:

$${\eta }_t=Y_t-r_t,t=1,\dots ,T.$$

(9)

Define η(r) = (η₁,…, η_T). We then specify a test for randomness in these residuals, R(η(r)) where:

$$R(\eta (r))=\{{}_{0:\text{do not reject randomness in}\eta (r)}^{1:\text{reject randomness in}\eta (r)}$$

(10)

For example, R might be the Wald–Wolfowitz runs test [28], a nonparametric test for the independence of binary random variables. We will return to this idea shortly when we propose our extension to Davies et al.’s work. We also define a “complexity” measure on r, ψ(r). For example, ψ might measure the number of extrema of r or the integrated squared second-derivative (“wiggliness”) of r,

$$\psi (r)={\displaystyle \int {(r_t^{″})}^{2}dt.}$$

(11)

Once R and ψ are specified, we seek the r that solves:

$$\underset{r}{min}\psi (r)$$

(12)

$$\text{subject to}R(\eta (r))=0.$$

(13)

That is, we seek the minimally complex regression function $\widehat{r}$, such that the residuals “look random”. This approach has been operationalized by Davies et al. in their runs method for nonparametric regression [15].

2.3. Computational Mechanics

A key part of Davies et al.’s method was the assumption that the residuals η_i should look “random”, where they operationalize random to mean that the residuals should appear like a realization from a white noise process. We could allow for the residuals to appear like realizations from more general stochastic processes, but we then need simple criteria to characterize the randomness of the residuals. Computational mechanics, a formalism for investigating stationary stochastic processes, provides such criteria. We now present a brief overview of computational mechanics. A high-level review may be found in [29]. A more mathematical treatment may be found in [16].

We restrict ourselves to a discrete time, discrete state stochastic process ${\left\{X_t\right\}}_{t\in \mathrm{\mathbb{Z}}}$ taking values from the finite alphabet $\mathcal{X}$. For example, when ${\left\{X_t\right\}}_{t\in \mathrm{\mathbb{Z}}}$ corresponds to a stochastic process defined over all bi-infinite binary strings, $\mathcal{X}=\{0,1\}$. We will use the standard convention of denoting a realization from this process at a fixed time t by x_t. For a time point t, we define the past of the process as:

$$X_{-\mathrm{\infty }}^{t-1}=(\dots ,X_{t-2},X_{t-1})$$

(14)

and the future (including the present) as:

$$X_t^{\mathrm{\infty }}=(X_t,X_{t+1},\dots ),$$

(15)

and denote the set of all semi-infinite pasts by ${\mathcal{X}}^{-}$ and all semi-infinite futures by ${\mathcal{X}}^{+}$. We will denote particular realizations of semi-infinite pasts and futures by $x_{-\mathrm{\infty }}^{t-1}$ and $x_t^{\mathrm{\infty }}$, respectively. Computational mechanics presents a particular model for use in the prediction of this process. For prediction, we ultimately desire to make a statement about the future of the process, conditioned on the particular past we have observed. That is, we seek:

$$P\left(X_t^{\mathrm{\infty }}|X_{-\mathrm{\infty }}^{t-1}=x_{-\mathrm{\infty }}^{t-1}\right)$$

(16)

While we might be able to predict using the entire past of the process, the insight of computational mechanics is that we can instead use a statistic that compresses the past as much as possible without losing any predictive ability. It can be shown that the unique minimal sufficient predictive statistic of the past $X_{-\mathrm{\infty }}^{t-1}$ for the future $X_t^{\mathrm{\infty }}$ of a conditionally stationary stochastic process is the equivalence class over predictive distributions. For two pasts $x_{-\mathrm{\infty }}^{t-1}$ and $y_{-\mathrm{\infty }}^{t-1}$, we define an equivalence relation, such that $x_{-\mathrm{\infty }}^{t-1}~y_{-\mathrm{\infty }}^{t-1}$ if:

$$P\left(X_t^{\mathrm{\infty }}|X_{-\mathrm{\infty }}^{t-1}=x_{-\mathrm{\infty }}^{t-1}\right)=P\left(X_t^{\mathrm{\infty }}|X_{-\mathrm{\infty }}^{t-1}=y_{-\mathrm{\infty }}^{t-1}\right)$$

(17)

as probability mass functions. In other words, two pasts are equivalent if they result in statistically-equivalent futures. Using this equivalence relation, we can define equivalence classes over pasts p, such that

$$[p]=\left\{x_{-\mathrm{\infty }}^{t-1}\in {\mathcal{X}}^{-}:P\left(X_t^{\mathrm{\infty }}|X_{-\mathrm{\infty }}^{t-1}=x_{-\mathrm{\infty }}^{t-1}\right)=P\left(X_t^{\mathrm{\infty }}|X_{-\mathrm{\infty }}^{t-1}=p\right)\right\}.$$

(18)

In other words, for each possible predictive distribution, we choose a candidate past p, and [p] represents all pasts that induce this predictive distribution. We can thus think of p as a particular past or as the label for this class of pasts. Typically, we will take the second perspective. We define our statistic $ϵ:{\mathcal{X}}^{-}\to S$ as mapping a past into the equivalence class for that past,

$$ϵ\left(X_{-\mathrm{\infty }}^{t-1}\right)=\left[X_{-\mathrm{\infty }}^{t-1}\right].$$

(19)

The statistic ϵ has been proven [16] to be the unique, minimal sufficient statistic of the past of a stationary stochastic process for its future. We can think of ϵ as partitioning the set of all pasts ${\mathcal{X}}^{-}$ based on the conditional futures they induce. The combination of the equivalence classes, as well as the allowed transitions between them is called the ϵ-machine or causal state model for the process ${\left\{X_t\right\}}_{t\in \mathrm{\mathbb{Z}}}$. The mapping by of the stochastic process to its predictive equivalence classes results in a new stochastic process ${\left\{S_t\right\}}_{t\in \mathrm{\mathbb{Z}}}$, called the causal state process. One of the important properties of this process is its relationship to the statistical complexity, denoted C_μ, of the stochastic process. The statistical complexity of a stochastic process is the average number of bits of its past necessary to optimally predict its future. For a conditionally stationary stochastic process, the statistical complexity is equivalent to the Shannon entropy of the causal state process,

$$C_{\mu }=H[S]$$

(20)

$$=-E\left[{\log }_{2}P(S)\right]$$

(21)

$$=-{\displaystyle \sum _{s\in S}P(S=s){\log }_{2}P(S=s)},$$

(22)

where $S$ is the set of equivalence classes and P (S = s) is the asymptotic probability associated with causal state s. The statistical complexity is also equivalent to the mutual information between the past of the process and the causal state associated with that past and, thus, captures the amount of information about the past stored in the causal state. A complementary quantity associated with a stochastic process is its entropy rate,

$$h_{\mu }=\underset{t\to \mathrm{\infty }}{\lim }H\left[X_t|X_{-\mathrm{\infty }}^{t-1}\right],$$

(23)

which represents the average uncertainty in the next symbol given the past. When the ϵ-machine representation of a stochastic process is available, the entropy rate is computable [30] in terms of the uncertainty in the next symbol conditional on the current causal state,

$$h_{\mu }=H\left[X_t|S_{t-1}\right]$$

(24)

$$=-E\left[{\log }_{2}P\left(X_t|S_{t-1}\right)\right]$$

(25)

$$=-{\displaystyle \sum _{s\in S}{\displaystyle \sum _{x\in X}P\left(X_t=x,S_{t-1}=s\right){\log }_{2}P\left(X_t=x|S_{t-1}=s\right)}}$$

(26)

$$=-{\displaystyle \sum _{s\in S}P\left(S_{t-1}=s\right){\displaystyle \sum _{x\in X}P\left(X_t=x|S_{t-}{}_1=s\right){\log }_{2}P\left(X_t=x|S_{t-}{}_1=s\right)},}$$

(27)

where, again, P (S_t−1 = s) is the asymptotic probability associated with causal state s.

The computational mechanics formalism requires knowledge of the full predictive distribution (16) in order to determine the equivalence relation that defines the ϵ-machine. Since this distribution is not known in practice, we must infer the ϵ-machine associated with ${\left\{X_t\right\}}_{t\in \mathrm{\mathbb{Z}}}$ using a statistical procedure. For this work, we use the causal state splitting reconstruction (CSSR) [31] algorithm. CSSR has been used in many application domains, including ecology [32], crystallography [33], neuroscience [34], anomaly detection [35] and social media analysis [36]. This algorithm provides an estimator for the ϵ-machine associated with a realization of the observed process ${\left\{X_t\right\}}_{t=1}^T$ by splitting candidate causal states. To do this, a maximum history length L_max is chosen, and all histories are initially placed in a single state. The value of L is then incremented from zero to L_max, and histories $x_{t-L}^{t-1}$ in a state are split if their one-step-ahead predictive distribution (called a morph in the computational mechanics literature):

$$P\left(X_t|X_{t-L}^{t-1}=x_{t-L}^{t-1}\right)$$

(28)

differs significantly (at size α) from the one-step-ahead predictive distribution associated with their causal state,

$$P\left(X_t|S_{t-1}=\widehat{ϵ}\left(x_{t-L}^{t-1}\right)\right).$$

The states resulting from this procedure are precausal, in the sense that they are optimal for one-step-ahead prediction. The precausal states are then refined to the causal states by taking advantage of the unifilarity of the ϵ-machine [30]. That is, for a given causal state s_t−1 and an emission symbol x_t, the causal state s_t at the next time step updates as s_t = T (s_t−1, x_t), where T (·, ·) is a one-to-one mapping from the previous causal state and the emission symbol to the next causal state. The precausal states are split to ensure this one-to-one mapping holds. The entire CSSR procedure results in an ϵ-machine that is a consistent estimator for the true ϵ-machine assuming the true stochastic process is conditionally stationary, has finitely many causal states and has finite-length suffixes of length L_max or smaller in each causal state [37].

2.4. Complexity Regularized Regression

Using the tools presented in the previous section, we now extend Davies et al.’s approach. Again, we compute the residuals:

$${\eta }_t=Y_t-r_t,t=1,\dots ,T.$$

(29)

We then transform the residuals η_t into binary random variables using the Heaviside function Θ to give:

$$B_t=\mathrm{\Theta }({\eta }_t)$$

(30)

$$=\{{}_{1:{\eta }_t>0}^{0:{\eta }_t\le 0}$$

(31)

This binary sequence ${\left\{B_t\right\}}_{t=1}^T$ is then used to infer a causal state model via the CSSR algorithm. Call this estimator for the causal state model $\widehat{ϵ}$. The estimator $\widehat{ϵ}$ consists of the estimates for the equivalence classes of pasts, the predictive distributions those equivalence classes induce and the allowed transitions between the equivalence classes.

We use the inferred causal state model $\widehat{ϵ}$ to extend Davies et al.’s approach in two ways. First, we replace the constraint term R(η(r)) by C_μ(B(r)), the statistical complexity of the causal state model inferred from the binarized residuals. For an independent and identically distributed stochastic process, C_μ = 0, and we see that if we enforce the constraint C_μ(B(r)) = 0, we recover the same criterion from Davies et al.’s runs test-based regularization term R(η(r)), though it should be noted that the runs test may be more powerful than using C_μ to test for independence. Second, instead of directly inferring $\widehat{r}$, we will assume a nonparametric model for $\widehat{r}$, indexed by a smoothness level λ, and infer the ${\widehat{r}}_{\lambda }$, such that:

$${\widehat{r}}_{\lambda }=\underset{r_{\lambda }}{\arg min}{C}_{\mu }(r_{\lambda }).$$

(32)

For example, with smoothing splines, λ might be the effective degrees of freedom. For kernel smoothing methods, λ might be the bandwidth of the kernel used. If we take ψ(r_λ) to be (11), then ψ(r_λ) will be monotonic in λ, and we can instead state our optimization problem as:

$$\widehat{\lambda }=\underset{\lambda }{\arg min}{C}_{\mu }(\lambda ).$$

(33)

Thus, we see that this method seeks the simplest regression function, as measured by λ, which makes the residuals have minimal statistical complexity. We call this method complexity-regularized regression (CRR).

2.4.1. Details for Operationalization

The statistical complexity of an ϵ-machine depends on both the number of causal states associated with the machine and the probabilities associated with those causal states. Thus, the number of causal states gives another proxy for the structure present in a stochastic process. In [38], the topological complexity of anϵ-machine was defined as the logarithm of the number of states N(ϵ) of the model ϵ,

$$C_0={\log }_{2}N(ϵ).$$

(34)

The topological complexity is an upper bound for the statistical complexity of a causal state model. Thus, we can take C₀ as a proxy for the statistical complexity of the causal state model. We do this for two reasons. First, statistical fluctuations inherent in inferring C_μ from finite data will have less of an impact on C₀. Second, by virtue of how the sequence ${\left\{B_t\right\}}_{t=1}^T$ is generated, changes in the number of states will be more useful than changes in the probabilities of the transitions between those states. Simply, topological changes in the causal state model are more useful for the task at hand. Thus, in practice, we choose:

$$\widehat{\lambda }=\underset{\lambda }{\arg min}{C}_0(\lambda ).$$

(35)

The CSSR algorithm has two parameters: α, a significance level used in the state-splitting step of the algorithm, and L_max, the maximal history to consider when inferring (19). The significance level α controls the probability that we do not assign a history to an existing causal state when it belongs to that causal state and is fixed at α = 0.001 for all experiments in this paper. The maximal history L_max balances the complexity of the causal state models that can be inferred by CSSR and the accuracy with which the one-step-ahead predictive distributions are inferred. Thus, the value of L_max controls the well-known bias-variance tradeoff present in all model selection problems [2]. If L_max is too small, the true causal state model will not be inferable using CSSR, because the histories will not resolve correctly into their true causal states. If L_max is too large relative to the length of the time series, the one-step-ahead predictive distributions will be poorly estimated, which will lead to spurious splitting of histories. A useful heuristic for choosing L_max, as recommended in [31], is to take it to be the largest value, such that the joint distribution is consistently estimated. For the class of stochastic processes that include those with finite-state ϵ-machine representations, this bound is given by:

$$L_{max}<\frac{{\log }_{2}T}{h_{\mu }+c},$$

(36)

where h_μ is the entropy rate of the stochastic process and c is some positive constant [39]. For all examples in this paper, we fix L_max = 5.

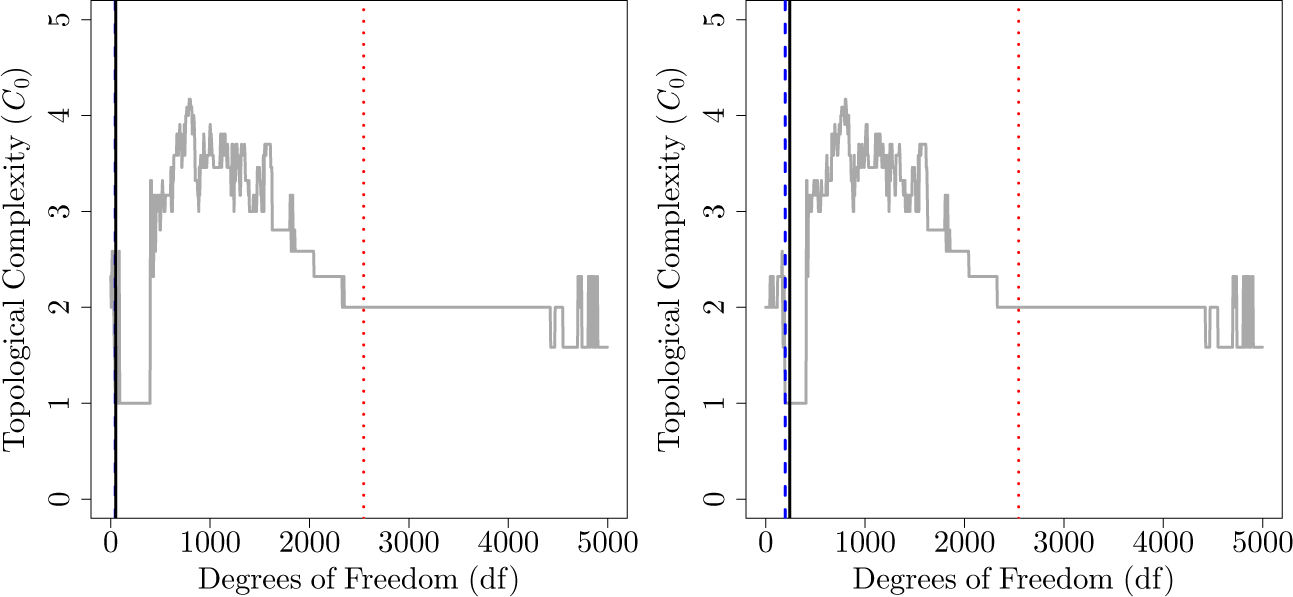
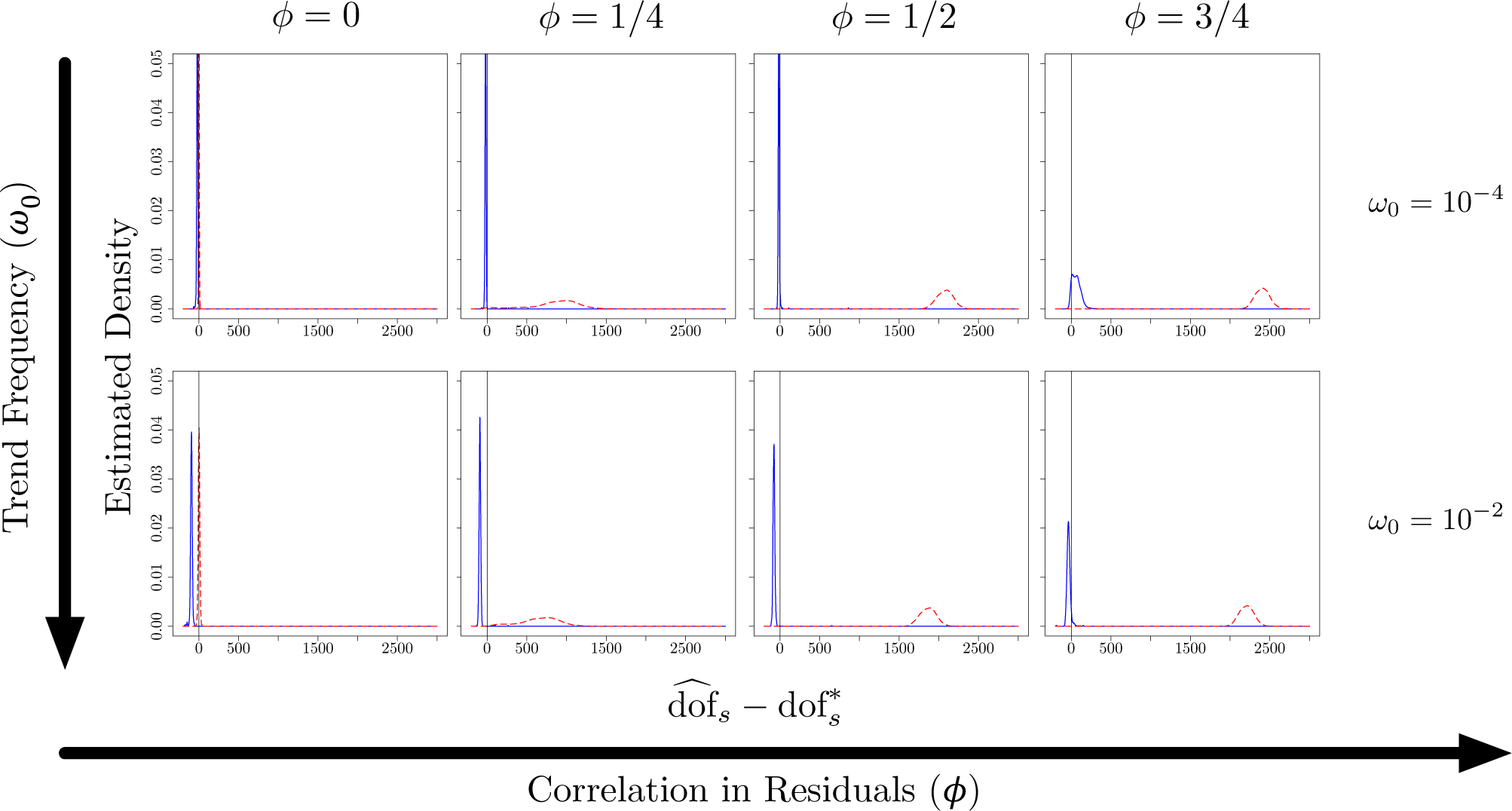
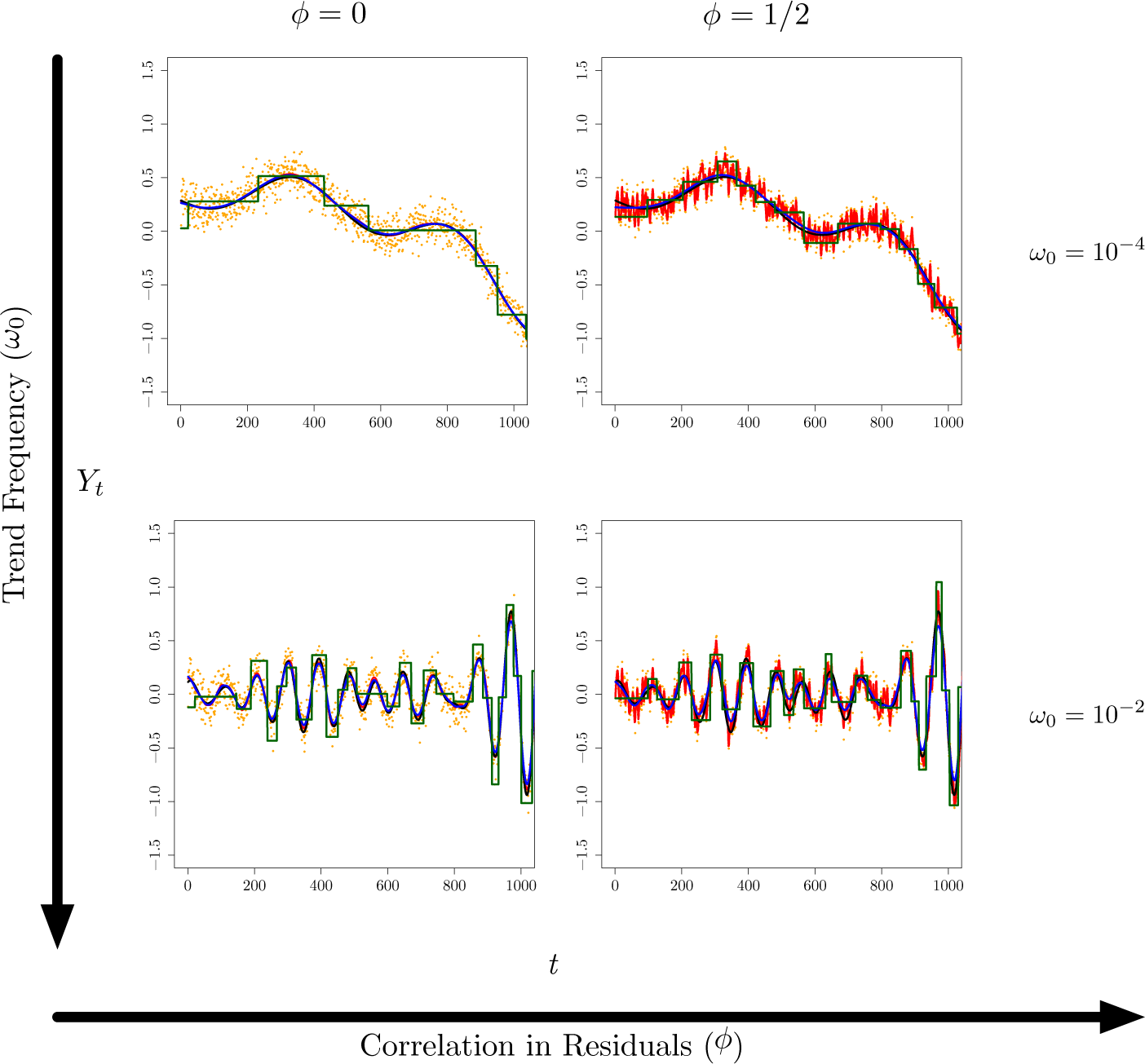
3. Simulation Experiments

In this section, we demonstrate CRR with a synthetic trend stationary time series that decomposes as in (1) into a trend plus residual activity about the trend. We take the trend to be the sum of a finite number of sinusoids with a single dominant frequency. Thus, we assume that the underlying trend has a single dominant scale. We allow serial correlations in the residuals by sampling them from a linear autoregressive process of order one. As mentioned in the Introduction, even for very weak serial correlation in such a process, standard methods, such as cross-validation, fail at choosing an appropriate smoothing parameter for the trend estimate. By varying the serial correlation in the residuals, we can explore how the performance of CRR compares to methods like cross-validation with increasing serial correlation.

3.1. The Generative Model

To test the performance of complexity regularized regression, we sampled 1000 regression curves, indexed by s = 1, 2, …, 1000, using the generative model:

$$r_{s,t}^{*}={\displaystyle \sum _{i=1}^{10}\cos (2\pi w_{s,i}t+{\delta }_{s,i})},t=0,1,\dots ,4999$$

(37)

where ${\omega }_{s,i}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{~}N({\omega }_0,{0.001}^2)$ and ${\delta }_{s,i}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{~}$ Uniform(0, 2π). For the high frequency examples, we take ${\omega }_0=\frac{1}{100}$, and for the low frequency examples, we take ${\omega }_0=\frac{1}{10,000}$. Thus, each regression curve is the sum of 10 sinusoids with random frequencies and phases, but with a single dominant scale dictated by ω₀. Each regression curve is then normalized, so that its range lies in [−1, 1], giving the final set of curves r_s,t, s = 1, …, 1000. The range-normalization was done to maintain the signal-to-noise ratio between the true regression curve and the residuals. The set ${\left\{r_{s,t}\right\}}_{s=1}^{1000}$ provides a test bed of trends that have a single principle scale (either at a low or high frequency) with variation in that structure dictated by the random frequencies and phase shifts. See Figure 2 for sample realizations from (37).

Using these true regression curves, we generate the observed values Y_s,t using the model:

$$Y_{s,t}=r_{s,t}+{\eta }_{s,t}$$

(38)

where the noise sequence is either white noise or an AR(1) process. In the white noise case, the residuals are taken to be ${\eta }_t\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{~}N(0,{\sigma }^2)$. In the correlated noise case, we take the residuals to be samples from an AR(1) process with variance σ² and lag-one coefficient ϕ. That is, the residuals are a realization of:

$${\eta }_t=\varphi {\eta }_{t-1}+{ϵ}_t,t=0,\dots ,4999$$

(39)

with ϵ_t ~ N(0, (1− ϕ²)σ²), t = 0, …, 4999. We take ϵ_t to have variance (1−ϕ²)σ², so that the pointwise variance of η_t is σ², making the pointwise noise comparable between the white noise and autoregressive processes. The serial correlation between any two residuals separated by a time lag h is given by:

$$\text{Corr}\left({\eta }_t,{\eta }_t{}_{+h}\right)={\varphi }^h.$$

(40)

Thus, for positive ϕ, nearby points will be correlated, with that correlation decaying exponentially in the time lag h. In the following numerical experiments, we take σ = 0:1 and vary ϕ ϵ {0:25; 0:5; 0:75}.

For each realization Y_s,t, a smoothing spline was used to infer a nonparametric regression function $\widehat{r}(t)$ [2]. A smoothing spline is the function that satisfies:

$$\widehat{r}(t)=\arg \underset{r\in C^2}{min}{\displaystyle \sum _{i=1}^n{(r(t_i)-y_i)}^2+{\displaystyle \int {\{r^{″}(t)\}}^{2}dt,}}$$

(41)

where C² is the space of twice differentiable functions. The solution to this optimization problem is a natural cubic spline with knots at each of the design points t_i, with coefficients regularized by an amount determined by the smoothing parameter λ ≥ 0. As λ goes to zero, the smoother reduces to the natural cubic spline interpolant of the points ${\left\{({\mathrm{t}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}})\right\}}_{i=1}^T$. As λ grows towards larger and larger values, the smoother does not allow any second-derivatives, and we recover the least-squares fit to the points. Thus, as described in (11), λ is the parameter that allows us to control the complexity of the regression function $\widehat{r}(t)$. In practice, we will use the effective degrees of freedom $\widehat{\mathrm{dof}}$ of $\widehat{r}(t)$ to control the complexity of the regression function. The effective degrees of freedom range c from one, which corresponds to the least squares fit, to n, which corresponds to the natural cubic spline interpolant of the data.

For CRR, the residuals were computed for each effective degree of freedom $\widehat{\mathrm{dof}}\in \{1,6,11,\dots ,5001\}$. The CRR degree of freedom ${\widehat{\mathrm{dof}}}^{*}$ was chosen as the smallest value that minimized C₀(λ). For cross-validation-based regression, we use generalized cross-validation (GCV), a standard cross-validation-based method for choosing the smoothing parameter for a linear smoother [2].

We measure the goodness-of-fit of the inferred $\widehat{r}$ by the mean-squared error between the true curve r and the inferred curve $\widehat{r}$ at the design points t ∈ {0, …, 4999},

$$\mathrm{MSE}(r,\widehat{r})=\frac{1}{5000}{\displaystyle \sum _{t=0}^{4999}{(r(t)-\widehat{r}(t))}^2}.$$

(42)

3.2. Simulation Results

We begin by walking through an example of using CRR for a particular realization from (37) with ϕ = 0.75, a case with large positive correlation in the residuals. After building the causal state models with the degrees of freedom for the smoothing spline ranging from one (a linear fit via least squares) to 5000 (a cubic spline interpolant), we can visualize how the topological complexity C₀ varies as the degrees of freedom increase. Two example plots are shown in Figure 3. The left and right panels correspond to low and high frequency trends r_s,t. The numbers of degrees of freedom chosen by generalized cross-validation and complexity regularized regression are indicated by the red and blue lines, respectively. By (35), the choice of 46 and 196 degrees of freedom for the low and high frequency trends correspond to the lowest degrees of freedom for which the number of causal states drops to its minimum, in this case two states.

Because we know the true value for r_s,t, in the simulation study, we can also compute the value dof^*, such that:

$${\mathrm{dof}}^{*}=\underset{\mathrm{dof}}{\arg min}\mathrm{MSE}(r,{\widehat{r}}_{\mathrm{dof}}).$$

(43)

This value represents the best choice of the smoothing parameter to minimize the mean-squared error given the data at hand, if we knew the true trend. The optimal value dof^* is indicated in Figure 3 by the black vertical line. We see that for both the low- and high-frequency trends, the degrees of freedom chosen by complexity-regularized regression are much closer than the generalized cross-validation values.

We then define the smoothing parameter bias for a given realization s using either tuning method as:

$$\text{Bias}\left(\widehat{\mathrm{dof}}\right)={\widehat{\mathrm{dof}}}_s-{\mathrm{dof}}_s^{*},$$

(44)

or the deviation of the data-driven value from the optimal value if we knew the true trend. Computing this bias across all thousand realizations from (37) gives a measure of how close the method came to recovering the true trend using a smoothing spline and the data at hand. See Figure 4 for the distribution of the smoothing parameter biases across all of the simulation conditions. A zero bias indicates that the data-driven method performed as well as possible, a positive bias indicates undersmoothing and a negative bias indicates oversmoothing. We see that except for the case where the residuals η_t are white noise, CRR results in a much lower bias, with a tendency to oversmooth the data. By comparison, GCV drastically undersmooths the data. This agrees with the theoretical result reported in [9], though their result was for kernel regressors, not smoothing splines. Both smoothing splines and kernel-based methods are linear smoothers, so we expect the theoretical result to extend to smoothing splines with small modifications.

Next, we examine the trends inferred for example low- and high-frequency trends as we vary the correlation in the residuals, shown in Figure 5. The top panels correspond to a low frequency trend, and the bottom panels correspond to a high frequency trend. As we move from left to right in the figure, the correlation in the residuals increases from zero to 0.5. As we saw from considering the smoothing parameter bias, the trend inferred using generalized cross-validation (red) undersmooths as we increase the correlation in the residuals, while the trend inferred using complexity regularized regression (blue) tends to track the true trend (grey) well, even for large values of correlation. We have also included the trend inferred using the Davies and Kovac run method (green) using the default tuning parameter values in the ftnonpar package for R.

Finally, we quantify the performance of each of the data-driven methods using the mean-squared error (42) between the inferred trend and the true trend. We computed the mean-squared error for each of the 1000 realizations across the frequency and residual conditions. These results are summarized in Figure 6, which shows the distribution of the mean-squared errors for each condition. We see that GCV performs extremely well when the residuals are uncorrelated. This is unsurprising, since GCV approximates leave-one-out cross-validation, and for uncorrelated residuals, leave-one-out cross-validation is a nearly unbiased estimator for the mean-squared error [3]. Thus, for this case, using GCV to choose the degrees of freedom will perform about as well as we can with smoothing splines. As we increase the correlation, however, we see a robustness in the performance of CRR that GCV does not share. In particular, as the residuals become more correlated, CRR maintains a low mean-squared error, while the mean-squared error for GCV increases with increasing correlation.

4. Financial Time Series

4.1. Modern Practices in Econometrics for Trend Stationary Time Series

In the study of time series occurring in macroeconomics, a common approach to analyzing systems of interest involves removing a (presumably) deterministic trend from the observations and then treating the residuals as realizations from a stationary stochastic process [40]. This can either be done in the time-domain, in the state-domain or in a mixture of the two. For time-domain smoothing, one of the most commonly-used tools for detrending data is the Hodrick–Prescott filter [41], which is essentially a special case of the smoothing spline [42]. In their original formulation, Hodrick and Prescott presented a heuristic choice of the smoothing parameter for quarterly data (such as the U.S. gross domestic product). Several authors have addressed how the choice of the smoothing parameter impacts the correlation structure of the residuals [43–45]. Data-driven approaches for choosing the smoothing parameter should be pursued, but as others have discussed [42], and we have demonstrated with our simulation study, care must be taken in the assumptions implicit to the chosen method. Other popular approaches include autoregressive models with a conditional mean that changes linearly in time [46]. It should be noted that the definition of a “trend” in econometric time series has remained open, even according to one of the leading researchers in the field [47]. Therefore, care must be taken in interpreting the results from an application of a method like CRR to such time series. In this spirit, we frame our study here as a worked example with real data, rather than a definitive statement about any “true” trends present in these time series.

We next apply complexity-regularized regression to a particular econometric time series: the closing prices of the Dow Jones Industrial Average from January 2, 1930, to December 31, 2009. This corresponds to 80 years of the market’s activity and covers 20,093 trading days. We divide the data into four double-decade periods (1930 to 1949, 1950 to 1969, 1970 to 1989, 1990 to 2009) and investigate how both the large timescale and intraday dynamics of the market have changed over these periods. We follow the same procedure for choosing the smoothing parameter as in the simulation experiments.

4.2. Macroscale Dynamics of the Market

Diagnostic plots for the topological complexity C₀ as a function of the degrees of freedom are shown in Figure 7. As before, we see that the generalized cross-validation procedure allows for many more degrees of freedom compared to the complexity regularization procedure. These diagnostic plots exhibit a property that did not occur in the simulation experiments: the minimizer (35) sometimes occurs at an isolated point that does not correspond to a “stable” location in the landscape of inferred states. For example, for the diagnostic plot for the 1930 to 1949 period, we see that the minimizer (35) occurs at an isolated point at one degree of freedom. Similarly, the minimizer for the 1970 to 1989 period occurs at an isolated point at 81 degrees of freedom. These isolated minimizers represent fragile ϵ-machines that do not persist with small perturbations in the trend. Because of this, we have modified the operationalization to choose (35), such that it corresponds to the smallest value λ that belongs to an “island” of some width in degrees of freedom. For this study, we have set the island length to two. We note that applying this modification to the operationalization does not alter the results from our simulation study.

The trends for each double-decade period are shown in Figure 8. To characterize the overall state of the market in each double-decade period, we next compute the average curvature of the trend,

$${\psi }_T(r)=\frac{1}{T}{\displaystyle {\int }_0^T{(r^{″}(t))}^{2}dt.}$$

(45)

The average curvature ψ_T (r) captures how quickly the market changes direction in its large-scale dynamics. This value, in addition to the number of trading days and the estimated degrees of freedom of the trend, are reported in

Table 1. The number of trading days (T), CRR degrees of freedom $({\widehat{\mathrm{dof}}}_{\mathrm{CRR}})$ and average curvature of the trend $({\psi }_T(\widehat{r}))$ for the four double-decade periods from 1930 to 2009.

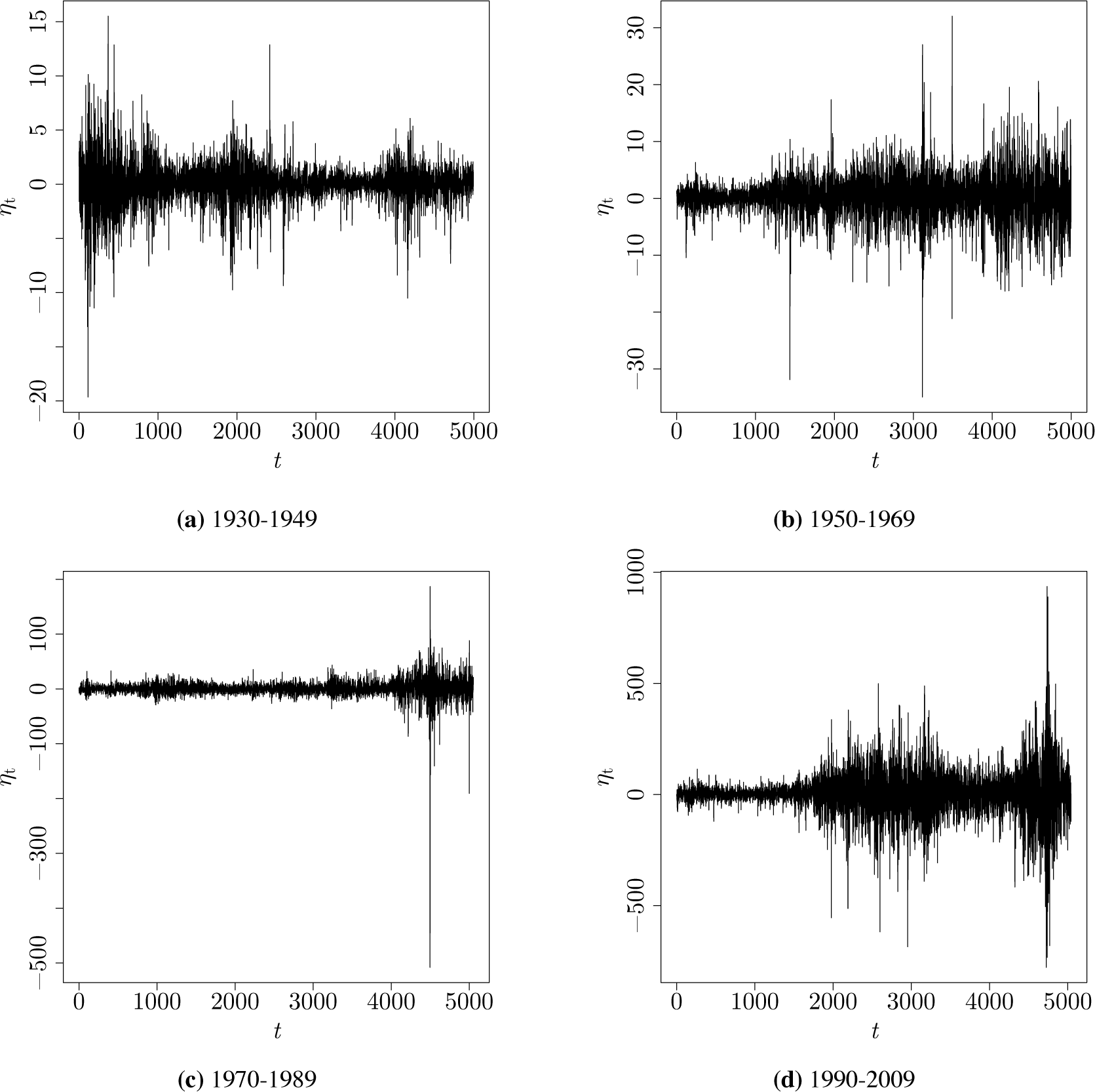
Time Period	T	$({\widehat{\mathrm{dof}}}_{\mathrm{CRR}})$	$({\psi }_T(\widehat{r}))$
1930–1949	4996	341	0.002727
1950–1969	5000	101	0.000361
1970–1989	5054	221	0.033354
1990–2009	5043	191	0.897089

for each double-decade period.

Table 1 demonstrates an important difference between the degrees of freedom and the average curvature: they capture two different senses of smoothness. In particular, the average curvature is scale-dependent. We see an instance of this with the trend from 1990 to 2009, which has a much larger average curvature than the other trends. By inspection of Figure 8, we see that this is because, during this double decade, the magnitude of the price of the market greatly increased. Thus, the “acceleration” of the trend during this time period has become larger, resulting in a larger average curvature. However, if we consider the degrees of freedom over time, which capture a scale-independent sense of the complexity of r, we see that long-term trend of the market exhibited greater complexity between 1930 and 1949 than during any of the other double-decade periods. We also note that the low number of degrees of freedom for 1950 to 1969 is most likely artificial: by inspection of Figure 7, we see that the optimal value occurs in a small island, and a value in the larger island around 200 might be more appropriate. This motivates considering the island length as a possible tuning parameter that may be set by the investigator.

4.3. Microscale Dynamics of the Market and the Associated Causal State Models

Previous work has considered the microscale dynamics of various markets using tools from computational mechanics. The authors in [48] used inter-day data from the Standard & Poor’s 500 index to construct causal state models. The authors in [49] constructed causal state models using high-frequency, single minute resolution data from the Standard & Poor’s 500 index, the Korean Stock Exchange (KOSPI) and the Nikkei index. Both papers used first-order differencing of either the price or log-price to detrend the time series before binarizing. Use of first-order differencing is closely related to an assumption that the trend in the time series can be approximated by a linear function, at least locally. This is equivalent to using a non-parametric regression method with a very small amount of smoothing, as we have seen occurs when using data-driven methods with correlated residuals. First-order differencing is also related to the Box–Jenkins approach to modeling time series, where higher-order differences of a time series are treated as realizations from a stationary autoregressive moving average (ARMA) model [1].

We also consider the computational structure of the microscale dynamics, but make no assumption on the trend being locally linear. Instead, we consider the residuals ${\{{\widehat{\eta }}_t\}}_{t=1}^T$ inferred from the CRR-based smoothing. These residuals for each double-decade period are shown in Figure 9. We see that the residual series, despite the detrending, are non-stationary: for example, the point-wise variance clearly changes over time. The same is true if we perform the detrending using first-order differences, as shown in Figure 10.

Next, we construct causal state models using the binarized residuals ${\left\{B_t\right\}}_{t=1}^T$. These causal state models are equivalent to those constructed in the smoothing parameter selection step of complexity-regularized regression, and we use CSSR with the same parameter values α = 0.001 and L_max = 5. The causal state models for the double-decade periods are shown in Figure 11. Each node corresponds to a causal state (an equivalence class over pasts), and each directed edge corresponds to an allowed transition out of that state, annotated with b | p, where b is the symbol emitted (either zero when below the trend or one when above the trend), and p is the probability of emitting that symbol, given the current causal state. We see that all four decades are characterized by the same two-state causal state model, with differing transition probabilities. The first state (B) represents when the market tends to remain above the prevailing trend, and a second state (S) represents when the market tends to remain below the prevailing trend. Interestingly, the causal state models for 1970 to 1989 and 1990 to 2009 are very similar, with only minor differences in the probabilities associated with the transitions out of state S.

The statistical complexity C_μ and the entropy rate h_μ of the binarized residuals are reported in

Table 2. The statistical complexities C_μ and entropy rates h_μ for the causal state models inferred from the binarized residuals for each double-decade period.

Time Period	Cμ (bits)	hμ (bits per symbol)
1930–1949	1.0	0.79
1950–1969	1.0	0.48
1970–1989	1.0	0.68
1990–2009	1.0	0.71

. As described previously, the statistical complexity characterizes the amount of memory in a stochastic process, in the sense that it quantifies the number of bits of the past necessary to optimally predict the future. The entropy rate characterizes the intrinsic randomness in the process [29], in the sense that the entropy rate quantifies the uncertainty in the future of the process after accounting for its entire past. Together, the entropy rate and statistical complexity give a picture of the predictability of the process and the computational overhead necessary to optimally perform the prediction. We see that for all four double-decade periods, the statistical complexity is one. That is, in order to predict whether or not the market will be above or below the prevailing trend the next day, we need only know whether the market is above or below the prevailing trend on the current day. This memory does not change from double-decade period to double-decade period. However, the entropy rate does differ, indicating that despite the similar memory, the intrinsic randomness of day-to-day fluctuations has changed over time.

5. Discussion and Future Work

When performing data-driven non-parametric regression, choosing the appropriate tuning parameter to learn from the data is paramount. Oversmoothing the data will miss out on important details, while undersmoothing the data will pick up spurious structure introduced by noise. We have proposed a method for choosing this tuning parameter in the situation where the residuals are correlated. We have seen that complexity-regularized regression outperforms generalized cross-validation, a popular data-driven approach, in the correlated case. Moreover, complexity-regularized regression does so with no assumptions on the properties of the residual process other than stationarity and short memory. Thus, our approach presents a non-parametric alternative to more standard methods [50], which assume a parametric form for the residual process. In addition, we have seen that complexity-regularized regression outperforms the original runs-based method of Davies et al., in the case of correlated residuals, while still maintaining the spirit of model-free regression.

To apply our method, we have removed a great deal of information from the residuals by only considering their signs in constructing a causal state model. A similar loss of information occurs when using, for instance, the Wald–Wolfowitz runs test. Keeping the magnitudes, as well as the signs, of the residual series should give a more accurate representation of its “randomness”. Recent work has extended the techniques of computational mechanics to continuous-valued, discrete-time stochastic processes [51] without the need to introduce a (somewhat arbitrary) discretization. This new formalism also associates a statistical complexity with any continuous-valued time series, with a similar interpretation in terms of the amount of past necessary to predict the future of a time series. The statistical complexity of the continuous-valued residuals would incorporate more information about the residuals and might improve the complexity regularization formalism.

We have seen from the DJIA example that, even after removing the most prominent trend in the data, non-trivial non-stationarities in the residuals remain. This is most likely due to the multi-scale nature of the time series, which presumably contains shorter timescale weekly and monthly seasonalities in addition to the longer timescale overall trend. To account for these non-stationarities, we could iteratively use complexity-regularized regression to generate a family of trends at different timescales. For example, we might consider the trend inferred using the methodology as representing the lowest frequency components of the trend. We could then treat the inferred residuals as a fresh input to complexity-regularized regression and estimate a higher-frequency trend in the residuals. We could continue in this manner until the residuals appear “random enough” by some criterion.

6. Conclusion

A new method for nonparametric regression has been proposed to handle the case of serially-correlated residuals, as commonly occurs in time series analysis. The method is “model-free,” in the sense presented in [27], i.e., we assume no model for the residuals and, instead, infer a regression curve to force the residuals to satisfy some criterion of randomness. The algorithm works by employing standard nonparametric regression estimators and choosing their smoothing parameter, so as to make the residuals look random, in that the statistical complexity of the binarized residuals is minimized. The approach was found to outperform GCV when the residuals are correlated.

We have applied complexity-regularized regression to analyzing the day-to-day price associated with the Dow Jones Industrial Average from 1930 to 2009. Our approach allows us to recover both long-term trends in the market and short-term behavior.