Ab Initio and Monte Carlo Approaches For the Magnetocaloric Effect in Co- and In-Doped Ni-Mn-Ga Heusler Alloys
Abstract
:1. Introduction
2. Construction of the Model Hamiltonian
 with respect to the action of the external magnetic field, where a shift of the structural transition temperature by the applied magnetic field had been modeled using the previous
with respect to the action of the external magnetic field, where a shift of the structural transition temperature by the applied magnetic field had been modeled using the previous
 Hamiltonian (using only the U1 parameter) for not too large magnetic fields. However, this is insufficient to model the martensitic transformation in the case of large magnetic fields. Therefore, we added to Equation (2) the second and third terms with dimensionless magnetoelastic constants U1 and U2. Somewhat similar terms (η4e2mμBH and η3e2(μBH)2) have been used in a Landau functional theory of elastic and magnetic interactions in [67].
Hamiltonian (using only the U1 parameter) for not too large magnetic fields. However, this is insufficient to model the martensitic transformation in the case of large magnetic fields. Therefore, we added to Equation (2) the second and third terms with dimensionless magnetoelastic constants U1 and U2. Somewhat similar terms (η4e2mμBH and η3e2(μBH)2) have been used in a Landau functional theory of elastic and magnetic interactions in [67]. , we take into account both the intra-domain and inter-domain exchange interactions using the Jij coupling constants; otherwise, only the intra-domain interactions are taken into account. Obviously, it follows from Equation (5) that in the case of a magnetic field, when the Zeeman energy is smaller than the magnetic anisotropy energy,
, we take into account both the intra-domain and inter-domain exchange interactions using the Jij coupling constants; otherwise, only the intra-domain interactions are taken into account. Obviously, it follows from Equation (5) that in the case of a magnetic field, when the Zeeman energy is smaller than the magnetic anisotropy energy,
 becomes small and, effectively, a limited number of atoms will participate in the inter-domain exchange interactions, resulting in a small total magnetization. In the case of a high magnetic field, when the field energy is much larger than the anisotropy energy,
becomes small and, effectively, a limited number of atoms will participate in the inter-domain exchange interactions, resulting in a small total magnetization. In the case of a high magnetic field, when the field energy is much larger than the anisotropy energy,
 approaches one, and all spins will participate in the inter-domain interactions aligning spins along the applied magnetic field. This leads to the disappearance of magnetic domains and to a maximum value of magnetization as a single crystal case.
approaches one, and all spins will participate in the inter-domain interactions aligning spins along the applied magnetic field. This leads to the disappearance of magnetic domains and to a maximum value of magnetization as a single crystal case.3. Computational Details
 /kBT)}.
/kBT)}. (see, Equation (5)) is performed for each MC step before the procedure of acceptance or rejection of independent variables qNi, qCo, qMn1(2) and σi. A uniform random number r is chosen from the interval [0, 1] and compared with the probability
(see, Equation (5)) is performed for each MC step before the procedure of acceptance or rejection of independent variables qNi, qCo, qMn1(2) and σi. A uniform random number r is chosen from the interval [0, 1] and compared with the probability
 : if r <
: if r <  , then interactions between randomly chosen atoms i and its neighbors from other domains are taken into account. Otherwise, if r >
, then interactions between randomly chosen atoms i and its neighbors from other domains are taken into account. Otherwise, if r >  , the interactions between atom i and its neighbors located in the same domain are taken into account. For each temperature the properties (internal energy of the system 〈
, the interactions between atom i and its neighbors located in the same domain are taken into account. For each temperature the properties (internal energy of the system 〈
 〉 and magnetic 〈m〉 and structural 〈∊〉 order parameters) were analyzed allowing 5 · 105 MC steps and 104 thermalization steps. For simplicity, we consider only two martensitic variants, i.e., the degeneracy factor p = 2. Values of spin states (i.e., the qNi, qCo, qMn1(2) variables) have been chosen randomly by using a number r with 0 ≤ r ≤ 1 and fixing qNi, qCo, qMn1(2) according to the scheme: if 0 ≤ r ≤ l/3, then qNi = l, l = 1, 2, 3, if 0 ≤ r ≤ k/4, then qCo = k, k = 1, …, 4, and if 0 ≤ r ≤ n/6, then qMn1(2) = n, n = 1, …, 6.
〉 and magnetic 〈m〉 and structural 〈∊〉 order parameters) were analyzed allowing 5 · 105 MC steps and 104 thermalization steps. For simplicity, we consider only two martensitic variants, i.e., the degeneracy factor p = 2. Values of spin states (i.e., the qNi, qCo, qMn1(2) variables) have been chosen randomly by using a number r with 0 ≤ r ≤ 1 and fixing qNi, qCo, qMn1(2) according to the scheme: if 0 ≤ r ≤ l/3, then qNi = l, l = 1, 2, 3, if 0 ≤ r ≤ k/4, then qCo = k, k = 1, …, 4, and if 0 ≤ r ≤ n/6, then qMn1(2) = n, n = 1, …, 6. for the competition of magnetic anisotropy and Zeeman energies.
for the competition of magnetic anisotropy and Zeeman energies.4. Computational Results and Discussion
4.1. Results of Ab Initio Calculations
4.2. Results of Monte Carlo Simulations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vasiliev, A.N.; Buchelnikov, V.D.; Takagi, T.; Khovailo, V.V.; Estrin, E.I. Shape-memory ferromagnets. Phys.-Uspekhi 2003, 46, 559–588. [Google Scholar]
- Planes, A.; Mañosa, L. Ferromagnetic shape-memory alloys. Mater. Sci. Forum 2006, 512, 145–152. [Google Scholar]
- Buchelnikov, V.D.; Vasiliev, A.N.; Koledov, V.V.; Taskaev, S.V.; Khovaylo, V.V.; Shavrov, V.G. Magnetic shape-memory alloys: Phase transitions and functional properties. Phys.-Uspekhi 2006, 49, 871–877. [Google Scholar]
- Entel, P.; Buchelnikov, V.D.; Gruner, M.E.; Hucht, A.; Khovailo, V.V.; Nayak, S.K.; Zayak, A.T. Shape Memory Alloys: A Summary of Recent Achievements. Mater. Sci. Forum 2008, 583, 21–41. [Google Scholar]
- Planes, A.; Mañosa, L.; Acet, M. Magnetocaloric effect and its relation to shape-memory properties in ferromagnetic Heusler alloys. J. Phys. Condens. Matter 2009, 21. [Google Scholar] [CrossRef]
- Martynov, V.V.; Kokorin, V.V. The crystal structure of thermally- and stress-induced martensites in Ni2MnGa single crystals. J. Phys. III 1992, 2, 739–749. [Google Scholar]
- Chernenko, V.A.; Amengual, A.; Cesari, E.; Kokorin, V.V.; Zasimchuk, I.K. Thermal and magnetic properties of stress-induced martensites in Ni-Mn-Ga alloys. J. Phys. IV 1995, 5. [Google Scholar] [CrossRef]
- Ullakko, K.; Huang, J.K.; Kantner, C.; O’Handley, R.C. Large magnetic-field-induced strains in Ni2MnGa single crystals. Appl. Phys. Lett 1996, 10, 1966–1968. [Google Scholar]
- Murray, S.J.; Marioni, M.A.; Allen, S.M.; O’Handley, R.C.; Lograsso, T.A. 6% magnetic-field-induced strain by twin-boundary motion in ferromagnetic Ni-Mn-Ga. Appl. Phys. Lett 2000, 77, 886–888. [Google Scholar]
- Sozinov, A.; Likhachev, A.; Lanska, N.; Ullakko, K. Giant magnetic-field-induced strain in NiMnGa seven-layered martensitic phase. Appl. Phys. Lett 2002, 80, 1746–1748. [Google Scholar]
- Sozinov, A.; Likhachev, A.A.; Lanska, N.; Ullakko, K.; Lindroos, V.K. 10% magnetic-field-induced strain in Ni-Mn-Ga seven-layered martensite. J. Phys. IV 2003, 112, 955–958. [Google Scholar]
- Karaca, H.E.; Karaman, I.; Basaran, B.; Chumlyakov, Y.I.; Maier, H.J. Magnetic field and stress induced martensite reorientation in NiMnGa ferromagnetic shape memory alloy single crystal. Acta Mater 2006, 54, 233–245. [Google Scholar]
- Martynov, V.V.; Kokorin, V.V. Shape memory and multistage superelasticity in Heusler-type Ni-Mn-Ga single crystals. Trans. Mater. Res. Soc. Jpn 1994, 18B, 839–844. [Google Scholar]
- Chernenko, V.A.; L’vov, V.; Pons, J.; Cesari, E. Superelasticity in high-temperature Ni-Mn-Ga alloys. J. Appl. Phys 2003, 93, 2394–2399. [Google Scholar]
- L’vov, V.A.; Rudenko, A.A.; Chernenko, V.A.; Cesari, E.; Pons, J.; Kanomata, T. Stress-induced martensitic transformation and superelasticity of alloys: Experiment and theory. Mater. Trans 2006, 46, 790–797. [Google Scholar]
- Aliev, A.; Batdalov, A.; Bosko, S.; Buchelnikov, V.D.; Dikshtein, I.; Khovailo, V.; Koledov, V.; Levetin, R.; Shavrov, V.; Takagi, T. Magnetocaloric effect and magnetization in Ni-Mn-Ga Heusler alloy in the vicinity of magnetostructural transition. J. Magn. Magn. Mater 2004, 272, 2040–2042. [Google Scholar]
- Albertini, F.; Paoluzi, A.; Pareti, L.; Solzi, M.; Villa, E.; Besseghini, S.; Passaretti, F. Phase transition and magnetocaloric entropy change in Mn-rich Ni2MnGa alloys. J. Appl. Phys 2006, 100. [Google Scholar] [CrossRef]
- Khovaylo, V.V.; Skokov, K.P.; Koshkid’ko, Y.S.; Koledov, V.V.; Shavrov, V.G.; Buchelnikov, V.D.; Taskaev, S.V.; Miki, H.; Takagi, T.; Vasiliev, A.N. Adiabatic temperature change at first-order magnetic phase transitions: Ni2.19Mn0.81Ga as a case study. Phys. Rev. B 2008, 78. [Google Scholar] [CrossRef]
- Fabbrici, S.; Porcari, G.; Cugini, F.; Solzi, M.; Kamarad, J.; Arnold, Z.; Cabassi, R.; Albertini, F. Co and In doped Ni-Mn-Ga magnetic shape memory alloys: A thorough structural, magnetic and magnetocaloric study. Entropy 2014, 16, 2204–2222. [Google Scholar]
- Han, Z.D.; Qian, B.; Wang, D.H.; Zhang, P.; Jiang, X.F.; Zhang, C.L.; Du, Y.W. Magnetic phase separation and exchange bias in off-stoichiometric Ni-Mn-Ga alloys. Appl. Phys. Lett 2013, 103. [Google Scholar] [CrossRef]
- Çakr, A.; Righi, L.; Albertini, F.; Acet, M.; Farle, M.; Aktúrk, S. Extended investigation of intermartensitic transitions in Ni-Mn-Ga magnetic shape memory alloys: A detailed phase diagram determination. J. Appl. Phys 2013, 114. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Gao, J.; Yang, S.; Ding, X.; Song, X.; Ren, X. Evidence for ferromagnetic strain glass in Ni-Co-Mn-Ga Heusler alloy system. Appl. Phys. Lett 2012, 101. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Wu, H.; Gao, J.; Yang, S.; Wang, D.; Ding, X.; Song, X.; Ren, X. Spontaneous strain glass to martensite transition in ferromagnetic Ni-Co-Mn-Ga strain glass. Appl. Phys. Lett 2013, 102. [Google Scholar] [CrossRef]
- Bozhko, A.D.; Vasiliev, A.N.; Khovailo, V.V.; Buchelnikov, V.D.; Dikshtein, I.E.; Seletskii, S.M.; Shavrov, V.G. Phase transitions in the ferromagnetic alloys Ni2+x Mn1−x Ga. JETP Lett 1998, 67, 227–232. [Google Scholar]
- Jin, X.; Marioni, M.; Bono, D.; Allen, S.M.; O’Handley, R.C.; Hsu, T.Y. Empirical mapping of Ni-Mn-Ga properties with composition and valence electron concentration. J. Appl. Phys 2002, 91, 8222–8224. [Google Scholar]
- Khovailo, V.V.; Novosad, V.; Takagi, T.; Filippov, D.A.; Levetin, R.Z.; Vasil’ev, A.N. Magnetic properties and magnetostructural phase transitions in Ni2+x Mn1−x Ga shape memory alloys. Phys. Rev. B 2004, 70. [Google Scholar] [CrossRef]
- Khovaylo, V.V.; Buchelnikov, V.D.; Kainuma, R.; Koledov, V.V.; Otsuka, M.; Shavrov, V.G.; Takagi, T.; Taskaev, S.V.; Vasiliev, A.N. Phase transitions in Ni2+x Mn1−x Ga with a high Ni excess. Phys. Rev. B 2005, 72. [Google Scholar] [CrossRef]
- Richard, M.; Feuchtwanger, J.; Schlagel, D.; Lograsso, T.; Allen, S.M.; O’Handley, R.C. Crystal structure and transformation behavior of Ni-Mn-Ga martensites. Scr. Mater 2006, 54, 1797–1801. [Google Scholar]
- Li, Z.; Zhang, Y.; Esling, C.; Zhao, X.; Zuo, L. Twin relationships of 5M modulated martensite in Ni-Mn-Ga alloy. Acta Mater 2011, 59, 3390–3397. [Google Scholar]
- Ranjan, R.; Banik, S.; Barman, S.R.; Kumar, U.; Mukhopadhyay, P.K.; Pandey, D. Powder x-ray diffraction study of the thermoelastic martensitic transition on Ni2Mn1.05Ga0.95. Phys. Rev. B 2006, 74. [Google Scholar] [CrossRef]
- Righi, L.; Albertini, F.; Villa, E.; Paoluzi, A.; Calestani, G.; Chernenko, V.; Besseghini, S.; Ritter, C.; Passaretti, F. Crystal structure of 7M modulated Ni-Mn-Ga martensitic phase. Acta Mater 2008, 56, 4529–4535. [Google Scholar]
- Wedel, B.; Suzuki, M.; Murakami, Y.; Wedel, C.; Suzuki, T.; Shindo, D.; Itagaki, K. Low temperature crystal structure of Ni-Mn-Ga alloys. J. Alloys Compd 1999, 290, 137–143. [Google Scholar]
- Söderberg, O.; Brown, D.; Aaltio, I.; Oksanen, J.; Syrén, J.; Pulkkinen, H.; Hannula, S.P. Microstructure and properties of Ni-Mn-Ga alloys produced by rapid solidification and pulsed electric current sintering. J. Alloys Compd 2011, 509, 5981–5987. [Google Scholar]
- Khovailo, V.V.; Abe, T.; Koledov, V.V.; Matsumoto, M.; Nakamura, H.; Note, R.; Ohtsuka, M.; Shavrov, V.G.; Takagi, T. Influence of Fe and Co on Phase Transitions in Ni-Mn-Ga Alloys. Mater. Trans 2003, 44, 2509–2512. [Google Scholar]
- Cong, D.Y.; Wang, S.; Wang, Y.D.; Ren, Y.; Zuo, L.; Esling, C. Martensitic and magnetic transformation in Ni-Mn-Ga-Co ferromagnetic shape memory alloys. Mater. Sci. Eng. A 2008, 473, 213–218. [Google Scholar]
- Ma, Y.; Yang, S.; Liu, Y.; Liu, X. The ductility and shape-memory properties of Ni-Mn-Co-Ga high-temperature shape-memory alloys. Acta Mater 2009, 57, 3232–3241. [Google Scholar]
- Glavatskyy, I.; Glavatska, N.; Söderberg, O.; Hannula, S.-P.; Hoffmann, J.-U. Transformation temperatures and magnetoplasticity of Ni-Mn-Ga alloyed with Si, In, Co or Fe. Scr. Mater 2006, 54, 1891–1895. [Google Scholar]
- Soto-Parra, D.E.; Moya, X.; Mañosa, L.; Planes, A.; Flores-Zúñiga, H.; Alvarado-Hernández, F.; Ochoa-Gamboa, R.A.; Matutes-Aquino, J.A.; Ríos-Jara, D. Fe and Co selective substitution in Ni2MnGa: Effect of magnetism on relative phase stability. Philos. Mag 2010, 90, 2771–2792. [Google Scholar]
- Rolfs, K.; Wimpory, R.C.; Petry, W.; Schneider, R. Effect of alloying Ni-Mn-Ga with Cobalt on thermal and structural properties. J. Phys. Conf. Ser 2010, 251. [Google Scholar] [CrossRef]
- Kumar, A.S.; Ramudu, M.; Seshubai, V. Effect of selective substitution of Co for Ni or Mn on the superstructure and microstructural properties of Ni50Mn29Ga21. J. Alloys Compd 2011, 509, 8215–8222. [Google Scholar]
- Fabbrici, S.; Kamarad, J.; Arnold, Z.; Casoli, F.; Paoluzi, A.; Bolzoni, F.; Cabassi, R.; Solzi, M.; Porcari, G.; Pernechele, C.; et al. From direct to inverse giant magnetocaloric effect in Co-doped NiMnGa multifunctional alloys. Acta Mater 2011, 59, 412–419. [Google Scholar]
- Kumar, A.S.; Ramudu, M.; Seshubai, V. Structural and magnetic investigations in the vicinity of first-order transformations in Ni-Mn-Ga-Co ferromagnetic shape memory alloys. Phase Trans 2012, 85, 1045–1059. [Google Scholar]
- Segui, C.; Cesari, E. Composition and atomic order effects on the structural and magnetic transformations in ferromagnetic Ni-Co-Mn-Ga shape memory alloys. J. Appl. Phys 2012, 111. [Google Scholar] [CrossRef]
- Pushin, V.G.; Korolev, A.V.; Kourov, N.I.; Kuranova, N.N.; Marchenkova, E.B.; Popov, A.G. On the effect of cobalt doping on thermoelastic martensitic transformations in ferromagnetic Heusler Ni50−x Cox Mn29Ga21 magnetically controlled shape memory alloys. Tech. Phys. Lett 2013, 39, 737–740. [Google Scholar]
- Khan, M.; Dubenko, I.; Stadler, S.; Ali, N. The structural and magnetic properties of Ni2Mn1−x Mx Ga (M = Co, Cu). J. Appl. Phys 2005, 97. [Google Scholar] [CrossRef]
- Kanomata, T.; Nunoki, S.; Endo, K.; Kataoka, M.; Nishihara, H.; Khovaylo, V.V.; Umetsu, R.Y.; Shishido, T.; Nagasako, M.; Kainuma, R.; et al. Phase diagram of the ferromagnetic shape memory alloys Ni2MnGa1x Cox. Phys. Rev. B 2012, 85. [Google Scholar] [CrossRef]
- Kumar, A.S.; Ramudu, M.; Seshubai, V. Site preference of magnetic atoms in Ni-Mn-Ga-M (M = Co, Fe) ferromagnetic shape memory alloys. Phys. Status Solidi B 2012, 249, 620–626. [Google Scholar]
- Porcari, G.; Fabbrici, S.; Pernechele, C.; Albertini, F.; Buzzi, M.; Paoluzi, A.; Kamarad, J.; Arnold, Z.; Solzi, M. Reverse magnetostructural transformation and adiabatic temperature change in Coand In-substituted Ni-Mn-Ga alloys. Phys. Rev. B 2012, 85. [Google Scholar] [CrossRef]
- Emre, B.; Yüce, S.; Stern-Taulats, E.; Planes, A.; Fabbrici, S.; Albertini, F.; Mañosa, L. Large reversible entropy change at the inverse magnetocaloric effect in Ni-Co-Mn-Ga-In magnetic shape memory alloys. J. Appl. Phys 2013, 113. [Google Scholar] [CrossRef]
- Segui, C. Effects of the interplay between atomic and magnetic order on the properties of metamagnetic Ni-Co-Mn-Ga shape memory alloys. J. Appl. Phys 2014, 115. [Google Scholar] [CrossRef]
- Entel, P.; Gruner, M.E.; Adeagbo, W.A.; Zayak, A.T. Magnetic field-induced changes in magnetic shape memory alloys. Mater. Sci. Eng. A 2008, 481–482, 258–261. [Google Scholar]
- Tan, C.-L.; Jiang, J.-X.; Tian, X.-H.; Cai, W. Effect of Co on magnetic property and phase stability of Ni-Mn-Ga ferromagnetic shape-memory alloys: A first-principles study. Chin. Phys. B 2010, 19. [Google Scholar] [CrossRef]
- Bai, J.; Raulot, J.-M.; Zhang, Y.; Esling, C.; Zhao, X.; Zuo, L. The effects of alloying element Co on Ni-Mn-Ga ferromagnetic shape memory alloys from first-principles calculations. Appl. Phys. Lett 2011, 98. [Google Scholar] [CrossRef]
- Zelený, M.; Sozinov, A.; Straka, L.; Björkman, T.; Nieminen, R.M. First-principles study of Co- and Cu-doped Ni2MnGa along the tetragonal deformation path. Phys. Rev. B 2014, 89. [Google Scholar] [CrossRef]
- Buchelnikov, V.D.; Entel, P.; Taskaev, S.V.; Sokolovskiy, V.V.; Hucht, A.; Ogura, M.; Akai, H.; Gruner, M.E.; Nayak, S.K. Monte Carlo study of the influence of antiferromagnetic exchange interactions on the phase transitions of ferromagnetic Ni-Mn-X alloys (X = In, Sn, Sb). Phys. Rev. B 2008, 78. [Google Scholar] [CrossRef]
- Entel, P.; Dannenberg, A.; Siewert, M.; Herper, H.C.; Gruner, M.E.; Buchelnikov, V.D.; Chernenko, V.V. Composition-dependent basics of smart Heusler materials from first-principles calculations. Mater. Sci. Forum 2011, 684, 1–29. [Google Scholar]
- Li, C.-M.; Luo, H.-B.; Hu, Q.-M.; Yang, R.; Johansson, B.; Vitos, L. Role of magnetic and atomic ordering in the martensitic transformation of Ni-Mn-In from a first-principles study. Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
- Sokolovskiy, V.V.; Buchelnikov, V.D.; Zagrebin, M.A.; Entel, P.; Sahool, S.; Ogura, M. First-principles investigation of chemical and structural disorder in magnetic Ni2Mn1+x Sn1−x Heusler alloys. Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
- Entel, P.; Siewert, M.; Gruner, M.E.; Herper, H.C.; Comtesse, D.; Arróyave, R.; Singh, N.; Talaparta, A.; Sokolovskiy, V.V.; Buchelnikov, V.D.; et al. Complex magnetic ordering as a driven mechanism of multifunctional properties of Heusler alloys from first-principles. Eur. Phys. J. B 2013, 86, 65–75. [Google Scholar]
- Comtesse, D.; Gruner, M.E.; Ogura, M.; Sokolovskiy, V.V.; Buchelnikov, V.D.; Grünebohm, A.; Arróyave, R.; Singh, N.; Gottschall, T.; Gutfleisch, O.; et al. First-principles calculation of the instability leading to giant inverse magnetocaloric effects. Phys. Rev. B 2014, 89. [Google Scholar] [CrossRef]
- Castán, T.; Vives, E.; Lindgard, P.-A. Modeling premartensitic effects in Ni2MnGa: A mean-field and Monte Carlo simulation study. Phys. Rev. B 1999, 60. [Google Scholar] [CrossRef]
- Buchelnikov, V.D.; Sokolovskiy, V.V.; Herper, H.C.; Ebert, H.; Gruner, M.E.; Taskaev, S.V.; Khovaylo, V.V.; Hucht, A.; Dannenberg, A.; Ogura, M.; et al. First-principles and Monte Carlo study of magnetostructural transition and magnetocaloric properties of Ni2+x Mn1−x Ga. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
- Buchelnikov, V.D.; Sokolovskiy, V.V.; Taskaev, S.V.; Khovaylo, V.V.; Aliev, A.A.; Khanov, L.N.; Batdalov, A.B.; Entel, P.; Miki, H.; Takagi, T. Monte Carlo simulations of the magnetocaloric effect in magnetic Ni-Mn-X (X = Ga, In) Heusler alloys. J. Phys. D Appl. Phys 2011, 44. [Google Scholar] [CrossRef]
- Sokolovskiy, V.V.; Buchelnikov, V.D.; Taskaev, S.V.; Khovaylo, V.V.; Ogura, M.; Entel, P. Quaternary Ni-Mn-In-Y Heusler alloys: A way to achieve materials with better magnetocaloric properties? J. Phys. D Appl. Phys 2013, 46. [Google Scholar] [CrossRef]
- Singh, N.; Arróyave, R. Magnetocaloric effects in Ni-Mn-Ga-Fe alloys using Monte Carlo simulations. J. Appl. Phys 2013, 113. [Google Scholar] [CrossRef]
- Entel, P.; Gruner, M.; Comtesse, D.; Sokolovskiy, V.V,; Buchelnikov, V.D. Interacting magnetic cluster-spin glasses and strain glasses in Ni-Mn based Heusler structured intermetallics. Phys. Status Solidi 2014, 1–14. [Google Scholar] [CrossRef]
- Ray, D.K.; Jardin, J.P. Elastic and magnetic interactions in a narrow twofold-degenerate band. Phys. Rev. B 1986, 33, 5021–5027. [Google Scholar]
- Murakami, Y.; Kainuma, R.; Shindo, D.; Tonomura, A. Magnetic microstructure analysis of ferromagnetic shape memory alloys and related compounds. Mater. Sci. Forum 2010, 684, 117–128. [Google Scholar]
- Ebert, H.; Ködderitzsch, D.; Minár, J. Calculating condensed matter properties using the KKR-Green’s function method-recent developments and applications. Rep. Prog. Phys 2011, 74. [Google Scholar] [CrossRef]
- Ebert, H. SPR-KKR Package, version 6.3; allowing to calculate the electronic structure of various periodic systems, including in particular systems with chemical disorder. Available online: http://ebert.cup.unimuenchen.de accessed on 17 September 2014.
- Liechtenstein, A.I.; Katsnelson, M.I.; Antropov, V.P.; Gubanov, V.A. Local spin-density functional-approach to the theory of exchange interactions in ferromagnetic metals and alloys. J. Magn. Magn. Mater 1987, 67, 65–74. [Google Scholar]
- Perdew, J.P.; Burke, K.; Enzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett 1996, 77, 3865–3868. [Google Scholar]
- Albertini, F.; Pareti, L.; Paoluzi, A.; Morellon, L.; Algaarabel, P.A.; Ibarra, M.R.; Righi, L. Composition and temperatue dependence of the magnetocrystalline anisotropy in Ni2+x Mn1−y Ga1−z (x + y + z = 0) Heusler alloys. Appl. Phys. Lett 2002, 81, 4032–4034. [Google Scholar]
- Enkovaara, J.; Ayuela, A.; Nordstöm, L.; Nieminen, R.M. Magnetic anisotropy in Ni2MnGa. Phys. Rev. B 2002, 65. [Google Scholar] [CrossRef]
- Gruner, M.E.; Entel, P.; Opahle, I.; Richter, M. Ab initio investigation of twin boundary motion in the magnetic shape memory Heusler alloy Ni2MnGa. J. Mater. Sci 2008, 43, 3825–3831. [Google Scholar]
- Şaşıoğlu, E.; Sandratskii, L.M.; Bruno, P. Role of conduction electrons in mediating exchange interactions in Mn-based Heusler alloys. Phys. Rev. B 2008, 77. [Google Scholar] [CrossRef]
- Anderson, P.W. Localized magnetic states in metals. Phys. Rev. B 1961, 124. [Google Scholar] [CrossRef]
- Şaşıoğlu, E.; Sandratskii, L.M.; Bruno,, P. First-principles calculation of the intersublattice exchange interactions and Curie temperatures of the full Heusler alloys Ni2MnX (X = Ga, In, Sn, Sb). Phys. Rev. B 2004, 70. [Google Scholar] [CrossRef]
- Kurtulus, Y.; Dronskowski, R.; Samolyuk, G.D.; Antropov, V.P. Electronic structure and magnetic exchange coupling in ferromagnetic full Heusler alloys. Phys. Rev. B 2005, 71. [Google Scholar] [CrossRef]
- Rusz, J.; Bergqvist, L.; Kudrnovský, J.; Turek, I. Exchange interactions and Curie temperatures in Ni2−x MnSb alloys: First-principles study. Phys. Rev. B 2006, 73. [Google Scholar] [CrossRef]
- Şaşıoğlu,, E. Nonzero macroscopic magnetization in half-metallic antiferromagnets at finite temperatures. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
- Meinert, M.; Schmalhorst, J.-M.; Reiss, G. Ab initio prediction of ferrimagnetism, exchange interactions and Curie temperatures in Mn2TiZ Heusler compounds. J. Phys. Condens. Matter 2011, 23. [Google Scholar] [CrossRef]
- Meinert, M.; Schmalhorst, J.-M.; Reiss, G. Exchange interactions and Curie temperatures of Mn2CoZ compounds. J. Phys. Condens. Matter 2011, 23. [Google Scholar] [CrossRef]
- Da Silva, C.G.; Falicov, L.M. Theory of magnetic properties of rare earth compounds (Localized moments and hybridization effects). J. Phys. C 1972, 5, 63–76. [Google Scholar]
- Shi, Z.-P.; Levy, P.M.; Fry, J.L. Interlayer magnetic coupling in metallic multilayer structures. Phys. Rev. B 1994, 49. [Google Scholar] [CrossRef]
- Ködderitzsch, D.; Ebert, H.; Rowlands, D.A.; Ernst, A. Relativistic formulation of the Korringa-Kohn-Rostoker nonlocal coherent-potential approximation. New J. Phys 2007, 9, 81–17. [Google Scholar]
- Özdŏgan, K.; Şaşıoğlu, E.; Galanakis, I. Engineering the electronic, magnetic, and gap-related properties of the quinternary half-metallic Heusler alloys. J. Appl. Phys 2008, 103. [Google Scholar] [CrossRef]
- Galanakis, I.; Şaşıoğlu, E. Variation of the magnetic properties of Ni2MnGa Heusler alloy upon tetragonalization: a first-principles study. J. Phys. D Appl. Phys 2011, 44. [Google Scholar] [CrossRef]
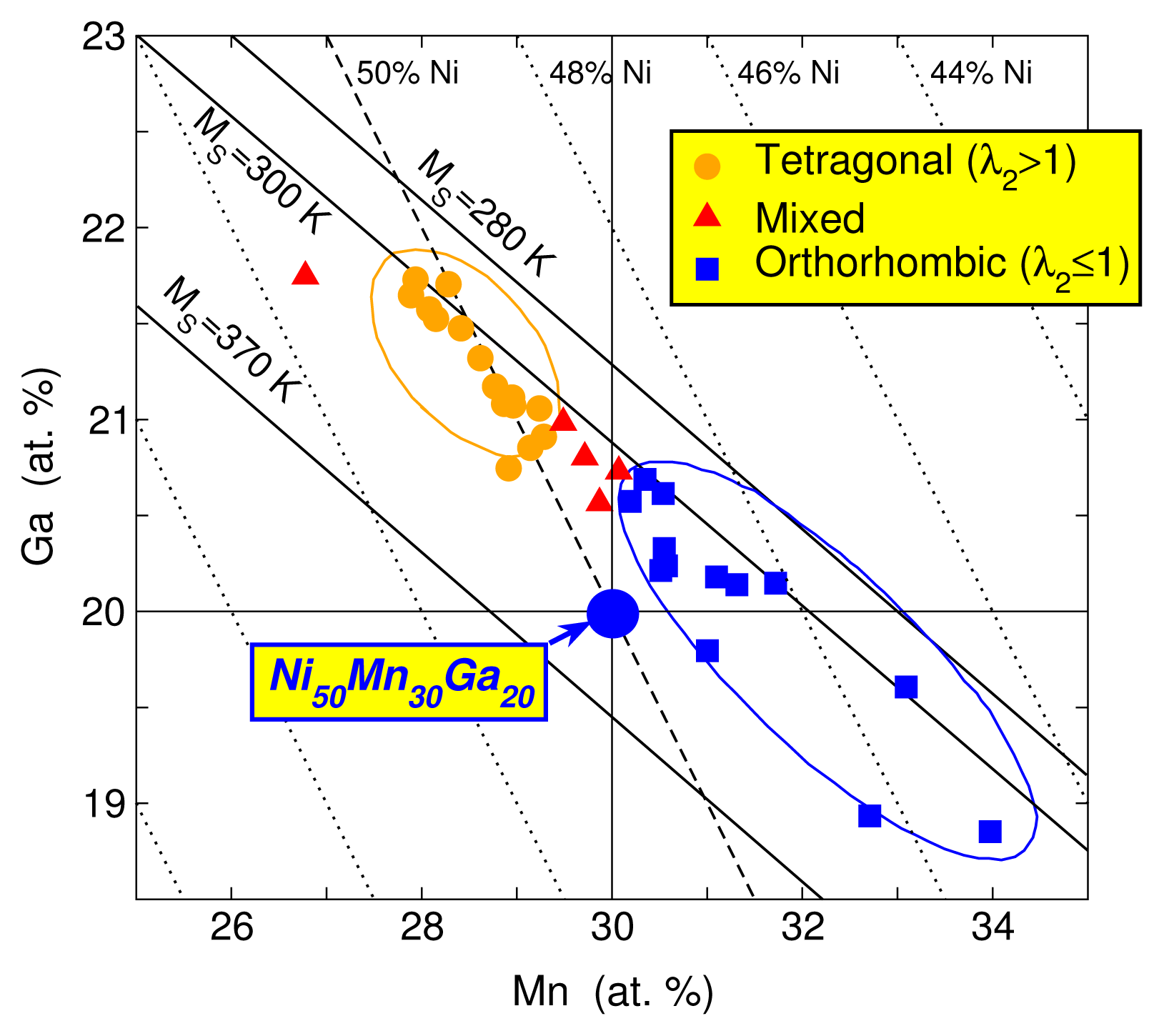





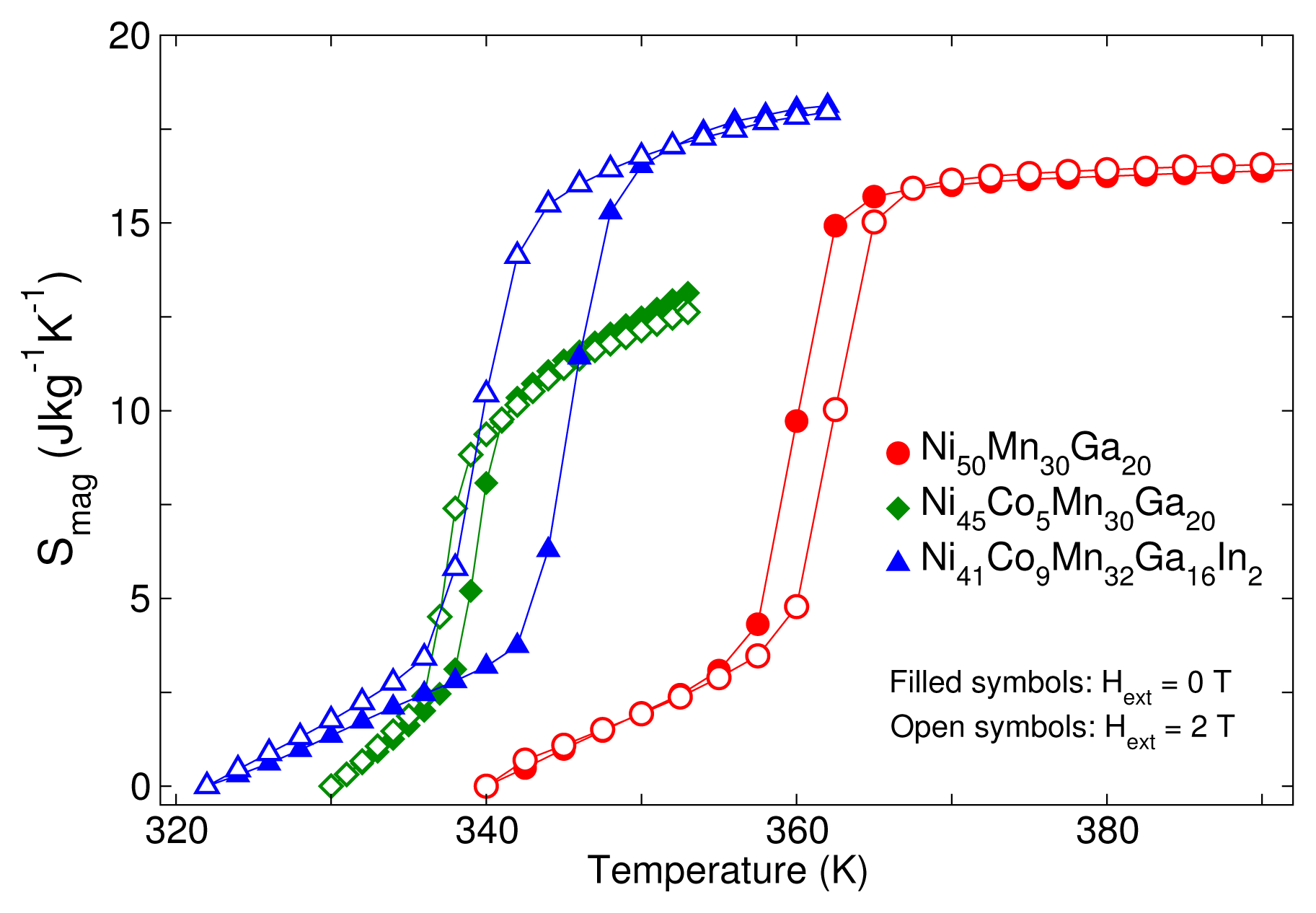

| Substitution of Co for Ni | Substitution of Co for Mn | Substitution of Co for Ga |
|---|---|---|
| Ni2+x−yCoyMn1−xGa | Ni2Mn1+x−yCoyGa1−x | Ni2Mn1+xGa1−x−yCoy |
| x = 0.16, 0 ≤ y ≤ 0.09 [34] | x = 0.16, 0.0 ≤ y ≤ 0.26 [40] | x = 0, 0 ≤ y ≤ 0.25 [38] |
| Ni2+x−yCoyMnGa1−x | Ni2+xMn1−yCoyGa1−x | x = 0, 0 ≤ y ≤ 0.2 [46] |
| x = 0.12, 0 ≤ y ≤ 0.56 [35] | x = 0.24, 0.16 ≤ y ≤ 0.32 [36] | x = 0.16, y = 0.088 [37] |
| x = 0.24, 0 ≤ y ≤ 0.32 [36] | Ni2+xMn1−x−yCoyGa | x = 0.16, 0 ≤ y ≤ 0.17 [47] |
| Ni2−yCoyMn1+xGa1−x | x = 0, 0 ≤ y ≤ 0.25 [45] | Tm increases, |
| x = 0, 0 ≤ y ≤ 0.2 [38] | x = 0, 0.03 ≤ y ≤ 0.2 [38] | TC weakly changes |
| x = 0.16, 0 ≤ y ≤ 0.16 [40] | x = 0.16, 0.04 ≤ y ≤ 0.14 [34] | |
| x = 0.16, 0 ≤ y ≤ 0.13 [42] | Tm increases, | |
| x = 0.16, 0 ≤ y ≤ 0.4 [44] | TC weakly changes | |
| x = 0.24, 0.20 ≤ y ≤ 0.24 [39] | ||
| 0 ≤ x ≤ 0.11, 0.068 ≤ x ≤ 0.232 [37] | ||
| 0.2 ≤ x ≤ 0.28, 0 ≤ y ≤ 0.36 [19,41] | ||
| 0.2 ≤ x ≤ 0.28, 012 ≤ y ≤ 0.32 [43] | ||
| Tm decreases, TC increases |
| Composition | J | K | U1 | U2 | ||||
|---|---|---|---|---|---|---|---|---|
| Ni50Mn30Ga20 | 6.6 | 0.5 | 0.5 | 3 | 0.1 | 0.1 | 0.00001 | 0.01 |
| Ni45Co5Mn30Ga20 | 6.2 | 0.5 | 2 | 0.5 | −0.1 | −0.1 | 0.00002 | 0.02 |
| Ni41Co9Mn32Ga16In2 | 6.3 | 0.5 | 0.4 | 0.2 | −0.2 | −0.8 | 0.00005 | 0.05 |
| Composition | μMn1 | μMn2 | μNi | μCo | μGa | μIn | μtot |
|---|---|---|---|---|---|---|---|
| Ni50Mn30Ga20 (c/a = 1) “ferri” | 3.547 | −3.746 | 0.242 | −0.077 | 3.219 | ||
| Ni50Mn30Ga20 (c/a = 1.31) “ferri” | 3.485 | −3.61 | 0.274 | −0.075 | 3.25 | ||
| Ni45Co5Mn30Ga20 (c/a = 1) “ferri” | 3.512 | −3.74 | 0.259 | 0.938 | −0.08 | 3.354 | |
| Ni45Co5Mn30Ga20 (c/a = 1.28) “ferri” | 3.459 | −3.614 | 0.263 | 0.619 | −0.079 | 3.268 | |
| Ni41Co9Mn32Ga16In2 (c/a = 1) “ferro” | 3.476 | 3.602 | 0.405 | 1.114 | −0.098 | −0.086 | 5.185 |
| Ni41Co9Mn32Ga16In2 (c/a = 1.28) “ferri” | 3.418 | −3.63 | 0.261 | 0.62 | −0.083 | −0.069 | 3.279 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sokolovskiy, V.; Grünebohm, A.; Buchelnikov, V.; Entel, P. Ab Initio and Monte Carlo Approaches For the Magnetocaloric Effect in Co- and In-Doped Ni-Mn-Ga Heusler Alloys. Entropy 2014, 16, 4992-5019. https://doi.org/10.3390/e16094992
Sokolovskiy V, Grünebohm A, Buchelnikov V, Entel P. Ab Initio and Monte Carlo Approaches For the Magnetocaloric Effect in Co- and In-Doped Ni-Mn-Ga Heusler Alloys. Entropy. 2014; 16(9):4992-5019. https://doi.org/10.3390/e16094992
Chicago/Turabian StyleSokolovskiy, Vladimir, Anna Grünebohm, Vasiliy Buchelnikov, and Peter Entel. 2014. "Ab Initio and Monte Carlo Approaches For the Magnetocaloric Effect in Co- and In-Doped Ni-Mn-Ga Heusler Alloys" Entropy 16, no. 9: 4992-5019. https://doi.org/10.3390/e16094992
APA StyleSokolovskiy, V., Grünebohm, A., Buchelnikov, V., & Entel, P. (2014). Ab Initio and Monte Carlo Approaches For the Magnetocaloric Effect in Co- and In-Doped Ni-Mn-Ga Heusler Alloys. Entropy, 16(9), 4992-5019. https://doi.org/10.3390/e16094992






