Abstract
The development of methods for time series analysis and prediction has always been and continues to be an active area of research. In this work, we develop a technique for modelling chaotic time series in parametric fashion. In the case of tonic-clonic epileptic electroencephalographic (EEG) analysis, we show that appropriate information theory tools provide valuable insights into the dynamics of neural activity. Our purpose is to demonstrate the feasibility of the maximum entropy principle to anticipate tonic-clonic seizure in patients with epilepsy.
1. Introduction
The processing of information by the brain is reflected in the dynamical changes of its electrical activity in time and frequency. Therefore, methods capable of describing the qualitative variations of the signals are required, such as the methods developed by Rosso et al. using wavelet analysis [1].
From the patient’s perspective, one of the most troubling aspects of epilepsy is the unpredictability of the occurrence of seizures. This fact has an impact on safety, patient anxiety and on the management of medications. The availability of a reliable predictor of an upcoming seizure would offer great value. An algorithm with high predictive accuracy and requiring relatively inexpensive computing resources would be very desirable.
In this paper an information theory approach is developed for modelling chaotic time series in parametric fashion. This technique can be used to predict the future behavior of these series, using just a small amount of data. Our working hypothesis is represented by a set of parameters that allows for good predictive power. The Maximum Entropy Principle (MEP) is used for the estimation of the parameters of the pertinent model, using associated time series data. We developed a method effective in anticipating seizures from the scalp recording. This prediction possibility would be of great importance since it would allow for preventive measures to be taken against tonic-clonic seizures. As the name implies, these seizures combine the characteristics of tonic seizures and clonic seizures. The tonic phase comes first: all muscles stiffen. Air being forced past the vocal cords causes a cry or groan. The person loses consciousness and falls. The tongue or cheek may be bitten, so bloody saliva may come out from the mouth. The person may turn a bit blue in the face. After the tonic phase comes the clonic phase: the arms and usually the legs begin to jerk rapidly and rhythmically, bending and relaxing at the elbows, hips, and knees. After a few minutes, the jerking slows and stops. Bladder or bowel control is sometimes lost as the body relaxes. Consciousness returns slowly, and the person may be drowsy, confused, agitated, or depressed. These seizures generally last 1 to 3 min.
The paper is organized as follows. In Section 2 we discuss how to model time series using information theory. We describe how the appropriate estimation of the model’s parameter values translates itself into a technique for time series prediction. In Section 3 these techniques are applied for the analysis of tonic-clonic electroencephalographic (EEG) time series so as to anticipate the seizure start. Some conclusions are given in Section 4.
2. Method
Given a signal x from a dynamical system D : ℝS → ℝS, the corresponding time series consists of a sequence of measurements {v(tn), n = 1, ··· ,N} on a system considered to be in a state described by x(tn) ∈ ℝS at discrete times tn, where N is the length of the time series.
As demonstrated by Takens in 1981 [2], for T ∈ ℝ, T > 0, there exists a functional form of the type,
where
and vi(t) = v(t − (i − 1)Δ), for i = 1, ··· ,d. Δ is the time lag and d is the embedding dimension of the reconstruction. T represents the anticipation time and it is of fundamental importance for a prediction model.
We will consider (as in [3]) a particular representation for the mapping function of Equation (1), expressing it—using Einstein’s summation notation—as an expansion of the form
where 1 ≤ ik ≤ d with 1 ≤ k ≤ np and np being an adequately chosen polynomial degree so as to series-expand the mapping F*. The number of parameters in Equation (3) corresponding to the terms of degree k depends on the embedding dimension and can be calculated using combination with repetitions,
Accordingly, the length of the vector of parameters, a, adopts the form
The computations are made on the basis of a specific information supply, given by M points of the series
Given the dataset in Equation (6), the parametric mapping in Equation (3) will be determined by the following condition,
which can be expressed in matrix form as,
where W is a matrix of size M × Nc, whose n-th row is [1,vi1(tn),vi1(tn)vi2(tn), ··· ,vi1(tn)vi2(tn), ··· ,vinp (tn)] (cf. Equation (3)) and (vT )n = v(tn + T), for n = 1, ··· ,M. In this work, we use the maximum entropy principle to characterize important probability distributions. Shannon’s entropy, defined for a discrete random variable, can be extended to situations for which the random variable under consideration is continuous.
In order to infer coefficients that are consistent with the data, we shall assume that each set a is realized with probability P(a). Thus, a normalized probability distribution over the possible sets a is introduced,
where da = da1da2 ·· daNc and Nc is the number of parameters of the model.
The problem then turns into finding P(a) subject to the requirement that the associated entropy H be maximized, since this is the best way of avoiding any bias. The expectation value of a is defined by
For the continuous random variable a with probability density function p(a) on I, where I = (−∞,∞), the entropy is given by
whenever it exists, and the relative entropy reads
where P0(a) is an appropriately chosen a priori distribution [4,5].
This measure resembles discrete entropy in many aspects, but unlike the entropy of a discrete random variable, the entropy for a continuous random variable may be infinitely large, negative, or positive (Ash, 1965 [6]). We characterize, via the maximum entropy principle, various probability distributions, subject to Equation (9) and Equation (8) as constraints, for the expectation ⟨a⟩ of a. The method for solving this constrained optimization problem is to use Lagrange multipliers for each of the operating constraints and maximize the following functional with respect to P(a),
where λ0 and λ are Lagrange multipliers associated, respectively, with the normalization condition and with the constraints, i.e., Equation (9) and Equation (8).
Taking the functional derivative with respect to P(a) we get
which implies that the maximum entropy distribution must have the form
If the a priori probability distribution P0(a) is chosen to be proportional to exp(
), where σ2 is the covariance matrix, a Gaussian form for the probability distribution P(a) is obtained, with
Considering Equation (8), the Lagrange multipliers λ can be eliminated:
and one can thus write
The matrixWt(WWt)−1 is known as the Moore–Penrose pseudo-inverse of the matrix W (see [7] and references therein). Consequently, this result shows that the maximum entropy principle coincides with a least square criterion. Once the pertinent parameters are determined, they are used to predict MP new series’ values,
where Ŵ is a matrix of size MP×Nc.
3. Application to EEG Time Series
3.1. Clinical Data and Experimental Setup
A scalp EEG signal is essentially a non-stationary time series that presents artefacts mainly due to eye movements, muscle activities (or electromyogram), among others. Artefacts related to muscle contractions are especially troublesome in the case of tonic-clonic epileptic seizures, where they reach very high amplitudes that contaminate the whole seizure recording.
In [8], Rosso, Martín and Plastino presented the analysis of twenty tonic-clonic secondary generalized epileptic records pertaining to eight patients showing the self-organization in brain electrical activity. The patient group consisted of four males and four females with a diagnosis of pharmaco-resistant epilepsy and no other accompanying disorders. From this data we chose one of the three seizures recorded for a female (39 years old) with epileptic focus in the left temporal lobe to be analyzed with the method we propose in this work. Scalp electrodes with bimastoideal reference were applied following the 10–20 international system. In Figure 1 we present the scalp EEG signal recorded in a central right location (C4 channel) [8]. This electrode was chosen after visual inspection of the EEG records, as the one with the minimum amount of artefacts. The signal was digitized at 409.6 Hz through a 12 bit A/D converter and filtered with an antialiasing eight pole lowpass Bessel filter, with a cut-off frequency of 50 Hz. Then, the signal was digitally filtered with a 1–50 Hz bandwidth Butterworth filter and stored, after decimation, at 102.4 Hz, in a PC hard drive. Recordings were performed under video control in order to have an accurate determination of the stages of the seizure. The different stages of the EEG signals (preseizure, seizure start, tonic phase, clonic phase, seizure end, and postseizure) were determined by a team of physicians. The preseizure state is the hypothetical state in which processes leading to the seizure onset start.
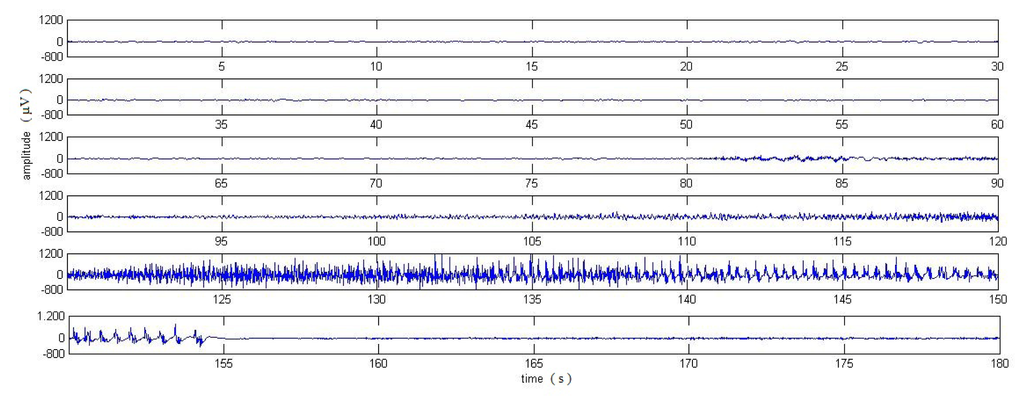
Figure 1.
Scalp EEG signal for a generalized epileptic tonic-clonic seizure. Preseizure stage (0–81 s), seizure start (81 s), tonic-clonic phase (82–155 s), seizure end (155 s), and postseizure (155–180 s).
According to physician diagnosis, the epileptic seizure starts at about to 81 s with a “discharge” of slow waves superposed by fast ones with lower amplitude. This discharge lasts approximately 8 s and has a mean amplitude of 100 μV. Afterwards, the seizure spreads, making the analysis of the EEG more complicated, due to muscle artefacts; however, it is possible to establish the beginning of the clonic phase at around 125 s, and the end of the seizure at 155 s, where one encounters an abrupt decay of the signal’s amplitude.
One of our goals was to model the EEG signals at the preseizure stage finding the corresponding parameters, in order to be able to predict a seizure’s start.
3.2. Maximum Entropy Prediction
The method described in Section 2 was applied to the EEG data corresponding to the preseizure stage. The data were subdivided into two parts. One of them was employed in order to adjust the parameters of the model, while the other served to check upon the subsequent predictive power. We include into the model polynomials up to cubic degree, np = 3. The frequency sample is Δ = 9.765 × 10−3 Hz. We considered 3000 series values, which corresponds to approximately 30 s, to obtain the parameter vector a. Using a d = 2 embedding dimension, the number of estimated parameters is Nc = 14. We consider an anticipation time T ≈ 1 s, corresponding to 60 samples.
In Figure 2, 81 seconds that encompass the preseizure stage taken from the original EEG series are displayed together with the MEP prediction. A zoom of the seizure start is presented in Figure 3 to show the prediction clearly. From t = 81 s to t = 81.6 s only predicted values are shown (prediction zone). It is important to note that the value of the anticipation time T allows one to predict the seizure start (ts = 81.5 s) one second before it happens.
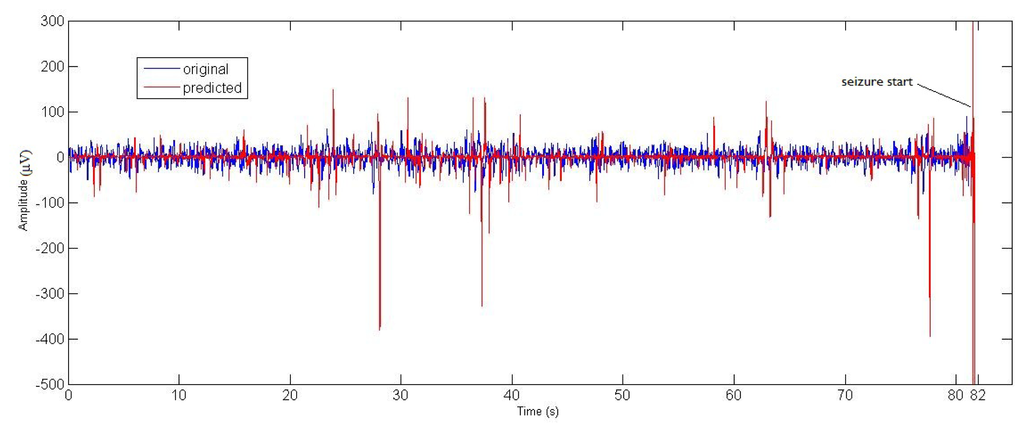
Figure 2.
Preseizure stage and seizure start. Original data (0–81 s) and MEP prediction (0–82 s).
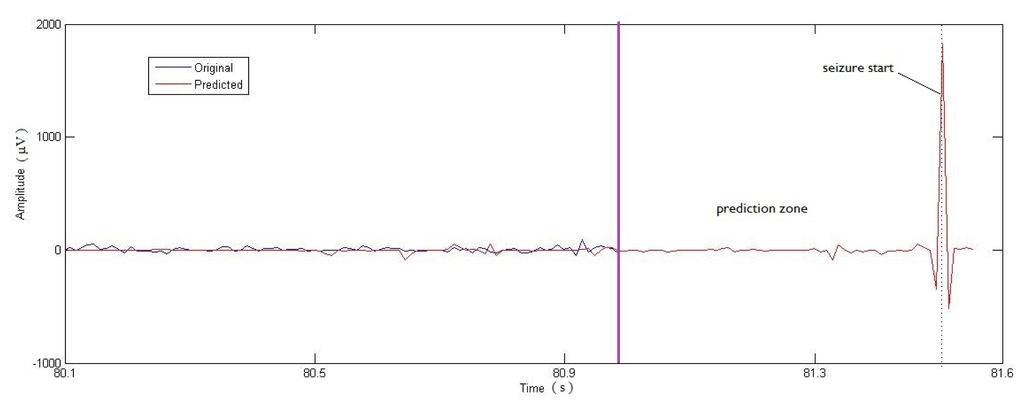
Figure 3.
Zoom from Figure 2. Prediction of seizure start (d = 2).
We analyzed the predictive power of the method for different anticipation time values. This is illustrated in Figures 4, 5 and 6, for 60, 30 and 5 samples, respectively. The best prediction was obtained for 5 samples (T ≈ 0.1 s), too short an interval for adopting preventive measures.
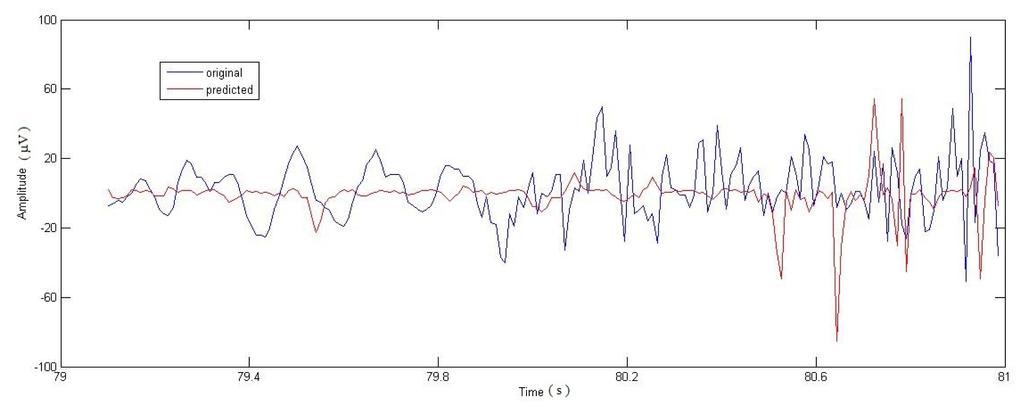
Figure 4.
Seizure start (79–81 s). T ≈ 1 s.
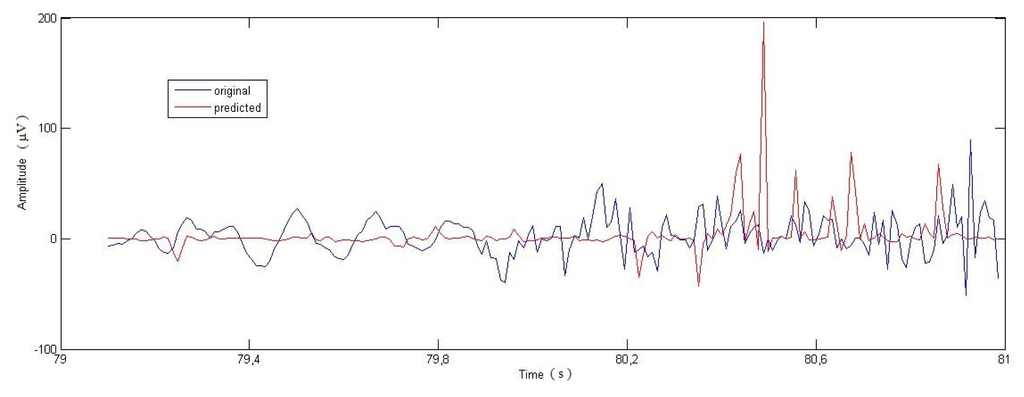
Figure 5.
Seizure start (79–81 s). T ≈ 0.5 s.
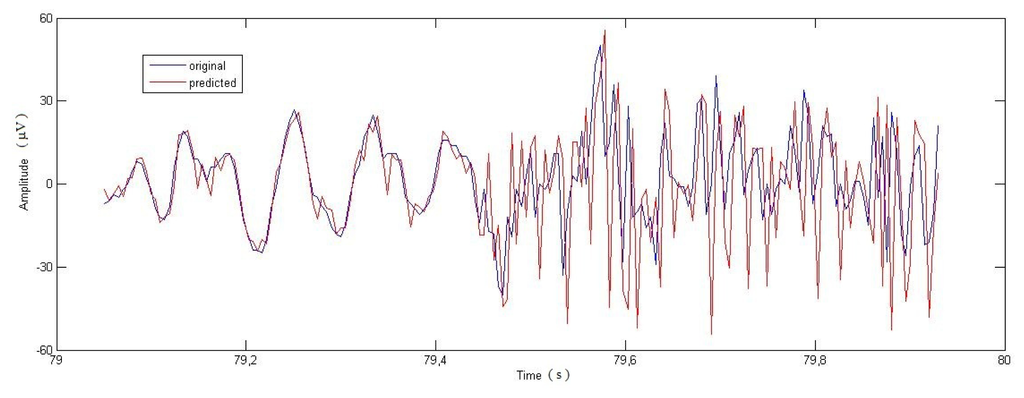
Figure 6.
Seizure start (79–81 s). T ≈ 0.1 s.
We also investigated the effect of varying the embedding dimension d. In Figure 7, results obtained with d = 3 are presented. Making pertinent comparisons, it can be noted that the predictive power becomes greater than that for d = 2 (Figure 3), but the concomitant number of parameters and consequently the computational cost also increase. For this reason d = 2 seems to be the most adequate choice.
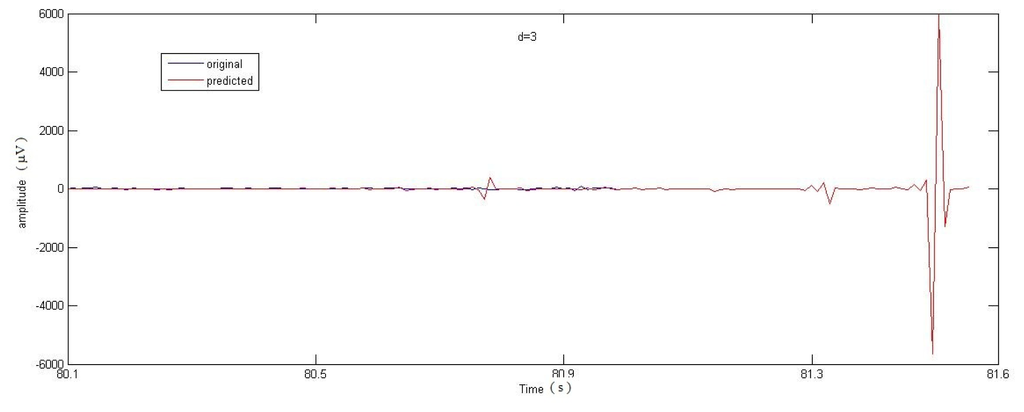
Figure 7.
Prediction of seizure start. Embedding dimension d = 3.
One critical point is the possible distortion due to spatial propagation of the seizure, since only data from the C4 electrode were analyzed and the source of the seizure was located in the left temporal location. For this reason, we also analyzed the T3 and T4 electrodes to compare with the C4 electrode results. Similar values for the time of the seizure start were obtained. As expected, due to its location, in the T3 electrode the seizure start was detected earlier, at t = 80.7 s.
4. Conclusions
We have devised an EEG analysis tool for prediction purposes. The pertinent technique models chaotic time series in parametric fashion. In the case of tonic-clonic epileptic EEG data, we have shown that appropriate information theory tools, associated with the maximum entropy principle, provide valuable insights into the dynamics of neural activity and allow one to anticipate the occurrence of the tonic-clonic transition. Successful detection and anticipation of the associated seizure start was thus obtained with the method we have here proposed. Although it would be desirable to have longer anticipation time than the ones here achieved, our finding seems encouraging and justifies further exploration.
Acknowledgments
The authors thank Osvaldo Anibal Rosso for his helpful suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rosso, O.A.; Martín, M.T.; Plastino, A. Brain electrical activity analysis using wavelet-based informational tools (II): Tsallis non-extensivity and complexity measures. Physica A 2003, 320, 497–511. [Google Scholar]
- Takens, F. Dynamical Systems and turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Proceedings of a Symposium Held at the University of Warwick 1979/80, Coventry, UK, 1979, Rand, D., Young, L.-S., Eds.; Lecture Notes in Mathematics, Volume 898; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Diambra, L.; Plastino, A. Modelling time series using information theory. Phys. Lett. A 1996, 216, 278–282. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J 1948, 27. [Google Scholar]
- Jaynes, E.T. Information Theory and Statistical Nechanics II. Phys. Rev 1957, 108, 171–190. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing, 2nd ed.; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Martín, M.T.; Plastino, A.; Vampa, V.; Judge, G. A parametric information-theory model for predictions in time series. Physica A 2014, 405, 63–69. [Google Scholar]
- Rosso, O.A.; Martín, M.T.; Plastino, A. Evidence of self-organization in brain electrical activity using wavelet-based informational tools. Physica A 2005, 347, 444–464. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).