A Novel Block-Based Scheme for Arithmetic Coding
Abstract
: It is well-known that for a given sequence, its optimal codeword length is fixed. Many coding schemes have been proposed to make the codeword length as close to the optimal value as possible. In this paper, a new block-based coding scheme operating on the subsequences of a source sequence is proposed. It is proved that the optimal codeword lengths of the subsequences are not larger than that of the given sequence. Experimental results using arithmetic coding will be presented.1. Introduction
For any discrete memoryless source (DMS, an independent identically distributed source—a typical example is a sequence of independent flips of an unbiased coin), Shannon’s lossless source coding theorem [1] shows that the optimal lossless compression rate is bounded by the entropy of the given source. Since then, there has been considerable interest in designing source codes and the objective is to make them matched to different applications. As regards the existing source codes, the most widely used algorithms are indubitably Huffman coding [2], arithmetic coding [3,4] and Lempel-Ziv coding [5,6]. Of these coding methods, arithmetic coding offers great potential for the combination of compression and encryption. Recently, many novel approaches on joint compression and encryption have been presented [7–14] and interested readers may find their corresponding cryptanalysis in [15–18].
The first exhibited coding method is the well-known Huffman coding, proved to be optimal by Huffman [2]. Due to the optimality of Huffman coding, it has been applied into many international standards, such as JPEG [19]. Later, with the appearance of arithmetic coding, Huffman coding has been replaced gradually and many new standards (such as JPEG2000 [20] and H.264 [21]) in multimedia have utilized modified versions of arithmetic coding to serve as their entropy coders.
The predecessor of arithmetic coding is Shannon-Fano-Elias coding. The extension of Shannon-Fano-Elias method to sequences is based on the enumerative methods presented by Cover [22]. Nevertheless, both of these codes suffer from precision problem. Fortunately, Rissanen and Langdon [3] successfully solve this problem and characterize the family of arithmetic codes through the notion of the decodability criterion which applies to all such codes. Actually, a practical implementation of arithmetic coding is due to Witten et al. [23] and a revisited version of arithmetic coding should be attributed to Moffat et al [24].
As is known, the prerequisite for the establishment of Shannon’s theorem is that the encoder should be optimal and work according to the distribution of the given source, which indicates the compression ratio is restricted by the entropy rate of the given DMS. The contribution of this paper is to draw freedom lines not bound by entropy rate constraint for a given DMS. The source sequence is first separated into two or more subsequences which are encoded independently. Then we consider a simple case that the length of each subsequence is the same and analyze the proposed coding scheme theoretically. Next, we prove that for general case, the sum of optimal codeword lengths of the subsequences is no longer than that of the original sequence. Moreover, the subsequences are encoded without interference, which facilities parallel computing. In addition, it should be noted that the coding algorithms adopted here are for a class of mean-optimal source codes. As a result, in the sequel, arithmetic coding is the main compression algorithm so as to achieve desired results.
The rest of this paper is arranged as follows: in the next section, the proposed scheme is described in detail. In Section 3, its constraint and feasibility are analyzed. In Section 4 we introduce a simple arithmetic coding scheme and present the experimental results as well. Finally, conclusions are drawn in Section 5.
2. Block-Based Coding
Let X be a random variable having value A or B:
Let Xn := X1X2…Xn be an independent and identically distributed sequence of length n generated according to this distribution and let nA and nB denote the number of times that symbols A and B appeared, respectively. Let x be a realization of X, then the optimal codeword length L of this sequence is given by [25]:
where here and throughout the sequel log(·):=log2(·). Let the given binary message sequence be divided into two subsequences of lengths n1 and n2, respectively. Let the number of symbols A and B in the first subsequence be n1A and n1B, respectively. For the second one, they are n2A and n2B. Denote the actual probability mass function of the source sequence as p(X). For the two subsequences, they are q(X) and r(X), respectively.
As the symbols of the given binary sequence is independent, we have [25]:
where H(Xn) is the entropy of the source sequence. Note that the entropy here refers to the information entropy presented by Shannon [1]. There are of course other kinds of entropies, interested readers can find them in [26–29]. Thus, the optimal codeword length of the source sequence can be rewritten as:

where L1 and L2 denote the respective codeword lengths of the two subsequences after encoding in accordance with the distribution of the source sequence. Actually, it can be easily found that the probability mass functions of the two subsequences and the source sequence are not necessarily the same. Therefore, after partitioning the real optimal codeword length of the first subsequence is:
For the second subsequence, the real optimal codeword length is expressed as:
From Equations (4)–(6), it seems that the source sequence has been encoded according to a wrong distribution after partitioning. In other words, an i.i.d. source sequence can be further compressed if it is divided into two subsequences. In the following subsections, we shall formally analyze this fact.
2.1. An Alphabet of Size Two
Consider a given binary sequence of length n. Without loss of generality, suppose that n is an even number and the two subsequences have the same length, i.e., n1 = n2. Then similar to the manner above, we have:
The optimal codeword length of the binary sequence can be given by:
After partition, it is easy to observe that , and n1A + n2A = nA. Therefore, we can obtain the following pair of equations:
and the sum of the optimal codeword lengths of these two subsequences is:
The above discussion leads to Theorem 1.
Theorem 1. For a given binary message Xn with length n (n ≥ 2), the sum of the optimal codeword length of the two equally-divided subsequences is no greater than that of the given message sequence as:
with equality holds if and only if n1A = n2A.
Proof of Theorem 1. From Equations (8)–(10), we have:
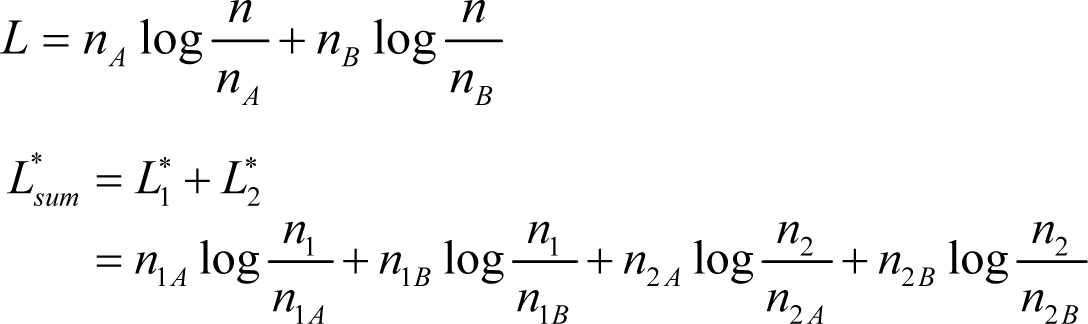
If n1A = n2A, we have:
as nA = n1A + n2A.
If n1A ≠ n2A, we can rewrite Equation (12) as:

Equation (13) implies that is a function of n1A since n and nA are constants for a given binary sequence. In order to make Equation (13) clear, here let F(t) and t denote and n1A, respectively. Then differentiating F(t) with respect to t yields:
After rearrangement, we have:
As nA − t ≥ 0, n − 2t ≥ 0, t ≥ 0 and n − 2nA + t ≥ 0, letting:
yields g(t) ≥ 0. Regarding Equation (16), there are two possible cases:
- (a)
If nA − t > t, i.e., , then g(t) > 1 and ;
- (b)
If nA − t < t, i.e., , then 0 < g(t) < 1 and .
The above two cases are visualized in Figure 1. It is clear that is concave and .
2.2. A Special Case for an Alphabet of Size 2
In this subsection, we shall demonstrate the case where the two subsequences are of arbitrary lengths while the sum of the two lengths are constant for a given source message sequence.
Theorem 2. For a given binary source sequence X1X2…Xn with length n (n ≥ 2), which takes values in {A, B} with probabilities p(A) and p(B), respectively. Let the binary sequence be partitioned into two subsequences with arbitrary lengths n1 and n2 (note that n1 + n2 = n), then the sum of the optimal codeword lengths of the two subsequences is no greater than the length of the given binary sequence, i.e., .
Before the formal proof is presented, the following lemma [25] is required:
Lemma 1: Let p(x) and q(x), x ∈ X, be two probability mass functions. Then D(p||q) ≥ 0 with equality holds if and only if p(x) = q(x) for all x. Here, D(·) represents the relative entropy.
Proof of Theorem 2. From the previous part, we have:
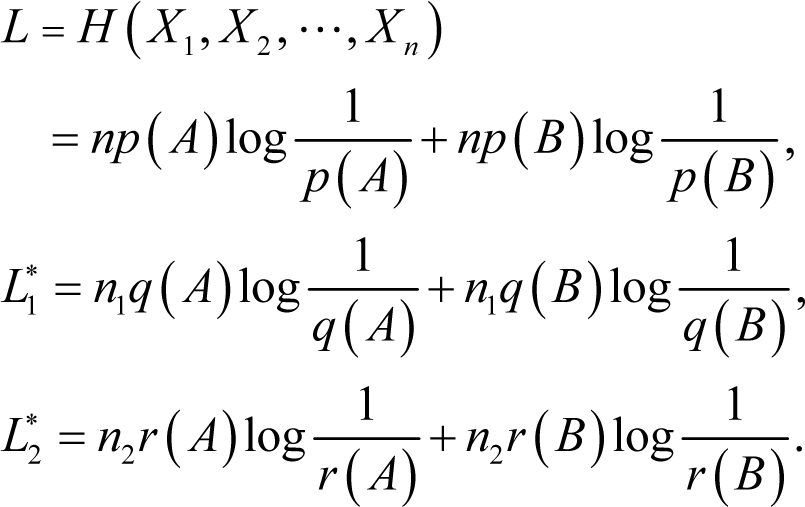
For symbol A, we have:
Now, expanding the first part of Equation (17) using Equation (18) with respect to the optimal codeword length of symbol A in the given source sequence, we have:
Similarly, for symbol B we have:
Combining Equations (19) and (20), we have:
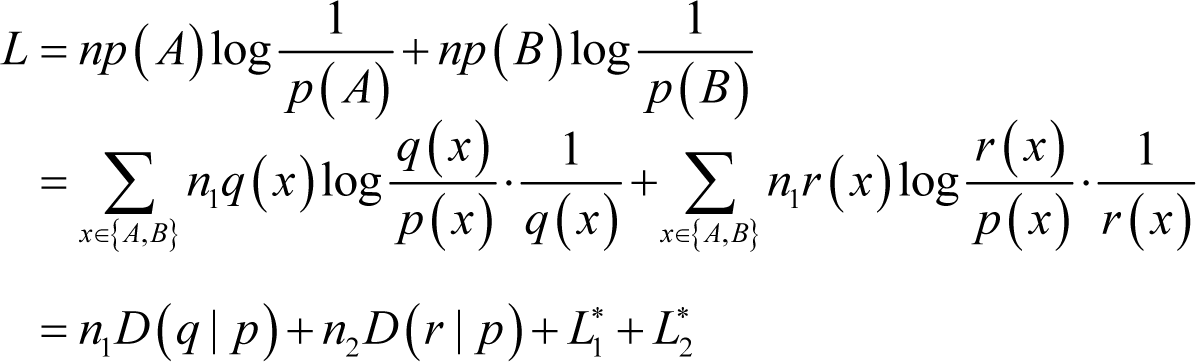
From Lemma 1, we know that:
If the equality holds, we have:
As a result, the proof of Theorem 2 has been shown. Additionally, we can see that Theorem 1 is a special case of Theorem 2 and Equation (21) can be considered as a coding scheme which is designed based on a wrong distribution [25].
2.3. An Alphabet of Size D > 2
In the above two subsections, we have discussed the case that the alphabet size is two. In this subsection, we shall deal with the case of alphabet size D > 2.
Consider an i.i.d. random variable Z taking value from the set {1,2,…, D} and a given discrete sequence Z1Z2…Zn of length n. Suppose that the number of occurrences of symbol i is ni for some i ∈ {1,2,…,D} and the corresponding probability is p(i). Obviously, we have:
Following the preceding method, we once more partition the given sequence into two subsequences ZA and ZB with length nA and nB, respectively. We further assume that the probability of symbol i is pA(i) and the number of times that symbol i occurred in ZA is niA. For ZB, they are pB(i) and niB, respectively. Similarly, we have:
and:
Then the entropies of the source sequence and the two subsequences are given by:
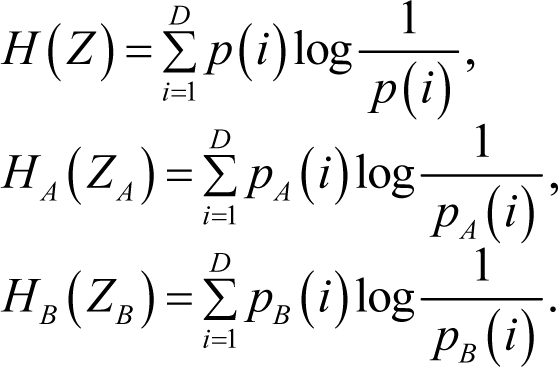
Their corresponding optimal codeword lengths:
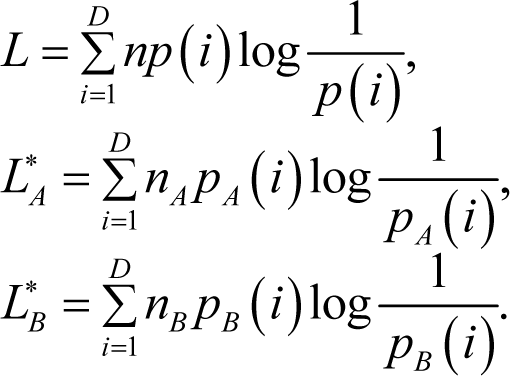
Similar to Theorem 2, we have the following theorem.
Theorem 3. For a discrete sequence from a multiple-symbol source, after partitioning it into two subsequences (ZA and ZB), its optimal codeword length with equality holds if and only if their probability mass functions satisfy p(i) = pA(i) = pB(i) for all i ∈ {1,2,…,D}.
Proof of Theorem 3. Let the source sequence be represented by Zn:= Z1Z2…Zn. As the source sequence is independent and identically distributed, we have:
Similar way to the proof of Theorem 2, we have:
Thus:
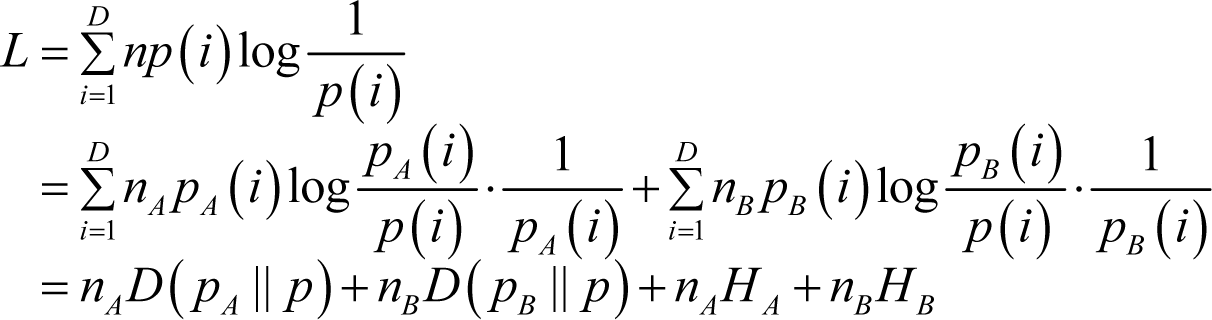
As:
we have:
with equality holds if and only if:
Now, we can see that not only binary sequences but also the non-binary ones can be further compressed by using the proposed method.
3. Constraint and Feasibility
In Section 2, we have studied the advantages of block-based coding. Particularly, as the source message is sufficiently large, we can repeat the partition operation. Nevertheless, this has the downside of increasing the size of the output file when the number of subsequences or alphabet size grows since more distributions will take up too much space in the output file. In this section, we shall show the constraint and feasibility of our approach.
For a given binary sequence x1x2…xn with length n and probability mass function p(x1,x2,…,xn), it can, without doubt, be encoded to a length of log(1/p (x1,x2,…,xn)) + 2 bits [25]. This means that if the source is i.i.d., this code achieves an average codeword length within 2 bits above the entropy. If the prefix-free restriction is removed, a codeword length of log(1/p (x1,x2,…,xn)) +1 bits can be achieved.
When the given message sequence x1x2…xn is partitioned into two subsequences of length n1 and n 2, the practical codeword lengths of the two subsequences can be given by:
Now, consider the following two special cases:
- (a)
Suppose that the message sequence is 010101…, i.e., equal number of zeros and ones. Obviously, it is not compressible. However, if we separate it into two subsequences alternatively, one subsequence will have all zeros while another will consist of all ones. Both subsequences have zero entropy and this is the ideal case;
- (b)
Suppose the message sequence is 010101… and the numbers of zeros and ones are both even numbers. After partitioned into three sequences, each one has equal probability of zero and one. According to the preceding analysis, the final codeword length will be within 2 bits above the codeword length before partitioning.
There is no doubt that the second special case exists. Thus, we suggest applying this work to binary arithmetic coding when the size of target input file is much smaller. On the other hand, since the subsequences after partition are encoded without interference, this fact implies that parallel coding is feasible. Peculiarly, if the file to be compressed is considerably large, then we can partition it into multiple subsequences and encode them in parallel.
4. Experimental Results
As an extension of Shannon-Fano-Elias coding, arithmetic coding is an efficient coding scheme for lossless compression. Unlike Huffman coding, the process of arithmetic coding does not require much additional memory as the sequence length increases. Therefore arithmetic coding has been adopted in quite a number of international standards. On the other hand, there is no need for a representative sample of sequence and the probability model can be updated with each symbol read, which indicates that adaptive coding can be utilized (but won’t perform well).
In order to further illustrate the superiority of the proposed coding scheme, we have performed a simple binary coding experiment. The operating procedures are described in Table 1 and one can refer to Figure 2 as well.
Eighteen standard test files from the Calgary Corpus [30] are compressed to show the performance of this compression method. The test results are listed in Table 2, where RT and RP represent the compression ratio of the traditional and the proposed schemes, respectively. Note that the proposed method is used to further improve the compression ratio instead of designing a new source coding algorithm. Consequently, we just compare the compression ratio of the proposed scheme with the traditional arithmetic coding algorithm.
Similarly, another experiment is performed by employing a fixed model with 256 possible source symbols. The detailed operating procedures are the same as that listed in Table 1 except that the source sequence is read in bytes rather than in bits. The corresponding test results are listed in Table 3.
So far, the compression ratios of most present compression algorithms cannot break the restriction of entropy. However, from Tables 2 and 3, it can be found that with extra relative entropy, the compression ratio of the proposed scheme is sometimes smaller than the entropy of the original sequence, which is highlighted in the two tables. The reason for this phenomenon can boil down to the following three aspects:
- (a)
The probability distribution of the source sequence;
- (b)
The partition method;
- (c)
The encoding function.
The first aspect is important since the compression ratio of a given source sequence depends on the probability distribution of the source sequence. As proved in Section 2, our method is able to work better than the traditional one because of the existence of the extra relative entropy. Meanwhile, a good partition method can increase the extra relative entropy. In other words, when there is a greater difference between the source sequence and the subsequence, the extra relative entropy will be larger and further the compression ratio will be higher. This fact exactly reflects the importance of Aspect (b). The importance of Aspect (c) is conspicuous and we no longer repeat it. In addition, as the subsequences are encoded independently, we can perform the coding by parallel processing which can obviously reduce the processing time.
5. Conclusions
In this paper, we have proved that the overall codeword length after sequence partition is no greater than the original one. The original sequence can be regarded as the case that the code is designed using a wrong distribution. Because of the existence of error in the encoding process, we cannot divide the sequence into multiple sequences infinitely. Nonetheless, if we perform the sequence separation properly according to the length of the original sequence, the expected codeword length can be achieved. This fact indirectly suggests that we can implement our scheme efficiently by parallel coding. Furthermore, since our work depends on the partition method, our future work will focus on how to partition different kinds of files and which kinds of files should be partitioned.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (No. 61271350), and the Fundamental Research Funds for the Central Universities (No. N120504005).
Author Contributions
Both authors contributed equally to the presented mathematical and computational framework and the writing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J 1948, 27, 379–423. [Google Scholar]
- Huffman, D.A. A method for the construction of minimum redundancy codes. Proc. IRE 1952, 40, 1098–1101. [Google Scholar]
- Rissanen, J.; Langdon, G., Jr. Arithmetic coding. IBM J. Res. Dev 1979, 23, 149–162. [Google Scholar]
- Langdon, G.; Rissanen, J. Compression of black-white images with arithmetic coding. IEEE Trans. Commun 1981, 29, 858–867. [Google Scholar]
- Ziv, J.; Lempel, A. A universal algorithm for sequential data-compression. IEEE Trans. Inf. Theory 1977, 23, 337–343. [Google Scholar]
- Ziv, J.; Lempel, A. Compression of individual sequences via variable-rate coding. IEEE Trans. Inf. Theory 1978, 24, 530–536. [Google Scholar]
- Cleary, J.; Irvine, S.; Rinsma-Melchert, I. On the insecurity of arithmetic coding. Comput. Secur 1995, 14, 167–180. [Google Scholar]
- Bergen, H.; Hogan, J. A chosen plaintext attack on an adaptive arithmetic coding algorithm. Comput. Secur 1993, 12, 157–167. [Google Scholar]
- Wen, J.; Kim, H.; Villasenor, J. Binary arithmetic coding with key-based interval splitting. IEEE Signal Process. Lett 2006, 13, 69–72. [Google Scholar]
- Kim, H.; Wen, J.; Villasenor, J. Secure arithmetic coding. IEEE Trans. Signal Process 2007, 55, 2263–2272. [Google Scholar]
- Wong, K.W.; Lin, Q.Z.; Chen, J.Y. Simultaneous Arithmetic Coding and Encryption Using Chaotic Maps. IEEE Trans. Circuits Syst 2010, 57, 146–150. [Google Scholar]
- Grangetto, M.; Magli, E.; Olmo, G. Multimedia selective encryption by means of randomized arithmetic coding. IEEE Trans. Multimedia 2006, 8, 905–917. [Google Scholar]
- Luca, M.B.; Serbanescu, A.; Azou, S.; Burel, G. A new compression method using a chaotic symbolic approach, Proceedings of the IEEE-Communications 2004, Bucharest, Romania, 3–5 June 2004; Available online: http://www.univ-brest.fr/lest/tst/publications/ (accessed on 18 June 2014).
- Nagaraj, N.; Vaidya, P.G.; Bhat, K.G. Arithmetic coding as a non-linear dynamical system. Commun. Nonlinear Sci. Numer. Simul 2009, 14, 1013–1020. [Google Scholar]
- Sun, H.M.; Wang, K.H.; Ting, W.C. On the Security of Secure Arithmetic Code. IEEE Trans. Inf. Forensics Secur 2009, 4, 781–789. [Google Scholar]
- Jakimoski, G.; Subbalakshmi, K.P. Cryptanalysis of Some Multimedia Encryption Schemes. IEEE Trans. Multimedia 2008, 10, 330–338. [Google Scholar]
- Pande, A.; Zambreno, J.; Mohapatra, P. Comments on “Arithmetic coding as a non-linear dynamical system”. Commun. Nonlinear Sci. Numer. Simul 2012, 17, 4536–4543. [Google Scholar]
- Katti, R.S.; Srinivasan, S.K.; Vosoughi, A. On the Security of Randomized Arithmetic Codes Against Ciphertext-Only Attacks. IEEE Trans. Inf. Forensics Secur 2011, 6, 19–27. [Google Scholar]
- Wallance, G.K. The JPEG Still image compression standard. Commun. ACM 1991, 34, 30–44. [Google Scholar]
- Taubman, D.S.; Marcellin, M.W. JPEG2000: Image Compression Fundamentals, Standards and Practice; Kluwer Academic: Norwell, MA, USA, 2002. [Google Scholar]
- Wiegand, T.; Sullivan, G.; Bjontegaard, G.; Luthra, A. Overview of the H.264/AVC video coding standard. IEEE Trans. Circuits Syst. Video Technol 2003, 13, 560–576. [Google Scholar]
- Cover, T.M. Enumerative source encoding. IEEE Trans. Inf. Theory 1973, 19, 73–77. [Google Scholar]
- Witten, I.H.; Neal, R.M.; Cleary, J.G. Arithmetic coding for data compression. Commun. ACM 1987, 30, 520–540. [Google Scholar]
- Moffat, A.; Neal, R.M.; Witten, I.H. Arithmetic coding revisited. ACM Trans. Inf. Sysy 1998, 16, 256–294. [Google Scholar]
- Cover, T.; Thomas, J. Elements of Information Theory; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Balasis, G.; Donner, R.V.; Potirakis, S.M.; Runge, J.; Papadimitriou, C.; Daglis, I.A.; Eftaxias, K.; Kurths, J. Statistical mechanics and information-theoretic perspectives on complexity in the Earth system. Entropy 2013, 15, 4844–4888. [Google Scholar]
- Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Kalimeri, M.; Anastasiadis, A.; Eftaxias, K. Investigating dynamical complexity in the magnetosphere using various entropy measures. J. Geophys. Res 2009. [Google Scholar] [CrossRef]
- Eftaxias, K.; Athanasopoulou, L.; Balasis, G.; Kalimeri, M.; Nikolopoulos, S.; Contoyiannis, Y.; Kopanas, J.; Antonopoulos, G.; Nomicos, C. Unfolding the procedure of characterizing recorded ultra low frequency, kHZ and MHz electromagnetic anomalies prior to the L’Aquila earthquake as preseismic ones–Part 1. Nat. Hazards Earth Syst. Sci 2009, 9, 1953–1971. [Google Scholar]
- Eftaxias, K.; Balasis, G.; Contoyiannis, Y.; Papadimitriou, C.; Kalimeri, M.; Athanasopoulou, L.; Nikolopoulos, S.; Kopanas, J.; Antonopoulos, G.; Nomicos, C. Unfolding the procedure of characterizing recorded ultra low frequency, kHZ and MHz electromagnetic anomalies prior to the L’Aquila earthquake as pre-seismic ones–Part 2. Nat. Hazards Earth Syst. Sci 2010, 10, 275–294. [Google Scholar]
- Calgary Corpus, Available online: ftp://ftp.cpsc.ucalgary.ca/pub/projects/text.compression.corpus (accessed on 8 February 2014).


| Input | Original sequence |
|---|---|
| Output | Codeword sequence |
| Step 1: | Read the source sequence to buffer in bits. |
| Step 2: | Find the middle symbol in the original sequence. |
| Step 3: | Divide the original sequence into two subsequences. |
| Step 4: | Encode the two subsequences according to their own probability models and then obtain two codeword sequences. |
| Step 5: | Combine the two codeword sequences. |
| File | Size (KB) | Entropy | RT (%) | RP (%) |
|---|---|---|---|---|
| bib | 111.261 | 0.985334 | 98.5350 | 98.5332 |
| book1 | 768.771 | 0.992689 | 99.2691 | 99.2690 |
| book2 | 610.856 | 0.993655 | 99.3656 | 99.3656 |
| geo | 102.400 | 0.858996 | 85.9014 | 85.9004 |
| news | 377.109 | 0.991326 | 99.1326 | 99.1329 |
| obj1 | 21.504 | 0.929604 | 92.9688 | 92.9641 |
| obj2 | 246.814 | 0.979415 | 97.9422 | 97.9418 |
| paper1 | 53.161 | 0.992549 | 99.2570 | 99.2551 |
| paper2 | 81.768 | 0.994734 | 99.4757 | 99.4732 |
| paper3 | 46.526 | 0.995974 | 99.6002 | 99.5981 |
| paper4 | 13.286 | 0.993788 | 99.3828 | 99.3828 |
| paper5 | 11.954 | 0.989678 | 98.9794 | 98.9711 |
| paper6 | 38.105 | 0.988634 | 98.8637 | 98.8663 |
| pic | 513.216 | 0.392885 | 39.2893 | 39.2893 |
| progc | 39.611 | 0.980897 | 98.0914 | 98.0914 |
| prog1 | 71.646 | 0.981620 | 98.1632 | 98.1632 |
| progp | 49.379 | 0.971435 | 97.1466 | 97.1445 |
| trans | 93.695 | 0.983281 | 98.3297 | 98.3286 |
| File | Size (KB) | Entropy | RT (%) | RP (%) |
|---|---|---|---|---|
| bib | 111.261 | 0.6501 | 65.04 | 65.06 |
| book1 | 768.771 | 0.5659 | 56.59 | 56.59 |
| book2 | 610.856 | 0.5991 | 59.91 | 59.82 |
| geo | 102.400 | 0.7058 | 70.58 | 70.55 |
| news | 377.109 | 0.6487 | 64.88 | 64.85 |
| obj1 | 21.504 | 0.7435 | 74.37 | 72.11 |
| obj2 | 246.814 | 0.7825 | 78.27 | 77.78 |
| paper1 | 53.161 | 0.6229 | 62.35 | 62.18 |
| paper2 | 81.768 | 0.5752 | 57.56 | 57.50 |
| paper3 | 46.526 | 0.5831 | 58.39 | 58.37 |
| paper4 | 13.286 | 0.5875 | 59.01 | 58.96 |
| paper5 | 11.954 | 0.6170 | 61.98 | 61.62 |
| paper6 | 38.105 | 0.6262 | 62.70 | 62.28 |
| pic | 513.216 | 0.1513 | 15.13 | 15.06 |
| progc | 39.611 | 0.6499 | 65.07 | 64.89 |
| prog1 | 71.646 | 0.5963 | 59.67 | 59.16 |
| progp | 49.379 | 0.6086 | 60.93 | 60.77 |
| trans | 93.695 | 0.6916 | 69.19 | 68.85 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hou, Q.-B.; Fu, C. A Novel Block-Based Scheme for Arithmetic Coding. Entropy 2014, 16, 3315-3328. https://doi.org/10.3390/e16063315
Hou Q-B, Fu C. A Novel Block-Based Scheme for Arithmetic Coding. Entropy. 2014; 16(6):3315-3328. https://doi.org/10.3390/e16063315
Chicago/Turabian StyleHou, Qi-Bin, and Chong Fu. 2014. "A Novel Block-Based Scheme for Arithmetic Coding" Entropy 16, no. 6: 3315-3328. https://doi.org/10.3390/e16063315
APA StyleHou, Q.-B., & Fu, C. (2014). A Novel Block-Based Scheme for Arithmetic Coding. Entropy, 16(6), 3315-3328. https://doi.org/10.3390/e16063315




