How to Determine Losses in a Flow Field: A Paradigm Shift towards the Second Law Analysis

Abstract

Assuming that CFD solutions will be more and more used to characterize losses in terms of drag for external flows and head loss for internal flows, we suggest to replace single-valued data, like the drag force or a pressure drop, by field information about the losses. These information are gained when the entropy generation in the flow field is analyzed, an approach that often is called second law analysis (SLA), referring to the second law of thermodynamics. We show that this SLA approach is straight-forward, systematic and helpful when it comes to the physical interpretation of the losses in a flow field. Various examples are given, including external and internal flows, two phase flow, compressible flow and unsteady flow. Finally, we show that an energy transfer within a certain process can be put into a broader perspective by introducing the entropic potential of an energy.

1. Introduction

Losses in a flow field usually are characterized and determined by friction factors and drag coefficients. These nondimensional numbers basically are head loss and drag force information gained empirically, i.e., by corresponding experiments. Since they refer to single “global” values, like a pressure drop or a force, they may be called single-valued factors and coefficients, respectively.

Today, and even more in the future, there is an alternative, however: Computational fluid dynamics (CFD), giving access to the flow field with all its details. Then, not only (single-valued) data with respect to the head loss or drag force are available, but the flow field as a whole is known.

From a thermodynamics point of view, this makes a big difference. Losses under these perspective are due to irreversibilities within a thermodynamic process (here, the flow), whereas head loss and drag force are the consequences. Then, however, it is attractive to relate the losses in a flow field immediately to the cause of it and not to certain consequences of it.

Irreversibilities in a flow field quite generally are related to the entropy and its generation in the flow field. This entropy generation is not directly accessible in an experiment, but can be immediately determined in a CFD solution. In such a solution, it appears as a field quantity that can be integrated in order to determine the overall irreversibilities and, thus, the overall losses in a flow field.

Choosing this alternative approach to find the losses in a flow field is the paradigm shift mentioned in the headline of this study: A shift from single-valued experimental data to the integration of numerical field values in order to characterize and quantity the losses in a flow field. Once the numerical code used is verified and the physical model behind it is validated, the alternative approach is highly attractive, as will be demonstrated with various examples given hereafter.

2. Losses and the Second Law of Thermodynamics

Losses in a flow field are losses of mechanical energy in favor of internal energy. Thermodynamically, this is a conversion process between two forms of energy (mechanical and internal) conserving the overall energy (according to the first law of thermodynamics). With the exergy concept (energy = exergy + anergy), this can be expressed as a loss of exergy or available work, corresponding to a devaluation of the energy in the flow field.

When these exergy losses are determined directly from the entropy generation in the flow field, the determination of a single value is replaced by the integration over the whole flow field. There are several advantages to this approach, which determines exergy losses instead of head loss and drag forces.

They are:

(1)

The higher accuracy of the final results;

(2)

Detailed information about the location of losses within the flow field;

(3)

A direct physical interpretation of the losses in terms of exergy losses; this information is not available from drag and friction results, since it also depends on the temperature level;

(4)

A unique assessment quantity for losses in the flow and in the temperature field when heat transfer is also involved.

In fluid mechanics, external and internal flows are commonly treated as flows that belong to two different categories. When losses are determined for these flows, drag is the target quantity for external flows, whereas internal flows are characterized by their pressure drop or head loss. In a non-dimensional form, they are expressed as drag coefficient ${\text{c}}_{\text{D}}$, friction factor f and head loss coefficient K (see [1], for example), which are:

$${\text{c}}_{\text{D}}\equiv \frac{F_{\text{D}}}{\frac{\varrho }{2}{u}_{\infty }^{2}A}(\text{drag}\text{coefficient,}\text{external}\text{flow}),$$

(1)

$$\text{f}\equiv \frac{(-\text{d}p/\text{d}x)D_{\text{h}}}{\frac{\varrho }{2}{u}_{\text{m}}^2}(\text{friction}\text{factor,}\text{pipe}\text{flow})$$

(2)

$$\text{K}\equiv \frac{\mathsf{\Delta }p}{\frac{\varrho }{2}{u}_{\text{m}}^2}(\text{head}\text{loss}\text{coefficient,}\text{internal}\text{flow})$$

(3)

In order to have a common form, the friction factor, f, for a pipe or channel of length L can be converted into a K-value by multiplying f by $L/D_{\text{h}}$, so that then, with $(-\text{d}p/\text{d}x)L=\mathsf{\Delta }p$, Equation (3) also holds for pipe and channel flows.

Here, $F_{\text{D}}$ is the drag force on the body, $\mathsf{\Delta }p$ is the pressure drop in a component, $u_{\infty }$ is the undisturbed oncoming flow and $u_{\text{m}}$ is the cross-section averaged velocity. In order to end up with non-dimensional ${\text{c}}_{\text{D}}$, f and K, the projected area, A, and the hydraulic diameter, $D_{\text{h}}$, are included. As far as ${\text{c}}_{\text{D}}$ according to Equation (1) is concerned, the drag force, $F_{\text{D}}$, is the appropriate quantity one needs when flow resistance is considered. It either corresponds to the load on a non-moving body subject to flow resistance or it corresponds to the mechanical power, $F_{\text{D}}{u}_{\infty }$, which gets lost when a body moves with $u_{\infty }$.

As far as f according to Equation (2) and K according to Equation (3) is concerned, the pressure gradient $(-\text{d}p/\text{d}x)$ or the pressure difference, $\mathsf{\Delta }p$, are somewhat problematic quantities. They correspond to the losses in a flow field only under certain circumstances, as for example that of a horizontal flow in constant cross-sections when $(-\text{d}p/\text{d}x)$ is used to quantify losses in a pipe flow. They are, nevertheless, introduced, since all these quantities can be measured.

2.1. The Alternative Approach in General

With a paradigm shift in mind, we address the physical source that causes $F_{\text{D}}$, $\text{d}p/\text{d}x$ and $\mathsf{\Delta }p$ mentioned before. All these quantities appear in a problem, because the physical processes involved are irreversible in a thermodynamic sense. In these processes, entropy is generated at the rate $\dot{S}\text{irr,D}$ of irreversibility. Translated into the descriptive auxiliary quantity “exergy”, this corresponds to the loss rate of exergy (or available work), which is:

$${\dot{E}}_{\text{L}}^{\text{E}}=T_0{\dot{S}}_{\text{irr}}$$

(4)

Here, $T_0$ is the environmental temperature in Equation (4), which is called the Gouy–Stodola theorem; see [2,3,4], for example.

For external flows, ${\dot{S}}_{\text{irr}}$ should be related to the drag force, $F_{\text{D}}$, while for internal flows, ${\dot{S}}_{\text{irr}}$, should be used instead of $\text{d}p/\text{d}x$ and $\mathsf{\Delta }p$. Altogether, this is a unique approach to the characterization and determination of losses in irreversible external and internal flow situations.

2.2. The Alternative Approach for External Flows

For external flows, the overall entropy generation rate due to dissipation, ${\dot{S}}_{\text{irr,D}}$, can be linked to the drag force, $F_{\text{D}}$, by considering the (lost) mechanical power:

$$P_{\text{L}}=F_{\text{D}}{u}_{\infty }$$

(5)

which is a dissipation rate. This rate is linked to the entropy generation through the ambienttemperature, T:

$$P_{\text{L}}=T{\dot{S}}_{\text{irr,D}}$$

(6)

With $F_{\text{D}}$ from Equations (5) and (6), the drag coefficient ${\text{c}}_{\text{D}}$ is (see Equation (1)),

$${\text{c}}_{\text{D}}=\frac{T}{\frac{\varrho }{2}{u}_{\infty }^{3}A}{\dot{S}}_{\text{irr,D}}$$

(7)

2.3. The Alternative Approach for Internal Flows

The lost mechanical power for internal flow, like for external flow, is due to the dissipation process involved, so that a general definition of a head loss coefficient K is:

$$\text{K}=\frac{\phi }{u_{\text{m}}^2/2}$$

(8)

with φ as the specific dissipation rate in the component in which the internal flow occurs. This dissipation rate is linked to the entropy generation by:

$$\phi =\frac{T}{\dot{m}}{\dot{S}}_{\text{irr,D}}$$

(9)

so that Equation (8) with $\dot{m}=\varrho u_{\text{m}}A$ now becomes:

$$\text{K}=\frac{T}{\frac{\varrho }{2}{u}_{\text{m}}^{3}A}{\dot{S}}_{\text{irr,D}}$$

(10)

This definition of the head loss coefficient is related to the conventional definition of K according to Equation (3). Both definitions are equivalent when $(-\text{d}p/\text{d}x)$ in Equation (2) and $\mathsf{\Delta }p$ in Equation (3) exactly account for the dissipation in the component that is characterized by f and K, respectively. Often, however, this is not the case, and f and K according to Equations (2) and (3) lack a clear physical interpretation; see [5] for a detailed discussion.

2.4. Advantage of the Alternative Approach

The alternative approach, from now on called the SLA approach (Second Law Analysis), is superior to indirect approaches in the four aspects already mentioned at the beginning of Section 2. While Aspects 2–4 are of a conceptual nature, the accuracy Aspect 1 needs special attention: Since the SLA approach is based on field information, the influence of boundary conditions can be analyzed within every calculation. It will turn out that the flow field in a quantifiable distance from the upstream boundary becomes independent of the boundary condition. For internal flow, developed flow occurs, which shows up in a plot of quasi-local values of the entropy generation; see, e.g., Figure 8 for $x/D_{\text{h}}=0$. Here, developed flow is indicated, since the entropy generation is invariant with the axial coordinate from the beginning, since a developed flow profile is explicitly set. In addition, information gained from the entire flow field is used, whereas values taken from relatively few cells at the boundaries (either the inlet and outlet for internal flow or fixed walls for external flows) might be largely affected by small errors.In [6], it is illustrated that the inaccurate determination of kinetic energy needed for an indirect approach can lead to very wrong results for the dissipation. This, however, is avoided when entropy generation is used as a field quantity instead of computing the dissipation from the extended Bernoulli equation.

Table 1. Drag and head loss coefficients; conventional and alternative definitions.

	conventional approach	alternative approach
external flow	${\displaystyle {\text{c}}_{\text{D}}=\frac{F_{\text{D}}}{\frac{\varrho }{2}{u}_{\infty }^{2}A}}$	${\displaystyle {\text{c}}_{\text{D}}=\frac{T}{\frac{\varrho }{2}{u}_{\infty }^{3}A}{\dot{S}}_{\text{irr,D}}}$
internal flow	${\displaystyle \text{K}=\frac{\mathsf{\Delta }p}{\frac{\varrho }{2}{u}_{\text{m}}^2}}$	${\displaystyle \text{K}=\frac{T}{\frac{\varrho }{2}{u}_{\text{m}}^{3}A}{\dot{S}}_{\text{irr,D}}}$

Table 1. Drag and head loss coefficients; conventional and alternative definitions.

	conventional approach	alternative approach
external flow	${\displaystyle {\text{c}}_{\text{D}}=\frac{F_{\text{D}}}{\frac{\varrho }{2}{u}_{\infty }^{2}A}}$	${\displaystyle {\text{c}}_{\text{D}}=\frac{T}{\frac{\varrho }{2}{u}_{\infty }^{3}A}{\dot{S}}_{\text{irr,D}}}$
internal flow	${\displaystyle \text{K}=\frac{\mathsf{\Delta }p}{\frac{\varrho }{2}{u}_{\text{m}}^2}}$	${\displaystyle \text{K}=\frac{T}{\frac{\varrho }{2}{u}_{\text{m}}^{3}A}{\dot{S}}_{\text{irr,D}}}$

Furthermore, the SLA approach leads to a unique definition of losses, irrespective of whether it is an external or an internal flow. The entropy generation rate, ${\dot{S}}_{\text{irr,D}}$, due to the dissipation of mechanical energy, immediately determines the loss rate of exergy (or available work) according to Equation (4). With this definition head loss coefficients for single components can be combined in order to evaluate the performance of whole systems, where, again, the entropy generation within a process is thecrucial quantity.

3. The Second Law Analysis (SLA) of a Flow Field

When drag and head loss coefficients are defined like in Equations (7) and (10) (also, see Table 1), losses are attributed to the overall entropy generation in the flow field. Since this ${\dot{S}}_{\text{irr}}$ will be determined by integrating local values ${\dot{S}}_{\text{irr}}^{‴}$, the basic equations are needed, from which ${\dot{S}}_{\text{irr}}^{‴}$ can be calculated. These equations constitute a mathematical/physical model of the flow under consideration. Since models have to be validated (see [7]), this also holds for the SLA-model introduced in this study. This aspect will be resumed once the details of the SLA-model are introduced after the literature about entropy and its generation is shortly reviewed next.

3.1. Literature about Entropy and the SLA Approach

There are a vast number of textbooks and monographs about thermodynamics that all have major parts with respect to entropy in it, like [2,3,4]. Special books about entropy range from easy-to-read introductions, like [8,9,10], over more comprehensive books, like [11,12], to very challengingones, like [13,14].

The SLA approach in which irreversibilities are identified and determined is described and applied in fundamental studies, like [15,16,17], for example.

Almost all studies that incorporate an SLA refer to one of the several important contributions by A. Bejan [15,18,19,20]. In these studies, entropy generation is often determined as an integral value within a finite solution domain, either by global balances or by the integration of the local entropy generation density. A general and systematic comparison of various approaches can be found in [21] and [22].

As far as internal flows are concerned, one can analyze a system as a whole or have a closer look into single components within a complex system. Studies about whole systems, like [23,24,25], aim at improving the system performance, though there is no systematic optimization strategy involved, like in the special study of [26], for example. Detailed studies about single components can be foundin [27], where a vortex tube is analyzed, in [28] for a diffuser, in [29] with a study about a cross-flow heat exchanger or in [30], where rectangular ducts are investigate, just to mention a few typical investigations out of the great number of studies based on the SLA approach.

The benefits of the SLA approach can also be seen in turbo-machinery applications. In [31], it is noted that entropy generation due to dissipation caused by viscous layers, vortices and shocks is the reason for reduced system performance. Therefore, local contributions to the entropy generation can be determined using adequate turbulence modeling, leading to an overall performance evaluation based on entropy generation considerations.

3.2. Local Entropy Generation Rates and Turbulence Modeling

The pivotal question in the SLA approach is how to determine the local entropy generation rate, ${\dot{S}}_{\text{irr,D}}^{‴}$, in a flow field, the integration of which leads to the (overall) entropy generation, ${\dot{S}}_{\text{irr,D}}$, in Equations (7) and (10). When the flow is laminar, the determination of ${\dot{S}}_{\text{irr,D}}$ is straight-forward, based on the thermodynamics relation (Cartesian coordinates; units: $\mathrm{W}/{\mathrm{m}}^3/\mathrm{K}$; see, e.g., [4]):

$$\begin{array}{c}{\dot{S}}_{\text{irr,D}}^{‴}=\frac{\mu }{T}\left(2\left[{\left(\frac{\partial u}{\partial x}\right)}^2+{\left(\frac{\partial v}{\partial y}\right)}^2+{\left(\frac{\partial w}{\partial z}\right)}^2\right]\right.+\hfill \\ \hfill \left.{\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)}^2+{\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right)}^2+{\left(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\right)}^2\right)\end{array}$$

(11)

In order to end up with the overall entropy generation rate, ${\dot{S}}_{\text{irr,D}}$, which appears in ${\text{c}}_{\text{D}}$ and K (see Table 1), this local quantity has to be integrated appropriately. This “appropriate” integration needs some special considerations when the flow losses of a conduit component in an otherwise fully developed internal flow should be determined; see Section 3.3 below.

When the flow is turbulent, ${\dot{S}}_{\text{irr,D}}^{‴}$ according to Equation (11) is adequate only for a direct numerical simulation (DNS)-approach with respect to the turbulence, as for the example shown in [32]. Since DNS solutions with their extraordinary computational demand cannot be used for solving technical problems, the time-averaged equations (Reynolds-averaged Navier–Stokes: RANS) are solved instead. Then, also, ${\dot{S}}_{\text{irr,D}}^{‴}$ has to be time averaged, leading to:

$${\dot{S}}_{\overline{\text{D}}}^{‴}={\dot{S}}_{\text{irr},\overline{\text{D}}}^{‴}+{\dot{S}}_{\text{irr},{\text{D}}^{\prime }}^{‴}$$

(12)

with the index “$\text{irr},\overline{\text{D}}$ ” for the entropy generation in the time-averaged velocity field and “$\text{irr},{\text{D}}^{\prime }$” for the time-averaged contribution of the fluctuating parts. Both parts are:

$$\begin{array}{cc}\hfill {\dot{S}}_{\text{irr},\overline{\text{D}}}^{‴}=& \frac{\mu }{T}\left(2\left[{\left(\frac{\partial \overline{u}}{\partial x}\right)}^2+{\left(\frac{\partial \overline{v}}{\partial y}\right)}^2+{\left(\frac{\partial \overline{w}}{\partial z}\right)}^2\right]\right.+\hfill \\ & \left.{\left(\frac{\partial \overline{u}}{\partial y}+\frac{\partial \overline{v}}{\partial x}\right)}^2+{\left(\frac{\partial \overline{u}}{\partial z}+\frac{\partial \overline{w}}{\partial x}\right)}^2+{\left(\frac{\partial \overline{v}}{\partial z}+\frac{\partial \overline{w}}{\partial y}\right)}^2\right)\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\dot{S}}_{\text{irr},{\text{D}}^{\prime }}^{‴}=& \frac{\mu }{T}\left(2\left[\overline{{\left(\frac{\partial u^{\prime }}{\partial x}\right)}^2}+\overline{{\left(\frac{\partial v^{\prime }}{\partial y}\right)}^2}+\overline{{\left(\frac{\partial w^{\prime }}{\partial z}\right)}^2}\right]\right.+\hfill \\ & \left.\overline{{\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)}^2}+\overline{{\left(\frac{\partial u^{\prime }}{\partial z}+\frac{\partial w^{\prime }}{\partial x}\right)}^2}+\overline{{\left(\frac{\partial v^{\prime }}{\partial z}+\frac{\partial w^{\prime }}{\partial y}\right)}^2}\right)\hfill \end{array}$$

(14)

With the result for a turbulent flow field from RANS equations, ${\dot{S}}_{\text{irr},\overline{\text{D}}}^{‴}$ according to Equation (13) can be determined, but not ${\dot{S}}_{\text{irr},{\text{D}}^{\prime }}^{‴}$ in Equation (14). Here, a turbulence model is needed. A simple model that basically relates ${\dot{S}}_{\text{irr},{\text{D}}^{\prime }}^{‴}$ to the turbulent dissipation rate ε and that can be justified in the limit of infinite Reynolds numbers (see [33]) reads:

$${\dot{S}}_{\text{irr},{\text{D}}^{\prime }}^{‴}=\frac{\varrho \epsilon }{T}$$

(15)

In our investigations, Menter’s $k-\omega$-SSTmodel is chosen due to its ability to integrate the Navier–Stokes equations in the low Re regime near the wall (without using damping corrections) and to adequately predict flow separation,; see [34]. Thus, our model for ${\dot{S}}_{\text{irr},{\text{D}}^{\prime }}^{‴}$ is:

$${\dot{S}}_{\text{irr},{\text{D}}^{\prime }}^{‴}={\beta }^{☆}\frac{\varrho \omega k}{T_m}$$

(16)

with ${\beta }^{☆}=0.09$. Here, ω is the characteristic frequency and k the kinetic energy of the turbulent fluctuations. As another benefit of this model in its low-Re formulation wall functions, strictly valid for unseparated shear flow at high Reynolds numbers only can be avoided. Due to today’s computer performance, the flow in the viscous sublayer can be fully resolved; the complete flow field is available for post-processing. Thus, cells adjacent to walls do not need a special treatment in order to compute the near wall entropy generation. The latter aspect would imply a special wall function for the entropy generation consistent with the wall function used to calculate the velocity field; see [35], for example. Additionally, the $k-\omega$-SST model is known to be robust with respect to the turbulent inflow boundary conditions. However, profiles for k and ω should be prescribe for internal flow. These profiles can be determined based on calculations of fully developed channel flow with periodic boundary conditions. The accuracy of the model (together with a grid of sufficient resolution and accurate numerical schemes) has been proven in [5], where losses due to a 90-degree bend are slightly overpredicted compared to reliable experimental data from [36], amongst others.

3.3. Overall Entropy Generation Rates

In order to end up with the overall entropy generation rate, ${\dot{S}}_{\text{irr},\text{D}}$, that appears in the drag and head loss coefficient, an integration of ${\dot{S}}_{\text{irr},\text{D}}^{‴}$ is required. This integration must cover all ${\dot{S}}_{\text{irr},\text{D}}$-effects due to the body or component that should be specified by the drag or head loss coefficient with respect to its losses. Here, the “due to” is important, since only those ${\dot{S}}_{\text{irr},\text{D}}^{‴}$ have to be taken into account that are caused by the body (external flow) or component (internal flow). When there is entropy generation in the flow field without the body or the component, already, only the additional entropy generation contributes to ${\text{c}}_{\text{D}}$ and K, respectively. For external flows, this kind of situation will be the exception (when, for example, the body would be placed in a shear flow), for internal flows; however, this is a situation that often occurs. Figure 1 schematically shows how ${\dot{S}}_{\text{irr,D}}$ is determined for a conduit component with a fully developed flow far upstream and far downstream of the component. The additional entropy generation upstream is $\mathsf{\Delta }{\dot{S}}_{\text{irr,D,u}}$; that downstream is $\mathsf{\Delta }{\dot{S}}_{\text{irr,D,d}}$. In order to characterize the range of up- and down-stream influence, $L_{\text{u}}$ and $L_{\text{d}}$ are introduced as those lengths on which 95% of the additional entropygeneration occurs.

Figure 1. Determination of the overall entropy generation rate due to a conduit component. $\mathsf{\Delta }{\dot{S}}_{\text{irr,D,u}}$ is the additional entropy generation upstream of the component, ${\dot{S}}_{\text{irr,D,c}}$ the entropy generation inside the component and $\mathsf{\Delta }{\dot{S}}_{\text{irr,D,d}}$ the additional entropy generation downstream of the component.

Figure 1. Determination of the overall entropy generation rate due to a conduit component. $\mathsf{\Delta }{\dot{S}}_{\text{irr,D,u}}$ is the additional entropy generation upstream of the component, ${\dot{S}}_{\text{irr,D,c}}$ the entropy generation inside the component and $\mathsf{\Delta }{\dot{S}}_{\text{irr,D,d}}$ the additional entropy generation downstream of the component.

According to these considerations, the overall entropy generation due to the body or component under consideration is

• for external flows:

  $${\dot{S}}_{\text{irr,D}}=\underset{V}{\int }\left({\dot{S}}_{\text{irr,D}}^{‴}-{\dot{S}}_{\text{irr,D0}}^{‴}\right)\text{d}V$$

  (17)

  with ${\dot{S}}_{\text{irr,D0}}^{‴}$ as the local entropy generation of the undisturbed flow (which often is zero) and V as the entire flow domain
• for internal flows:

  $$\underset{\phi \dot{m}/T_{\text{m}}}{\underbrace{{\dot{S}}_{\text{irr,D}}\phantom{{\int }_{V_{\text{c}}}}}}=\underset{\mathsf{\Delta }{\dot{S}}_{\text{irr,D,u}}=\mathsf{\Delta }{\phi }_u\dot{m}/T_{\text{m}}}{\underbrace{\underset{V_{\text{u}}}{\int }({\dot{S}}_{\text{irr,D}}^{\prime \prime \prime }-{\dot{S}}_{\text{irr,D}0}^{\prime \prime \prime })\text{d}V}}+\underset{{\dot{S}}_{\text{irr,D,c}}={\phi }_c\dot{m}/T_{\text{m}}}{\underbrace{\underset{V_{\text{c}}}{\int }{\dot{S}}_{\text{irr,D}}^{\prime \prime \prime }\text{d}V}}+\underset{\mathsf{\Delta }{\dot{S}}_{\text{irr,D,d}}=\mathsf{\Delta }{\phi }_d\dot{m}/T_{\text{m}}}{\underbrace{\underset{V_{\text{d}}}{\int }({\dot{S}}_{\text{irr,D}}^{\prime \prime \prime }-{\dot{S}}_{\text{irr,D}0}^{\prime \prime \prime })\text{d}V}}$$

  (18)

  with ${\dot{S}}_{\text{irr,D}0}^{‴}$ as the local entropy generation of the fully developed flow in the up- and down-stream adjacent channels and $V_{\text{u}}$, $V_{\text{c}}$ and $V_{\text{d}}$ according to Figure 1.

In both cases the impact of the body and the component decays asymptotically with the distance, i.e., ${\dot{S}}_{\text{irr,D}}^{‴}-{\dot{S}}_{\text{irr,D}0}^{‴}$ exactly becomes zero at an infinite distance only. In a numerical calculation, the solution domain in most cases will be finite, so that a certain “truncation error” will occur. This error can be kept small, however, and will not pose a problem when it is smaller than the discretization error of the numerical solution procedure. Numerical solutions in finite solution domains are those in the so-called near-flow field. neglecting effects “at infinity”.

3.4. Entropy Generation versus Dissipation in a Flow Field

Sometimes, it is argued that there is no need to refer to the entropy generation, ${\dot{S}}_{\text{irr,D}}$, in a flow field, since the dissipation $\mathsf{\Phi }=T{\dot{S}}_{\text{irr,D}}$ is the actually needed quantity. It turns out, however, that ${\dot{S}}_{\text{irr,D}}$ is the more fundamental and definitely preferable quantity, because:

• from a thermodynamics point of view, dissipation is quantified by the entropy generation involved in this process and not vice versa;
• entropy generation is immediately linked to the loss of exergy (see Equation (4)), but dissipation is not; how much exergy is lost in a dissipative process is determined by the entropy generated;
• when further mechanisms, which are irreversible in character, are involved (like heat transfer), their irreversibility can be characterized by a further entropy generation in the flow field and added to that due to dissipation; the overall loss (of exergy) in a flow field is then uniquely accounted for by the overall entropy generation.

4. Examples for External Flows

Though a greater variety of problems has been dealt with for internal flows (see Section 5), we first want to show the applicability of the SLA approach for two very different external flow situations. Comparing the SLA results with well-established analytical results for the first and experimental results for the second example is part of the validation requirements for the SLA model, already mentioned at the beginning of Section 3.

4.1. Drag of a Flat Plate for Laminar Boundary Layer Flow

Laminar flow over a flat plate of finite length is a benchmark case for the higher order boundary layer theory, described in [37], for example. This theory is an asymptotic theory for $\text{Re}\to \infty$, the results of which can be applied as approximate solutions for finite values of the Reynolds number. Especially when higher order terms are taken into account, the approximation is excellent even for Reynolds numbers of the order $\mathcal{O}\left(1\right)$.

Such a higher order result for the flat plate of finite length, L, is:

$${\text{c}}_{\text{D}}=2[1.328{\text{Re}}^{-1/2}+2.67{\text{Re}}^{-7/8}]+\mathcal{O}\left({\text{Re}}^{-1}\right)$$

(19)

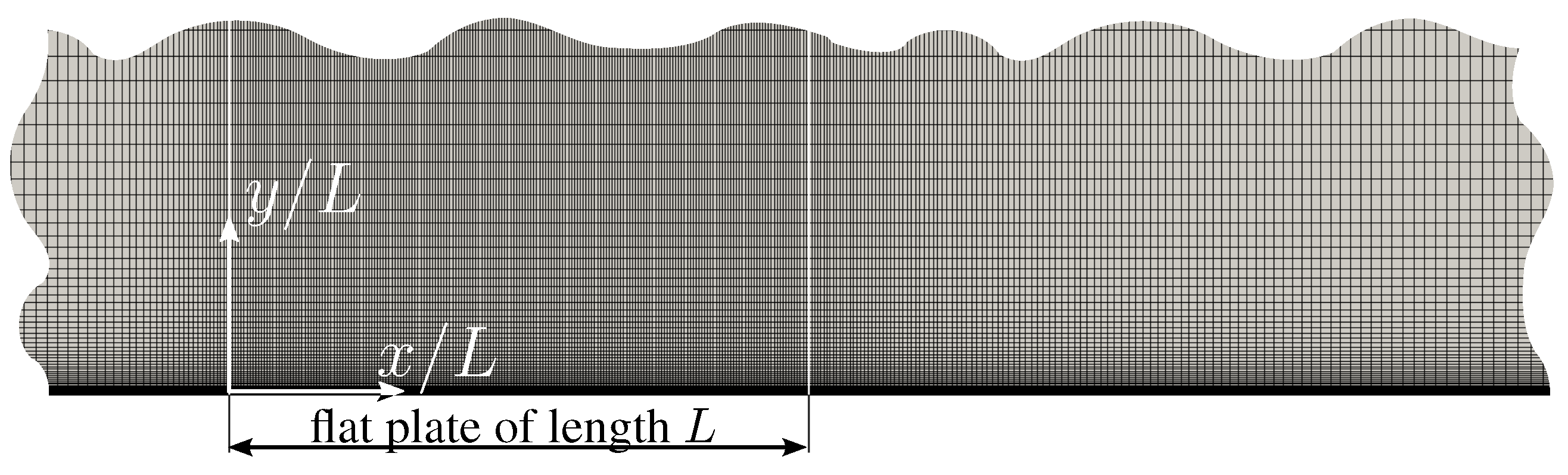
Here, the second term on the rhs comes in as the influence of the trailing edge determined by the so-called triple deck theory; see, for example, [38] for more details. The drag coefficient according to Equation (19) will be compared to the results we get from our SLA approach, integrating the local entropy generation in the near-flow field. This is done by discretizing the two-dimensional steady Navier–Stokes equations with a grid shown in Figure 2. There is a grid refinement in the vicinity of the flat plate, which is discretized using 280 cells stream-wise and 140 cells in the lateral direction. The aspect ratio of the cells adjacent to the surface is two more details of the grid structure, and the numerical solution procedures are given in [39].

Figure 2. Discretization of the near-flow field around the flat plate; the plate is located between $x/L=0$ and 1.

Figure 2. Discretization of the near-flow field around the flat plate; the plate is located between $x/L=0$ and 1.

In Figure 3(a–c), ${\dot{S}}_{\text{irr,D}}^{\prime }$ along the x-coordinate is shown, which is the entropy generation within the (x,y)-plane at $x=\text{const}$. This ${\dot{S}}_{\text{irr,D}}^{\prime }$ is referred to ${\dot{S}}_{\text{irr,D}}/L$ and, thus, dimensionless.

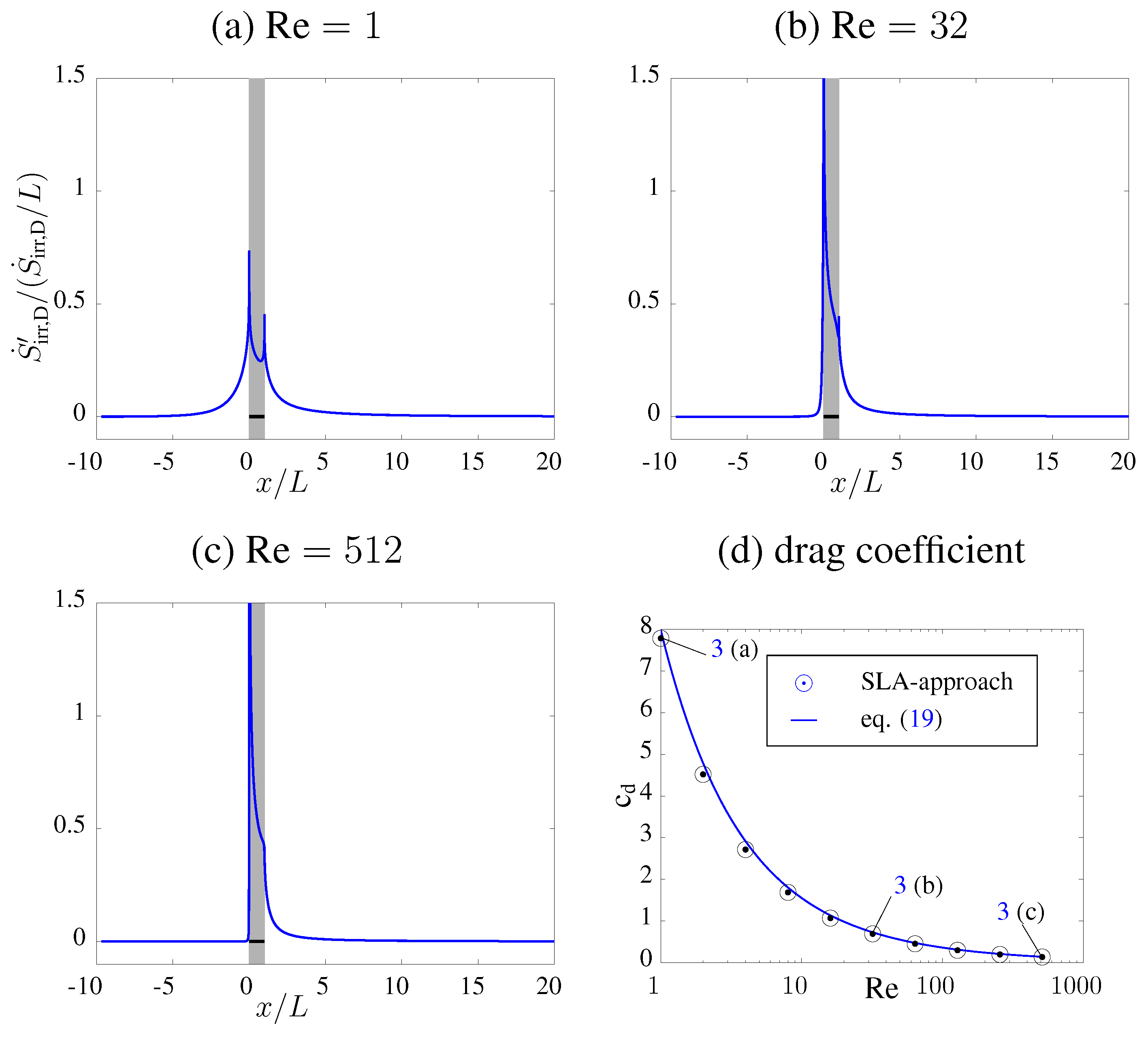
Figure 3. (a–c): Distribution of ${\dot{S}}_{\text{irr,D}}^{\prime }$ along the x-axis, non-dimensionalized with the overall entropy generation rate, ${\dot{S}}_{\text{irr,D}}$, and the length of the plate, L. The location of the flat plate is between $x/L=0$ and 1. (d) Drag coefficient ${\text{c}}_{\text{D}}\left(\text{Re}\right)$.

Figure 3. (a–c): Distribution of ${\dot{S}}_{\text{irr,D}}^{\prime }$ along the x-axis, non-dimensionalized with the overall entropy generation rate, ${\dot{S}}_{\text{irr,D}}$, and the length of the plate, L. The location of the flat plate is between $x/L=0$ and 1. (d) Drag coefficient ${\text{c}}_{\text{D}}\left(\text{Re}\right)$.

With an increasing Reynolds number $\text{Re}=u_{\infty }L/\nu$, the entropy generation occurs more and more in the vicinity of the plate (and the wake), thus showing the increasing boundary layer character of the flow.

At $\text{Re}=512$, there is almost no upstream influence. Since entropy generation only occurs where velocity gradients are (see Equation (11)), an almost undisturbed upstream flow field has almost zero ${\dot{S}}_{\text{irr,D}}^{\prime }$ values. Entropy generation and, thus, the losses in the flow field, are shifted downstream when the Reynolds number is increased.

Figure 3d shows ${\text{c}}_{\text{D}}$-data determined by the SLA approach compared to the asymptotic results according to Equation (19). Slightly increasing deviations for $\text{Re}\to 0$ may be explained by the missing higher order terms, $\mathcal{O}\left({\text{Re}}^{-1}\right)$, in the asymptotic result in Equation (19).

4.2. Drag of a Rising Bubble

In order to show the wide applicability of the SLA approach and that results gained by this method are meaningful with respect to a physical interpretation, we consider the flow around a rising bubble and determine its drag from the entropy generation in the surrounding flow field.

When a single bubble has a diameter $D<1.5\mathrm{mm}$, the high surface tension leads to the almost perfect spherical shape of the bubble, and the path it takes on its way upwards is straight; see [40] for details. Such a case can be modeled by a fixed bubble with a homogeneous oncoming flow in the direction of the gravity vector, $\overrightarrow{g}$. At the bubble surface, no shear stress occurs, since the gas motion inside the bubble has a negligible momentum, due to the low density compared to that of the surrounding water. Then, however, the bubble surface is totally mobile, which can be accounted for by a total slip velocity boundary condition at the surface of the spherical bubble.

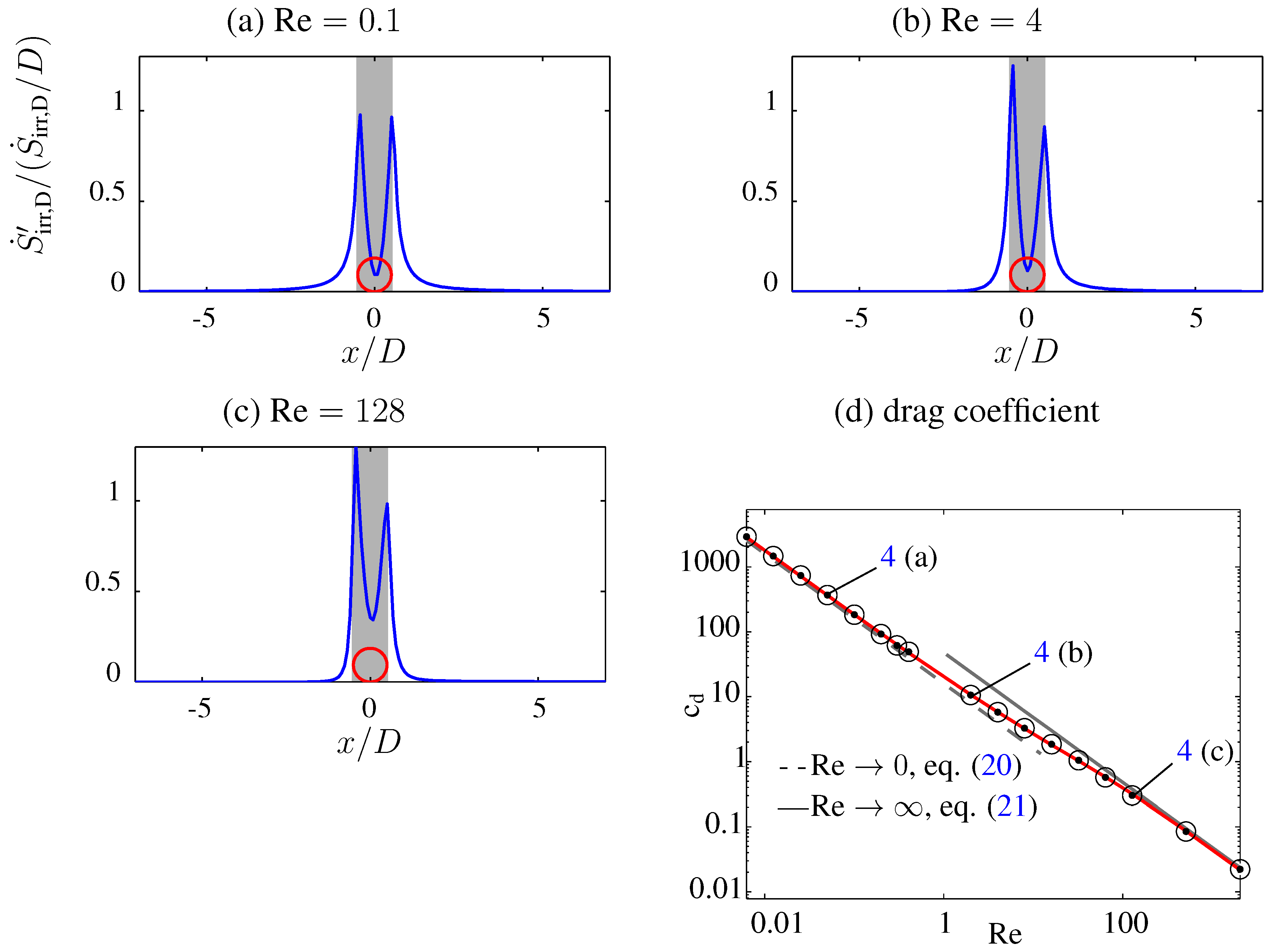
The circumference of the sphere is discretized with 544 cells with an aspect ratio of 3.6, leading to 140,000 cells of the axisymmetric grid with a streamwise extent of $34D$ and a lateral extent of $10D$. More details of the grid and the solution procedure can be found in [39]; some results are shown in Figure 4(a–c). Again, the entropy generation, ${\dot{S}}_{\text{irr,D}}^{\prime }$, in a plane at constant values x are shown; here, for three Reynolds numbers $\text{Re}=u_{\infty }D/\nu$.

For spherical bubbles, there are asymptotic solutions for $\text{Re}\to 0$, associated with the names, Hadamard and Rybczinsky; see [41], and for $\text{Re}\to \infty$, see [42]. They are given in terms of drag coefficients ${\text{c}}_{\text{D}}$; see Equation (1),

$$\begin{array}{ccc}\hfill {\text{c}}_{\text{D}}=16/\text{Re}& & \text{for}\text{Re}\to 0\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill {\text{c}}_{\text{D}}=48/\text{Re}& & \text{for}\text{Re}\to \infty \hfill \end{array}$$

(21)

In Figure 4d, both asymptotes are shown together with our SLA results. There is a smooth transition between the asymptotic results for small and large Reynolds numbers showing that the integrated entropy generation corresponds to the losses in the flow field for the whole Reynolds number range oflaminar flow.

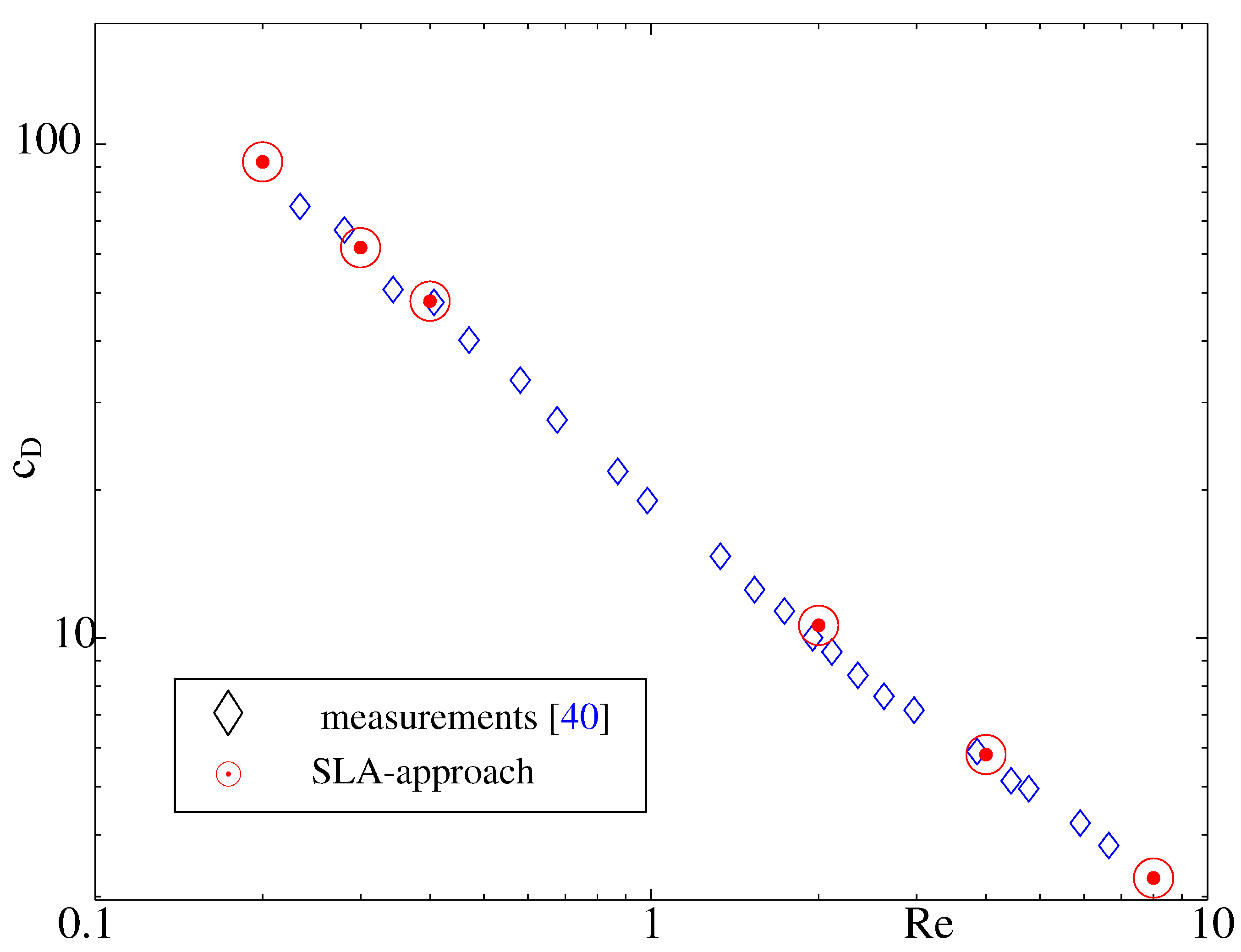
A comparison with experimental data in oil (see [40]), as part of the validation of the SLA approach, is given in Figure 5; here, with a close coincidence of experimental and theoretical data.

Figure 4. (a–c): Distribution of ${\dot{S}}_{\text{irr,D}}^{\prime }$ along the x-axis, non-dimensionalized with the overall entropy generation rate, ${\dot{S}}_{\text{irr,D}}$, and the diameter, D, of the bubble. (d): drag coefficient.

Figure 4. (a–c): Distribution of ${\dot{S}}_{\text{irr,D}}^{\prime }$ along the x-axis, non-dimensionalized with the overall entropy generation rate, ${\dot{S}}_{\text{irr,D}}$, and the diameter, D, of the bubble. (d): drag coefficient.

Figure 5. Drag coefficient for rising bubbles; validation of the SLA approach.

Figure 5. Drag coefficient for rising bubbles; validation of the SLA approach.

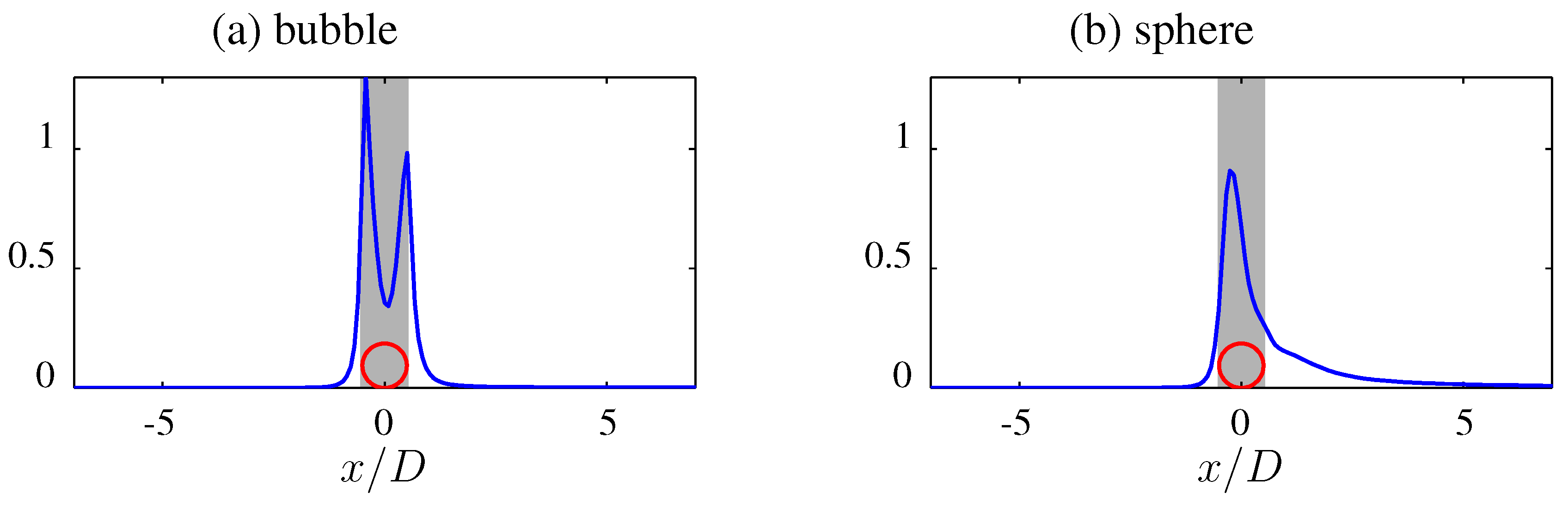
For the physical interpretation, it is interesting to compare the entropy generation field around a rising bubble (slip at the boundary) and the corresponding sphere (non-slip at the boundary).

Due to the change in boundary conditions from slip to non-slip, the velocity gradients near the bubble and sphere surfaces are fundamentally different and, as a consequence, also, the local entropygeneration rates.

This can be demonstrated for the cross-section averaged entropy generation rates, ${\dot{S}}_{\text{irr,D}}^{\prime }$, for both cases; see Figure 6. With the slip condition, there is no boundary layer at the bubble surface, and even for higher Reynolds numbers, no flow separation. With the non-slip condition, separation occurs for moderate to high Reynolds numbers and an appreciable amount of entropy generation can be found in the wake behind the sphere.

Figure 6. Entropy generation ${\dot{S}}_{\text{irr,D}}^{\prime }/({\dot{S}}_{\text{irr,D}}/D)$ for $\text{Re}=128$. (a) Bubble: slip at the boundary; (b) sphere: non-slip at the boundary. More details can be found in [39].

Figure 6. Entropy generation ${\dot{S}}_{\text{irr,D}}^{\prime }/({\dot{S}}_{\text{irr,D}}/D)$ for $\text{Re}=128$. (a) Bubble: slip at the boundary; (b) sphere: non-slip at the boundary. More details can be found in [39].

5. Examples for Internal Flows in Conduit Components

Conduit components, like straight channels, bends, trijunctions, channel entrances and exits, are often combined in pipe or channel systems. For such a system, flow losses are important to know, since they determine the power needed to maintain a certain flow rate through the system.

Combining head loss coefficients for single components always, then, is a problem when losses in the flow field do not completely occur in the component itself (as with a straight channel), but partly outside of it, mostly downstream (as with a bend).

Another problem is the influence of wall roughness, especially for turbulent flow. It can be relatively strong in fully-developed flow situations, like in straight pipes, but is often neglected in components, like bends or junctions, since, then, the head loss due to disturbed flow profiles is dominating.

With these considerations in mind, we give several examples addressing the problems of wall roughness, downstream influence and the combination of components.

5.1. Straight Pipes and Channels

Pipes and channel with respect to their losses are characterized by friction factors f, which are closely related to the general head loss coefficient, K (see Table 1) by:

$$\text{f}=\text{K}{D}_{\text{h}}/L$$

(22)

with $D_{\text{h}}$ as the hydraulic diameter and L as the length of the pipe or channel.

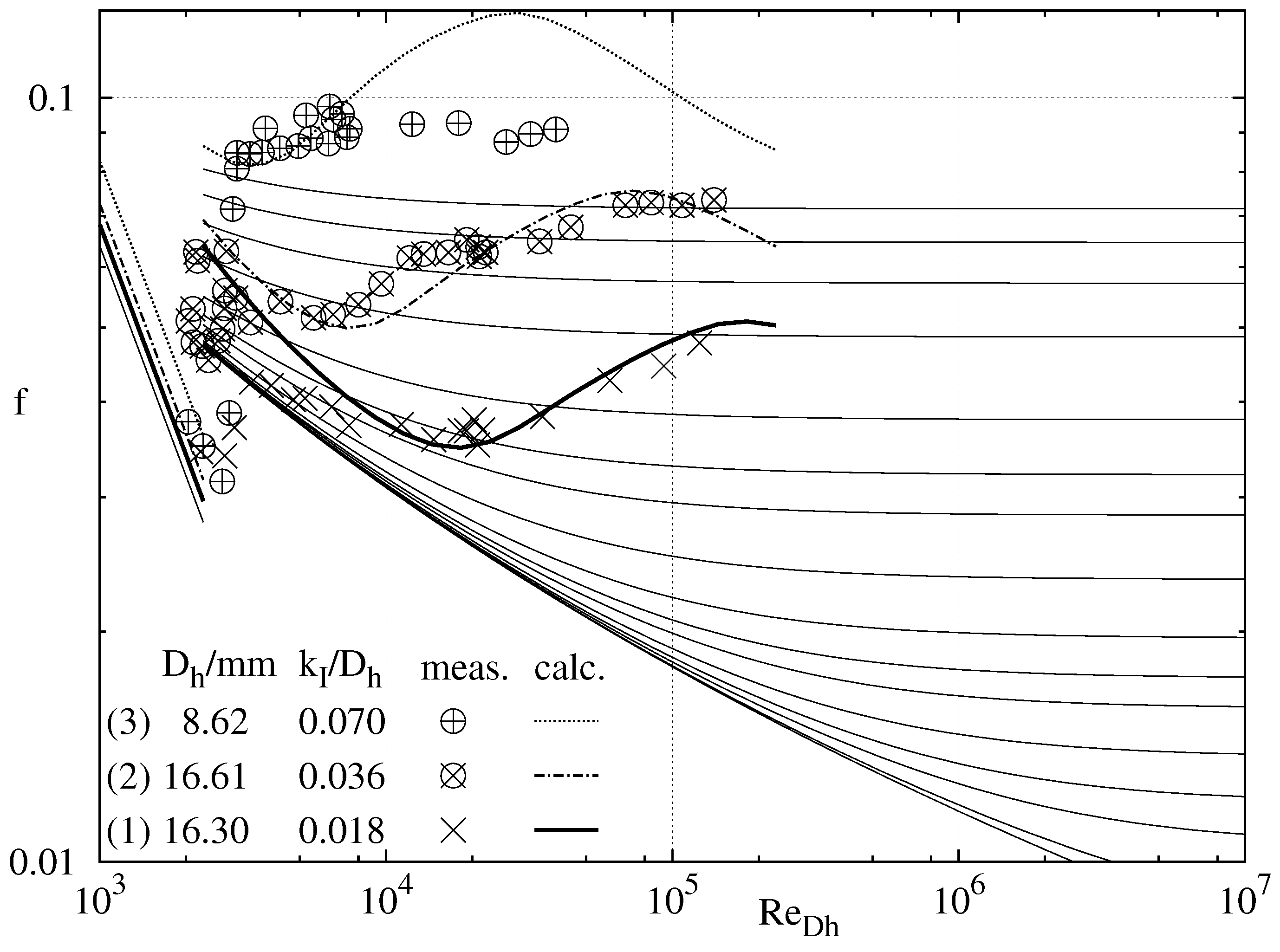
When roughness effects are included, a systematic analysis will always incorporate regular roughness elements, which follows the same idea as introducing (regular) sand roughness in experiments, which leads to the famous Moody chart; see [43] and [44]. In [45], we applied the SLA approach to the flow through a pipe with special roughness elements, called Loewenherz-roughness, [46]. Figure 7 shows both the experiments and our SLA results. It can be seen that f for these roughness elements does not follow the general trend of the Moody chart with respect to the lines for increasing sand roughness height. This, however, is also predicted in our SLA results; for a detailed discussion, see [45].

Figure 7. Experimental data and SLA results for three different pipes with rough walls and turbulent flow; experimental data are from [46].

Figure 7. Experimental data and SLA results for three different pipes with rough walls and turbulent flow; experimental data are from [46].

With the same kind of analysis, we could show that, contrary to the common belief, there is also a definite roughness effect in laminar pipe and channel flows; see [47,48,49].

5.2. Ninety-Degree Bend and Bend Combinations

In many pipe or channel systems, 90-degree bends can be found, either as single conduit components or as combinations, i.e., close together. Then, the problem of mutual interactions occurs, as will be discussed in the following.

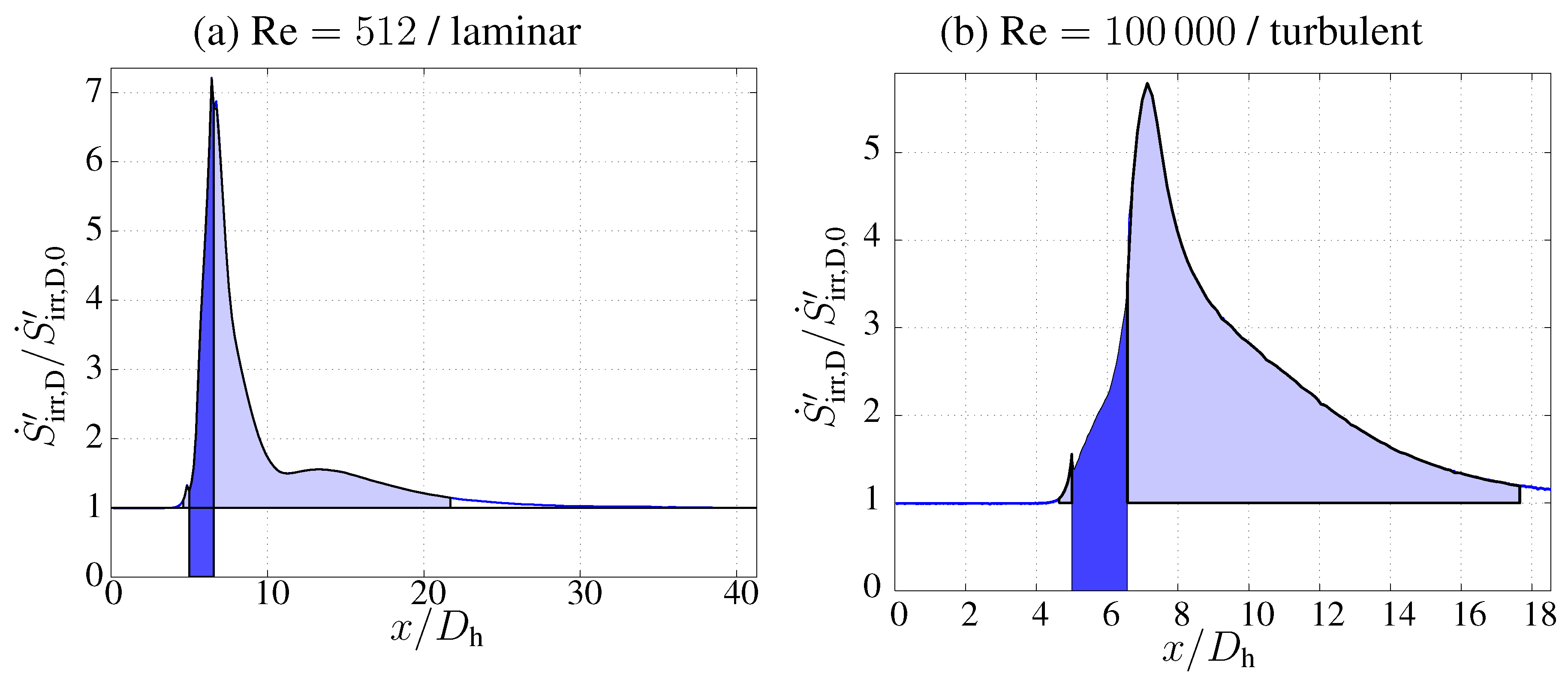
For a single 90-degree bend, applying the SLA analysis is straight-forward, when the peculiarities described in Figure 1 and Equation (18) are taken into account. Figure 8 shows two examples of how the entropy generation is distributed along the flow path, one for laminar flow ($\text{Re}=512$) and one for turbulent flow ($\text{Re}=100000$). In both cases, most of the (additional) entropy generation occurs downstream of the bend. This is why conduit components cannot be combined with a small distance between the single components and, nevertheless, be described by summing up the single head loss coefficients. Then, instead, these combinations must be treated as one new component and be characterized by its own K-value.

Figure 8. Distribution of ${\dot{S}}_{\text{irr,D}}^{\prime }$ along the centerline coordinate, x. (a) $\text{Re}=512$, with more details in [50]; (b) $\text{Re}=\mathrm{100,000}$, with more details in [5].

Figure 8. Distribution of ${\dot{S}}_{\text{irr,D}}^{\prime }$ along the centerline coordinate, x. (a) $\text{Re}=512$, with more details in [50]; (b) $\text{Re}=\mathrm{100,000}$, with more details in [5].

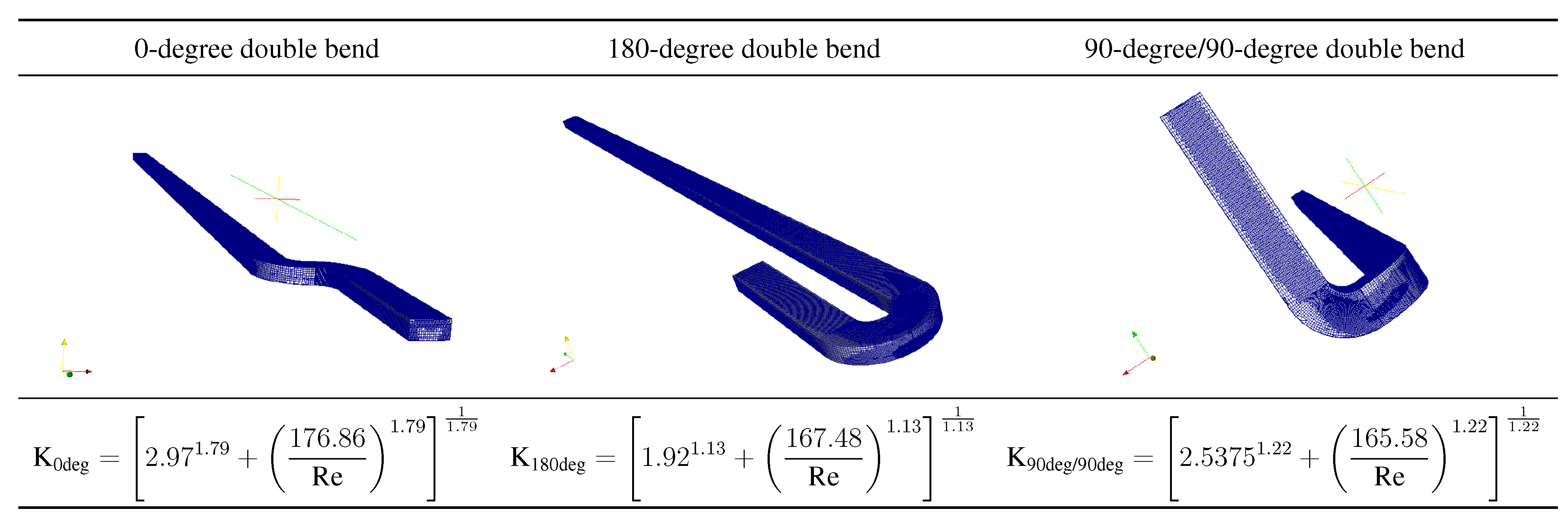
Such combinations of two 90-degree bends are shown in Figure 9 with the associated K-coefficients determined by the SLA approach. Table 2 shows that only for very low Reynolds numbers (with little downstream additional entropy generation), the K-value of a double bend is almost twice the value of the corresponding single bend. For high Reynolds numbers and, therefore, strong downstream effects, the downstream bend is placed where otherwise, the strong additional entropy generation of the upstream bend would occur. That is why a double bend has K-values that are always smaller than twice the single bend K-values, as can be seen in Table 2 for increasing Reynolds numbers.

Figure 9. Geometry and K-value of double bend combinations; laminar flow; more details in [50].

Figure 9. Geometry and K-value of double bend combinations; laminar flow; more details in [50].

Table 2. Comparison of K-values for three different 90-degree bend combinations with twice the K-value of a single 90-degree bend; more details in [50]; laminar flow.

Re	2 × 90-degree bend	0-degree double bend	180-degree double bend	90-degree/90-degree double bend
4	44.38	43.76	43.76	43.51
8	22.50	22.20	22.14	22.05
16	11.82	11.67	11.57	11.59
32	6.93	6.71	6.63	6.76
64	4.51	4.35	4.31	4.60
128	4.53	3.15	3.06	3.53
256	4.34	3.06	2.31	2.90
512	4.54	3.18	2.20	2.68

Table 2. Comparison of K-values for three different 90-degree bend combinations with twice the K-value of a single 90-degree bend; more details in [50]; laminar flow.

Re	2 × 90-degree bend	0-degree double bend	180-degree double bend	90-degree/90-degree double bend
4	44.38	43.76	43.76	43.51
8	22.50	22.20	22.14	22.05
16	11.82	11.67	11.57	11.59
32	6.93	6.71	6.63	6.76
64	4.51	4.35	4.31	4.60
128	4.53	3.15	3.06	3.53
256	4.34	3.06	2.31	2.90
512	4.54	3.18	2.20	2.68

5.3. Branching Conduit Components

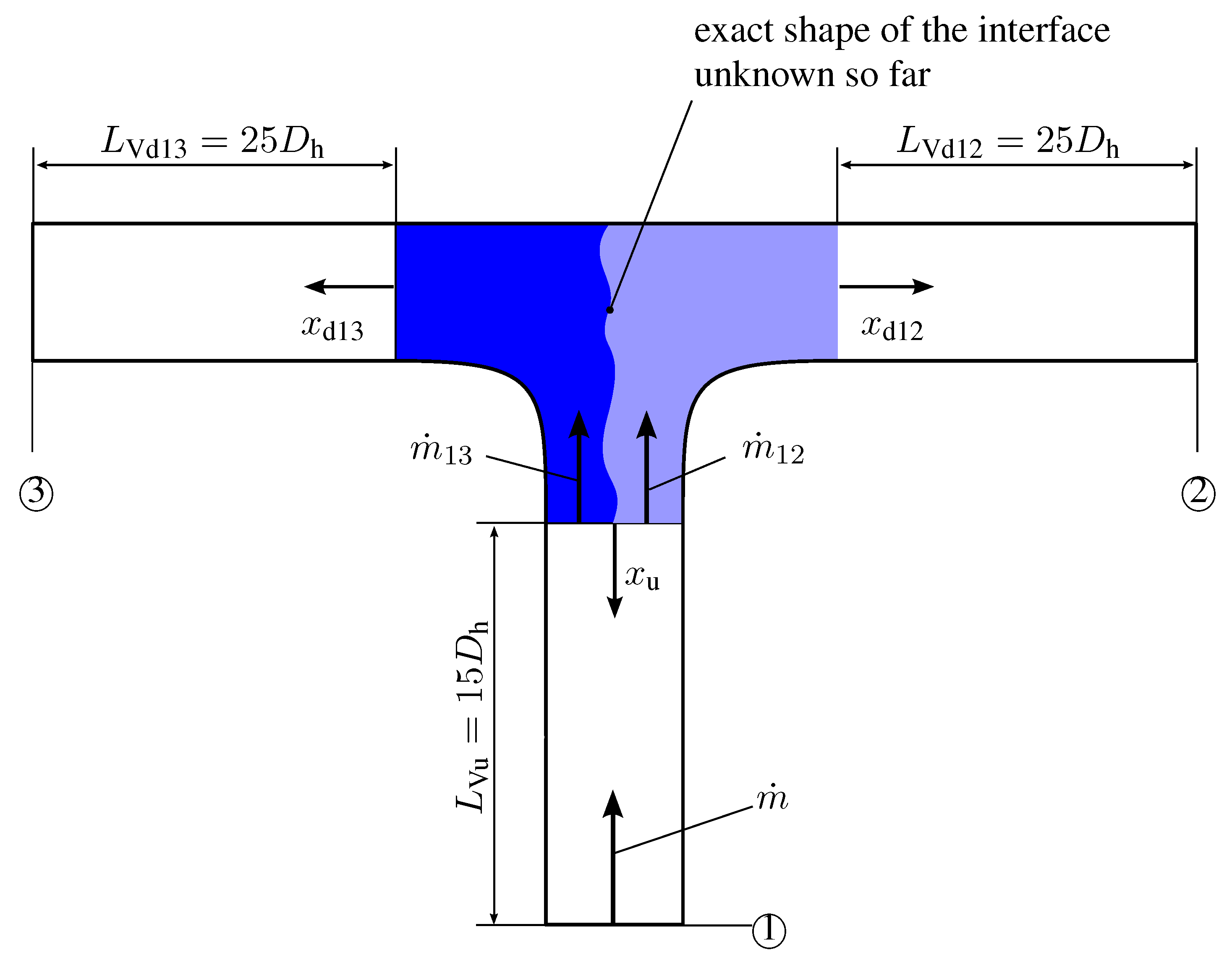
When, in conduit components, the flow is divided or combined in a T-shaped junction, a new aspect appears compared to a situation in which the flow is uniquely confined all along the component. In Figure 10, the case of flow division in a T-junction is sketched. Due to the splitting of $\dot{m}$ into ${\dot{m}}_{12}$ and ${\dot{m}}_{13}$, an interface exists that needs special attention. On this interface, shear stresses occur, leading to forces with moving points of action and, thus, to an energy transfer between the two adjacent flows. This energy transfer will be named diffusion and is a transfer of mechanical energy from one flow to the other.

Figure 10. Dividing of the mean flow rate, $\dot{m}$, into ${\dot{m}}_{12}$ and ${\dot{m}}_{13}$ for the symmetric T-junction with a square cross-section $A=D_{\text{h}}^2$. Corners are described by circular arcs of radius $R=D_{\text{h}}$. $L_{\text{Vu}}$, $L_{\text{Vd12}}$, $L_{\text{Vd13}}$: lengths over which effects are accounted for numerically upstream and downstream.

Figure 10. Dividing of the mean flow rate, $\dot{m}$, into ${\dot{m}}_{12}$ and ${\dot{m}}_{13}$ for the symmetric T-junction with a square cross-section $A=D_{\text{h}}^2$. Corners are described by circular arcs of radius $R=D_{\text{h}}$. $L_{\text{Vu}}$, $L_{\text{Vd12}}$, $L_{\text{Vd13}}$: lengths over which effects are accounted for numerically upstream and downstream.

From a thermodynamic point of view, this is very different in character compared to the dissipation in the flow field, which is a transfer from mechanical to internal energy within a certain flow. Both effects, however, affect the head loss coefficient, which then is not named correctly anymore. Since the diffusion part is no “loss”, K should be named the head change coefficient whenever diffusion effects are involved.

Taking this into account, the definition in analogy to K according to Equation (8) for single mass flow rates, now for branched flows, calling ${\text{K}}_{\text{ij}}$ the head change coefficient, is:

$${\text{K}}_{\text{ij}}=\frac{{\phi }_{\text{ij}}-d_{\text{ij}}}{u_{\text{m}}^2/2}$$

(23)

In order to determine these ${\text{K}}_{\text{ij}}$, the specific dissipation rates, ${\phi }_{\text{ij}}$, as well as the specific stress work rates, $d_{\text{ij}}$, have to be determined.

They are:

$${\phi }_{\text{ij}}={\dot{S}}_{\text{ij}}{T}_{\text{m}}/{\dot{m}}_{\text{ij}}=T_{\text{m}}\underset{V_{\text{ij}}}{\int }{\dot{S}}_{\text{irr,D}}^{‴}\text{d}V/{\dot{m}}_{\text{ij}}$$

(24)

$$d_{\text{ij}}={\dot{D}}_{\text{ij}}/{\dot{m}}_{\text{ij}}=\underset{V_{\text{ij}}}{\int }{\dot{D}}^{‴}\text{d}V/{\dot{m}}_{\text{ij}}$$

(25)

with the local entropy generation rate, ${\dot{S}}_{\text{irr,D}}^{‴}$ in ($\mathrm{W}/{\mathrm{m}}^3/\mathrm{K}$), according to Equation (11), which also can be written in vector form as:

$${\dot{S}}_{\text{irr,D}}^{‴}=\frac{\overrightarrow{\overrightarrow{\tau }}:\nabla \overrightarrow{u}}{T}$$

(26)

and the local stress work rate, ${\dot{D}}^{‴}$ ($\mathrm{W}/{\mathrm{m}}^3$),

$${\dot{D}}^{‴}=\nabla ·\left(\overrightarrow{\overrightarrow{\tau }}\overrightarrow{u}\right).$$

(27)

Here, $d_{\text{ij}}$ appears as a volume integral equivalent to the surface integral incorporating the shear stress after the theorem of Gauss has been applied, replacing the surface by a volume integral.

Once the splitting parameter, r, is fixed in terms of:

$$\begin{array}{cc}\hfill {\dot{m}}_{\text{12}}& =\text{r}\dot{m}\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill {\dot{m}}_{\text{13}}& =(1-\text{r})\dot{m}\hfill \end{array}$$

(29)

(when only two partial flows are involved) ${\text{K}}_{\text{ij}}$, according to Equation (23), is well defined. In order to determine ${\phi }_{\text{ij}}$ and $d_{\text{ij}}$, details about the flow field must be available in terms of ${\dot{S}}_{\text{irr,D}}^{‴}$ and ${\dot{D}}^{‴}$. Since these quantities have to be integrated over the volume, $V_{\text{ij}}$, one also has to know the exact part of the flow field within the T-junction that belongs to ${\dot{m}}_{\text{12}}$ and ${\dot{m}}_{\text{13}}$, respectively.

For that purpose, a further equation for an artificial variable, $a\in [0,1]$, can be solved, which is:

$$\frac{\partial a}{\partial t}+\overrightarrow{u}·\nabla a=0.$$

(30)

Since this equation contains convection, but no diffusion and no dissipation terms, the quantity, a, is merely convected through the flow field. If a is set to $a=1$ in one exit of the T-junction and $a=0$ in the other, the integration of Equation (30) leads to the a-field, in which the boundary between both partial flows is indicated by the jump of a between zero and one. After some further considerations with respect to the finite volumes cut by the interface, the two partial flow fields can be identified within the overall numerical solution, and ${\text{K}}_{12}$ and ${\text{K}}_{13}$ according to Equation (23) can be determined.

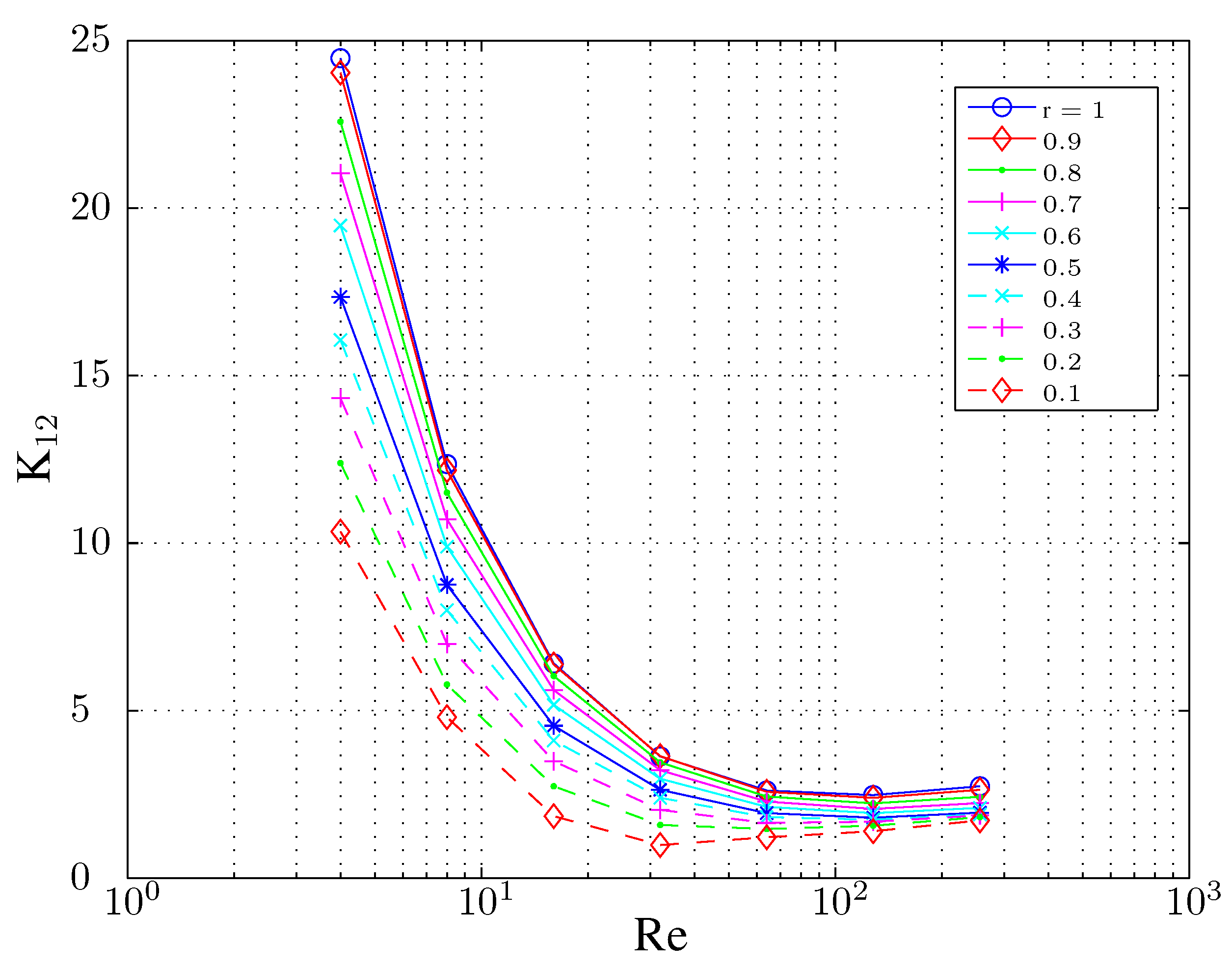
Figure 11 shows ${\text{K}}_{12}\left(\text{Re}\right)$ for the T-junction in Figure 10 with the splitting parameter, r, increased by 10% steps.

Figure 11. Head change coefficient $K_{12}$ for the partial flow with ${\dot{m}}_{12}$; more details in [51].

Figure 11. Head change coefficient $K_{12}$ for the partial flow with ${\dot{m}}_{12}$; more details in [51].

Basically, this is the whole information about the T-junction, since the complementary coefficient ${\text{K}}_{13}$, as well as the overall coefficient, K, follow from ${\text{K}}_{12}$, according to:

$${\text{K}}_{13}(\text{r},\text{Re})={\text{K}}_{12}(1-\text{r},\text{Re})$$

(31)

and:

$$\text{K}\equiv \frac{({\dot{S}}_{\text{irr,D,12}}+{\dot{S}}_{\text{irr,D,13}})T_0/\dot{m}}{u_{\text{m}}^2/2}=\text{r}{\text{K}}_{12}+(1-\text{r}){\text{K}}_{13}$$

(32)

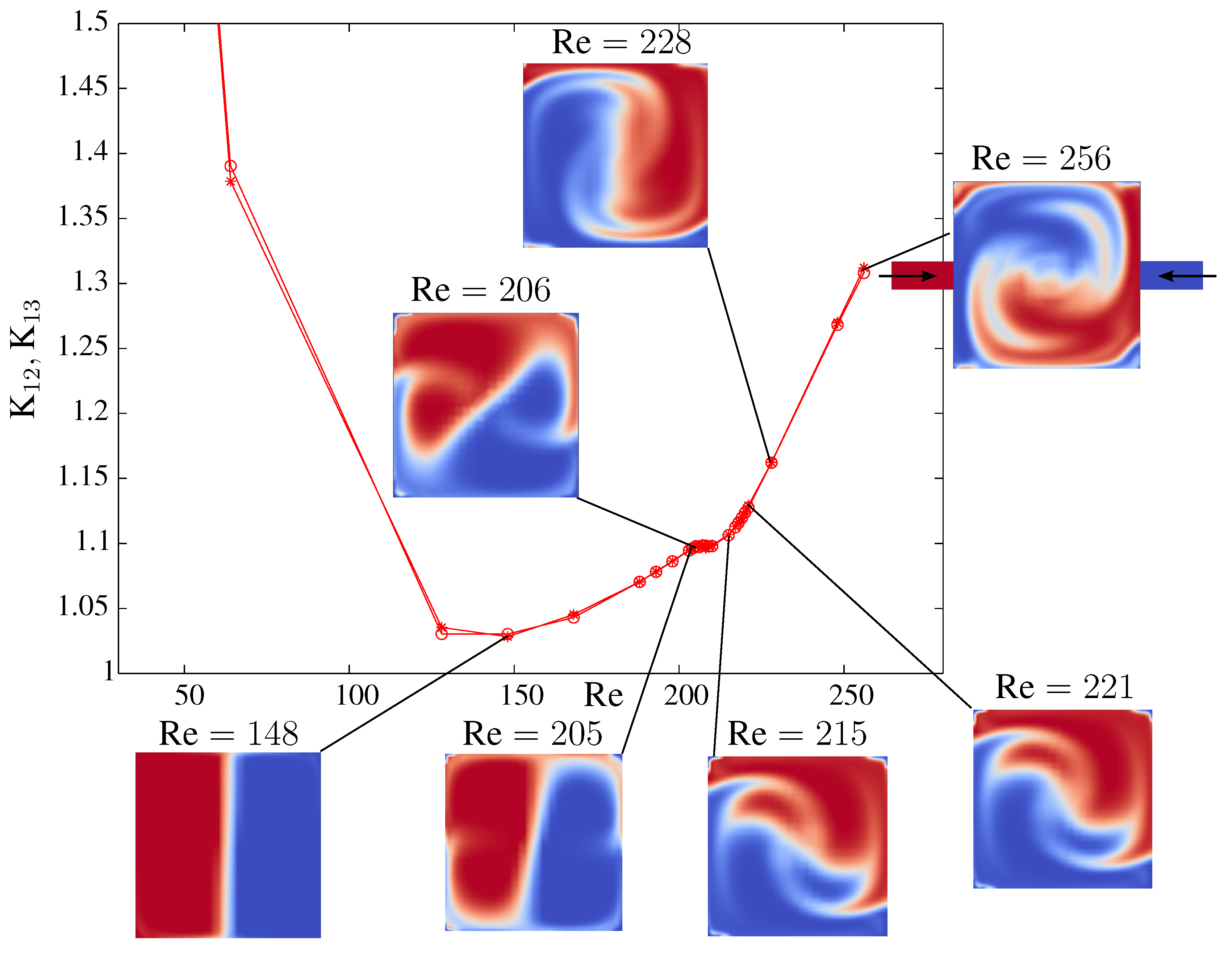
When a T-junction is used in order to combine (instead of divide) two partial flows, many aspects of the SLA approach are similar. It turns out, however, that in the downstream part of the T-junction, after the partial flows are combined, a phenomenon may occur that is called engulfment; see [52]. It is a strong mixing of the two partial flows and happens once the Reynolds number is higher than a certain critical Reynolds number. In the example shown in Figure 12, the onset of engulfment can be observed for Reynolds numbers $\text{Re}>205$; more details can be found in [53].

Figure 12. Head change coefficients for engulfed and symmetric flows. Onset of engulfment at $\text{Re}>205$. Small pictures show indicator field a at the end of the combining duct.

Figure 12. Head change coefficients for engulfed and symmetric flows. Onset of engulfment at $\text{Re}>205$. Small pictures show indicator field a at the end of the combining duct.

5.4. Loss Coefficients for Compressible Flows

Compared to the incompressible case, some new aspects have to be taken into account when the SLA approach is applied. It turns out that with the consideration of local entropy generation, a sound physical interpretation is possible. For laminar internal flows, the major new aspects are:

(1)

Density changes due to variations in pressure and temperature, and thus, there is no longer a fully developed flow far upstream and downstream of a conduit component.

(2)

The impact of a component in terms of an additional entropy generation due to the component again can be cast into the three parts: $\mathsf{\Delta }{\dot{S}}_{\text{irr,u}}$, ${\dot{S}}_{\text{irr,c}}$ and $\mathsf{\Delta }{\dot{S}}_{\text{irr,d}}$; see Figure 1. While $\mathsf{\Delta }{\dot{S}}_{\text{irr,u}}$ is a finite value, due to the gradual deviation of ${\dot{S}}_{\text{irr}}^{‴}$ from the undisturbed value, $\mathsf{\Delta }{\dot{S}}_{\text{irr,d}}$ is no longer finite, since ${\dot{S}}_{\text{irr}}^{‴}$ in the downstream part does not return to its undisturbed value. There is, however, a certain fixed shift, $\mathsf{\Delta }x$, in the streamwise coordinate by which $\mathsf{\Delta }{\dot{S}}_{\text{irr,d}}$ becomes finite again, and ${\dot{S}}_{\text{irr}}$, due to the component, is recovered.

(3)

For incompressible, flow K according to Equation (10) could be called the “head loss coefficient”, and it could be immediately attributed to the specific dissipation in the flow field due to the validity of Equation (9). For compressible flow, still, K according to Equation (10) can be used as a “loss coefficient”. It should be named the “exergy loss coefficient”, however, since exergy and not total head is the quantity that gets lost, and the (exergy) loss cannot be fully attributed to the specific dissipation; for details see [54].

Since, however, exergy is related to the ambient temperature, a “reference exergy loss coefficient”:

$${\text{K}}_{\text{RE}}=\frac{T_{\text{R}}}{\frac{u_{\text{m}}^2}{2}\dot{m}}{\dot{S}}_{\text{irr}}$$

(33)

analogous to Equation (10), is introduced. Here, $T_{\text{R}}$ and $u_{\text{m}}$ are the temperature and velocity at a reference point. The “exergy loss coefficient”, ${\text{K}}_{\text{E}}$, then, is:

$${\text{K}}_{\text{E}}=\frac{T_{\infty }}{T_{\text{R}}}{\text{K}}_{\text{RE}}$$

(34)

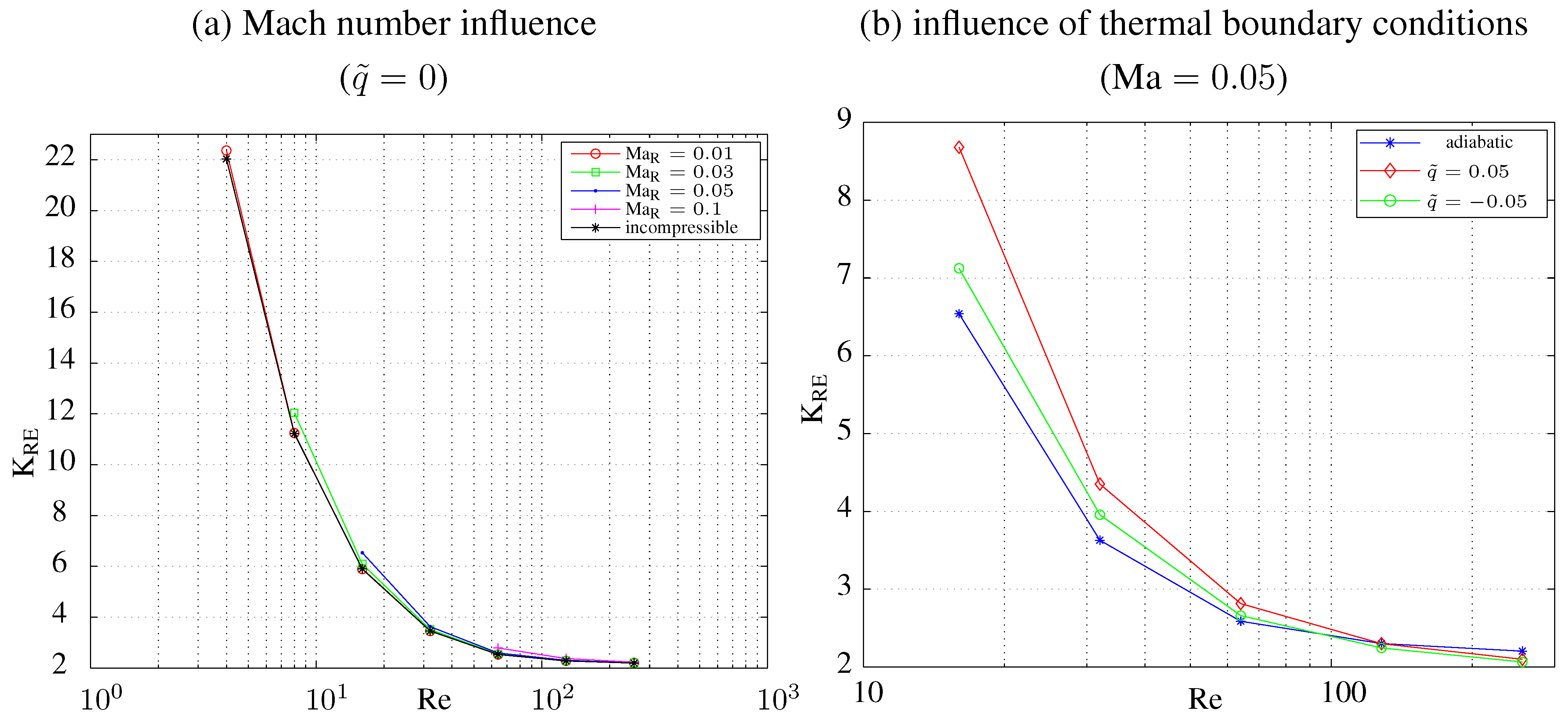
In Figure 13, reference exergy loss coefficients ${\text{K}}_{\text{RE}}$ are shown for various Reynolds numbers Re, Mach numbers ${\text{Ma}}_{\text{R}}=u_{\text{m}}/\sqrt{\kappa R{T}_{\text{R}}}$ and heat transfer rates $\tilde{q}=q{D}_{\text{h}}/\left(\lambda T_{\text{R}}\right)$. Here, an ideal gas is assumed $(\kappa ,R)$, and the thermal boundary conditions are heating $(\tilde{q}>0)$, adiabatic $(\tilde{q}=0)$ and cooling $(\tilde{q}<0)$. Mach numbers do not exceed ${\text{Ma}}_{\text{R}}=0.1$; they are, however, defined with the reference quantities at $x=0$ and take higher values downstream based on local values.

Altogether, it turns out that the Mach number influence is weak, at least for adiabatic walls. At low Reynolds numbers, important for flows in micro devices, there is a non-negligible influence of the thermal boundary conditions, however.

Figure 13. Reference exergy loss coefficients for compressible flow; more details in [54].

Figure 13. Reference exergy loss coefficients for compressible flow; more details in [54].

5.5. Loss Coefficients for Unsteady Flows

For an unsteady flow, the K-definition in Equations (8) and (10), respectively, can be used, as well; then being an instantaneous value, however. K changes with time, as does the flow field (which determines the instantaneous values of ${\dot{S}}_{\text{irr,D}}^{‴}$ and, thus, of K). For the special situation of a periodically unsteady flow, K can be integrated over a period (or multiple periods) leading to a (time) mean value, ${\text{K}}_{\text{m}}$. Then there also is a (time) mean mass flow rate, ${\dot{m}}_{\text{m}}$, and it can be determined how ${\text{K}}_{\text{m}}\left({\dot{m}}_{\text{m}}\right)$ compares to $\text{K}\left({\dot{m}}_{\text{m}}\right)$, i.e., the equivalent steady result.

For that purpose, a sinusoidally modulated mass flow rate:

$$\dot{m}\left(t\right)={\dot{m}}_{\text{m}}+{\dot{m}}_{\text{A}}\text{sin}\left(2\pi ft\right)$$

(35)

is introduced in [55].

Here, f is the frequency and ${\dot{m}}_{\text{A}}$ the amplitude of the sinusoidal modulation of the mass flow rate. In nondimensional form with:

$$\text{F}=\frac{D_{\text{h}}^2}{\nu }f,\tau =\frac{\nu }{D_{\text{h}}^2}t,\dot{\text{M}}=\frac{\dot{m}}{{\dot{m}}_{\text{m}}},{\dot{\text{M}}}_{\text{A}}=\frac{{\dot{m}}_{\text{A}}}{{\dot{m}}_{\text{m}}}$$

(36)

the unsteady mass flow rate is:

$$\dot{\text{M}}=1+{\dot{\text{M}}}_{\text{A}}\text{sin}\left(2\pi \text{F}\tau \right)$$

(37)

For this mass flow rate and laminar flow, there is an analytical solution for the velocity in a circular duct and, thus, for the entropy generation field (see [55] for details) from which ${\text{K}}_{\text{m}}$ can be determined.

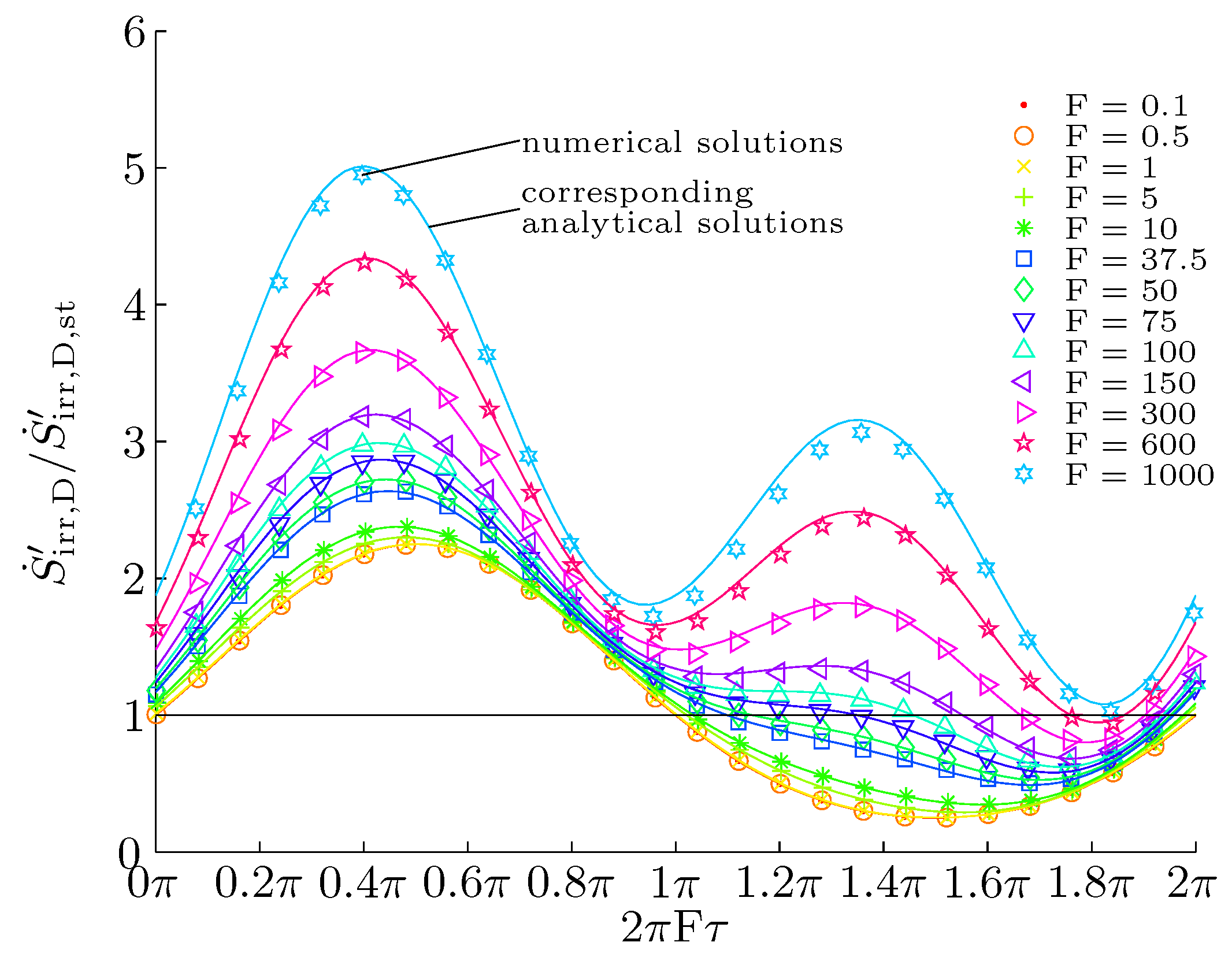
Within one period, the ratio of ${\dot{S}}_{\text{irr,D}}^{\prime }$ and the corresponding value, ${\dot{S}}_{\text{irr,D,st}}^{\prime }$, for the steady case varies, as shown in Figure 14. With increasing frequencies, the symmetry around the ${\dot{S}}_{\text{irr,D}}^{\prime }/{\dot{S}}_{\text{irr,D,st}}^{\prime }=1$ line gets more and more lost, because ${\dot{S}}_{\text{irr,D}}^{\prime }$ quite generally exceeds ${\dot{S}}_{\text{irr,D,st}}^{\prime }$. Integrating the ratio, ${\dot{S}}_{\text{irr,D}}^{\prime }/{\dot{S}}_{\text{irr,D,st}}^{\prime }$, over one period leads to the unsteadiness coefficient:

$${\text{C}}_{\text{un}}=\underset{0}{\overset{1}{\int }}\frac{{\dot{S}}_{\text{irr,D}}^{\prime }}{{\dot{S}}_{\text{irr,D,st}}^{\prime }}\text{d}\left(\text{F}\tau \right)$$

(38)

which also determines ${\text{K}}_{\text{m}}$, according to:

$${\text{K}}_{\text{m}}={\text{C}}_{\text{un}}{\text{K}}_{\text{st}}$$

(39)

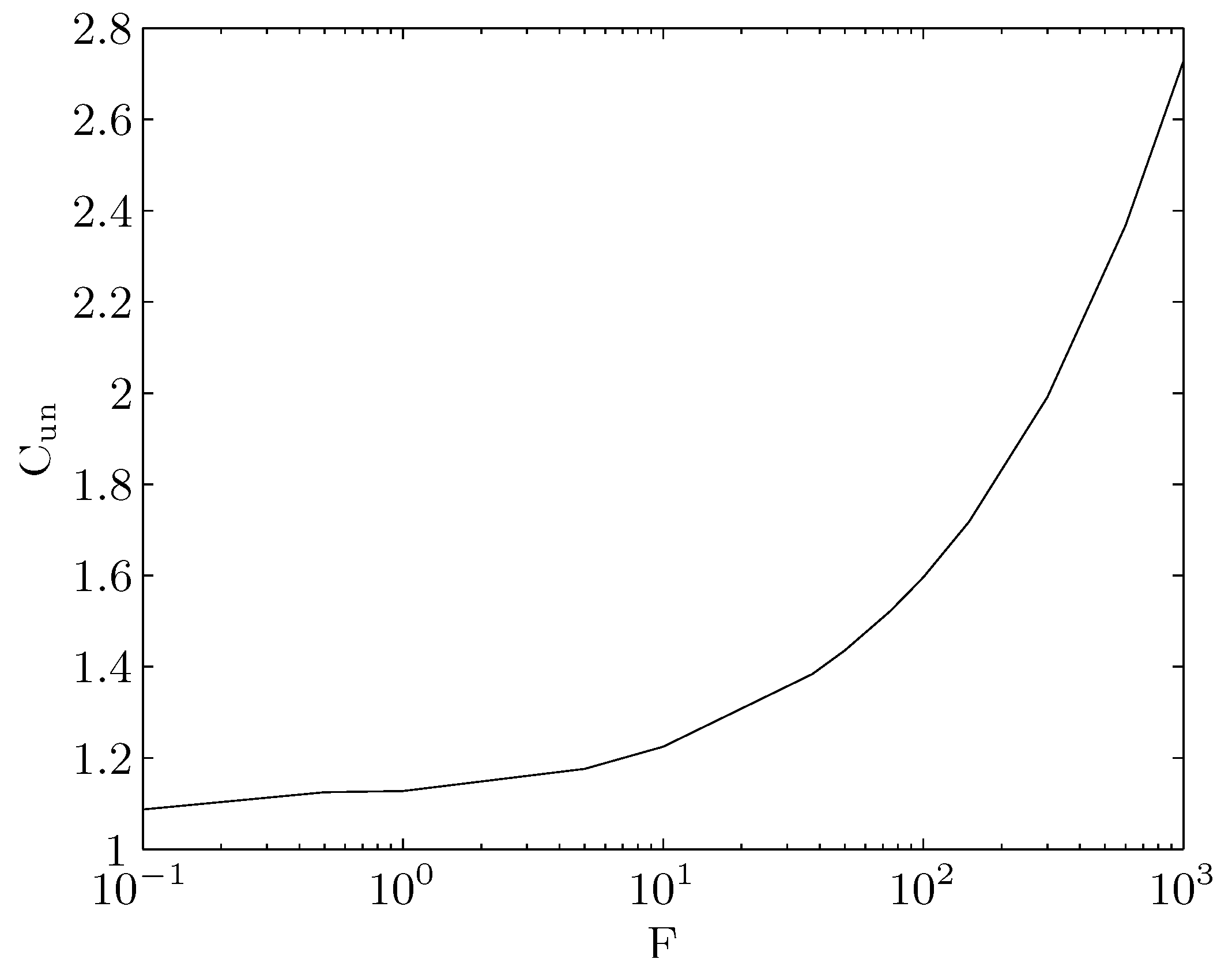
Figure 15 shows how ${\text{C}}_{\text{un}}$ increases with F for the same value of ${\dot{M}}_{\text{A}}$ as in Figure 14. Note that F is a nondimensional frequency, which has to be rescaled when real values are of interest. For the pipe flow of water and a hydraulic diameter $D_{\text{h}}=0.01\mathrm{m}$, for example, $\text{F}={10}^3$ corresponds to a frequency $f\approx 10\mathrm{Hz}$ and has an unsteadiness coefficient of almost three.

In [55], these consideration have also been extended to a 90-degree bend as a standard conduit component. Results are qualitatively similar to those shown before, except that now, an explicit Reynolds number dependence appears in the unsteadiness coefficient, ${\text{C}}_{\text{un}}$.

Figure 14. Cross-section entropy generation in a circular duct along one period.$\dot{M}$, according to Equation (37) with ${\dot{\text{M}}}_{\text{A}}=0.5$F: nondimensional frequency data taken from [55].

Figure 14. Cross-section entropy generation in a circular duct along one period.$\dot{M}$, according to Equation (37) with ${\dot{\text{M}}}_{\text{A}}=0.5$F: nondimensional frequency data taken from [55].

Figure 15. Unsteadiness coefficient for the mass flow rate of Figure 14.

Figure 15. Unsteadiness coefficient for the mass flow rate of Figure 14.

6. Flow with Heat Transfer

In non-isothermal flows, heat transfer occurs, which is strongly affected by the flow and, therefore, called convective heat transfer. As long as the fluid properties (density, viscosity) are constant values, the flow is not affected by the heat transfer, however. Then, also, the loss coefficients are the same as those for isothermal flows.

There is, however, an additional exergy loss in the temperature field, which happens within the energy that is transferred thermally. In order to assess convective heat transfer situations, both aspects (losses of exergy in the flow and in the temperature field) have to be taken into account. This can easily and systematically be done by also considering the entropy generation in the temperature field. Its local value (Cartesian coordinates; units ($\mathrm{W}/{\mathrm{m}}^3/\mathrm{K}$) (see, e.g., [4]) is for laminar flow:

$${\dot{S}}_{\text{C}}^{‴}=\frac{k}{T^2}\left({\left(\frac{\partial T}{\partial x}\right)}^2+{\left(\frac{\partial T}{\partial y}\right)}^2+{\left(\frac{\partial T}{\partial z}\right)}^2\right)$$

(40)

and for turbulent flow with ${\dot{S}}_{\text{C}}^{‴}={\dot{S}}_{\overline{\text{C}}}^{‴}+{\dot{S}}_{{\text{C}}^{\prime }}^{‴}$:

$$\begin{array}{cc}\hfill {\dot{S}}_{\overline{\text{C}}}^{‴}& =\frac{k}{{\overline{T}}^2}\left({\left(\frac{\partial \overline{T}}{\partial x}\right)}^2+{\left(\frac{\partial \overline{T}}{\partial y}\right)}^2+{\left(\frac{\partial \overline{T}}{\partial z}\right)}^2\right)\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill {\dot{S}}_{{\text{C}}^{\prime }}^{‴}& =\frac{k}{{\overline{T}}^2}\left(\overline{{\left(\frac{\partial T^{\prime }}{\partial x}\right)}^2}+\overline{{\left(\frac{\partial T^{\prime }}{\partial y}\right)}^2}+\overline{{\left(\frac{\partial T^{\prime }}{\partial z}\right)}^2}\right)\hfill \end{array}$$

(42)

Since now, exergy losses are uniquely described by the overall entropy generation rates, ${\dot{S}}_{\text{irr,D}}$ and ${\dot{S}}_{\text{C}}$, the sum of these two values corresponds to the total loss of exergy in a convective heat transfer situation.

When a conduit component is part of a system in which the loss of exergy counts (as, for example, in a power cycle), conduit components and their possible modifications can be assessed by this total exergy loss. For certain modifications, often, changes in ${\dot{S}}_{\text{irr,D}}$ and ${\dot{S}}_{\text{C}}$ have an opposing trend (one increasing, one decreasing), so that optimal modifications can be identified by the minimal total loss of exergy. An example for this kind of assessment can be found in [56,57,58,59,60,61].

In Figure 16, the total entropy generation per length ${\dot{S}}_{\text{irr}}^{\prime }$ in a pipe with wall roughness as the sum of the entropy generation, ${\dot{S}}_{\text{irr,D}}^{\prime }$, in the flow and ${\dot{S}}_{\text{C}}^{\prime }$ in the temperature field is shown. For each roughness parameter, ${\text{k}}_{\text{S}}$, there is a minimum and, thus, an optimal Reynolds number for this device; for more details, see [60].

Figure 16. Influence of wall roughness ${\text{k}}_{\text{S}}\le 0.5$ on the entropy generation rates; all values refer to ${\dot{S}}_{\text{irr},\circ }^{\prime }$ (at ${\text{Re}}_{\text{opt,s}}$).

Figure 16. Influence of wall roughness ${\text{k}}_{\text{S}}\le 0.5$ on the entropy generation rates; all values refer to ${\dot{S}}_{\text{irr},\circ }^{\prime }$ (at ${\text{Re}}_{\text{opt,s}}$).

When the physical properties of the fluid are no longer constants, a systematic approach then can be based on a Taylor series expansion of the properties with respect to the temperature; see [62,63,64].

7. Conduit Components As Part of a System

The loss of exergy determined by the entropy generation in a component in general is a partial devaluation of the energy involved. Devaluation here means that the exergy part of the energy is reduced and the anergy part increased. This, however, can be put in a wider perspective, taking into account that a certain energy transferred in a conduit component started as primary energy and finally will end as part of the internal energy of the environment. The overall process can be called a devaluation chain with respect to the energy with the specific process under consideration, just as one part of it.

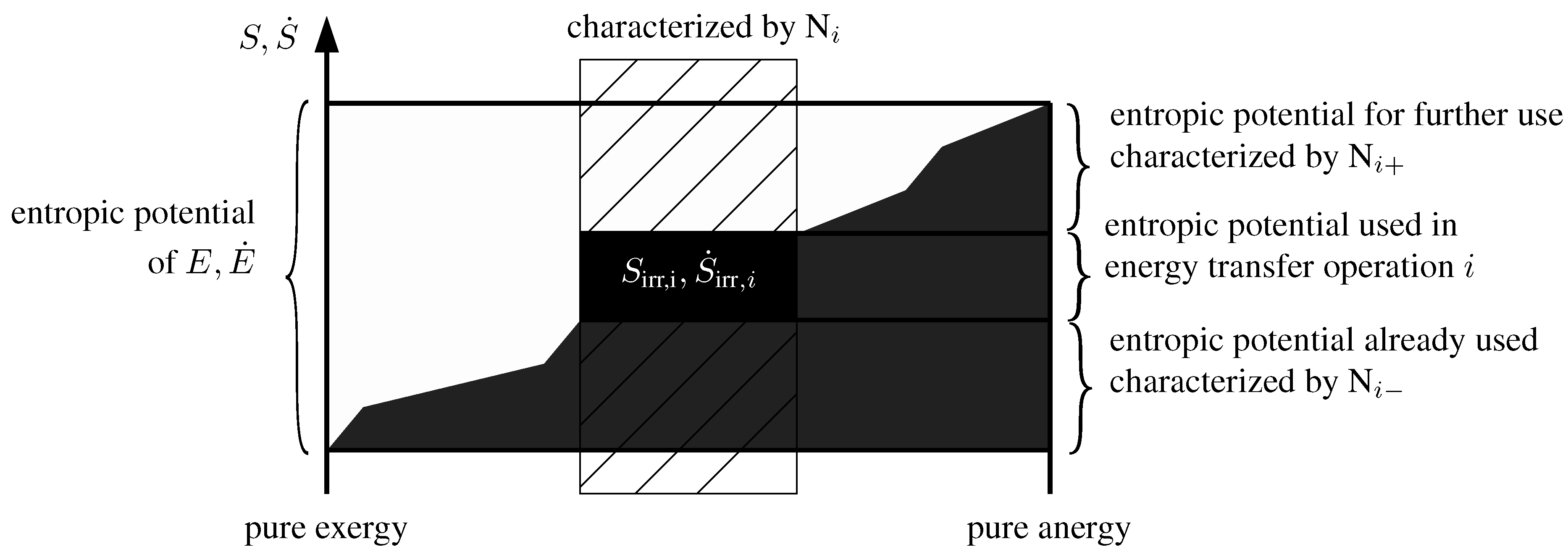
In [65], we introduced the entropic potential of an energy, E, as ${\dot{S}}_{\infty }=E/T_0$, with $T_0$ being the ambient temperature. Figure 17 shows how a certain energy transfer operation, i (in a component), is part of the devaluation chain with respect to E. In Figure 18, the entropic potential of E is shown together with how a certain process, i, participates in it by its so-called energy devaluation number:

$${\text{N}}_i=\frac{{\dot{S}}_{\text{irr},i}}{{\dot{S}}_{\infty }}$$

(43)

This number is always between zero and one with both limits as:

• ${\text{N}}_i=0$: reversible energy transfer operation;
• ${\text{N}}_i=1$: energy transfer operation that completely devaluates the energy (rate).

When the overall devaluation of the energy, E or $\dot{E}$, prior to the energy transfer operation under consideration, is given by the energy devaluation number, ${\text{N}}_{i-}$, and that after by ${\text{N}}_{i+}$, the overall devaluation corresponds to:

$${\text{N}}_{i-}+{\text{N}}_i+{\text{N}}_{i+}=1$$

(44)

Figure 17. Energy devaluation by consecutive energy transfer operations illustrated by the decrease of exergy during the energy transfer operations. Progress in time for finite energies (progress in process steps for finite energy rates).

Figure 17. Energy devaluation by consecutive energy transfer operations illustrated by the decrease of exergy during the energy transfer operations. Progress in time for finite energies (progress in process steps for finite energy rates).

8. The Second Law Analysis Based on DNS Results for Turbulent Flows

A further step to get closer to the physics of losses in a flow field is a DNS-analysis (direct numerical simulation) when the flow is turbulent. Since, then, the computational demands are extremely high (CPU times of several weeks on high performance computers and with highly parallelized CFD codes), such studies will be performed only for fundamental investigations that may get the character of benchmark solutions. These kind of solutions are important tools for the development and/or improvement of turbulence models.

Figure 18. The entropic potential and its use on the way the energy becomes part of the internal energy of the environment; here, the contribution of an energy transfer operation, i.

Figure 18. The entropic potential and its use on the way the energy becomes part of the internal energy of the environment; here, the contribution of an energy transfer operation, i.

For example, the important aspect of how turbulence is affected by wall roughness is studied with an DNS-SLA approach in [66] and [67]. In both studies, wall roughness on one wall of a plane channel results from a regular arrangement of certain bars on the otherwise smooth wall with geometrical details given in Figure 19 and Table 3.

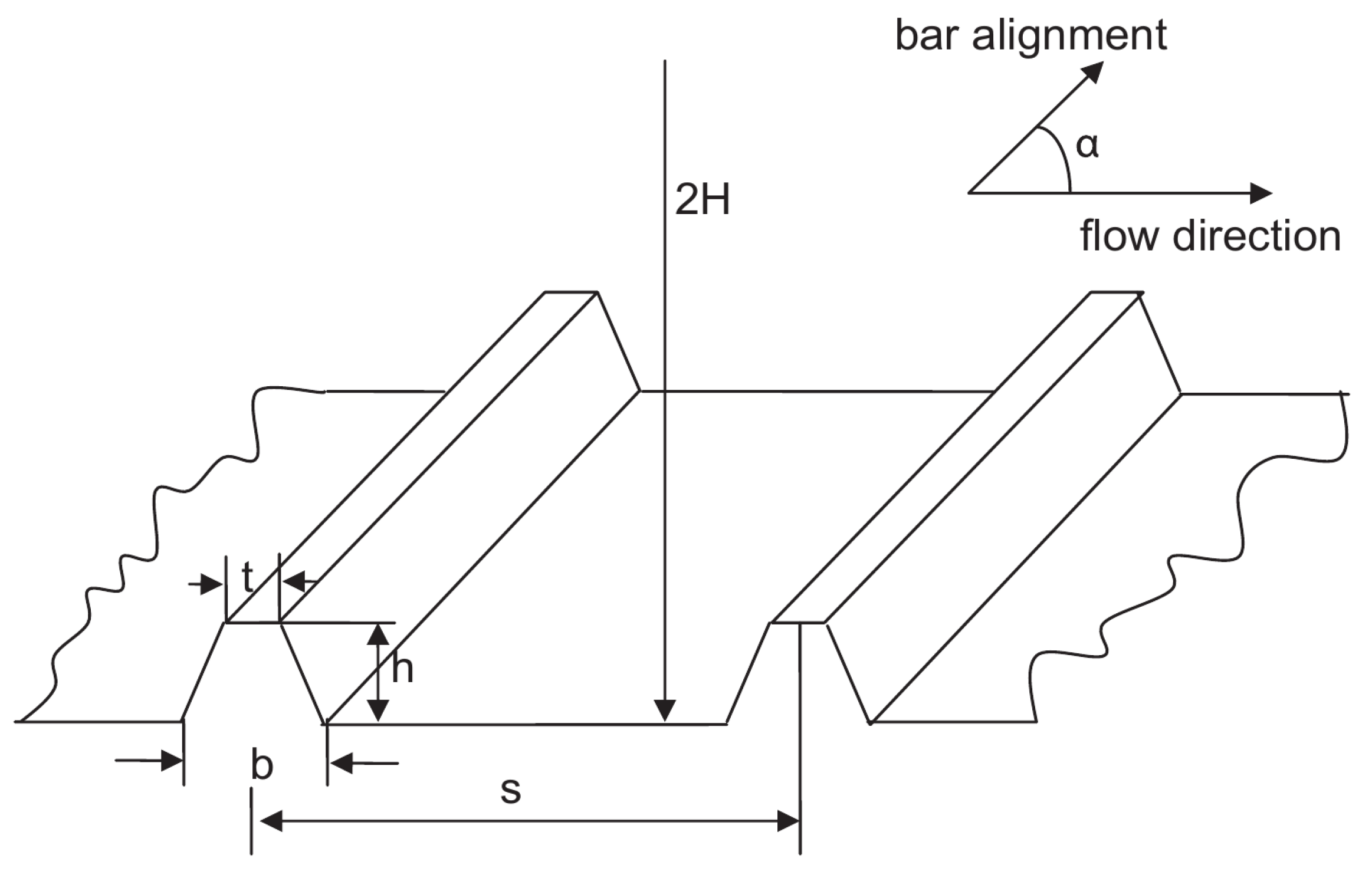
Figure 19. Geometrical arrangement of general regular wall roughness. H: Half channel height; h: Height of the roughness elements; b: Bottom width of the roughness elements; t: Top width of the roughness elements; s: Spacing of the roughness elements; α: Inclination angel with respect to the flow direction.

Figure 19. Geometrical arrangement of general regular wall roughness. H: Half channel height; h: Height of the roughness elements; b: Bottom width of the roughness elements; t: Top width of the roughness elements; s: Spacing of the roughness elements; α: Inclination angel with respect to the flow direction.

Table 3. Wall roughness test cases in [66] and [67].

Test Case	$h/H$	$h/s$	$h/b$	$t/b$	α		Ref.
SW	-	-	-	-	-	smooth wall	[66]
R	$0.034$	$0.14$	1	1	90 degrees
						obstacles
B1	$0.01$	$0.2$	10	1	0 degrees		[67]
B2	0.02	$0.4$	20	1	0 degrees
B3	0.03	$0.6$	30	1	0 degrees
B4	0.04	$0.8$	40	1	0 degrees
B5	0.05	$0.4$	20	1	0 degrees
						blades
W1	$0.02$	$0.4$	$0.866$	0	0 degrees
W2	0.02	$0.4$	$1.866$	0	0 degrees
					wedges

Table 3. Wall roughness test cases in [66] and [67].

Test Case	$h/H$	$h/s$	$h/b$	$t/b$	α		Ref.
SW	-	-	-	-	-	smooth wall	[66]
R	$0.034$	$0.14$	1	1	90 degrees
						obstacles
B1	$0.01$	$0.2$	10	1	0 degrees		[67]
B2	0.02	$0.4$	20	1	0 degrees
B3	0.03	$0.6$	30	1	0 degrees
B4	0.04	$0.8$	40	1	0 degrees
B5	0.05	$0.4$	20	1	0 degrees
						blades
W1	$0.02$	$0.4$	$0.866$	0	0 degrees
W2	0.02	$0.4$	$1.866$	0	0 degrees
					wedges

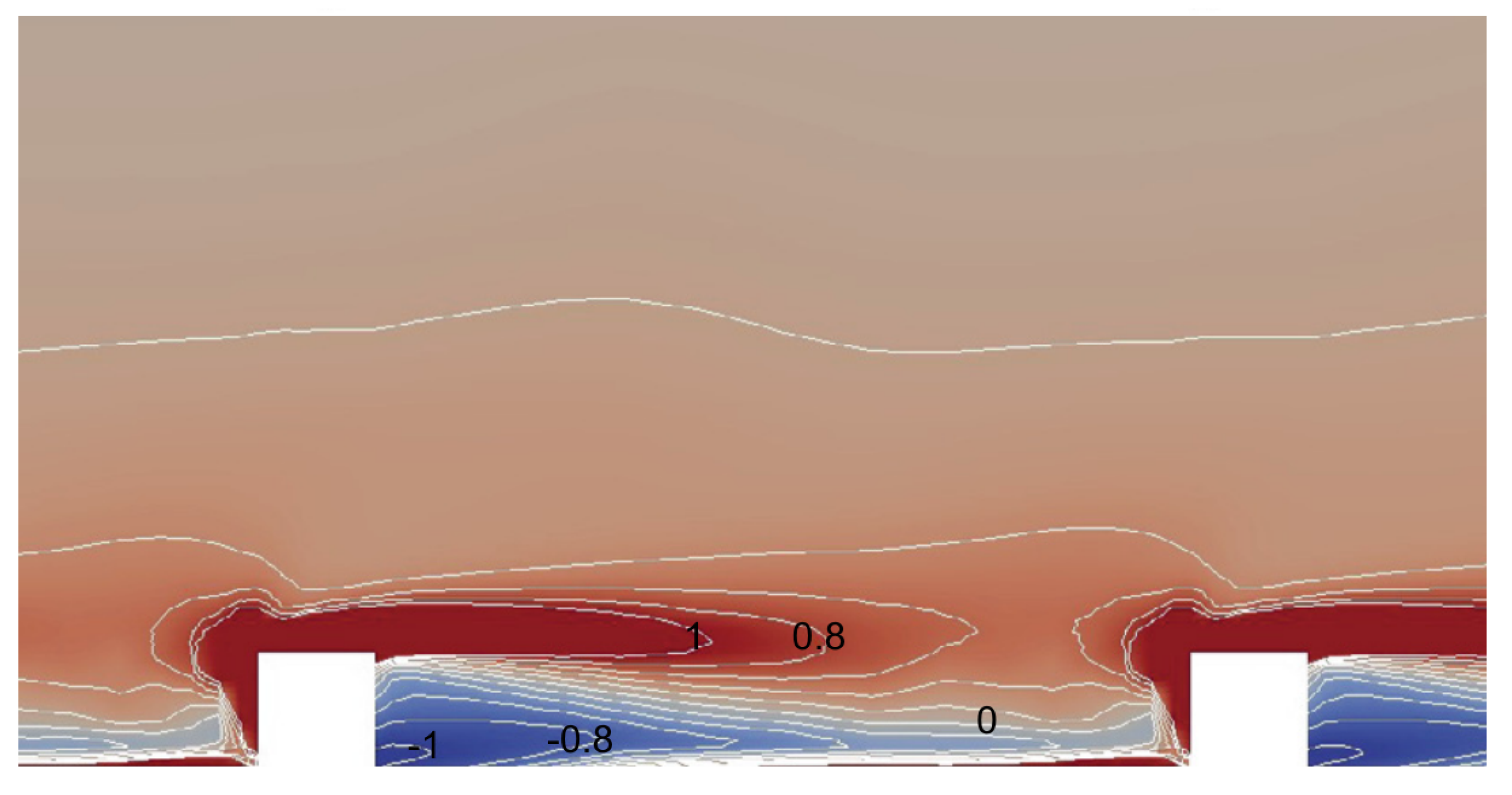
When the bars are perpendicular to the main flow direction, they act like densely arranged obstacles on the wall and increase the entropy generation and, thus, the losses in the flow field. This can be seen in Figure 20, where the actual entropy generation minus that for the corresponding smooth wall is shown as an example taken from [66].

Figure 20. Conventionally rough wall: local change of entropy generation rate minus this quantity for a smooth wall (Re = 5,600); further details in [66].

Figure 20. Conventionally rough wall: local change of entropy generation rate minus this quantity for a smooth wall (Re = 5,600); further details in [66].

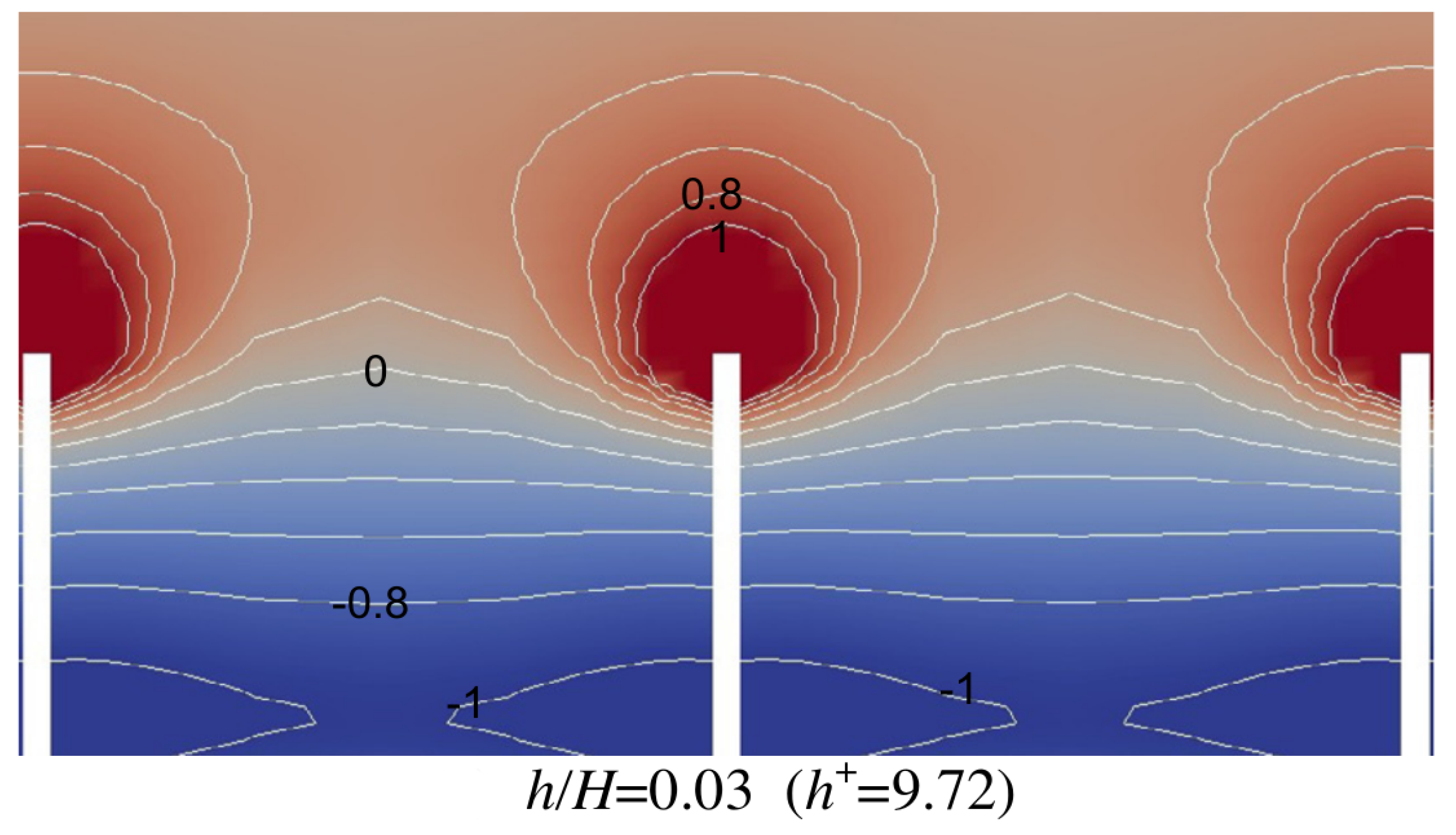
When the bars are in line with the main flow direction, however, a very different situation occurs. Then, the losses in the flow field can be reduced compared to the corresponding smooth wall case. This kind of wall roughness is called shark skin type roughness. In [67], its physical mechanism is analyzed based on DNS results. It is called the lift off and alignment (LOA) mechanism, which acts on the turbulent structures near the wall. Figure 21, which again shows the difference, now, between the entropy generation over the shark skin textured wall and the smooth wall, may give an impression of this mechanism; for further details, see [67].

Figure 21. Shark skin-textured walls: Local change of entropy generation rates minus this quantity for a smooth wall (Re = 5,600); further details in [67].

Figure 21. Shark skin-textured walls: Local change of entropy generation rates minus this quantity for a smooth wall (Re = 5,600); further details in [67].

9. Conclusions

We suggest to take a chance and use all the information available when a detailed numerical solution of a flow is known. In a post-processing step, the entropy generation in the flow (and also the temperature) field can be determined locally and, subsequently, integrated in order to determine the overall value of the entropy generation.

This entropy generation is the key quantity with respect to losses in a flow field. These losses can be identified as losses of exergy corresponding to a devaluation of the energy involved in a transfer process.

Combining thermo-dynamical and fluid mechanical considerations is the paradigm shift mentioned in the headline of this paper.