Finite-Time Chaos Suppression of Permanent Magnet Synchronous Motor Systems
Abstract
: This paper considers the problem of the chaos suppression for the Permanent Magnet Synchronous Motor (PMSM) system via the finite-time control. Based on Lyapunov stability theory and the finite-time controller are developed such that the chaos behaviors of PMSM system can be suppressed. The effectiveness and accuracy of the proposed methods are shown in numerical simulations.1. Introduction
The PMSM system had been appealing to more and more industry engineers for many AC motor applications. Recently, there have been many researches presenting numerous kinds of control methods for PMSM systems [1–3]. The permanent magnet synchronous motor (PMSM) plays an important role in industrial applications due to its simple structure, high power density, low maintenance cost, and high efficiency [4–7]. In these two decades, the dynamic characteristics and stability analysis of PMSM had emerged as a new and attractive research field, such as bifurcation, chaos, and limit cycle dynamic behaviors [8–13], etc. Among chaos phenomenon which is a deterministic nonlinear dynamical system that has been generally developed over the past two decades, in fields such as engineering science, medical science, biological engineering, and secure communication. Chaotic systems are very complex, dynamic nonlinear systems and their response possesses intrinsic characteristics such as broadband noise-like waveforms, prediction difficulty, and sensitivity to initial condition variations, etc. Moreover, many profound theories and methodologies [14–18] have been developed to deal with this issue. For the chaos suppression of permanent magnet synchronous motor systems, some kinds of control design and determination of stability have been conferred [19–28]. Some control methods had been studied to stabilize PMSM systems, such as optimal Lyapunov exponents placement [19], passive control [20], fuzzy control [21–23], impulsive control [24,25], sensorless control [26,27], and the cascade adaptive approach [28]. Therefore, chaos suppression aimed at eliminating the undesired chaotic behavior has become an important issue in the field of nonlinear control. From the viewpoint of control theory, chaos suppression can be considered as a stability problem. Recently, secure communication has received a lot attention with regards to the internet and personal information. An increasing number of studies have addressed secure communication via the chaos theory. In past research reports, chaos systems have been an attractive topic for their potential applications in secure communication [29–32]. In recent years, digital chaos signals have been extensively used in commercial applications, such as multimedia systems, mobile and wireless communications [33–35]. In [36], by using XOR logic operation, a chaotic watermark was obtained between the binary watermark and the binary chaotic image, and then the chaotic watermark was embedded into an order less image of each block of the least significant bit.
On the other hand, based on its unique powerful advantages, a particular property of asymptotic stability, finite-time stability has received a lot attention recently. It is surely more useful for some problems or applications to obtain the finite-time stable element than convergence within infinity time. Moreover, the finite-time control techniques have demonstrated better robustness and disturbance rejection properties. Based on proposed fractional controllers, the finite-time stability and the settling time can be guaranteed and computed [37–49]. However, few studies have focused on the finite-time suppression chaos of permanent magnet synchronous motor (PMSM) systems.
Motivated by the above discussion, this paper aims to achieve the finite-time chaos suppression for the permanent magnet synchronous motor (PMSM) system by the proposed controllers. Based on finite-time stability theory, the chaos suppression of PMSM is analyzed. Finally, an example is given to illustrate the usefulness of the obtained results.
2. Preliminaries
In order to derive the main results, the following definition and lemma are needed:
Definition [46]
Consider the nonlinear dynamical system modeled by:
where the system state variable x ∈ Rn. If there exists a constant T > 0 (may depend on the initial system state x(0)), such that:
and || x(t) ||≡ 0, if t ≥ T, then system ẋ=g(x) is finite-time stable.
Lemma [44]
Assume that a continuous, positive-definite function V(t) satisfies the following differential inequality:
where ρ > 0 and 0 < λ < 1 are two constants. Then, for any given t0, V(t) satisfies the following inequality:
V(t) ≡ 0, ∀t ≥ tr, with tr given by:
3. Problem Formulation and Main Results
Based on d-q axis, the dynamic model of a permanent synchronous motor with a smooth air gap can be described by the following differential equation [8]:
where id, iq, and w are state variables, which denote d, q axis stator currents, w is the motor angular speed, respectively. T̃L, ũd, and ũq are the external load torque, the direct- and quadrature axis stator voltage components of the motor, respectively. γ and σ are system operating parameters. In this paper, we only consider the case that the system is unforced. This case can be thought of as that, after an operating period of the system, the external inputs are set to zero, namely, T̃L = ũd = ũq = 0. Then, the system (6) becomes:
or:
where x1 = id, x2 = iq, x3 = w.
This paper aims at proposing a controller to suppression chaotic oscillation for PMAM in finite time, we add the single control u(t) to system (8) and then the controlled PMSM system can be expressed by:
To achieve this aim, we propose the main results based on the finite-time stability theory (Definition). According to the Lyapunov stability theorem and the Lemma, if there is a feedback controller such that V ≤ −ρVλ(t) where is the defined Lyapunov function and ρ > 0 and 0 < λ < 1 are two real constants, the system’s state variables converging to zero reaching in finite-time can be obtained. Therefore, the proposed controller u(t) is designed as:
where ρ is gain which is positive constant.
Theorem 1
Based on the proposed designed controller in Equation (10), the system’s state variables in (9) will converge to zero in finite-time and the finite-time suppression chaotic oscillation for PMAM can be achieved.
Proof
Define the Lyapunov function:
where V(t) is a legitimate Lyapunov function candidate, the time derivatives of V(t), along the trajectories of system (9) with (10) satisfy:
By substituting the feedback controller (10), one can obtain:
From the above equation, we can obtain:
and:
It implies:
Therefore, we can get:
From the Definition and Lemma, x1(t), x2(t) and x3(t) can converge to zero in finite-time. The finite-time suppression chaotic oscillation for PMAM is guaranteed, completing the proof.
Remark
In order to avoid chattering, sgn(x(t)) is replaced by in the simulation, where υ is an appropriate minimal value.
4. Numerical Simulation and Analysis
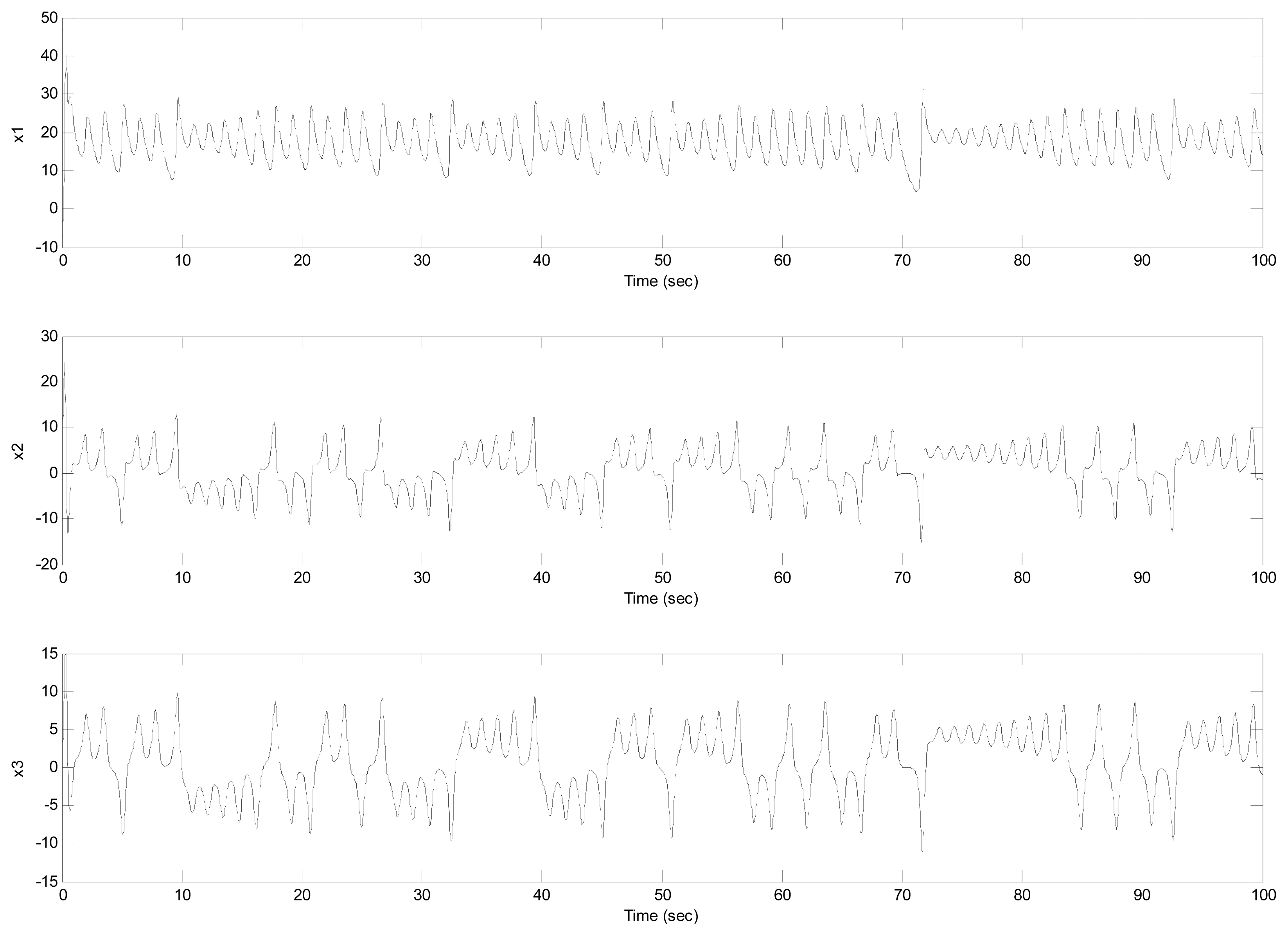
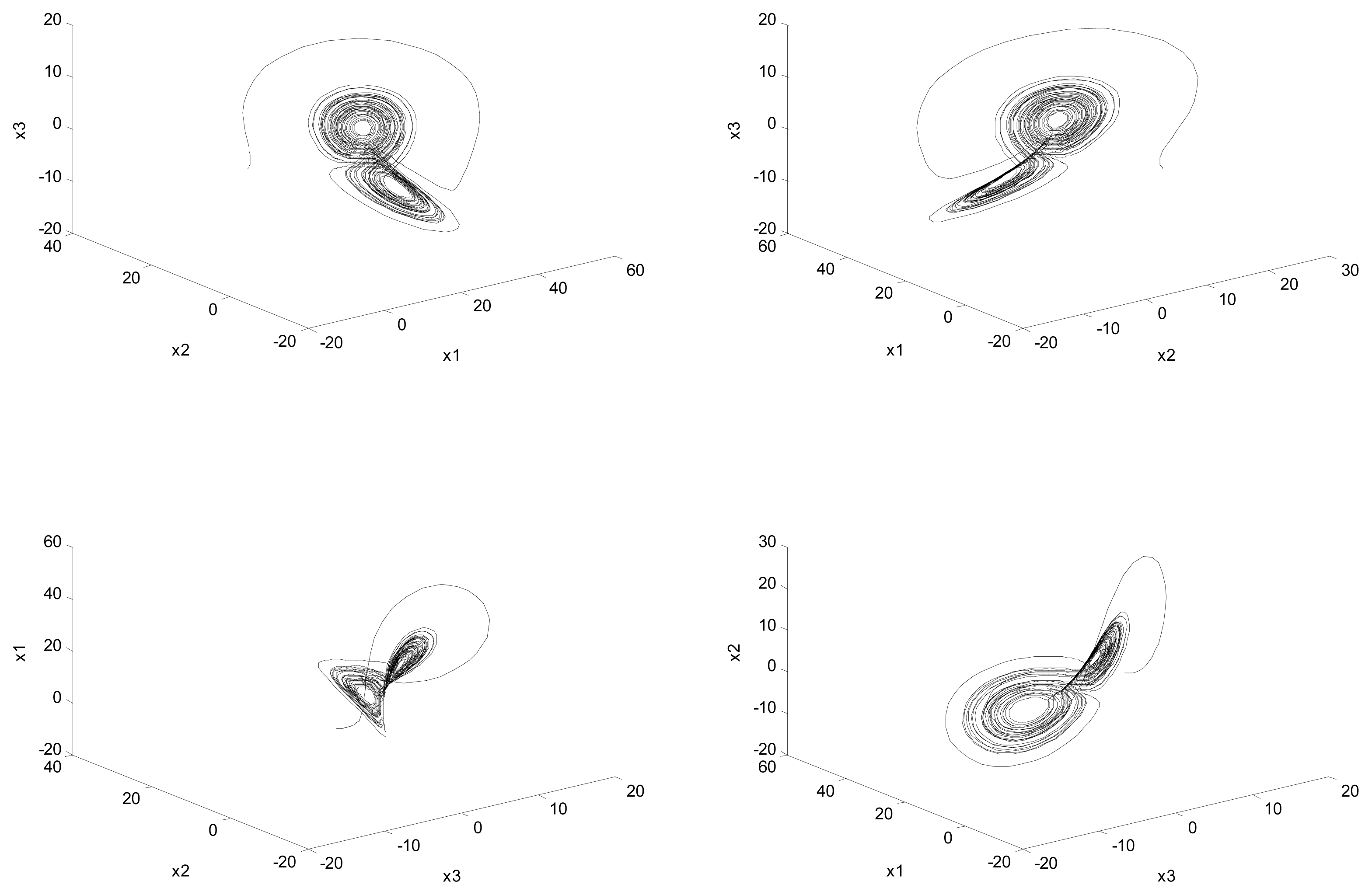
In this section, a numerical example is presented to demonstrate and verify the performance of the proposed results. Finite-time chaos suppression on PMSM via the finite-time stability theory will be conducted. Typical chaotic attractors behavior of PMSM is shown in Figures 1 and 2 with parameters given by γ = 20, σ = 5.46 [8].
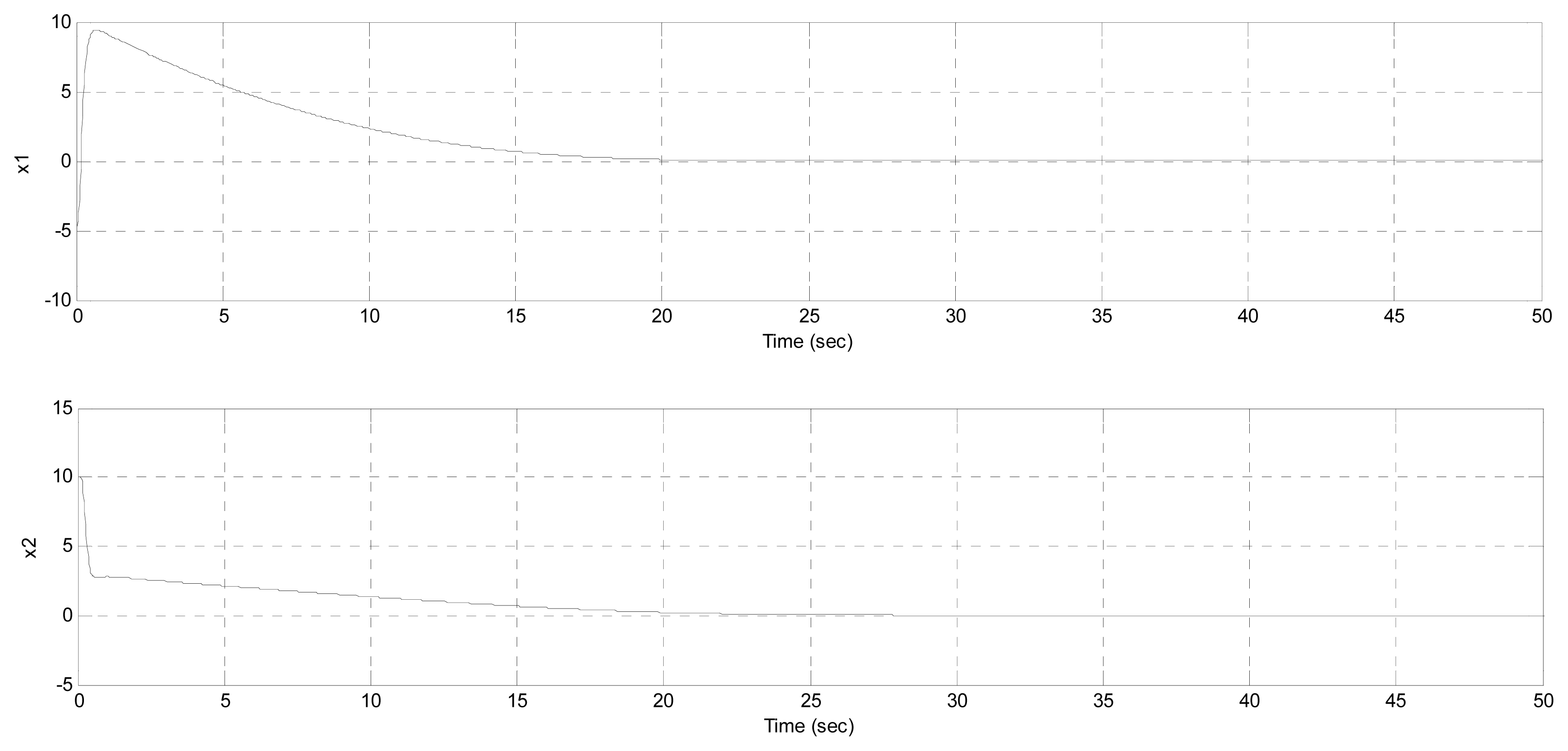
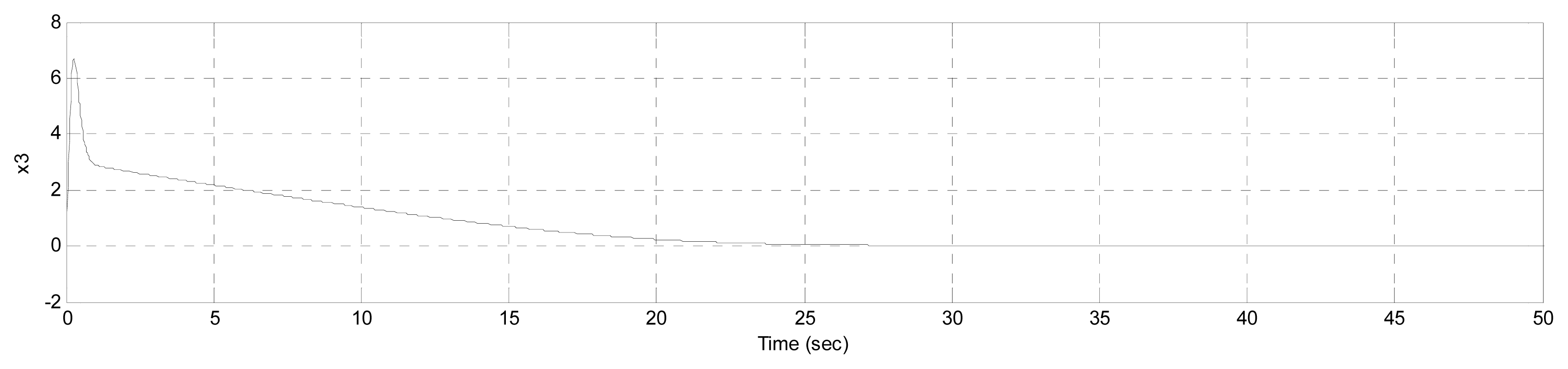
The simulation was done with a four order Runge-Kutta integration algorithm in Matlab 7 with the control parameters are set as ρ = 0.2 and λ = 0.7; the initial conditions x(0) = [−5 10 −1]T. The system state responses trajectory of the controller design shown in Figure 3 depicts the time responses of the control input of u(t).
It is seen clearly that the PMSM state reaches the desired goal in finite-time chaos suppression. From the simulation results, the effectiveness of the proposed method and the designed controller is shown.
5. Conclusions
In conclusion, the finite-time control of chaos suppression for PMSM systems was presented. Based on finite-time stability theory, the proposed control law is very effective according to the theoretical method and simulation results. The proposed controller is simple and easy to implement. This study should prove helpful to maintain industrial servo driven systems’ secure operation and applies chaos control methods to the plant. Numerical simulation displayed the feasibility and usefulness of the central discussion.
Acknowledgments
The author thanks the Ministry of Science and Technology, Taiwan for supporting this work under Grant NSC 102-2622-E-269-003-CC3 and NSC 102-2221-E-269-021. The author also wishes to thank the anonymous reviewers for providing constructive suggestions.
Conflicts of Interest
The author declares no conflict of interest.
References
- Krishnan, R. Electric Motor Drives, Modeling, Analysis, and Control; Prentice Hall, Inc: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Luo, Y.; Chen, Y.Q.; Pi, Y.G. Cogging effect minimization in PMSM position servo system using dual high-order periodic adaptive learning compensation. ISA Trans 2010, 49, 479–488. [Google Scholar]
- Accetta, A.; Cirrincione, M.; Pucci, M. TLS EXIN based neural sensorless control of a high dynamic PMSM. Control Eng. Practice 2012, 20, 725–732. [Google Scholar]
- Babak, N.M.; Farid, M.T.; Sargos, F.M. Mechanical Sensorless Control of PMSM with Online Estimation of Stator Resistance. IEEE Trans. Ind. Appl 2004, 40, 457–471. [Google Scholar]
- Bolognani, S.; Zigliotto, M.; Zordan, M. Extended-Range PMSM Sensorless Speed Drive Based on Stochastic Filtering. IEEE Trans. Power Electron 2001, 16, 110–117. [Google Scholar]
- Xu, Z.; Faz Rahma, M. Direct torque and flux regulation of an ipm synchronous motor drive using variable structure control approach. IEEE Trans. Power Electron 2007, 22, 2487–2498. [Google Scholar]
- Rossi, C.; Tonielli, A. Robust control of permanent magnet motors: Vss techniques lead to simple hardware implementations. IEEE Trans. Ind. Electron 1994, 41, 451–460. [Google Scholar]
- Li, Z.; Park, J.B.; Joo, Y.H.; Zhang, B.; Chen, G.R. Bifurcation and chaos in a permanent magnet synchronous motor. IEEE Trans. Circuits Syst. I, Fundam. Theory 2002, 49, 383–387. [Google Scholar]
- Wei, D.Q.; Luo, X.S.; Wang, B.H.; Fang, J.Q. Robust adaptive dynamic surface control of chaos in permanent magnet. Phys. Lett. A 2007, 363, 71–77. [Google Scholar]
- Wei, D.; Luo, X.; Fang, J.; Wang, B. Controlling chaos in permanent magnet synchronous motor based on the differential geometry methods. Acta Phys. Sin 2006, 55, 54–59. [Google Scholar]
- Luo, Y. Current rate feedback control of chaos in permanent magnet synchronous motor. Proc. CSU-EPSA 2006, 18, 31–34. [Google Scholar]
- Ren, H.; Liu, D. Nonlinear feedback control of chaos in permanent magnet synchronous motor. IEEE Trans. Circuits Syst. II, Exp. Briefs 2006, 53, 45–50. [Google Scholar]
- Li, J.; Ren, H. Partial decoupling control of chaos in permanent magnet synchronous motor. IET Contr. Theory Appl 2005, 22, 637–640. [Google Scholar]
- Salarieh, H.; Alasty, A. Adaptive synchronization of two chaotic systems with stochastic unknown parameters. Commun. Nonlinear Sci. Numer. Simul 2009, 14, 508–519. [Google Scholar]
- Liu, C.; Li, C.; Li, C. Quasi-synchronization of delayed chaotic systems with parameters mismatch and stochastic perturbation. Commun. Nonlinear Sci. Numer. Simul 2011, 16, 4108–4119. [Google Scholar]
- Hu, A.; Xu, Z. Stochastic linear generalized synchronization of chaotic systems via robust control. Phys. Lett. A 2008, 372, 3814–3818. [Google Scholar]
- Sun, Y.; Cao, J.; Wang, Z. Exponential synchronization of stochastic perturbed chaotic delayed neural networks. Neurocomputing 2007, 70, 2477–2485. [Google Scholar]
- Tang, Y.; Qiu, R.; Fang, J.A.; Miao, Q.; Xia, M. Adaptive lag synchronization in unknown stochastic chaotic neural networks with discrete and distributed time-varying delays. Phys. Lett. A 2008, 372, 4425–4433. [Google Scholar]
- Ataei, M.; Kiyoumarsi, A.; Ghorbani, B. Control of chaos in permanent magnet synchronous motor by using optimal Lyapunov exponents placement. Physics Letters A 2010, 374, 4226–4230. [Google Scholar]
- Qi, D.L.; Wang, J.J.; Zhao, G.Z. Passive control of permanent magnet synchronous motor chaotic systems. J. Zhejiang Univ. Sci. A 2005, 6, 728–732. [Google Scholar]
- Elmas, C.; Ustun, O.; Sayan, H. A neuro-fuzzy controller for speed control of a permanent magnet synchronous motor drive. Expert Syst. Appl 2008, 34, 657–664. [Google Scholar]
- Yu, J.; Chen, B.; Yu, H.S.; Gao, J.W. Adaptive fuzzy tracking control for the chaotic permanent magnet synchronous motor drive system via backstepping. Nonlinear Anal.-Real World Appl 2011, 12, 671–681. [Google Scholar]
- Kuo, C.; Hsu, C.; Tsai, C. Control of permanent magnet synchronous motor with a fuzzy slide-mode controller. Int. J. Adv. Manuf. Technol 2007, 32, 757–763. [Google Scholar]
- Wei, Q.; Wang, X.Y.; Hu, X.P. Impulsive control in permanent magnet synchronous motor. Sci. Res. Essays 2013, 8, 670–675. [Google Scholar]
- Li, D.; Wang, S.L.; Zhang, X.H.; Yang, D. Impulsive control for permanent magnet synchronous motors with uncertainties: LMI approach. Chin. Phys. B 2010, 19, 010506. [Google Scholar]
- Seok, J.K.; Lee, J.K.; Lee, D.C. Sensorless speed control of nonsalient permanent-magnet synchronous motors using rotor-position-tracking PI controller. IEEE Trans. Ind. Appl 2006, 53, 399–405. [Google Scholar]
- Wallmark, O.; Harnefors, L. Sensorless control of salient PMSM drives in the transition region. IEEE Trans. Ind. Appl 2006, 53, 1179–1187. [Google Scholar]
- Wei, W.; Zou, M.; Jiang, T.Q.; Liu, Z.W. Control chaos in permanent magnet synchronous motors by cascade adaptive approach. Adv. Appl. Mech 2011, 96, 128–129. [Google Scholar]
- Huang, C.K.; Tsay, S.C.; Wu, Y.R. Implementation of chaotic secure communication systems based on OPA circuits. Chaos Solitons Fractals 2005, 23, 589–600. [Google Scholar]
- Li, Z.G.; Xu, D.L. A secure communication scheme using projective chaos synchronization. Chaos Solitons Fractals 2004, 22, 477–481. [Google Scholar]
- Liao, T.L.; Tsai, S.H. Adaptive synchronization of chaotic systems and its application to secure communications. Chaos Solitons Fractals 2000, 11, 1387–1396. [Google Scholar]
- Chen, H.C.; Chang, J.F.; Yan, J.J.; Liao, T.L. EP-based PID control design for chaotic synchronization with application in secure communication. Expert Syst. Appl 2008, 34, 341169–341177. [Google Scholar]
- Lau, F.C.M.; Tse, C.K. Chaos-Based Digital Communication Systems: Operating Principles, Analysis Methods and Performance Evaluation; Springer: Berlin, Germany, 2003. [Google Scholar]
- Sandhu, G.S.; Berber, S. Investigation on Operations of a Secure Communication System based on the Chaotic Phase Shift Keying Scheme. In Information Technology and Applications, Proceeding of the Third International Conference on Information Technology and Applications, Sydney, Australia, 4–7 July 2005; 2, pp. 584–587.
- Tam, W.M.; Lau, C.M.; Tse, C.K.; Lawrance, A.J. Exact Analytical Bit Error Rates for Multiple Access Chaos-Based Communication Systems. IEEE Trans. Circuits Syst. II, Exp. Briefs 2004, 51, 473–481. [Google Scholar]
- Chen, Y.L.; Yau, H.T.; Yang, G.J. A maximum entropy-based chaotic time-variant fragile watermarking scheme for image tampering detection. Entropy 2013, 15, 3170–3185. [Google Scholar]
- Moulay, E.; Perruquetti, W. Finite time stability and stabilization of a class of continuous systems. J. Math. Anal. Appl 2006, 323, 1430–1443. [Google Scholar]
- Amato, F.; Ariola, M.; Cosentino, C. Finite-time control of discrete-time linear systems: Analysis and design conditions. Automatica 2010, 46, 919–924. [Google Scholar]
- Yang, Y.; Li, J.; Chen, G. Finite-time stability and stabilization of nonlinear stochastic hybrid systems. J. Math. Anal. Appl 2009, 356, 338–345. [Google Scholar]
- Chen, W.; Jiao, L.C. Finite-time stability theorem of stochastic nonlinear systems. Automatica 2010, 46, 2105–2108. [Google Scholar]
- Jammazi, C. On a sufficient condition for finite-time partial stability and stabilization: applications. IMA J. Math. Control Inf 2010, 27, 29–56. [Google Scholar]
- Zhang, Y.; Liu, C.; Mu, X. Robust finite-time H∞ control of singular stochastic systems via static output feedback. Appl. Math. Comput 2012, 218, 5629–5640. [Google Scholar]
- Wan, Z.L.; Hou, Y.Y.; Liao, T.L.; Yan, J.J. Partial Finite-Time Synchronization of Switched Stochastic Chua’s Circuits via Sliding-Mode Control. Math. Probl. Eng 2011, 2011, 162490. [Google Scholar]
- Yin, J.; Khoo, S.; Man, Z.; Yu, X. Finite-time stability and instability of stochastic nonlinear systems. Automatica 2011, 47, 2671–2677. [Google Scholar]
- Zhou, J.; Xu, S.; Shen, H. Finite-time robust stochastic stability of uncertain stochastic delayed reaction–diffusion genetic regulatory networks. Neurocomputing 2011, 74, 2790–2796. [Google Scholar]
- Bhat, S.P.; Bernstein, D.S. Finite-Time Stability of Homogeneous Systems. Proceedings of the American Control Conference, IEEE, Albuquerque, NM, USA, 4–6 June, 1997.
- Aghababa, M.P.; Aghababa, H.P. Finite-time stabilization of uncertain non-autonomous chaotic gyroscopes with nonlinear inputs. Appl. Math. Mech 2012, 33, 155–164. [Google Scholar]
- Aghababa, M.P.; Aghababa, H.P. Chaos suppression of rotational machine systems via finite-time control method. Nonlinear Dyn 2012, 69, 1881–1888. [Google Scholar]
- Meng, Z.; Sun, C.; An, Y.; Cao, J.; Gao, P. Chaos Anti-Control of Permanent Magnet Synchronous Motor Based on Model Matching. Proceeding of International Conference on Electrical Machines and Systems, Seoul, Korea, 8–11 Octorber 2007; pp. 1748–1752.
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hou, Y.-Y. Finite-Time Chaos Suppression of Permanent Magnet Synchronous Motor Systems. Entropy 2014, 16, 2234-2243. https://doi.org/10.3390/e16042234
Hou Y-Y. Finite-Time Chaos Suppression of Permanent Magnet Synchronous Motor Systems. Entropy. 2014; 16(4):2234-2243. https://doi.org/10.3390/e16042234
Chicago/Turabian StyleHou, Yi-You. 2014. "Finite-Time Chaos Suppression of Permanent Magnet Synchronous Motor Systems" Entropy 16, no. 4: 2234-2243. https://doi.org/10.3390/e16042234
APA StyleHou, Y.-Y. (2014). Finite-Time Chaos Suppression of Permanent Magnet Synchronous Motor Systems. Entropy, 16(4), 2234-2243. https://doi.org/10.3390/e16042234



