Parameter Estimation for Spatio-Temporal Maximum Entropy Distributions: Application to Neural Spike Trains
Abstract
: We propose a numerical method to learn maximum entropy (MaxEnt) distributions with spatio-temporal constraints from experimental spike trains. This is an extension of two papers, [10] and [4], which proposed the estimation of parameters where only spatial constraints were taken into account. The extension we propose allows one to properly handle memory effects in spike statistics, for large-sized neural networks.1. Introduction
With the evolution of multi-electrode array (MEA) acquisition techniques, it is currently possible to simultaneously record the activity of a few hundred neurons up to a few thousand [1]. Stevenson et al. [2] reported that the number of recorded neurons doubles approximately every eight years. However, beyond the mere recording of an increasing number of neurons, there is a need to extract relevant information from data in order to understand the underlying dynamics of the studied network, how it responds to stimuli and how the spike train response encodes these stimuli. In the realm of spike train analysis, this means having efficient spike sorting techniques [3–6], but also efficient methods to analyze spike statistics. The second aspect requires using canonical statistical models, whose parameters have to be tuned (“learned”) from data.
The maximum entropy method (MaxEnt) offers a way of selecting canonical statistical models from first principles. Having its root in statistical physics, MaxEnt consists of fixing a set of constraints, determined as the empirical average of features measured from the spiking activity. Maximizing the statistical entropy given those constraints provides a unique probability, called a Gibbs distribution, which approaches, at best, data statistics in the following sense: among all probability distributions that match the constraints, this is the one that has the smallest Kullback-Leibler divergence with the data ([7]). Equivalently, it satisfies the constraints without adding additional assumption on the statistics [8].
Most studies have focused on properly describing the statistics of spatially-synchronized patterns of neuronal activity without considering time-dependent patterns and memory effects. In this setting, pairwise models [9,10] or extensions with triplets and quadruplets interactions [11–13] were claimed to correctly fit ≈ 90 to 99% of the information. However, considering now the capacity of these models to correctly reproduce spatio-temporal spike patterns, the performances drop-off dramatically, especially in the cortex [14,15] or in the retina [16].
Taking into account spatio-temporal patterns requires introducing memory in statistics, described as a Markov process. MaxEnt extends easily to this case (see Section 2.2 and the references therein for a short description) producing Gibbs distributions in the spatio-temporal domain. Moreover, rigorous mathematical methods are available to fit the parameters of the Gibbs distribution [16]. However, the main drawback of these methods is the huge computer memory they require, preventing their applications to large-scale neural networks. Considering a model with memory depth D (namely, the probability of a spike pattern at time t depends on the spike activity in the interval [t–D, t–1]), there are 2N(D+1) possible patterns. The method developed in [16] requires one to handle a matrix of size 2N(D+1) × 2N(D+1). Therefore, it becomes intractable for N(D + 1) > 20.
In this paper, we propose an alternative method to fit the parameters of a spatio-temporal Gibbs distribution with larger values of the product, N(D + 1). We have been able to go up to N(D + 1) (~ 120) on a small cluster (64 processors AMD Opteron(tm) 2, 300 MHz). The method is based on [17] and [18], who proposed the estimation of parameters in spatial Gibbs distributions. The extension in the spatio-temporal domain is not straightforward, as we show, but it carries over to the price of some modifications. Combined with parallel Monte Carlo computing developed in [19], this provides a numerical method, allowing one to handle Markovian spike statistics with spatio-temporal constraints.
The paper is organized as follow. In Section 2, we recall the theoretical background for spike trains with a Gibbs distribution. We discuss both the spatial and spatio-temporal case. In the next section, 3, we explain the method to fit the parameters of MaxEnt distributions. As we mathematically show, the convex criterion used by [17] still applies for spatio-temporal constraints. However, the method used by [18] to avoid recomputing the Gibbs distribution at each parameters change cannot be directly used and has to be adapted using a linear response scheme. In the last section, 4, we show benchmarks evaluating the performance of this method and discuss the computational obstacles that we encountered. We made tests with both synthetic and real data. Synthetic data were generated from known probability distributions using a Monte Carlo method. Real data correspond to spike trains obtained from retinal ganglion cells activity (courtesy of M.J. Berry and O. Marre). The method shows a satisfying performance in the case of synthetic data. Real data analysis is not systematic, but instead used as an illustration and comparison with the paper of Schneidman et al. 2006 ([9]). As we could see in the example, the performance on real data, although satisfying, is affected by the large number of parameters in the distribution, a consequence of the choice to work with canonical models (Ising, pairwise with memory). This effect is presumably not related to our method, but to a standard problem in statistics.
Some of our notations might not be usual to some readers. Therefore, we added a list of symbols at the end of the paper.
2. Gibbs Distributions in the Spatio-Temporal Domain
2.1. Spike Trains and Observables
2.1.1. Spike Trains
We consider the joint activity of N neurons, characterized by the emission of action potentials (“spikes”). We assume that there is a minimal time scale, δ, set to one without loss of generality, such that a neuron can at most fire a spike within a time window of size δ. This provides a time discretization labeled with an integer time, n. Each neuron activity is then characterized by a binary variable. We use the notation, ω, to differentiate our binary variables ∈ {0, 1} to the notation, σ or S, used for “spin” variables ∈ {−1, 1}. ωk(n) = 1 if neuron k fires at time n, and ωk(n) = 0, otherwise.
The state of the entire network in time bin n is thus described by a vector , called a spiking pattern. A spike block is a consecutive sequence of spike patterns, , representing the activity of the whole network between two instants, n1 and n2.
The time-range (or “range”) of a block, , is n2–n1+1, the number of time steps from n1 to n2. Here is an example of a spike block with N = 4 neurons and range R = 3:
A spike train or raster is a spike block, , from some initial time, zero, to some final time, T. To alleviate the notations, we simply write ω for a spike train. We note Ω, the set of spike trains.
2.1.2. Observables
An observable is a function,


Typically, an observable does not depend on the full raster, but only on a sub-block of it. The time-range (or “range”) of an observable is the minimal integer R > 0, such that, for any raster, ω, . The range of the observable is one; the range of ωk1(n1)ωk2 (n2) is n2 – n1 + 1. From now on, we restrict to observables of range R, fixed and finite. We set D = R – 1.
An observable is time-translation invariant if, for any time n > 0, we have
whenever
. The two examples above are time-translation invariant. The observable λ(n1)ωk1(n1)ωk2(n2), where λ is a real function of time, is not time-translation invariant. Basically, time-translation invariance means that

2.1.3. Monomials
Prominent examples of time-translation invariant observables with range R are products of the form:
where pu, u = 1. . . r are pairs of spike-time events (ku, nu), ku = 1. . . N being the neuron index and nu = 0. . . D being the time index. Such an observable, called monomial, takes therefore values in { 0, 1 } and is one, if and only if ωku(nu) = 1, u = 1. . . r (neuron k1 fires at time n1, . . .; neuron kr fires at time nr). A monomial is therefore a binary observable that represents the logic-AND operator applied to a prescribed set of neuron spike events.
We allow the extension of the definition (1) to the case where the set of pairs p1, . . . , pr is empty, and we set m∅︀ = 1. For a number, N, of neurons and a time range, R, there are, thus, 2N R such possible products. Any observable of range R can be represented as a linear combination of products (1). Monomials constitute therefore a canonical basis for observable representation. To alleviate notations, instead of labeling monomials by a list of pairs, as in (1), we shall label them by an integer index, l.
2.1.4. Potential
Another prominent example of an observable is the function called “energy” or potential in the realm of the MaxEnt. Any potential of range R can be written as a linear combination of the 2N R possible monomials (1):
where some coefficients, λl, in the expansion may be zero. Therefore, by analogy with spin systems, monomials somewhat constitute spatio-temporal interactions between neurons: the monomial contributes to the total energy, λ(ω), of the raster, ω, if and only if neuron k1 fires at time n1, . . . , and neuron kr fires at time nr in the raster, ω. The number of pairs in a monomial (1) defines the degree of an interaction: Degree 1 corresponds to “self-interactions”, Degree 2 to pairwise, and so on. Typical examples of such potentials are the Ising model [9,10,20]:
where considered events are individual spikes and pairs of simultaneous spikes. Another example is the Ganmor–Schneidman–Segev (GSS) model [11,12]:
where, additionally to 3, simultaneous triplets of spikes are considered (we restrict the form (4) to a triplet, although Ganmor et al. were also considering quadruplets). In these two examples, the potential is a function of the spike pattern at a given time. Here, we choose this time equal to zero, without loss of generality, since we are considering time-translation invariant potentials. More generally, the form (2) affords the consideration of spatio-temporal neurons interactions: this allows us to introduce delays, memory and causality in spike statistics estimation. A simple example is a pairwise model with delays, such as:
where ‘PR’ stands for ‘pairwise with range R’, which takes into account the events where neuron i fires s time steps after a neuron, j, with s = 0. . . D.
2.2. The Maximum Entropy Principle
Assigning equal probabilities (uniform probability distribution) to possible outcomes goes back to Laplace and Bernoulli ([21]) (“principle of insufficient reason”). Maximizing the statistical entropy without constraints is equivalent to this principle. In general, however, one has some knowledge about data, typically characterized by the empirical average of the prescribed observables (e.g., for spike trains, firing rates, the probability that a fixed group of neurons fire at the same time, the probability that K neurons fire at the same time [22]); this constitutes a set of constraints. The maximum entropy principle (MaxEnt) is a method to obtain, from the observation of a statistical sample, a probability distribution that approaches, at best, the statistics of the sample, taking into account these constraints without additional assumptions [8]. Maximizing the statistical entropy given those constraints provides a distribution as far as possible from the uniform one and as close as possible to the empirical distribution. For instance, considering the empirical mean and variance of the sample of a random variable as constraints results in a Gaussian distribution.
Although some attempts have been made to extend MaxEnt to non-stationary data [23–26], it is mostly applied in the context of stationary statistics: the average of an observable does not depend explicitly on time. We shall work with this hypothesis. In its simplest form, the MaxEnt also assumes that the sample has no memory: the probability of an outcome at time t does not depend on the past. We first discuss the MaxEnt in this context in the next section, before considering the case of processes with memory in Section 2.2.2.
2.2.1. Spatial Constraints
In our case, the natural constraints are represented by the empirical probability of occurrence of characteristic spike events in the spike train or, equivalently, by the average of specific monomials. Classical examples of constraints are the probability that a neuron fires at a given time (firing rate) or the probability that two neurons fire at the same time. For a raster, ω, of length T, we note
, the empirical distribution, and
, the empirical average of the observable,

In this context, the MaxEnt problems is stated as follows. Find a probability distribution, μ, that maximizes the entropy:
(where the sum holds on the 2N possible spike patterns, ω(0)), given the constraints:
The average of monomials, predicted by the statistical model, μ (noted here as μ [ml ]), must be equal to the average, , measured in the sample. There is, additionally, the probability normalization constraint:
This provides a variational problem:
where is the set of (stationary) probabilities on spike trains. One searches, among all stationary probabilities ν ∈ , for the one which maximizes the right hand side of (9). There is a unique such probability, μ = μλ, provided N is finite and λl > – ∞. This probability depends on the parameters, λ.
Stated in this form, the MaxEnt is a Lagrange multipliers problem. The sought probability distribution is the classical Gibbs distribution:
where Zλ = ∑ω(0) eλ[ ω(0) ] is the partition function, whereas . Note that the time index (here, zero) does not play a role, since we have assumed μλ to be stationary (time-translation invariant).
The value of λls is fixed by the relation:
Additionally, note that the matrix is positive. This ensures the convexity of the problem and the uniqueness of the solution of the variational problem.
Note that we do not expect, in general, μλ to be equal to the (hidden) probability shaping the observed sample. It is only the closest one satisfying the constraints (7) [7]. The notion of closeness is related to the Kullback-Leibler divergence, defined in the next section.
It is easy to check that the Gibbs distribution (10) obeys:
for any spike block, . Indeed, the potential of the spike block, , is , whereas the partition function on spike blocks is . Equation (12) expresses that spiking patterns occurring at different times are independent under the Gibbs distribution (10). This is expected: since the constraints shaping μλ take only into account spiking events occurring at the same time, we have no information on the causality between spike generation or on memory effects. The Gibbs distributions obtained when constructing constraints only with spatial events leads to statistical models where spike patterns are renewed at each time step, without reference to the past activity.
2.2.2. Spatio-Temporal Constraints
On the opposite side, one expects that spike train generation involves causal interactions between neurons and memory effects. We would therefore like to construct Gibbs distributions taking into account information on the spatio-temporal interactions between neurons and leading to a statistical model, not assuming anymore that successive spikes patterns are independent. Although the notion of the Gibbs distribution extends to processes with infinite memory [27], we shall concentrate here on Gibbs distributions associated with Markov processes with finite memory depth D; that is, the probability of having a spike pattern, ω(n), at time n, given the past history of spikes reads . Note that those transition probabilities are assumed not to depend explicitly on time (stationarity assumption).
Such a family of transition probabilities, , defines a homogeneous Markov chain. Provided (this is a sufficient, but not a necessary condition. In the remainder of the paper, we shall work with this assumption) for all , there is a unique probability, μ, called the invariant probability of the Markov chain, such that:
In a Markov process, the probability of a block, , for n2 – n1 + 1 > D, is:
the Chapman–Kolmogorov relation [28]. To determine the probability of , one has to know the transition probabilities and the probability, . When attempting to construct a Gibbs distribution obeying (14) from a set of spatio-temporal constraints, one has therefore to determine simultaneously the family of transition probabilities and the invariant probability. Remark that setting:
we may write (14) in the form:
The probability of observing the spike pattern, , given the past of depth D has an exponential form, similar to (10). Actually, the invariant probability of a Markov chain is a Gibbs distribution in the following sense.
In view of (14), probabilities must be defined as whatever, even if n2 – n1 is arbitrarily large. In this setting, the right objects are probabilities on infinite rasters [28]. Then, the entropy rate (or Kolmogorov–Sinai entropy) of μ is:
where the sum holds over all possible blocks, . This reduces to (6) when μ obeys (12).
The MaxEnt takes now the following form. We consider a set of L spatio-temporal spike events (monomials), whose empirical average value, , has been computed. We only restrict to monomials with a range at most equal to R = D + 1, for some D > 0. This provide us a set of constraints of the form (7). To maximize the entropy rate (17) under the constraints (7), we construct a range-R potential . The generalized form of the MaxEnt states that there is a unique probability measure μλ ∈ , such that [29]:
This is the extension of the variational principle (9) to Markov chains. It selects, among all possible probability, ν, a unique probability, μλ, which realizes the supremum. μλ is called the Gibbs distribution with potential λ.
The quantity, ℘ [ λ ], is called topological pressure or free energy density. For a potential of the form (2) [30,31]:
This is the analog of (11), which allows one to tune the parameters, λl. Thus, ℘ [ λ ] plays the role of log Zλ in (10). Actually, it is equal to log Zλ when restricting to the memoryless case (In statistical physics, the free energy is −kT log Z. The minus sign comes from the minus sign in the Hamiltonian). ℘ [ λ ] is strictly convex thanks to the assumption , which guarantees the uniqueness of μλ.
Note that μλ has not the form (10) for D > 0. Indeed a probability distribution, e.g., of the form with:
the potential of the block , and:
the “n-time steps” partition function does not obey the Chapman–Kolmogorov relation (14).
However, the following holds [29,32–34].
There exist A, B > 0, such that, for any block, :
We have:
In the spatial case, Zn [ λ] = Zn [ λ ] and ℘ [ λ] = log Z [ λ ], whereas A = B = 1 in (22). Although (23) is defined by a limit, it is possible to compute ℘ [ λ ] as the log of the largest eigenvalue of a transition matrix constructed from λ (Perron–Frobenius matrix) [35]. Unfortunately, this method does not apply numerically as soon as NR > 20.
These relations are crucial for the developments made in the next section.
To recap, a Gibbs distribution in the sense of [18] is the invariant probability distribution of a Markov chain. The link between the potential λ and the transition probabilities
(respectively, the potential [15]) is given by:
, where


To finish this section, let us introduce the Kullback-Leibler divergence, dKL(ν, μ), which provides a notion of similarity between two probabilities, ν, μ. We have dKL(ν, μ) ≥ 0 with equality, if and only if μ = ν. The Kullback-Leibler divergence between an invariant probability ν ∈ and the Gibbs distribution, μλ, with potential λ is given by dKL ( ν, μλ) = ℘ [ λ ] – ν [λ ] –
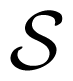
3. Inferring the Coefficients of a Potential from Data
Equation (11) or (19) provides an analytical way to compute the coefficients of the Gibbs distribution from data. However, they require the computation of the partition function or of the topological pressure, which becomes rapidly intractable as the number of neurons increases. Thus, researchers have attempted to find alternative methods to compute reliably and efficiently the λls. An efficient method has been introduced in [17] and applied to spike trains in [18]. Although these papers are restricted to Gibbs distributions of the form (10) (models without memory), we show in this section how their method can be extended to general Gibbs distributions.
3.1. Bounding the Kullback-Leibler Divergence Variation
3.1.1. The Spatial Case
The method developed in [17] by Dudik et al. is based on the so-called convex duality principle, used in mathematical optimization theory. Due to the difficulty in maximizing the entropy (which is a concave function), one looks for a convex function that easier to investigate. Dudik et al. showed that, for spatially constrained MaxEnt distributions, finding the Gibbs distribution amounts to finding the minimum of the negative log likelihood (we have adapted [17] to our notations. Moreover, in our case, corresponds to the empirical average on a raster, ω, whereas π in [17] corresponds to an average over independent samples):
Indeed, in the spatial case, the Kullback-Leibler divergence between the empirical measure, , and the Gibbs distribution at μλ is:
so that, from (24):
where we used .
Since ℘ is convex and linear in λ, is convex. Its unique minimum is given by (11).
Moreover, we have:
with Δλ = λ′ –λ. From (10):
and since P [λ] = log Z [λ] in the spatial case:
Therefore:
The idea proposed by Dudik et al. is then to bound this difference by an easier-to-compute convex quantity, with the same minimum as , and to reach this minimum by iterations on λ. They proposed a sequential and a parallel method. Let us summarize first the sequential method. The goal here is not to rewrite their paper [17], but to explain some crucial elements that are not directly appliable to the spatio-temporal case.
In the sequential case, one updates λ as λ′ = λ + δel, for some l, where el is the canonical basis vector in direction l, so that Δλ = δml, and:
Using the following property:
for x ∈ [0, 1], and since ml ∈ {0, 1}, we have:
This bound, proposed by Dudik et al., is remarkably clever. Indeed, it replaces the computation of the average μλ [eδml], which is computationally hard, by the computation of μλ [ml ], which is computationally easy. Finally,
In the parallel case, the computation and results differ. One now updates λ as . Moreover, one has to renormalize the mls in in order that Equation (34) below holds. We have, therefore, .
Thus,
Using the following property [36]:
for δl ∈ ℝ and , we have:
Since log(1 + x) ≤ x for x > −1, Dudick et al. obtain:
provided . (this constraint has to be checked during iterations). Finally, using the definition of .
To be complete, let us mention that Dudik et al. consider the case where some error, εl, is allowed in the estimation of the coefficient, λl. This relaxation on the parameters alleviates the overfitting.
In this case, the bound on the right-hand side in (33) (sequential case) becomes:
whereas the right-hand side in (35) becomes with:
The minimum of these functions is easy to find, and one obtains, for a given λ, the variation, δ, required to lower bound the log-likelihood variation. The authors have shown that both the sequential and parallel method produce a sequence, λ(k), which converges to the minimum of as k → +∞. Note, however, that one strong condition in their convergence theorem is εl > 0. This requires a sharp estimate of the error, εl, which cannot be solely based on the central limit theorem or on Hoeffding inequality in our case, because when the empirical average, , is too small, the minima of F, computed in [18], may not be defined.
3.1.2. Extension to the Spatio-Temporal Case
We now show how to extend these computations to the spatio-temporal case, provided one replaces the log-likelihood, , by the Kullback-Leibler divergence (24). The main obstacle is that the Gibbs distribution does not have the form, . We obtain, thus, a convex criterion to minimize Kullback-Leibler divergence variation, hence reaching the minimum, .
Replacing ν in Equation (24) by , the empirical measure, one has:
because the entropy, , cancels. This is the analog of (27). The main problem now is to compute ℘ [ λ′] – ℘[ λ ].
From (22), we have:
so that:
Since , from (23):
Therefore:
This is the extension of (29) to the spatio-temporal case. In the spatial case, it reduces to (29) from (12). This equation is obviously numerically intractable, but it has two advantages: on the one hand, it allows one to extend the bounds, (33) (sequential case) and (35) (parallel case), and on the other hand, it can be used to get a δ-power expansion of ℘ [ λ′]–℘ [ λ ]. This last point is used in Section 3.2.3.
To get the analog of (33) in the sequential case where , one may still apply (31) which holds, provided:
Therefore, compared to the spatial, we have to replace ml by in . We have, therefore:
From the time translation invariance of μλ, we have:
so that:
At first glance this bound is not really useful. Indeed, from (40), we obtain:
Since this holds for any δ, this implies ℘ [ λ′] = ℘ [ λ ]. The reason for this is evident. Renormalizing ml, as we did to match the condition imposed by the bound (31), is equivalent to renormalizing δ by . As n → +∞, this perturbation tends to zero and λ′ = λ. Therefore, the clever bound (31) would here be of no interest if we were seeking exact results. However, the goal here is to propose a numerical scheme, where, obviously, n is finite. We replace, therefore, the limit n → +∞ by a fixed n in the computation of ℘ [ λ′ ] – ℘[ λ ]. Keeping in mind that ml must also be renormalized in and using , the Kullback-Leibler divergence (38) obeys:
the analog of (33).
In the parallel case, similar remarks hold. In order to apply the bound (34), we have to renormalize the mls in . As for the spatial case, we also need to check that . (this constraint is not a guarantee and has to be checked during iterations). One obtains finally:
the analog of (35).
Compared with the spatial case, we see, therefore, that n must not be too large to have a reasonable Kullback-Leibler divergence variation. It must not be too small, however, to get a good approximation of the empirical averages.
3.2. Updating the Target Distribution when the Parameters Change
When updating the parameters, λ, one has to compute again the average values, μλ [ml ], since the probability, μλ, has changed. This has a huge computational cost. The exact computation (e.g., from (11, 19)) is not tractable for large N, so approximate methods have to be used, like Monte Carlo [19]. Again, this is also CPU time consuming, especially if one recomputes it again at each iteration, but at least it is tractable.
In this spirit, Broderick et al. [18] propose generating a Monte Carlo raster distributed according to μλ and to use it to compute μλ′ when || λ′ – λ || is sufficiently small. We explain their method, limited to the spatial case, in the next section, and we explain why it is not applicable in the spatio-temporal case. We then propose an alternative method.
3.2.1. The Spatial Case
The average of ml is obtained by the derivative of the topological pressure, ℘ [λ ]. In the spatial case, where ℘(λ) = log Zλ, we have:
Using (28), one finally obtains:
which is Equation (18) in [18]. Using this formula, one is able to compute the average of ml with respect to the new probability, μλ′, only using the old one, μλ.
3.2.2. Extension to the Spatio-Temporal Case
We now explain why the Broderick et al. method does not extend to the spatio-temporal case. The main problem is that if one tries to obtain the analog of the equality (45), one obtains, in fact, an inequality:
where A, B are the constants in (22). They are not known in general (they depend on the potential), and they are different. However, in the spatial case A = B = 1, whereas , because the potential has range one. Then, one recovers (45). Let us now explain how we obtain (46).
The averages of quantities are obtained by the derivative of the topological pressure (Equation (19)). We have:
Assuming that the limit and the derivative commute (see, e.g., [37]), gives:
From (22):
and:
Therefore:
3.2.3. Taylor Expansion of the Pressure
The idea is here to use a Taylor expansion of the topological pressure. This approach is very much in the spirit of [38], but extended here to the spatio-temporal case. Since λ′ = λ + δ, we have:
The second derivative of the pressure is given by [29,32–34]:
where:
is the correlation function between ml, mk at time n, computed with respect to μλ. (51) is a version of the fluctuation-dissipation theorem in the spatio-temporal case. σn is the time shift applied n times. The third derivatives can be computed, as well, by taking the derivative (51) and using (47). This generates terms with third order correlations, and so on [37]. Up to second order, we have:
Since the observable are monomials, they only take the values zero or one, and the computation of χjl is straightforward, reducing to counting the occurrence of time pairs, t, t + n, such that mj(t) = 1 and ml(t + n) = 1.
On practical grounds, we introduce a parameterΔ = ||λ′ − λ||, which measures the variation in the parameters after updating. If Δ is small enough (smaller than some Δc), the terms of order three in the Taylor expansion are negligible; then, we can use (53). Otherwise, if Δ is big, we compute a new Monte Carlo estimation of (as described in [19]). We explain in Section 4.2 how Δc was chosen in our data. Then, we use the following trick. If ||δ|| > Δc, we compute the new value μλ′ [mj]. If , we use the linear response approximation (53) of μλ′. Finally, if , we use μλ [ml] instead of μλ′ [ml] in the next iteration of the method. Thus, in the case, ||δ|| < Δc, we use the Gibbs distribution computed at some time step, say n, to infer the values at the next iteration. If we do that several successive time steps, the distance to the original value, λn, of the parameters increases. Therefore, we compute the norm ||λn − λn+k|| at each time step, k, and we do not compute a new raster until this norm is larger than Δc.
3.3. The Algorithms
We have two algorithms, sequential and parallel, which are very similar to Dudik et al. Especially, the convergence of their algorithms, proven in their paper, extends to our case, since it only depends on the shape of the cost functions (36, 37). We describe here the algorithms coming out from the presented mathematical framework, in a sequential and parallel version. We iterate the algorithms until the distance is smaller than some ηc. We use the Hellinger distance:
3.3.1. Sequential Algorithm
δ is the learning rate by which we change the value of a parameter, λl. η is the convergence criterion (54)). Δ is the parameter allowing us to decide whether we update the parameter change by computing a new Gibbs sample or by the Taylor expansion. Fl is given by Equation (36)
3.4. Parallel Algorithm
The implementation of those algorithms consists of an important part in software developed at INRIA (Institut National de Recherche en Informatique et en Automatique) and called EnaS (Event Neural Assembly Simulation). The executable is freely available at [39].
4. Results
In this section, we perform several tests on our method. We first consider synthetic data generated with a known Gibbs potential and recover its parameters. This step also allows us to tune the parameter, Δc, in the algorithms. Then, we consider real data analysis, where the Gibbs potential form is unknown. This last step is not a systematic study that would be out of the scope of this paper, but simply provided as an illustration and comparison with the paper of Schneidman et al. 2006 [9].
4.1. Synthetic Data
Synthetic data are obtained by generating a raster distributed according to a Gibbs distribution, whose potential (2) is known. We consider two families of Gibbs potentials. For each family, there are L > N monomials, whose range belongs to { 1, . . . , R }. Among them, there are N “rate monomials” ωi(D), i = 1. . . N, whose average gives the firing rate of neuron i, denoted ri; the L − N other monomials, with degree k > 1, are chosen at random with a probability law ~ e−k, which favors, therefore, pairwise interactions. The difference between the two families comes from the distribution of coefficients, λl.
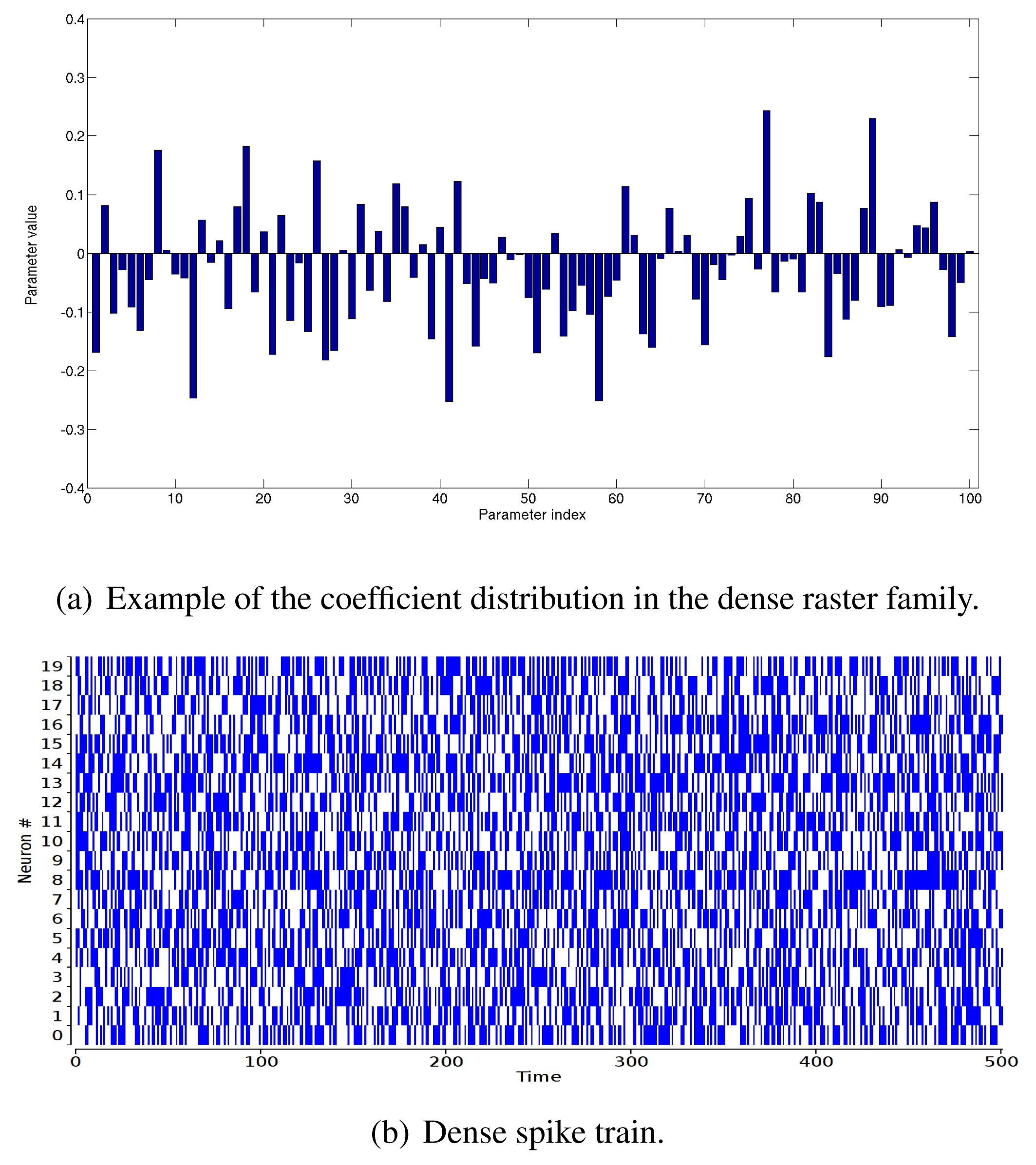
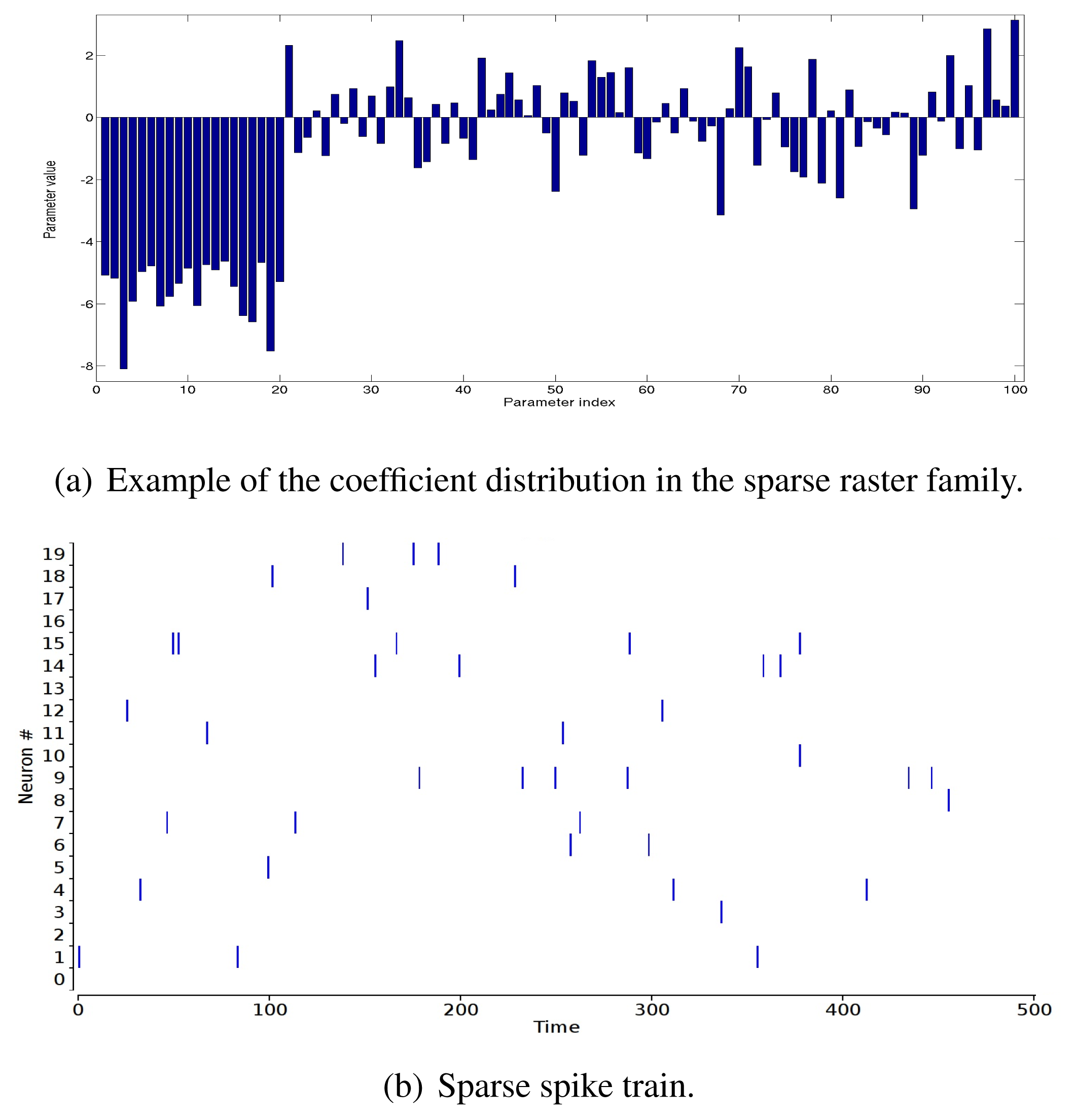
“Dense” raster family. The coefficients are drawn with a Gaussian distribution with mean zero and variance to ensure a correct scaling of the coefficients dispersion as L increases (Figure 1(a)). This produces typically a dense raster (Figure 1(b)) with strong multiple correlations.
“Sparse” raster family. The rate coefficients in the potential are very negative: the coefficient, hi, of the rate monomial, ωi(D), is , where ri ∈ [0 : 0.01] with a uniform probability distribution. Other coefficients are drawn with a Gaussian distribution with mean 0.8 and variance one (Figure 2(a)). This produces a sparse raster (Figure 2(b)) with strong multiple correlations.
4.2. Tuning Δc
For small N, R (NR ≤ 20), it is possible to exactly compute the topological pressure using the transfer matrix technique [16]. We have therefore a way to compare the Taylor expansion (51) and the exact value.
If we perturb λ by an amount, δ, in the direction, l, this induces a variation on μλ [ml], l = 1. . . L, given by the Taylor expansion (53). To the lowest order μλ′ [ml] = μλ [ml] + O(1), so that:
is a measure of the relative error when considering the lowest order expansion.
In the same way, to the second order:
so that:
is a measure of the relative error when considering the next order expansion.
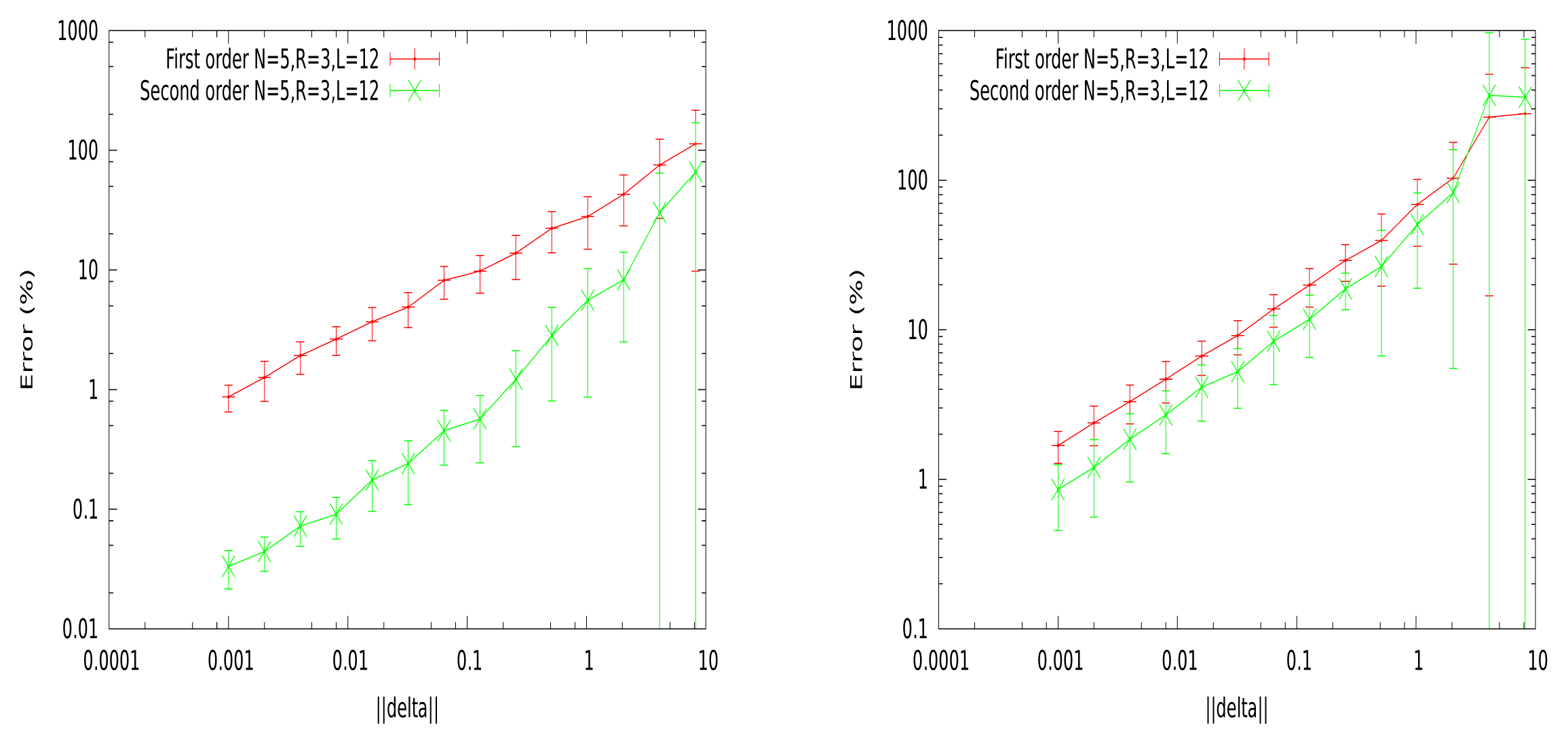
In Figure 3, we show the relative errors, ε (1), ε (2) (in percent), as a function of δ. For each point, we generate 25 potentials, with N = 5, R = 3, L = 12. For each of these potentials, we randomly perturb the λjs, with a random sign, so that the norm of the perturbation ||δ|| is fixed. The linear response, χ, is computed from a raster of length T = 100, 000.
These curves show a big difference between the dense and sparse case. In the dense case, the second order error is about 5% for Δc = 1, whereas we need a Δc ~ 0.03 to get the same 5% in the sparse case. We choose to align on the sparse case, and in typical experiments, we take Δc = 0.1, corresponding to about 10% of the error on the second order.
4.3. Computation of the Kullback-Leibler Divergence
To compute the Kullback-Leibler divergence between the empirical distribution, , and the fitted predicted distribution, μλ, we need to know the value of the pressure, ℘ [λ], the empirical probability of the potential, , and the entropy, . For small networks, we can compute the pressure using the Perron–Frobenius theorem ([16]). However, for large scales, since we cannot compute the pressure, computing the Kullback-Leibler divergence is not direct and exact. We compute an approximation using the following technique. From Equation (18) and (24), we can write:
From the parameters, λ, we compute a spike train distributed as μλ using the Monte Carlo method ([19]). From this spike train, we compute the monomials averages, μλ[ml], and the entropy,
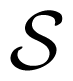
4.4. Performances on Synthetic Data
Here, we test the method on synthetic data, where the shape of the sought potential is known: only the λls have to be estimated. Experiments were designed according to the following steps:
We start from a potential . The goal is to estimate the coefficient values, , knowing the set, , of monomials spanning the potential.
We generate a synthetic spike train (ωs) distributed according to the Gibbs distribution of λ*.
We take a potential λ = ∑l∈ λlml with random initial coefficients λl. Then, we fit the parameters, λl, to the synthetic spike train, .
We evaluate the goodness of fit.
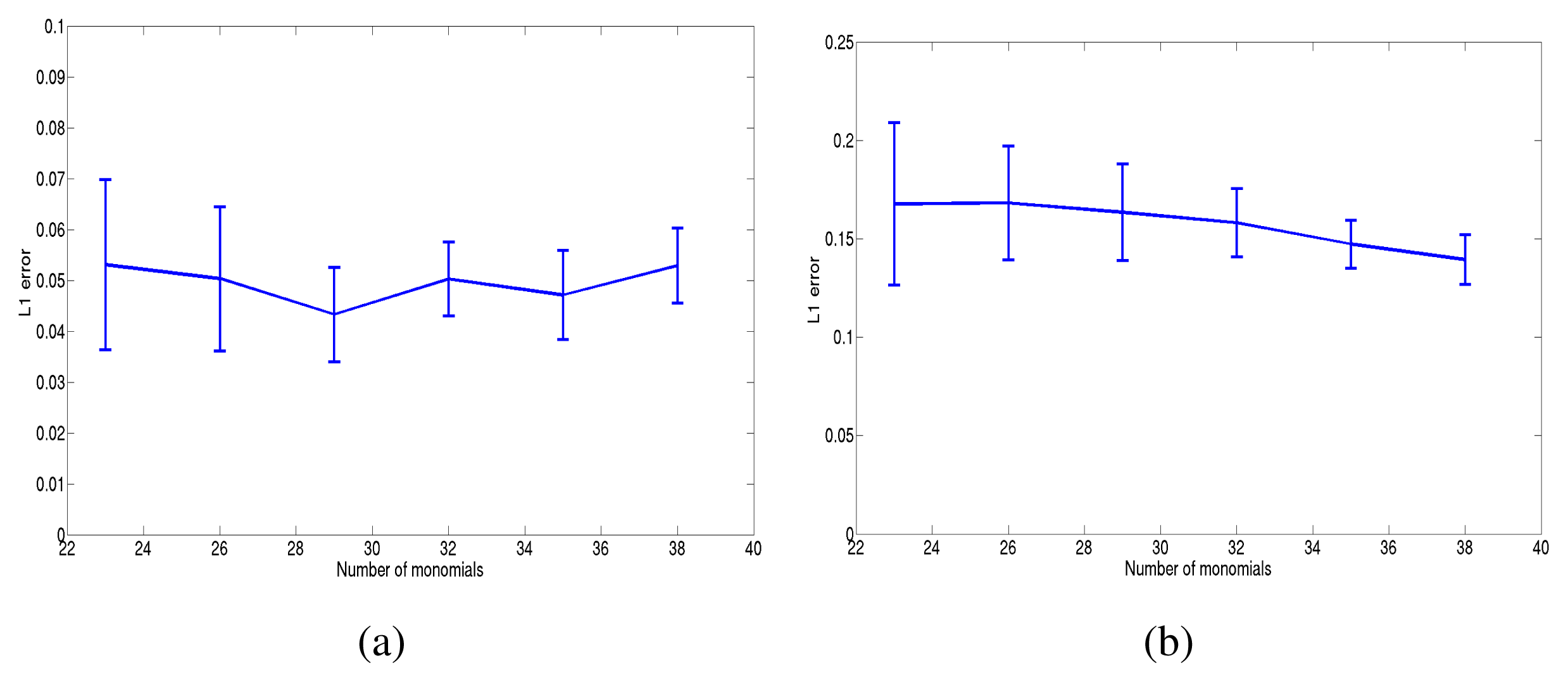
For the last step (goodness of fit), we have used three criteria. The first one simply consists of computing the L1 error , where is the final estimated value. d1 is then averaged on 10 random potentials. Figure 4 shows the committed error in the case of sparse and dense potentials. The method showed a good performance, both in the dense and sparse case, for large N × R ~ 60.
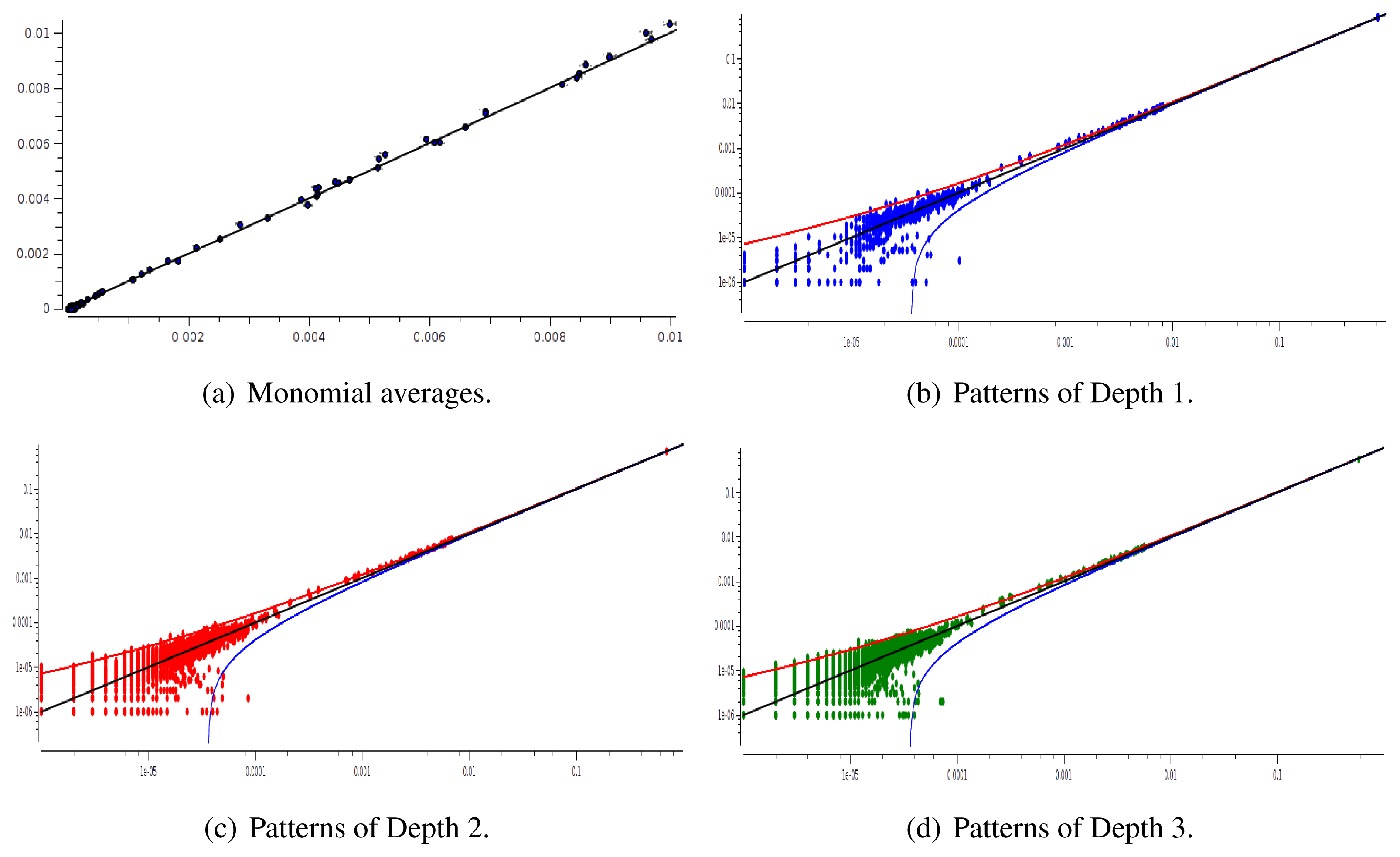
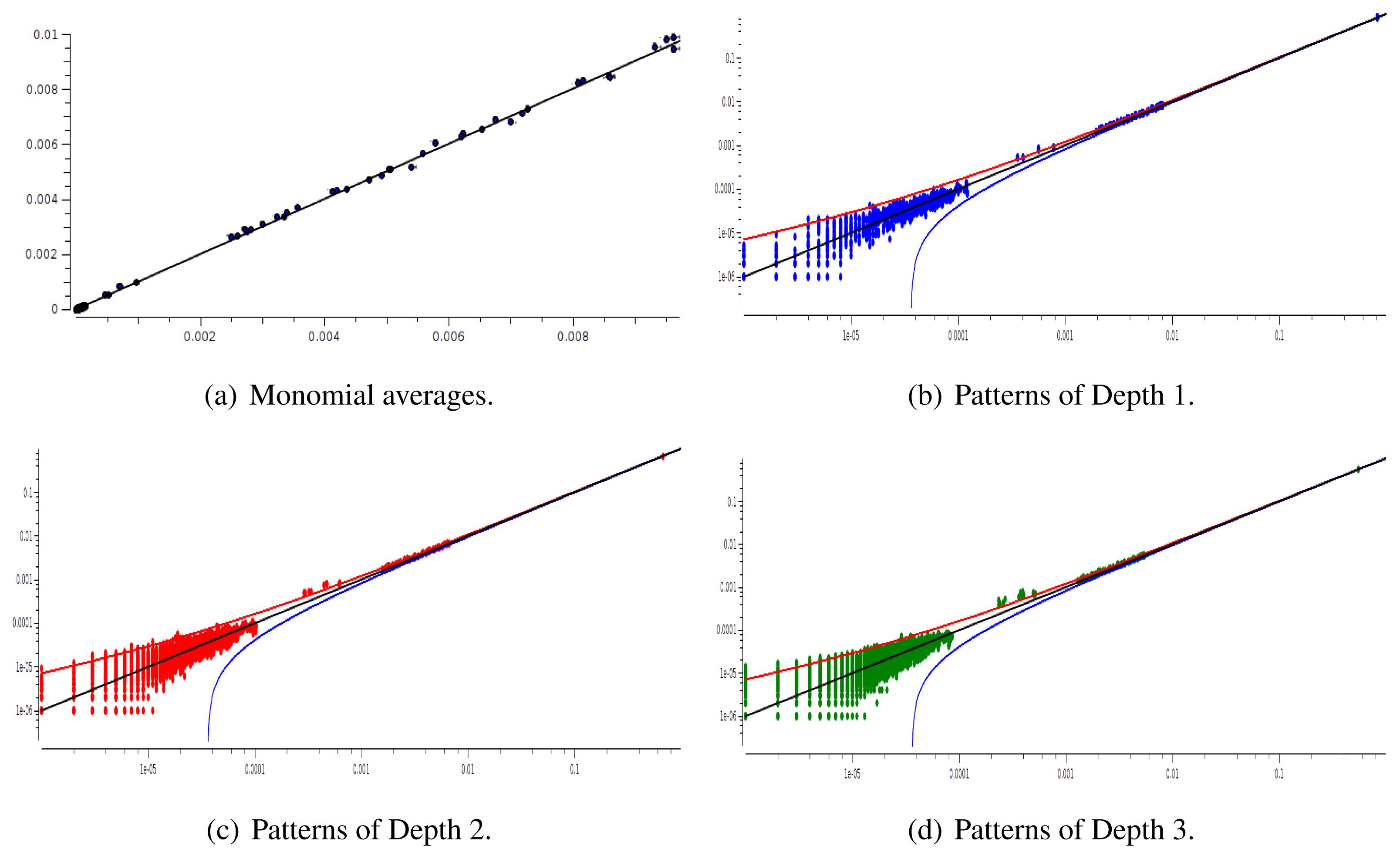
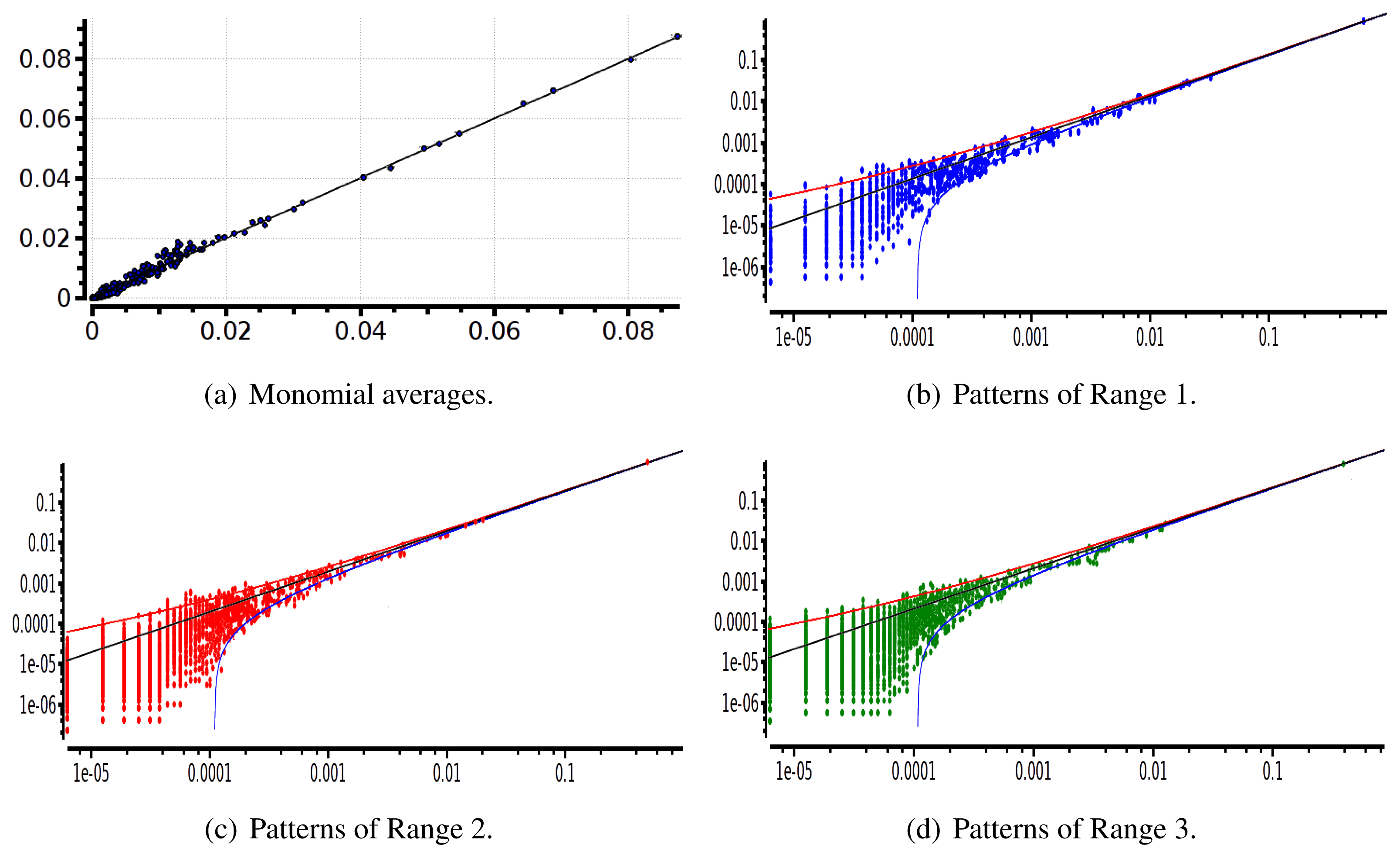
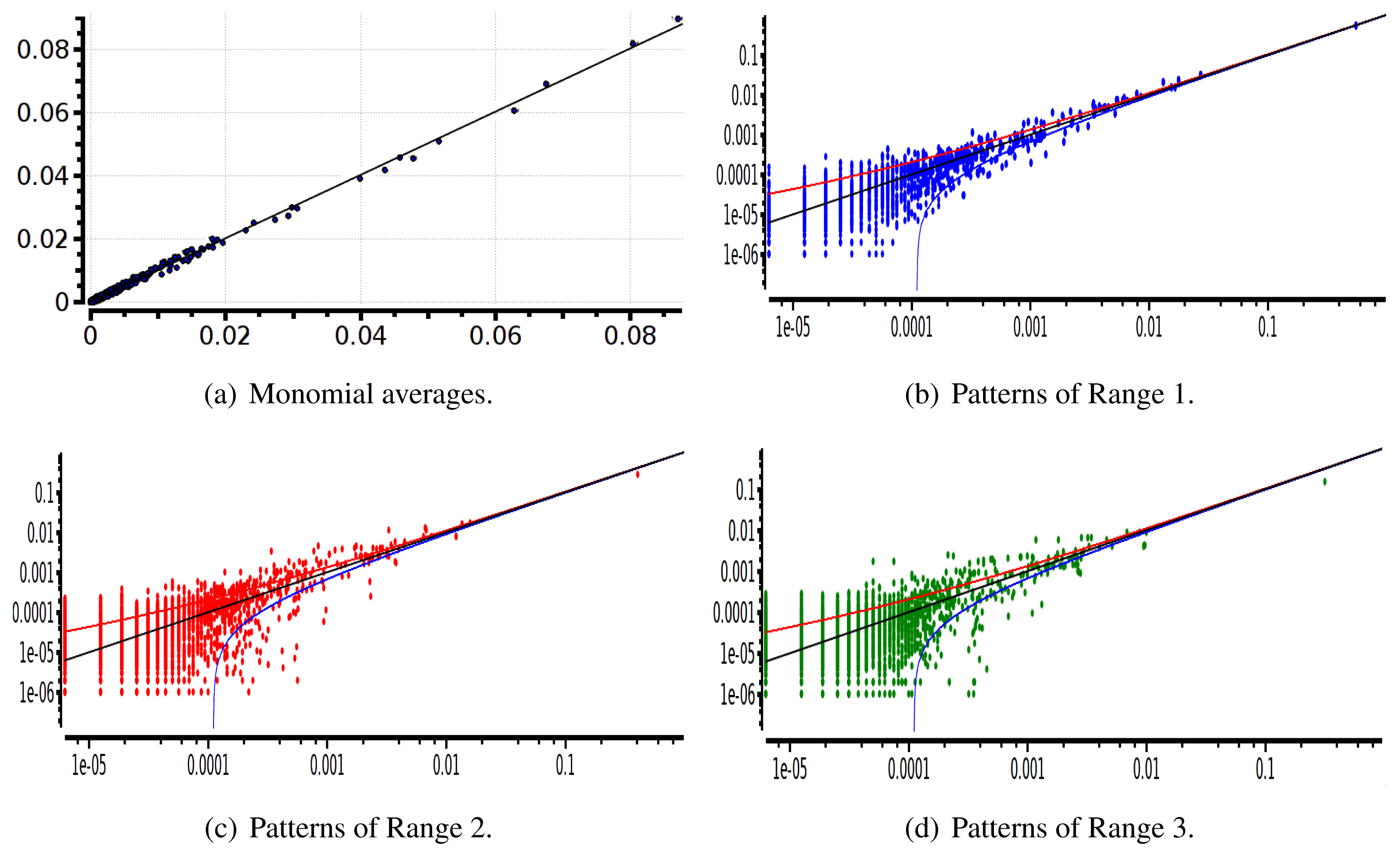
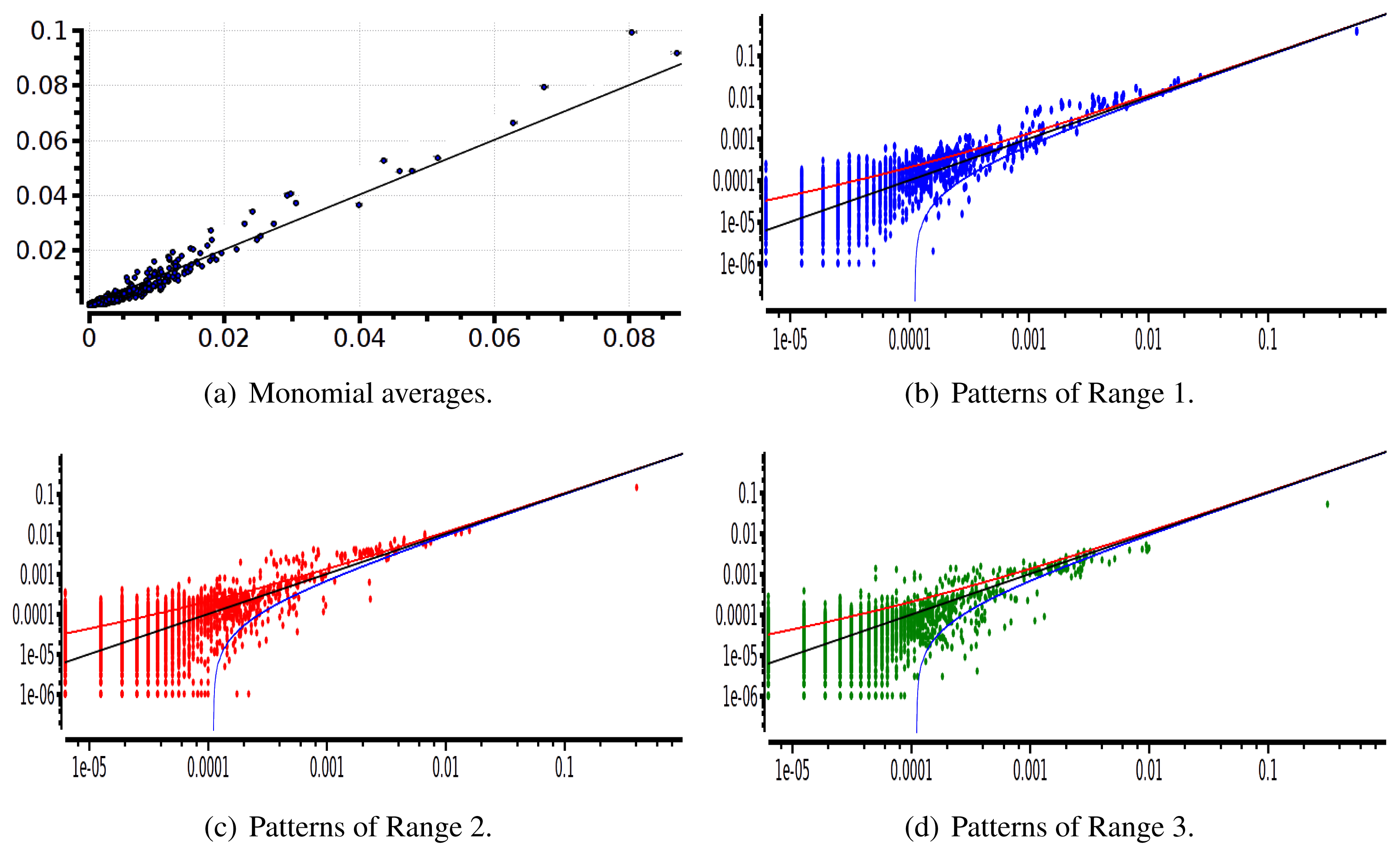
The main advantage of this criterion is that it provides an exact estimation of the error made on coefficient estimation. Its drawback is that we have to know the shape of the potential that generated the raster: this is not the case anymore for real neural network data. We therefore used a second criterion: confidence plots. For each spike block, , appearing in the raster, ωs, we draw a point in a two-dimensional diagram with, on abscissa, the observed empirical probability, , and, on ordinate, the predicted probability, . Ideally, all points should align on the diagonal y = x (equality line). However, since the raster is finite, there are finite-sized fluctuations ruled by the central limit theorem. For a block, , generated by a Gibbs distribution, μλ, and having an exact probability, , the empirical probability, , is a Gaussian random variable with mean and mean-square deviation . The probability that is therefore of about 99, 6%. This interval is represented by confidence lines spreading around the diagonal. As a third criterion, we have used the Kullback-Leibler divergence (55).
We have plotted two examples in Figures 5 and 6 for sparse data types:
4.5. The Performance on Real Data
Here, we show the inferring of the MaxEnt distribution on real spike trains. We analyzed a data set of 20 and 40 neurons with spatial and spatio-temporal constraints (data courtesy of M. J. Berry and O. Marre, 40 is the maximal number of neurons in this data set). Data are binned at 20 ms. We show the confidence plots and an example of convergence curves using the Hellinger distance. The goal here is to check the goodness of fit, not only for spatial patterns (as done in [9–12]), but also for spatio-temporal patterns.
Figure 7 shows the evolution of the Hellinger distance during the parameter update both in the parallel and sequential update process.
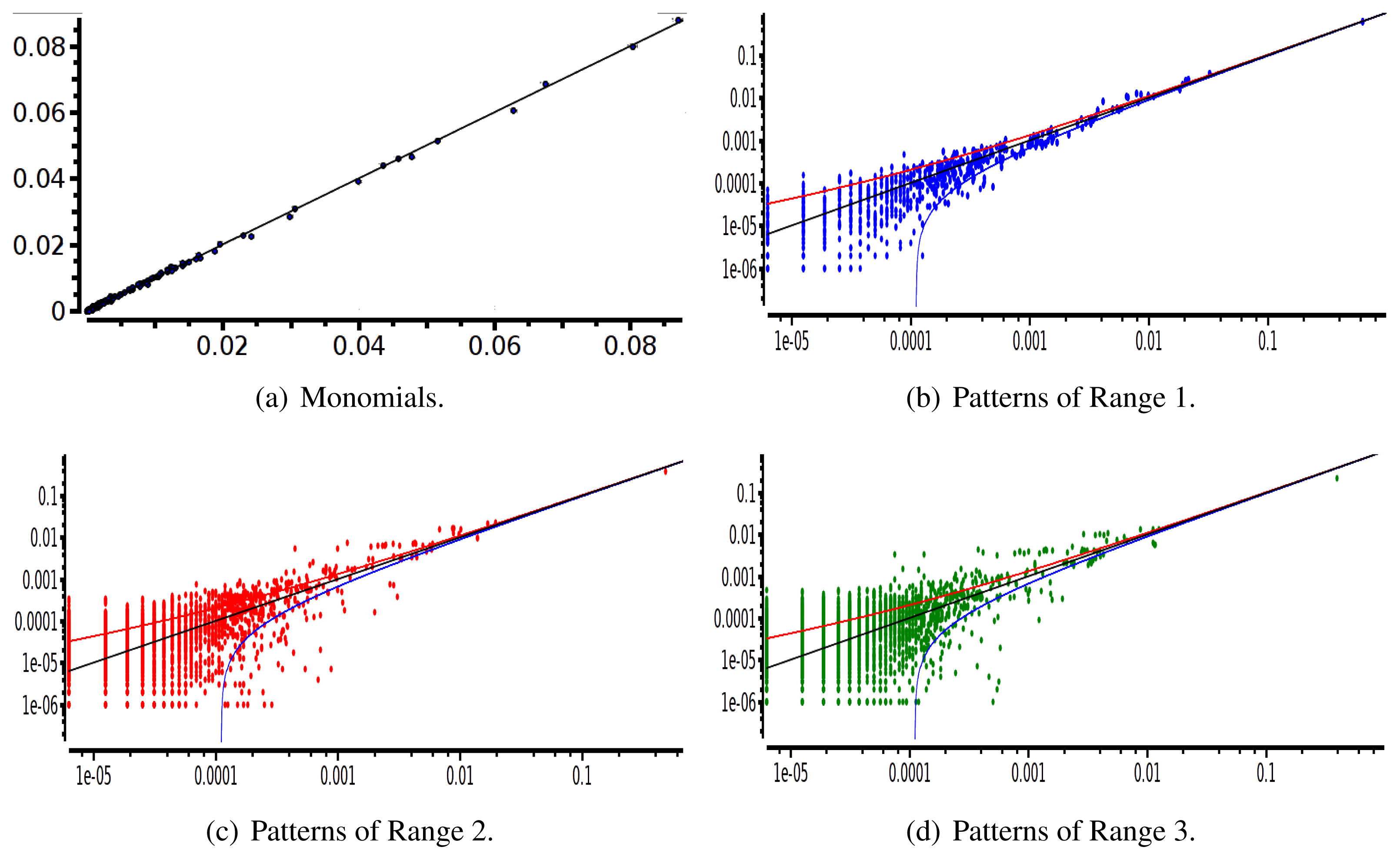
After estimating the parameters of an Ising and pairwise model of range R = 2 on a set of 20 neurons, we evaluate the confidence plots. Figures 8 and 9 show, respectively, the confidence plots for patterns of Ranges 1, 2 and 3 after fitting with an Ising model and the pairwise model of range R = 2. Our results on 20 neurons confirm the observations made in [16] for N = 5, R = 2: a pairwise model with memory performs quite better than an Ising model to explain spatio-temporal patterns.
We then made the same analysis for 40 neuron. Figures 10 and 11 show, respectively, the confidence plots for patterns of Ranges 1, 2 and 3 after fitting with an Ising model and the pairwise model of range R = 2. In this case, we were not able to obtain a good convergence for N = 40, R = 2. This is presumably due to the insufficient length of the data set, which does not allow us to estimate accurately the probability of some monomials. This aspect is discussed in the next section.
5. Discussion and Conclusion
The method shows better performances for synthetic data than for real data, although we did not make extensive studies of real data. The main reason, we believe, is that in the second case, we do not know the form of the potential. As a consequence, we stick to existing canonical forms of potentials, e.g., Ising and pairwise. The main problem with this approach is that the number of parameters to estimate dramatically grows with NR. The increase is moderate for the Ising model ( symmetric pairwise couplings), but it becomes prohibitively large even for pairwise range R models. On the opposite, our analysis of synthetic data used a relatively small number of parameters to fit.
The large number of parameters has two drawbacks: the increasing of the computation time and errors in the estimation. Let us comment on the second problem. It is not intrinsic to our method, nor is it intrinsic to MaxEnt; this is a well-known problem, which arises already when doing linear regression analysis. Increasing the number of parameters may eventually lead to catastrophic estimations, where the addition of a degree of freedom can seriously hinder the resolution.
In the case of MaxEnt, the situation can be described as follows. We generate a finite raster, , from a known distribution, μλ*, with a potential of the form (2). Denote μλ* [m] as the vector with entries μλ* [ml] and as the vector with entries . From (19), we have μλ* [m] = ∇λ*℘. This exact solution is obtained when the Gibbs distribution, μλ*, can be exactly sampled, namely, for an infinite raster. For a finite raster, if T is large enough to apply the central limit theorem, the empirical distribution, , is Gaussian with mean μλ [m] and covariance given by (51). We have, therefore, , where β is a centered Gaussian with covariance . Solving (19), where the exact probability, μλ*, is replaced by the empirical one, , one obtains an approximate solution of λ, λ* with: λ = λ* + ε, where: . Therefore, ∇λ℘ = μλ* [m] + β = ∇λ*+ε℘ = ∇λ*℘ + εχ + O(||ε||2). Hence, ε = χ−1β. χ is invertible, since ℘ is convex.
The fluctuations of the estimated solution, λ, around the exact solution, λ*, are therefore Gaussian, centered, with covariance
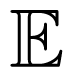
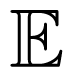
At this stage, the main question is therefore: can we have an idea of the potential shape from data before fitting the parameters? This question is not only related to the goodness of fit, but it is also a question of concept. Is is useful to represent a pairwise distribution for 40 neurons with nearly 2,000 parameters? The idea would then be to filter irrelevant monomials. For that, a feature selection method is useful and should complement this work. There are many directions we can take in favor of the feature selection; for instance, selecting the features on the threshold ([41,42]), using a χ2 method ([43]), as well as the incremental feature selection algorithm ([44], [45]). Other methods based on periodic orbit sampling ([46]) and information geometry ([47,48]) are under current investigation.
We have presented a method to fit the parameters of the MaxEnt distribution with spatio-temporal constraints. In the process of exploring the dynamics of neural data, we hypothesize the model, fit it and, finally, judge the quality of the suggested model. Hence, this work is positioned as an important intermediate step in neural coding using the MaxEnt framework, opening the door for analyzing the dynamics of large networks, not being limited to spatial and/or traditional MaxEnt models.
Finally, we would like to highlight two points that should be investigated in further studies:
The effect of binning. In many experimental studies, data is binned. Basically, binning was used in order to account for time spiking sensitivity, which is not the same for all the biological neural networks. For instance, [9] used 20 ms of binning for retinal spike trains. In the present paper, we have used the same as these authors, but we have not considered the effect of binning on our statistical estimations. This is certainly a matter of further investigations, especially because, to our best knowledge, no systematic study on the binning effects on statistics has been done. In particular, three distinct dimensions should be considered:
- –
The statistical dimension: how does binning biases statistics? Could binning introduce spurious effects, such as, e.g., creating fallacious long-range correlations?
- –
The computational dimension: how does the performance of the algorithm change with the bin size?
- –
The biological dimension: cross-correlograms are not the same in all brain areas. Therefore, the optimal bin size is expected to depend on the investigated area.
Maximum entropy: There are several methods now in use to model the spatio-temporal correlations in ensembles of neurons. The generalized linear model (GLM) approach uses the maximum likelihood and point-process to assess connectivity (e.g., [10]). Reverse correlation methods can also work well (e.g., [49]). Finally, there are causality metrics, like Granger causality or transfer entropy ([50]). Some of these methods have been compared in [51], but further investigations should be helpful, starting from synthetic data, where statistics is under good control. Especially, how does maximum entropy perform compared to these others methods?
Our method allows one to investigate these two questions on numerical grounds although such an investigation should be completed by mathematical insights, using the properties of spatio-temporal Gibbs distributions.
6. List of symbols
| ωi(n) | Spike event |
| ω(n) | Spike pattern |
Spike block | |
| ω | Spike train |
| T | Length (in time) of the spike train |
| N | Number of neurons |
| R | Model range |
| D | Model memory (R = D − 1) |
| ml(ω) | Monomial number l |
| m | Vector of monomials |
| L | Total number of parameters (monomials) in the model |
| λl | Parameter number l |
| λ | Parameters vector |
Gibbs potential | |
| Zλ | Partition function |
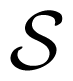 | Entropy |
| ℘ | Topological pressure |
Empirical probability measured on the spike train, ω, of length T | |
| μλ | Gibbs density with parameters λ |
Set of invariant probabilities | |
Learning rate or the value by which we update the parameters, λl | |
| δ | Vector of learning rates |
| dKL | Kullback-Leibler divergence |
| Cjk | Correlation between two monomials, j and k |
| χ | Hessian matrix (second derivative of the pressure) |
| Δ | Root sum square of the learning rates |
| β | Fluctuations on the monomials averages |
| ε | Fluctuations on the parameters (relaxation) |
Acknowledgments
We thank the reviewers for helpful remarks and constructive criticism. We also warmly acknowledge M.J. Berry and O. Marre for providing us MEA recordings from the retina and G. Tkacik, who provided us the references, [17,18], and helped us in the algorithm design. This work was partially supported by the ERC-NERVI number 227747, KEOPS ANR-CONICYT, and European FP7 projects RENVISION (FP7-600847), BRAINSCALES (FP7-269921).
Conflicts of Interest
The authors declare no conflicts of interest.
- Author’s contributionReal data was provided by M.J. Berry and O. Marre from Princeton university. The authors contributed equally to the presented mathematical and computational framework and the writing of the paper.
References
- Ferrea, E.; Maccione, A.; Medrihan, L.; Nieus, T.; Ghezzi, D.; Baldelli, P.; Benfenati, F.; Berdondini, L. Large-scale, high-resolution electrophysiological imaging of field potentials in brain slices with microelectronic multielectrode arrays. Front. Neural. Circ 2012, 6. [Google Scholar]
- Stevenson, I.H.; Kording, K.P. How advances in neural recording affect data analysis. Nat. Neurosci 2011, 14, 139–142. [Google Scholar]
- Marre, O.; Amodei, D.; Deshmukh, N.; Sadeghi, K.; Soo, F.; Holy, T.; Berry, M., II. Mapping a Complete Neural Population in the Retina. J. Neurosci 2012, 43, 14859–14873. [Google Scholar]
- Hill, D.N.; Mehta, S.B.; Kleinfeld, D. Quality Metrics to Accompany Spike Sorting of Extracellular Signals. J. Neurosci 2011, 31, 8699–8705. [Google Scholar]
- Litke, A.M.; Bezayiff, N.; Chichilnisky, E.J.; Cunningham, W.; Dabrowski, W.; Grillo, A.A.; Grivich, M.; Grybos, P.; Hottowy, P.; Kachiguine, S.; Kalmar, R.S.; Mathieson, K.; Petrusca, D.; Rahman, M.; Sher, A. What does the eye tell the brain?: Development of a system for the large scale recording of retinal output activity. IEEE Trans. Nucl. Sci 2004, 51, 1434–1440. [Google Scholar]
- Quiroga, R.Q.; Nadasdy, Z.; Ben-Shaul, Y. Unsupervised spike detection and sorting with wavelets and superparamagnetic clustering. Neural Comput 2004, 16, 1661–1687. [Google Scholar]
- Csiszár, I. On the computation of rate-distortion functions (Corresp.). Inform. Theory, IEEE T on 1974, 20, 122–124. [Google Scholar]
- Jaynes, E. Information theory and statistical mechanics. Phys. Rev 1957, 106, 620. [Google Scholar]
- Schneidman, E.; Berry, M.; Segev, R.; Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 2006, 440, 1007–1012. [Google Scholar]
- Pillow, J.W.; Shlens, J.; Paninski, L.; Sher, A.; Litke, A.M.; Chichilnisky, E.J.; Simoncelli, E.P. Spatio-temporal correlations and visual signaling in a complete neuronal population. Nature 2008, 454, 995–999. [Google Scholar]
- Ganmor, E.; Segev, R.; Schneidman, E. Sparse low-order interaction network underlies a highly correlated and learnable neural population code. Proc. Natl. Acad. Sci. USA 2011, 108, 9679–9684. [Google Scholar]
- Ganmor, E.; Segev, R.; Schneidman, E. The architecture of functional interaction networks in the retina. J. Neurosci 2011, 31, 3044–3054. [Google Scholar]
- Tkačik, G.; Schneidman, E.; Berry, M.J., II; Bialek, W. Spin glass models for a network of real neurons. arXiv preprint arXiv:0912.5409. 2009. [Google Scholar]
- Tang, A.; Jackson, D.; Hobbs, J.; Chen, W.; Smith, J.L.; Patel, H.; Prieto, A.; Petrusca, D.; Grivich, M.I.; Sher, A.; Hottowy, P.; Dabrowski, W.; Litke, A.M.; Beggs, J.M. A Maximum Entropy Model Applied to Spatial and Temporal Correlations from Cortical Networks. In Vitro. J. Neurosci 2008, 28, 505–518. [Google Scholar]
- Marre, O.; El Boustani, S.; Frégnac, Y.; Destexhe, A. Prediction of spatiotemporal patterns of neural activity from pairwise correlations. Phys. Rev. Lett 2009, 102. [Google Scholar]
- Vasquez, J.C.; Marre, O.; Palacios, A.G.; Berry, M.J.; Cessac, B. Gibbs distribution analysis of temporal correlation structure on multicell spike trains from retina ganglion cells. J. Physiol. Paris 2012, 106, 120–127. [Google Scholar]
- Dudík, M.; Phillips, S.; Schapire, R. Performance Guarantees for Regularized Maximum Entropy Density Estimation. Proceedings of the 17th Annual Conf. on Comp. Learn Theory, 2004.
- Broderick, T.; Dudik, M.; Tkacik, G.; Schapire, R.E.; Bialek, W. Faster solutions of the inverse pairwise Ising problem. arXiv:0712.2437. 2007. [Google Scholar]
- Nasser, H.; Marre, O.; Cessac, B. Spatio-temporal spike train analysis for large scale networks using the maximum entropy principle and Montecarlo method. J. Stat. Mech 2013, 2013, P03006. [Google Scholar]
- Schaub, M.T.; Schultz, S.R. The Ising decoder: reading out the activity of large neural ensembles. arXiv:1009.1828. 2010. [Google Scholar]
- Garibaldi, U.; Penco, M.A. Probability Theory and Physics Between Bernoulli and Laplace: The Contribution of J H. Lambert (1728–1777). Proceeding of the Fifth National Congress on the History of Physics, Rome, 1985; 9, pp. 341–346.
- Tkacik, G.; Marre, O.; Mora, T.; Amodei, D.M.B., 2nd; Bialek,, W. The simplest maximum entropy model for collective behavior in a neural network. J. Stat. Mech 2013, P03011. [Google Scholar]
- Jaynes, E.T. Where do we stand on maximum entropy. In The Maximum Entropy Formalism; Levine, D., Tribus, M., Eds.; MIT Press: Cambridge, MA, USA, 1978; pp. 15–118. [Google Scholar]
- Jaynes, E.T. The minimum entropy production principle. Ann. Rev. Phys. Chem 1980, 31, 579–601. [Google Scholar]
- Jaynes, E. Macroscopic prediction. In Complex Systems - Operational Approaches in Neurobiology, Physics, and Computers; Springer: Berlin, Germany, 1985; pp. 254–269. [Google Scholar]
- Otten, M.; Stock, G. Maximum caliber inference of nonequilibrium processes. J. Chem. Phys 2010, 133, 034119. [Google Scholar]
- Fernandez, R.; Maillard, G. Chains with complete connections : General theory, uniqueness, loss of memory and mixing properties. J. Stat. Phys 2005, 118, 555–588. [Google Scholar]
- Gikhman, I.; Skorokhod, A. The Theory of Stochastic Processes; Springer: Berlin, Germany, 1979. [Google Scholar]
- Chazottes, J.; Keller, G. Pressure and Equilibrium States in Ergodic Theory. Isr. J. Math 2008, 131. [Google Scholar]
- Ruelle, D. Statistical Mechanics: Rigorous Results; Benjamin: New York, NY, USA, 1969. [Google Scholar]
- Keller, G. Equilibrium States in Ergodic Theory; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Ruelle, D. Thermodynamic Formalism; Addison-Wesley: Reading, MA, USA, 1978. [Google Scholar]
- Bowen, R. Lecture Notes in Mathatics; Springer-Verlag: 1975; Volume 470. [Google Scholar]
- Georgii, H.O. Gibbs Measures and Phase Transitions (De Gruyter Studies in Mathematics); Springer: Berlin, Germany, 1988. [Google Scholar]
- Vasquez, J.C.; Palacios, A.; Marre, O., II; M.J.B.; Cessac, B. Gibbs distribution analysis of temporal correlation structure on multicell spike trains from retina ganglion cells. J. Physiol. Paris 2012, 106, 120–127. [Google Scholar]
- Collins, M.; Schapire, R.E.; Singer, Y. Logistic Regression, AdaBoost and Bregman Distances. Mach. Lear 2002, 48, 253–285. [Google Scholar]
- Mayer, V.; Urbański, M. Thermodynamical formalism and multifractal analysis for meromorphic functions of finite order. Memoir. Am. Math. Soc 2010, 203. [Google Scholar]
- Kappen, H.; Rodriguez, F. Boltzmann Machine learning using mean field theory and linear response correction. In NIPS; Kearns, M., Ed.; MIT Press: Cambridge, MA, USA, 1998; Volume 12, pp. 280–286. [Google Scholar]
- Event neural assembly Simulation: v3 version, Available online: http://enas.gforge.inria.fr/v3/download.html accessed on 21 April 2014.
- Strong, S.; Koberle, R.; de Ruyter van Steveninck, R.; Bialek, W. Entropy and information in neural spike trains. Phys. Rev. Let 1998, 80, 197–200. [Google Scholar]
- Rosenfeld, R.; Carbonell, J.; Rudnicky, A. Adaptive Statistical Language Modeling: A Maximum Entropy Approach. In Technical report; School of Computer Science, Carnegie Mellon University, 1994. [Google Scholar]
- Koeling, R. Chunking with maximum entropy models. In Proceeding ConLL ’00 Proceedings of the 2nd Workshop on Learning Language in Logic and the 4th conference on Computational Natural Language Learning; Volume 7, pp. 139–141. Association for Computational Linguistics: Stroudsburg, PA, USA, 2000. [Google Scholar]
- Chen, S.F.; Rosenfeld, R. Efficient Sampling and Feature Selection in Whole Sentence Maximum. Ent. Lang Mod 1999. [Google Scholar]
- Berger, A.L.; Pietra, S.A.D.; Pietra, V.J.D. A Maximum Entropy approach to Natural Language Processing. Comp. Lang 1996, 22, 39–71. [Google Scholar]
- Zhou, Y.; Wu, L. A fast algorithm for feature selection in conditional maximum entropy modeling. Proceedings of the Empirical Methods in Natural Language Processing (EMNLP 2003), Sapporo, Japan, July 2003; pp. 153–159.
- Cessac, B.; Cofre, R. Estimating maximum entropy distributions from periodic orbits in spike trains. research report RR-8329; INRIA, 2013. [Google Scholar]
- Nakahara, H.; Amari, S. Information-Geometric Decomposition in Spike Analysis. Adv. Neural Inform. Process. Syst 2001, 253–260. [Google Scholar]
- Amari, S. Information geometry on hierarchy of probability distributions. IEEE T. Inf. Theory 2001, 47, 1701–1711. [Google Scholar]
- Chichilnisky, E.J. A simple white noise analysis of neuronal light responses. Network Comput. Neural Syst 2001, 12, 199–213. [Google Scholar]
- Li, Z.; Li, X. Estimating Temporal Causal Interaction between Spike Trains with Permutation and Transfer Entropy. PloS One 2013, 8, e70894. [Google Scholar]
- Truccolo, W.; Hochberg, L.R.; Donoghue, J.P. Collective dynamics in human and monkey sensorimotor cortex: predicting single neuron spikes. Nature Neurosci 2009, 13, 105–111. [Google Scholar]

© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Nasser, H.; Cessac, B. Parameter Estimation for Spatio-Temporal Maximum Entropy Distributions: Application to Neural Spike Trains. Entropy 2014, 16, 2244-2277. https://doi.org/10.3390/e16042244
Nasser H, Cessac B. Parameter Estimation for Spatio-Temporal Maximum Entropy Distributions: Application to Neural Spike Trains. Entropy. 2014; 16(4):2244-2277. https://doi.org/10.3390/e16042244
Chicago/Turabian StyleNasser, Hassan, and Bruno Cessac. 2014. "Parameter Estimation for Spatio-Temporal Maximum Entropy Distributions: Application to Neural Spike Trains" Entropy 16, no. 4: 2244-2277. https://doi.org/10.3390/e16042244
APA StyleNasser, H., & Cessac, B. (2014). Parameter Estimation for Spatio-Temporal Maximum Entropy Distributions: Application to Neural Spike Trains. Entropy, 16(4), 2244-2277. https://doi.org/10.3390/e16042244




