Co and In Doped Ni-Mn-Ga Magnetic Shape Memory Alloys: A Thorough Structural, Magnetic and Magnetocaloric Study
Abstract
: In Ni-Mn-Ga ferromagnetic shape memory alloys, Co-doping plays a major role in determining a peculiar phase diagram where, besides a change in the critical temperatures, a change of number, order and nature of phase transitions (e.g., from ferromagnetic to paramagnetic or from paramagnetic to ferromagnetic, on heating) can be obtained, together with a change in the giant magnetocaloric effect from direct to inverse. Here we present a thorough study of the intrinsic magnetic and structural properties, including their dependence on hydrostatic pressure, that are at the basis of the multifunctional behavior of Co and In-doped alloys. We study in depth their magnetocaloric properties, taking advantage of complementary calorimetric and magnetic techniques, and show that if a proper measurement protocol is adopted they all merge to the same values, even in case of first order transitions. A simplified model for the estimation of the adiabatic temperature change that relies only on indirect measurements is proposed, allowing for the quick and reliable evaluation of the magnetocaloric potentiality of new materials starting from readily available magnetic measurements.PACS Codes: 75.30.Sg; 81.30.Kf1. Introduction
In 1996, pioneering work by Ullakko, and O’Handley (and his group) in collaboration with Kokorin introduced a new magnetoelastic effect, the magnetic field induced variant reorientation (MIR) in Ni2MnGa Heusler alloys [1]. Since then “ferromagnetic shape memory” materials, characterized by the coexistence of martensitic transformation and magnetic order, have become an emerging class of materials where new properties and potential fields of applications have constantly come to light [2]. The strong coupling between magnetic and structural degrees of freedom is at the basis of their extraordinary phenomenology that offers also exciting matter for basic investigation [3]. While MIR up to 12% in the martensitic phase due to a magnetostructural coupling on the mesoscopic scale was mainly found in NiMnGa alloys [4,5], giant properties changes obtained by inducing structural transition by external fields (i.e., magnetic field, pressure, stress) were mainly shown in off-stoichiometric Mn-rich Heuslers composed of different IIIA-VA elements (i.e., In, Sn, Sb) [6]. Magnetic superelasticity and strain recovery [7,8], giant magnetoresistance [9] magnetothermal conductivity [10], magnetocaloric [11–14] and barocaloric [15] effects were demonstrated, making these materials very interesting for multifunctional applications, also allowing the multiple exploitation of external fields. Moreover, exchange bias [16] and ferromagnetic strain glass behavior have been recently evidenced [17].
The ternary phase diagram of the NiMnGa system has been mapped to search for new shape memory alloys and for a systematic study of the relationship between martensitic transformation and Curie temperature [18–20]. It has been shown that martensitic and magnetic transformation temperatures show a dependency of electrons per atom following Hume-Rothery concepts. In, Sn, Sb based families of alloys show a linear dependence of martensitic transformation on valence electrons number [21,22]. It has also been recently shown that chemical order plays a primary role in determining martensitic properties [23,24].
Remarkably, the crystallographic structure of the martensitic phase can be tuned by changing composition from modulated (commensurate and incommensurate) monoclinic 10M and 14M structures to non-modulated tetragonal [25–27]. Structural relationships between lattice parameters in the martensitic phase and austenitic and martensitic lattice parameters determine respectively the maximum possible strain achievable by magnetic field induced variant reorientation and by magnetic field induced transformation (MFIS) in single crystals. In polycrystalline isotropic materials the volume discontinuities between austenite and martensite determine the maximum strain achievable by MFIS. In addition, the discontinuities of lattice parameters and volume enable the possibility to drive the martensitic transformation by external fields (stress and pressure) but influence the thermal hysteresis of martensitic transformation, a detrimental effect for applications.
Modeling the magnetic interactions in martensite and austenite and tuning the magnetization discontinuity (ΔM) at the transformation is a crucial goal to drive the martensitic transformation temperature by magnetic fields and to enable giant magnetic field induced effects, and it has been one of the main goals of our research in this field [20,28–31]. In previous papers we demonstrated that in ternary off-stoichiometric Ga-alloys (both in the case of Ni-rich at expenses of Mn and in Mn-rich at expenses of Ga) it is possible to merge martensitic and Curie temperature in a wide temperature range, obtaining a direct first order transformation from ferromagnetic martensite to paramagnetic austenite on heating [20]. As a consequence ΔM maximization and a much higher magnetocaloric effect (Isothermal entropy change, Δs, increased up to 4-times in Ni-rich composition) were obtained [12].
Interestingly, the Mn-Mn distances in these alloys are close to the limit where the interactions switch from ferromagnetic to antiferromagnetic. That is why they show a variety of magnetic properties depending on even minor changes in the stoichiometry, the atomic order, the lattice parameters and the symmetry of the alloy (whether it is in the high temperature or low temperature phase). We have recently shown that in Mn-rich Ni-Mn-Ga alloys, Co substitution produces important changes in magnetism and structure [32]. Chemical disorder in the Mn-rich Heusler alloys is responsible for competing ferromagnetic and antiferromagnetic interaction (magnetic frustration) because the extra Mn atoms occupy lattice sites of the Ga-sublattice which interact antiferromagnetically with the Mn atoms on the Mn-sublattice because of shorter interatomic Mn-Mn distances [22,33] Co affects differently the magnetic interactions of the two phases in the Mn-rich alloy, strengthening the ferromagnetic interactions in austenite while weakening the ferromagnetic behavior of martensite. As a result, the quaternary alloys show lower Curie temperature for the martensitic phase (TCM) than the austenitic one (TCA). When the martensitic instability temperature (TM) is tuned between the two Curie temperatures, an inverse magnetostructural transition, from low moment martensite to high moment austenite, occurs (on heating), characterized by a negative field dependence of the transformation temperature (dTM/μ0dH). Owing to the improved ferromagnetic interactions in austenite and to the increased distance between TM and TCA with respect to the ternary compound, very high values of magnetization discontinuity can be achieved, and also of |dTM/μ0dH|. We showed that a 10-fold increase in magnetization discontinuity and a 6-fold increase in critical temperatures sensitivity can be obtained by substituting up to 9 at% Ni with Co in the parent phase Ni50Mn30Ga20 [34].
Thus, a metamagnetic behaviour like In, Sn, Sb-based alloys and inverse magnetocaloric effect has been observed also for Ga alloys, by Co-doping in the Mn-rich stoichiometric region [34]. The high values recently obtained for Co-doped In and Ga-based alloys of magnetocaloric [14,35,36] and barocaloric effect [15,37] make them promising for solid state refrigeration and multifunctional applications, even if important drawbacks, mainly linked to hysteresis and poor mechanical properties, must be overcome.
In the present paper we will examine in depth the effects of Co and In doping on Mn-rich NiMnGa alloys, focusing on four representative samples of the series characterized by different number of first and second order phase transitions of different nature (e.g., from ferro to para or from para to ferro, on heating). In the first part of the paper we will present a thorough study of the intrinsic magnetic and structural properties, including their dependence on hydrostatic pressure, that are at the basis of their multifunctional behavior. We will then discuss their magnetocaloric properties, taking advantage of complementary calorimetric and magnetic techniques, and showing that if a proper measurement protocol is adopted they all merge to same values, even in the case of first order transitions.
2. Results and Discussion
2.1. Critical Temperatures and Magnetic Properties
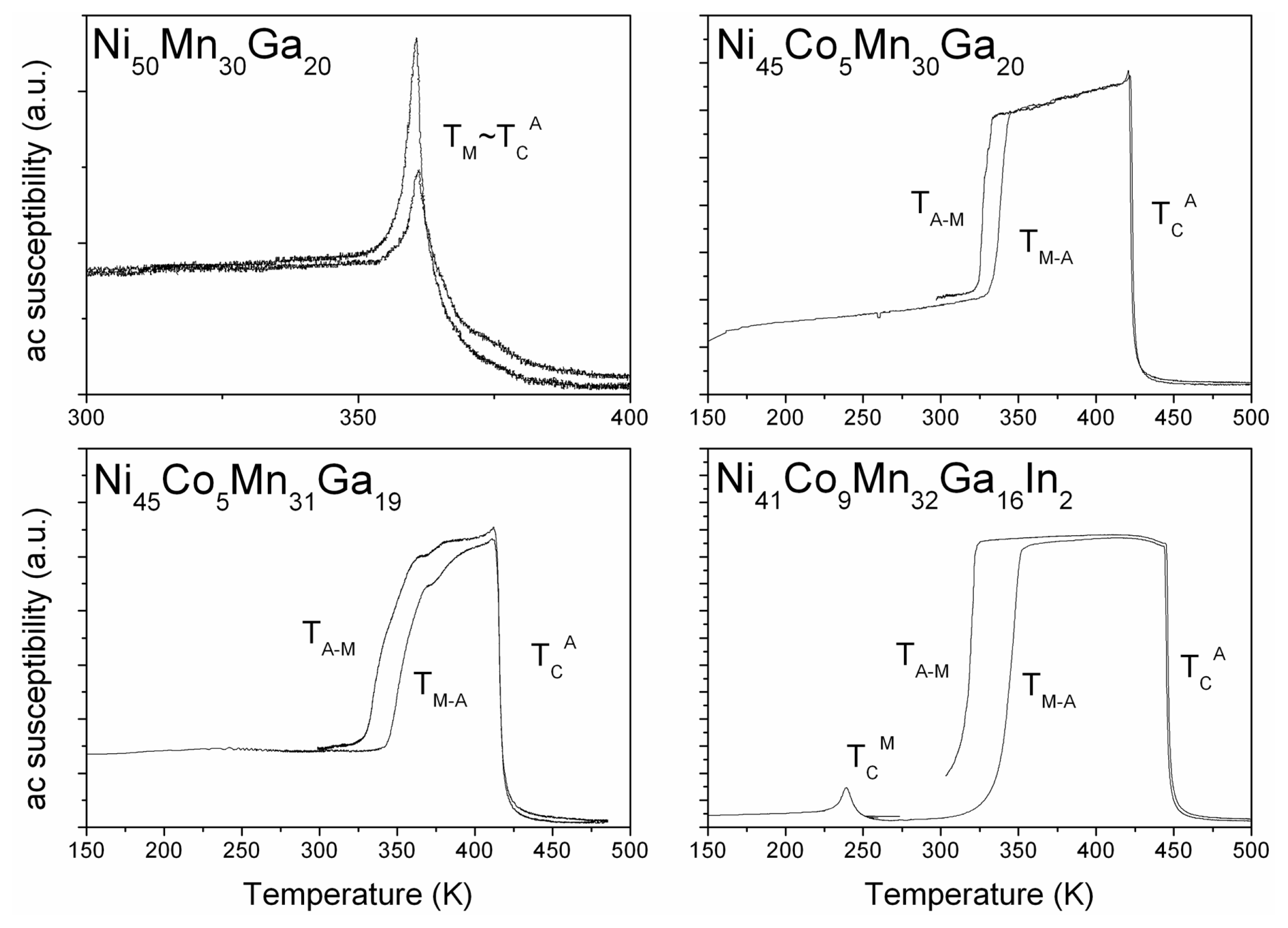
In this work we have chosen four Co and In-doped Ni2MnGa samples that provide an excerpt of the various magnetic configurations where the martensitic transformation is realized. Tables 1 and 2 report the critical temperatures and the magnetic and structural figures of interest for the analysis of magnetocaloric effect. In order to minimize the role of temperature in this comparison, the three doped samples were chosen with similar TM values (Figure 1).
The ternary compound Ni50Mn30Ga20 shows coincidence of the magnetic and structural transitions across a ferromagnetic martensite to paramagnetic austenite transformation on heating. The critical temperature is approximately 370 K. Due to the partial antiferromagnetic alignment of the extra Mn atoms in the Mn-rich composition and due to the vicinity to the Curie temperature, the magnetization jump ΔM is negative on heating (Figure 2), being approximately −9.5 A·m2/Kg, and the field drag on the transition is quite limited (dTM/μ0dH = +0.45 K/T).
Two quaternary compounds, Ni45Co5Mn30Ga20 (sample 5–30) and Ni45Co5Mn31Ga19 (sample 5–31), display the transformation temperature TM between two ferromagnetic phases. In fact, by Co doping, the austenitic Curie temperature is pushed to higher values (TC A = 420 K) while the martensitic transformation temperature is lowered (TM in the range 330–350 K). Due to enhanced ferromagnetism in austenite, the magnetization jump at the transformation turns to positive values. When compared to the ternary compound, the magnetization discontinuity has reversed sign while field sensitivity of the martensitic transformation is negative and increases three times in absolute value (Table 2 and Figure 2).
A notable effect on the structural stability of the quaternary alloy can also be achieved by partial substitution of the group p element, Ga, with homovalent In. The peculiarity of this substitution is the selective effect that can be achieved: in fact, by substituting small amounts of Ga with In (around 2 or 3 at.%), the martensitic transformation temperature is lowered while the Curie temperatures are almost unchanged [29]. The In-doped sample chosen for this review, Ni41Co9Mn32Ga16In2, shows a so-called paramagnetic gap preceding TM, due to a substantial shift of TC M below both TC A and TM. The resulting reverse transformation between a very low moment martensite and a high magnetization austenite allows for maximum values of magnetization discontinuity. In this sample both ΔM and |dTM/μ0dH| reach the highest values of this series (Table 2), increasing of more than one order of magnitude with respect to the ternary parent sample. (dTM/μ0dH changing from +0.45 to −5.5 K/T)
2.2. Structural Characterization
In order to get a better understanding of the magnetostructural behavior of these alloys it is necessary to study the structural evolution across the transformation. The samples presented here show that even slight changes in composition result in notable differences. For instance, the two quaternary samples share similar composition, similar magnetic figures (critical temperatures, and dTM/μ0dH) and similar hysteresis; nonetheless, sample 5–30 shows a much steeper transformation with respect to sample 5–31 (5 K vs. 13 K transition width). Provided that the two samples share similar dTM/μ0dH values, the steeper transition of sample 5–30 allows for complete transformation in a lower applied field. The difference in steepness reflects differently on the magnetization jump at the transition: in fact, the steeper the transition, the more ΔMiso (the maximum achievable ΔM, calculated among the heating and the cooling branches of the transformation) is similar to the transition jump, ΔMM-A. On the other hand, broader transitions like the one of sample 5–31 show that ΔMiso can be consistently higher than ΔMM-A.
One of the causes contributing to such a difference may be ascribed to the structural features of the different samples, thus it is interesting to determine the crystal structure of these materials and to follow their evolution across the structural transformation. The crystal structure of the martensitic phase is in both cases tetragonal, non-modulated; nonetheless, the temperature evolution of the X-ray diffraction patterns allows for the determination of different crystal volume discontinuities at the transformation (see for instance Figure 3): sample 5–31 has indeed a higher volume discontinuity than sample 5–30 (ΔV/V ≈ 0.55% versus ≈ 0.45%, see Table 2).
The magnetic figures introduced above provide only a partial description of the magnetostructural transformation occurring in these alloys. The martensitic transformation is a first order diffusionless process involving a change in the lattice parameters and in the symmetry of the crystal. Its dynamics depends on the stress accumulated at the border between martensite and austenite, the so-called invariant plane. Symmetry rules and the metric of the two phases, i.e., the mismatch occurring at the invariant plane, [38] determine the entity of the energy barrier which has to be overcome. As we are dealing with polycrystalline alloys, extrinsic contributions to the energy barrier of the transformation arise, too: a complex stress-strain relation among the differently oriented crystallites provides a landscape of energy barriers that heavily influence the width of the martensitic transformation and the thermal hysteresis.
While metric considerations on the lattice matching of the two phases at the invariant plane [38] is a good predictor of the thermal hysteresis, it appears that, at least for series sharing the same martensitic symmetry, the volume discontinuity can be considered a good descriptor of the transformation width; in fact the In doped sample, which show the highest discontinuity in Volume (up to 0.9%), also shows the broader transformation of the series, as reported in Table 2. The parent sample does not follow such a rule; although it shows the lower volume discontinuity of the series (ΔV/V ≈ 0.2), its transformation width is comparable with sample 5–31 and even double than sample 5–30. Nonetheless, several features differentiate it from the doped samples, the most important being the different symmetry of the martensitic phase, which in this case is the 7M modulated monoclinic [30]. Also, the presence of the concurrent Curie transition may actually affect the magnetic profile of the transformation. A common feature of all the samples is the sign of the volume discontinuity, which is always positive on heating; this is due to the austenitic phase having always a higher volume than the martensitic one.
The hysteretic nature of the martensitic transformation poses a serious limit to the cycling operation of these alloys [39]. Therefore, the mitigation of cycling irreversibility, either by intrinsic or extrinsic means, is mandatory. The search for new compositions with better martensite-austenite interface matching or the development of proper microstructural configurations are promising routes. A straightforward way to overcome hysteresis and non-negligible transformation width is to rely on values of critical temperature sensitivity to external fields high enough to move the transformation temperature outside of the hysteresis region in moderate fields, taking in mind the bivalent role played by dTM/μ0dH in determining the magnetocaloric properties [14]. For the sake of applications in energy efficient devices, whether magnetocaloric engines or magneto-thermal energy generators, it is necessary to provide high reversibility in low fields (typically below 2T, the maximum limit of permanent magnets).
On the other hand, the enhanced volume discontinuity that was measured on these alloys allows for improved multifunctionality, i.e., it opens up the possibility of simultaneous shift of the transformation by different fields. Magnetic measurements under hydrostatic pressure were carried out to study the pressure sensitivity of TM, dTM/dp; due to increased stability of the most packed structure, martensite, the hydrostatic pressure drives the martensitic temperature to higher values, the opposite of magnetic field application. The dTM/dp parameters for Co-doped samples, reported in Table 2, are higher than in the ternary compound, and for the In-doped sample reach unprecedented values among the entire class of Ni-Mn based Heuslers [14,29,37]. The In doped sample shows values of dTM/dp up to 6 K/kbar, 6 times higher than the ternary alloy.
As expected, the trend of the magnetization and volume discontinuities, as well as that of the critical temperature sensitivities to external forces, are coherent, i.e., higher discontinuities provide higher sensitivity of the critical temperature to the corresponding external force (Figure 4).
In our samples the enhanced response to pressure results in a substantial equivalence between 1T and 1 kbar in affecting the transformation temperature. We introduce here a magnetic field-pressure equivalence parameter, HPR = |(dTM/μ0dH)/(dTM/dp)|, that can be useful to compare the relative field and pressure sensitivity of different alloys (Table 2).
On the other hand, and additional parameter, the product of the two sensitivities, HPP = |(dTM/μ0dH)×(dTM/dp)|, can be introduced to account for the increased multifunctionality potential shown by doped alloys (Table 2). By Co and In doping Ni2MnGa, such multifunctional index is increased by almost two order of magnitudes; this means that both magnetic field and pressure are able to substantially shift the transformation. Such improved sensitivity to both fields, coupled to the opposite effect that magnetic field and pressure display (i.e., magnetic field shifts TM to lower temperatures, pressure shifts TM to higher ones) allows for the exploitation of new concept devices where hysteresis can be effectively canceled out by a subsequent application of field and pressure [14]. Figure 5 shows this concept on the In-doped sample: the 5T isofield curves are shifted even outside the thermal hysteresis by the application of 4.5 kbar, effectively overcoming hysteresis.
2.3. Calorimetry in Magnetic Field
The thermodynamic properties of the presented samples are studied by measuring the temperature and magnetic field dependence of the specific heat across the martensitic transformation (Figure 6). When dealing with magnetocaloric characterization, in-field differential scanning calorimetry (DSC), is indeed the technique which offers the largest amount of information [40]. By comparing the four panels of Figure 6, partial substitution of Ni by Co does not seem to affect the martensitic specific heat baseline (cp ~ 500 J/(Kg·K) at 320 K). The same is not verified for the high temperature phase: the specific heat of austenite in the parent alloy (Ni50Mn30Ga20) has lower values than the other materials due to the paramagnetic nature of the high temperature phase.
Field dependent calorimetry experiments confirm the values of dTM/μ0dH and hysteresis width already deduced from magnetization measurements.
It can be noticed that while the direct ferro-para system and the Co-doped alloys with ferro-ferro inverse transformation show the same dTM/μ0dH values across the heating and the cooling transformations, the In-doped sample shows unique features. In this case the magnetic field shifts more the cooling branch than the heating one. This behavior, already reported for NiMnSn-based systems [41], is due to the consistently larger ΔM jump across the cooling branch and results in a wider hysteresis in applied field: from 17.7 K in zero field to 20.3 K in 1.8 T. Also, the smaller specific heat peak values reflect a markedly broadened in-field martensitic transformation.
The latent heat λ of the fully transformed transition can be calculated by integrating the cp profiles after subtraction of the baseline (see Figure 7). Two features stick out from these plots: the value corresponding to the fully transformed process and the field effect on it.
The parent alloy shows the larger latent heat, pointing out how the effort to increase the MCE by enhancing the volume and the magnetization jump contributes indeed to increase the |dTM/μ0dH| while the maximum entropy change (calculated as ΔST = λ/TM) is depressed. This behavior is striking when comparing the parent alloy with the In-doped one. In the parent sample the ΔST of the fully induced process is about −18.5 J/(Kg·K) with dTM/μ0dH = +0.45 K/T, while in the In-doped sample a huge negative dTM/μ0dH = −5.5 K/T (comparable with the systems reported in [14]) can be used to trigger up to 6 J/(Kg·K).
The second interesting aspect is the action of the field on the fully induced latent heat. Within the error bars the direct and the ferro-ferro transformations are characterized by a constant transformation latent heat, as measured both on heating and cooling, both in applied and zero field. (Figure 7). The alloy characterized by the “low moment” martensite also in this case displays a peculiar behavior: both for the heating and cooling transformation, the latent heat measured in magnetic field is consistently lower than the corresponding zero field measure. From Figure 7 it can be observed that the stronger decrease of latent heat is realized when the transformation occurs at lower temperature; following the Brillouin-like increase of magnetization of ferromagnetic austenite by lowering the temperature, it appears that the latent heat decreases with ΔM increasing. This phenomenon could be related to a thermodynamic arrest mechanism already pointed out in the literature for Ni-Mn based Heusler alloys showing a reverse magnetostructural transition [42,43]. However, further studies are needed to achieve a better and complete understanding of this feature.
The field dependent specific heat curves are a powerful tool for a comprehensive measurement of the magnetocaloric effect: in fact, by integration it is possible to obtain the entropy-temperature curves across the transformation at different field values. The isentropic and isothermal differences between the two curves represent the adiabatic temperature change, ΔTad(T), and isothermal entropy change, Δsiso(T), respectively.
Table 3 reports the magnetocaloric data of the samples, both the transition entropy change of the fully induced transformation (calculated from latent heat and magnetic Clausius-Clapeiron relation) and the magnetocaloric effect Δsiso and ΔTad induced in a 1.8 T field.
The maximum entropy change calculated from the latent heat, ΔsT, matches quite well the results of magnetic Clausius-Clapeyron equation, Δsc-c. The difference shown for the In-doped sample arises from the different pieces of sample used in the different techniques. As reported in [36], proper measurement protocols have to be followed for the reliable analysis of first order transformation materials.
In Figure 8 we compare the temperature behavior of the isothermal entropy change induced by a field span of 1.8 T, Δsiso, calculated by both the magnetic measurements and the field dependent calorimetry. For clarity of the picture, only the heating branch of the transformation is considered. Magnetization isothermal curves have been planned to pick up the full irreversible effect; we took care to cross the cooling martensitic branch before starting every isothermal M(H) curve to avoid the presence of “ghost peaks” in the Δsiso(T) curve [44], and calculated the entropy change by exploiting the Maxwell relation. The calorimetric Δsiso values are the isothermal difference between the entropy curves in 0 T and 1.8 T obtained from integration of the specific heat curves of Figure 7. A quite good agreement between the two techniques is observed for all the studied samples (Figure 8). Magnetization measurements and DSC for the Co-substituted alloys have been performed on exactly the same fragment, while the Δsiso curves of the parent Ni50Mn30Ga20 sample were obtained from two different samples sharing the same composition: this justifies the slight peak shift (around 3 K) of the two Δs curves.
The maximum values of Δsiso (Table 3) are consistently lower than the ones estimated by latent heat: this demonstrates that the applied field change of 1.8 T is not enough to fully induce the transformation in either of the presented samples. By comparing the four samples, the two ferro-ferro inverse alloys, samples 5–30 and 5–31, show the maximum Δsiso of the series. The lower values shown by the parent sample and the In-doped alloy originate from different features: in the first case, the low value of dTM/μ0dH prevents the applied magnetic field of 1.8 T to fully induce the transformation; in the latter case, both the widening of the transformation and a much lower latent heat concur in obtaining a low Δsiso value.
The most interesting question relates at this point to how the large |dTM/μ0dH| values of the Co substituted alloys can enhance the MCE. The parameter dTM/μ0dH is well known to set an upper limit to the adiabatic temperature change, while at the same time it gives a rough indication of whether our material may be promising for applications (thanks to the possibility of fully induce the transformation in lower magnetic fields) [45,46].
We noticed that the magnetostructural transformation in these systems can be described, in the frame of a simple geometrical model, by a peculiar relation linking the field induced adiabatic temperature change ΔTad with dTM/μ0dH, with the martensite specific heat value cp Mart, the transformation temperature TM and the isothermal entropy change Δsiso [35,36,47]:
Here ΔTM = (dTM/μ0dH)·μ0ΔH is the effective transformation shift in temperature induced by a magnetic field variation μ0ΔH. The usefulness of this equation is that it gives the chance to estimate the ΔTad merely from indirect magnetization measurements. The specific heat of the low temperature phase can be safely taken from literature, while the remaining parameters can be deduced from isofield magnetization curves. It is important to stress that this relation holds for purely first-order systems and when the field-induced transition shift is smaller than the transformation width [35].
The non-negligible error propagation gives to the calculated ΔTad an uncertainty of about 30%–40%. The adiabatic temperature change obtained from direct measurements, field dependent DSC and calculated by using the Equation (1) is reported in Figure 9 for samples 5–30 and 5–31. A remarkable convergence of the three experimental techniques is realized: as discussed in [35], these results corroborate the reliability of the presented model for the estimation of the magnetocaloric effect by indirect methods, and highlight how the Maxwell relation for the calculation of isothermal entropy change Δsiso can correctly describe the magnetocaloric effect even of first order transformations. The ΔTad of these systems seems to increase in proportion to Co content, which means that there is a direct correlation between ΔTad, ΔM and dTM/μ0dH.
Equation (1) gives also interesting information about the relation linking ΔTad with dTM/μ0dH and Δsiso. The first consideration is that ΔTad is not directly proportional either to dTM/μ0dH or Δsiso. This is a direct consequence of the fact that the infinitesimal relation dTad = (TM/cp)dsiso cannot be straightforwardly extrapolated to finite differences due to the dependence on magnetic field and temperature of the specific heat, cp(H,T). On the other hand, eq. 1 relies on the simple value of the specific heat far from the transition region, cp Mart. Second, and perhaps even more interesting, it can be appreciated that the adiabatic temperature change tends to its upper limit set by the parameter dTM/μ0dH when cp Mart/TM→0. This condition is approached for relatively low values of the specific heat of the low temperature phase, and sets an additional figure of merit for the search of promising magnetocaloric materials endowed with high adiabatic temperature change [48].
3. Experimental Section
The samples were grown by arc melting stoichiometric amounts of pure elements in an inert atmosphere; homogenization was obtained by subsequent annealing in an inert atmosphere at 1173 K for 72 h followed by water quenching. The final compositions of the grown samples were verified by energy dispersive spectroscopy and were close to the nominal values with a maximum deviation of <1%. The magnetic and magnetostructural critical temperatures were identified by temperature dependence measurements of the initial a.c. susceptibility. The isothermal and isofield magnetic properties were measured in SQUID magnetometers (maximum field 5 T, temperature range 5–500 K).
Magnetic measurements under hydrostatic pressure were performed in a SQUID magnetometer by a purpose-built Cu(Be) pressure cell. Unit cell volumes of the parent and product phases were evaluated by X-ray diffraction at the transformation temperatures using a Thermo ARL X’tra diffractometer equipped with a solid-state Si(Li) Peltier detector and an environmental chamber.
The specific heat measurements, which allowed for the latent heat and magnetocaloric analysis, were performed with purpose built differential scanning calorimeter able to work up to 1.8 T and between 255 K and 390 K. This setup exploits Peltier cells both as active and passive elements [36]. ΔTad was evaluated for a field change up to 1.9 T at a maximum field rate of <2.2 T/s. The direct probe operates in vacuum (10−4 mbar) and uses a Cernox HT-BR temperature sensor connected to the sample with a thermo conductive paste.
4. Conclusions
We have shown that in Mn-rich Ni2MnGa Heusler compounds the chemical substitution with Co and In has profound effects both on the magnetic properties and the structural stability. In particular, it is possible to tune the magnetic properties of austenite and martensite independently, allowing for the martensitic transformation to occur between ferromagnetic phases, or between ferro-martensite para-austenite or even enabling an inverse transformation between para-martensite and a strongly ferromagnetic austenite. This reflects also on the magnetocaloric properties: in this sense the Ga based alloys are attractive for their unique feature to switch from direct to inverse giant MCE by compositional change.
The doped alloys show enhanced magnetic and structural discontinuities across the martensitic transformation, which allow for an increased drive of the structural instability through external stimuli; remarkably, the In-doped sample show the highest value of dTM/dp (up to 6 K/kbar) for this class of materials.
Since the enhanced response with respect to magnetic field and pressure seems somehow entangled in these alloys, we have suggested two index parameters (the ratio and the product of the critical temperature dependence to external fields) that describe their multifunctionality; such parameters could also be considered for the evaluation and comparison of other classes of materials.
We have reviewed the magneto-thermodynamic properties of the presented samples by several different techniques, providing a comprehensive analysis of the giant magnetocaloric effect across the martensitic transformation. We have proved the convergence of the results obtained from different techniques, and highlighted some detrimental features connected to the magnetostructural transformation, such as inhomogeneity and partial cycling effects, that should be taken care of in order to provide affordable characterization of first order materials. The doped alloys show quite high values of adiabatic temperature change, estimated up to −2.3 K for the In-doped sample.
Finally, we have proposed a simplified model for the estimation of the adiabatic temperature change that relies only on indirect measurements, allowing for the quick and reliable evaluation of the magnetocaloric potentiality of new materials starting from readily available magnetic measurements.
Acknowledgments
The financial support from the 2007–2013 FESR Operative program of the Emilia Romagna Region (Activity I.1.1) is acknowledged. Part of this work has been performed in the framework of the CNR-AS CR 2009–2012 and 2013–2015 bilateral Agreements.
Conflicts of Interest
The authors declare no conflict of interest.
- Author ContributionsSimone Fabbrici, Franca Albertini and Giacomo Porcari wrote the manuscript. Simone Fabbrici synthesized the samples and performed temperature dependent X-ray diffraction experiments. Simone Fabbrici, Riccardo Cabassi, Giacomo Porcari, Francesco Cugini and Massimo Solzi performed magnetic measurements. Giacomo Porcari, Francesco Cugini and Massimo Solzi performed calorimetric measurements. Jiri Kamarad, Zdenek Arnold performed magnetic measurements under pressure. Franca Albertini supervised the research. All authors have read and approved the final manuscript.
References
- Ullakko, K.; Huang, J.K.; Kanter, C.; O’Handley, R.C.; Kokorin, V.V. Large magnetic-field-induced strains in Ni2MnGa single crystals. Appl. Phys. Lett 1996, 69. [Google Scholar] [CrossRef]
- Acet, M.; Manosa, L.; Planes, A. Magnetic-Field-Induced Effects in Martensitic Heusler-Based Magnetic Shape Memory Alloys. In Handbook of Magnetic Materials; 19Buschow, K.H.J., Ed.; Elsevier: Amsterdam, The Netherlands, 2011; Chapter 4pp. 231–289. [Google Scholar]
- Siewert, M.; Gruner, M.E.; Hucht, A.; Herper, H.C.; Dannenberg, A.; Chakrabarti, A.; Singh, N.; Arroyave, R.; Entel, P. A First-Principles Investigation of the Compositional Dependent Properties of Magnetic Shape Memory Heusler Alloys. Adv. Eng. Mater 2012, 14, 530–546. [Google Scholar]
- Sozinov, A.; Likhachev, A.A.; Lanska, N.; Ullakko, K. Giant magnetic-field-induced strain in NiMnGa seven-layered martensitic phase. Appl. Phys. Lett 2002, 80, 1746–1748. [Google Scholar]
- Sozinov, A.; Lanska, N.; Soroka, A.; Zou, W. 12% magnetic field-induced strain in Ni-Mn-Ga-based non-modulated martensite. Appl. Phys. Lett 2013, 102, 021902. [Google Scholar]
- Planes, A.; Manosa, L.; Acet, M. Magnetocaloric effect and its relation to shape-memory properties in ferromagnetic Heusler alloys. J. Phys. Condens. Matter 2009, 21, 233201. [Google Scholar]
- Karaca, H.E.; Karaman, I.; Basaran, B.; Ren, Y.; Chumlyakov, Y.I.; Maier, H.J. Magnetic Field-Induced Phase Transformation in NiMnCoIn Magnetic Shape-Memory Alloys—A New Actuation Mechanism with Large Work Output. Adv. Funct. Mater 2009, 19, 983–998. [Google Scholar]
- Kainuma, R.; Imano, Y.; Ito, W.; Sutou, Y.; Morito, H.; Okamato, H.; Kitakami, S.; Oikawa, O.; Fujita, A.; Kanomata, T.; et al. Magnetic-field-induced shape recovery by reverse phase transformation. Nature 2006, 439, 957–960. [Google Scholar]
- Sharma, V.K.; Chattopadhyay, M.K.; Shaeb, K.H.B.; Chouhan, A.; Roy, S.B. Large magnetoresistance in Ni50Mn34In16 alloy. Appl. Phys. Lett 2006, 89, 222509. [Google Scholar]
- Zhang, B.; Zhang, X.X.; Yu, S.Y.; Chen, J.L.; Cao, Z.X.; Wu, G.H. Giant magnetothermal conductivity in the Ni-Mn-In ferromagnetic shape memory alloys. Appl. Phys. Lett 2007, 91, 012510. [Google Scholar]
- Hu, F.X.; Shen, B.G.; Sun, J.R. Magnetic entropy change in Ni51.5Mn22.7Ga25.8 alloy. Appl. Phys. Lett 2000, 76, 3460–3462. [Google Scholar]
- Pareti, L.; Solzi, M.; Albertini, F.; Paoluzi, A. Giant entropy change at the co-occurrence of structural and magnetic transitions in the Ni2.19Mn0.81Ga Heusler alloy. Eur. Phys. J. B 2003, 32, 303–307. [Google Scholar]
- Krenke, T.; Duman, E.; Acet, M.; Wassermann, E.F.; Moya, X.; Manosa, L.; Planes, A. Inverse magnetocaloric effect in ferromagnetic Ni-Mn-Sn alloys. Nat. Mater 2005, 4, 450–454. [Google Scholar]
- Liu, J.; Gottschall, T.; Skokov, K.P.; Moore, J.D.; Gutfleisch, O. Giant magnetocaloric effect driven by structural transitions. Nat. Mater 2012, 11, 620–626. [Google Scholar]
- Mañosa, L.; González-Alonso, D.; Planes, A.; Bonnot, E.; Barrio, M.; Tamarit, J.L.; Aksoy, S.; Acet, M. Giant solid-state barocaloric effect in the Ni-Mn-In magnetic shape-memory alloy. Nat. Mater 2010, 9, 478–481. [Google Scholar]
- Khan, M.; Dubenko, I.; Stadler, S.; Ali, N. Exchange bias behavior in Ni-Mn-Sb Heusler alloys. Appl. Phys. Lett 2007, 91, 072510. [Google Scholar]
- Wang, Y.; Huang, C.; Gso, J.; Yang, S.; Ding, X.; Song, X.; Ren, X. Evidence for ferromagnetic strain glass in Ni-Co-Mn-Ga Heusler alloy system. Appl. Phys. Lett 2012, 101, 101913. [Google Scholar]
- Chernenko, V.A.; Cesari, E.; Kokorin, V.V.; Vitenko, I.N. The development of new ferromagnetic shape memory alloys in Ni-Mn-Ga System. Scripta Metallurgica et Materialia 1995, 33, 1239–1244. [Google Scholar]
- Khovaylo, V.V.; Buchelnikov, V.D.; Kainuma, R.; Koledov, V.V.; Ohtsuka, M.; Shavrov, V.G.; Takagi, T.; Taskaev, S.V.; Vasiliev, A.N. Phase transitions in Ni2+x Mn1−x Ga with a high Ni excess. Phys. Rev. B 2005, 72, 224408. [Google Scholar]
- Albertini, F.; Solzi, M.; Paoluzi, A.; Righi, L. Magnetocaloric Properties and Magnetic Anisotropy by Tailoring Phase Transitions in NiMnGa Alloys. In Advances in Shape Memory Materials; Book Series: Materials Science Forum; Volume 583, Chernenko, V.A., Ed.; Trans Tech Publications: Zurich, Switzerland, 2008; pp. 169–196. [Google Scholar]
- Aksoy, S.; Acet, M.; Wassermann, E.F.; Krenke, T.; Moya, X.; Manosa, L.; Planes, A.; Deen, P.P. Structural properties and magnetic interactions in martensitic Ni-Mn-Sb alloys. Philos. Mag 2009, 89, 2093–2109. [Google Scholar]
- Entel, P.; Dannenberg, A.; Siewert, M.; Herper, H.C.; Gruner, M.E.; Buchelnikov, V.; Chernenko, V.A. Composition-Dependent Basic of Smart Heuslers Materials from First Principles Calculations. In Advances in Shape Memory Materials; Book Series: Materials Science Forum; Volume 684, Chernenko, V.A., Ed.; Trans Tech Publications: Zurich, Switzerland, 2011; pp. 1–29. [Google Scholar]
- Barandiaran, J.M.; Chernenko, V.A.; Cesari, E.; Salas, D.; Gutierrez, J.; Lazpita, P. Magnetic field and atomic order effect on the martensitic transformation of a metamagnetic alloy. J. Phys. Condens. Matter 2013, 25, 484005. [Google Scholar]
- Entel, P.; Siewert, M.; Grune, M.E.; Herper, H.C.; Comtesse, D.; Arroyave, R.; Singh, N.; Talapatra, A.; Sokolovskiy, V.; Buchelnikov, V.D.; et al. Complex magnetic ordering as a driving mechanism of multifunctional properties of Heusler alloys from first principles. Eur. Phys. J. B 2013, 86, 1–11. [Google Scholar]
- Righi, L.; Albertini, F.; Calestani, G.; Pareti, L.; Paoluzi, A.; Ritter, C.; Algarabel, P.A.; Morellon, L.; Ibarra, M.R. Incommensurate modulated structure of the ferromagnetic shape-memory Ni2MnGa martensite. J. Solid State Chem 2006, 179, 3526–3533. [Google Scholar]
- Righi, L.; Albertini, F.; Pareti, L.; Paoluzi, A.; Calestani, G. Commensurate and incommensurate “5M” modulated crystal structures in Ni-Mn-Ga martensitic phases. Acta Mater 2007, 55, 5237–5245. [Google Scholar]
- Righi, L.; Albertini, F.; Villa, E.; Paoluzi, A.; Calestani, G.; Chernenko, V.A.; Besseghini, S.; Ritter, C.; Passaretti, F. Crystal structure of 7M modulated Ni-Mn-Ga martensitic phase. Acta Mater 2008, 56, 4529–4535. [Google Scholar]
- Albertini, F.; Pareti, L.; Paoluzi, A.; Morellon, L.; Algarabel, P.A.; Ibarra, M.R.; Righi, L. Composition and temperature dependence of the magnetocrystalline anisotropy in Ni2+xMn1+yGa1+z (x + y + z = 0) Heusler alloys. Appl. Phys. Lett 2002, 81, 4032–4034. [Google Scholar]
- Albertini, F.; Fabbrici, S.; Paoluzi, A.; Kamarad, J.; Arnold, Z.; Righi, L.; Solzi, M.; Porcari, G.; Pernechele, C.; Serrate, D.; et al. Reverse Magnetostructural Transitions by Co and In Doping NiMnGa Alloys: Structural, Magnetic, and Magnetoelastic Properties. In Advances in Magnetic Shape Memory Materials; Book Series: Materials Science Forum; Volume 684, Chernenko, V.A., Ed.; Trans Tech Publications: Zurich, Switzerland, 2011; pp. 151–163. [Google Scholar]
- Righi, L.; Albertini, F.; Fabbrici, S.; Paoluzi, A. Crystal Structures of Modulated Martensitic Phases of FSM Heusler Alloys. In Advances in Shape Magnetic Memory Materials; Book Series: Materials Science Forum; Volume 684, Chernenko, V.A., Ed.; Trans Tech Publications: Zurich, Switzerland, 2011; pp. 105–116. [Google Scholar]
- Righi, L.; Albertini, F.; Paoluzi, A.; Fabbrici, S.; Villa, E.; Calestani, G.; Besseghini, S. Incommensurate and Commensurate Structural Modulation in Martensitic Phases of FSMA. In Ferromagnetic Shape Memory Alloys II; Book Series: Materials Science Forum; Chernenko, V.A., Barandiaran,, J.M., Eds.; Trans Tech Publications: Zurich, Switzerland, 2010; pp. 33–41. [Google Scholar]
- Fabbrici, S.; Albertini, F.; Paoluzi, A.; Bolzoni, F.; Cabassi, R.; Solzi, M.; Righi, L.; Calestani, G. Reverse magnetostructural transformation in Co-doped NiMnGa multifunctional alloys. Appl. Phys. Lett 2009, 95, 022508. [Google Scholar]
- Enkovaara, J.; Heczko, O.; Ayuela, A.; Nieminem, R.M. Coexistence of ferromagnetic and antiferromagnetic order in Mn-doped Ni2MnGa. Phys. Rev. B 2003, 67, 212405. [Google Scholar]
- Fabbrici, S.; Kamarad, J.; Arnold, Z.; Casoli, F.; Paoluzi, A.; Bolzoni, F.; Cabassi, R.; Solzi, M.; Porcari, G.; Pernechele, C.; et al. From direct to inverse giant magnetocaloric effect in Co-doped NiMnGa multifunctional alloys. Acta Mater 2011, 59, 412–419. [Google Scholar]
- Porcari, G.; Fabbrici, S.; Pernechele, C.; Albertini, F.; Buzzi, M.; Paoluzi, A.; Kamarad, J.; Arnold, Z.; Solzi, M. Reverse magnetostructural transformation and adiabatic temperature change in Co-, In-substituted Ni-Mn-Ga alloys. Phys. Rev. B 2012, 85, 024414. [Google Scholar]
- Porcari, G.; Cugini, F.; Fabbrici, S.; Pernechele, C.; Albertini, F.; Buzzi, M.; Mangia, M.; Solzi, M. Convergence of direct and indirect methods in the magnetocaloric study of first order transformations: the case of Ni-Co-Mn-Ga Heusler alloys. Phys. Rev. B 2012, 86, 104432. [Google Scholar]
- Manosa, L.; Moya, X.; Planes, A.; Gutfleisch, O.; Lyubina, J.; Barrio, M.; Tamarit, J.L.; Aksoy, S.; Krenke, T.; Acet, M. Effects of hydrostatic pressure on the magnetism and martensitic transition of Ni-Mn-In magnetic superelastic alloys. Appl. Phys. Lett 2008, 92, 012515. [Google Scholar]
- Cui, J.; Chu, Y.S.; Famodu, O.; Furuya, Y.; Hattrick-Simpers, J.; James, R.D.; Ludwig, A.; Thienhaus, S.; Wuttig, M.; Zhang, Z.; et al. Combinatorial search of thermoelastic shape-memory alloys with extremely small hysteresis width. Nat. Mater 2006, 5, 286–290. [Google Scholar]
- Emre, B.; Yuce, S.; Stern-Taulats, E.; Planes, A.; Fabbrici, S.; Albertini, F.; Manosa, L. Large reversible entropy change at the inverse magnetocaloric effect in Ni-Co-Mn-Ga-In magnetic shape memory alloys. J. Appl. Phys 2013, 113, 213905. [Google Scholar]
- Basso, V.; Sasso, C.P.; Küpferling, M. A Peltier cells differential calorimeter with kinetic correction for the measurement of cp(H,T) and Δs(H,T) of magnetocaloric materials. Rev. Sci. Instrum 2010, 81, 113904. [Google Scholar]
- Khovaylo, V.V.; Skokov, K.P.; Gutfleisch, O.; Miki, H.; Takagi, T.; Kanomata, T.; Koledov, V.V.; Shavrov, V.G.; Wang, G.; Palacios, E.; et al. Peculiarities of the magnetocaloric properties in Ni-Mn-Sn ferromagnetic shape memory alloys. Phys. Rev. B 2010, 81, 214406. [Google Scholar]
- Ito, W.; Ito, K.; Umetsu, R.Y.; Kainuma, R.; Koyama, K.; Watanabe, K.; Fujita, A.; Oikawa, K.; Ishida, K.; Kanomata, T. Kinetic arrest of martensitic transformation in the NiCoMnIn metamagnetic shape memory alloy. Appl. Phys. Lett 2008, 92, 021908. [Google Scholar]
- Xu, X.; Ito, W.; Umetsu, R.Y.; Koyama, K.; Kainuma, R.; Ishida, K. Kinetic Arrest of Martensitic Transformation in Ni33.0Co13.4Mn39.7Ga13.9 Metamagnetic Shape Memory Alloy. Mat. Trans 2010, 51, 469–471. [Google Scholar]
- Caron, L.; Ou, Z.Q.; Nguyen, T.T.; Cam Thanh, D.T.; Tegus, O.; Brück, E. On the determination of the magnetic entropy change in materials with first-order transitions. J. Magn. Magn. Mater 2009, 321, 3559–3566. [Google Scholar]
- Pecharsky, V.K.; Gschneidner, K.A., Jr.; Pecharsky, A.O.; Tishin, A.M. Thermodynamics of the magnetocaloric effect. Phys. Rev. B 2001, 64, 144406. [Google Scholar]
- Skokov, K.P.; Mueller, K.H.; Moore, J.D.; Liu, J.; Karpenkov, A.Y.; Krautz, M.; Gutfleisch, O. Influence of thermal hysteresis and field cycling on the magnetocaloric effect in LaFe11.6Si1.4. J. All. Comp 2013, 552, 310–317. [Google Scholar]
- Porcari, G. Magnetocaloric Effect across First Order Transformations of Energy Conversion Materials. Ph.D. Thesis, University of Parma, Parma, Italy, 2013. [Google Scholar]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Some common misconceptions concerning magnetic refrigerant materials. J. Appl. Phys 2001, 90, 4614–4622. [Google Scholar]








| Sample ID | Nominal composition | TCM [K] | TCA [K] | TM-A [K] | TA-M [K] | Hysteresis [K] | Transition width [K] |
|---|---|---|---|---|---|---|---|
| Parent | Ni50Mn30Ga20 | -- | 368 | 375 | 368 | 7 | 10 |
| 5–30 | Ni40Co5Mn30Ga20 | -- | 420 | 337 | 327 | 10 | 5 |
| 5–31 | Ni40Co5Mn31Ga19 | -- | 420 | 353 | 341 | 12 | 13 |
| In-doped | Ni41Co9Mn32Ga16 In2 | 245 | 448 | 343 | 321 | 22 | 35 |
| Sample ID | ΔMM-A [Am2/Kg] | ΔMiso [Am2/Kg] | dTM/Δ0dH [K/T] | ΔV/V % | dTM/dp [K/kbar] | HPR |(dTM/0dH)/(dTM/dp)|[kbar/T] | HPP |(dTM/0dH)×(dTM/dp)|[K2/(T·kbar)] |
|---|---|---|---|---|---|---|---|
| Parent | −9.5 | −7.5 | +0.45 | 0.2 | 1.0 | 0.4 | 0.4 |
| 5–30 | 15 | 16.5 | −1.2 | 0.45 | 1.3 | 0.92 | 1.56 |
| 5–31 | 16 | 21.5 | −1.3 | 0.55 | 2.5 | 0.52 | 3.25 |
| In-doped | 60 | 72 | −5.5 | 0.9 | 6.0 | 0.91 | 33 |
| Sample | Latent heat (J·kg−1) | ΔsT (Jkg−1K−1) | ΔsC-C (Jkg−1K−1) | Δsiso(1.8 T) (Jkg−1K−1) | ΔTad(1.8 T) (K) |
|---|---|---|---|---|---|
| Ni50Mn30Ga20 | 6900 | −19 | −21 | −3.7 | +0.8 |
| Ni45Co5Mn30Ga20 | 4900 | 14 | 12.5 | +6 | −1.45 |
| Ni45Co5Mn31Ga19 | 4500 | 12.5 | 12 | +5 | −1.5 |
| Ni41Co9Mn32Ga16In2 | 2300 | 6 | 11 | +4.5 | −2.3 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fabbrici, S.; Porcari, G.; Cugini, F.; Solzi, M.; Kamarad, J.; Arnold, Z.; Cabassi, R.; Albertini, F. Co and In Doped Ni-Mn-Ga Magnetic Shape Memory Alloys: A Thorough Structural, Magnetic and Magnetocaloric Study. Entropy 2014, 16, 2204-2222. https://doi.org/10.3390/e16042204
Fabbrici S, Porcari G, Cugini F, Solzi M, Kamarad J, Arnold Z, Cabassi R, Albertini F. Co and In Doped Ni-Mn-Ga Magnetic Shape Memory Alloys: A Thorough Structural, Magnetic and Magnetocaloric Study. Entropy. 2014; 16(4):2204-2222. https://doi.org/10.3390/e16042204
Chicago/Turabian StyleFabbrici, Simone, Giacomo Porcari, Francesco Cugini, Massimo Solzi, Jiri Kamarad, Zdenek Arnold, Riccardo Cabassi, and Franca Albertini. 2014. "Co and In Doped Ni-Mn-Ga Magnetic Shape Memory Alloys: A Thorough Structural, Magnetic and Magnetocaloric Study" Entropy 16, no. 4: 2204-2222. https://doi.org/10.3390/e16042204
APA StyleFabbrici, S., Porcari, G., Cugini, F., Solzi, M., Kamarad, J., Arnold, Z., Cabassi, R., & Albertini, F. (2014). Co and In Doped Ni-Mn-Ga Magnetic Shape Memory Alloys: A Thorough Structural, Magnetic and Magnetocaloric Study. Entropy, 16(4), 2204-2222. https://doi.org/10.3390/e16042204





