A Two-stage Method for Solving Multi-resident Activity Recognition in Smart Environments
Abstract
: To recognize individual activities in multi-resident environments with pervasive sensors, some researchers have pointed out that finding data associations can contribute to activity recognition and previous methods either need or infer data association when recognizing new multi-resident activities based on new observations from sensors. However, it is often difficult to find out data associations, and available approaches to multi-resident activity recognition degrade when the data association is not given or induced with low accuracy. This paper exploits some simple knowledge of multi-resident activities through defining Combined label and the state set, and proposes a two-stage activity recognition method for multi-resident activity recognition. We define Combined label states at the model building phase with the help of data association, and learn Combined label states at the new activity recognition phase without the help of data association. Our two stages method is embodied in the new activity recognition phase, where we figure out multi-resident activities in the second stage after learning Combined label states at first stage. The experiments using the multi-resident CASAS data demonstrate that our method can increase the recognition accuracy by approximately 10%.1. Introduction
Activity recognition has appeared as an Ambient Intelligence (AmI) feature to facilitate the development of applications that are aware of users’ presence and context and are adaptive and responsive to their needs and habits. Such assistive technologies have been widely adopted in smart home systems and healthcare applications involving only a single resident [1,2], and have delivered promising results for offering thoughtful services to an elderly resident [3,4,5], and providing responsive help in emergencies [6]. Now the interest in designing smart environments that can reason about multiple residents is growing. However, earlier work includes finding out global behaviors and preferences of a group residents [7,8] and little is focused on recognizing the activity of every resident in a multi-resident environment. The focus of our study is how to recognize individual activities in multi-resident environments.
Moving from a single resident to multiple ones, many researchers often resort to asking residents to carry wearable devices [9] or capturing their behavior with video cameras [10]. However, this might erode the human-centric advantages of AmI since wearable sensors may cause inconvenience, and camera-based solutions may raise residents’ privacy concerns. Therefore some researchers have preferred to deploy non-obtrusive and pervasive sensors such as pressure sensors, reed switches, motion sensors and temperature sensors for tuning activity reasoning in a multi-resident environment.
For multi-resident activity recognition using non-obtrusive sensors, most of the related studies have involved data association, i.e., associating sensor data with the right person. In [11], Wilson and Atkeson first introduced the concept of data association and pointed out that we need some way of determining which occupant generated what observation. Most recent work also looked into the benefits of data association in activity estimation. Singla et al. [12] first modeled the independent and joint activities among multiple residents using a single Hidden Markov model (HMM), then with manual data association, they modeled one HMM for one resident. Based on the Conditional Random Field (CRF), Hsu et al. [13] proposed an iterative procedure to train and infer the activities and data association in turns, and their empirical studies proved that good data association can greatly improve the accuracy of multi-resident activity recognition. Provided with data association, Chiang and Hsu [14] improve the accuracy of activity estimation by modeling interactions among residents. Wang et al. [15] proposed using Coupled Hidden Markov Model (CHMM) and Factorial Conditional Random Field (FCRF) to model interaction processes.
Besides data association in training activity recognition models, however, previous methods either need or infer data association when recognizing new multi-resident activities based on new observations from sensors. For the training dataset, it is easy to find out data associations because which resident is carrying out activity is known at each moment. For new observations from sensors, it is hard to find out the data association because we don’t know which resident is carrying out the activity. The problem is that activity estimation in a multi-resident context greatly degrades when data association is not available or is induced in a low quality [12,13]. Learning data association is interesting but not easy, and even harder with unreliable data signaled by non-obtrusive and pervasive sensors, and also it may vary from application to application, so there is not such a strong underlying association for recognition algorithms to use.
In the smart homes setting, there are activities that can be done independently, jointly or exclusively, so we believe that there is some simple knowledge in activities (i.e. pattern, global features and trends) that is invariant and easy to set up in the multi-resident context. For instance, two residents may be used to carrying out activities collaboratively (playing chess), one may do one activity when the other is doing another (resident B is used to sleeping when resident A is watching TV), or one can exclusively carry out some activity (resident B must do other thing when a computer is used by resident A, since there are only one computer in the home). Data association can be a kind of simple knowledge, but not the other way around in that simple knowledge does not indicate the association between sensor data and a particular person. Considered seriously, the so-called “simple knowledge” is beyond data association by expressing something like “what is done together”, and “what is done individually”; it aims to exploit some properties of multi-residents’ behavior, either spatial or temporal, which are handy and widely valid in most smart environments.
To exploit simple knowledge in multi-resident activities, we define one Combined label and use the states to signify two or more activities that are performed simultaneously and independently by multiple residents. By learning the states of the Combined label, we can gain the global features and trends of multi-resident activities, and our goal is to find the most likely Combined label states sequence that could have generated the original sensor event sequence and then use the Combined label states to figure out multi-resident activities. In doing so, this paper proposes a two-stage method for multi-resident activity recognition to improve the performance. There are two phases in our model defined as model building phase and new activity recognition phase. Our two stages method embodied in the new activity recognition phase. We build and train activity recognition model at model building phase using training dataset. At new activity recognition phase, our method learns Combined label states at first stage, and then maps the Combined label states to multi-resident activities at the second stage.
Compared to previous methods, our method builds activity recognition models using a training dataset with the help of data association, while does not need data association when recognizing new multi-resident activities based on new observations from sensors. This is dictated by two reasons: first, for the training dataset, we need the simple knowledge to build State Event Matrix to create the State Event Set and to build the activity recognition model offline; second, the State Event Matrix is built based on inverse mapping from the Combined label states to the State Event Set where Combined label states are inferred by the learned activity recognition model and State Event Sets are learned from the training dataset.
The paper is organized as follows: Section 2 will introduce our two-stage method for multi-resident activity recognition in detail. Then, we will verify our method in the Section 3. Finally, we summarize this paper in Section 4.
2. Two-Stage Method for Multi-Resident Activity Recognition
In this section, we begin with the problem statement, and give some definitions. After that, two typical activity recognition models like HMM and CRF are briefly introduced. Finally, we propose our two-stage multi-resident activity recognition method.
2.1. Problem Statement
Activity recognition is often done with a learned state space model with hidden variables to infer a multi-resident activity sequence {y1, y2, …, yT} from an observation sequence {x1, x2, …, xT}, where yt, t = 1, 2, …, T, are activity label vectors with the dimension equal to the number of residents and xt, t = 1, 2, …, T, are observation vectors with the dimension equal to the number of sensors.
Learning such a model often needs some training data, namely historical sensor data and their action labels, and the training data set is denoted as {(x1, y1), (x2, y2),…, (xT0, yT0)}. To formalize the problem, we will give a multi-resident scenario:
Scenario
In one home set, two residents with resident ID = 1 and resident ID = 2 randomly performed three activities labeled by 1, 2 and 3. Sometimes they are doing something together, sometimes they are doing things separately, and sometimes they are doing something meaningless (labeled by 0). So we have labeled dataset {(x1, y1), (x2, y2),…, (x7, y7)}, where xi, i = 1, 2, …, 7, are observations and y1 = (0, 0), y2 = (1, 0), y3 = (1, 0), y4 = (3, 0), y5 = (1, 1), y6 = (1, 1), y7 = (3, 3) are the activity label vector of the two residents.
2.2. Some Definitions
Definition 1 (Single-label Problem)
Single-label learning is phrased as the problem of finding a model that maps inputs x to a scalar output y.
Definition 2 (Multi-label Problem)
Multi-label learning is phrased as the problem of finding a model that maps inputs x to a vector y, rather than a scalar output.
For an observation sequence x1:T = {x1, x2, …, xT}, it is a Single-label Problem if there is a sequence of labels y1:T = {y1, y2, …, yT}, where yt, t = 1, 2, …, T, are single-label vectors that best explains the sequence, and it is Multi-label Problem if there is a sequence of labels y1:T = {y1, y2, …, yT}, where yt, t = 1, 2, …, T, are multi-label vectors that best explains the sequence.
Multi-resident activity recognition is a Multi-label Problem if we regard one resident as one label and regard one activity as one state. The activities label for two residents at time step t is a two-dimensional label and denoted as , where , i = 1, 2 is the activity ID at time step t that triggered the signals and performed by the i-th resident.
In the above two resident scenario, if we count all activities of two residents that can happen concurrently, we can get 4 × 4 = 16 different two-dimensional label vectors which are included in set {(0, 0), (0, 1), …, (3, 3)}. However, due to the fact some activities do not occur concurrently in real life, there are only seven two-dimensional label vectors, and some of them are the same. For example, a person cannot perform “using computer” if the computer is occupied by another person and the combined state denoted that two persons perform ‘using computer’ simultaneously is illegal.
To reduce the complexity of labeling, we introduced concept of State Event, State Event Matrix M and State Event Set A.
Definition 3 (State Event)
For any observation xt with m different labels, we define State Event as ( ), where is the state of the i-th label at time step t.
Therefore, State Event is multi-dimensional vector which represent the possible states of all individual labels at the same time step. In multi-resident scenario, we use State Event to present the multi-resident activities at the same time step, and State Event ( ) to present the activities of all residents at time step t and present the activity of the i-th resident at time step t.
Definition 4 (State Event Matrix M)
For any observation xt with m different labels, we define State Event Matrix M as:
where the i-th row is the i-th State Event, the j-th column represents the state of j-th label, and T is the State Event number which equals to the total training data number.
Definition 5 (State Event Set A)
where K is the total number of different State Events and all State Event can be found in set A.
According to the definition of M, the State Event Matrix M1 of the above multiple-resident scenario can be expressed as:
As M1 shows, the second State Event and the third State Event are the same, the 5-th State Event and 6-th State Event are the same, and all State Event are included in the State Event Set A1 = {(0, 0), (1, 0), (3, 0), (1, 1), (3, 3)}.
To represent the possible states of all individual labels simultaneously, we define a Combined label C and a mapping f as follows.
Definition 6 (Combined label C)
Combined label C is single variable with state set B = {0, 1, …, K−1}, where K is the total number of different State Events.
Definition 7 (Mapping f)
The mapping f maps the State Event set to state set B as:
where ( ) is the k-th different State Event if and only if Ck is the k-th states of C.
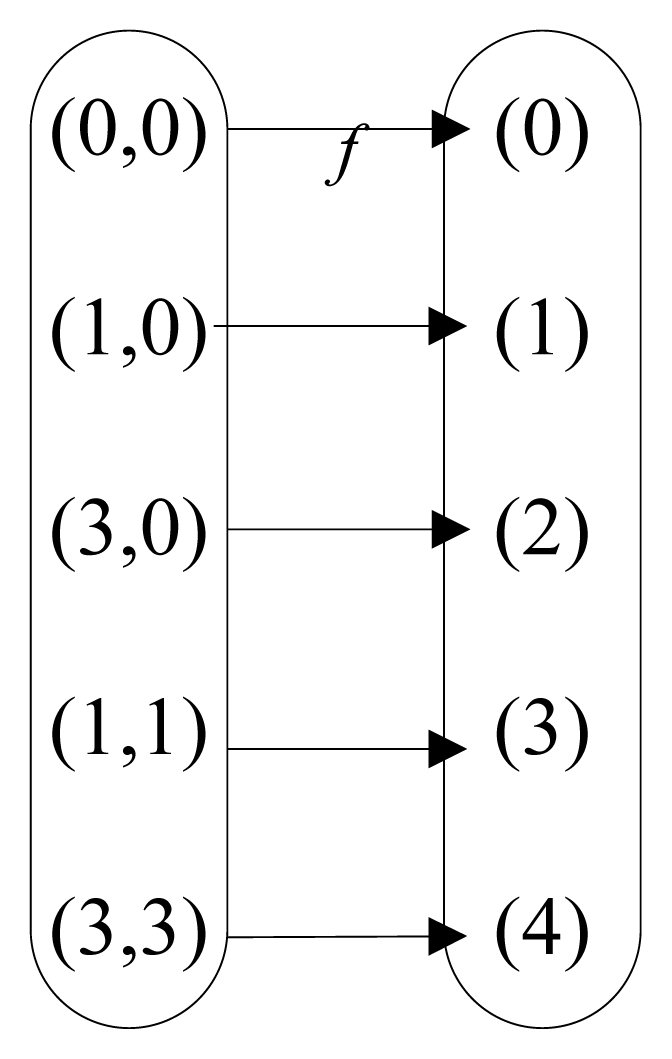
In our multi-resident scenario, the State Event Set is A1 = {(0, 0), (1, 0), (3, 0), (1, 1), (3, 3)}, the Combined label state set is B1 = {0, 1, 2, 3, 4}, and the mapping between A1 and B1 is clearly listed as Figure 1.
Similarly, we can map State Event at time t to the states set B as:
and if and only if Ci = Cj.
The mapping between State Event Matrix M1 and states set B1 is defined as:
Representing the possible states of all individual labels at the same time as Combined label states C, we can get Figure 2b instead of Figure 2a and the states of y1, y2 can be inferred on the basis of the states of C. For example, in our multi-resident scenario, when C = 1, there are y1 = 1, y2 = 0, and when C = 3, there are y1 = 1, y2 = 1. Therefore, the multi-label problem is converted to a single-label problem. Thus, multi-resident activities can be recognized by finding out the states of Combined label C and backward reasoning State Event based on inverse mapping f−1, and then find the state of individual labels which present activities of single resident in our case. Apparently, given the mapping from Combined label states set to State Event set, above method can recognize multi-resident activities base on Combined label states.
If there is a need to know the data association, i.e. tracking the resident, we can also find out data association based on the states of Combined label C. For example, given C = 1, we can figure out y1 = 1, y2 = 0, where y1 = 1 represents that the first person is carrying out the first activity while y2 = 0 represents the second person do not trigger signals at this time step. Because the first state is non-zero, we say that the first person triggered the signals and generated the observations.
2.3. Hidden Markov Model
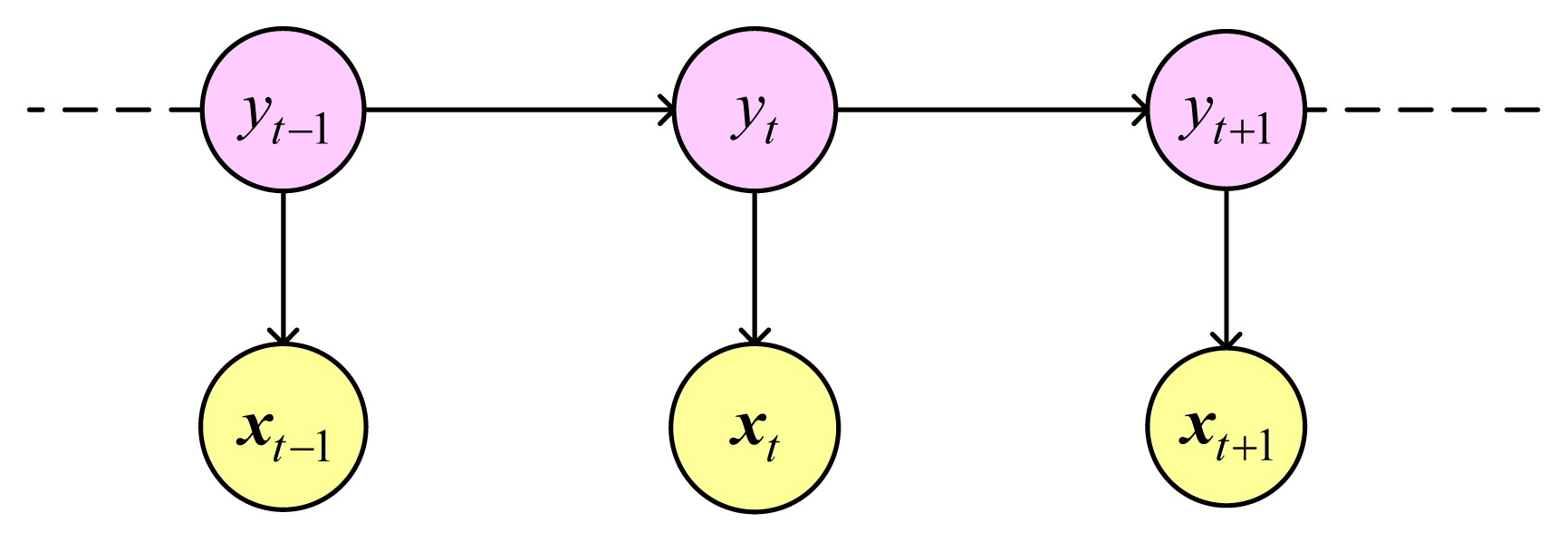
The Hidden Markov Model (HMM) is a generative probabilistic model and is the development of the Naive Bayes in sequence direction. The model consists of a hidden variable y and an observable variable x at each time step. There are two dependency assumptions in HMM. Firstly, the hidden variable at time t, namely yt, depends only on the previous hidden variable yt−1. Secondly, the observable variable at time t, namely xt, depends only on the hidden variable yt at that time slice. Figure 3 is graph structure of HMM.
HMM models joint probability as follows:
Thus, HMM can be modeled using three probability distributions: initial state distributions p(y1), transition probability distribution p(yt|yt−1) and observation distribution p(xt|yt).
Given a labeled dataset {(xt, yt)}, t = 1, 2, …, T, we can calculate the initial state distributions πi = p(y1 = i), i = 1, 2, …, K, which represents the belief about which state the HMM is in when the first sensor event is seen. For a state (activity) a, this is calculated as the ratio of instances for which the activity label is a. The transition probability aij = p(yt = j|yt−1 = i), i, j = 1, 2, …, K, signifies the likelihood of transitioning from a given state to any other state in the model and captures the temporal relationship between the states. For any two states a and b, the probability of transitioning from state a to state b is calculated as the ratio of instances having activity label a followed activity label b, to the total number of instances.
The observation distribution is factorized as:
where each sensor observation is modeled as an independent Bernoulli distribution, given by:
where uni = p(xn|y = i) (i = 1, 2, …, K, n = 1, 2, …, N) is calculated by finding the frequency of the n-th sensor event as observed for each activity.
For a novel observation sequence x1:T1 = {x1, x2, …, xT1}, we can efficiently find the sequence of activities that maximizes p(y1:T1|x1:T1) using the Viterbi algorithm [16].
2.4. Conditional Random Field
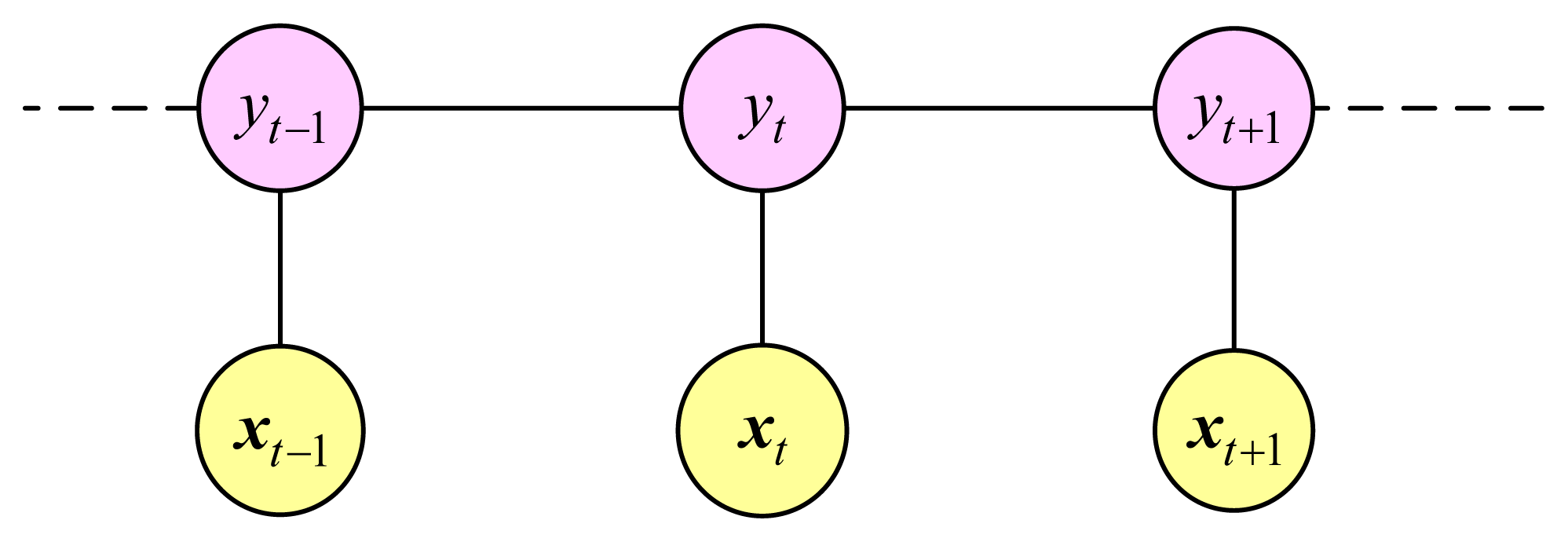
A Conditional Random Field (CRF) is an undirected graphical model and the main idea of the model is that of a maximum entropy model. CRF models the conditional probability of a particular label sequence Y given a sequence of observations X [17]. Figure 4 is graph structure of a linear-chain CRF (LCRF). Like other undirected graphical models, LCRF is a discriminative model where the relations between two connected nodes are represented as potentials which are not like a probability restricted to a value between 0 and 1.
LCRF is commonly trained by maximizing the conditional likelihood of a labeled training set to estimate the weight vector θ. The log conditional likelihood is defined as:
The feature function fk (x, yt−1, yt, t) is either a state function sk (yt, x, t) or a transition function tk (yt−1, yt, x, t). State functions sk depend on a single label state and observations in the model while transition functions tk depend on pairs of label states. For each state functions, there are:
where , (n = 1, 2, …, N) is defined as:
For each label pair (y′, y″), the transitions function tk is defined as:
The gradient of Equation (10) Error! Reference source not found.is defined as:
Given a function and its gradient, training the model becomes a matter of numerical optimization. In the case of LCRF, the objective function is convex and first order methods such as gradient ascent are directly applicable, although in practice more efficient algorithms such as conjugate gradient offer better performance. In addition to first order methods, an approximate second order method, limited memory BFGS [18] can also been used. For a novel observation sequence x = {x1, x2, …, xT1}, the sequence of activities that best fits to the data is found using the Viterbi algorithm [16].
2.5. Two-Stage Method for Multi-Resident Activity Recognition
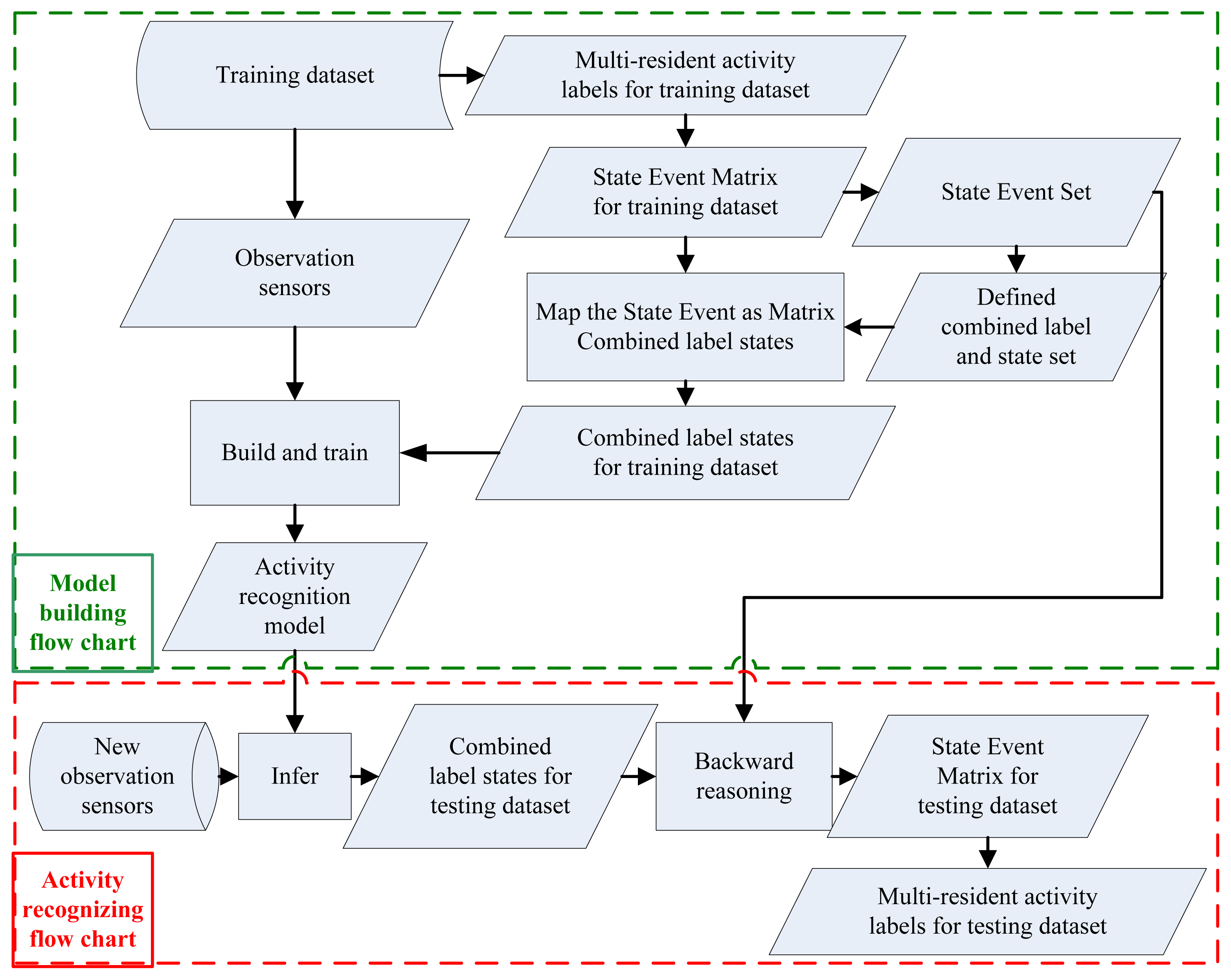
The flow charts of our multi-resident activity recognition method are shown in Error! Reference source not found.. The top is the model building flow chart and the bottom is the activity recognizing flow chart. There are two phases in our model defined as model building phase and new activity recognition phase, while our two stages method is embodied in the new activity recognition phase. In the new activity recognition phase, we learn Combined label states at the first stage, and figure out the multi-resident activities from Combined label states at the second stage.
Based on the training dataset, we first build the State Event Matrix using multi-resident activity labels (Definition 4). Then, we create State Event Set (Definition 5), define Combined label and the corresponding Combined label state set (Definition 6), build the mapping f from State Event Set to Combined label state set (Definition 7). Finally, we obtain Combined label states from the State Event Matrix using the mapping f. After mapping multi-resident activities in the training dataset to the states in the Combined label state set, typical activity recognition models (e.g., HMM and CRF) will be built and train based on the training dataset.
When new sensors are coming, we will infer Combined label state for every observation using built typical activity recognition model firstly, and then inversely map Combined label states as State Event Matrix using f−1. State Event Matrix is composed of State Event which represents the multi-resident activities at the same time step. For example, State Event ( ) represents the activities of all residents at time step t and every component presents the activity of the i-th resident at time step t. So from State Event Matrix we can obtain multi-resident activities easily.
There are two kinds of State Event Matrixes: the State Event Matrix corresponding to the training dataset and the State Event Matrix corresponding to the testing dataset. The State Event Matrix corresponding to the training dataset is defined by multi-resident activity labels where data association is given. The State Event Matrix corresponding to the testing dataset is obtained by backward reasoning Combined label states to State Event Set based on inverse mapping f−1, where Combined label states are inferred based on observations from sensors using the trained activity recognition model. Algorithm 1 (in Table 1) and Algorithm 2 (in Table 2) are the automatic generation processes of the State Event Matrix that correspond to the training dataset and the State Event Matrix that corresponds to the testing dataset, where m is resident number, T is samples number in the training dataset and T1 is observations number in the testing dataset.
Table 3 is the procedure of our two-stage method for recognizing multi-resident activities with HMM (TSM-HMM) and with CRF (TSM-CRF).
3. Validation
This section is organized as follows: after introducing the dataset and giving some measurement criteria, this section will carry out two experiments.
3.1. Dataset Preparation
In this section, we will validate our two-stage method for multi-resident activity recognition using a dataset used in literature [12] and collected in the CASAS project in the WSU smart apartment Testbed where two residents are performing activities of daily living (ADL).
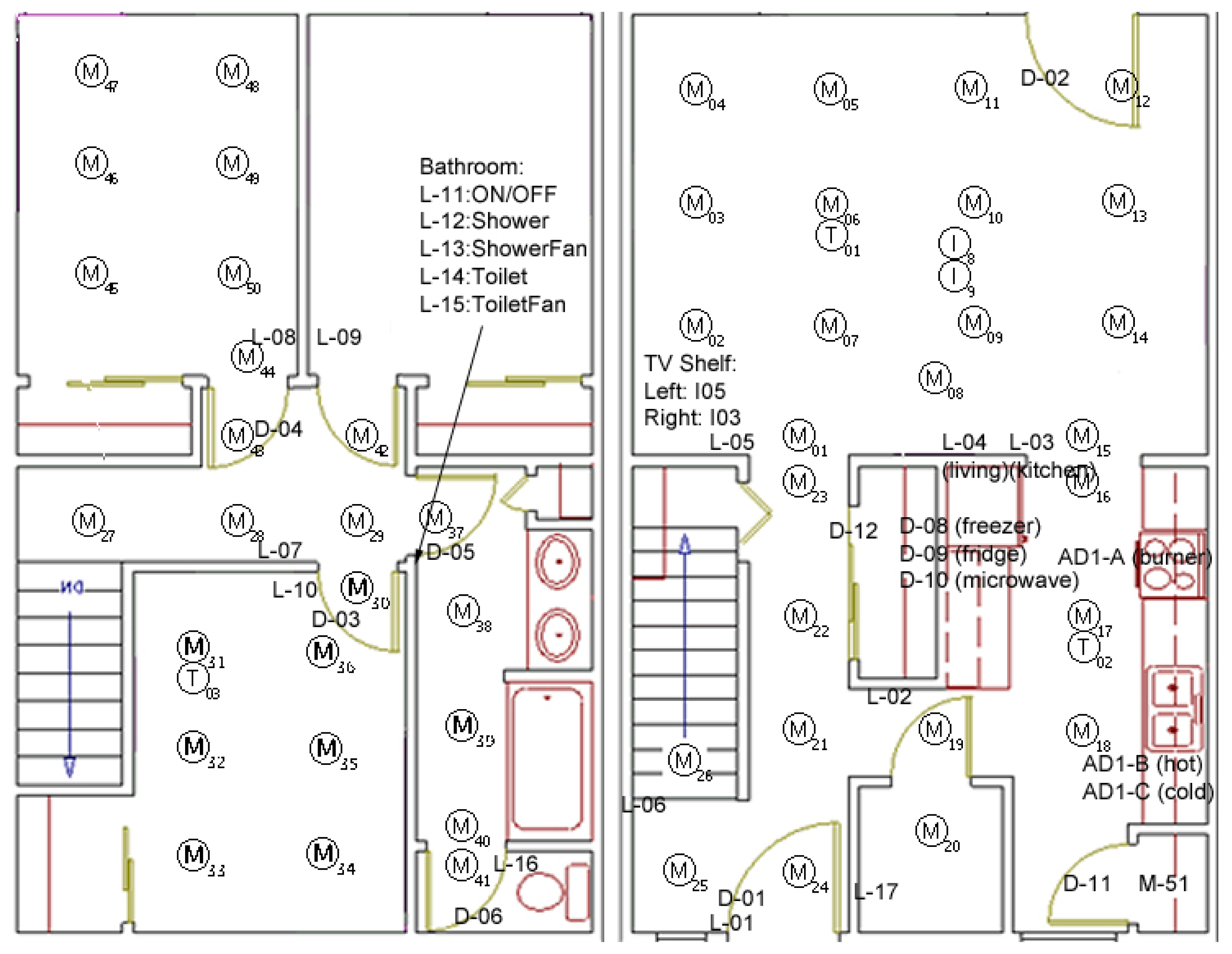
Sensor
The Testbed is equipped with motion and temperature sensors as well as analog sensors that monitor water and stove burner use (see Figure 6). The motion sensors are located on the ceiling approximately one meter apart to locate the resident, the Voice over IP (VOIP) technology captures phone usage and switch sensors to monitor usage of the phone book, a cooking pot, and the medicine container.
Activities
There are 26 files in this dataset and there are approximately 400 to 800 sensor events in each file. Each file corresponds to one pair participants who perform fifteen activities in the apartment. The data represents the observation of two residents asked to perform 15 activities, which are listed as follows:
- (1)
Filling medication dispenser: Fill medication dispenser in the kitchen using items obtained from the cabinet. Return items to the cabinet when done.
- (2)
Hanging up clothes: Hang up clothes in the hallway closet. The clothes are laid out on the couch in the living room.
- (3)
Moving furniture: Move the couch and coffee table to the other side of the living room. Request help from other person.
- (4)
Reading magazine 1: Sit on the couch and read a magazine.
- (5)
Watering plants: Water plants located around the apartment. Use the watering can located in the hallway closet. Return the watering can to the closet when finished.
- (6)
Sweeping floor: Sweep the kitchen floor using the broom and dust pan located in the kitchen closet. Return the tools to the closet when finished.
- (7)
Playing checkers: Play a game of checkers for a maximum of five minutes.
- (8)
Preparing dinner: Set out ingredients for dinner in the kitchen (Preparing dinner).
- (9)
Setting table: Set dining room table for dinner.
- (10)
Reading magazine 2: Read a magazine on the living room couch.
- (11)
Paying bill: Simulate paying an electric bill.
- (12)
Gathering food: Gather food for a picnic from the kitchen cupboard and pack them in a picnic basket.
- (13)
Retrieving dishes: Retrieve dishes from a kitchen cabinet.
- (14)
Packing supplies: Pack supplies in the picnic basket.
- (15)
Packing food: Pack food in the picnic basket and bring the basket to the front door of the apartment.
Among these activities, individual activities are those performed by a resident and independent from other’s activities, whereas cooperative activities are those performed by one or more residents simultaneously and dependently.
Knowledge representation and activity analysis
The output of a sensor event and its annotation is either in the format of (Date, Time, Sensor ID, Value, Resident ID, and Activity ID) which means there is one resident who triggered the signals, or in the format of (Date, Time, Sensor ID, Value, Resident ID, Activity ID, Resident ID, Activity ID) which means there are two residents who triggered the signals.
Without considering the date and time feature, the observation at time step t can be denoted as a n-dimensional vector where the i-th value is 1 if the i-th sensor changed state, otherwise the i-th value is 0 (e.g., xt = (0, 1, 0, 0, 0) means there are total five sensors and the second sensor change state at time step t).
For n residents, we use a vector (A1, …, An) to represent what activities they were doing, where Ai, i = 1, …, n, are their activity ID that was performed, respectively. If one resident is not in the sensing range or some other physical factors impaired the sensing, what the resident is doing is unknown. In this case we denote the known activity as ‘0’. For two residents, their activity label vector at time step t (both in individual and cooperative terms) is denoted as (A1, A2). Therefore, (0, A2) means that the first resident performed one unknown activity and he/she did not triggered any sensing signals while the second resident performed the activity A2. Similarly, (A1, 0) means that the first resident performed activity A1 and the activity of the second resident was not sensed at some time step, whereas (0, 0) means the activities of both residents are unknown. The unknown state means more and is essentially a disjunction of all possible activities. In the CASAS case, we have:
The activity label vectors and their frequency of the dataset are shown in Table 4. The frequency represents the occurrence counts of activity label vectors. It shows that some concurrent activities don’t occur at all in this dataset, some happen rarely, while some occur frequently. This is because there are 15 activities that can be detected in ideal conditions for each resident at a time step. So there are 16 labels for each resident (including label 0 which means that the resident performed unknown activity but did not trigger the signals). For two residents, there are 16 × 16 = 256 two-dimensional labels theoretically, but there are only 27 different two-dimensional labels in the CASAS dataset, since some concurrent activities don’t occur at all in reality.
3.2. Measurement Criteria
In the first experiment, we use the measurement criteria used in [12] to validate our two-stage method for multi-resident activity recognition in the first experiment, where accuracy is defined by comparing correctly labeled activities with total activities and the average indicates that it is averaged across all possible activities.
Activity recognition is a multi-label classification problem in essence, so we choose the corresponding measures [19] to evaluate the performance of our models in the second experiment. Quality of the overall classification is assessed in two ways: Macro-averaging and Micro-averaging. We use Macro-averaging because it treats all classes equally and take β = 1 which weights recall and precision evenly. The multi-label classification measurement criteria are list as follows:
where l is the total cluster number, tpi is the number that correctly recognized as the i-th class (true positives), tni is the number that correctly recognized but do not belong to the i-th class (true negatives), and fpi is the number that incorrectly recognized as the i-th class (false positives) while fni is the number that incorrectly recognized but do not belong to the i-th class (false negatives).
3.3. Experiment 1
This experiment will carry out the two-stage method with threefold cross validation and compare the result with previous method. For training dataset, we map multi-resident activity labels as Combined label states C0 after defining Combined label state C and building mapping f and f−1. Then, we train HMM and CRF with training sensors and Combined label states. For testing the dataset with only testing sensors, we first estimate Combined label state using the trained model. The average accuracies of Combined label states for HMM and CRF are 65.46% and 67.61%, respectively, which represent not the multi-resident activity recognition accuracy but the multi-resident activity knowledge recognition accuracy.
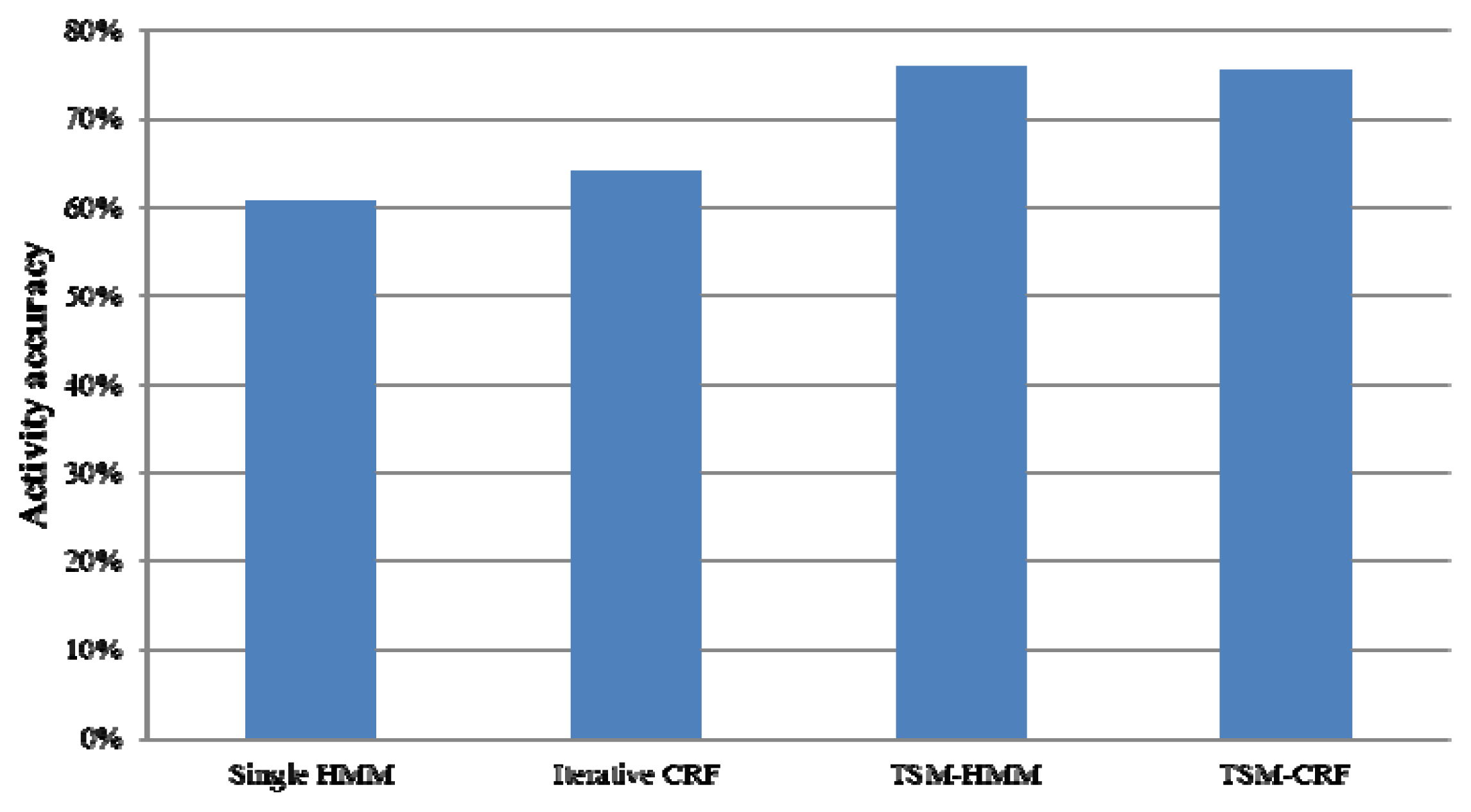
To get multi-resident activity labels, we map Combined label states to multi-resident activity labels with the built mapping f−1. Figure 7 gives the average recognition accuracies of four models in recognizing multi-resident activities. Singla et al. [12] gave an average accuracy of 60.60% by a single HMM and Hsu et al. [13] gave an average accuracy of 64.16% by Iterative CRF. However, TSM-HMM gets an average accuracy of 75.77% and TSM-CRF obtains an average accuracy of 75.38% which are apparently higher than the single HMM and the Iterative CRF.
TSM-HMM and TSM-CRF for multi-resident activity recognition outperform single HMM and Iterative CRF and gets good recognition results for the following reasons. Firstly, the previous single resident activity recognition model is not suitable for multi-resident activity recognition. In HMM implementation, a single model is implemented for both residents. The model not only needs to represent transitions between activities performed by one person, but also needs to represent transitions between residents and transitions between different activities performed by different residents. Secondly, the activity recognition using Iterative CRF depends on the recognition accuracy of data association and the activity recognition accuracy will be low when data association is recognized badly. Fortunately, our methods don’t use data association when recognizing multi-resident activities, thus avoid the deviation caused by the data association error. In addition, our methods can learn the knowledge in the multi-resident context and capture global features and trends of multi-resident activities which cannot be captured by previous single resident recognition method.
In many AmI applications, find out the data association is very meaningful. With the State Event of all the test dataset, the TSM-HMM and the TSM-CRF can find data association easily. If the i-th value of the State Event vector is non-zero, we say that the i-th resident has triggered an observed sensor. The data association accuracies of different strategies are shown in Table 5. TSM-HMM gets data association accuracy of 84.19% and TSM-CRF gets 82.88%, which are higher than the iterative training and transition table provided by Iterative CRF.
3.4. Experiment 2
This experiment will compare the effective of TSM-HMM and TSM-CRF for multi-resident activity recognition using multi-label classification measurement criteria and analyze the relations between Combined label states and multi-residents activities. In the experiment, we take 80% of the dataset for training and 20% for testing. Table 6 is the multi-resident activity recognition results for two models with the measures for multi-label classification. As the table shows, TSM-HMM is slightly lower than TSM-CRF in the ‘Precision’ while is better than TSM-CRF in the “Average Accuracy”, “Recall” and “Fscore”. Also, TSM-HMM gets lower “Error Rate”.
This is because a separate model p(x|y) is learned in HMM for each class and Bayes rule is used to calculate the posterior probability p(y|x) for a novel point. But in the case of CRF, a single model is used for all classes when calculating p(y|x) directly and parameters are learned by maximizing the conditional likelihood p(y|x). There are many Combined label states in multi-resident scenario that do not involve many types of sensors and thus they will make less intrinsic actions. Since Combined label states are important in our two-stage method, the result of TSM-HMM is slightly better than TSM-CRF.
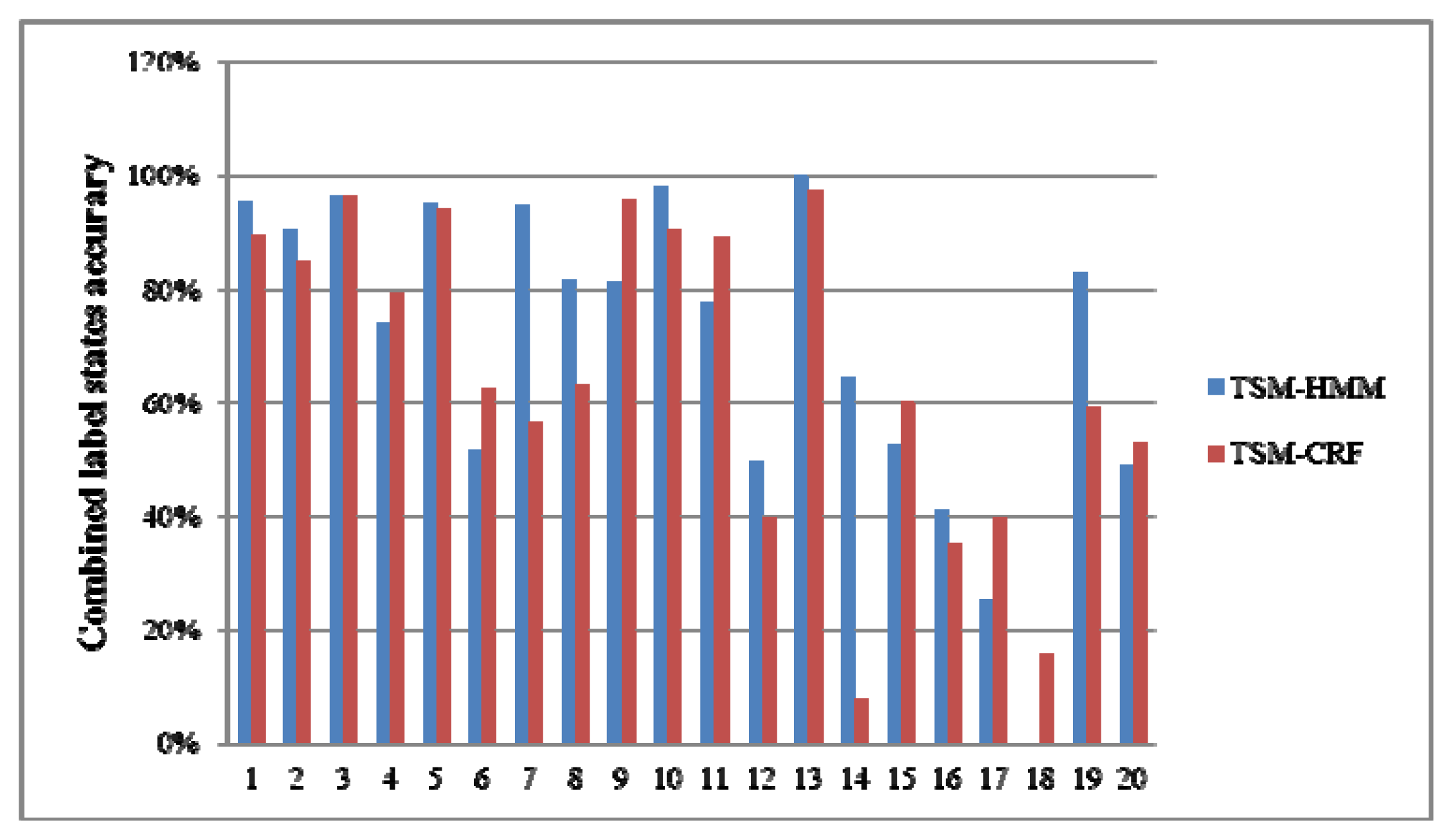
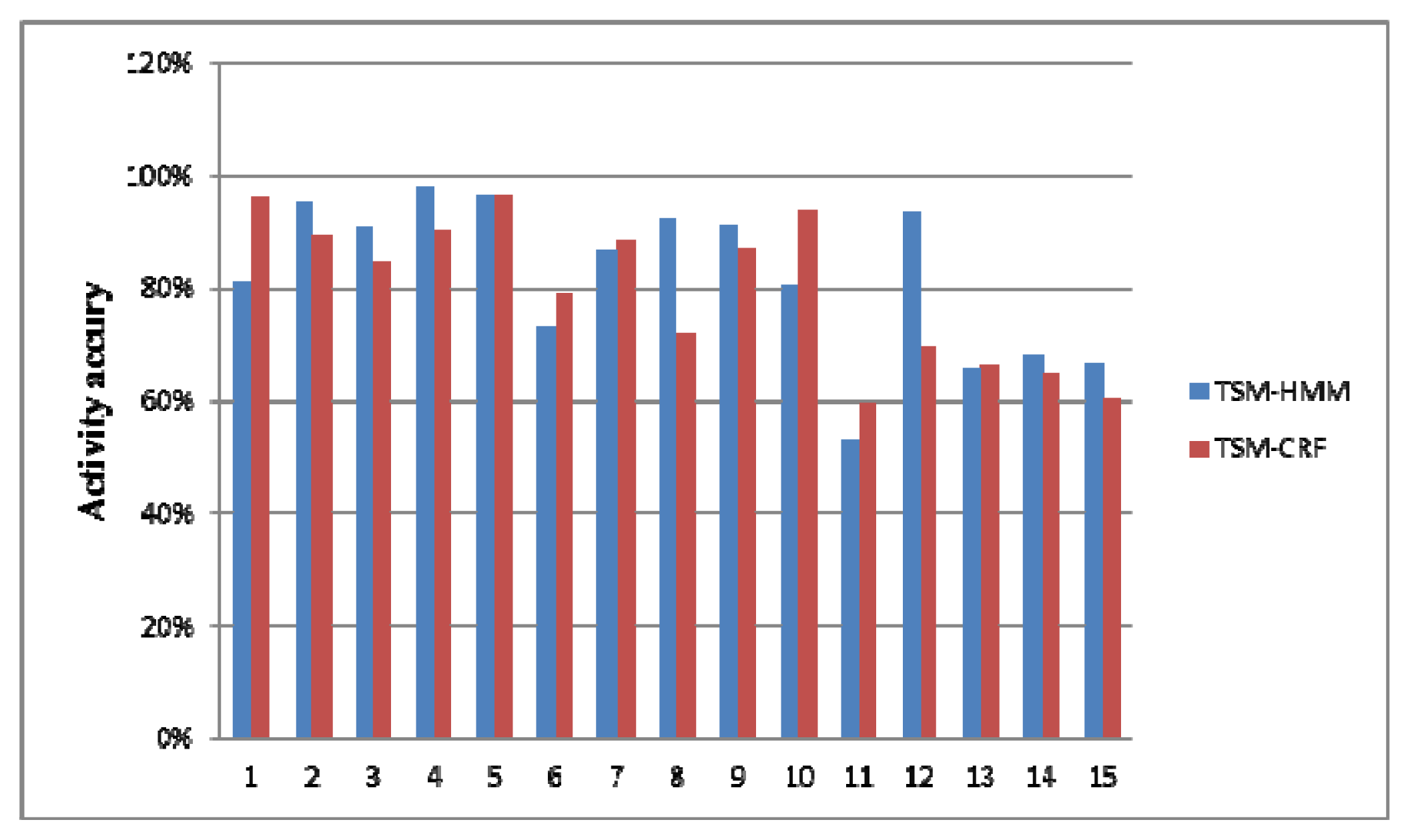
Table 7 is the Combined label states in the test dataset and corresponding multi-resident activity labels. Figure 8 shows the recognition accuracies of Combined label states. Figure 9 is the recognition accuracies of multi-resident activities. As they show, the accuracies of activities 1–5 are the same as Combined label states 9, 1, 2, 10, 3. This is because those activities are performed separately by one resident. The activity 12 is performed separately by one resident, but the accuracy is higher than Combined label state 17. The activity 15 is only existed in Combined label state 20, but the accuracy is higher than Combined label state 20. This is because our method can capture the knowledge in the multi-resident activities.
4. Conclusions
Multi-resident activity recognition is an important yet challenging problem when allowing elderly people to be better assisted with context-aware services. In order to reason about multi-resident activities, this paper exploits some simple knowledge about multi-resident activities by defining a Combined label and the state set, and proposes a two-stage activity recognition method for multi-resident activity recognition after the typical activity recognition model is build. The simple knowledge we use is not the same as the data association in that it encodes spatial and temporal constraints without indicating which occupant generated what observation. This method converts multi-label problems into single-label problems by treating multi-resident activities at the same moment as a Combined label state and can capture global activity features and trends of multi-residents from sensor data in smart environments.
We validated the algorithm by recognizing multi-resident activities from the CASAS dataset. In the first experiment, we compared our two-stage method with previous multi-resident activity recognition methods. The results show that our method can recognize multiple-resident activities with higher accuracy. In the second experiment, we compared TSM-HMM and TSM-CRF in terms of multi-label classification measurement criteria, and also analyzed the relations between Combined label states and multi-residents activities. Any contribution to multi-resident activity recognition will bring us to live better. In future, we will build models to learn more about global activity features and trends, and then use them to recognize complex activities in multi-resident environments.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (No. 61175056, No. 61073056), the Fundamental Research Funds for the Central Universities (No. 3132013335), and IT Industry Development of Jilin Province.
Conflict of Interest
The author has no conflict of interest to declare.
- Author ContributionsThe author Rong Chen conceived and designed the study, the author Yu Tong collected and analyzed the data. The two authors both contribute to the paper written, revised and proofreading.
References
- Van Kasteren, T.; Noulas, A.; Englebienne, G.; Krose, B. Accurate activity recognition in home setting. Proceedings of 10th International Conference Ubiquitous Computing, Seoul, South Korea, 21–24 September 2008; ACM: New York, NY, USA, 2008; pp. 1–9. [Google Scholar]
- Patterson, D.J.; Fox, D.; Kautz, H.; Philipose, M. Fine-grained activity recognition by aggregating abstract object usage. Proceedings of the Ninth IEEE International Symposium on Wearable Computers, Osaka, Japan, 18–21 October 2005; IEEE Computer Society: Washington, DC, USA, 2005; pp. 44–51. [Google Scholar]
- Chernbumroong, S.; Cang, S.; Atkins, A.; Yu, H. Elderly activities recognition and classification for applications in assisted living. Expert Syst. Appl 2013, 40, 1662–1674. [Google Scholar]
- Mocanu, S.; Mocanu, I.; Anton, S.; Munteanu, C. AmIHomCare: A Complex Ambient Intelligent System for Home Medical Assistance. Proceedings of the 10th International Conference on Applied Computer and Applied Computational Science, Venice, Italy, 8–10 March 2011; World Scientific and Engineering Academy and Society: Stevens Point, WI, USA, 2011; pp. 181–186. [Google Scholar]
- Van Kasteren, T.; Englebienne, G.; Kröse, B. An activity monitoring system for elderly care using generative and discriminative models. Pers. Ubiquit. Comput 2010, 14, 489–498. [Google Scholar]
- Mocanu, I.; Florea, A.M. A model for activity recognition and emergency detection in smart environments. Proceedings of The First International Conference on Ambient Computing, Applications, Services and Technologies, Barcelona, Spain, 23–29 October 2011; Emonet, R., Curran Associates, Inc: Red Hook, NY, USA, 2011; pp. 13–19. [Google Scholar]
- Lin, Z.; Fu, L. Multi-user preference model and service provision in a smart home environment. Proceedings of the IEEE International Conference on Automation Science and Engineering, CASE’07, Scottsdale, AZ, USA, 22–25 September 2007; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2007; pp. 759–764. [Google Scholar]
- Roy, N.; Roy, A.; Das, S.K.; Basu, K. A cooperative learning frame work for mobility-aware resource management in multi-inhabitant smart homes. Proceedings the Second Annual International Conference on Mobile and Ubiquitous Systems: Networking and Services, San Diego, CA, USA, 17–21 July 2005; IEEE Computer Society: Washington, DC, USA, 2005; pp. 393–403. [Google Scholar]
- Wang, L.; Gu, T.; Tao, X.; Lu, J. Sensor-based human activity recognition in a multi-user scenario. Proceedings of the Third European Conference on Ambient Intelligence, Salzburg, Austria, 18–21 November 2009; Tscheligi, M., Markopoulos, P., Wichert, R., Mirlacher, Th., Meschterjakov, A., Reitberger, W., Eds.; Springer-Verlag: Berlin, Germany, 2009; pp. 78–87. [Google Scholar]
- McCowan, I.; Gatica-Perez, D.; Bengio, S.; Lathoud, G.; Barnard, M.; Zhang, D. Automatic analysis of multimodal group actions in meetings. IEEE Trans. Pattern Anal. Mach. Intell 2005, 27, 305–317. [Google Scholar]
- Wilson, D.H.; Atkeson, C. Simultaneous Tracking and Activity Recognition (STAR) Using Many Anonymous, Binary Sensors. Proceedings of The Third International Conference on Pervasive Computing, Munich, Germany, 8–13 May 2005; Gellersen, HW., Want, R., Schmidt, A., Eds.; Springer-Verlag: Berlin, Germany, 2005; pp. 62–79. [Google Scholar]
- Singla, G.; Cook, D.J.; Schmitter-Edgecombe, M. Recognizing independent and joint activities among multi-residents in smart environments. J. Ambient Intell. Human. Comput 2010, 1, 57–63. [Google Scholar]
- Hsu, K.C.; Chiang, Y.T.; Lin, G.Y.; Lu, C.H.; Jen Hsu, J.Y.; Fu, L.C. Strategies for inference mechanism of conditional random fields for multi-resident activity recognition in a smart home. Proceedings of the 23rd International Conference on Industrial Engineering and Other Applications of Applied Intelligent Systems, Cordoba, Spain, 1 June 2010; Springer-Verlag: Berlin, Germany, 2010; pp. 417–426. [Google Scholar]
- Chiang, Y.T.; Hsu, K.C. Interaction Models For Multi-Resident Activity Recognition in a Smart Home. Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010.
- Wang, L.; Gu, T.; Tao, X.P.; Chen, H.H.; Lu, J. Recognizing multi-user activities using wearable sensors in a smart home. Pervas. Mobile Comput 2011, 7, 287–298. [Google Scholar]
- Viterbi, A.J. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans. Inform. Theory 1967, 13, 260–269. [Google Scholar]
- Lafferty, J.; McCallum, A.; Pereira, F. Conditional random fields: Probabilistic models for segmenting and labeling sequence data. Proceedings of the International Conference on Machine Learning, Williamstown, MA, USA, 28 June–1 July 2001; Morgan Kaufmann Publishers Inc: San Francisco, CA, USA, 2001; pp. 282–289. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited memory bfgs method for large scale optimization. Math. Program 1989, 45, 503–528. [Google Scholar]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag 2009, 45, 427–437. [Google Scholar]

| Automatic generation process of State Event Matrix for the training dataset |
|---|
| Input: Multi-resident activity label:
, t=1,...,T, i = 1,...,m. Output: State Event Matrix M |
|
| Automatic generation process of State Event Matrix for the testing dataset |
|---|
| Input: Observations sensor in the testing dataset: x = {xt}, t = 1,…,T1; Activity recognition model: ARM; Inverse mapping f−1; State Event Set A Output: State Event Matrix M1 |
|
| Two-stage method for multi-resident activity recognition |
|---|
Input:
|
| Step 1. Model the State Events of training data based on multi-labels y0, cluster and get State Event Set A. Step 2. Define Combined label C and the corresponding state set, build mapping f and map State Events of every training data as Combined label states C0 using f. Step 3. Train activity recognition models such as HMM and CRF with x0 and C0, and finally get model parameters. Step 4. Infer Combined label states C1 use trained model and testing observation x1. Step 5. Backward reasoning using f−1 and get estimated State Event for every testing observation. Step 6. Figure out activity labels y1 based on the estimated State Event. |
| (A1, A2) | Frequency |
|---|---|
| (0, 0) | 3 |
| (0, 2) | 1568 |
| (0, 3) | 668 |
| (0, 4) | 1 |
| (0, 5) | 545 |
| (0, 7) | 1529 |
| (0, 8) | 432 |
| (0, 11) | 891 |
| (0, 13) | 1309 |
| (0,15) | 748 |
| (1,0) | 1175 |
| (4,0) | 864 |
| (6,0) | 1505 |
| (6,7) | 350 |
| (9,0) | 866 |
| (9,8) | 280 |
| (10,0) | 660 |
| (10,1) | 1 |
| (10,11) | 284 |
| (10,15) | 2 |
| (12,0) | 1179 |
| (12,13) | 272 |
| (13,0) | 4 |
| (13,13) | 865 |
| (14,0) | 387 |
| (14,15) | 845 |
| (15,0) | 1 |
| Strategies | Data association accuracy |
|---|---|
| Transition table | 50.99% |
| Iterative training | 72.87% |
| TSM-HMM | 84.19% |
| TSM-CRF | 82.88% |
| TSM-HMM | TSM-CRF | |
|---|---|---|
| Average Accuracy | 0.9740 | 0.9725 |
| Error Rate | 0.0260 | 0.0275 |
| Precision | 0.8003 | 0.8005 |
| Recall | 0.8192 | 0.7991 |
| Fscore | 0.4048 | 0.3999 |
| State | Label |
|---|---|
| 1 | (0,2) |
| 2 | (0,3) |
| 3 | (0,5) |
| 4 | (0,7) |
| 5 | (0,8) |
| 6 | (0,11) |
| 7 | (0,13) |
| 8 | (0,15) |
| 9 | (1,0) |
| 10 | (4,0) |
| 11 | (6,0) |
| 12 | (6,7) |
| 13 | (9,0) |
| 14 | (9,8) |
| 15 | (10,0) |
| 16 | (10,11) |
| 17 | (12,0) |
| 18 | (13,13) |
| 19 | (14,0) |
| 20 | (14,15) |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, R.; Tong, Y. A Two-stage Method for Solving Multi-resident Activity Recognition in Smart Environments. Entropy 2014, 16, 2184-2203. https://doi.org/10.3390/e16042184
Chen R, Tong Y. A Two-stage Method for Solving Multi-resident Activity Recognition in Smart Environments. Entropy. 2014; 16(4):2184-2203. https://doi.org/10.3390/e16042184
Chicago/Turabian StyleChen, Rong, and Yu Tong. 2014. "A Two-stage Method for Solving Multi-resident Activity Recognition in Smart Environments" Entropy 16, no. 4: 2184-2203. https://doi.org/10.3390/e16042184
APA StyleChen, R., & Tong, Y. (2014). A Two-stage Method for Solving Multi-resident Activity Recognition in Smart Environments. Entropy, 16(4), 2184-2203. https://doi.org/10.3390/e16042184





