A Fuzzy Parallel Processing Scheme for Enhancing the Effectiveness of a Dynamic Just-in-time Location-aware Service System
Abstract
: Location-aware service systems are a hot topic in diverse research fields including mobile commerce, ambient intelligence, remote sensing and ubiquitous computing. However, the timeliness and efficiency of such systems are two issues that have rarely been emphasized. For this reason, this study tries to establish a location-aware service system in which both the timeliness and efficiency of service provision are addressed. To this end, some innovative treatments have been used in the proposed methodology. First, the uncertainty of detecting a user’s location using the global positioning system is considered by modeling the location and speed of the user with fuzzy numbers. Subsequently, a fuzzy integer-nonlinear programming model is formulated to address the problem of finding the dynamic just-in-time service location and path for the user. To help solve the problem, the maximum entropy weighting function and the basic defuzzification distribution (BADD) method are applied to defuzzify the fuzzy variables. In addition, to enhance the efficiency of solving the problem, a fuzzy parallel processing scheme is also proposed for decomposing the problem into smaller pieces that can be handled by separate processing modules. An illustrative example is used to illustrate the proposed methodology. Finally, the effectiveness of the proposed methodology has been confirmed with an experiment. According to the results, using the proposed methodology the waiting time could be reduced by 60%.1. Introduction
Users in a dynamic environment may encounter unexpected events, leading to some needs that must be met. How the environment supports this is the goal of ambient intelligence (AmI). AmI is a vision in which an environment supports the people inhabiting it in an unobtrusive/transparent, interconnected, adaptable, dynamic, embedded, and intelligent manner [1,2]. For example, a user may need an AmI system to provide him/her information, such as the nearest parking space [3]. Sometimes, a user needs an AmI system to help him/her make a decision, such as choosing the right restaurant for lunch [4]. After obtaining and analyzing a user’s needs, an AmI system responds the required information or answer to the user through a variety of channels, such as voice prompts, screen messages, eco-feedback, and others.
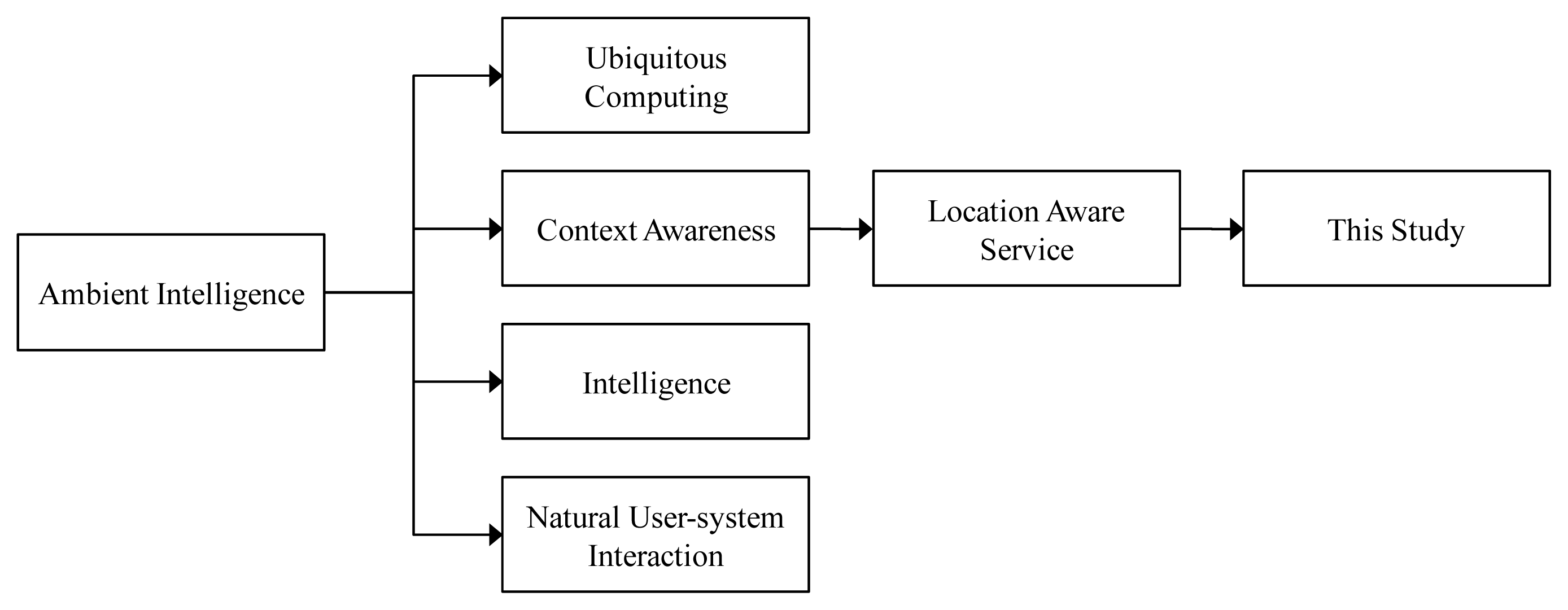
AmI can be roughly divided into four categories – ubiquitous computing, context awareness, intelligence, and natural user-system interaction (see Figure 1). This study aims to explore a particular topic in context awareness – location-aware services (LASs). A LAS is a special context-aware service (CAS) that utilizes the location of a user to adapt the service accordingly [5]. Dialing an emergency number from a cell phone, car or marine navigation systems, and package tracking systems are typical LAS examples. Krevl and Ciglarič [6] proposed a framework for developing location-based distributed applications. The framework comprises of three layers – the client layer, the application/server layer, and the database layer. According to Park et al.’s opinion, it is not easy to provide LASs because of latency, limited display, and intermittent connectivity to the backend database [7]. Nevertheless, according to Zickuhr [8], until 2012 about three-quarters of smartphone owners have used LASs. The mobile 911 service, mentioned in Zhu et al. [9], sends a request to find medical helps for those in the immediate vicinity. Aalto et al. [10] established a LAS system for delivering permission-based location-aware mobile advertisements to a user’s cell phone using Bluetooth positioning and wireless application protocol (WAP) push. Aittola et al. [11] provided a LAS to guide readers in a library to books and collections they may be interested in. Similarly, Bohnenberger et al. [12] implemented a LAS system that gives a shopper direction through a shopping mall. The reasoning was based on three factors: the types of products that the shopper was interested in, the shopper’s current location, and the purchase history of the shopper.
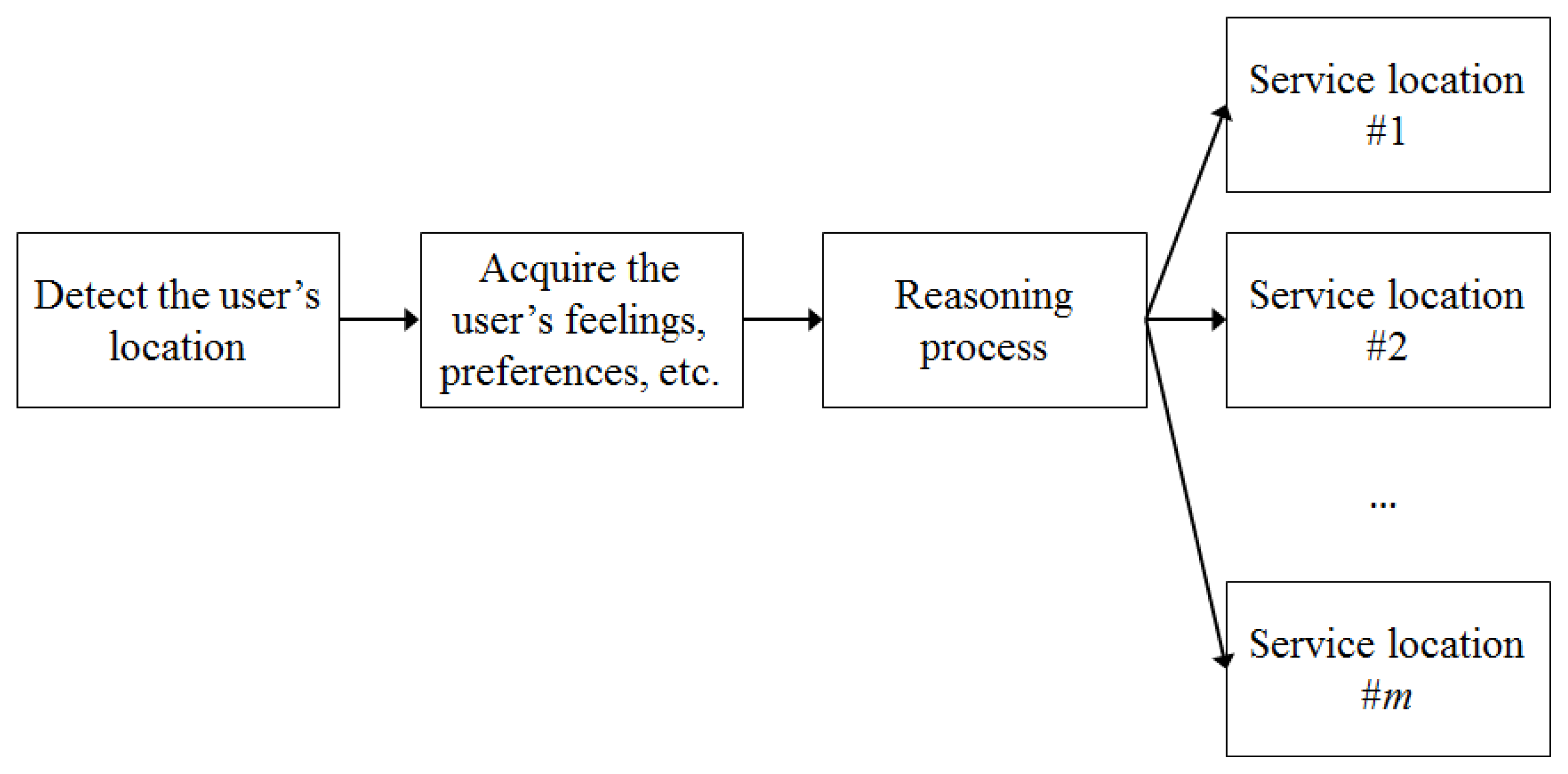
The existing LASs can be generalized to a four-step procedure (see Figure 2). However, the existing LAS systems have the following problems:
- (1)
A LAS system usually has multiple service providers. Balancing the loads on these providers, thereby improving the quality of service (QoS), is an important issue. In Abrougui et al.’s opinion [13], a LAS request should be allowed to use a less crowded service provider via a less congested route.
- (2)
In addition, some service providers may not be trustworthy. Reporting a user’s location to such service providers is risky, as warned by Chow et al. [14]. Zhu et al. [9] identified that security, privacy, and location-awareness are important in service discovery for both roaming users and services.
- (3)
There is considerable uncertainty when detecting a user’s location. For example, the detection error may be up to 20 meters when using the global positioning system on a cell phone [15], which is large enough to mislead the recommendation process. Such uncertainty has rarely been discussed in past studies.
- (4)
More emphasis is put on the correctness of a service than on the timeliness of providing the service. Some LAS systems attempt to suggest the nearest service location to the user; however, timeliness is a different concept that forces the LAS system to get along with a user’s pace.
For these reasons, a dynamic just-in-time LAS system is to be developed in this study. As the name implies, with this system, the service requested by a user will be just ready when the user reaches the service location. The objectives to be achieved by the dynamic just-in-time LAS system include:
- (1)
After considering the needs of a user, the dynamic just-in-time LAS system chooses from some service locations the most suitable one, and recommends it to the user.
- (2)
When a user arrives at the service location, the service requested by the user is just ready, and he/she does not need to wait.
- (3)
The requested service cannot be ready before the arrival of the user because of security or preservation issues.
This study is based on the following assumptions:
- (1)
Users can communicate with the dynamic just-in-time LAS system through their portable handheld devices.
- (2)
The location of a user can be detected in some way.
- (3)
Only service locations located on the way from a user’s location to his/her destination will be considered.
- (4)
The required service is to be satisfied by a static location, rather than by a nomadic provider.
- (5)
A user does not need to change his/her pace.
The development of the dynamic just-in-time LAS system follows the generalized procedure shown in Figure 2. In addition, its reasoning capability has been enhanced with fuzzy logic and parallel processing. In the literature, applications of fuzzy logic to LASs can be seen. For example, linguistic variables were used to help a user express his/her needs and/or evaluate his/her satisfaction of a recommendation [16,17]. Then, some fuzzy inference rules were established to process such linguistic information, and make a recommendation [18]. Chen et al. [3] recommended the best parking station to a user, for which some fuzzy inference rules were established to compare the alternatives. In this study,
- (1)
Fuzzy numbers are used to approximate a user’s location and speed, and the preparation time of a service. As a result, the time to reach a service location is also a fuzzy number.
- (2)
If a user reaches the recommended service location before the requested service is ready, he/she must wait. To minimize the waiting time, a fuzzy integer-nonlinear programming (FINLP) problem is formulated. To solve the FINLP problem, Liu’s method [19], which is a combination of the maximum entropy weighting function and the basic defuzzification distribution (BADD), was applied to defuzzify the fuzzy variables and parameters, so as to convert the problem into a crisp one.
- (3)
To help solve the FINLP problem, a fuzzy Dijkstra’s algorithm is proposed.
On the other hand, parallel processing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that a large problem can often be divided into smaller ones, which are then solved concurrently (“in parallel”) [20]. Parallel processing is considered in this study because of the following reasons:
- (1)
Multiple service locations mean multiple possible destinations. When the available times of these possible destinations are different, the traditional Dijkstra’s algorithm for a single destination can hardly be applied.
- (2)
In practical applications, there may be hundreds of people accessing a LAS system simultaneously. Parallel processing is therefore required to distribute the needs to multiple servers.
The remaining of this paper is organized in the following manner: the architecture of the dynamic just-in-time LAS system is described in Section 2. The problem of minimizing the waiting time of a user is formulated as a FINLP problem, as described in Section 3. To help solve the FINLP problem, a fuzzy Dijkstra’s algorithm based on the fuzzy parallel processing scheme is proposed in Section 4. An example is used to illustrate the applicability of the proposed methodology. In addition, to further elaborate the effectiveness of the proposed methodology, an experiment has been carried out, as detailed in Section 5. Finally, this paper is concluded in Section 6.
2. The Dynamic Just-in-Time LAS System
The proposed dynamic just-in-time LAS system starts from the detection of a user’s location using the GPS system on the cell phone. According to the statistics in [15], the accuracy of the existing GPS systems on cell phones is about 20 meters. In contrast, the Federal Communications Commission of U.S. has mandated a program called E911 that requires the location of any cell phone used to call 911 can be determined to within 50 to 100 meters [21].
2.1. Estimate a User’s Location and Speed
Assume the latitude and longitude of a user at time t are indicated with la(t) and lo(t), respectively; the estimation error of the GPS is r. Then, the fuzzy location of the user can be determined as ((la(t) − r, la(t), la(t) + r), (lo(t) − r, lo(t), lo(t) + r)), given in triangular fuzzy numbers. In addition, from at least two times of detection, the user’s fuzzy speed s̃ can also be estimated:
where (−) denotes fuzzy subtraction, and:
According to the arithmetic for triangular fuzzy numbers [22], there are four outcomes of Equation (1):
- (1)
If α1α3 ≤ 0 and β1β3 ≤ 0,
- (2)
If α1α3 > 0 and β1β3 ≤ 0,
- (3)
If α1α3 ≤ 0 and β1β3 > 0,
- (4)
If α1α3 > 0 and β1β3 > 0,
2.2. System Architecture
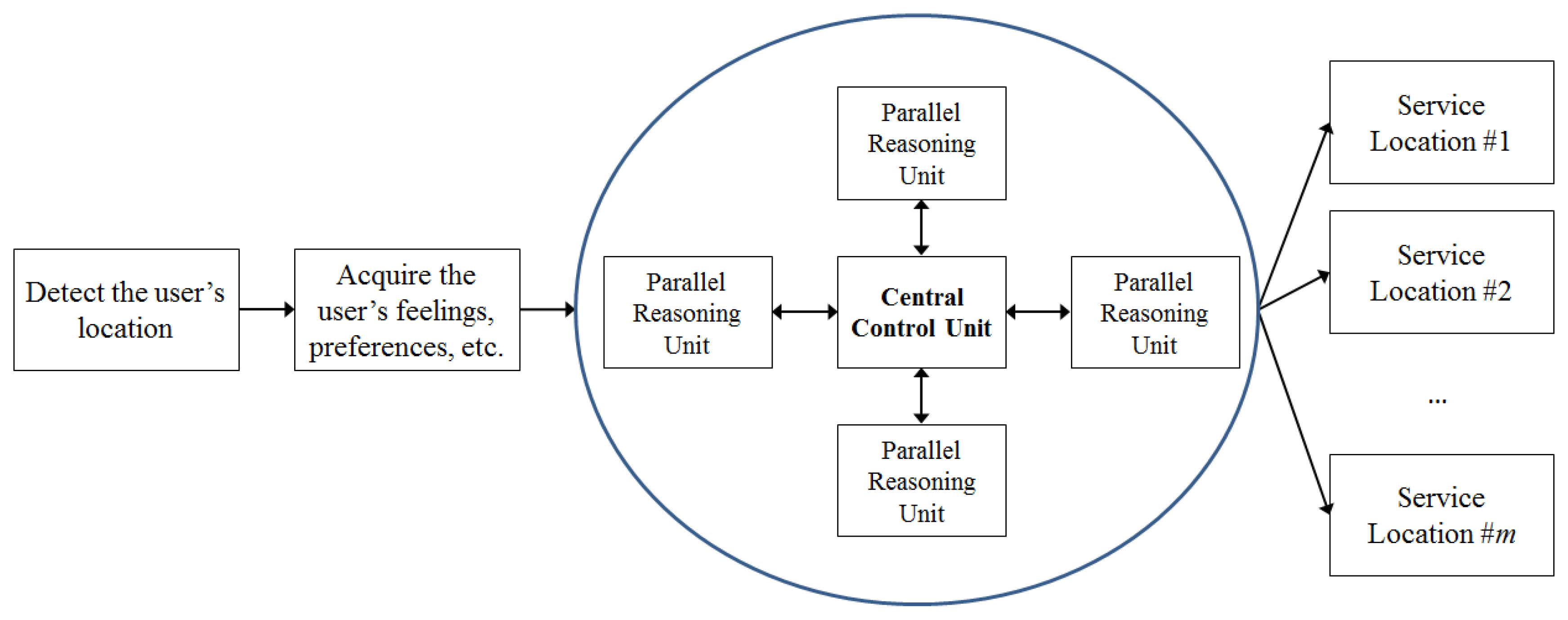
Subsequently, a user will be asked to input his/her request – including the service content, destination, and other information. Such information as well as the user’s location and speed are transmitted from the cell phone to the backend reasoning module. The backend reasoning module is composed of a central control unit and several parallel reasoning units (see Figure 3). The reasoning module attempts to find the dynamic just-in-time service location to minimize the waiting time of a user. In theory, such a task can be formulated as a FINLP problem, which will be described in the next section:
- (1)
In theory, the parallel reasoning units can be realized by separate computing clouds that apply the same or different methods (such as optimizers, decision trees, and algorithms) to solve different parts of the problem.
- (2)
The requests of different customers can be processed by different parallel reasoning units.
- (3)
A complex request can be decomposed into several simpler ones that can be efficiently handled by these parallel reasoning units concurrently.
The central control unit requests each parallel reasoning unit to evaluate a part of the problem. The optimization results are then returned to the central control unit to be aggregated. All communications are done by sending simple object access protocol (SOAP) messages. An example is given in Figure 4.
Finally, the user is informed of the dynamic just-in-time service location with a message on his/her cell phone.
3. Finding the Dynamic Just-in-Time Service Location
Chen and Wu [23] have proved that the dynamic just-in-time path problem is in fact a restricted longest path problem. In this study, a FINLP problem is solved to find the dynamic just-in-time service location to minimize the waiting time of a user. The variables and parameters used in the FINLP model are defined in Table 1.
3.1. FINLP Model
To find the fuzzy dynamic just-in-time path to a service location, the following FINLP problem is formulated and solved:
s.t.:
The objective function is to minimize the waiting time. Constraint (13) forces the ready time of the required service to be later than the available time of the service location. Equation (14) derives the distance to a node from the distances to the node’s predecessors. Among the paths to a node, only one of them will be chosen, as required by Equation (15).
The FINLP problem has to be converted into an equivalent crisp problem to be solved. The most common way for this is to defuzzify each fuzzy variable [24]. In this paper, the maximum entropy weighting function BADD defuzzification method [19] was applied, because it is very flexible in representing the attitude of a decision maker. For a fuzzy variable à defined in [a, b], the defuzzified value is:
where γ is a free parameter in [0, ∞]; f(x) is the weighting function; . When γ = 1 and f(x) = 1/(b–a):
It becomes a defuzzification method with neutral valuation and confidential attitude. As a result, the objective function becomes:
Constraint (13) becomes:
In addition, constraint (14) can be expanded into:
Therefore:
Finally, the following INLP problem can be solved instead:
subject to:
3.2. A Systematic Procedure
In a fuzzy dynamic just-in-time LAS system, there are multiple service locations to choose from. The one that minimizes the waiting time is named the fuzzy dynamic just-in-time service location. To determine that, the following procedure is followed:
- (1)
Find the fuzzy dynamic just-in-time path to each service location by solving the above-mentioned model. Assume the optimal objective function value associated with service location k is Z*(k).
- (2)
Find the value of k that minimizes Z*(k), indicated with k*. Service location k* is the fuzzy dynamic just-in-time service location.
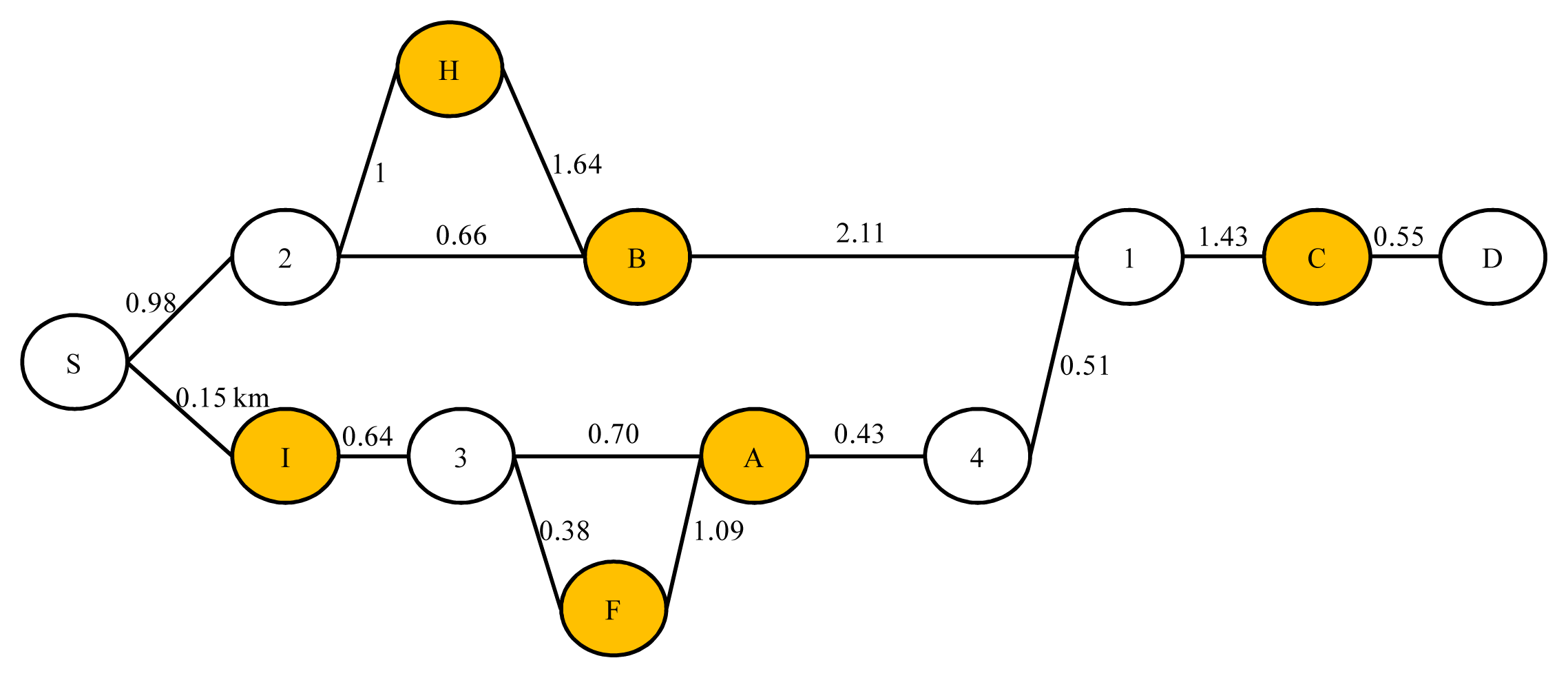
An illustrative example is given in Figure 5, in which the travel time of each path is estimated with a triangular fuzzy number. In this example, there are three service locations: nodes 7, 8, and 9. Assume p̃ = (16, 18, 23); tc = 0. The available times of the three service locations were summarized in Table 2.
First, the fuzzy dynamic just-in-time path to each of the three service locations is to be found. Take service location 3 (node 9) as an example, the Lingo codes for finding the fuzzy dynamic just-in-time path to this service location are shown in Figure 6. The optimal objective function value is 12.33. The fuzzy dynamic just-in-time path to this service location is 1->4->7->9. In the same way, the fuzzy dynamic just-in-time paths to the other service locations have been obtained, and were summarized in Table 3. In this example, the fuzzy dynamic just-in-time service location is node 8.
4. The Modified Fuzzy Dijkstra’s Algorithm and the Fuzzy Parallel Processing Scheme
Chen and Wang [23] proposed a fuzzy Dijkstra algorithm to find the dynamic just-in-time path in a fuzzy dynamic just-in-time LAS system, as demonstrated in Figure 7. Chen and Wang’s fuzzy Dijkstra method has the following drawbacks:
- (1)
Chen and Wang’s fuzzy Dijkstra method does not consider the available time of a service location. In fact, if the available times of the service locations are different, Chen and Wang’s fuzzy Dijkstra method can hardly be applied since it is difficult to know which service location the current route is leading to.
- (2)
Chen and Wang’s fuzzy Dijkstra method does not consider the uncertainties of the available time and the service preparation time.
To tackle these, Chen and Wang’s fuzzy Dijkstra algorithm needs to be modified. First, in Chen and Wang’s fuzzy Dijkstra algorithm, the suitability of a node was defined as:
according to the maximum entropy weighting function BADD defuzzification method, while in this study it is defined as:
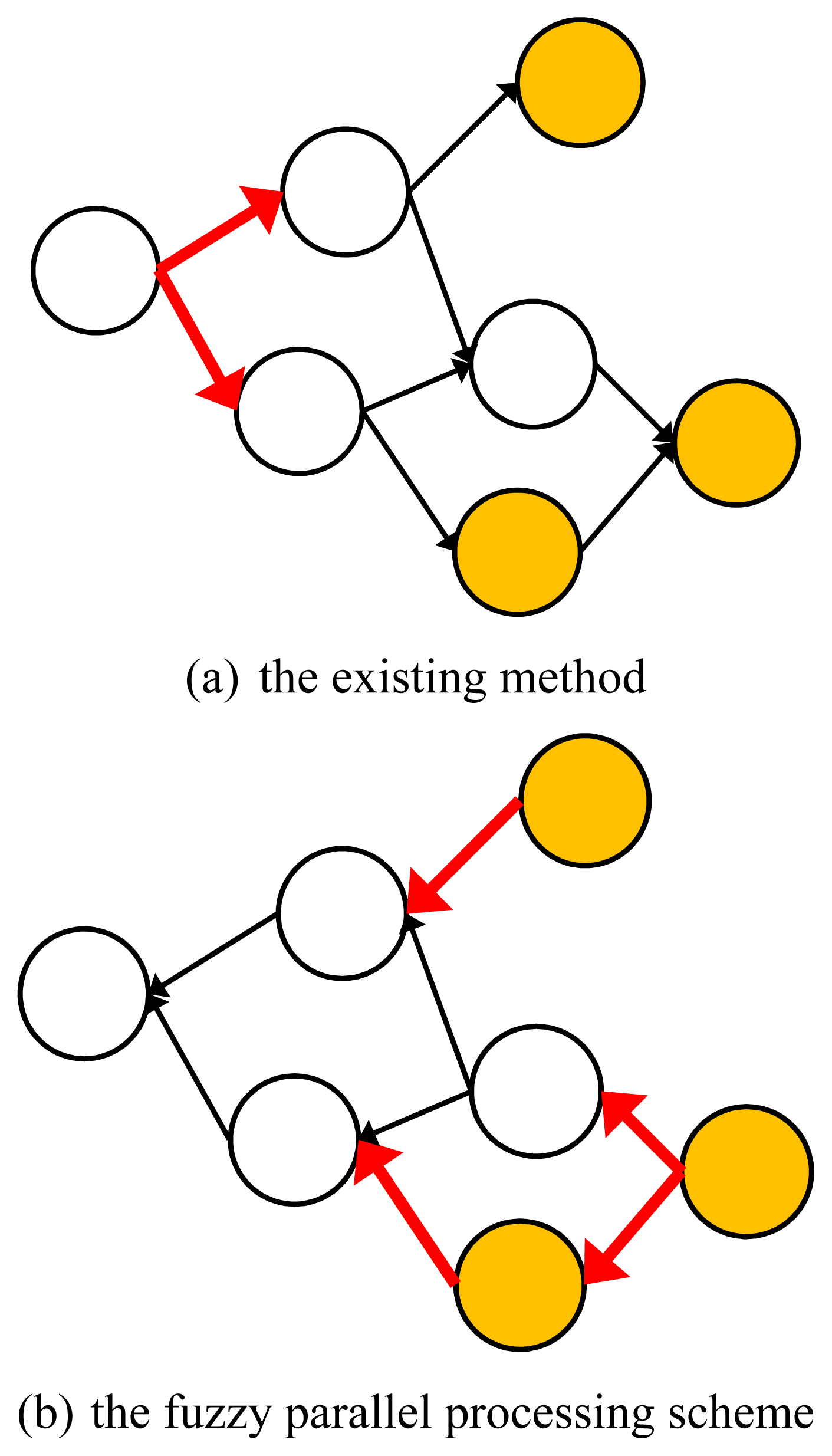
Subsequently, in Chen and Wang’s fuzzy Dijkstra algorithm, the evaluation starts from a single location, i.e., the start location or node 1 (see Figure 8(a)). However, the fuzzy dynamic just-in-time service location problem is different from the traditional shortest or longest path problem in which there is only a single destination. In a fuzzy dynamic just-in-time service location problem, there are usually multiple service locations to choose from, that is, multiple destinations.
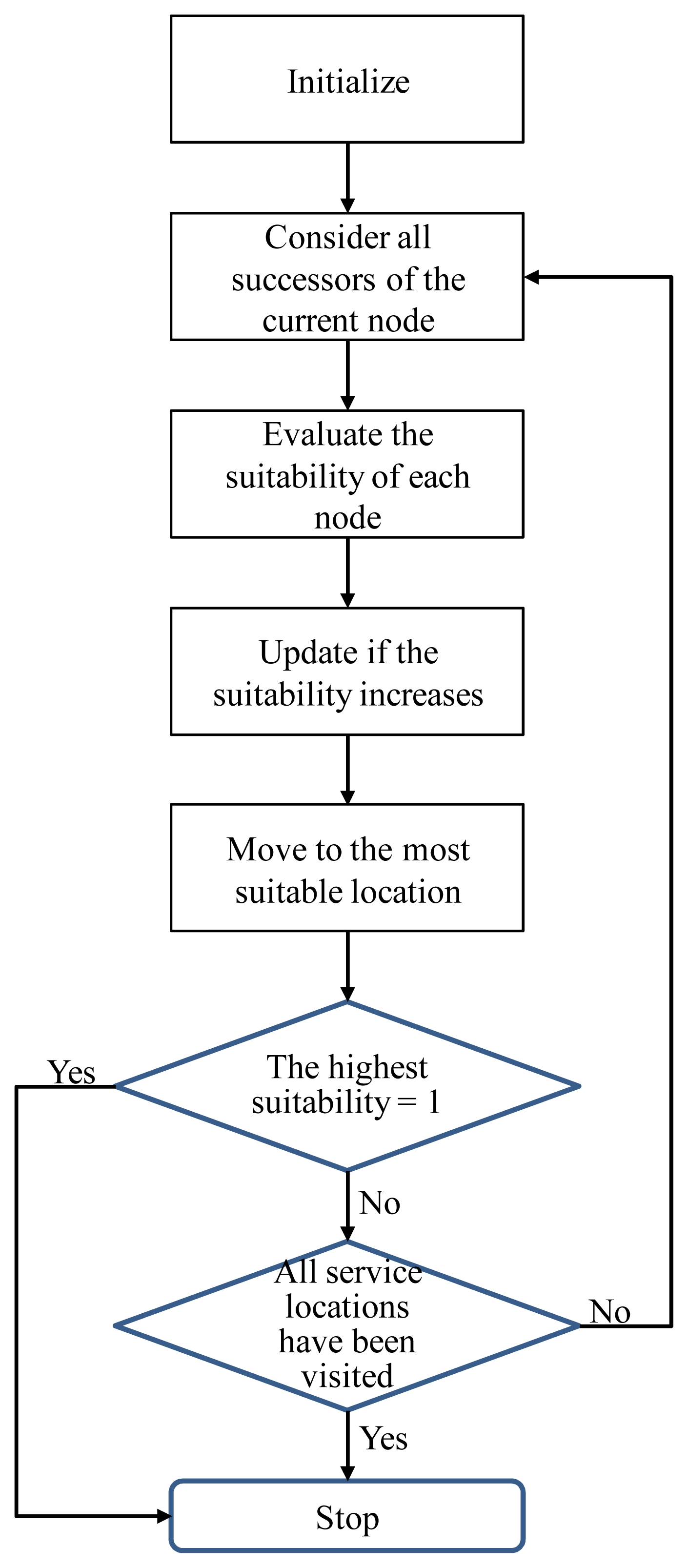
The evaluation can start from any of the service locations, rather than from the start location. In this way, a user goes back until he/she reaches node 1. This reduces the size of the problem. In addition, the evaluations from different service locations can be done simultaneously as if they are independent of each other. In this manner, the overall efficiency can be improved (see Figure 8(b)). After effective aggregation, the results will be no different. To achieve this, the following fuzzy parallel processing scheme is proposed:
- (1)
(Parallel operation) Set d̃(k) = 0; k = 1 ~ m, and d̃i = ∞ for i ≠ (k). Set the current node to service location k.
- (2)
(Parallel operation) Evaluate the suitability of node i according to Equation (38); i = 1 ~ (k).
- (3)
(Parallel operation) If there is no unvisited service location on the path from the current node to the start location, go to step (4); otherwise, consider all predecessors of the current node. For each predecessor, calculate the distance and evaluate the suitability. Update the suitability if it increases.
- (4)
(Parallel operation) Mark the current node as visited.
- (5)
(Parallel operation) If the highest suitability is 1, or the start location has been visited, go to step (6); otherwise, set the current node to “unvisited” and assign the highest suitability to the current node and return to step (3).
- (6)
(Aggregation) The service location with the highest suitability determines the fuzzy dynamic just-in-time service location. Stop.
If the time required for the evaluation starting from service location k is te(k), the time to find the fuzzy dynamic just-in-time service location will be with the fuzzy parallel processing scheme. In contrast, the time is if the existing non-parallel-processing method is applied.
4.1. An Illustrative Example
The previous example is used to illustrate the application of the fuzzy parallel processing scheme as follows:
- (1)
The initial setting is shown in Table 4.
- (2)
(Round 1) The predecessors of each service location are considered. Their distances and suitability values are calculated and evaluated, as shown in Table 5. Mark all service locations as visited. Set the current nodes to nodes 4, 5, and 7, respectively.
- (3)
(Round 2) The predecessors of nodes 4, 5 and 7 are considered. Their distances and suitability values are calculated and evaluated, as shown in Table 6. The route starting from service location 1 (node 7) has reached the start location, so stop. Set the current nodes of the other routes to nodes 2 and 4, and continue.
- (4)
(Round 3) The predecessors of nodes 2 and 4 are considered. Their distances and suitability values are calculated and evaluated, as shown in Table 7. Both routes have reached the start location, so stop.
- (5)
(Aggregation) The highest suitability with a value of 0.75 is achieved by the route starting from service location 2 (node 8), and the fuzzy dynamic just-in-time path is 1->2->5->8. The waiting time is ((16, 18, 23) + 0) (−) (10, 14, 19) = (−3, 4, 13); however, that is adjusted to (0, 4, 13) since the waiting time cannot be negative. The defuzzified value is 5.67.
In contrast, if the traditional non-parallel method is applied, the results are shown in Table 8. Since we don’t know which service location the current route is leading to, the available times of the service locations are not considered during the evaluation process.
In total, seven rounds are required, and the dynamic just-in-time route is 1->4->7->9. The waiting time is ((16, 18, 23) + (7, 9, 11)) (−) (11, 16, 20) = (3, 11, 23) or 12.33 equivalently. The results by the two methods are compared in Table 9. Obviously,
- (1)
The fuzzy parallel processing scheme did reduce the number of rounds required to find the dynamic just-in-time service location and path, which is beneficial to the efficiency of the proposed dynamic just-in-time LAS system.
- (2)
The proposed methodology also reduced the waiting time by considering the available time of each service location. As mentioned previously, it is not easy to achieve this using the traditional non-parallel-processing method.
- (3)
The dynamic just-in-time paths found by the two methods were not the same, showing that without considering the availability of service and the uncertainties of parameters, the result may be misleading.
- (4)
For a dynamic just-in-time LAS system involving n nodes, the complexity (i.e. the number of the required steps) of Chen and Wang’s fuzzy Dijkstra’s algorithm is less than (n + 5)·n· (n – 1) / 2, while that of the proposed methodology is less than , in which (k) ≤ n.
5. Experiment
To further elaborate the effectiveness of the proposed methodology, an experiment has been carried out. The experimental region (see Figure 9) is located in the Seatwen District, Taichung City of Taiwan, with an area of 16.88 km2. The six stores of a fast-food chain (indicated with red pins in Figure 9) constitute a ubiquitous service network. These stores are equipped with drive-through facilities that are expected to provide instant services to drivers. However, in real situations, most drivers have to spend 5~25 minutes on waiting, ordering, and payment. Ordering by cell phones is expected to eliminate some of the processing and waiting time; however, more improvements are still possible.
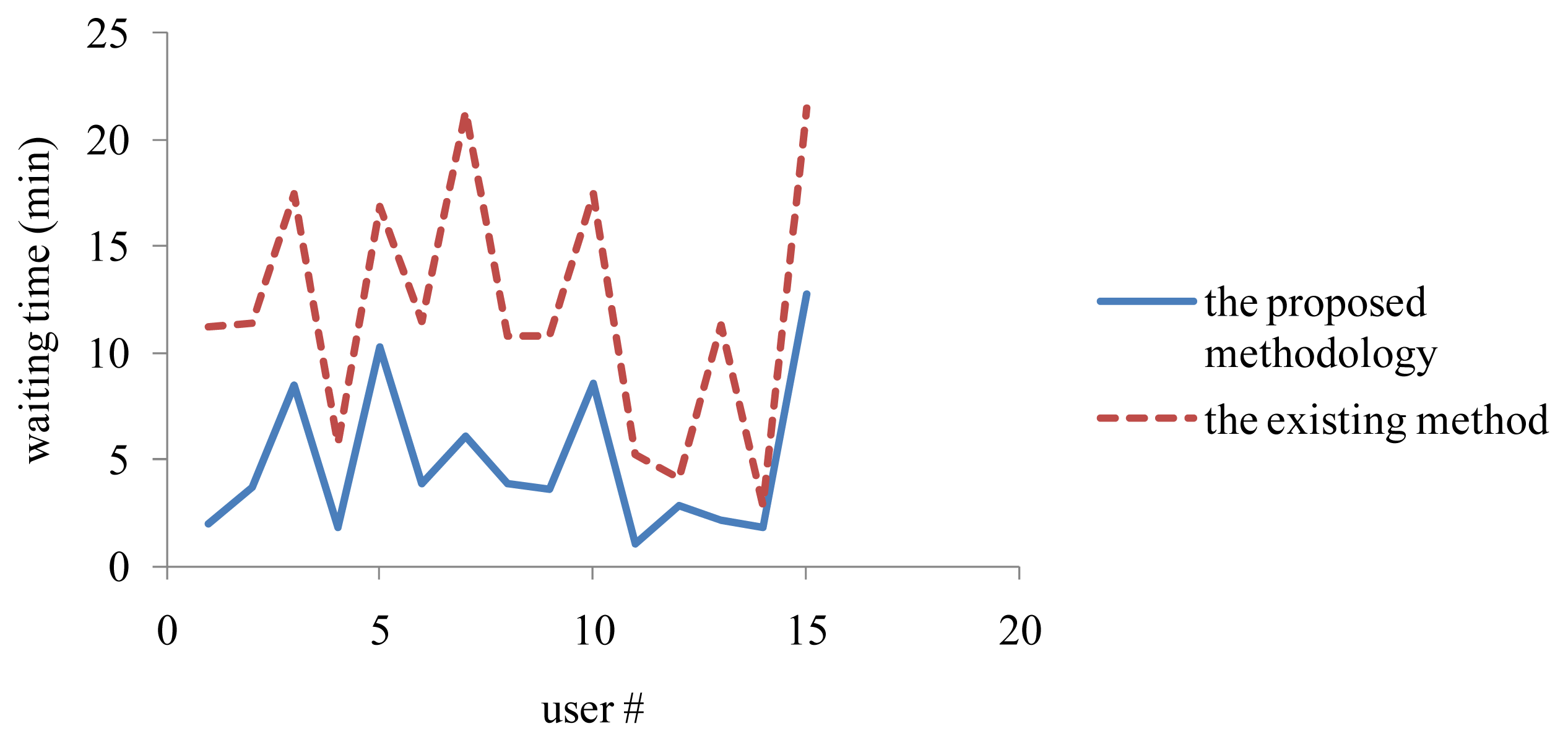
The experimental region was abstracted into a traffic network, as shown in Figure 10. Fifteen users, starting from various locations to the same destination but with unequal speeds, sent their requests through their cell phones to the system server to order food from the six shops. The collected data were summarized in Table 10. The recommendation results and performances were shown in Table 11. The existing LAS system usually recommends a user to the nearest service location via the shortest path. So, we also estimated the waiting times of users if they were guided in this way. The average waiting time of users using the proposed methodology and the existing LAS system are compared in Figure 11. On average, the waiting time of users could be reduced by 60% using the proposed methodology.
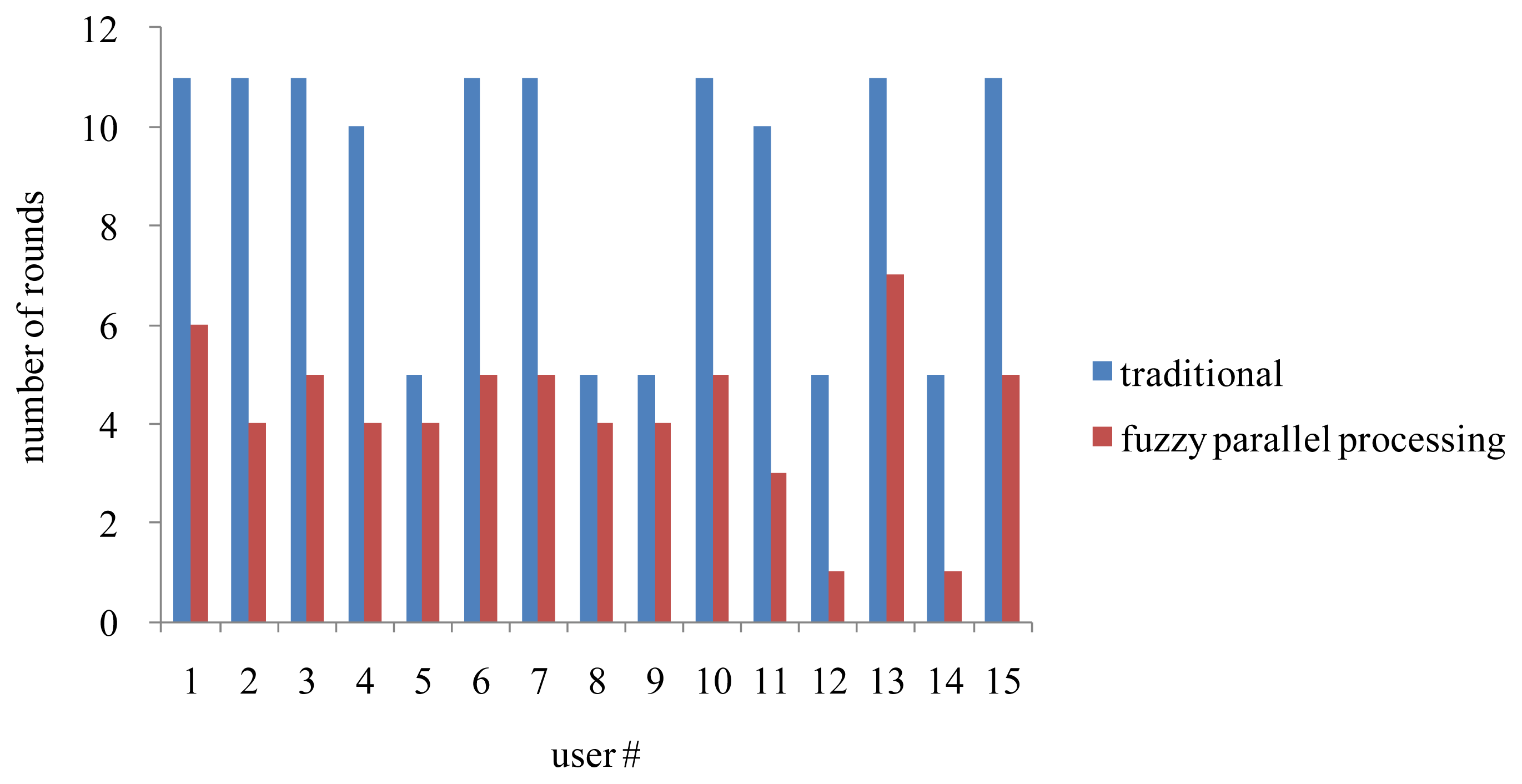
Subsequently, to assess the efficiency of the proposed fuzzy parallel processing scheme, the number of rounds required to achieve the optimal solution was recorded for each user, and compared with that using the traditional non-parallel-processing method. The results were summarized in Figure 12. As it can be seen, much fewer rounds were required to achieve the optimal solution using the fuzzy parallel processing scheme, which supported its validity as a means of accelerating the recommendation process.
6. Conclusions
The timeliness and efficiency of a LAS system have rarely been discussed in past studies. To investigate these, some important treatments have been taken in this study to design a dynamic just-in-time LAS system. First, the uncertainties in the location and speed of a user and the available time of a service location are modeled with fuzzy numbers. Subsequently, a FINLP model is established to solve the problem of finding the dynamic just-in-time service location and path for each user. To help solve the problem, the maximum entropy weighting function BADD defuzzification method is applied to defuzzify the fuzzy variables and parameters in the FINLP problem. In addition, the existing fuzzy Dijkstra’s algorithm is enhanced with a fuzzy processing scheme that decomposes the FINLP problem into several smaller parts to be efficiently solved, thereby being able to respond to a user’s request within shorter time.
An illustrative example is provided to assess the applicability of the proposed methodology. In addition, an experiment has been carried out to further elaborate the effectiveness of the proposed methodology, and to make a comparison with the existing method. The experimental results showed that the proposed methodology was able to reduce the number of rounds to find the dynamic just-in-time path, which contributed to its better efficiency. In addition, after considering the available time of each service location, the proposed methodology was able to find a service location that is more suitable for a specific user, as revealed by the reduction in the average waiting time.
In the future, how to extend the FINLP model to consider cases involving multiple users is worth exploring. Further, services can be static or roaming. Adjusting the established FINLP model to deal with roaming services is another important issue.
Acknowledgement
This study was financially supported by the National Science Council of Taiwan.
Conflicts of Interests
The author declares no conflict of interest.
References
- Ducatel, K.; Bogdanowicz, M.; Scapolo, F.; Leijten, J.; Burgelman, J.-C. Scenarios for ambient intelligence in 2010. In IST Advisory Group Final Report; European Commission: Brussels, Spain, 2001. [Google Scholar]
- Cook, D. J.; Augusto, J. C.; Jakkula, V. R. Ambient intelligence: technologies, applications, and opportunities. Technical Report 2007. [Google Scholar]
- Chen, Z.; Xia, J. B. Development of fuzzy logic forecast models for location-based parking finding services. Math. Probl. Eng 2013, 473471. [Google Scholar]
- Tung, H.; Soo, V. A personalized restaurant recommender agent for mobile e-service. IEEE International Conference on e-Technology. e-Commerce and e-Service, Taipei, Taiwan, 28–31 March 2004; pp. 259–262.
- Dey, A.K. Understanding and using context. Personal and Ubiquitous Computing 2001, 5, 20–24. [Google Scholar]
- Krevl, A.; Ciglarič, M. A framework for developing distributed location based applications. 20th International Parallel and Distributed Processing Symposium, Rhodes Island, Greece, 25–29, April 2006.
- Park, M.-H.; Hong, J.-H.; Cho, S.-B. Location-based recommendation system using Bayesian user’s preference model in mobile devices. Lect. Notes Comput. Sci 2007, 4611, 1130–1139. [Google Scholar]
- Zickuhr, K. Three-quarters of smartphone owners use location-based services; Pew Research Center’s Internet & American Life Project. Available online: http://pewinternet.org/Reports/2012/Location-based-services.aspx accessed on 2 April 2014.
- Zhu, F.; Mutka, M.; Ni, L. Splendor: a secure, private, and location-aware service discovery protocol supporting mobile services. Proceedings of the First IEEE International Conference on Pervasive Computing and Communications, Texas, USA, 23–26 March 2003.
- Aalto, L.; Göthlin, N.; Korhonen, J.; Ojala, T. Bluetooth and WAP push based location-aware mobile advertising system. The 2nd Annual International Conference on Mobile Systems, Applications, and Services, Boston, USA, June 6–9, 2004.
- Aittola, M.; Ryhänen, T.; Ojala, T. SmartLibrary – location-aware mobile library service. Lect. Notes Comput. Sci 2003, 2795, 411–416. [Google Scholar]
- Bohnenberger, T.; Jameson, A.; Krüger, A.; Butz, A. Location-aware shopping assistance: evaluation of a decision-theoretic approach. Lect. Notes Comput. Sci 2002, 2411, 155–169. [Google Scholar]
- Abrougui, K.; Boukerche, A.; Ramadan, H. Efficient load balancing and QoS-based location aware service discovery protocol for vehicular ad hoc networks. EURASIP J. Wireless Commun. Netw 2012, 96. [Google Scholar]
- Chow, C.-Y.; Mokbel, M.F.; Liu, X. A peer-to-peer spatial cloaking algorithm for anonymous location-based service. Proceedings of the 14th Annual ACM International Symposium on Advances in Geographic Information Systems, Virginia, USA, 10–11 November; pp. 171–178.
- Kaasinen, E. User needs for location-aware mobile services. Pervasive Ubiquitous Comput 2003, 7, 70–79. [Google Scholar]
- Kotsakis, E.; Ketselidis, M. Modeling personalized and context sensitive behavior for location aware services by employing fuzzy logic. In Recent Advances in Circuits, Systems and Signal Processing; WSEAS Press: Athens, Greece, 2002; pp. 244–249. [Google Scholar]
- Anagnostopoulos, C.; Hadjiefthymiades, S. Advanced fuzzy inference engines in situ ation aware computing. Fuzzy Sets Syst 2010, 161, 498–521. [Google Scholar]
- Mateo, R.M.A.; Lee, M.; Joo, S.-C.; Lee, J. Location-aware data mining for mobile users based on neuro-fuzzy system. Lect. Notes Artif. Intelli 2006, 4223, 1269–1278. [Google Scholar]
- Gottlieb, A.; Almasi, G.S. Highly Parallel Computing; Benjamin/Cummings: Redwood City, California, 1989. [Google Scholar]
- Map-GPS-Info.com. GPS cell phone - portable navigation and safety, Available online: http://www.maps-gps-info.com/gpcp.html accessed on 2 April 2014.
- Zimmermann, H.J. Fuzzy Set Theory and Its Applications; Kluwer Academic Publishers: Dordrecht, Germany, 1991. [Google Scholar]
- Chen, T.; Wu, H.-C. Finding the just-in-time service location and path in a ubiquitous service network. Int. J. Internet Manuf. Serv 2013. in press. [Google Scholar]
- Chen, T. A fuzzy mid-term single-fab production planning model. J. Intell. Manuf 2003, 14, 273–285. [Google Scholar]
- Liu, X. Parameterized defuzzification with maximum entropy weighting function - Another view of the weighting function expectation method. Math. Comput. Mod 2007, 45, 177–188. [Google Scholar]




| Variables/Parameters | Meanings |
|---|---|
| i | n nodes in the traffic network indicated with node i = 1 ~ n |
| k | m service locations in the traffic network indicated with service location k = 1 ~ m |
| l̃ij | the length of the path connecting nodes i and j. i, j = 1 ~ n; i ≠ j l̃ij = ∞ if there is no connection between two nodes l̃ij = ∞ if i > j |
| d̃i | the distance from the start point to node i d̃i = d̃j (+)l̃ij ∀j < i d̃1 = 0; d̃n = max d̃i |
| d̃(k) | the distance from the start point to service location k |
| p̃ | the service preparation time |
| r | the positioning accuracy |
| s̃ | the user’s speed |
| tc | the current time |
| ṽi | the available time of node i |
*(+): fuzzy addition
| k | Node # | ṽk |
|---|---|---|
| 1 | 7 | (8, 10, 11) |
| 2 | 8 | 0 |
| 3 | 9 | (7, 9, 11) |
| k | Node # | Z(k) | ṽk |
|---|---|---|---|
| 1 | 7 | 16.33 | 1->4->7 |
| 2 | 8 | 4.67 | 1->2->5->8 |
| 3 | 9 | 12.33 | 1->4->7->9 |
| (Service location 1/Node 7) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 0 | - | - | - | - |
| si | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - | - | - | - |
| Visited | |||||||||||
| (Service location 2/Node 8) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 0 | - | - | - |
| si | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - | - | - |
| Visited | |||||||||||
| (Service location 3/Node 9) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 0 | - | - |
| si | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - | - |
| Visited | |||||||||||
| (Service location 1/Node 7) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | ∞ | ∞ | (2, 4, 4) | (6, 7, 8) | ∞ | ∞ | 0 | - | - | - | - |
| si | 0 | 0 | 0.12 | 0.24 | 0 | 0 | 0 | - | - | - | - |
| Visited | Yes | ||||||||||
| (Service location 2/Node 8) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | ∞ | ∞ | ∞ | ∞ | (5, 7, 8) | (3, 5, 8) | ∞ | 0 | - | - | - |
| si | 0 | 0 | 0 | 0 | 0.35 | 0.28 | 0 | 0 | - | - | - |
| Visited | Yes | ||||||||||
| (Service location 3/Node 9) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | ∞ | ∞ | ∞ | ∞ | ∞ | (1, 3, 4) | (2, 4, 4) | ∞ | 0 | - | - |
| si | 0 | 0 | 0 | 0 | 0 | 0.10 | 0.12 | 0 | 0 | - | - |
| Visited | Yes | ||||||||||
| (Service location 1/Node 7) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | (9, 12, 16) | ∞ | (2, 4, 4) | (6, 7, 8) | ∞ | ∞ | 0 | - | - | - | - |
| si | 0.43 | 0 | 0.12 | 0.24 | 0 | 0 | 0 | - | - | - | - |
| Visited | Yes | Yes | |||||||||
| (Service location 2/Node 8) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | ∞ | (8, 11, 15) | ∞ | ∞ | (5, 7, 8) | (3, 5, 8) | ∞ | 0 | - | - | - |
| si | 0 | 0.60 | 0 | 0 | 0.35 | 0.28 | 0 | 0 | - | - | - |
| Visited | Yes | Yes | |||||||||
| (Service location 3/Node 9) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | ∞ | ∞ | (4, 8, 8) | (8, 11, 12) | ∞ | (1, 3, 4) | (2, 4, 4) | ∞ | 0 | - | - |
| si | 0 | 0 | 0.24 | 0.37 | 0 | 0.10 | 0.12 | 0 | 0 | - | - |
| Visited | Yes | Yes | |||||||||
| (Service location 2/Node 8) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | (10, 14, 19) | (8, 11, 15) | ∞ | ∞ | (5, 7, 8) | (3, 5, 8) | ∞ | 0 | - | - | - |
| si | 0.75 | 0.60 | 0 | 0 | 0.35 | 0.28 | 0 | 0 | - | - | - |
| Visited | Yes | Yes | Yes | ||||||||
| (Service location 3/Node 9) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | (11, 16, 20) | ∞ | (4, 8, 8) | (8, 11, 12) | ∞ | (1, 3, 4) | (2, 4, 4) | ∞ | 0 | - | - |
| si | 0.56 | 0 | 0.24 | 0.37 | 0 | 0.10 | 0.12 | 0 | 0 | - | - |
| Visited | Yes | Yes | Yes | ||||||||
| (Initial setting) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | 0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | - | - |
| si | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - | - |
| Visited | Current | ||||||||||
| (Round 1) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | 0 | (2, 3, 4) | (1, 2, 5) | (3, 5, 8) | ∞ | ∞ | ∞ | ∞ | ∞ | - | - |
| si | 0 | 0.16 | 0.14 | 0.28 | 0 | 0 | 0 | 0 | 0 | - | - |
| Visited | Yes | Current | |||||||||
| (Round 2) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | 0 | (2, 3, 4) | (1, 2, 5) | (3, 5, 8) | ∞ | ∞ | (9, 12, 16) | ∞ | ∞ | - | - |
| si | 0 | 0.16 | 0.14 | 0.28 | 0 | 0 | 0.65 | 0 | 0 | - | - |
| Visited | Yes | Yes | Current | ||||||||
| (Round 3) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | 0 | (2, 3, 4) | (1, 2, 5) | (3, 5, 8) | ∞ | ∞ | (9, 12, 16) | ∞ | (11, 16, 20) | - | - |
| si | 0 | 0.16 | 0.14 | 0.28 | 0 | 0 | 0.65 | 0 | 0.82 | - | - |
| Visited | Yes | Yes | Yes | Current | |||||||
| (Round 4) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | 0 | (2, 3, 4) | (1, 2, 5) | (3, 5, 8) | ∞ | ∞ | (9, 12, 16) | ∞ | (11, 16, 20) | - | - |
| si | 0 | 0.16 | 0.14 | 0.28 | 0 | 0 | 0.65 | 0 | 0.82 | - | - |
| Visited | Yes | Current | Yes | Yes | Yes | ||||||
| (Round 5) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | 0 | (2, 3, 4) | (1, 2, 5) | (3, 5, 8) | (5, 7, 11) | (3, 5, 10) | (9, 12, 16) | ∞ | (11, 16, 20) | - | - |
| si | 0 | 0.16 | 0.14 | 0.28 | 0.40 | 0.32 | 0.65 | 0 | 0.82 | - | - |
| Visited | Yes | Yes | Yes | Current | Yes | Yes | |||||
| (Round 6) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | 0 | (2, 3, 4) | (1, 2, 5) | (3, 5, 8) | (5, 7, 11) | (3, 5, 10) | (9, 12, 16) | (10, 14, 19) | (11, 16, 20) | - | - |
| si | 0 | 0.16 | 0.14 | 0.28 | 0.40 | 0.32 | 0.65 | 0.75 | 0.82 | - | - |
| Visited | Yes | Yes | Yes | Yes | Yes | Current | Yes | ||||
| (Round 7) | |||||||||||
| Node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| d̃i | 0 | (2, 3, 4) | (1, 2, 5) | (3, 5, 8) | (5, 7, 11) | (3, 5, 10) | (9, 12, 16) | (10, 14, 19) | (11, 16, 20) | - | - |
| si | 0 | 0.16 | 0.14 | 0.28 | 0.40 | 0.32 | 0.65 | 0.75 | 0.82 | - | - |
| Visited | Yes | Yes | Yes | Yes | Yes | Yes | Yes | ||||
| Chen and Wang’s fuzzy Dijkstra method | The parallel processing scheme | |
|---|---|---|
| No. of rounds | 7 | 5 |
| Dynamic just-in-time route | 1->4->7->9 | 1->2->5->8 |
| Waiting time | (3, 11, 23) | (0, 4, 13) |
| Defuzzified waiting time | 12.33 | 5.67 |
| User # | Start Location | Speed (km/hr) | Service Preparation Time |
|---|---|---|---|
| 1 | S | (20, 22, 25) | (10, 12, 13) |
| 2 | S | (30, 35, 40) | (8, 12, 15) |
| 3 | S | (43, 45, 47) | (15, 18, 20) |
| 4 | S | (30, 32, 35) | (5, 6, 7) |
| 5 | 2 | (46, 50, 55) | (15, 18, 20) |
| 6 | S | (50, 52, 55) | (8, 12, 15) |
| 7 | S | (20, 25, 31) | (18, 22, 25) |
| 8 | 2 | (40, 45, 50) | (8, 12, 15) |
| 9 | 2 | (36, 45, 55) | (10, 12, 13) |
| 10 | S | (38, 40, 43) | (15, 18, 20) |
| 11 | S | (10, 13, 16) | (5, 6, 7) |
| 12 | 3 | (10, 12, 15) | (5, 6, 7) |
| 13 | S | (24, 26, 28) | (8, 12, 15) |
| 14 | 2 | (10, 13, 16) | (5, 6, 7) |
| 15 | S | (35, 40, 50) | (18, 22, 25) |
| User # | Recommended Service Location | Dynamic Just-in-time Path | Suitability | Waiting Time (min) (Estimated) | Waiting Time (min) (Actual) |
|---|---|---|---|---|---|
| 1 | C | S->I->3->A->4->1->C | 0.90 | 1.74 | 1.97 |
| 2 | C | S->2->B->1->C | 0.77 | 3.45 | 3.67 |
| 3 | C | S->2->H->B->1->C | 0.54 | 8.11 | 8.52 |
| 4 | A | S->I->3->F->A | 0.70 | 1.79 | 1.84 |
| 5 | C | 2->H->B->1->C | 0.42 | 10.26 | 10.25 |
| 6 | C | S->2->H->B->1->C | 0.70 | 3.64 | 3.89 |
| 7 | C | S->2->H->B->1->C | 0.81 | 5.32 | 6.11 |
| 8 | C | 2->H->B->1->C | 0.71 | 3.78 | 3.87 |
| 9 | C | 2->H->B->1->C | 0.72 | 3.34 | 3.62 |
| 10 | C | S->2->H->B->1->C | 0.60 | 6.99 | 8.61 |
| 11 | F | S->I->3->F | 0.93 | 1.07 | 1.06 |
| 12 | A | 3->A | 0.58 | 2.50 | 2.89 |
| 13 | C | S->I->3->F->A->4->1->C | 0.92 | 2.13 | 2.16 |
| 14 | H | 2->H | 0.80 | 1.54 | 1.79 |
| 15 | C | S->2->H->B->1->C | 0.50 | 10.81 | 12.77 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, T. A Fuzzy Parallel Processing Scheme for Enhancing the Effectiveness of a Dynamic Just-in-time Location-aware Service System. Entropy 2014, 16, 2001-2022. https://doi.org/10.3390/e16042001
Chen T. A Fuzzy Parallel Processing Scheme for Enhancing the Effectiveness of a Dynamic Just-in-time Location-aware Service System. Entropy. 2014; 16(4):2001-2022. https://doi.org/10.3390/e16042001
Chicago/Turabian StyleChen, Toly. 2014. "A Fuzzy Parallel Processing Scheme for Enhancing the Effectiveness of a Dynamic Just-in-time Location-aware Service System" Entropy 16, no. 4: 2001-2022. https://doi.org/10.3390/e16042001
APA StyleChen, T. (2014). A Fuzzy Parallel Processing Scheme for Enhancing the Effectiveness of a Dynamic Just-in-time Location-aware Service System. Entropy, 16(4), 2001-2022. https://doi.org/10.3390/e16042001




