Abstract
The introduction of the partial information decomposition generated a flurry of proposals for defining an intersection information that quantifies how much of “the same information” two or more random variables specify about a target random variable. As of yet, none is wholly satisfactory. A palatable measure of intersection information would provide a principled way to quantify slippery concepts, such as synergy. Here, we introduce an intersection information measure based on the Gács-Körner common random variable that is the first to satisfy the coveted target monotonicity property. Our measure is imperfect, too, and we suggest directions for improvement.1. Introduction
Partial information decomposition (PID) [] is an immensely suggestive framework for deepening our understanding of multivariate interactions, particularly our understanding of informational redundancy and synergy. In general, one seeks a decomposition of the mutual information that n predictors X1, . . ., Xn convey about a target random variable, Y. The intersection information is a function that calculates the information that every predictor conveys about the target random variable; the name draws an analogy with intersections in set theory. An anti-chain lattice of redundant, unique and synergistic partial information is then built from the intersection information.
As an intersection information measure, [] proposes the quantity:
where DKL is the Kullback–Leibler divergence. Although Imin is a plausible choice for the intersection information, it has several counterintuitive properties that make it unappealing []. In particular, Imin is not sensitive to the possibility that differing predictors, Xi and Xj, can reduce uncertainty about Y in nonequivalent ways. Moreover, the min operator effectively treats all uncertainty reductions as the same, causing it to overestimate the ideal intersection information. The search for an improved intersection information measure ensued and continued through [–], and today, a widely accepted intersection information measure remains undiscovered.
Here, we do not definitively solve this problem, but explore a candidate intersection information based on the so-called common random variable []. Whereas Shannon mutual information is relevant to communication channels with arbitrarily small error, the entropy of the common random variable (also known as the zero-error information) is relevant to communication channels without error []. We begin by proposing a measure of intersection information for the simpler zero-error information case. This is useful in and of itself, because it provides a template for exploring intersection information measures. Then, we modify our proposal, adapting it to the Shannon mutual information case.
The next section introduces several definitions, some notation and a necessary lemma. We extend and clarify the desired properties for intersection information. Section 3 introduces zero-error information and its intersection information measure. Section 4 uses the same methodology to produce a novel candidate for the Shannon intersection information. Section 5 shows the successes and shortcoming of our candidate intersection information measure using example circuits and diagnoses the shortcoming’s origin. Section 6 discusses the negative values of the resulting synergy measure and identifies its origin. Section 7 summarizes our progress towards the ideal intersection information measure and suggests directions for improvement. Appendices are devoted to technical lemmas and their proofs, to which we refer in the main text.
2. Preliminaries
2.1. Informational Partial Order and Equivalence
We assume an underlying probability space on which we define random variables denoted by capital letters (e.g., X, Y and Z). In this paper, we consider only random variables taking values on finite spaces. Given random variables X and Y, we write X ≼ Y to signify that there exists a measurable function, f, such that X = f(Y ) almost surely (i.e., with probability one). In this case, following the terminology in [], we say that X is informationally poorer than Y ; this induces a partial order on the set of random variables. Similarly, we write X ≽ Y if Y ≼ X, in which case we say X is informationally richer than Y.
If X and Y are such that X ≼ Y and X ≽ Y, then we write X ≅= Y. In this case, again following [], we say that X and Y are informationally equivalent. In other words, X ≅= Y if and only if one can relabel the values of X to obtain a random value that is equal to Y almost surely and vice versa.
This “information-equivalence” can easily be shown to be an equivalence relation, and it partitions the set of all random variables into disjoint equivalence classes. The ≼ ordering is invariant within these equivalence classes in the following sense. If X ≼ Y and Y ≅= Z, then X ≼ Z. Similarly, if X ≼ Y and X ≅= Z, then Z ≼ Y. Moreover, within each equivalence class, the entropy is invariant, as shown in Section 2.2.
2.2. Information Lattice
Next, we follow [] and consider the join and meet operators. These operators were defined for information elements, which are σ-algebras or, equivalently, equivalence classes of random variables. We deviate from [] slightly and define the join and meet operators for random variables.
Given random variables X and Y, we define X ⋏ Y (called the join of X and Y ) to be an informationally poorest (“smallest” in the sense of the partial order ≼ ) random variable, such that X ≼ X ⋎ Y and Y ≼ X ⋎ Y. In other words, if Z is such that X ≼ Z and Y ≼ Z, then X ⋎ Y ≼ Z. Note that X ≼ Y is unique only up to equivalence with respect to ≅=. In other words, X ⋎ Y does not define a specific, unique random variable. Nonetheless, standard information-theoretic quantities are invariant over the set of random variables satisfying the condition specified above. For example, the entropy of X ⋎ Y is invariant over the entire equivalence class of random variables satisfying the condition above. Similarly, the inequality Z ≼ X ⋎ Y does not depend on the specific random variable chosen, as long as it satisfies the condition above. Note, the pair (X, Y ) is an instance of X ⋎ Y.
In a similar vein, given random variables X and Y, we define X ⋏ Y (called the meet of X and Y ) to be an informationally richest random variable (“largest” in the sense of ≽ ), such that X ⋏ Y ≼ X and X ⋏ Y ≼ Y. In other words, if Z is such that Z ≼ X and Z ≼ Y, then Z ≼ X ⋏ Y. Following [], we also call X ⋏ Y the common random variable of X and Y.
An algorithm for computing an instance of the common random variable between two random variables is provided in []; it generalizes straightforwardly to n random variables. One can also take intersections of the σ-algebras generated by the random variables that define the meet.
The ⋎ and ⋏ operators satisfy the algebraic properties of a lattice []. In particular, the following hold:
commutative laws: X ⋎ Y ≅= Y ⋎ X and X ⋏ Y ≅= Y ⋏ X;
associative laws: X ⋎ (Y ⋎ Z) ≅= (X ⋎ Y ) ⋎ Z and X ⋏ (Y ⋏ Z) ≅= (X ⋏ Y ) ⋏ Z;
absorption laws: X ⋎ (X ⋏ Y ) ≅= X and X ⋏ (X ⋎ Y ) ≅= X;
idempotent laws: X ⋎ X ≅= X and X ⋏ X ≅= X;
generalized absorption laws: if X ≼ Y, then X ⋎ Y ≅= Y and X ⋏ Y ≅= X.
Finally, the partial order ≼ is preserved under ⋎ and ⋏, i.e., if X ≼ Y, then X ⋎ Z ≼ Y ⋎ Z and X ⋏ Z ≼ Y ⋏ Z.
Let H(·) represent the entropy function and H (·|·) the conditional entropy. We denote the Shannon mutual information between X and Y by I(X:Y ). The following results highlight the invariance and monotonicity of the entropy and conditional entropy functions with respect to ≅= and ≼ []. Given that X ≼ Y if and only if X = f(Y ), these results are familiar in information theory, but are restated here using the current notation:
- (a)
If X ≅= Y, then H(X) = H(Y ), H(X|Z) = H(Y |Z), and H(Z|X) = H(Z|Y ).
- (b)
If X ≼ Y, then H(X) ≤ H(Y ), H(X|Z) ≤ H(Y |Z), and H(Z|X) ≥ H(Z|Y ).
- (c)
X ≼ Y if and only if H(X|Y ) = 0.
2.3. Desired Properties of Intersection Information
We denote (X:Y ) as a nonnegative measure of information between X and Y. For example, could be the Shannon mutual information; i.e., (X:Y ) ≡ I(X:Y ). Alternatively, we could take to be the zero-error information. Yet, other possibilities include the Wyner common information [] or the quantum mutual information []. Generally, though, we require that (X:Y ) = 0 if Y is a constant, which is satisfied by both the zero-error and Shannon information.
For a given choice of , we seek a function that captures the amount of information about Y that is captured by each of the predictors X1, . . ., Xn. We say that I∩ is an intersection information for if I∩(X:Y) = (X:Y ). There are currently 11 intuitive properties that we wish the ideal intersection information measure, I∩, to satisfy. Some are new (e.g., lower bound (LB), strong monotonicity (M1), and equivalence-class invariance (Eq)), but most were introduced earlier, in various forms, in [–]. They are as follows:
(GP) Global positivity: I∩(X1, . . ., Xn :Y ) ≥ 0.
(Eq) Equivalence-class invariance: I∩(X1, . . ., Xn :Y ) is invariant under substitution of Xi (for any i = 1, . . ., n) or Y by an informationally equivalent random variable.
(TM) Target monotonicity: If Y ≼ Z, then I∩(X1, . . ., Xn :Y ) ≤ I∩(X1, . . ., Xn :Z).
(M0) Weak monotonicity: I∩(X1, . . ., Xn, W :Y ) ≤ I∩(X1, . . ., Xn :Y ) with equality if there exists a Z ∈ {X1, . . ., Xn} such that Z ≼ W.
(S0) Weak symmetry: I∩(X1, . . ., Xn :Y ) is invariant under reordering of X1, . . ., Xn.
The next set of properties relate the intersection information to the chosen measure of information between X and Y.
(LB) Lower bound: If Q ≼ Xi for all i = 1, . . ., n, then I∩(X1, . . ., Xn :Y ) ≥ (Q:Y ). Note that X1 ⋏ · · · ⋏ Xn is a valid choice for Q. Furthermore, given that we require I∩(X:Y ) = (X:Y ), it follows that (M0) implies (LB).
(Id) Identity: I∩(X, Y :X ⋎ Y ) = (X : Y ).
(LP0) Weak local positivity: For n = 2 predictors, the derived “partial information” defined in [] and described in Section 5 are nonnegative. If both (GP) and (M0) are satisfied, as well as I∩(X1, X2 :Y ) ≥ (X1 :Y ) + (X2 :Y ) – (X1 ⋎ X2 :Y ), then (LP0) is satisfied.
Finally, we have the “strong” properties:
(M1) Strong monotonicity: I∩(X1, . . ., Xn, W :Y ) ≤ I∩(X1, . . ., Xn :Y ) with equality if there exists Z ∈ {X1, . . ., Xn, Y } such that Z ≼ W.
(S1) Strong symmetry: I∩(X1, . . ., Xn :Y ) is invariant under reordering of X1, . . ., Xn, Y.
(LP1) Strong local positivity: For all n, the derived “partial information” defined in [] is nonnegative.
Properties (LB), (M1) and (Eq) are introduced for the first time here. However, (Eq) is satisfied by most information-theoretic quantities and is implicitly assumed by others. Though absent from our list, it is worthwhile to also consider continuity and chain rule properties, in analogy with the mutual information [,].
3. Candidate Intersection Information for Zero-Error Information
3.1. Zero-Error Information
Introduced in [], the zero-error information, or Gács–Körner common information, is a stricter variant of Shannon mutual information. Whereas the mutual information, I(A:B), quantifies the magnitude of information A conveys about B with an arbitrarily small error ε > 0, the zero-error information, denoted I0(A:B), quantifies the magnitude of information A conveys about B with exactly zero error, i.e., ε = 0. The zero-error information between A and B equals the entropy of the common random variable A ⋏ B,
Zero-error information has several notable properties, but the most salient is that it is nonnegative and bounded by the mutual information,
3.2. Intersection Information for Zero-Error Information
For the zero-error information case (i.e., = I0), we propose the zero-error intersection information as the maximum zero-error information, I0(Q:Y ), that a random variable, Q, conveys about Y, subject to Q being a function of each predictor X1, . . ., Xn:
In Lemma 7 of Appendix 7.3, it is shown that the common random variable across all predictors is the maximizing Q. This simplifies Equation (2) to:
Most importantly, the zero-error information satisfies nine of the 11 desired properties from Section 2.3, leaving only (LP0) and (LP1) unsatisfied. See Lemmas 1, 2, and 3 in Appendix 7.3 for details.
4. Candidate Intersection Information for Shannon Information
In the last section, we defined an intersection information for zero-error information that satisfies the vast majority of the desired properties. This is a solid start, but an intersection information for Shannon mutual information remains the goal. Towards this end, we use the same method as in Equation (2), leading to I⋏, our candidate intersection information measure for Shannon mutual information:
In Lemma 8 of Appendix 7.3, it is shown that Equation (4) simplifies to:
Unfortunately, I⋏ does not satisfy as many of the desired properties as . However, our candidate, I⋏, still satisfies seven of the 11 properties; most importantly, the coveted (TM) that, until now, had not been satisfied by any proposed measure. See Lemmas 4, 5 and 6 in Appendix 7.3 for details. Table 1 lists the desired properties satisfied by Imin, I⋏ and . For reference, we also include Ired, the proposed measure from [].

Lemma 9 in Appendix 7.3 allows a comparison of the three subject intersection information measures:
Despite not satisfying (LP0), I⋏ remains an important stepping-stone towards the ideal Shannon I∩. First, I⋏ captures what is inarguably redundant information (the common random variable); this makes I⋏ necessarily a lower bound on any reasonable redundancy measure. Second, it is the first proposal to satisfy target monotonicity. Lastly, I⋏ is the first measure to reach intuitive answers in many canonical situations, while also being generalizable to an arbitrary number of inputs.
5. Three Examples Comparing Imin and I⋏
Example Unq illustrates how Imin gives undesirable (some claim fatally so []) decompositions of redundant and synergistic information. Examples Unq and RdnXor illustrate I⋏’s successes and example ImperfectRdn illustrates I⋏’s paramount deficiency. For each, we give the joint distribution Pr(x1, x2, y), a diagram and the decomposition derived from setting Imin or I⋏ as the I∩ measure. At each lattice junction, the left number is the I∩ value of that node, and the number in parentheses is the I∂ value (this is the same notation used in []). Readers unfamiliar with the n = 2 partial information lattice should consult [], but in short, I∂ measures the magnitude of “new” information at this node in the lattice beyond the nodes lower in the lattice. Specifically, the mutual information between the pair, X1 ⋎ X2 and Y, decomposes into four terms:
In order, the terms are given by the redundant information that X1 and X2 both provide to Y, the unique information that X1 provides to Y, the unique information that X2 provides to Y and finally, the synergistic information that X1 and X2 jointly convey about Y. Each of these quantities can be written in terms of standard mutual information and the intersection information, I∩, as follows:
These quantities occupy the bottom, left, right and top nodes in the lattice diagrams, respectively. Except for ImperfectRdn, measures I⋏ and reach the same decomposition for all presented examples.
5.1. Example Unq (Figure 1)
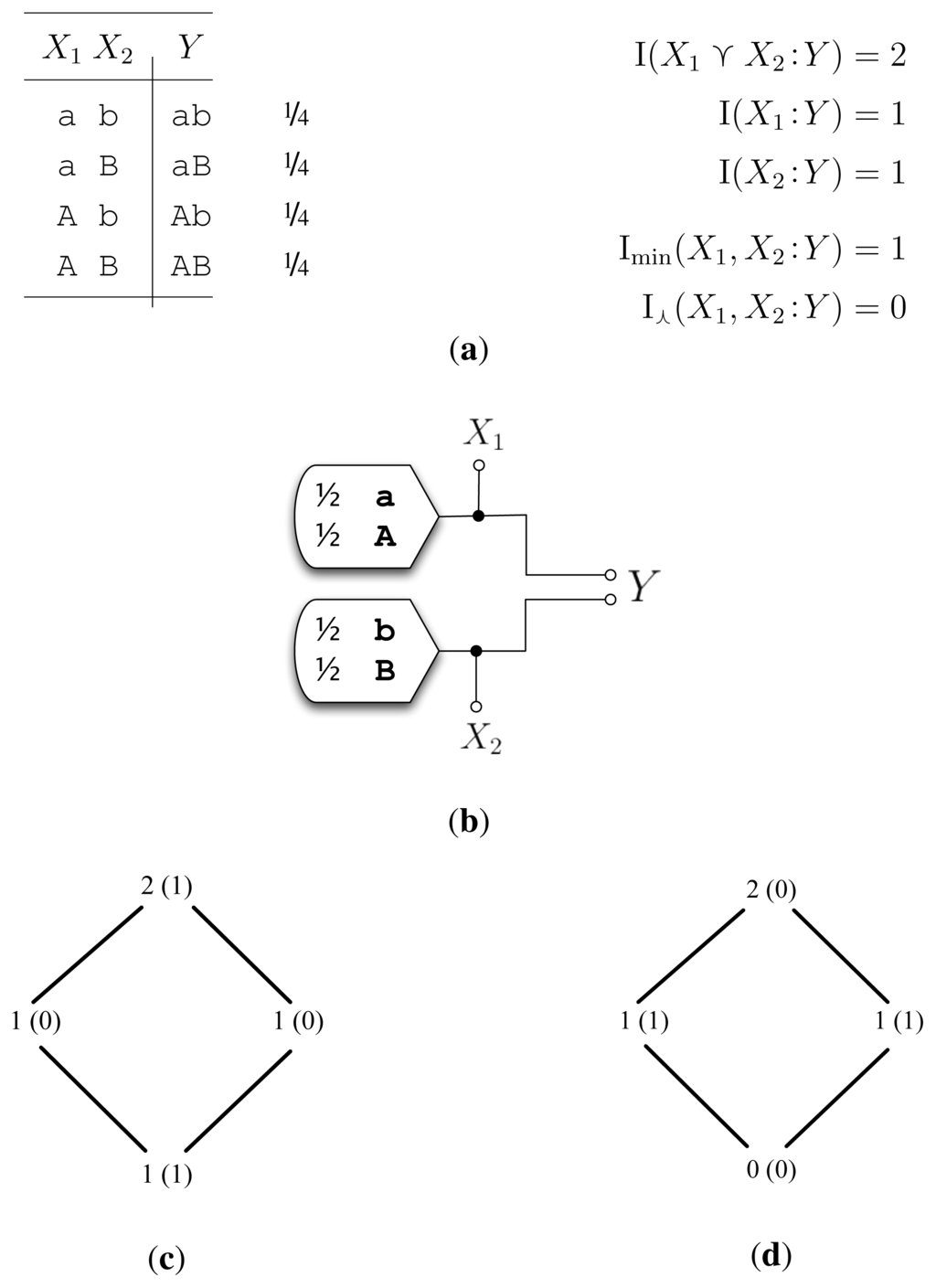
The desired decomposition for example Unq is two bits of unique information; X1 uniquely specifies one bit of Y, and X2 uniquely specifies the other bit of Y. The chief criticism of Imin in [] was that Imin calculated one bit of redundancy and one bit of synergy for Unq (Figure 1c). We see that unlike Imin, I⋏ satisfyingly arrives at two bits of unique information. This is easily seen by the inequality,
Therefore, as I(X1 :X2) = 0, we have I⋏ (X1, X2 :Y) = 0 bits leading to I∂(X1 : Y) = 1 bit and I∂(X2 : Y ) = 1 bit (Figure 1d).
5.2. Example RdnXor (Figure 2)
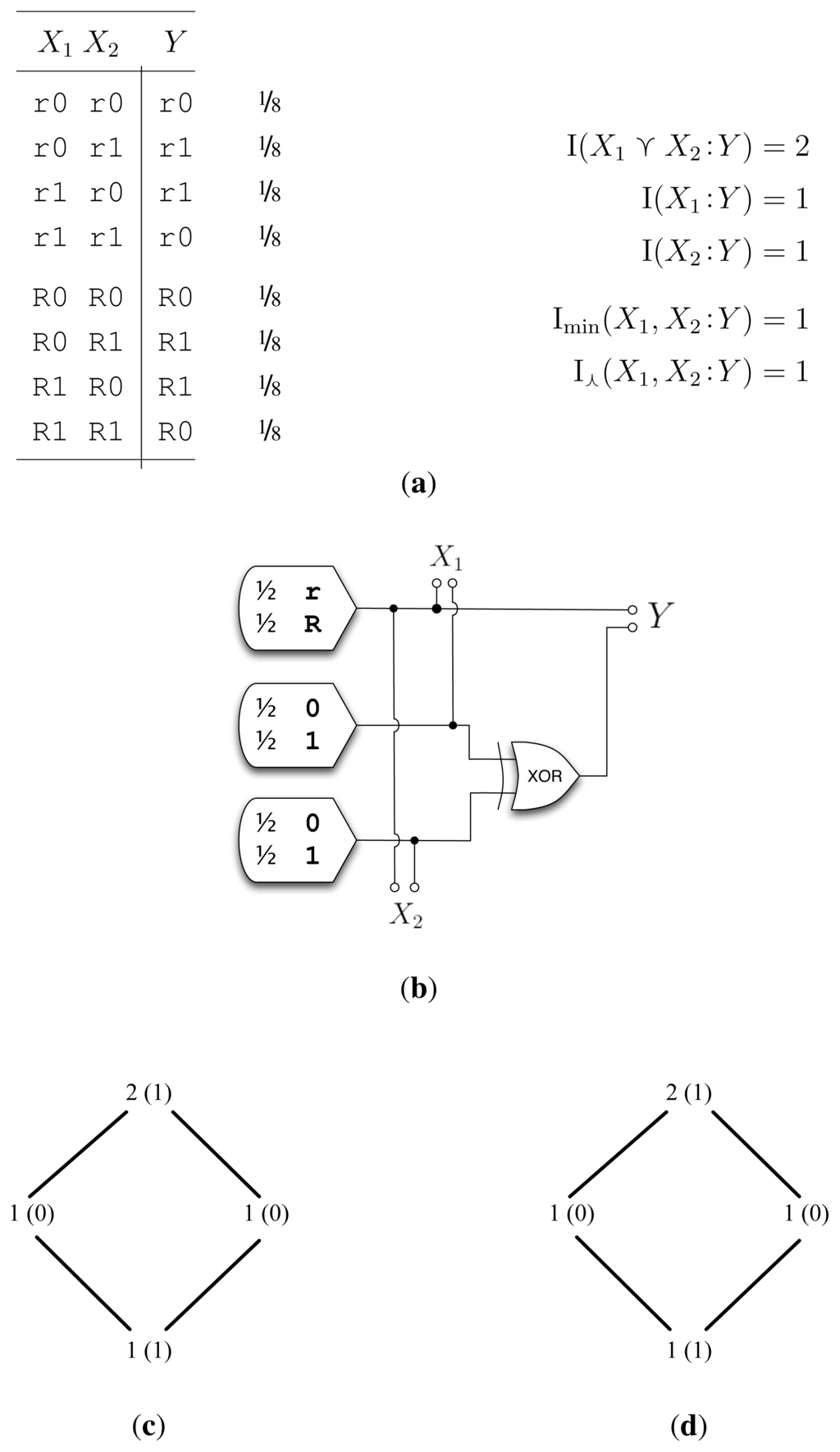
In [], RdnXor was an example where Imin shined by reaching the desired decomposition of one bit of redundancy and one bit of synergy. We see that I⋏ finds this same answer. I⋏ extracts the common random variable within X1 and X2—the r/R bit—and calculates the mutual information between the common random variable and Y to arrive at I⋏(X1, X2 :Y ) = 1 bit.
5.3. Example ImperfectRdn (Figure 3)
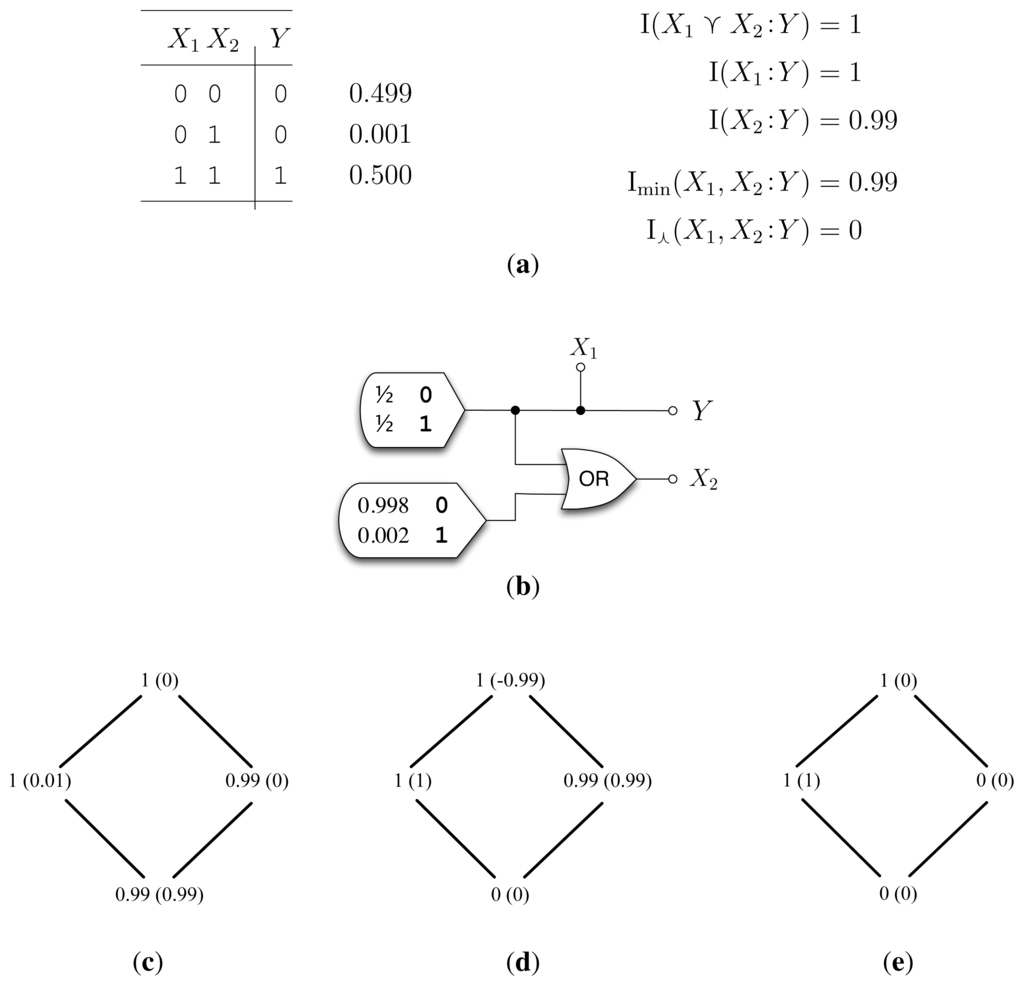
ImperfectRdn highlights the foremost shortcoming of I⋏: It does not detect “imperfect” or “lossy” correlations between X1 and X2. Given (LP0), we can determine the desired decomposition analytically. First, I(X1 ⋎ X2 :Y) = I(X1 :Y) = 1 bit, and thus, I (X2 :Y |X1) = 0 bits. Since the conditional mutual information is the sum of the synergy I∂(X1, X2 :Y ) and unique information I∂(X2 :Y ), both quantities must also be zero. Then, the redundant information I∂(X1, X2 :Y ) = I(X2 :Y )–I∂(X2 : Y ) = I(X2 :Y ) = 0.99 bits. Having determined three of the partial informations, we compute the final unique information: I∂(X1 :Y ) = I(X1 :Y ) – 0.99 = 0.01 bits.
How well do Imin and I⋏ match the desired decomposition of ImperfectRdn? We see that Imin calculates the desired decomposition (Figure 3c); however, I⋏ does not (Figure 3d). Instead, I⋏ calculates zero redundant information, that I∩(X1, X2 :Y) = 0 bits. This unpleasant answer arises from Pr(X1 = 0, X2 = 1) > 0. If this were zero, then both I⋏ and Imin reach the desired one bit of redundant information. Due to the nature of the common random variable, I⋏ only sees the “deterministic” correlations between X1 and X2; add even an iota of noise between X1 and X2, and I⋏ plummets to zero. This highlights the fact that I⋏ is not continuous: an arbitrarily small change in the probability distribution can result in a discontinuous jump in the value of I⋏. As with traditional information measures, such as the entropy and the mutual information, it may be desirable to have an I∩ measure that is continuous over the simplex.
To summarize, ImperfectRdn shows that when there are additional “imperfect” correlations between A and B, i.e., I(A:B|A ⋏ B) > 0, I⋏ sometimes underestimates the ideal I∩(A, B:Y ).
6. Negative Synergy
In ImperfectRdn, we saw I⋏ calculate a synergy of −0.99 bits (Figure 3d). What does this mean? Could negative synergy be a “real” property of Shannon information? When n = 2, it is fairly easy to diagnose the cause of negative synergy from the equation for I∂(X1 ⋎ X2 : Y ) in Equation (7). Given (GP), negative synergy occurs if and only if,
where I∪ is dual to I∩ and related by the inclusion-exclusion principle. For arbitrary n, this is I∪(X1, . . ., Xn : Y ) ≡ ∑ S⊆{X1,...,Xn}(−1)|S|+1 I∩ (S1, . . ., S|S| :Y). The intuition behind I∪ is that it represents the aggregate information contributed by the sources, X1, . . ., Xn, without considering synergies or double-counting redundancies.
From Equation (8), we see that negative synergy occurs when I∩ is small, probably too small. Equivalently, negative synergy occurs when the joint random variable conveys less about Y than the sources, X1 and X2, convey separately; mathematically, when I(X1 ⋎ X2 :Y ) < I∪(X1, X2 : Y ). On the face of it, this sounds strange. No structure “disappears” after X1 and X2 are combined by the ⋎ operator. By the definition of ⋎, there are always functions f1 and f2, such that X1 ≅= f1(Z) and X2 ≅= f2(Z). Therefore, if your favorite I∩ measure does not satisfy (LP0), it is too strict.
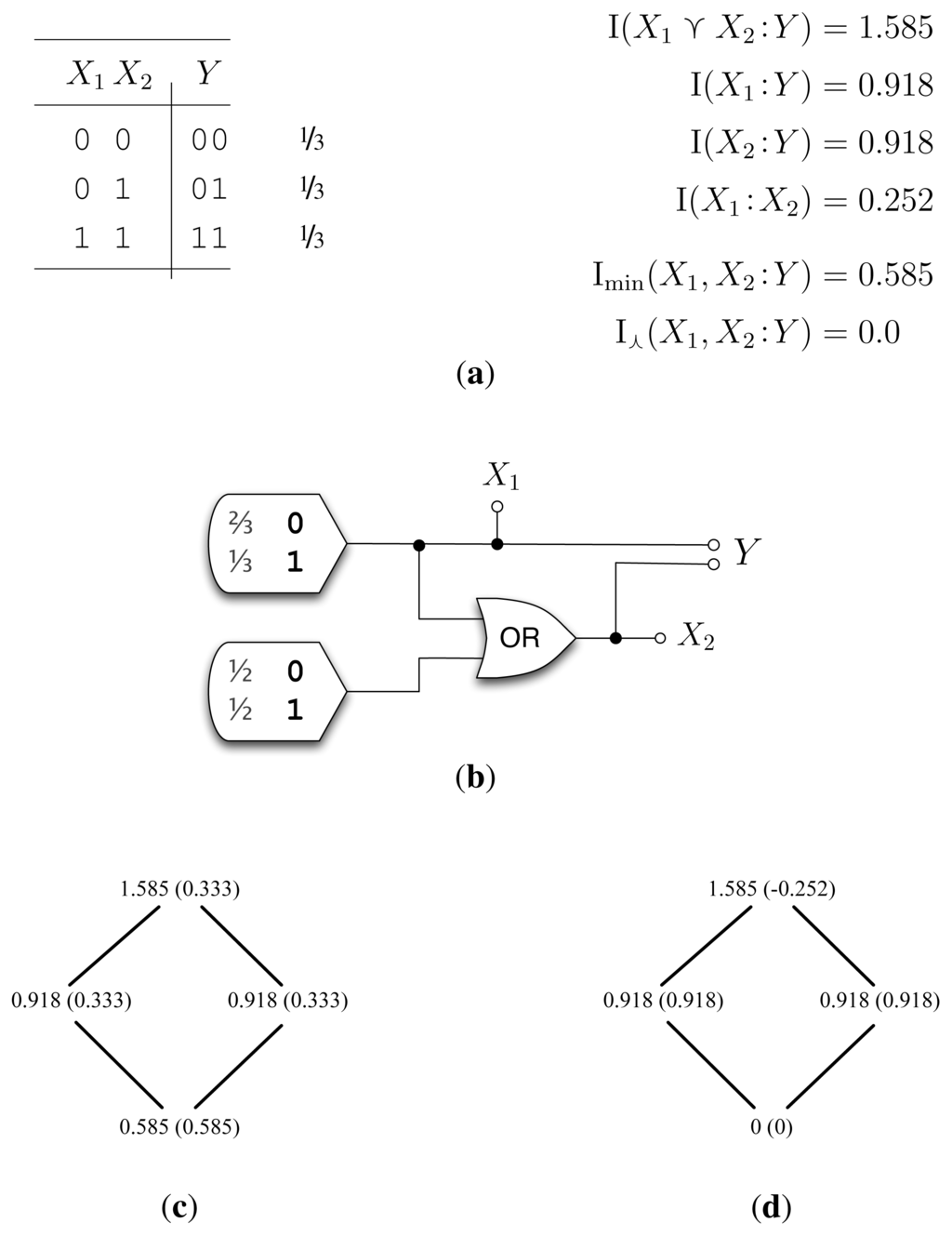
This means that our measure, , does not account for the full zero-information overlap between I0(X1 :Y ) and I0(X2 :Y ). This is shown in the example, Subtle (Figure 4), where calculates a synergy of −0.252 bits. Defining a zero-error, I∩, that satisfies (LP0) is a matter of ongoing research.
7. Conclusions and Path Forward
We made incremental progress on several fronts towards the ideal Shannon I∩.
7.1. Desired Properties
We have expanded, tightened and grounded the desired properties for I∩. Particularly,
(LB) highlights an uncontentious, yet tighter lower bound on I∩ than (GP).
Inspired by I∩(X1 :Y ) = (X1 :Y ) and (M0) synergistically implying (LB), we introduced (M1) as a desired property.
What was before an implicit assumption, we introduced (Eq) to better ground one’s thinking.
7.2. A New Measure
Based on the Gács–Körner common random variable, we introduced a new Shannon I∩ measure. Our measure, I⋏, is theoretically principled and the first to satisfy (TM). A point to keep in mind is that our intersection information is zero whenever the distribution Pr(x1, x2, y) has full support; this dependence on structural zeros is inherited from the common random variable.
7.3. How to Improve
We identified where I⋏ fails; it does not detect “imperfect” correlations between X1 and X2. One next step is to develop a less stringent I∩ measure that satisfies (LP0) for ImperfectRdn, while still satisfying (TM). Satisfying continuity would also be a good next step.
Contrary to our initial expectation, Subtle, showed that does not satisfy (LP0). This matches a result from [], which shows that (LP0), (S1), (M0) and (Id) cannot all be simultaneously satisfied, and it suggests that is too strict. Therefore, what kind of zero-error informational overlap is not capturing? The answer is of paramount importance. The next step is to formalize what exactly is required for a zero-error I∩ to satisfy (LP0). From Subtle, we can likewise see that within zero-error information, (Id) and (LP0) are incompatible.
Acknowledgments
Virgil Griffith thanks Tracey Ho, and Edwin K. P. Chong thanks Hua Li for valuable discussions. While intrepidly pulling back the veil of ignorance, Virgil Griffith was funded by a Department of Energy Computational Science Graduate Fellowship; Edwin K. P. Chong was funded by Colorado State University’s Information Science & Technology Center; Ryan G. James and James P. Crutchfield were funded by Army Research Office grant W911NF-12-1-0234; Christopher J. Ellison was funded by a subaward from the Santa Fe Institute under a grant from the John Templeton Foundation.
Appendix
By and large, most of these proofs follow directly from the lattice properties and also from the invariance and monotonicity properties with respect to ≅= and ≼.
A. Properties of
Lemma 1
satisfies (GP), (Eq), (TM), (M0), and (S0), but not (LP0).
Proof
(GP) follows immediately from the nonnegativity of the entropy. (Eq) follows from the invariance of entropy within the equivalence classes induced by ≅=. (TM) follows from the monotonicity of the entropy with respect to ≼. (M0) also follows from the monotonicity of the entropy, but now applied to ⋏iXi ⋏ W ⋏ Y ≼ ⋏iXi ⋏ Y. If there exists some j, such that Xj ≼ W, then generalized absorption says that ⋏iXi ⋏ W ⋏ Y ≅= ⋏iXi ⋏ Y, and thus, we have the equality condition. (S0) is a consequence of the commutativity of the ⋏ operator. To see that (LP0) is not satisfied by the , we point to the example, Subtle (Figure 4), which has negative synergy. One can also rewrite (LP0) as the supermodularity law for common information, which is known to be false in general. (See [], Section 5.4.)
Lemma 2
satisfies (LB), (SR), and (Id).
Proof
For (LB), note that Q ≼ X1 ⋏ · · · ⋏ Xn for any Q obeying Q ≼ Xi for i = 1, . . ., n. Then, apply the monotonicity of the entropy. (SR) is trivially true given Lemma 7 and the definition of zero-error information. Finally, (Id) follows from the absorption law and the invariance of the entropy.
Lemma 3
satisfies (M1) and (S1), but not (LP1).
Proof
(M1) follows using the absorption and monotonicity of the entropy in nearly the same way that (M0) does. (S1) follows from commutativity, and (LP1) is false, because (LP0) is false.
B. Properties of I⋏
The proofs here are nearly identical to those used for .
Lemma 4
I⋏ (X1, . . ., Xn :Y ) satisfies (GP), (Eq), (TM), (M0), and (S0), but not (LP0).
Proof
(GP) follows from the nonnegativity of mutual information. (Eq) follows from the invariance of entropy. (TM) follows from the data processing inequality. (M0) follows from applying the monotonicity of the mutual information I(Y : · ) to ⋏iXi ⋏ W ≼ ⋏iXi. If there exists some j, such that Xj ≼ W, then generalized absorption says that ⋏iXi ⋏ W ≅= ⋏iXi, and thus, we have the equality condition. (S0) follows from commutativity, and a counterexample for (LP0) is given by ImperfectRdn (Figure 3).
Lemma 5
I⋏ (X1, . . ., Xn :Y ) satisfies (LB) and (SR), but not (Id).
Proof
For (LB), note that Q ≼ X1 ⋏ · · · ⋏ Xn for any Q obeying Q ≼ Xi for i = 1, . . ., n. Then, apply the monotonicity of the mutual information to I(Y : · ). (SR) is trivially true given Lemma 8. Finally, (Id) does not hold, since X ⋏ Y ≼ X ⋎ Y, and thus, I⋏ (X, Y :Y ⋏ Y) = H(X ⋏ Y ).
Lemma 6
I⋏ (X1, . . ., Xn :Y ) does not satisfy (M1), (S1), or (LP1).
Proof
(M1) is false due to a counterexample provided by ImperfectRdn (Figure 3), where I⋏ (X1 :Y) = 0.99 bits and I⋏ (X1, Y :Y) = 0 bits. (S1) is false, since I⋏ (X, X:Y ) ≠ I⋏ (X, Y :X). Finally, (LP1) is false, due to (LP0) being false.
C. Miscellaneous Results
Lemma 7
Simplification of .
Proof
Recall that I0(Q:Y ) ≡ H(Q ⋏ Y ), and note that ⋏iXi is a valid choice for Q. By definition, ⋏iXi is the richest possible Q, and so, monotonicity with respect to ≼ then guarantees that H( ⋏iXi ⋏ Y ) ≥ H(Q ⋏ Y ).
Lemma 8
Simplification of I⋏.
Proof
Note that ⋏iXi is a valid choice for Q. By definition, ⋏iXi is the richest possible Q, and so, monotonicity with respect to ≼ then guarantees that I(Q:Y ) ≤ I(⋏iXi :Y ).
Lemma 9
I⋏ (X1, . . ., Xn :Y ) ≤ Imin (X1, . . ., Xn : Y )
Proof
We need only show that I( ⋏iXi : Y ) ≤ Imin (X1, . . ., Xn : Y ). This can be restated in terms of the specific information: I( ⋏iXi : y) ≤ mini I (Xi : y) for each y. Since the specific information increases monotonically on the lattice (cf. Section 2.2 or []), it follows that I( ⋏iXi : y) ≤ I(Xj : y) for any j.
Conflicts of Interest
The authors declare no conflicts of interest.
- Author ContributionsEach of the authors contributed to the design, analysis, and writing of the study.
References
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. 2010. arXiv:1004.2515 [cs.IT]. [Google Scholar]
- Griffith, V.; Koch, C. Quantifying Synergistic Mutual Information. In Guided Self-Organization: Inception; Prokopenko, M., Ed.; Springer: Berlin, Germany, 2014. [Google Scholar]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared Information—New Insights and Problems in Decomposing Information in Complex Systems. Proceedings of the European Conference on Complex Systems 2012, Brussels, Belgium, 3–7 September 2012; Gilbert, T., Kirkilionis, M., Nicolis, G., Eds.; Springer Proceedings in Complexity; Springer: Berlin, Germany, 2013; pp. 251–269. [Google Scholar]
- Lizier, J.; Flecker, B.; Williams, P. Towards a synergy-based approach to measuring information modification. Proceedings of the 2013 IEEE Symposium on Artificial Life (ALIFE), Singapore, 16–17 April 2013; pp. 43–51.
- Gács, P.; Körner, J. Common information is far less than mutual information. Probl. Control Inform. Theor 1973, 2, 149–162. [Google Scholar]
- Wolf, S.; Wullschleger, J. Zero-error information and applications in cryptography. Proc. IEEE Inform. Theor. Workshop 2004, 4, 1–6. [Google Scholar]
- Li, H.; Chong, E.K.P. On a Connection between Information and Group Lattices. Entropy 2011, 13, 683–708. [Google Scholar]
- Wyner, A.D. The common information of two dependent random variables. IEEE Trans. Inform. Theor 1975, 21, 163–179. [Google Scholar]
- Cerf, N.J.; Adami, C. Negative Entropy and Information in Quantum Mechanics. Phys. Rev. Lett 1997, 79, 5194–5197. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley: New York, NY, USA, 1991. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).