Robust Control of a Class of Uncertain Fractional-Order Chaotic Systems with Input Nonlinearity via an Adaptive Sliding Mode Technique
Abstract
: In this paper, the problem of stabilizing a class of fractional-order chaotic systems with sector and dead-zone nonlinear inputs is investigated. The effects of model uncertainties and external disturbances are fully taken into account. Moreover, the bounds of both model uncertainties and external disturbances are assumed to be unknown in advance. To deal with the system’s nonlinear items and unknown bounded uncertainties, an adaptive fractional-order sliding mode (AFSM) controller is designed. Then, Lyapunov’s stability theory is used to prove the stability of the designed control scheme. Finally, two simulation examples are given to verify the effectiveness and robustness of the proposed control approach.1. Introduction
Although fractional calculus is a mathematical topic with more than 300 years of history, its application to physics and engineering has attracted lots of attentions only in the recent years. It has been found that with the help of fractional calculus, many systems in interdisciplinary fields can be described more accurately, such as viscoelastic systems [1], dielectric polarization [2], electrode-electrolyte polarization [3], finance systems and electromagnetic waves [4]. That is to say, fractional calculus provides a superb instrument for the description of the memory and hereditary properties of various materials and processes.
Chaotic systems are a well-known class of complex nonlinear systems, which have several special properties, such as extraordinary sensitivity to system initial conditions, chaotic attractors, and fractal motions. Meanwhile, it has been proven that some fractional-order differential systems can behave chaotically, e.g., the fractional-order Duffing system [5], fractional-order Chen-Lee system [6], fractional-order Lorenz system [7], fractional-order hyperchaotic Chen system [8], fractional-order Qi system [9], and so on. The research of chaotic systems has attracted considerable attentions, for example, Gyorgyi [10] calculated the entropy in chaotic systems. Steeb et al. [11] applied the maximum entropy formalism into the study of chaotic systems. Aghababa [12] used the finite-time theory to realize finite-time synchronization of chaotic systems. Lu [13] developed a nonlinear observer to synchronize the chaotic systems. Chen et al. [14,15] researched the synchronization of fractional-order chaotic neural networks. With the development of sliding mode control (SMC) technique, SMC approach has became a universal method to realize the stabilization or synchronization of chaotic systems [16–20]. It is well known that the system on the sliding manifold has desired properties such as good stability, disturbance rejection ability, and tracking capability.
In this paper, the following class of fractional-order chaotic systems are considered :
The fractional-order system (1) was introduced by [20], and it should be noted that many chaotic systems can be modeled in this form, such as the Chen, Lorenz, Liu, and Lu systems, etc. Some control techniques have been reported for stabilizing this type of system. For example, Sadras et al. [21] introduced a sliding mode controller to stabilize a special case of system (1). Chen et al. [22] developed a fractional-order sliding surface to guarantee asymptotic stability of the system in the presence of uncertainties. Inspired by [22], Yin et al. [23] provided an adaptive fractional-order sliding mode technique to realize the robust stabilization of this system with unknown bounded uncertainties. It is worth noting that there is a drawback in abovementioned literatures, that is, the stability of the sliding mode dynamics is not researched. Recently, Faieghi et al. [24] firstly applied the fractional Lyapunov stability theory to demonstrate global stability of the sliding mode dynamics. Yuan et al. [25] employed the continuous frequency distributed model of fractional integrator to analyze asymptotic stability of this kind of sliding mode dynamics. However, in [24,25], the nonlinear items of the controlled system were required to be directly eliminated, resulting in a complex controller unsuitable for practical realization. On the other hand, all approaches in the aforementioned works are only focused on the linear and direct application of control inputs. In practice, input nonlinearity is often encountered in various chaotic systems and can be a cause of instability. Thus, it is obvious that the effects of input nonlinearity must be taken into account when analyzing and implementing a control scheme. Recently, Aghababa [26–28] considered the impacts of nonlinear inputs in the stabilization and synchronization of integer-order chaotic systems. However, to the best of our knowledge, there is little information available in the literature about the stabilization of fractional-order chaotic systems with nonlinear inputs.
Motivated by the above discussions, the problem of stabilizing a class of uncertain fractional-order chaotic systems with nonlinear inputs is addressed in this paper. Two kinds of nonlinear inputs including sector nonlinear inputs and dead-zone nonlinear inputs are researched, respectively. In order to stabilize system (1), an adaptive fractional-order sliding mode (AFSM) controller is proposed, which is associate with time-varying feedback gains, can deal with the nonlinear items of the controlled system. After that, the Lyapunov’s stability theory is used to demonstrate the stability of the proposed control scheme.
To sum up, our approach makes the following contributions: (i) it researches the stabilization of a class of fractional-order chaotic systems with unknown bounded model uncertainties and external disturbances; (ii) two kinds of control input nonlinearities including sector and dead-zone nonlinearities are considered; (iii) based on a fractional-order integral type sliding surface, adaptive sliding mode input control and some adaptation laws, a novel sliding mode control scheme is proposed.
The remainder of this paper is organized as follows: in Section 2, the relevant definitions, lemmas and numerical methods for solving the fractional-order differential equations are given. Main results are presented in Section 3. Some numerical simulations are provided in Section 4 to show the effectiveness of the proposed method. Finally, conclusions are put forth in Section 5.
2. Preliminaries
2.1. Definitions and Lemma
The most frequently used definitions for the general fractional calculus are Riemann-Liouville definition, Caputo definition and Grunwald-Letnikov definition.
Definition 1. The α-th-order Riemann-Liouville fractional integration is given by :
Definition 2. For n−1 < α≤n, n ∈ R, the Riemann-Liouville fractional derivative definition of order α is defined as:
Definition 3. The Caputo fractional derivative definition of order α is described as:
Definition 4. The Grunwald-Letnikov fractional derivative definition of order α is written as:
Lemma 1. (Barbalat’s Lemma [29]) If ε R → R is a uniformly continuous function for t ≥ 0, and if the limit of the integral exist and is finite, then .
2.2. Numerical Method for Solving Fractional Differential Equations
The PC (Predictor, Corrector) method which was proposed by Diethelm et al. in [30] is generally used to solve fractional differential equations (FDE). Consider the following fractional differential equation:
During the process of numerical computation, the trapezoidal quadrature product is used to replace the integral, and the nodes tj(j = 0,1,2, …, n+1) are taken with respect to the weight function (tn+1−·)α−1, that is to say:
Let h = T/N, tn = nh, n = 0,1, …, N, and Xh(tn) be approximation for X(tn). If Xh(tj) is calculated, then Xh(tn+1) can be computed by means of the following formula:
To calculate the values of and , we should use the predictor formula, the following numerical approximation formula is applied:
Hence, for approximating the Equation (7), the predictor formula is given by:
In this method, the error is:
Thus, with the help of the aforementioned method, we can obtain the numerical solution of a fractional differential equation.
3. Main Results
Consider system (1) is perturbed by model uncertainty and external disturbance, and a nonlinear control input is added to the second equation of system (1), then the proposed fractional-order chaotic system can be rewritten as:
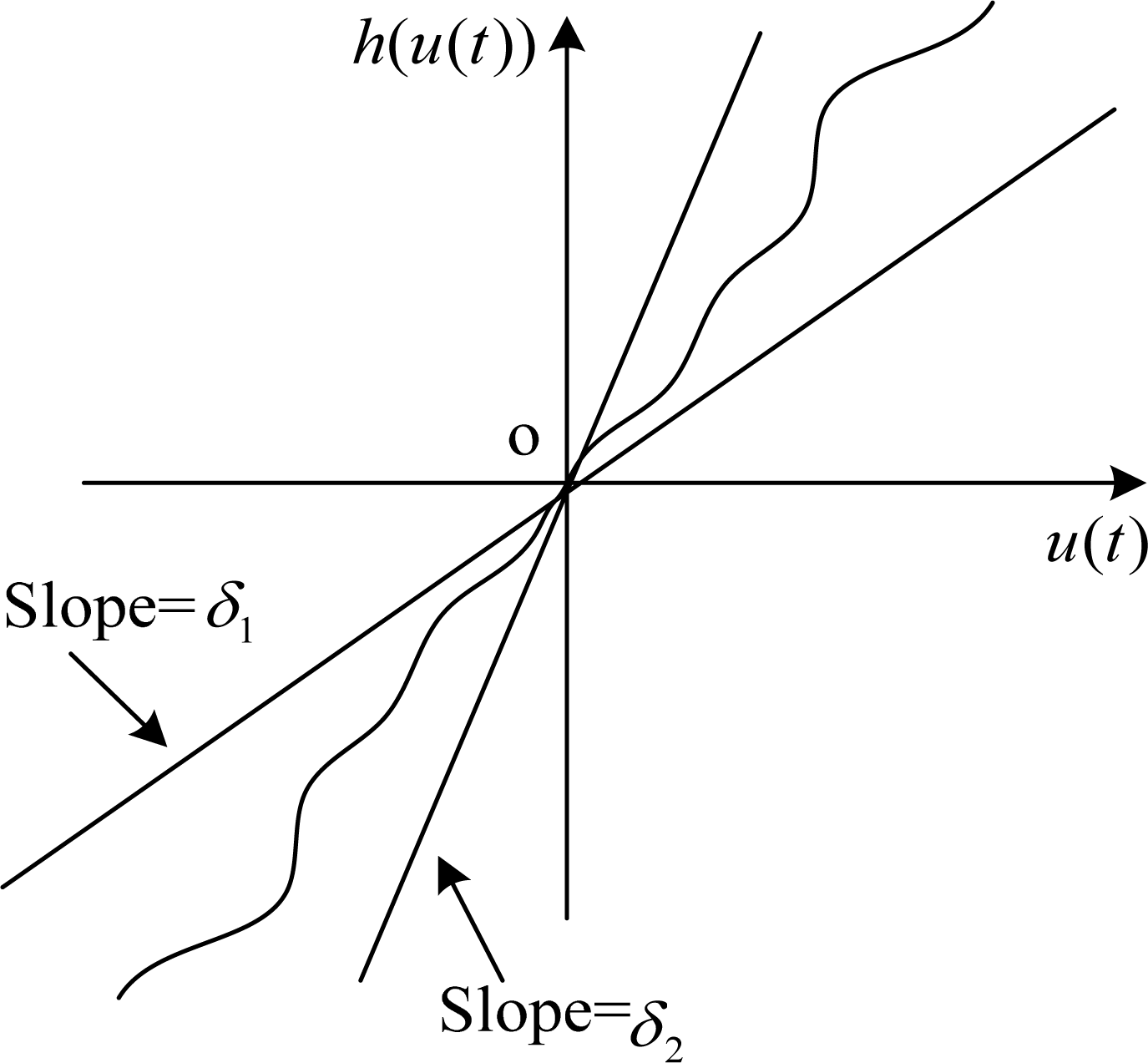
Then the presented nonlinear function of input in Equation (15) is called sector nonlinear input. A typical sector nonlinear function is shown in Figure 1.
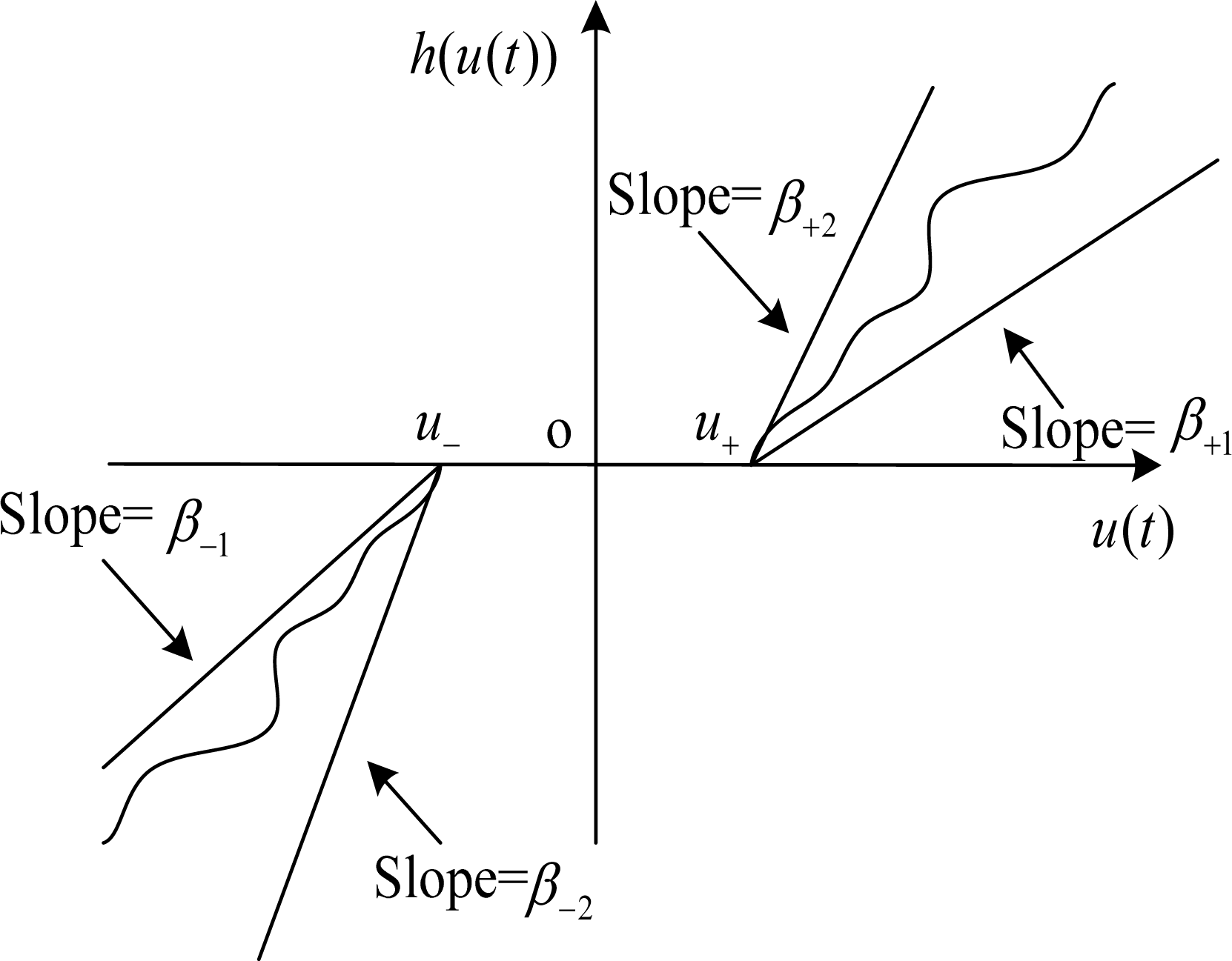
The dead-zone nonlinear function is described as follows:
Before introducing our approach, we firstly give an assumption.
Assumption 1. The model uncertainty and external disturbance are assumed to be bounded by:
Letting θ̂(t) and ψ̂(t) be estimations for θ and ψ, respectively, which are updated by the following adaptive laws:
Generally, the design procedure of an AFSM controller involves two steps. The first step is to establish an appropriate sliding surface with the desired properties. The second step is to design a robust control law to ensure the occurrence of sliding motion. In this paper, we select the following fractional-order integral type sliding surface:
When the system (14) operates in the sliding mode, the following equalities are satisfied:
Theorem 1. Consider the sliding mode dynamics (23), the system is asymptotically stable.
Proof: According to the continuous frequency distributed model of fractional integrator [31–33], the fractional-order sliding mode dynamics (23) is exactly equivalent to the following infinite dimensional ordinary differential equations:
Taking the derivative of V1(t) with respect to time, it yields:
Since μi(ω) > 0, α, r are non-negative constants, and η is a positive constant, so according to the analysis results of Reference [34], we have V̇1(t) < 0, which implies that the fractional-order sliding mode dynamics (23) is asymptotically stable. Therefore, the proof is completed.
Once a proper sliding surface has been designed, it is followed by designing an adaptive control law to force the state trajectories of system (14) onto the sliding surface and stay on it forever. The control law for the nonlinearities defined in Equations (15) and (16) are given by Equations (27) and (28), respectively:
Theorem 2. Consider the fractional-order chaotic system (14) with unknown bounded uncertainties and sector nonlinear input, then the closed-loop system consisting of uncertain system (14) and controller (27) will converge to the sliding surface s = 0
Proof: Selecting a positive Lyapunov function for system (14):
Taking the time derivative of both sides of Equation (30), one obtains:
Inserting ṡ from Equation (21) into (31), and according to the second state equation of Equation (14), we have:
It is clear that:
According to Equations (15) and (27), we known that:
One can conclude from Equation (34) that:
Multiplying both sides of Equation (35) by |s|, and using |s| sgn(s) = s with sgn2(s) = 1, we get:
Substituting Equation (36), the adaptive laws (19) and (29) into (33), and using Assumption 1, one has:
Integrating (38) from zero to t, it yields:
Since V̇2(t)≤0, V2(0) − V2(t) ≥ 0 is positive and finite, then we can obtain that exists and is finite. With this in mind, according to Barbalat’s lemma:
Owing to the fact Q(t) > 0, Equation (40) implies that s → 0 as t → ∞. Therefore, the state trajectories of the controlled system (14) can be forced onto the predefined sliding surface. Hence, the proof is completed. On the basis of Theorem 2, if system (14) subject to dead-zone nonlinear input, then we have the following theorem.
Theorem 3. Consider the fractional-order chaotic system (14) with unknown bounded uncertainties and dead-zone nonlinear input. Then the closed-loop system consisting of uncertain system (14) and controller (28) will converge to the sliding surface s = 0
Proof: In a similar way as in the Proof of Theorem 2, we get:
According to Equations (16), (17), and (28), when s < 0, it is apparent that u(t) > u+, and:
From Equation (42), since γ = β−1 > 0, K(t) > 0, then one has:
Multiplying both sides of Equation (43) by |s|, and using |s| sgn(s) = s with sgn2(s) = 1 it yields:
When s > 0, through the similar operations, the inequality (44) still holds. Substituting (44), the adaptive laws (19) and (29) into (41), in the same way to the case of Equation (37), we can obtain V̇2(t) ≤ 0. By Barbalat’s lemma, we have . Thus, the proof is completed.
4. Simulation Results
In this section, two illustrative examples are presented to verify the feasibility and effectiveness of the propose control scheme.
4.1. Numerical Simulation Considering Sector Nonlinear Input
Consider an uncertain fractional-order Chen system with sector nonlinear input, which is described by:
It is obvious that δ1 = 0.4, γ = 5/2. In this simulation, set the control parameters as λ0 = λ1 = λ2 = λ3 = 15, η = 1, ρ1 = 0.1, ρ2 = 0.2, let h = 0.01, (q1, q2, q3) = (0.9, 0.92, 0.94), (a,b,c) = (35,3,28), θ̂(0) = ψ̂(0) = 0, k0(0) = k1(0) = k2(0) = k3(0) = 0.2. According to the initialization method in [35], the initial conditions for fractional differential equations with order between 0 and 1 are constant function of time, so the initial conditions for system (45) can be chosen randomly as:
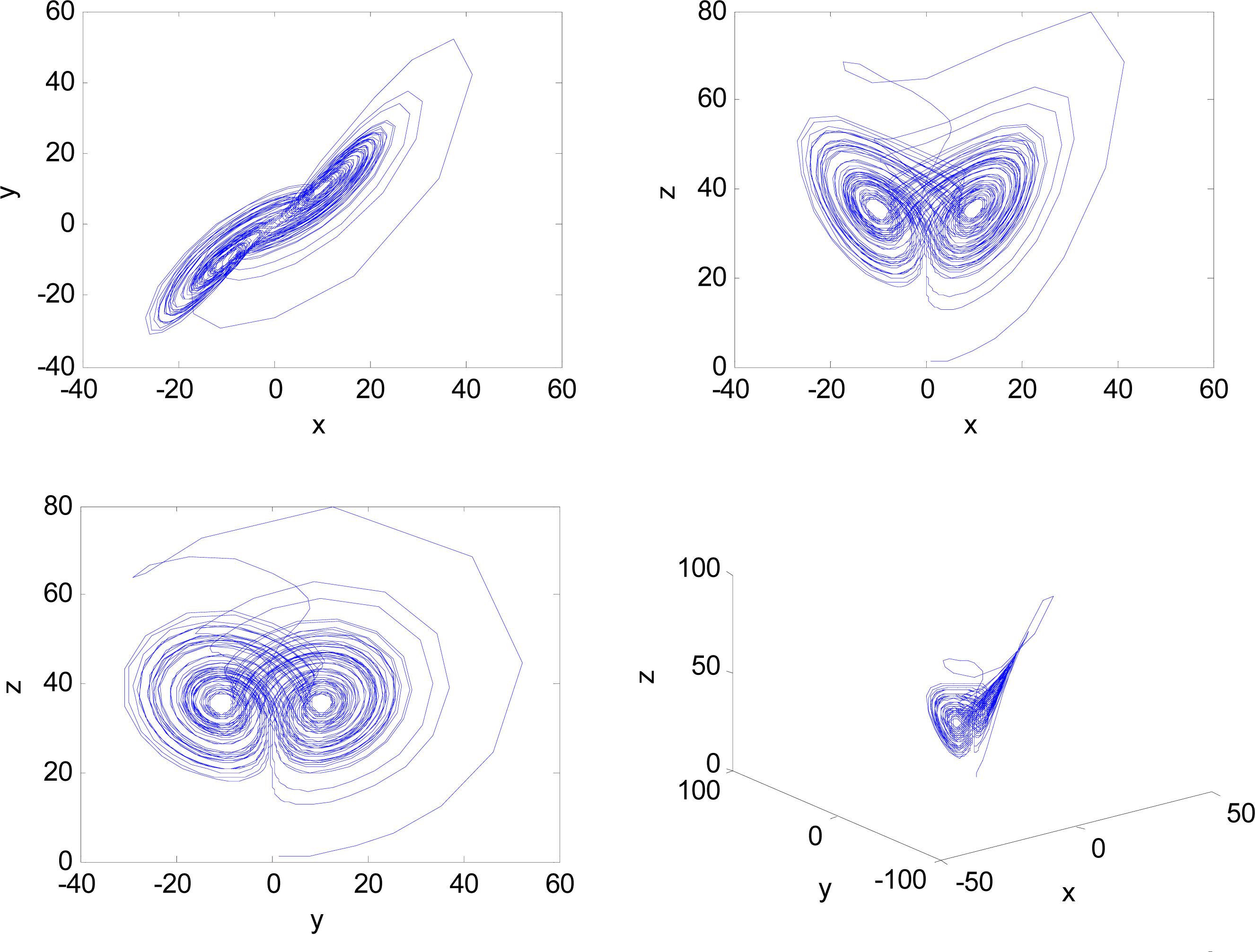
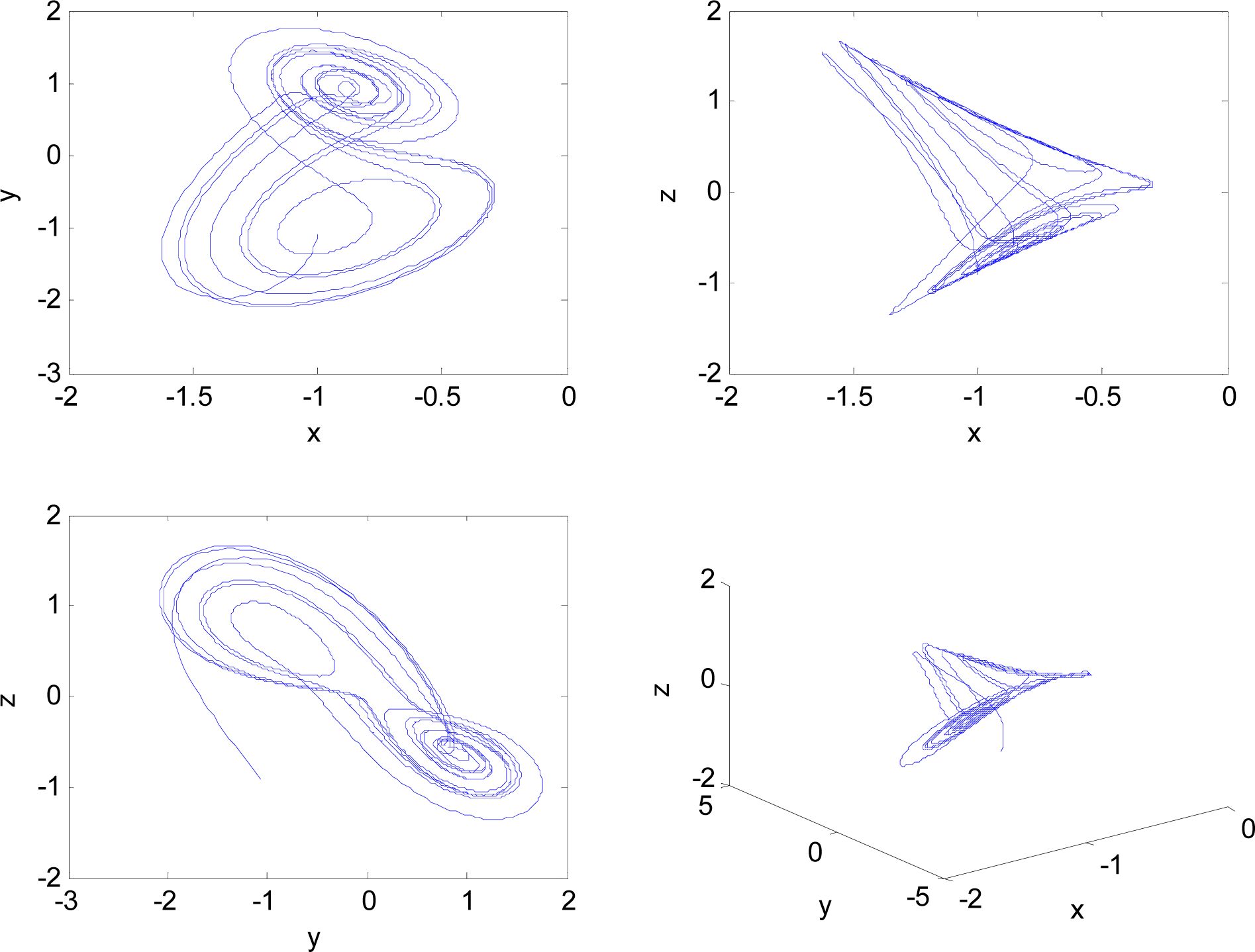
With the above fractional orders and initial conditions, system (45) possesses a chaotic behavior, as shown in Figure 3.
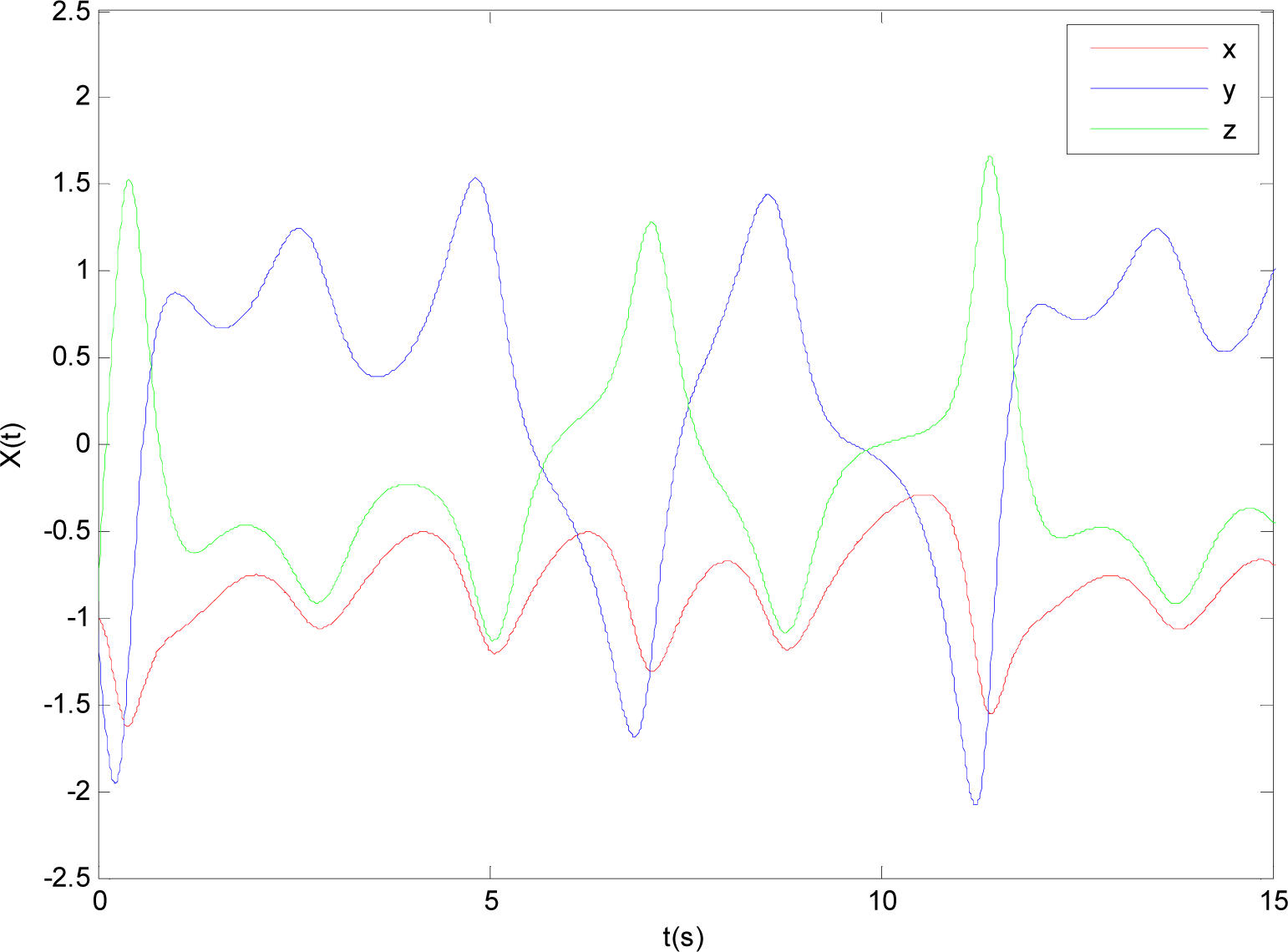
To observe the control effect of AFSM controller, the state trajectories of Equation (45) without control are firstly given in Figure 4.
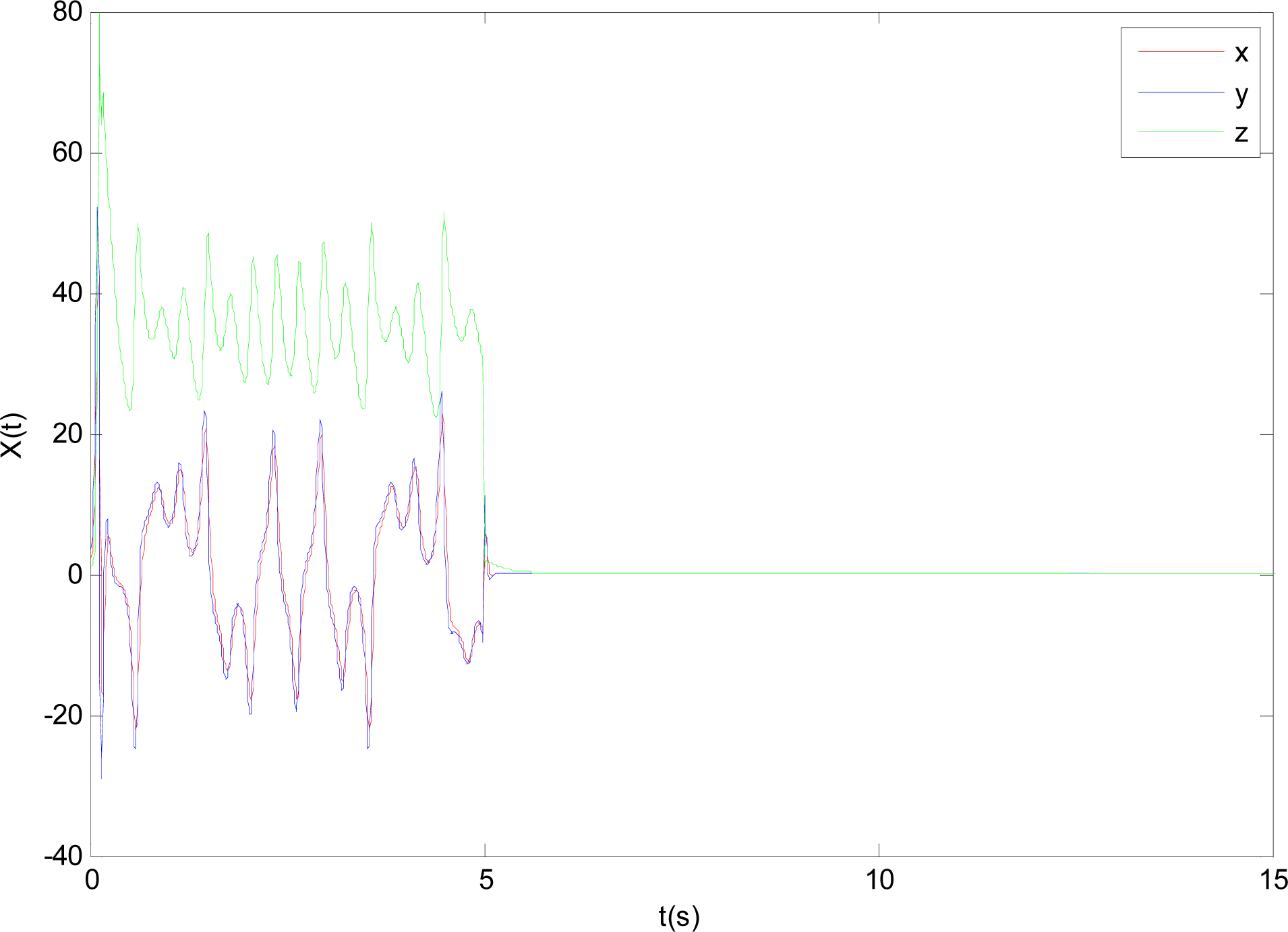
When the controller is activated at t = 5s, we can obtain the desired time responses of system (45), shown in Figure 5. It is not difficult to see that all state trajectories converge to zero asymptotically, which implies that a class of uncertain fractional-order chaotic systems (14) with sector nonlinear input can be stabilized.
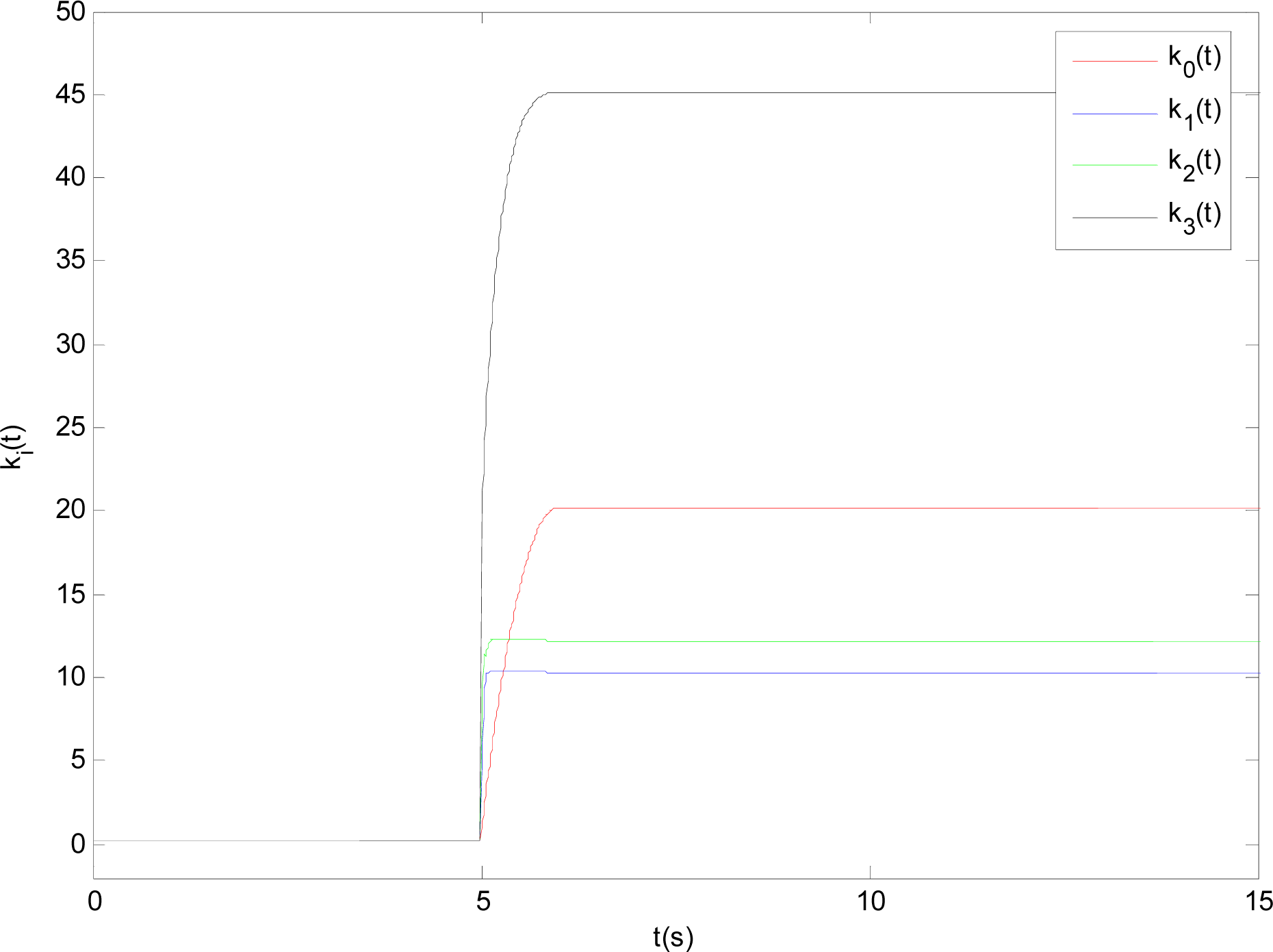
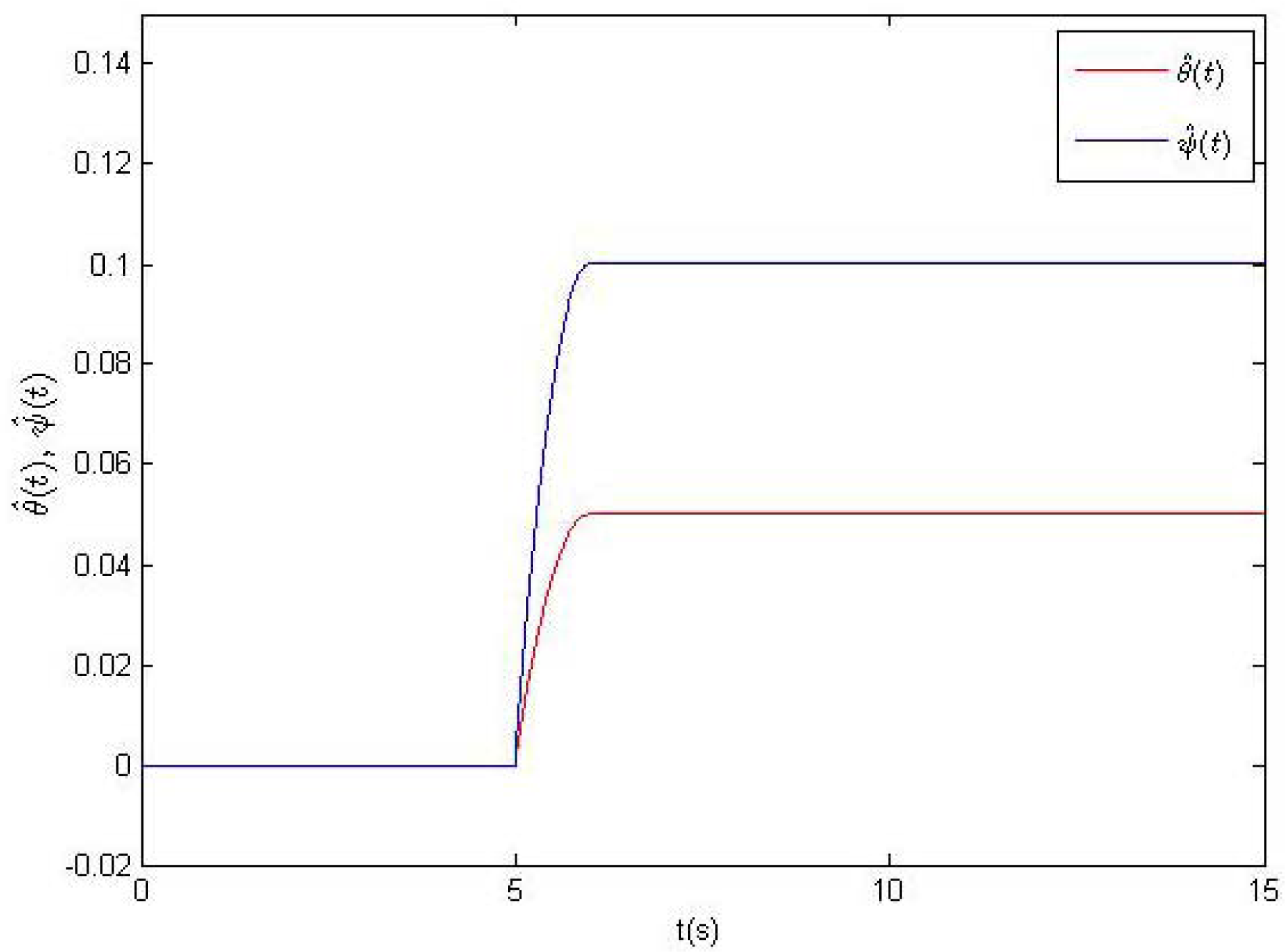
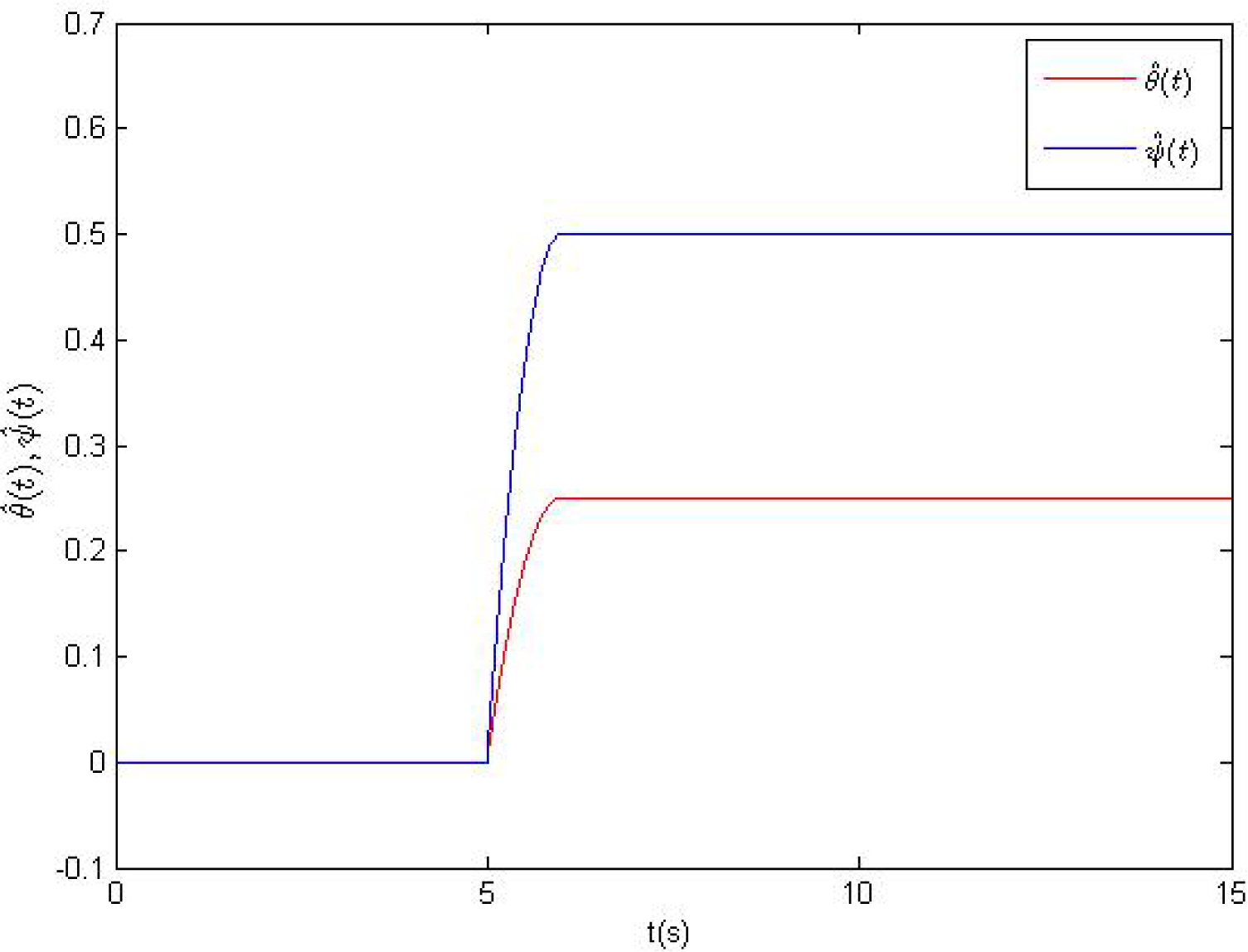
The time evolutions of feedback gains ki(t), i = 0,1,2,3 and the estimations θ̂(t), ψ̂(t) are presented in Figures 6 and 7, respectively. From Figures 6 and 7, it is clear that all time-varying feedback gains ki(t), i = 0,1,2,3 and the estimations θ̂(t), ψ̂(t) converge to some fixed values, which verify the feasibility of the introduced method.
4.2. Numerical Simulation Considering Dead-Zone Nonlinear Input
In this simulation, we consider the uncertain fractional-order Liu system with dead-zone nonlinear input, which is written as:
It is obvious that β+1 = 0.7, β−1 = 0.3, γ = 10/3. In this simulation, set the control parameters as λ0 = λ1 = λ2 = λ3 = 10, η = 1, ρ1 = 0.5, ρ2 = 1, let h = 0.01, (q1, q2, q3) = (0.98, 0.98, 0.98), (a,b,c,k,m,e) = (1,2,5,5,4,4,1), θ̂(0) = ψ̂(0) = 0, k0(0) = k1(0) = k2(0) = k3(0) = 0.1. The initial conditions for systems (48) can be chosen randomly as:
The chaotic behaviors of system (48) are displayed in Figures 8 and 9.
When the controller is activated at t = 5s, we get the desired state trajectories of (48), shown in Figure 10.
From Figure 10 we can observe that system (48) is stabilized by the proposed sliding mode control approach, and all state trajectories tend to zero asymptotically. Time evolutions of feedback gains ki(t), i = 0,1,2,3 and the estimations θ̂(t), ψ̂(t) are illustrated in Figures 11 and 12, respectively. All these simulation results demonstrate that our method is strongly robust to unknown model uncertainties and external disturbances. Therefore, the proposed approach is effective and feasible.
5. Conclusions
In this paper, an adaptive fractional-order sliding mode controller is designed to stabilize a class of uncertain fractional-order chaotic systems with nonlinear inputs. The bounds of model uncertainties and external disturbances are assumed to be unknown in advance. Techniques for stabilizing this type of systems are demonstrated in detail. On the basis of the Lyapunov stability theorem, some sufficient conditions are given to guarantee the stabilization. Finally, two simulation examples are presented to verify the effectiveness and robustness of the proposed control scheme.
Acknowledgments
The author would like to thank the editors and referees for their constructive comments and suggestions. This work is supported by the National Natural Science Foundation of China (61273119) and the National Nature Science Foundation of China (61374038).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bagley, R.L.; Calico, R.A. Fractional order state equations for the control of viscoelastically damped structure. J. Guidance Control Dyn 1991, 14, 304–311. [Google Scholar]
- Sun, H.H.; Abdelwahad, A.A.; Oharal, B. Linear approximation of transfer function with a pole of fractional power. IEEE Trans. Autom. Control 1984, 29, 441–444. [Google Scholar]
- Ichise, M.; Nagayanagi, Y.; Kojima, T. An analog simulation of non-integer order transfer functions for analysis of electrode process. J. Electroanal. Chem. Interfacial Electrochem 1971, 33, 253–265. [Google Scholar]
- Heaviside, O. Electromagnetic Theory; Chelsea: New York, NY, USA, 1971. [Google Scholar]
- Gao, X.; Yu, J. Chaos in the fractional order periodically forced complex Duffing’s oscillators. Chaos Solitons Fractals 2005, 26, 1125–1133. [Google Scholar]
- Chen, C.M.; Chen, H.K. Chaos and hybrid projective synchronization of commensurate and incommensurate fractional order Chen-Lee systems. Nonlinear Dyn 2010, 62, 851–858. [Google Scholar]
- Grigorenko, I.; Grigorenko, E. Chaotic dynamics of the fractional Lorenz system. Phys. Rev. Lett 2003, 91, 034101. [Google Scholar]
- Wu, X.J.; Lu, Y. Generalized projective synchronization of the fractional-order Chen hyperchaotic system. Nonlinear Dyn 2009, 57, 25–35. [Google Scholar]
- Zhang, R.X.; Yang, S.P. Robust chaos synchronization of fractional-order chaotic systems with unknown parameters and uncertain perturbations. Nonlinear Dyn 2012, 69, 983–992. [Google Scholar]
- Gyorgyi, G.; Szepfalusy, P. Calculation of the entropy in chaotic systems. Phys. Rev. A 1985, 31, 3477–3479. [Google Scholar]
- Steeb, W.H.; Solms, F.; Stoop, R. Chaotic systems and maximum entropy formalism. J. Phys. Math. Gen 1994, 27, 399–402. [Google Scholar]
- Aghababa, M.P. Finite-time chaos control and synchronization of fractional-order nonautonomous chaotic (hyperchaotic) systems using fractional nonsingular terminal sliding mode technique. Nonlinear Dyn 2012, 69, 247–267. [Google Scholar]
- Lu, J.G. Nonlinear observer design to synchronize fractional-order chaotic system via a scalar transmitted signal. Phys. A 2006, 359, 107–118. [Google Scholar]
- Chen, L.P.; Qu, J.F.; Chai, Y.; Wu, R.C.; Qi, G.Y. Synchronization of a class of fractional-order chaotic neural networks. Entropy 2013, 15, 3265–3276. [Google Scholar]
- Chen, L.P.; Chai, Y.; Wu, R.C.; Sun, J.; Ma, T.D. Cluster synchronization in fractional-order complex dynamical networks. Phys. Lett. A 2012, 376, 2381–2388. [Google Scholar]
- Yang, C.C; Qu, C.J. Adaptive terminal sliding mode control subject to input nonlinearity for synchronization of chaotic gyros. Commun. Nonlinear Sci. Numer. Simul 2012, 18, 682–691. [Google Scholar]
- Yang, C.C. Synchronization of rotating pendulum via self-learning terminal sliding-mode control subject to input nonlinearity. Nonlinear Dyn 2013, 72, 695–705. [Google Scholar]
- Abooee, A.; Haeri, M. Stabilisation of commensurate fractional-order polytopic non-linear differential inclusion subject to input non-linearity and unknown disturbances. IET Control Theory Appl 2013, 7, 1624–1633. [Google Scholar]
- Pisano, A.; Rapaic, M.R.; Jelicic, Z.D.; Usai, E. Sliding mode control approaches to the robust regulation of linear multivariable fractional-order dynamics. Int. J. Robust Nonlinear Control 2010, 20, 2045–2056. [Google Scholar]
- Yin, C.; Zhou, S.M.; Chen, W.F. Design of sliding mode controller for a class of fractional-order chaotic systems. Commun. Nonlinear Sci. Numer. Simul 2012, 17, 356–366. [Google Scholar]
- Dadras, S.; Momeni, H.R. Control of a fractional-order economical system via sliding mode. Phys. A 2010, 389, 2434–2442. [Google Scholar]
- Chen, D.Y.; Liu, Y.; Ma, X.; Zhang, R. Control of a class of fractional-order chaotic systems via sliding mode. Nonlinear Dyn 2011, 67, 893–901. [Google Scholar]
- Yin, C.; Dadras, S.; Zhong, S.M.; Chen, Y.Q. Control of a novel class of fractional-order chaotic systems via adaptive sliding mode control approach. Appl. Math. Model 2013, 37, 2469–2483. [Google Scholar]
- Faieghi, M.R.; Delavari, H.; Baleanu, D. A note on stability of sliding mode dynamics in suppression of fractional-order chaotic systems. Comput. Math. Appl 2013, 66, 832–837. [Google Scholar]
- Yuan, J.; Shi, B.; Ji, W.Q. Adaptive sliding mode control of a novel class of fractional chaotic systems. Adv. Math. Phys 2013, 2013, 576709. [Google Scholar]
- Aghababa, M.P. Adaptive control for electromechanical systems considering dead-zone phenomenon. Nonlinear Dyn 2014, 75, 157–174. [Google Scholar]
- Aghababa, M.P.; Aghababa, H.P. Robust synchronization of a chaotic mechanical system with nonlinearities in control inputs. Nonlinear Dyn 2013, 73, 363–376. [Google Scholar]
- Aghababa, M.P.; Heydari, A. Chaos synchronization between two different chaotic systems with uncertainties, external disturbances, unknown parameters and input nonlinearities. Appl. Math. Model 2012, 36, 1639–1652. [Google Scholar]
- Khalil, H.K. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Diethelm, K.; Ford, N. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn 2002, 29, 3–22. [Google Scholar]
- Trigeassou, J.C.; Maamri, N.; Sabatier, J.; Oustaloup, A. State variables and transients of fractional order differential systems. Comput. Math. Appl 2012, 64, 3117–3140. [Google Scholar]
- Trigeassou, J.C; Maamri, N.; Sabatier, J.; Oustaloup, A. Transients of fractional-order integrator and andderivatives signal. Image Video Process 2012, 6, 359–372. [Google Scholar]
- Trigeassou, J.C.; Maamri, N. Initial conditions and initialization of linear fractional differential equations. Signal Process 2011, 91, 427–436. [Google Scholar]
- Trigeassou, J.C.; Maamri, N.; Sabatier, J.; Oustaloup, A. A. Lyapunov approach to the stability of fractional differential equations. Signal Process 2011, 91, 437–445. [Google Scholar]
- Sabatier, J., Agrawal, O.P., Tenreiro Machado, J.A., Eds.; Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering; Springer: Heidelberg, Germany, 2007.



© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tian, X.; Fei, S. Robust Control of a Class of Uncertain Fractional-Order Chaotic Systems with Input Nonlinearity via an Adaptive Sliding Mode Technique. Entropy 2014, 16, 729-746. https://doi.org/10.3390/e16020729
Tian X, Fei S. Robust Control of a Class of Uncertain Fractional-Order Chaotic Systems with Input Nonlinearity via an Adaptive Sliding Mode Technique. Entropy. 2014; 16(2):729-746. https://doi.org/10.3390/e16020729
Chicago/Turabian StyleTian, Xiaomin, and Shumin Fei. 2014. "Robust Control of a Class of Uncertain Fractional-Order Chaotic Systems with Input Nonlinearity via an Adaptive Sliding Mode Technique" Entropy 16, no. 2: 729-746. https://doi.org/10.3390/e16020729
APA StyleTian, X., & Fei, S. (2014). Robust Control of a Class of Uncertain Fractional-Order Chaotic Systems with Input Nonlinearity via an Adaptive Sliding Mode Technique. Entropy, 16(2), 729-746. https://doi.org/10.3390/e16020729



