Dynamical Stability and Predictability of Football Players: The Study of One Match
Abstract
: The game of football demands new computational approaches to measure individual and collective performance. Understanding the phenomena involved in the game may foster the identification of strengths and weaknesses, not only of each player, but also of the whole team. The development of assertive quantitative methodologies constitutes a key element in sports training. In football, the predictability and stability inherent in the motion of a given player may be seen as one of the most important concepts to fully characterise the variability of the whole team. This paper characterises the predictability and stability levels of players during an official football match. A Fractional Calculus (FC) approach to define a player’s trajectory. By applying FC, one can benefit from newly considered modeling perspectives, such as the fractional coefficient, to estimate a player’s predictability and stability. This paper also formulates the concept of attraction domain, related to the tactical region of each player, inspired by stability theory principles. To compare the variability inherent in the player’s process variables (e.g., distance covered) and to assess his predictability and stability, entropy measures are considered. Experimental results suggest that the most predictable player is the goalkeeper while, conversely, the most unpredictable players are the midfielders. We also conclude that, despite his predictability, the goalkeeper is the most unstable player, while lateral defenders are the most stable during the match.1. Introduction
The study of sports performance has developed over the years trying to improve the feedback provided to coaches and their staff [1]. From rudimentary systems, using only observation, to new technological-based approaches, many procedures can be developed to increase the understanding of a given sport [2]. Therefore, present day research proposes methods and techniques that can help analyse sports performance [3].
Football is one of the most popular sports in the World [4]. Scientific areas, such as engineering and mathematics, have been interested in providing their insights to further understand this sport in the last few years. The major contribution of mathematical tools resides in the field of human movement analysis with fast and efficient systems, providing quantitative measures to sports coaches [5]. Nevertheless, the technological devices and related methods should always be applied considering the aim of the analysis.
Tactical analyses of performance, whether at the individual or collective levels, are of interest to coaches and sport researchers [5]. However, the lack of knowledge about advanced methods to analyse the dynamics of football players (space-time series) is responsible for the lack of studies focusing on the tactical performance of football matches [3]. In this sense, mathematics and engineering can provide valuable contributions to sports science in the performance analysis area.
By benefiting from these scientific fields, it is possible to analyze football players’ variability in terms of dynamic trajectory [6]. Such variability was studied from a spatio-temporal point-of-view, by understanding the main factors and constraints that affect players’ actions [7]. In spite of the regular dynamics of a football game [8], and considering the tactical behavior of players, the variability of players’ trajectories can be seen as an interesting indicator in characterising football players within their specific tactical zones.
1.1. Variability Analysis in Sport
The discussion about variability arises in the scope of systems theory, where the notion of nonlinearity was initially introduced [9]. By studying the variability of football players, the foundations were laid for a whole series of possible new methods to identify and classify their performance. Nevertheless, the assertive implementation of these notions requires quantitative methods. Therefore, some nonlinear methods, such as the approximate entropy [10], or the Lyapunov exponents [11], were adopted to study human performance features. It should be highlighted that, contrarily to traditional methods (e.g., standard variation, coefficient of variation), nonlinear methods can provide additional information about the structure of the variability that evolves over time [9].
In invasive team sports (e.g., football, basketball and others), players are generally confined to a specific area (tactical region) depending on their role [7]. Nevertheless, the variability of a given player not only depends on his specific actions (i.e., at the microscopic level) but also on the team as a whole (i.e., the specific role in the team’s strategy at the mesoscopic level) [12]. In some cases, the emergent behaviours can be different in their regularity, depending upon the team’s strategy [10].
In the current state-of-the-art, only a few papers have analysed the variability of displacement of football players [13–15]. All these studies focused on the variability within each sub-phase (e.g., 1 vs. 1 player, 2 vs. 2 players) without considering the full match dynamics (e.g., 11-a-side game). Generally, studies around sub-phases have presented the variability in the emergent behaviours by means of different player strategies, so as to achieve the final result [15]. Despite their importance towards an understanding of the player’s decision-making processes, the variability can be associated with other important indicators. For instance, performance indices such as distance covered, speed, or intensity, should be considered so as to understand the player’s variability in the 11-a-side match. This analysis can be a step forward to distinguish players that show similar results to the previously described indicators.
All the same, the variability of trajectories can also be classified as stable or non-stable. Actually, the notion of “stability” is quite different from the one of “variability”. Stability is not only the resistance to a perturbation, but also the ability to return to the equilibrium point (e.g., initial position, tactical position, among others). The existence of a stable equilibrium point implies the existence of a “restoring force” which is directed towards the equilibrium point. Thus, we assume that there is a steady-state point to which players converge. The truth is that they are “only” attracted to that point, that is, they convergence to an equilibrium point that is defined by their tactical position. The “stability” can be understood, in the context of football, as the capability that a player reveals in keeping his trajectories within a specific region (such as their tactical position on the field). A similar assumption can be made about the “predictability” of players. By definition, predictability is the degree to which a correct prediction of a system’s state can be made. In the context of a player’s trajectory, the predictability is related to whether one can predict where the player will be, by knowing his trajectory so far. This is in line with the concept of predictability in mathematics, wherein a process is classified as predictable if it is possible to know the “next” state at the present time.
Despite the complexity of a player’s trajectory outside their specific tactical region during a football match, it is mostly certain that, eventually, the player will return to his own tactical region. Even when players change their strategic position, they return to their specific strategic position most of the time [16]. Hence, we can formulate that in, a rather simplistic way, a player can be considered more or less stably based, even when he remains outside his tactical region.
1.2. Statement of Contribution and Paper Organization
Players’ dynamics have been studied at the individual and collective level. This paper introduces a new approach for variability analysis, thus providing some new insights around football players’ behaviour. Moreover, this paper introduces a new set of parameters to easily distinguish players with regards to their activity profiles in official matches. These indices can provide deeper information about players’ behaviour while improving the sports training quality. For the study of the player’s variability, in terms of dynamic trajectory, the concepts associated with the Fractional Calculus (FC) mathematical formalism are adopted [17]. One of the first studies applying FC to trajectory analysis was introduced by Couceiro, Clemente and Martins [17] by estimating the next position of a player based on his previous trajectory. This was proposed for improving the accuracy of automatic tracking methods. As suggested by the authors, using the fractional coefficient of a player over the time, one can analyse his level of predictability. Therefore, the purpose of the current study is to determine the predictability level and, as a consequence, the stability of football players, comparing these values side-by-side with traditional football indicators, such as distance covered, player’s directions and the space covered by each player.
Having these ideas in mind, this paper is organized as follows: Section 2 describes two alternative methods typically used in the football context, namely, Shannon’s entropy applied to heat maps and the approximate entropy as a variability measure applied to kinematic variables. Section 3 shows how FC may be applied to mathematically describe a football player’s trajectory. This is further exploited in Section 4 where the fractional coefficient is used to estimate the next position of a football player, thus shaping the player’s predictability. Section 5 presents an analytical procedure for designing an attraction domain related with the player’s maintenance of his own tactical position. Sections 6 and 7 consider the case study of one football match that relates the newly introduced indicators with traditional indices, discussing the predictability and the stability of each player while considering their tactical positions. Section 7 presents the conclusions.
2. A Brief Overview of Entropy in Sports
As previously stated, entropy-based measures have been the most typical nonlinear methods applied in the sports context. Therefore, this section describes two entropy methods used to study the variability of football players’ trajectories.
2.1. Shannon’s Entropy
Heat maps are a classical method to analyse a given player’s variability. Generally, heat maps represent the spatial distribution of a player over the field by considering the time spent at a certain position, that is, the frequency distribution (histogram) of each player’s coordinates [12]. However, the analysis of heat maps in the football context have not benefited from any complementary metrics that may provide more assertive results. The Shannon’s entropy can be applied to images providing relevant information about the spatial variability of players. The entropy formula applied to images can be defined as [18]:
Consider the following example:
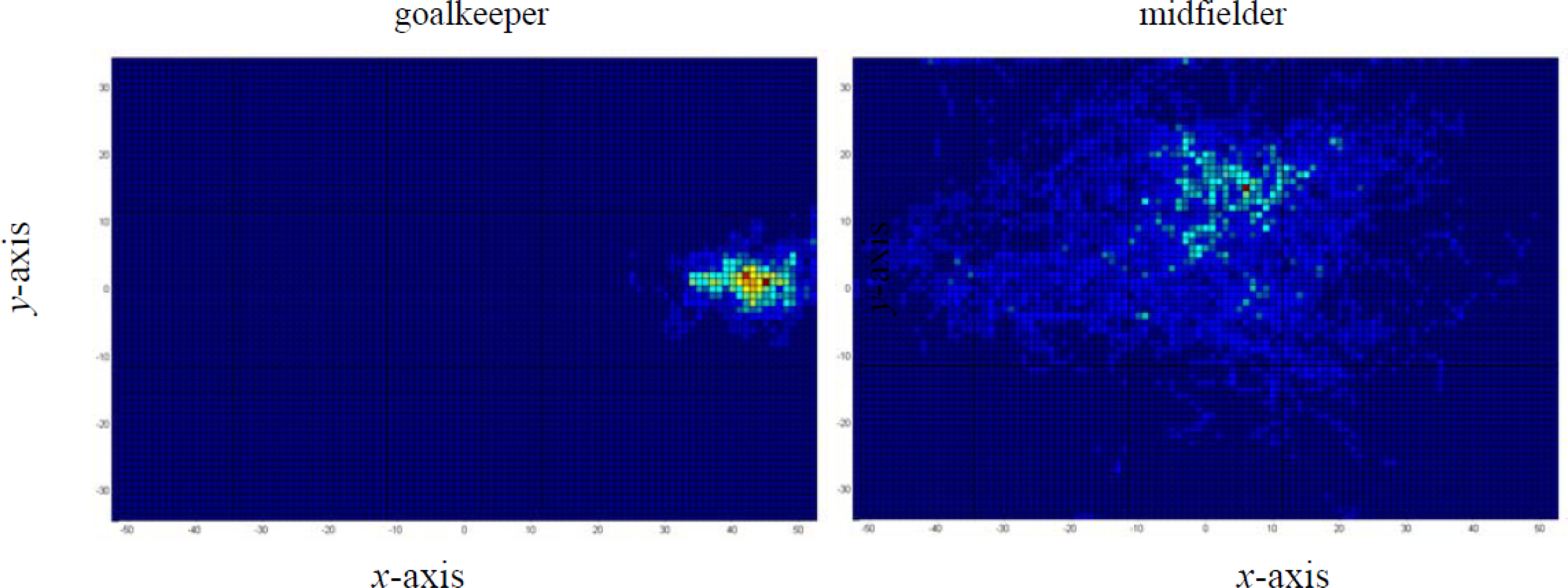
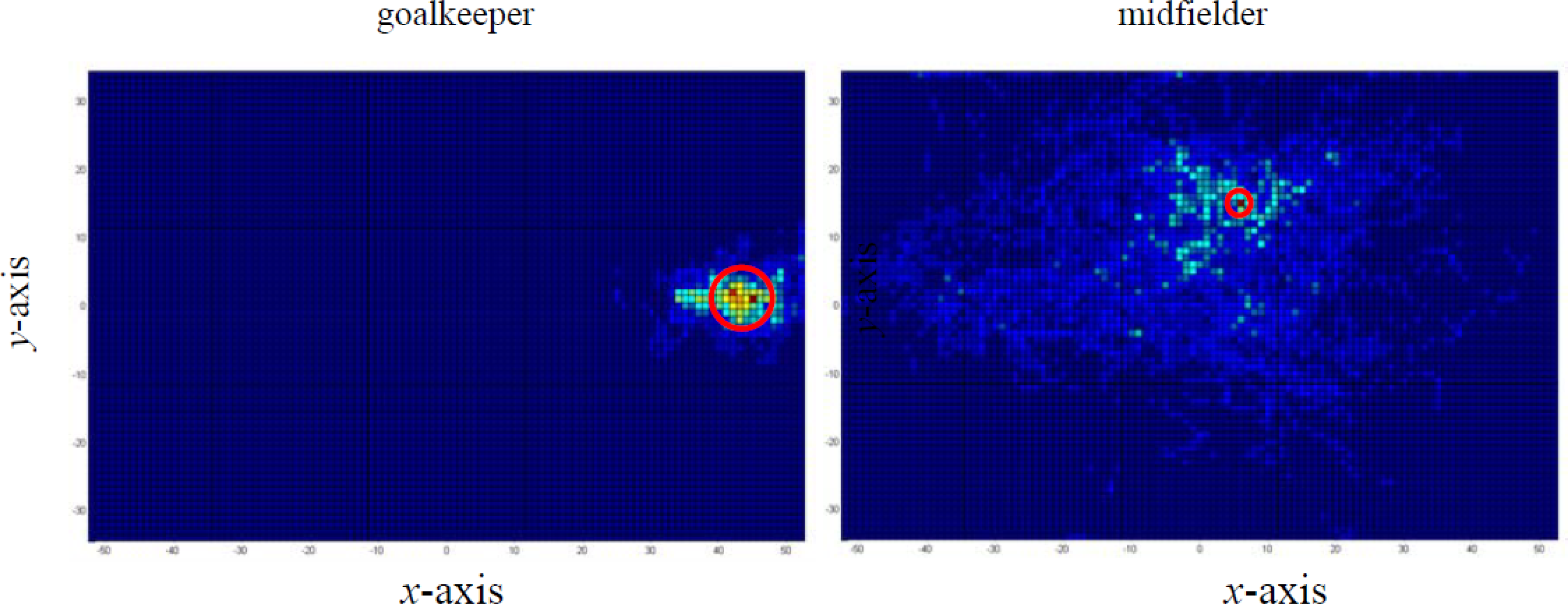
Example 1: Let us consider a resolution of 1 m2 for a football field of 104 × 68m. This results in a total number of cells Nc = 7072. The heat map representation of two players of an 11-a-side football team, considering their position at each discretization interval of 1 s, is depicted in Figure 1.
The data comes from an all “useful” time periods in one football match. By other words, only the instants where the ball is playable in the field are considered. As one may observe, it is possible to identify that the goalkeeper has a reduced area of action, thus spending more time around the same places and, consequently, increasing the intensity of colours. On the other hand, the dispersion is high on the midfielder player, thus reducing the time spent around the same place and, therefore, decreasing the intensity in any given place. The goalkeeper presents lower spatial variability than the midfielder, and is characterized by an entropy measure of E = 0.804. On the other hand, the midfielder presents an entropy of E = 2.449.
2.2. Approximate Entropy Calculus
Pincus, Gladstone and Ehrenkranz [19] described the techniques for estimating the Kolmogorov entropy of a process represented by a time series and the related statistics approximate entropy. Let us consider that the whole data of t samples (i.e., seconds) is represented by a time-series as u(1),u(2),…,u(N), from measurements equally spaced in time. These samples form a sequence of vectors x(1),x(2),… x(N−m+1) ∈ ℝ1×m, each one defined by the array x(i) = [u(i) u(i+1) … u(i+m−1)] ∈ℝ1×m. The parameters Nt, m, and ɛ must be fixed for each calculation. The parameter Nc represents the length of the time series (i.e., number of data points of the whole series), m denotes the length of sequences to be compared and ɛ is the tolerance for accepting matches. Thus, one can define:
From the , it is possible to define:
Let us define the following relation:
On the basis of calculations that included the theoretical analysis performed by Pincus et al [19], the authors derived a preliminary conclusion that choices of ɛ of the standard deviation of the data ranging from 0.1 to 0.2 would produce reasonable statistical validity of ApEn.
Consider the following example.
Example 2: Let us represent the distance covered by the lateral defender at each second over a match as depicted in Figure 2.
From this example, the distance covered by the lateral defender results in an approximate entropy value of ApEn =0.545 for ɛ = 0.2 of the standard deviation and m=2[19], thus being classified as a chaotic system (cf., Table 1).
The entropy may not capture the adequate level of variability of a given player over time if applied on some type of signals. For example, when applied to the spatial distribution (cf., Example 1), the entropy simply returns the spatial variability of a player without considering his trajectory over time. On the other hand, when applied to the distance covered (cf., Example 2), it yields the level of variability without considering the direction of the player trajectory. Other techniques can be applied in the sports context. For instance, by adopting the insights from Couceiro, Clemente and Martins [17], one can define a player’s variability, at each instant, using the FC memory properties as a predictability level. Therefore, the FC approach for the human variability understanding will be discussed in next section.
3. Player’s Motion from the View of Fractional Calculus
Fractional Calculus (FC) may be considered as a generalisation of integer-order calculus, thus accomplishing what integer-order calculus cannot [20]. As a natural extension of the integer (i.e., classical) derivatives, fractional derivatives provide an excellent tool for the description of memory and hereditary properties of processes [21]. An important property revealed by the FC formulation is that while an integer-order derivative just implies a finite series, the fractional-order derivative requires an infinite number of terms.
Despite FC’s potentialities only a limited number of applications based on FC have been reported so far within the sport sciences literature [17,22]. One of them was the development of a correction metric for golf putting to prevent the inaccurate performance of golfers when facing the golf lipout phenomenon [21]. The authors extended a performance metric using the Grünwald–Letnikov approximate discrete equation to integrate a memory of the ball’s trajectory. A more recent study by the same authors benefited from FC to overcome automatic tracking problems of football players [17]. As a prediction method based on the memory of past events, FC features offer a new perspective on understanding players’ motion.
3.1. Fractional Calculus: Preliminaries
The concept of Grünwald–Letnikov fractional differential is presented by the following definition:
Definition 1 [23]: Let Γ be the gamma function defined as:
The signal Dα[x(t)] given by
An important property revealed by Equation (10) is that while an integer-order derivative just implies a finite series, the fractional-order derivative requires an infinite number of terms. Therefore, integer derivatives are “local” operators while fractional derivatives have, implicitly, a “memory” of all past events. However, the influence of past events decreases over time. The formulation in Equation (10) inspires a discrete time calculation presented by the following definition:
Definition 2 [23]: The signal Dα[x[t]] given by:
The series presented in Equation (11) can be implemented by a rational fraction expansion which leads to a superior compromise in what concerns the number of terms versus the quality of the approximation. That being said, it is possible to extend an integer discrete difference, i.e., classical discrete difference, to a fractional-order one, using the following definition:
Definition 3 [24]: The classical integer “direct” discrete difference of signal x[t] is defined as follows:
The features inherent to FC make this mathematical tool well suited to describe many phenomena, such as irreversibility and chaos, because of its inherent memory property. In this line of thought, the dynamic phenomena of a player’s trajectory configure a case where FC tools may fit adequately.
3.2. Fractional Calculus Approach for the Study of Football Players Trajectories
Both in manual and automatic multi-player tracking systems, a matrix containing the planar position of each player n of team δ over time is generated:
Definition 4 [17]: Consider the matrix:
In our case, the 11-a-side football game will be analysed. Therefore, by Definition 4, we have Nδ =11. Using Definitions 1, 2 and 3, considering players’ dynamics and following the insights from [17], one can define an approximation of player n next position, i.e., , as:
Example 3: Let us adopt the example of players’ spatial distribution alongside the football field introduced in Example 1. Figure 3 represents the tactical region of each player by means of the standard deviation of their own heat map (histogram) [25]. It is possible to identify that the TR have different sizes depending on the in-game mission of each player. For instance, although the midfielder presents a larger dispersion along the field when compared to the goalkeeper, his standard deviation is smaller. The standard deviation of the goalkeeper’s trajectory is 4.69 m while the one of the midfielder’s trajectory is 2.46 m. Put differently, one can state that, although the midfielder’s spatial distribution is generally larger than the goalkeeper’s, the midfielder wanders approximately 68% of the time around the same tactical position (position with higher intensity on the heat map).
Note that the FC approach on Expression (15) should be accomplished for small sampling periods (e.g., T ≤ 1 s), as players may not be able to drastically change their velocity between two consecutive samples. Moreover, such strategy increases the memory requirements as it memorizes the last r positions of each player, i.e., [rNδ]. Nonetheless, the truncation order r does not need to be too large and will always be inferior to the current iteration/time t, i.e., r≤ t. For example, let us consider a the truncation order r= 10, sampling period T= 1 s and fractional coefficient . Considering the last 10 previous samples, results in an attenuation of players’ position at time t−9 (i.e., the x[t+1−10] of approximately 99.5 (i.e., ).
Note that the influence of past events (i.e., previous positions) of a given player depend on the fractional coefficient α (cf., [22]). Hence, analysing the fractional coefficient α may be a source of useful information to understand the level of predictability of each player.
4. Predictability
As one may observe in Equation (15), a problem arises regarding the calculation of the fractional coefficient α. A player’s trajectory can only be correctly defined by adjusting the fractional coefficient α along time. In other words, α will vary from player to player and from iteration to iteration. Hence, one should find out the best fitting α for player n at time t, i.e., αn[t], based on its last known positions so far. The value of αn[t] will be the one that yields a smaller error between the approximated position and the real one from the corresponding element of matrix Xδ[t], denoted as . This value αn[t] will be used to assess the next possible position and, again, will be systematically updated at each t. This reasoning may be formulated by the following minimization problem:
We will not focus upon the best type of optimization method. In this paper, the solution of Equation (16) is based on golden section search and parabolic interpolation [26,27]. Successive parabolic interpolation allows finding the minimum distance by successively fitting parabolas to the optimization function at three unique points and, at each iteration, by replacing the “oldest” point with the minimum value of the fitted parabola. This method is alternated with the golden section search, hence increasing the probability of convergence without hampering the convergence rate. For a more detailed description about this optimization methods please refer to [26,27].
The solution of Equation (16) consists of the most adequate fractional coefficient for player n at time t, i.e., αn[t]. To clarify how αn[t] varies over time depending on a player’s trajectory let us introduce the following example:
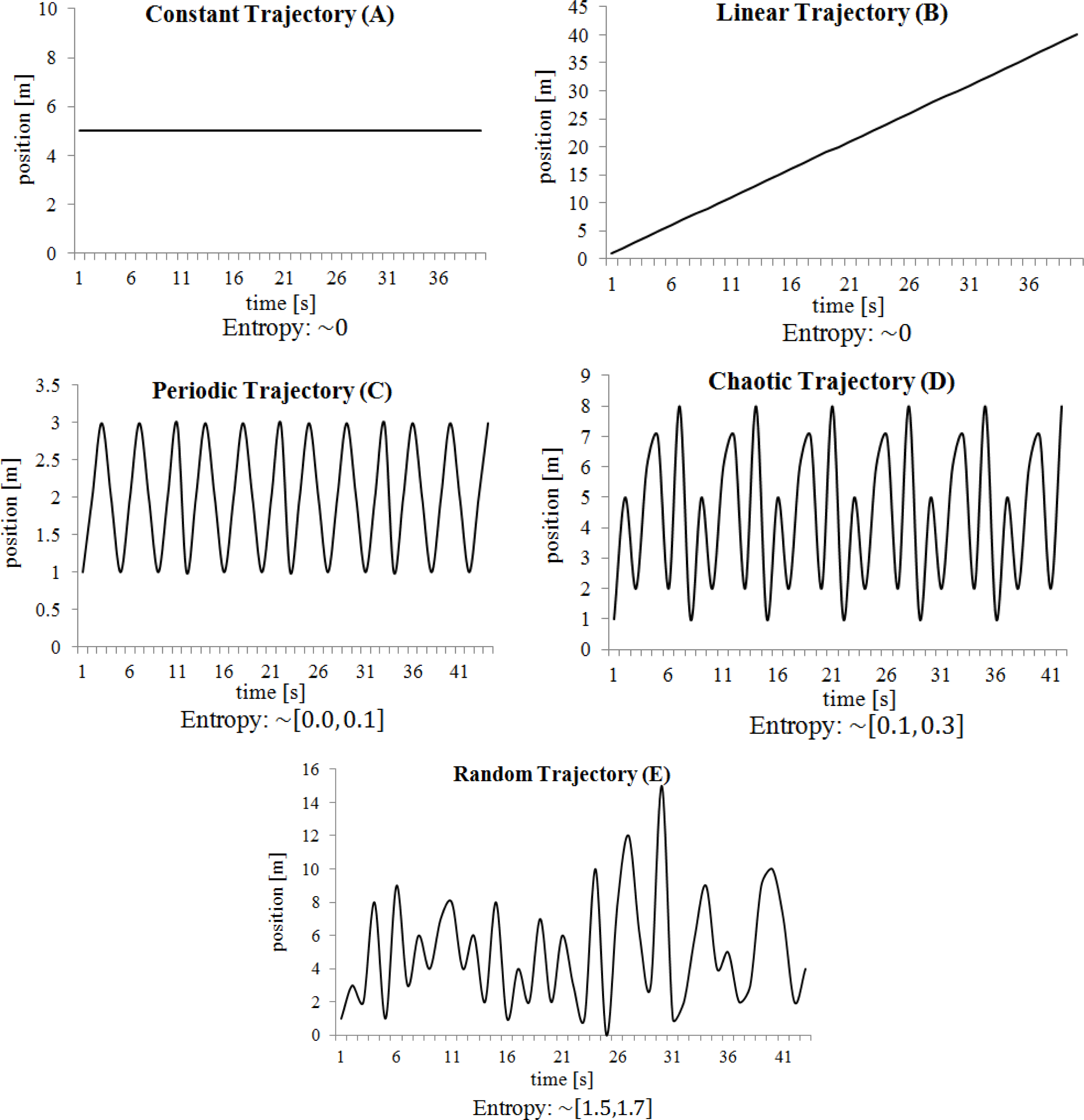
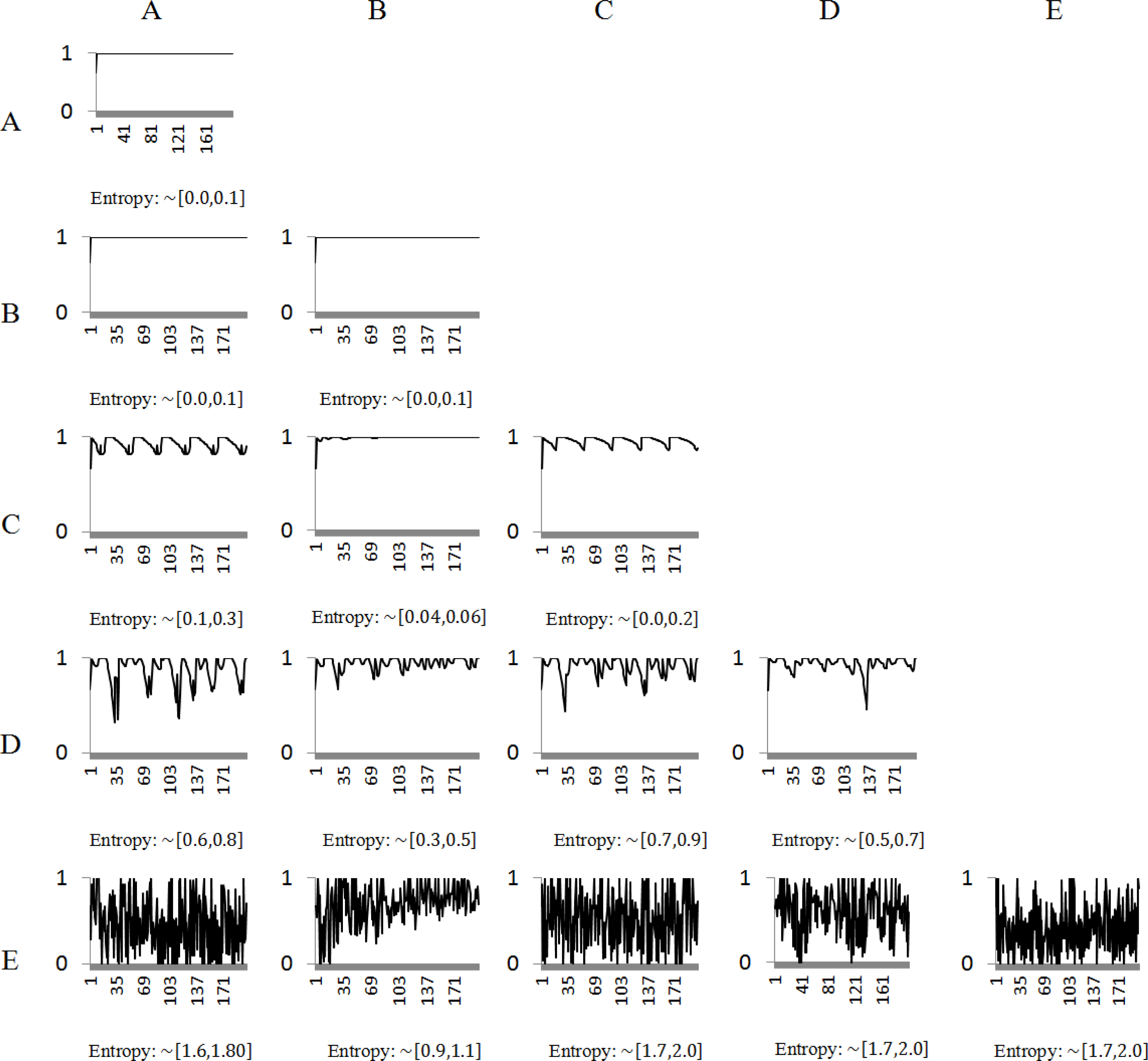
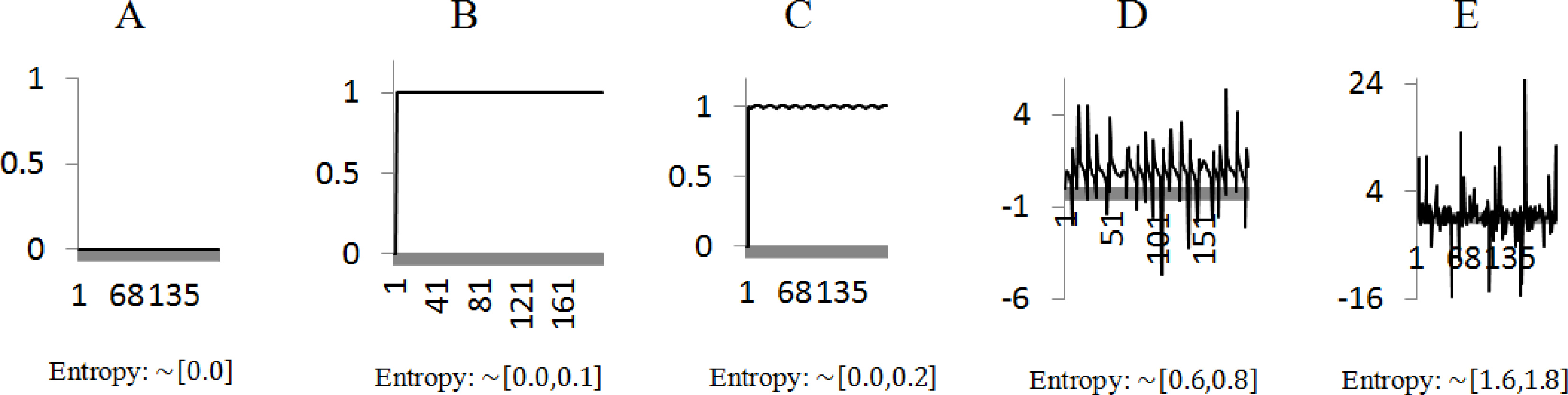
Example 4: Consider five illustrative unidimensional player’s trajectories:
The fractional coefficient αn[t] was calculated, at each sample t, each pairwise combinations of the 5 different unidimensional signals represented in Figure 4 are combined into bidimensional (x, y)-coordinates to exemplify the fractional coefficient variation. To improve the understanding of the fractional coefficient variability, the approximate entropy of αn[t] is also presented in Figure 5.
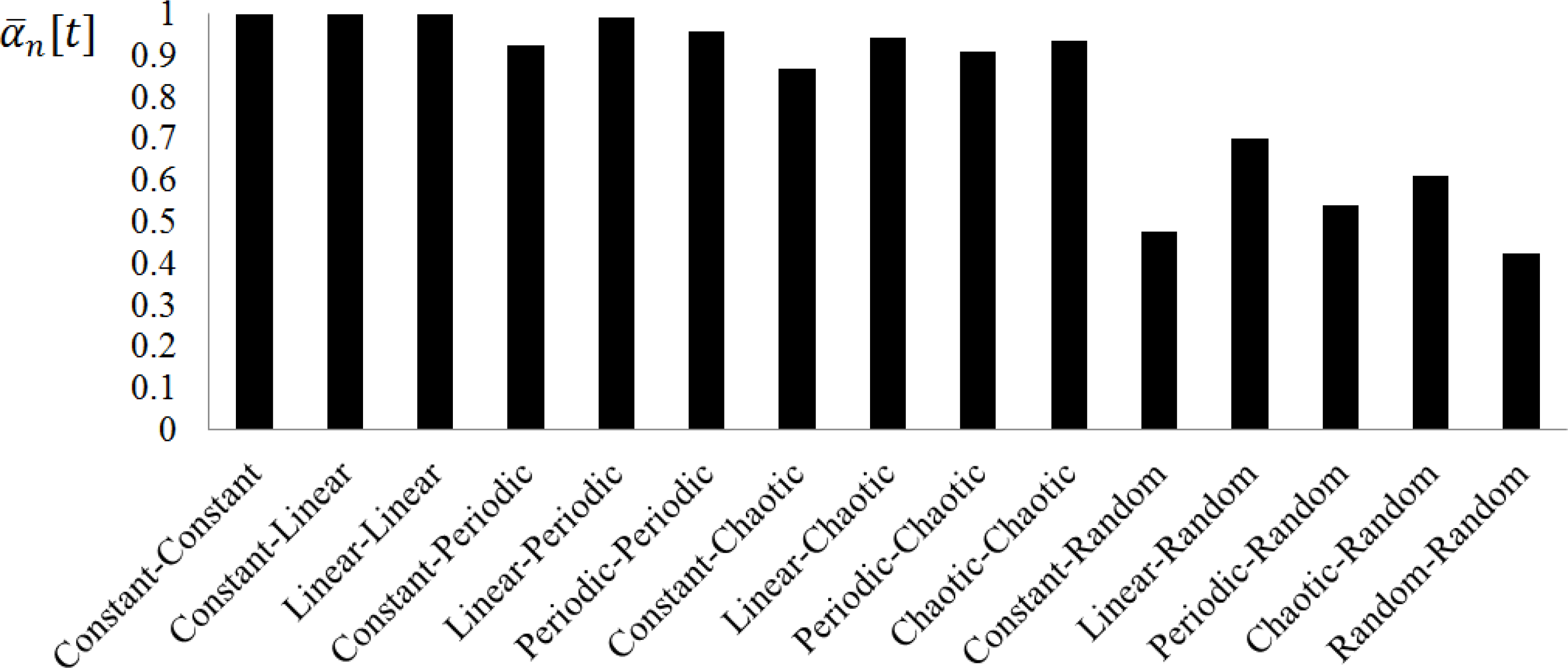
As previously stated, one may observe that the closer to 1 the values of αn[t] are, the higher predictable player n is. In other words, a value of αn[t] =1 means that equation (13) can accurately predict the next position based on the previous ones, i.e.,. Therefore, for constant trajectories (A-A), i.e., without moving at all, the fractional coefficients. αn[t] gets closer to a constant value of 1 and, as a result, a low approximate entropy, thus being highly predictable. These results are also the same for the constant-linear (A-B) trajectories, as well as for the linear-linear (B-B) trajectories, i.e., with constant speed. Regarding the periodic trajectories, one can observe an increase of the approximate entropy (ApEn ≈ 0.3) and the fractional coefficient αn[t] varies periodically. Also, it should be highlighted that the constant signal does not contribute towards a better predictability of the player’s trajectory. This occurs not only in the periodic-constant (A-C), but also in the chaotic-constant (A-D) and random-chaotic (A-E). The results are worse when the trajectory along one of the axis is constant yields worse results than when they are linear. These results suggest that a constant trajectory (i.e., when the player’s motion is only variable along one of the axis), does not have any effect in the fractional coefficient calculation. For a chaotic trajectory, the fractional coefficient variability decreases considerably, presenting values close to αn[t] =0.4 in some situations. This variability is only exceeded by the random trajectories, in which the fractional coefficient in some situations may even get close to αn[t] =0, thus resulting in approximate entropy values in the range ApEn= [0.9, 2.0]. To summarize these results, Figure 6 depicts the average value of the fractional coefficient, i.e., αn[t], for each case.
The mean values for the fractional coefficient are approximately αn[t] ≈0.99 for the A-A, A-B and B-B pairs. This value indicates that the trajectories are highly predictable. For all combinations, the linear trajectories increase the fractional coefficients, thus increasing the predictability of the player. On the other hand, the random trajectories decrease the mean values of the fractional coefficient, being more unpredictable. The most curious cases may be observed for constant trajectories paired with other trajectories that decrease the fractional coefficients, thus suggesting its neutrality regarding the players’ unpredictability.
By defining a single time-variant parameter retrieved from players’ planar trajectories, one can classify athletes’ predictability based on their behaviour in the field. In brief, we can discuss that player’s predictability can be used to define his decision-making. However, there is the need to define a value, or a range of values, of αn[t] in which one can classify players as predictable or unpredictable, without resorting to the definition of any arbitrary or problem-specific conditions. Therefore, the next section presents an attraction domain supported by stability analysis theory.
5. Stability
The main problem when analysing a player’s dynamics comes from its nonlinearity and variability over time. However, one can consider that each player converges to an equilibrium point defined by the attractor point (initial position xn0) inherent in their initial TP. Therefore, this section presents the stability analysis of football players based on the Equation (15). In order to classify players as stable or unstable, one can formulate the following problem.
5.1. Problem Formulation
Consider a trajectory from player n described by an Equation (15), in which the fractional coefficient αn[t] dictates its level of predictability. The goal is to find the attraction domain 𝒜 such that, if coefficients αn[t] ∈ 𝒜;, then the global asymptotic stability of the system in Equation (15) is guaranteed. In other words, the attraction domain 𝒜 represents the region wherein the football player may be considered both predictable and stable.
5.2. General Approach
As previously stated, the position returned by Equation (15) may not match the real position from the corresponding element of matrix Xδ[t], i.e., . For having Equation (15) as a function of the signal xn[t], one can start by calculating the velocity vector of player n as [17]:
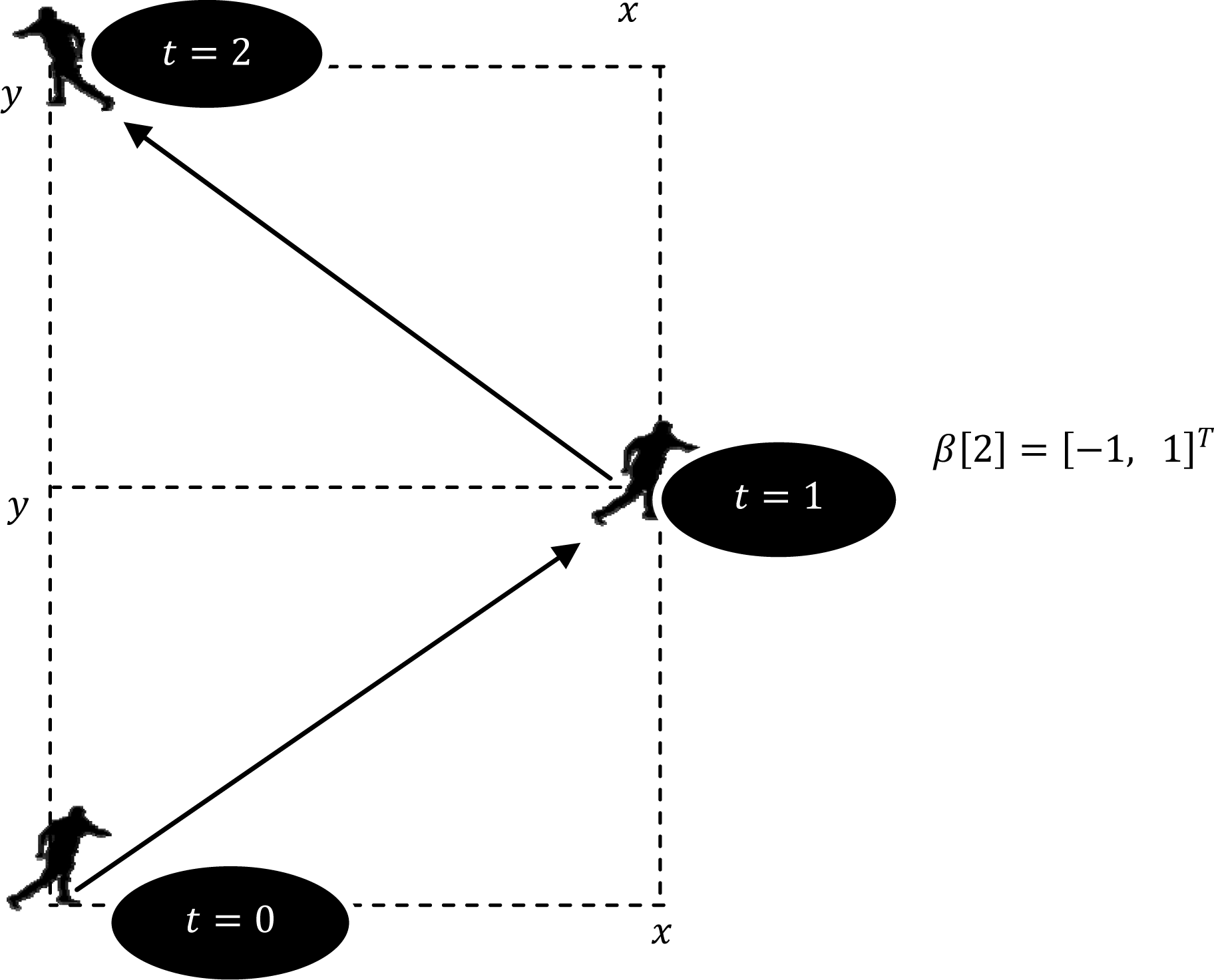
As before, let us analyse the stability vector βn[t] considering the examples of Figure 4:
Example 5: Contrarily to the fractional coefficient, that varies according to the combination of two trajectories (one for each planar coordinate), the stability vector returns a different value for each coordinate. Moreover, as previously stated in Definition 4, since the (x, y) coordinates of a player n planar position are independent, one can simply analyse one of the components. Let us consider the identification of each coordinate as τ= {1, 2} in such a way that xn[t] =[x[t] y[t]]T= .
Combining Equations (17) and (18), we can calculate the element τ from the stability vector βn[t] at time t:
As a result, the trajectories of Figure 4, namely, constant (A), linear (B), periodic (C), chaotic (D) and random (E), produce the following values of in Figure 8.
It is possible to verify that the random trajectory is the one that results in higher values of entropy for the stability vector βn[t], similarly to what was observed on the results for alpha results. In fact, the entropy values for the stability vector βn[t] are consistent with those retrieved for the fractional coefficient (Example 4).
Having defined all the coefficients that may explain a football player’s trajectory, let us now solve the problem formulated in Section 5.1.
5.3. Attraction Domain
To better understand where the predictability and the stability of a player can be interpreted, let us consider Equations (17) and (18) and rewrite Equation (15) as:
At this point, let us assume both coefficients as time-invariant, i.e., βn[t] =βn and αn[t] =αn for ∀ t. This is an assumption that is only taken for the purposes of finding the attraction domain wherein both coefficients may be defined to ensure player’s convergence to the initial TP at coordinate xn0.
The equilibrium point can be defined as a constant position solution of Equation (20), such that, when each player n reaches at time t, the velocity vn[t] is zero (i.e., players will stop at the equilibrium point ). Supposing that the initial TP at coordinate xn0 is constants (i.e., the player converges to his own initially defined TP), the particular solution of each player can be obtained replacing xn[t+1−k],k, t ∈ ℕ0, by in Equation (20), yielding:
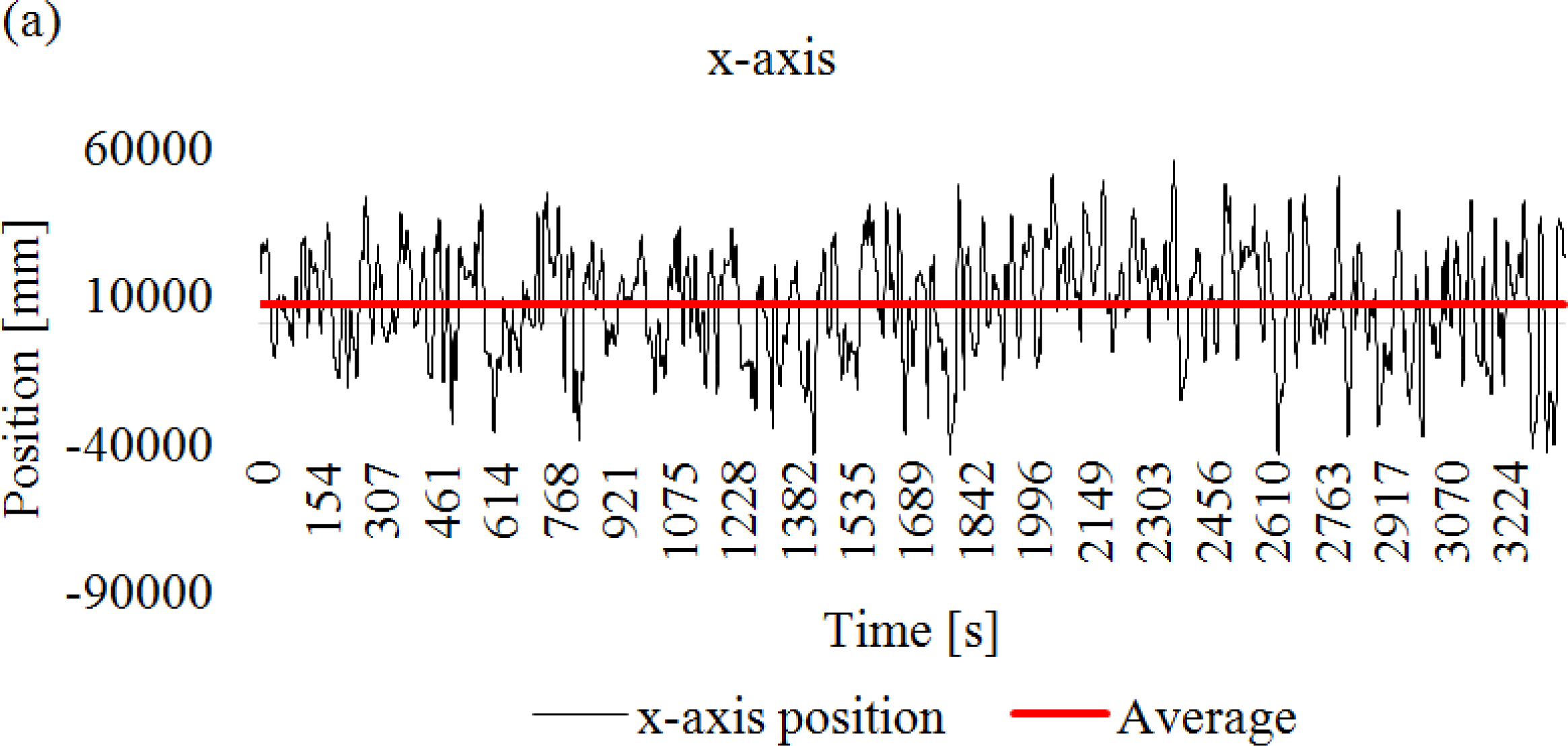
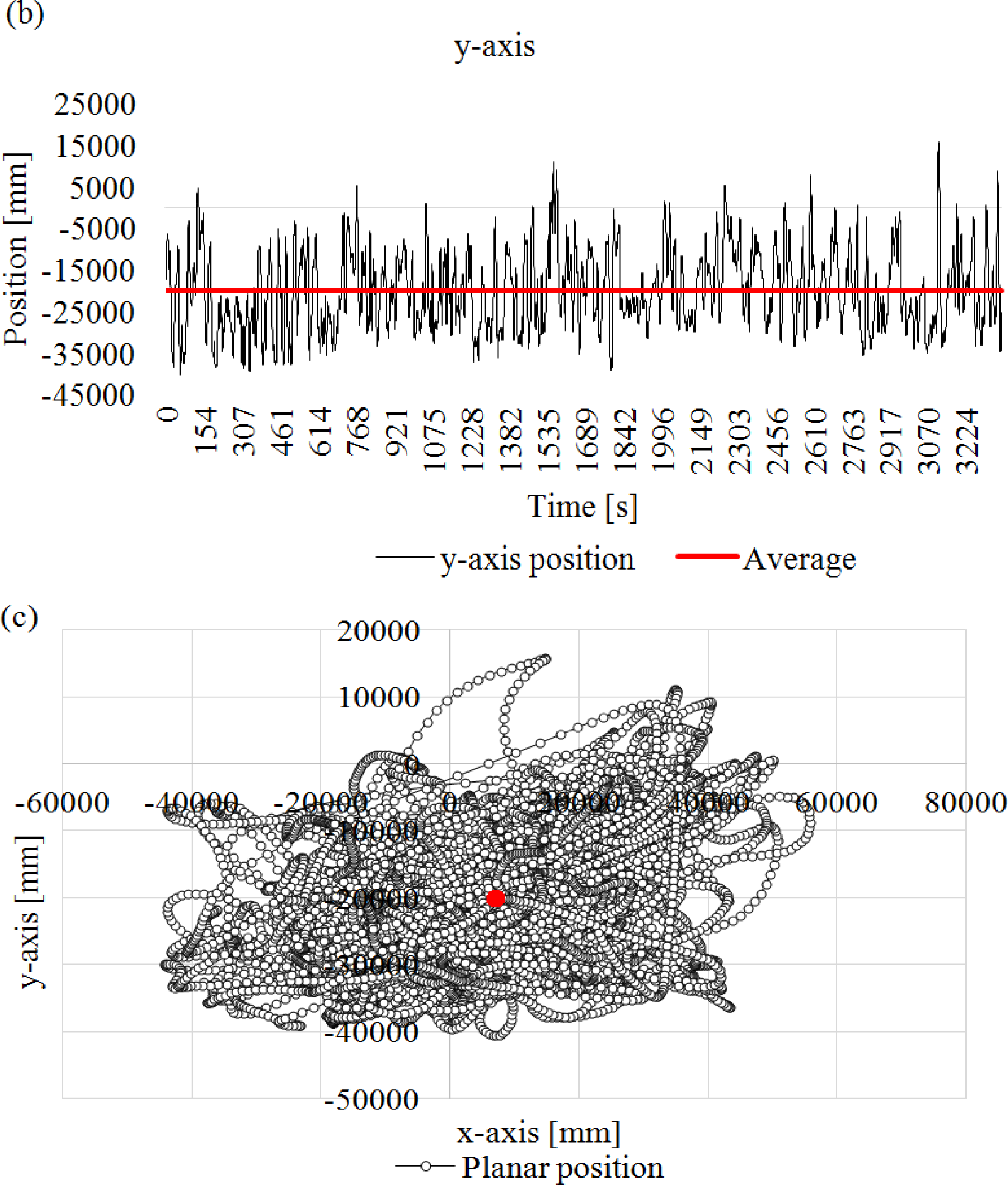
Example 6: The following charts represent the trajectory of the lateral defender during a football match (Figure 9).
It is possible to observe that from time to time the player returns to his own tactical region (defined by the red horizontal lines in Figures 9a,b or the red point in Figure 9c. This is a typical behaviour of football players. When the opponent team approaches the team’s goal in the defensive phase, the lateral defender should cover the interior space, thus approaching the y-axis centre of the field. In the offensive phase, particularly in counterattack situations, the lateral defender should support his midfielder, thus running along the x-axis. Nevertheless, in both cases, the lateral defender will return, at some point, to his own equilibrium point.
In synthesis, each player should converge to the particular solution from Equation (19), based on the following theorems [28]:
Theorem 1 [28]: All solutions of Equation (20) converge to as t→ ∞, if and only if the homogeneous difference equation of (20) is asymptotically stable.
Theorem 2 [28]: The homogeneous difference equation of (20) is asymptotically stable if and only if all roots of the corresponding characteristics equation have modulus smaller than one.
In order to study the stability of the homogeneous difference Equation (20), let us truncate the series at r= 4 and consider a sampling time of T= 1. Once again, let us consider the identification of each coordinate (x, y) as τ= {1, 2}, in such a way that xn[t] =[x[t] y[t]]T = . Under those conditions, one can rewrite Equation (20) in the following form:
Based on Equation (22), it yields the following characteristic equation:
Due to the complexity in obtaining the roots of the characteristics equation of homogeneous difference Equation (23), a result based on Jury-Marden’s Theorem [29] is established, ensuring that all roots of the real polynomial p(λ) have modulus smaller than one.
Theorem 3 [29]: Consider the real polynomial p(y) =a0yn +a1yn–1 +⋯+an–1 y+an,a0 >0. Construct an array having two initial rows:
Considering Theorem 3 and the characteristic Equation (23), let us present the following result:
Proposition 1: All roots of p(λ) have modulus smaller than one if and only if the following conditions are met.
Proof: The real polynomial p(λ) described in Equation (23) can be rewritten as:
Furthermore, one can construct an array having two initial rows defined as:
By Theorem 3, we consider that all roots of polynomial p(λ) have modulus less than one if and only if d21 >0, dξ1 <0, for ξ = 3,4,5.
Hence:
Solving Equation (29) we obtain Equation (24).
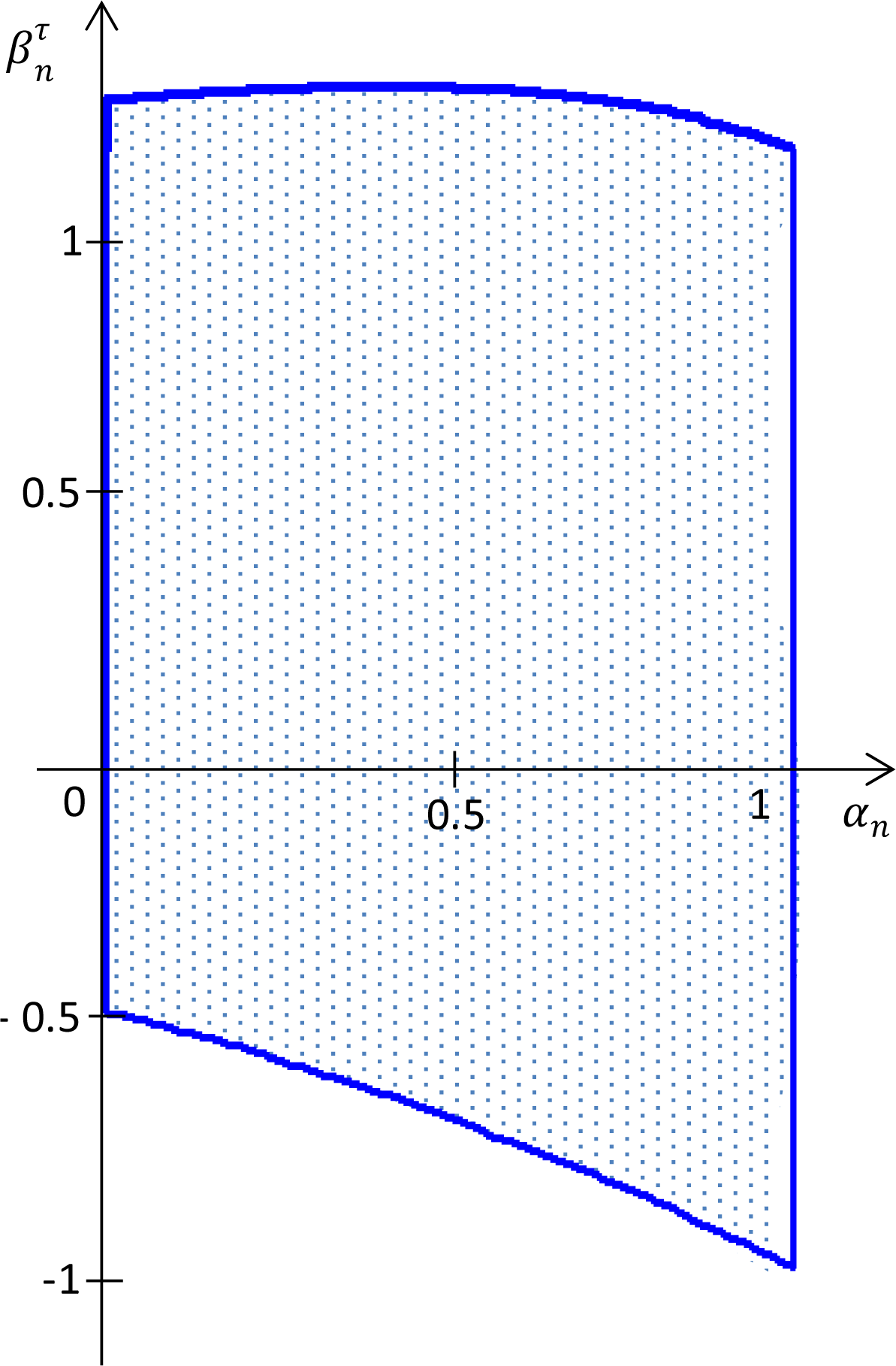
Consequently, by Proposition 1, Theorem 1 and Theorem 2, the conditions in Equation (23) are obtained, so that all solutions of Equation (20) converge to resulting in an attraction domain represented in Figure 10.
Let us present a new example to clarify the definition of attraction domain.
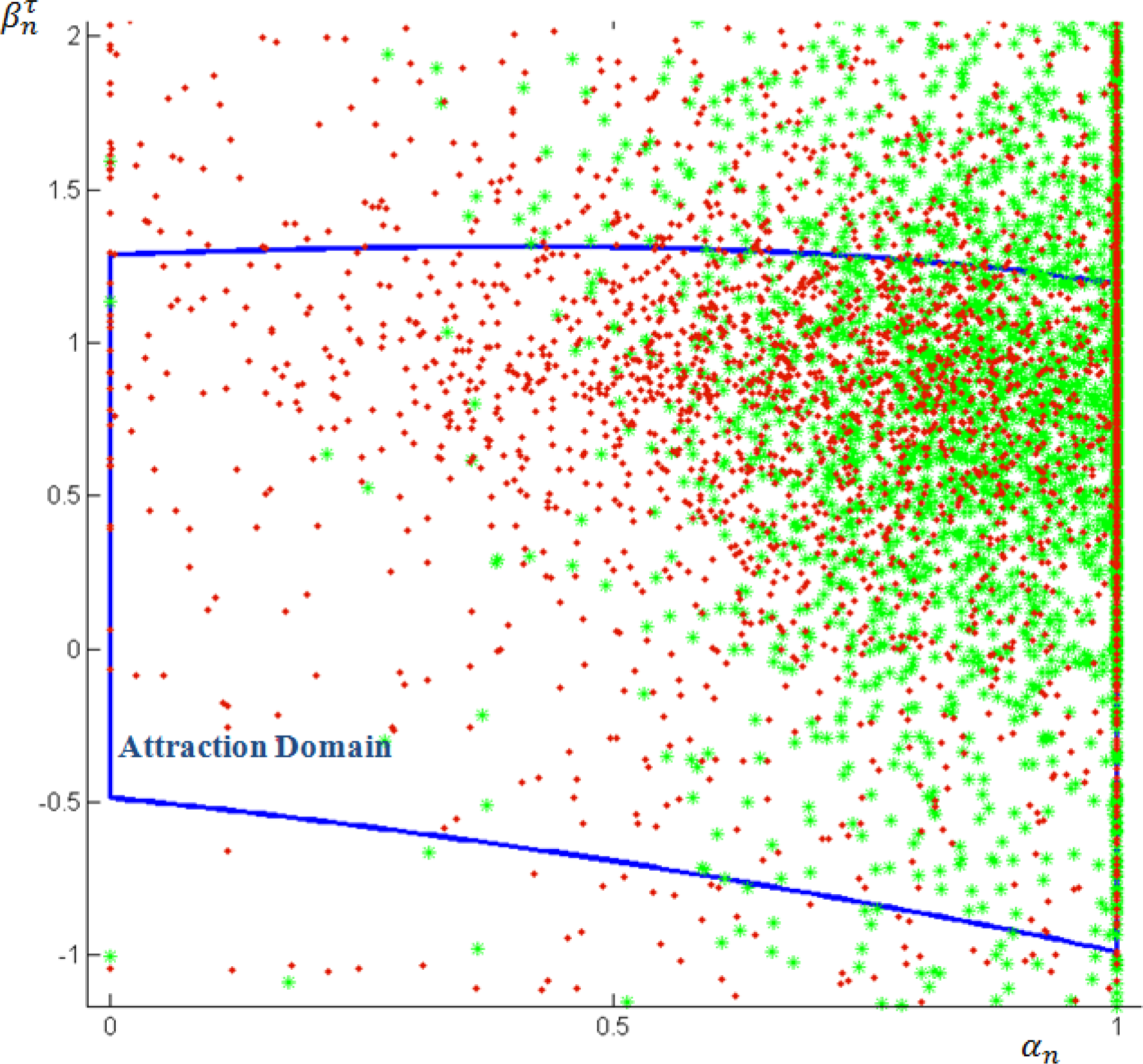
Example 7: The predictability and stability coefficients along the x-axis, and αn[t], both for the goalkeeper and the lateral defender, were retrieved and represented on top of the attraction domain from Figure 10.
It is possible to observe in Figure 11 that the goalkeeper has a high number of points outside the area from the attraction domain 𝒜. Nevertheless, his trajectory coefficients are closer to the threshold αn =1, meaning that the goalkeeper presents a larger predictability. Therefore, although the lateral defender can be classified as more stable, his motion it is more difficult to predict. This may be explained by the specific tactical missions. The goalkeeper, when his team is in the offensive phase, usually moves in order to reduce the open space with his teammates, which increases the size of his TR. Nevertheless, the goalkeeper’s movements are usually more linear, since he does not face as many constraints as his teammates (e.g., playing dyads, continuous interaction with teammates, among others), and, consequently, it is more predictable. The lateral defender should cover his own tactical region, producing a large amount of trajectory coefficients within the attraction domain. Nevertheless, as an outfield player, he performs more unpredictable trajectories.
6. Experimental Results: A Case Study of a Football Match
In this section, three main indicators will be considered: (i) the distance covered; (ii) the distribution frequency on the field (using heat maps); and (iii) the fractional coefficient measure of each player.
During the 90 min of a regular match, the distances covered by top level players are in the order of magnitude of 10∼12 km for the field players, and about 4 km for the goalkeeper [30–33]. In Reilly’s study [34], it was possible to observe that players under different contexts cover average distances between 7∼11.5 km, indicating that outfield players should be able to cover 8∼13 km during the course of the match [35]. Some studies [32,36–38] show that defenders cover distances between 7 and 12 km, while midfielders cover distances between 9 and 13 km, and attackers between 7 and 11 km. Despite this important information, some questions remain open. One of the main questions is: how to differentiate two players that cover the same distance during the match? To answer this question, one may resort to the heat maps as previously addressed in this work. Although heat maps can be used for several different analyses, their main applications has been to provide a deeper understanding of the spatial distribution of players [39] and ball [40].
Position information about players may be analysed using the heat maps, representing the probability distribution of the player’s positions, during a match, on the field [16]. Similarly to this work, some studies around heat maps segmented the football field into 1 m2 resolution. Also, the player’s position has been commonly discretized at each second, in which a given cell gets the value 1 to signal the player presence [40], or 0 otherwise. However, even the use of heat maps to characterize the players spatial distribution does not provides a way to analyse the level of predictability of each player. Note that heat maps do not consider players’ dynamics, since the trajectory is ignored. That is, they only represent the spatial distribution considering the players’ positions without involving the notion of time.
In spite of these limitations, the variability of the fractional coefficient over time are used here to provide some more relevant information on how a player can be predictable (or unpredictable) and differentiate him from his teammates. Moreover, the stability levels of each player should be considered to understand how they tend to play under their specific tactical regions. All these variables will be analysed and discussed in the next section.
6.1. Data Collection
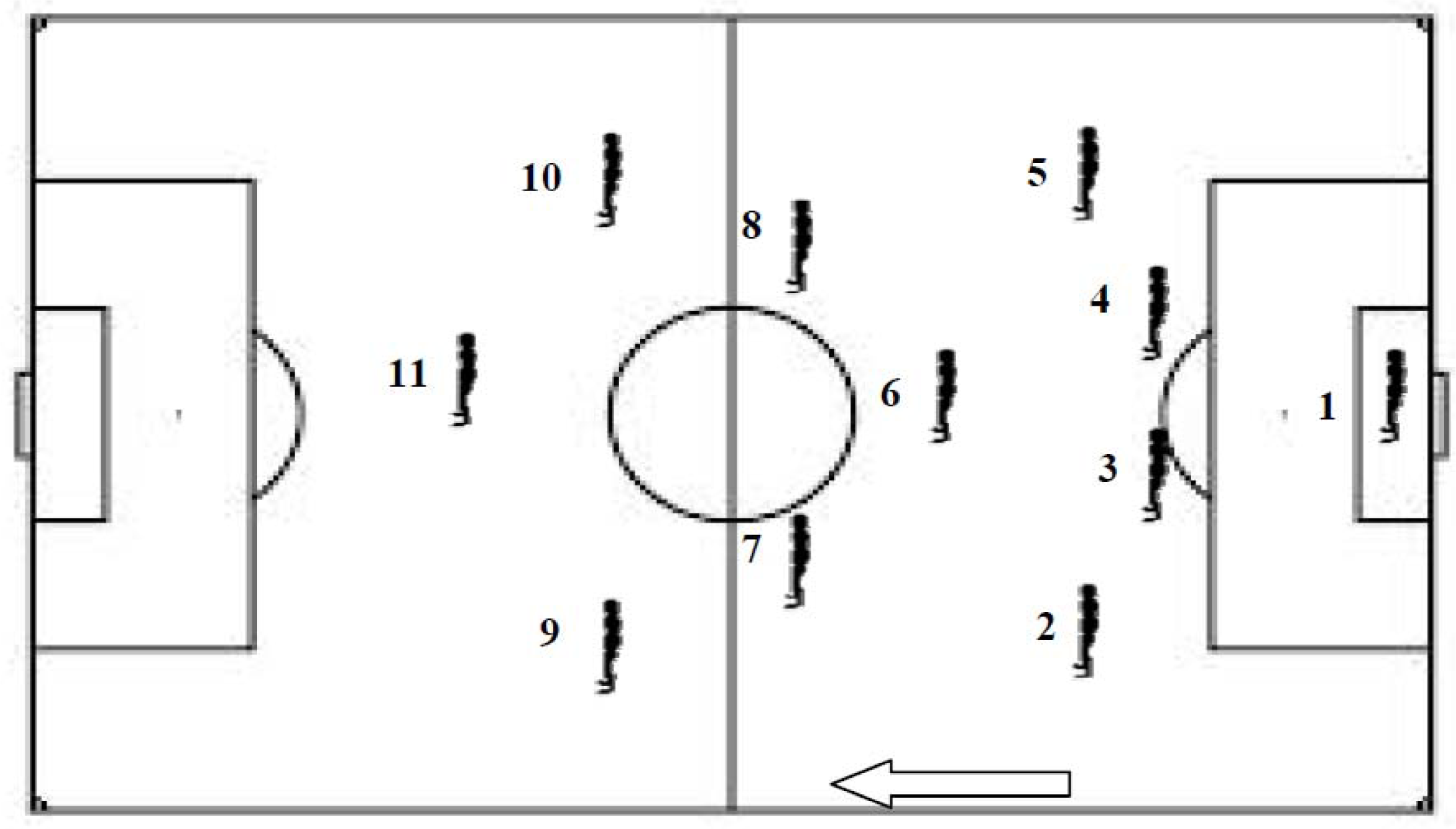
To evaluate the accuracy of the proposed method, one official football match from the first professional Portuguese League was analysed. All the players’ position in the field was acquired using a single camera (GoPro Hero with 1280 × 960 resolution), with capacity to process images at 30 Hz (i.e., 30 frames per second). The movements of the 22 players (goalkeepers included) from the two competing teams were recorded during the entire game. After capturing the football match, the physical space was calibrated using direct linear transformation (DLT) [41], thus producing the Cartesian planar positioning of all players and the ball over time. The whole process inherent in this approach, such as the detection and identification of players’ trajectories, the space transformation and the computation of metrics, was handled, using the high-level calculation package MATLAB. The tracking of football players was carried out manually and the positional data of each player was sorted based on the fractional methodology described in our previous work [3]. From the outcome of Couceiro et al. [3], a downsampling of the acquired data to 4 Hz was adopted (i.e., sampling period of T = 250 ms). For a matter of efficiency, only playing periods were considered, hence excluding all the pause moments in which the ball was not in the field (i.e., ball out-of-bounds). This resulted in 3372 s (56.2 min) of useful match time (13,488 samples). For this study, each player was analysed considering their specificities and they were numbered as depicted in Figure 12.
The analysis of the fractional coefficient inherent to player’s trajectory will be divided into two components, that is, over time and the overall final outcome. For both cases, the fractional coefficient of each player will be compared with the traditional performance indicators. Throughout the analysis, the results will be discussed for all players and compared based on the four main football positions: goalkeeper (player 1), defenders (players 2–5), midfielders (players 6–8), and forwards (players 9–11).
6.2. Results and Discussion
Table 2 depicts the overall values of the distance covered, average values, standard deviation and entropy of the fractional coefficient, and entropy of the heat maps.
Players 7 and 8 covered the largest overall distance (12.520 and 12.556 km, respectively). On the other hand, the goalkeeper (player 1: 3.508 km) and central defenders (player 3: 9.075 km; player 4: 9.355 km) covered smaller overall distances. Both cases are in line with the literature [30,42,43]. Generally, the largest distances are covered by midfielders since they act as links between defence and attack [36,42]. Bangsbo [44] reported that elite defenders and forwards cover approximately the same average distance, which is significantly less than the distance covered by midfield players. This study shows that central defenders, excluding goalkeepers since they are more constrained than other players, cover (with a large difference) a smaller distance than any other tactical position.
In terms of heat maps entropy, the results are in line with the overall distance. All the midfielders have a larger entropy than the remaining teammates (player 7: E = 2.470; player 8: E = 2.449; player 6: E = 2.372). On the other hand, the goalkeeper (player 1) presents the lower entropy value (E = 0.515), followed by the right forward (player 10) with E = 2.024, and the central defender(player 3) with E = 2.083. These results can be easily explained by the tactical roles of each position. In football, midfielders act as a link between the defenders and the forwards [42]. Therefore, they present a higher level of participation in the periods of time with or without ball possession. Also, as the goalkeeper and the central defenders have different roles in specific confined TR, they present a smaller spatial distribution (lower heat maps entropy). Conversely, lateral positions (defenders and forwards) have a larger TR. In some cases, the lateral defenders participate in offensive attempts. The inverse is observed in the lateral forwards players, because they regularly help in the defensive moments. Hence, the low values of entropy from player 10 can be explained by his reduced participation in the defensive phase.
The fractional coefficients show that the midfielders are the most unpredictable players. Players 6 and 7 are characterised by values close to αn[t] =0.68. These values are in line with the combination linear-random trajectories. This tendency makes sense since midfielders cover more distances. On the other hand the goalkeeper’s trajectory is defined by larger fractional coefficient values (αn[t] =0.86). This result is in line with the combination constant-chaotic. In point of fact, this also makes sense since the goalkeeper stays most of the time around the same tactical region. The remaining players are somewhere between the combination constant-chaotic and linear-random, with more tendency for the linear-random.
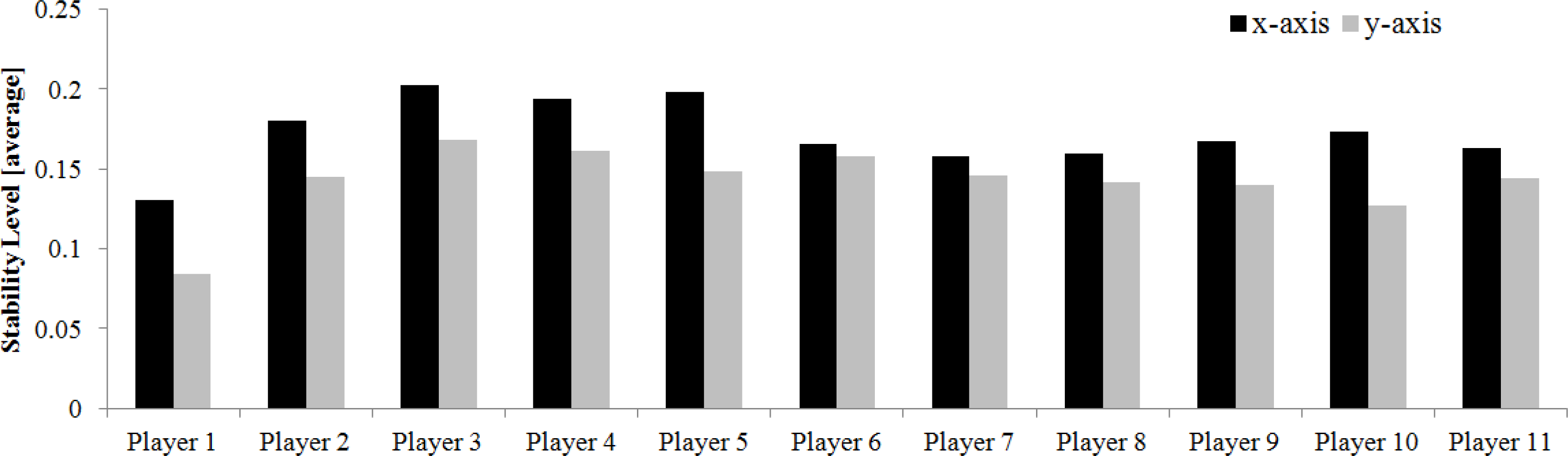
Going further on this analysis, the attraction domain previously defined was considered so as to study the number of times that each player remained within their stability region. In a quantitative point-of-view, if a player’s trajectory is classified as stable (based on and αn[t]), then the stability is defined as 1. Otherwise, the stability is defined as -1. Putting differently, a player that is as often within the stable region and the unstable one, will have an overall stability level of 0. From this analysis it is possible to obtain the stability values per player on the x-axis and y-axis coordinates (see Figure 13).
From the results shown, it is possible to observe that the goalkeeper (player 1) is the more unstable elements in both axes. On the other hand, defenders (players 2–5) are the elements with higher stability values. These values can be supported by the specific tactical missions of each player. Defenders should keep a large defensive stability by remaining in their tactical position, giving some equilibrium to the team. As a point of interest, a considerable number of goals suffered results from the defensive instability. Therefore, defenders should maintain their trajectories within their specific regions so as to ensure the possibility of recovering the ball in the offensive attempts by the opponent team. In contrast, the goalkeeper’s TR is evidently smaller than all his teammates. As such, at many moments of the match (mainly in the offensive situations) the goalkeeper moves outside his TR, towards his remaining teammates. Such movements decrease the goalkeeper’s stability.
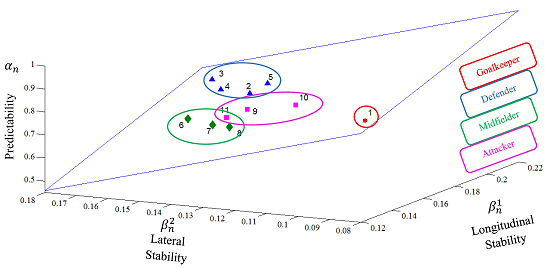
Using both concepts (predictability and stability) it is possible to observe that one player can be highly predictable (in terms of trajectory) while unstable (going outside his TR). On the other hand, a highly unpredictable player can be very stable if he stays most of the time inside his TR. Therefore, those two concepts are different and they provide an interesting set of information for coaches and their staff. The predictability level can be used to classify the oscillations during the football match while the stability level can be used to identify player’s responsiveness to his TR. To illustrate the relationship between predictability and stability, let us present Figure 14. The 3D chart on Figure 14 depicts how the level of stability on the x-axis, , is related to the level of stability on the y-axis, , and the level of predictability represented by the fractional coefficient αn
As one may observe, the relationship between these measures is represented by a plane. Moreover, as already concluded from Figure 13, although players are more stable in the x-axis, there is a clear dependency between the stability on both axes. On the other hand, the level of predictability seems to vary in a significant manner depending on the positional main role of players. For instance, it is possible to divide the points into four clusters, wherein the goalkeeper (red circle) represents the first cluster, the defenders represent the second cluster (blue triangles), the central players represent the third cluster (green lozenges) and the forwards represent the forth cluster (purple squares).
The information retrieved from the fractional coefficient cannot be compared neither with the outcome provided by the total distance covered nor with the heat maps entropy. The distance covered can be the same for all players, without providing a specific characteristic about the behaviour of the player. The heat maps entropy only provides information about the spatial distribution of players on the field. This distribution may also be similar for two players without describing their trajectory over time. Only understanding the specific properties of each football player’s trajectory can improve the performance analysis and, likewise, improve the quality of the football training.
6.3. Practical Remarks
The information retrieved from the fractional coefficient cannot be compared with either the outcome provided by the total distance covered, or with the heat maps entropy. The distance covered can be the same for all players, without providing any specific characteristic about the behaviour of the player. The heat maps entropy only provides information about the spatial distribution of players on the field. This distribution may also be similar for two players without describing their trajectory over time. Only understanding the specific properties of each football player’s trajectory can improve the performance analysis and, likewise, to improve the quality of the football training.
We should note that we are not redefining the concept of variability. Instead, this work proposes to analyse such variability by studying the regularity of players in returning to their own TR (stability), and by studying how predictable their trajectory may be (predictability). Stability, in science, is defined as its resistance to perturbations. In fact, this is a typical property shared by many dynamical systems, in which we could state that the stability is not only the resistance to a perturbation, but also the ability to return to the equilibrium point (or initial position) [45]. The existence of a stable equilibrium point implies the existence of a “restoring force” which is directed towards the equilibrium point. For instance, in the simple pendulum case study, this is a combination of the tension in the string and the force of gravity. Nevertheless, as opposed to the simple pendulum, the results presented here classify football players as non-linear dynamical systems, thus presenting chaotic or even stochastic trajectories. Although we assume that there is a steady-state point from which players converge, the truth is that they converge to an equilibrium point which is defined by their TR. In other words, a player’s orbit spirals in towards the equilibrium. The same can be said about the predictability of players. By definition, predictability is the degree to which a correct estimation of a system’s state can be made. This is in line with the concept of predictability in mathematics, wherein a process is classified as predictable if it is possible to know the “next” state at the present time.
In many situations, the choice regarding the players from the first team is based on each player’s specific properties so as to adjust the team against their opponents. As such, one may choose between more stable players to focus on the defence, or more unpredictable ones to focus on the attack. The fractional coefficient can also be a useful method to improve the understanding about decision-making in sports. The main techniques used so far for this specific issue have been the approximate entropy and the Lyapunov exponent. Nevertheless, the applicability of such methods depends on the variable that better explains the level of predictability. For a more specific tactical analysis, one should go further into understanding the fractional coefficient variability by resorting to stability theory. This is very important in understanding the player’s regularity on returning to his own TR. The stability confined to on attraction region has a great potential for use by coaches to classify the tactical oscillations of players, thus adjusting or readjusting the desired tactical behaviours. Also, the opponent coach can use this information to identify some unstable points and exploit them during the match. Nevertheless, it should be highlighted that neither the fractional coefficient, nor the stability analysis per se, are the ultimate answer to one’s needs in the context of football. Such team sport, as a complex and dynamic game, should be analysed using collective nonlinear methods. The classical perspective of the performance analysis has been overtaken using new technologies to improve the understanding of the individual and tactical parameters, mainly trying to explain the process variables. For the collective analysis, some metrics have been proposed based on the position of players over time [3,46,47]. Nevertheless, for the individual performance, the researchers have been emphasizing on the notational information (i.e., product variables) and kinematical information [43]. This paper provides a new take-home message on the individual performance of a football match, with the main purpose being the understanding of the specific properties of each player and their dynamical behaviour during the match.
It is noteworthy that the herein proposed methodology proposed here was evaluated using one match. Its usefulness for coaches and sports analysts needs to be further assessed over multiple matches, with and without professional players. Note, however, that this requires the use of automatic tracking systems, such as AMISCO Pro and ProZone [48]. These systems provide online information to coaches and their staff about players’ movements (e.g., energy spent by a player). Nevertheless, despite of their efficiency and autonomous properties, player-to-player occlusion, similar player appearance, number of players changing over time, variability of players’ motion and noises or video blur present themselves as open problems [49]. Therefore, although generally autonomous, these tracking systems still require some human input as well as continual online verification by an operator to make sure that players are correctly tracked by the computer program [48]. Hence, beyond their expensive devices (e.g., many high-definition video cameras), those systems may benefit from the outcome provided by the fractional calculus methodology provided in this paper and previously presented in Couceiro et al. [17], to accurately and autonomously estimate a given player’s position over time.
7. Conclusions
New technological devices and mathematical methods have been used recently to analyse the performance of football players. Despite these developments, a gap still remains on understanding a player’s dynamical behaviour during the match. Some of the most important variables one may look at are inherent in a player’s variability, which one may classify based on the predictability and stability of his trajectory. This study proposed an approach to measure the predictability and stability levels of player’s trajectories based on the concepts inherent in Fractional Calculus. Furthermore, the variability of each player was measured using the well-known Shannon’s entropy and the approximate entropy. The fractional coefficient, explaining a given player’s trajectory, was used in order to estimate his predictability. The addition of a new parameter, herein denoted here as the stability vector, gave rise to an attraction domain defining the player’s stability. The results showed that the goalkeeper was the most predictable and unstable player. The most unpredictable players were the midfielders while the most stable players were the defenders. All this information can be used by coaches to adjust and readjust the team’s strategy, as well as the tactical behaviour of players.
Acknowledgments
This work was supported by a PhD scholarship (SFRH/BD /73382/2010) by the Portuguese Foundation for Science and Technology (FCT). Also, this paper reports research work carried out within the project “Towards a technological approach of the match analysis: Using tactical metrics to evaluate football teams” from the Instituto de Telecomunicações, granted by the Portuguese Foundation for Science and Technology (FCT) with the ref. PEst-OE/EEI/LA0008/2011.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hughes, M.D.; Bartlett, R.M. The use of performance indicators in performance analysis. J. Sports Sci 2002, 20, 739–754. [Google Scholar]
- Yue, Z.; Broich, H.; Seifriz, F.; Mester, J. Mathematical analysis of a soccer game. Part I: Individual and collective behaviors. Stud. Appl. Math 2008, 121, 223–243. [Google Scholar]
- Clemente, F.M.; Couceiro, M.S.; Martins, F.M.M.; Mendes, R. An online tactical metrics applied to football game. Res. J. Appl. Sci 2013, 5, 1700–1719. [Google Scholar]
- Figueroa, P.J.; Leite, N.J.; Barros, R.M.L. Tracking soccer players aiming their kinematical motion analysis. Comput. Vis. Image Underst 2006, 101, 122–135. [Google Scholar]
- Leser, R.; Baca, A.; Ogris, G. Local Positioning Systems in (Game) Sports. Sensors 2011, 11, 9778–9797. [Google Scholar]
- Travassos, B.; Araújo, D.; Davids, K.; Vilar, L.; Esteves, P.; Vanda, C. Informational constraints shape emergent functional behaviours during performance of interceptive actions in team sports. Psychol. Sport Exerc 2012, 13, 216–223. [Google Scholar]
- Frencken, W.; Poel, H.; Visscher, C.; Lemmink, K. Variability of inter-team distances associated with match events in elite-standard soccer. J. Sports Sci 2012, 30, 1207–1213. [Google Scholar]
- Passos, P.; Milho, J.; Fonseca, S.; Borges, J.; Araújo, D.; Davids, K. Interpersonal distance regulates functional grouping tendencies of agents in team sports. J. Motor Behav 2011, 43, 155–163. [Google Scholar]
- Harbourne, R.T.; Stergiou, N. Movement variability and the use of nonlinear tools: Principles to guide physical therapist practice. Phys. Ther 2009, 89, 267–282. [Google Scholar]
- Fonseca, S.; Milho, J.; Passos, P.; Araújo, D.; Davids, K. Approximate entropy normalized measures for analyzing social neurobiological systems. J. Motor Behav 2012, 44, 179–183. [Google Scholar]
- Lamoth, C.J.C.; van Lummel, R.C.; Beek, P.J. Athletic skill level is reflected in body sway: A test case for accelometry in combination with stochastic dynamics. Gait Posture 2009, 29, 546–551. [Google Scholar]
- Martins, F.M.L.; Clemente, F.M.; Couceiro, M.S. From the individual to the collective analysis at the football game. Proceedings of International Conference on Mathematical Methods in Engineering, Porto, Portugal, 22–26 July 2013; pp. 217–231.
- Passos, P.; Araújo, D.; Davids, K.; Gouveia, L.; Serpa, S.; Milho, J.; Fonseca, S. Interpersonal pattern dynamics and adaptive behavior in multi-agent neurobiological systems: A conceptual model and data. J. Motor Behav 2009, 41, 445–459. [Google Scholar]
- Correia, V.; Araújo, D.; Davids, K.; Fernandes, O.; Fonseca, S. Territorial gain dynamics regulates success in attacking sub-phases of team sports. Psychol. Sport Exerc 2011, 12, 662–669. [Google Scholar]
- Headrick, J.; Davids, K.; Renshaw, I.; Araújo, D.; Passos, P.; Fernandes, O. Proximity-to-goal as a constraint on patterns of behaviour in attacker-defender dyads in team games. J. Sports Sci 2012, 30, 247–253. [Google Scholar]
- Beetz, M.; von Hoyningen-Huene, N.; Kirchlechner, B.; Gedikli, S.; Siles, F.; Durus, M.; Lames, M. ASpoGAMo: Automated Sports Game Analysis Models. Int. J. Comput. Sci. Sport 2009, 8, 4–21. [Google Scholar]
- Couceiro, M.S.; Clemente, F.M.; Martins, F.M.L. Analysis of football player’s motion in view of fractional calculus. Cent. Eur. J. Phys 2013, 11, 714–723. [Google Scholar]
- Sabuncu, M.R. Entropy-based Image Registration; Ph.D. Thesis, Princeton University, Princeton, NJ, USA; 2006. [Google Scholar]
- Pincus, S.M.; Gladstone, I.M. A regularity statistic for medical data analysis. J. Clin. Monit 1991, 7, 335–345. [Google Scholar]
- Zhou, S.; Cao, J.; Chen, Y. Genetic algorithm-based identification of fractional-order systems. Entropy 2013, 15, 1624–1642. [Google Scholar]
- Couceiro, M.S.; Martins, F.M.L.; Rocha, R.P.; Ferreira, N.M.F. Introducing the Fractional Order Robotic Darwinian PSO. Proceedings of 9th International Conference on Mathematical Problems in Engineering, Aerospace and Sciences, ICNPAA 2012, Vienna, Austria, 10–14 July 2012.
- Couceiro, M.S.; Dias, G.; Martins, F.M.L.; Luz, J.M.A. A fractional calculus approach for the evaluation of the golf lip-out. Sig. Imag. Video Process 2012, 6, 437–443. [Google Scholar]
- Machado, J.A.T.; Silva, M.F.; Barbosa, R.S.; Jesus, I.S.; Reis, C.M.; Marcos, M.G.; Galhano, A.F. Some applications of fractional calculus in engineering. Math. Probl. Eng 2010, 2010, 639801. [Google Scholar]
- Ostalczyk, P.W. A note on the Grünwald-Letnikov fractional-order backward-difference. Phys. Scripta 2009, T136, 1–5. [Google Scholar]
- Young, I.T.; Gerbrands, J.J.; van Vliet, L.J. Fundamentals of Image Processing; Delft University of Technology: Delft, The Netherlands, 1998. [Google Scholar]
- Forsythe, G.E.; Malcolm, M.A.; Moler, C.B. Computer Methods for Mathematical Computations; Prentice Hall: Englewood Cliffs, NJ, USA, 1977. [Google Scholar]
- Brent, R.P. Algorithms for Minimization without Derivatives; Prentice-Hall: Englewood Cliffs, NJ, USA, 1973. [Google Scholar]
- Elaydi, S. An Introduction to Difference Equations, 3rd ed; Springer: Berlin, Germany, 2005. [Google Scholar]
- Barnett, S. Polynomials and Linear Control Systems; Marcel Dekker, Inc: New York, NY, USA, 1983. [Google Scholar]
- Di Salvo, V.; Baron, R.; Cardinale, M. Time motion analysis of elite footballers in European cup competitions. J. Sports Sci. Med 2007, 6, 14–15. [Google Scholar]
- Wisløff, U.; Helgerud, J.; Hoff, J. Strength and endurance of elite football players. Med. Sci. Sports Exerc 1998, 30, 462–467. [Google Scholar]
- Mohr, M.; Krustrup, P.; Bangsbo, J. Match performance of high-standard football players with special reference to development of fatigue. J. Sports Sci 2003, 21, 519–528. [Google Scholar]
- Stølen, T.; Chamari, K.; Castagna, C.; Wisløff, U. Physiology of Football: An Update. Sports Med 2005, 35, 501–536. [Google Scholar]
- Reilly, T. Physiological aspects of football. Biol. Sport 1994, 11, 3–20. [Google Scholar]
- Carling, C.; Williams, A.M.; Reilly, T. Handbook of Soccer Match Analysis: A Systematic Approach to Improving Performance; Taylor & Francis Group: London, UK and New York, NY, USA, 2005. [Google Scholar]
- Reilly, T.; Thomas, V. A motion analysis of work-rate in different positional roles in professional football match-play. J. Hum. Movement Stud 1976, 2, 87–97. [Google Scholar]
- Rienzi, E.; Drust, B.; Reilly, T.; Carter, J.E.; Martin, A. Investigation of anthropometric and work-rate profile of elite South American international football players. J. Sports Med. Phys. Fit 2000, 40, 162–169. [Google Scholar]
- Di Salvo, V.; Baron, R.; Tschan, H.; Calderon Montero, F.; Bachl, N.; Pigozzi, F. Performance characteristics according to playing position in elite football. Int. J. Sports Med 2007, 28, 222–227. [Google Scholar]
- Clemente, F.; Couceiro, M.; Martins, F.; Dias, G.; Mendes, R. Influence of task constraints on attacker trajectories during 1v1 sub-phase in soccer practice. Sport Logia 2012, 8, 13–20. [Google Scholar]
- Duque, C. Priors for the Ball Position in Football: Match using Contextual Information. Master Thesis, Royal Institute of Technology, School of Computer Science and Communication, Stockholm, Sweden. 2010. [Google Scholar]
- Abdel-Aziz, Y.; Karara, H. Direct linear transformation from comparator coordinates into object space coordinates in close-range photogrammetry. Presented at ASP Symposium on Close-Range Photogrammetry, Falls Church, VA, USA; 1971. [Google Scholar]
- Bloomfield, J.; Polman, R.; O'Donoghue, P. Physical demands of different positions in FA Premier League soccer. J. Sports Sci. Med 2007, 6, 63–70. [Google Scholar]
- Barros, R.M.L.; Misuta, M.S.; Menezes, R.P.; Figueroa, P.J.; Moura, F.A.; Cunha, S.A.; Anido, R.; Leite, N.J. Analysis of the distances covered by first division Brazilian soccer players obtained with an automatic tracking method. J. Sports Sci. Med 2007, 6, 233–242. [Google Scholar]
- Bangsbo, J. The physiology of soccer—with special reference to intense intermittent exercise. Acta Physiol. Scand. Suppl 1994, 619, 1–156. [Google Scholar]
- McGinnis, P. Biomechanics of Sport and Exercise; Human Kinetics: Champaign, IL, USA, 2013. [Google Scholar]
- Bartlett, R.; Button, C.; Robins, M.; Dutt-Mazumder, A.; Kennedy, G. Analysing team coordination patterns from player movement trajectories in football: Methodological considerations. Int. J. Perform. Anal. Sport 2012, 12, 398–424. [Google Scholar]
- Frencken, W.; Lemmink, K. Team Kinematics of Small-Sided Football Games: A Systematic Approach. In Science and Football VI; Routledge Taylor & Francis Group: Oxon, UK, 2008; pp. 161–166. [Google Scholar]
- Carling, C.; Bloomfield, J.; Nelsen, L.; Reilly, T. The role of motion analysis in elite soccer. Sports Med 2008, 38, 839–862. [Google Scholar]
- Liu, J.; Tong, X.; Li, W.; Wang, T.; Zhang, Y. Automatic player detection, labeling and tracking in broadcast soccer video. Pattern Recognit. Lett 2009, 30, 103–113. [Google Scholar]


| Signal | Approximate Entropy Values |
|---|---|
| Periodic function | ∼0 |
| Chaotic system (e.g., Lorenz attractor) | 0.1 |
| Random time series | 1.5 |
| Overall Distance [km] | αn AVG | αn STD | Heat Maps Entropy | Distance Entropy | αn Entropy | ||
|---|---|---|---|---|---|---|---|
| Goalkeeper | Player 1 | 3.508 | 0.86 | 0.14 | 0.804 | 0.515 | 0,386 |
| Defenders | Player 2 | 10.976 | 0.77 | 0.24 | 2.205 | 0.504 | 0,455 |
| Player 3 | 9.075 | 0.74 | 0.25 | 2.083 | 0.531 | 0,381 | |
| Player 4 | 9.355 | 0.73 | 0.26 | 2.151 | 0.511 | 0,353 | |
| Player 5 | 10.916 | 0.76 | 0.24 | 2.192 | 0.510 | 0,479 | |
| Midfielders | Player 6 | 11.263 | 0.68 | 0.30 | 2.372 | 0.543 | 0,372 |
| Player 7 | 12.520 | 0.69 | 0.29 | 2.470 | 0.547 | 0,363 | |
| Player 8 | 12.556 | 0.68 | 0.30 | 2.449 | 0.562 | 0,398 | |
| Forwards | Player 9 | 11.747 | 0.74 | 0.26 | 2.338 | 0.512 | 0,364 |
| Player 10 | 10.783 | 0.76 | 0.25 | 2.024 | 0.507 | 0,455 | |
| Player 11 | 11.117 | 0.71 | 0.27 | 2.333 | 0.546 | 0,389 | |
| Overall | 10,347 | 0.74 | 0.25 | 0.526 | 2.129 | 0.400 | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Couceiro, M.S.; Clemente, F.M.; Martins, F.M.L.; Machado, J.A.T. Dynamical Stability and Predictability of Football Players: The Study of One Match. Entropy 2014, 16, 645-674. https://doi.org/10.3390/e16020645
Couceiro MS, Clemente FM, Martins FML, Machado JAT. Dynamical Stability and Predictability of Football Players: The Study of One Match. Entropy. 2014; 16(2):645-674. https://doi.org/10.3390/e16020645
Chicago/Turabian StyleCouceiro, Micael S., Filipe M. Clemente, Fernando M. L. Martins, and José A. Tenreiro Machado. 2014. "Dynamical Stability and Predictability of Football Players: The Study of One Match" Entropy 16, no. 2: 645-674. https://doi.org/10.3390/e16020645
APA StyleCouceiro, M. S., Clemente, F. M., Martins, F. M. L., & Machado, J. A. T. (2014). Dynamical Stability and Predictability of Football Players: The Study of One Match. Entropy, 16(2), 645-674. https://doi.org/10.3390/e16020645