Automatic Sleep Stages Classification Using EEG Entropy Features and Unsupervised Pattern Analysis Techniques

Abstract

Sleep is a growing area of research interest in medicine and neuroscience. Actually, one major concern is to find a correlation between several physiologic variables and sleep stages. There is a scientific agreement on the characteristics of the five stages of human sleep, based on EEG analysis. Nevertheless, manual stage classification is still the most widely used approach. This work proposes a new automatic sleep classification method based on unsupervised feature classification algorithms recently developed, and on EEG entropy measures. This scheme extracts entropy metrics from EEG records to obtain a feature vector. Then, these features are optimized in terms of relevance using the Q-α algorithm. Finally, the resulting set of features is entered into a clustering procedure to obtain a final segmentation of the sleep stages. The proposed method reached up to an average of 80% correctly classified stages for each patient separately while keeping the computational cost low.

1. Introduction

Humans devote approximately one third of their life to sleep [1]. The biological rationale of this need remains unknown. However, there have been some attempts to elucidate the role of sleeping in human beings. It has been related to plasticity [2], and also to the reorganization of memory [3,4].

Unfortunately, sleep disorders and/or deprivation affect a great number of subjects worldwide. This entails a huge impact on public and individual health, including economic costs, reduced quality of life, co-morbidities, and even early mortality [5]. These are the main reasons why sleep is a subject of intense systematic research interest, including sleep stages detection and characterization.

Polysomnography (PSG) is the most commonly used technique in medicine for the diagnosis and understanding of the sleep phenomena [6]. PSG is a multimodal recording of different bio-signals during the whole sleep period at night. The Electroencephalogram (EEG) can be used to indirectly study the dynamics of the neural activity [7], which is time-varying during night-time [8] (pp. 193–208, Chapter 10).

Sleep is a highly nonstationary and nonlinear process whose statistics are time-varying but remain constant inside a short period of time known as sleep stage. Sleep analysis considers 5 different stages: wake (W), drowsiness (N1), light sleep (N2), deep sleep (N3), and rapid eye movement sleep (REM) [9].

The scoring and classification of sleep stages is manually performed by experts who analyze the PSG records in small time windows or epochs (commonly 30 s duration). This task is difficult, subjective and is often an exasperating time consuming process, thus leading to a low reliability and differences among scorers [10,11]. In order to effectively address these issues, automatic classification schemes have been progressively introduced as an objective way to assist the experts during this process [12,13].

The most commonly used techniques for automatic sleep stage classification are still supervised however. Namely, they require user intervention or manual data annotation. Among these techniques, neural networks (NN) [14] yield very good results, with up to 80% classification accuracy [14,15]. Other approaches have achieved 95% accuracy in more specific applications, such as differentiating alert states from drowsy and sleep states. All these supervised approaches strongly depend on the predefined scorer’s labels [16], and therefore they lack of flexibility, adaptability, and reusability.

In this work, a novel unsupervised classification scheme for sleep stage determination based on EEG records is proposed. This technique computes entropy metrics from the signals to build a feature vector. This vector is optimized in terms of relevance using the recently developed Q-α based approach [17] in order to reduce computational cost. The resulting weighted feature vector is processed by a J-means clustering algorithm to obtain the final stage classification. The segmentation accuracy rate achieved in the experiments was up to 80% for each patient separately, comparable to that obtained with supervised methods.

2. Method

A representative experimental set was processed using the method proposed. A vector of EEG entropy features was computed for different epochs of 30 s of duration. For comparative purposes, a number of entropy metrics were utilized. Spare features were removed using the Q-α algorithm, and the final vectors were clustered according to a J-means scheme. Results were assessed both in terms of classification accuracy and computational burden. Each step of the method proposed is described in Sections 2.2–2.4 (see flow chart in Figure 1), including the experimental dataset employed for validation (Section 2.1).

2.1. Experimental Dataset

The EEG signals used in the experiments were drawn from the SC Sleep-EDF Database [Expanded] [18]. This database is freely available through Physionet [19].

Specifically, only the Fpz-Cz and Pz-Oz EEG channels were analyzed [20]. These signals correspond to Caucasian normal males and females aged 25 to 34 years old, taking no medication. In total, 39 records sampled at 100 Hz and filtered from 0.5 to 100 Hz were employed in the experiments. Further details of the database can be found at [18,21].

Sleep stages were scored manually using Rechtschaffen and Kales (R & K) criteria [22]. Stage labels were provided together with the database by Physionet [19], using additionally recorded signals, and according to standard scoring rules [22]. Epochs marked as movement and unscored were rejected for further analysis (61 epochs). Information about the inter-rater reliability for sleep scoring can be found in [10,11]. For the specific purposes of the present study, sleep stages 3 and 4 were merged into a single deep sleep stage (N3).

2.2. Feature Extraction

Given an input discrete time series $x=\{x_1,\cdots ,x_N|x_i\in ℝ,i\in \mathbb{Z}>0\}$ length N, a vector V ∈ ℝ^q is formed by q points, being q the number of features $\psi =\{{\psi }_1,\cdots ,{\psi }_q|{\psi }_j\in ℝ,j\in \mathbb{Z}>0\}$ used (number of 30 s epochs).

The aim of the feature extraction stage was to compare the performance of different entropy estimators when applied to the experimental set, and find out if some metrics are more sensitive to EEG patterns. The changes in sleep stages cause changes in the EEG, and these changes are also expected to be reflected in the entropy results, as observed in many other works, see [8] (pp. 193–208, Chapter 10) and [18,20,23]. The specific features computed in this study using the standard algorithms were: Fractal Dimension (FD), Detrended Fluctuation Analysis (DFA), Shannon entropy (H), Approximate Entropy (ApEn), Sample Entropy (SampEn), and Multiscale Entropy (MSE). A total of q = 34 complexity measures were included in the analysis.

2.2.1. Fractal Dimension

The estimation of the FD was applied in order to account for signal complexity and scale invariance. FD statistically quantifies how well a fractal matches the input data at different scales.

The method to compute FD was based on the box counting algorithm [24,25]. FD is estimated as the slope of the straight line fitted to the curve formed by the sequence (ln(L), (S(L)/L)), where L is the size of the box, and S(L) is the number of boxes. If the sampling interval of the input time series is ∆t and the box size is L = n∆t, the number of boxes S(L) can be obtained from:

$$S(n\mathrm{\Delta }t)={\displaystyle \sum _{i=1}^{\mathrm{mod}(N/n)}|\max (\mathrm{\Delta }{x}_i)-\min (\mathrm{\Delta }{x}_i)|}$$

(1)

where $\mathrm{\Delta }{x}_i=x_{n(i-1)+1,}{x}_{n(i-1)+2},\cdots ,x_{n(i-1)+n+1}$. The FD of x is estimated by counting the number of boxes needed to cover the curve [24]. A fractal dimension index was calculated for both EEG channels referred as FD.Fpz-Cz and FD.Pz-Oz (features ψ₁, ψ2).

2.2.2. Detrended Fluctuation Analysis

It is not a true entropy estimator, but DFA is a measure that allows the detection of long-range power-law correlations in a time series [26]. The first step to obtain DFA is to compute the integrated time series as $y=\{y_k={\displaystyle {\sum }_{i=1}^k{x}_i}\}$. Then, y is divided into N/L boxes of length L (the parameter L defines the time-scale). In each box, a line is fitted and its ordinate, denoted by $y_k^L$, is taken as the trend of the time series in that box. The integrated time series is detrended by subtracting $y_k^L$ and the root mean square fluctuation is computed according to:

$$f(L)=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=k}^N{(y_i-y_i^L)}^2}}$$

(2)

This process is repeated for different scales L. Finally, the scaling exponent that represents the DFA value is obtained from the slope of a linear fitting between (log₁₀(L), log₁₀(f(L))). Three features were calculated from the DFA for each channel, the scaling exponents of the whole epoch (DFA-α), and scaling exponents (DFA-a1 and DFA-a2) before and after the relative estimated error correction (features ψ₃ − ψ₈). A detailed description of this algorithm can be found in [27].

2.2.3. Shannon Entropy

This is a measure of the data spread. It was calculated for each channel according to:

$$H(x)=-{\displaystyle \sum _{i}p(x_i)\log (p(x_i))}$$

(3)

where p(x_i) is the probability p(x = x_i). In this work, we considered $p(x_i)=x_i^2$. This entropy measure has already been used in sleep EEG signal processing, yielding high values in wakefulness and REM sleep stages, and low values in N3 stages [28]. Shannon entropy was calculated for each channel independently (features ψ₉ and ψ₁₀).

2.2.4. Approximate Entropy

ApEn is related to the predictability or regularity of a time series. It was devised as an approximation of the Kolmogorov entropy of an underlying process [29].

The ApEn algorithm is basically a search for the repetitive patterns of length m commencing at sample i in which the distance induced by the maximum norm differs up to an error threshold r [30]. The ApEn statistic, given an input value for parameters m and r, is defined as:

$$\text{ApEn}(m,r,N)={\mathrm{\Phi }}_m(r)-{\mathrm{\Phi }}_{m+1}(r)$$

(4)

where

$${\mathrm{\Phi }}_m(r)=\epsilon \left\{\ln \left(\frac{c_i^m\left(r\right)}{N-m+1}\right)\right\}$$

(5)

being $c_i^m(r)$ the number of vectors ${\mathrm{x}}_i\in {ℝ}^m$ such that $d({\mathrm{x}}_i,{\mathrm{x}}_j)<r,{\mathrm{x}}_i=\{x_i,x_{i+1},\cdots ,x_{i+m-1}\}$, 1 ≤ i, j≤N − m+1. ApEn was computed for both Fpz-Cz and Pz-Oz channels (features ψ₁₁ and ψ₁₂).

2.2.5. Sample Entropy

SampEn was an evolution of ApEn devised to solve the bias of ApEn due to counting self-matches. SampEn exhibits better statistical properties [30] than ApEn. It is computed in a similar fashion, but the final step becomes:

$$\text{SampEn}(m,r,N)=-\ln \left(\frac{A^m(r)}{B^m(r)}\right)$$

(6)

where B^m(r) is defined as the mean of the number of vectors x_i ∈ ℝ^m, such that d(x_i, x_j) < r with i ≠ j, divided by N − m + 1. The value of A^m(r) is defined similarly for x_i ∈ ℝ^m+1. SampEn was calculated for two template lengths (m = 0 and m = 1) for each channel (features ψ₁₃ – ψ₁₆).

2.2.6. Multiscale Entropy

MSE is an estimator of the complexity of a time series in which entropy measures are applied at different time-scales. The calculation is carried out in two steps [31]. First, a coarse grained time series is constructed for the different scales τ considered (1 < τ ≤ 9 in this work), from the original signal x:

$$y_j^{(\tau )}=\frac{1}{\tau }{\displaystyle \sum _{i=(j-1)\tau +1}^{j\tau }{x}_i}$$

(7)

Second, an auxiliary single-scale entropy measure (we chose SampEn) is computed over the resulting coarse-grained series. MSE was computed for scales n = 1, 2,…,9 for the two channels (features ψ₁₇ – ψ₃₄)

2.3. Feature Relevance Analysis

The previous feature extraction stage yields a set of p vectors V ∈ ℝ^q, where the q components correspond to the features computed as described in Section 2.2. Next, in order to reduce the computational cost of the classification stage and improve the classification speed, a dimensionality reduction method, termed feature relevance analysis, takes place. This method provides a reduced subset q′ < q of the input features in p, but maximizing the preserved relevant discriminatory information. This optimization is carried out following a matrix projection scheme, similar to that used in Principal Component Analysis (PCA) methods. The output of this stage is a feature significance quantitative score that, using a threshold, enables or disables the exclusion of that feature. The value selected for the threshold was an accumulated variance criterion of 98% [32].

Specifically, this work applies a relevance analysis method based on the Q-α algorithm recently developed by us, and applied successfully to Electrocardiographic records [17]. This relevance analysis was applied to each patient separately. Features were retained in the final set if they were found relevant for at least 20 subjects.

The Q-α algorithm is an optimization procedure. Given a matrix W that contains the p feature vectors V of length q, W ∈ ℝ^p×q the objective is to find a new matrix $\widehat{\mathbf{W}}$ with q′ < q features, $\widehat{\mathbf{W}}$ ∈ ℝ^p×q′. To obtain $\widehat{\mathbf{W}}$, it is necessary to solve the optimization problem given by the general expression:

$$\underset{\mathbf{Q},\mathbf{A}}{\max }tr({\mathbf{Q}}^T\mathbf{AAQ})$$

(8)

where A is a symmetric, positive, affinity matrix given by A = Wdiag (α) W^T, tr is the matrix trace, α a weight vector α ∈ ℝ^q with ||α|| = 1, and Q an orthonormal p × p matrix. The difference between W and $\widehat{\mathbf{W}}$ can be determined by the Euclidean norm with regard to A, i.e., $\Vert W-\widehat{W}{\Vert }_A^2$, where the squared is used to simplify. It can be shown that $\Vert W-\widehat{W}{\Vert }_A^2=tr(A){\displaystyle \sum }_{i=(q-q^{\prime })+1}^q{\lambda }_i$ denotes the i-th eigenvector from W^TW. Thereby, the purpose of minimizing this difference is that it could be represented in terms of the maximization of its complement, such as tr (W^TAW). Because A = Wdiag (α) W^T, with an initial value of α = 1_q, Equation (8) could be introduced as:

$$\begin{array}{l}tr({\mathbf{Q}}^T{\mathbf{WW}}^T{\mathbf{WW}}^T\mathbf{Q})=\\ tr({\mathbf{Q}}^T\mathbf{AAQ})={\displaystyle \sum _{i=1}^r{\lambda }_i^2}\end{array}$$

(9)

The Equations (8) and (9) are analogous to the quadratic optimization problem described by [33] and is solved by the algorithm Q-α. This stage is also unsupervised since the 98% variance criterion fixes when the Q-α finishes the search without user intervention or training datasets. This method sorts the features according to their relevance measured in terms of contribution to whole variance, and when the threshold is reached, no more features are included in the final feature set. A full description of the method could be found in [17].

2.4. Sleep Stages Unsupervised Classifier

The automatic classification is based on a J-means approach [34]. The objective of this stage is to obtain an optimal partition of the feature vectors in $\widehat{\mathbf{W}}$ in such a way that the resulting disjoint clusters correspond to different sleep stages. Additional clusters can be added in order to collect outliers, namely, artifacts that can not be classified as any sleep stage because their dissimilarity to any centroid is too large (noise, movement artifacts, interferences, sensor contact issues).

The algorithm attains a local optimum by heuristic reassignment of neighborhoods using a jumping paradigm [34], as follows:

• Initialization: A standard k-means clustering is used to set an initial partition of the feature vectors and the centroids. This reduces the temporal cost of the partition calculation.
• Search: Given a tolerance threshold (4 standard deviations of the intra-cluster distance), find the unoccupied points (feature vectors that do not belong to any cluster).
• Update: Add a new cluster centroid at some unoccupied location and find the index of the best centroid to delete. Update the partition according to the new centroids.
• Finalize: If a local minimum is found in the previous iteration, stop. For each resulting cluster, a sleep stage can be assigned as the most frequent class (using a k-Neighbors method), which in clinical practice could be done by a whole cluster manual scoring. Otherwise return to step 2.

3. Results and Discussion

The experiments were carried out using a standard Windows 8 personal computer and MATLAB® environment tools. The most relevant features obtained were (using feature names and EEG channels): FD.Fpz-Cz, FD.Pz-Oz, H.Fpz-Cz, DFA-α.Fpz-Cz, dfa-α.pz-oz, DFA-a1.Pz-Oz, ApEn.Fpz-Cz, ApEn.Pz-Oz, MSE1.Pz-Oz, SampEn2.Pz-Oz.

Classification methods were tested for each subject independently (1048 ± 223 epochs per subject). Mean results are presented in

Table 1. Recall and precision for sleep stages identification using the set of relevant features. Results expressed as mean(variance).

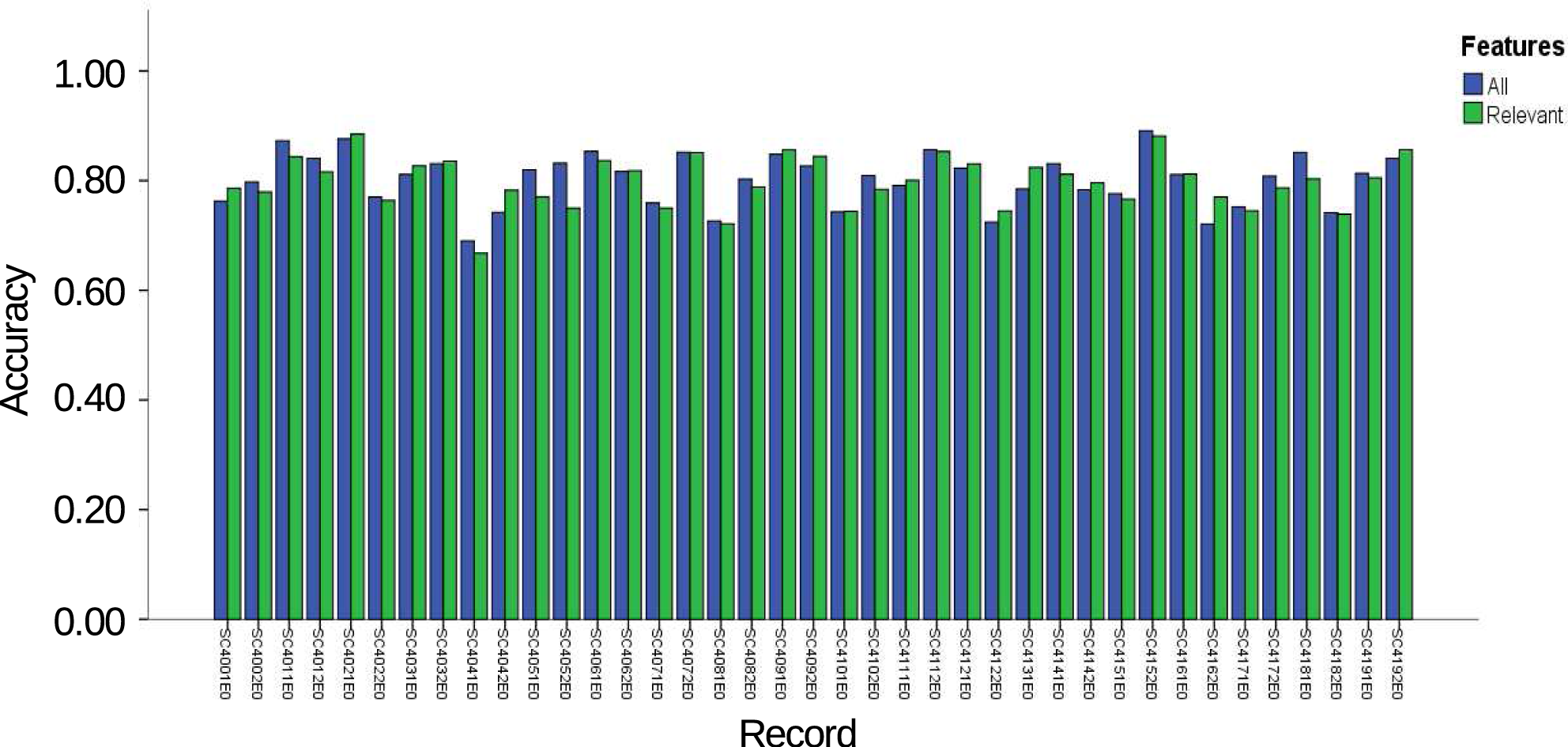
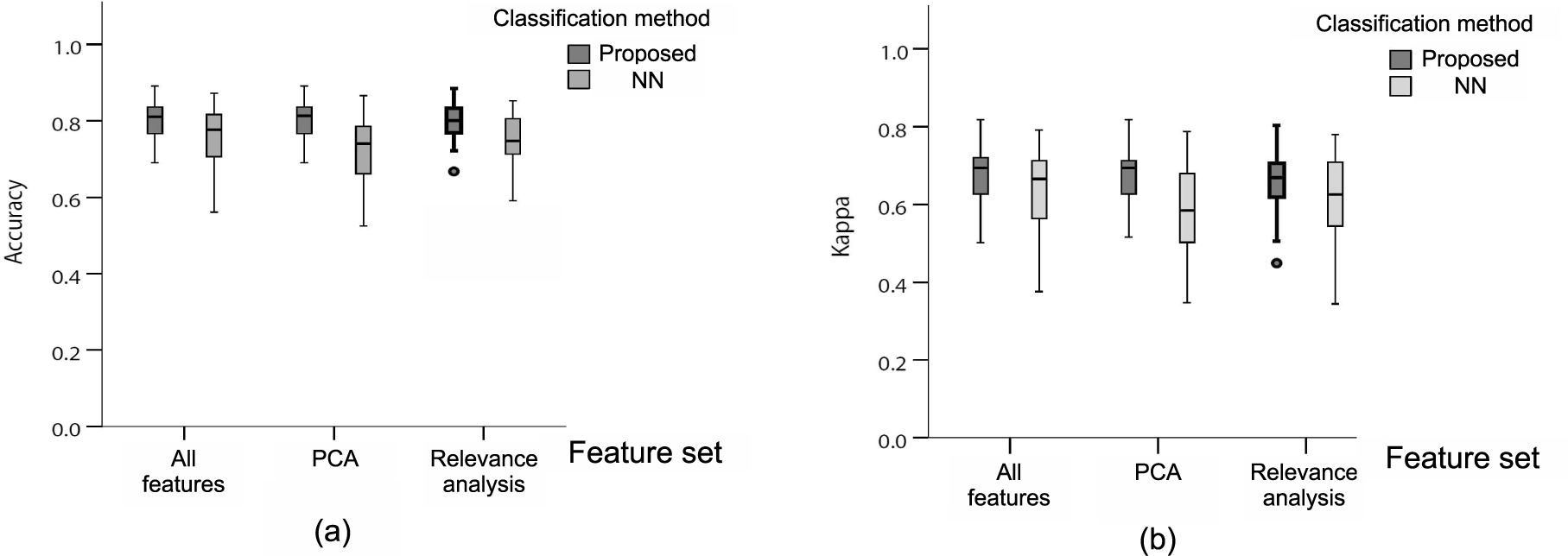
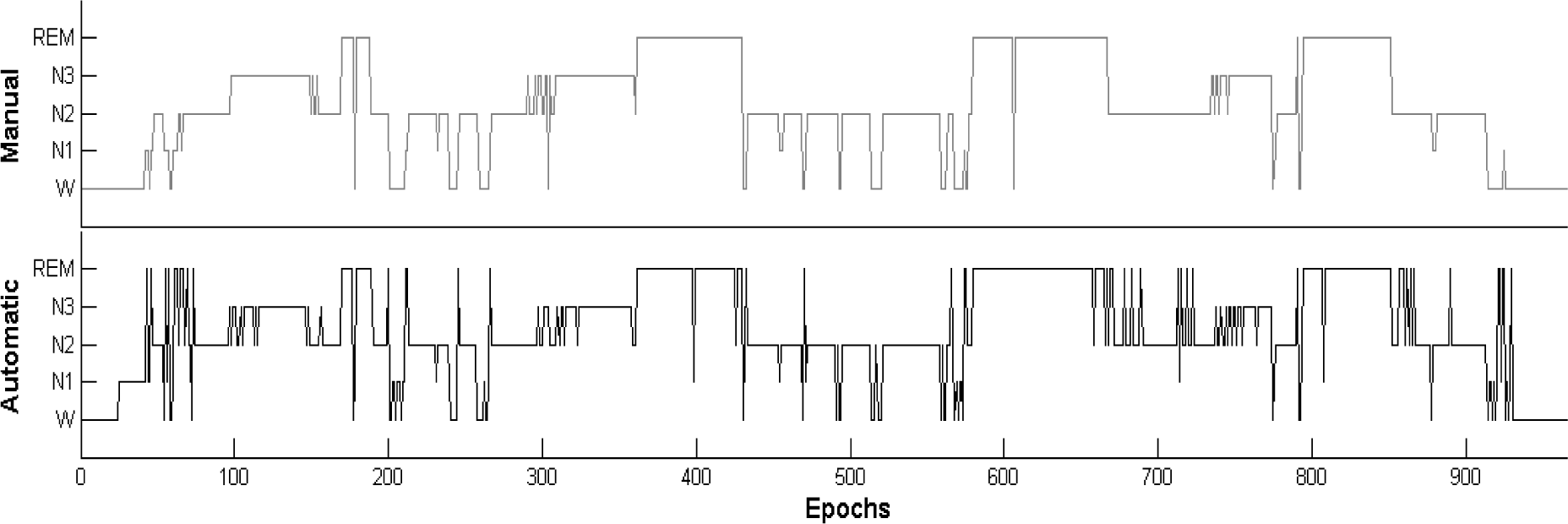
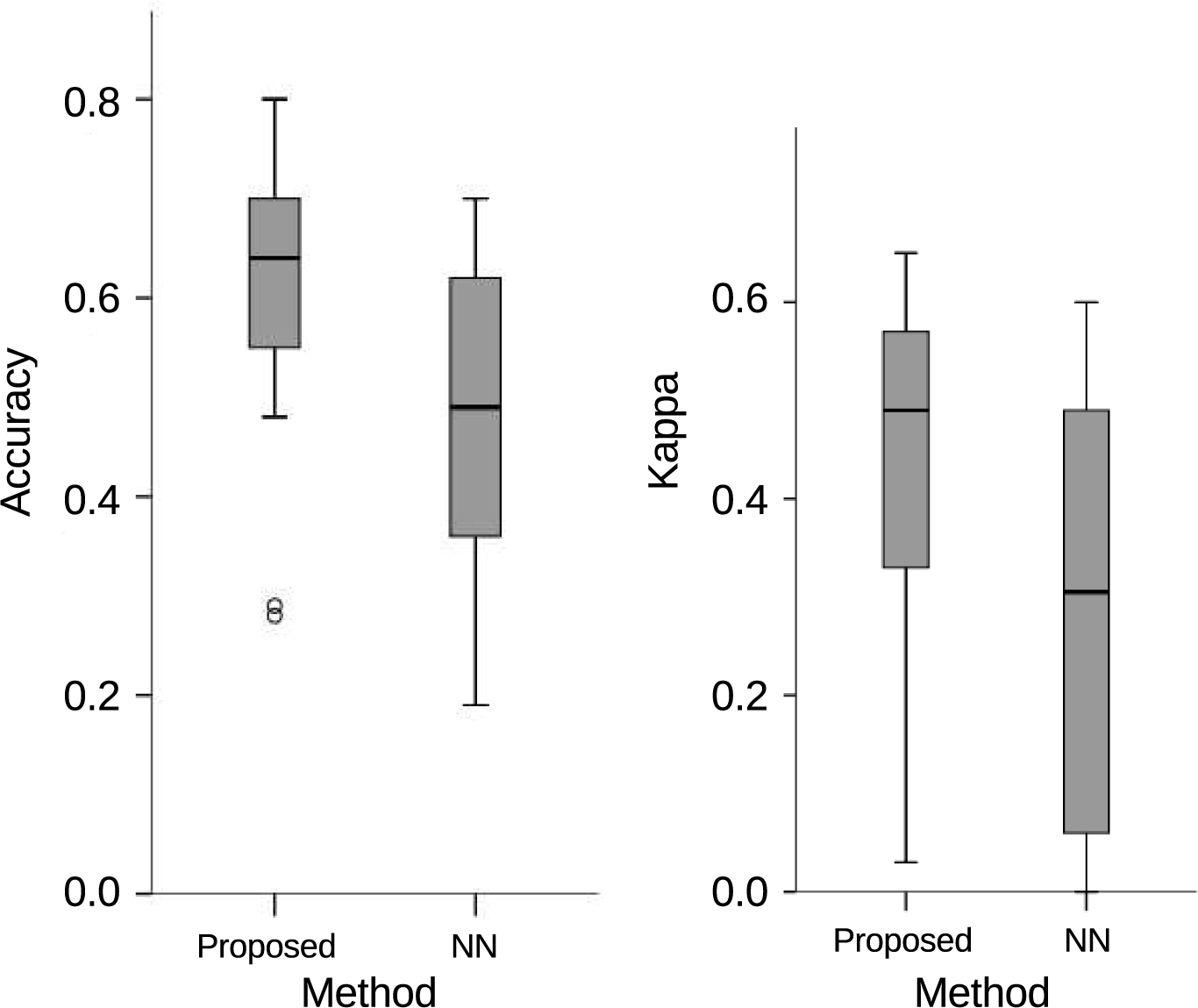
Stage	J-means		NN
	Recall	Precision	Recall	Precision
N1	0.15 (0.28)	0.14 (0.26)	0.35 (0.23)	0.42 (0.24)
N2	0.91 (0.07)	0.84 (0.07)	0.84 (0.09)	0.89 (0.10)
N3	0.59 (0.43)	0.39 (0.29)	0.43 (0.22)	0.46 (0.24)
REM	0.38 (0.44)	0.34 (0.40)	0.75 (0.26)	0.52 (0.31)
W	0.84 (0.16)	0.87 (0.10)	0.93 (0.08)	0.73 (0.18)

and

Table 2. Performance achieved depending on the specific entropy metric employed and other common features for Sleep stage detection using the method proposed. Time is normalized (1.00 corresponds to the slowest case).

Feature	Accuracy	Kappa	Time
FD	0.78 (0.06)	0.61 (0.13)	0.62 (0.04)
DFA	0.75 (0.06)	0.56 (0.14)	0.62 (0.05)
H	0.65 (0.09)	0.37 (0.12)	0.81 (0.10)
ApEn	0.74 (0.05)	0.54 (0.12)	0.56 (0.02)
SampEn	0.73 (0.06)	0.51 (0.16)	0.63 (0.04)
MSE	0.69 (0.06)	0.42 (0.13)	0.88 (0.08)
Absolute Power	0.74 (0.06)	0.53 (0.11)	1.00 (0.29)
Asymmetry	0.70 (0.07)	0.46 (0.08)	0.63 (0.03)
Central Power	0.70 (0.07)	0.47 (0.11)	0.69 (0.04)
Coherence	0.70 (0.07)	0.46 (0.12)	0.69 (0.04)
Phase Coherence	0.67 (0.08)	0.38 (0.12)	0.75 (0.04)
Power Ratios	0.80 (0.05)	0.67 (0.08)	0.75 (0.05)
Relative Power	0.77 (0.06)	0.61 (0.11)	0.69 (0.03)

, for each patient in Figure 2, and globally in Figure 3, including results from standard PCA. Table 1 shows the performance in terms of Recall (T_p/(T_p + F_n)) and Precision (T_p/(T_p + F_p)) related to each sleep stage. The parameters T_p, F_n, and F_p are the normal values used to quantify the quality of classification results: true positives, false negatives, and false positives, respectively. For comparative purposes, this table also includes the results obtained using a supervised classification approach based on Neural Networks (NN).

The method proposed exhibited comparable results to that of NN, despite being NN a supervised method (it includes labeled training patterns). The NN method outperforms the method proposed when detecting N1 and REM stages, but the opposite is found when detecting N2, N3 and REM sleep. These results support the studies that propose the use of unsupervised clustering techniques in order to address the sleep stage classification problem [35]. The performance archived by this sleep stage detection algorithm is similar (or superior) to previous results, for both supervised [23,36] and unsupervised applications [35]. Clustering methods do not depend on a previous training process, and therefore tend to be less influenced by signal differences among subjects or specific conditions [37]. The final partition groups are then scored. As an example, Figure 4 depicts a comparison between manual and automatic scoring results.

Recall and precision for sleep stages, with both classification methods, indicated better recognition of wakefulness and N2 stage (Table 1). These results are analogous to previous studies for automatic sleep stage scoring [38]. Also, results about the poor classification of N1 stage have been observed in previous inter-scorers agreement studies, specially when using the R&K rules [10,11], maybe due to the similarity of the EEG activity described between REM and drowsy states [8], stages to which electromyographic (EMG) and electrooculographic (EOG) activity are fundamental for manual classification. In further studies, the inclusion of such signals could improve the performance. In fact, some works highlight the importance of these signals in automatic classification [39]. Some approaches even used a single electrode site to discriminate among sleep stages with Kappa values up to 0.74 using a supervised neural network approach [40], although no information about the signal features was included or specifications about the classifier.

Inter-scorer agreement for sleep stages has been reported to be around 0.68 Kappa and 76.8 accuracy. Similar results have been achieved using the proposed method (Figure 3). Also, our results are comparable to those found by novel automatic classification techniques that group epochs into wakefulness, REM and NREM sleep stages [41]. In this later study the use of six polygraphic channels (including EEG, EMG and EOG) led to a Kappa value around 0.51 ± 0.14, compared to manual scoring.

In another study [42], using linear discriminant analysis and entropy measures alone, they reached sensitivity and Kappa levels up to 76% and 0.65% respectively, which were higher than the ones obtained with the same measure in this work. Nevertheless, although we use the same SampEn and embedding dimension for Multiscale Entropy, the r value was set to a fixed value of 0.2 instead of including the standard deviation, which could account for the result difference.

In Table 2, the results are shown as the accuracy level ((T_p + T_n)/(T_p + F_n + T_n + F_p)), Kappa statistic [43], and normalized computing time. These results are listed as a function of the specific entropy metric used for feature extraction: FD, DFA, H, ApEn, SampEn, and MSE. Although the results are quite similar both in terms of accuracy and computational cost, ApEn seems to reach an optimal tradeoff between these two issues, and FD yields the most accurate results. On the contrary, H and MSE offer a poorer performance, and should be discarded in favor of other entropy metrics.

Table 2 also shows the results achieved using the same method proposed in this paper, but computing classical features employed in most of the similar sleep stages studies instead of entropy metrics: the absolute power, power asymmetry, central power, coherence, phase coherence, power ratios, and relative power. Examples of application of these features and more details about them can be found in [36,44,45]. The classification results are similar to those obtained with the entropy metrics. Only the features based on the Power Ratios seem to outperform the previous results, but at a significantly higher computational cost. In fact, the main strength of the entropy features seems to be a general lower computational cost, with equal or even better accuracy.

In addition, the relevance analysis does not significantly appear to harm the classification performance of the method, as shown in Figure 3. The three cases tested: using all the raw features extracted, reducing the number of features using a standard feature selection method based on PCA, or the proposed relevance analysis method, yield a similar performance for Kappa and Accuracy. Furthermore, the NN method seems to be more sensitive to the feature selection stage, and in most of these experiment variants, the new method still outperforms NN.

This method has a very important novelty, which is using a non-supervised approach. Usually, this kind of methods perform worse than supervised ones since they do not have as much carefully selected input information and user feedback as these last have. The method proposed, not only does not underperform in comparison to supervised methods, but even exhibits a slightly better performance. It improves the classification accuracy, but also exhibits faster calculations when the features selected were based on entropy estimators. Maybe the improvement is not very big in quantitative terms, but from the implementation point of view, this method can be more easily introduced in daily clinical practice since required user feedback is minimized. This method reaches a trade-off between being accurate enough as supervised methods, but requiring far less user intervention, the main advantage of unsupervised methods.

The sleeping brain has been described as a complex system with continuous, rather than discrete, transitions [46]. To study similarity of stages among subjects, the proposed method was applied to the whole set of subjects merged into a single matrix of 40,826 epochs by 56 relevant features.

With this method, a low similarity between subjects was found, specially in stages N1 and REM sleep. The low recall and precision values for these stages could be due to intra-subjects variability in the EEG signals, as described in [47,48]. Furthermore, these results are consistent with previous reports that suggest a significant EEG similarity between these stages [8], reflected in low discrimination values for both automatic classification [42,49] or inter-scorer agreement [11].

The global clustering time using PCA (0.30 ± 0.16 s) or the proposed Q-α optimization (0.20 ± 0.11 s) are lower than that needed for the complete set of features (0.69 ± 0.44 s). Therefore, the method proposed reduces considerably the computation time needed for an unsupervised sleep stage classification, while preserving the relevant features, and therefore, the accuracy [17]. Hence, the Q-α relevance analysis can be recommended as a competitive clustering technique for sleep stage classification, along with an FD, ApEn, or Power Ratio feature extraction method.

The performance was further validated using a different experimental database. It is also available at Physionet from a study of temazepam effects on sleep [19,50]. It contains 22 sleep files of male and female subjects (aged 18 to 79) sampled at 100 Hz. Half of the records were from subjects that took temazepam before going to sleep.

These additional results show a reduction of accuracy and Kappa values (Figure 5). This could be due to the greater subject variability in this dataset. For instance, age range and temazepam have different effects on sleep EEG dynamics [51]. However, this reduction is higher with the NN approach compared to the proposed one. The resulting confusion matrix is presented in

Table 3. Confusion matrix for the automatic procedure computing the whole set of 40,826 epochs for all the patients together to test inter-subject variability.

		Prediction outcome
		W	N1	N2	N3	REM
Actual value	W	3333	2046	1074	21	329
	N1	177	1082	624	39	882
	N2	884	915	8155	1198	6647
	N3	42	69	1539	4255	400
	REM	484	1017	1738	25	3851

.

4. Conclusions

This paper describes a new method to automatically detect sleep stages on EEG records, which is of great medical and social interest. This method proposes to use entropy metrics as the features of the EEG epochs to be analyzed, and also introduces a feature selection stage to reduce the algorithm cost.

The core of the method is the so-called Q-α relevance analysis. This method has been successfully used in similar applications to ECG signals [17], and it is exported in this work to the new field of EEG relevant feature selection. The reduction of the number of features is confirmed not to damage the performance of the method, keeping the segmentation capability almost intact, as should be expected.

The study explores the capabilities of a plurality of entropy metrics for comparative purposes. The results confirm the validity of the approach, from which it can be concluded that almost any metric could perform satisfactorily, specially ApEn and FD.

The experiments were repeated using more classical methods in this field such as NN. Furthermore, the feature extraction stage was also replaced by a standard stage based on other signal parameters. In all cases, the performance of the new method was at least as accurate as the references assessed, or even more on most cases, but at a low computational cost, and being an unsupervised method (no user intervention needed).

Most elements of the proposed method are already implemented in a MATLAB^® library called EEGLAB, an open source tool for assisted sleep staging. This software application was previously presented in [52].

Current efforts in most entropy-based EEG studies are still mainly focused on the identification of certain patterns (such as seizure detection [53]). Other works employ entropy as a metric for diagnostic purposes, to discriminate among subjects with neural alterations (citeGarn2014 Bachiller2014. Our results, in addition to proposing a suitable method for automatic sleep stages detection, also suggest a differential effect of sleep stages on EEG entropy features. These results have been also supported by studies of anesthesia depth [54]. EEG features are also very important to understand sleep dynamics. A comparison of the entropy features among sleep stages, along with an analysis of the significance or meaning of this kind of features, is still object of research work.

In summary, we proposed in this paper a method to classify sleep stages based on computing entropy metrics of EEG records, optimizing the resulting set using a relevance analysis, and including a clustering algorithm to obtain the final partition. Such a method exhibits better flexibility and adaptability in comparison to other supervised methods. It also reduces the computational cost, which is very important, taking into account the impending electronic health record explosion.