Ab intio Investigation of the Thermochemistry and Kinetics of the SO2 + O3− → SO3− + O2 Reaction in Aircraft Engines and the Environment
Abstract
:1. Introduction
2. Methods
3. Result and Discussion
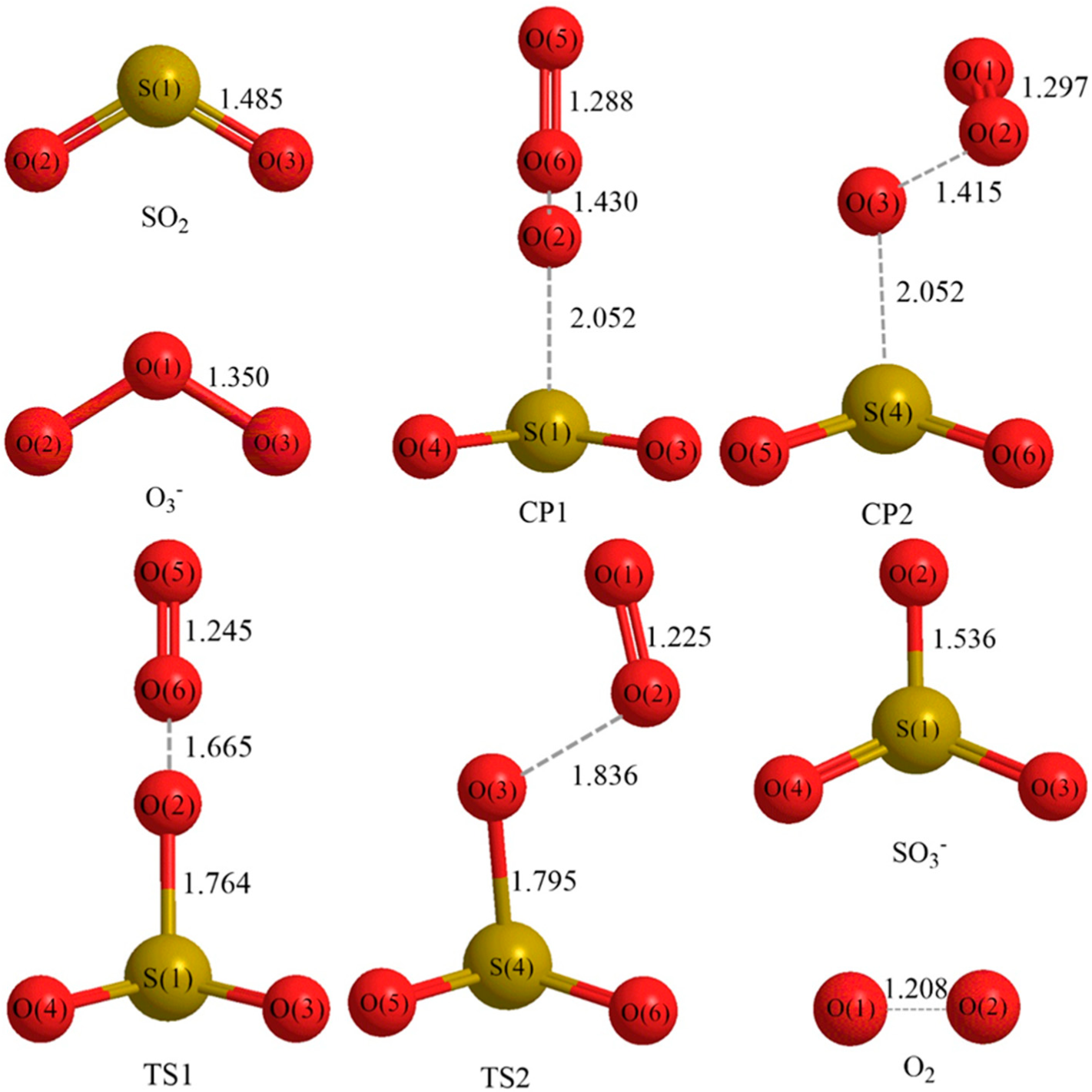
3.1. Reaction Mechanism
3.2. Thermochemical Analysis
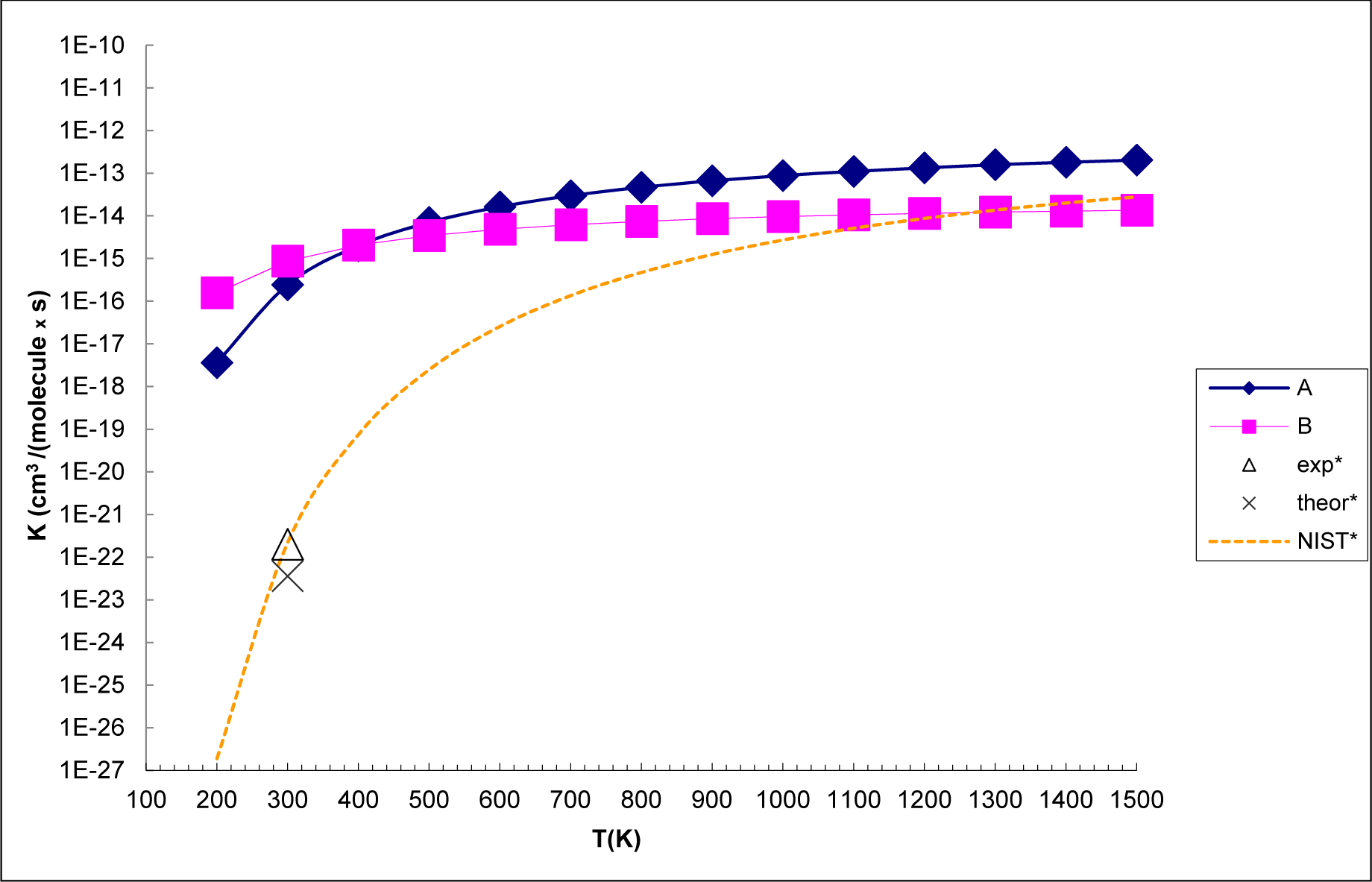
3.3. Reaction Kinetics
4. Conclusions
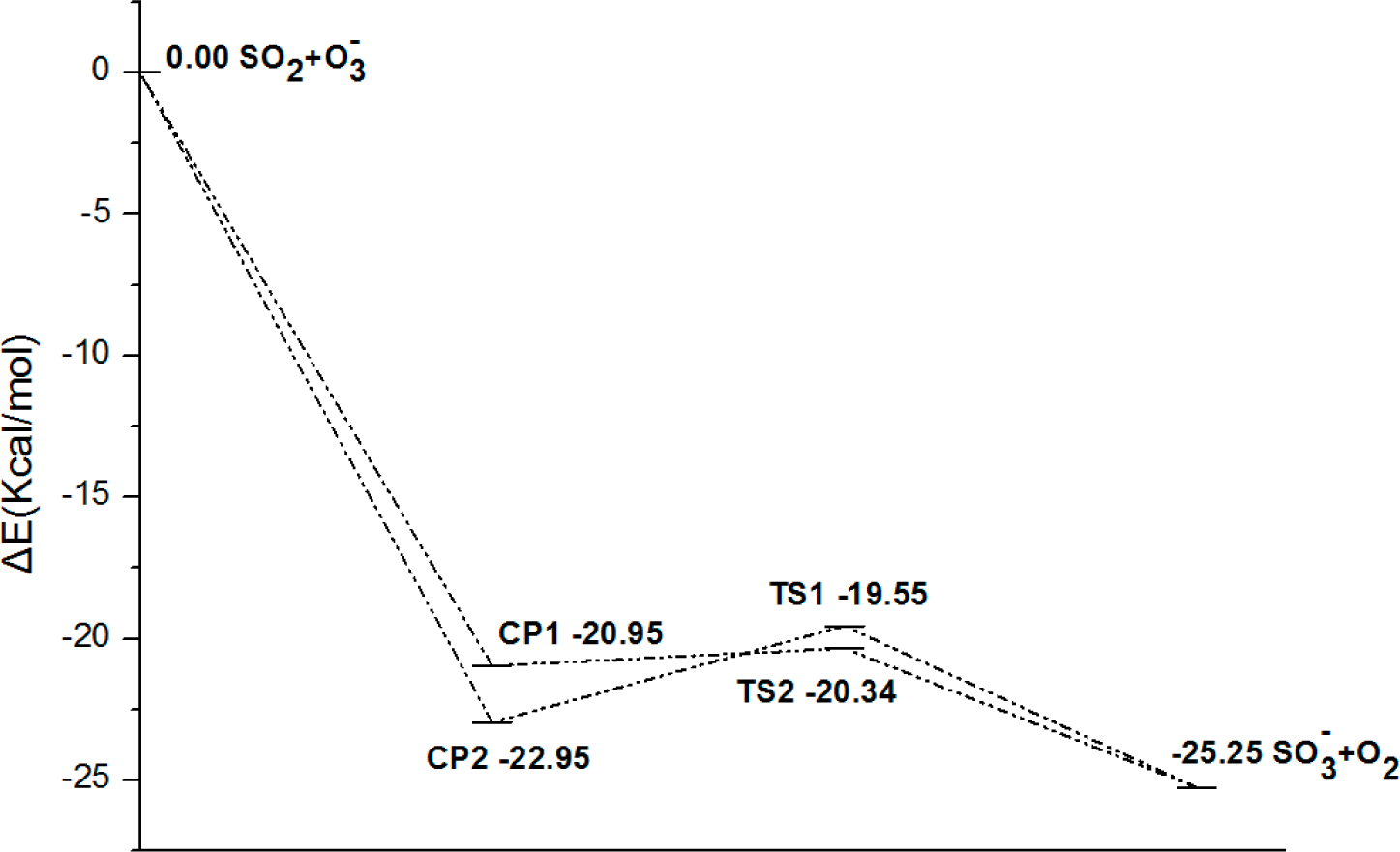
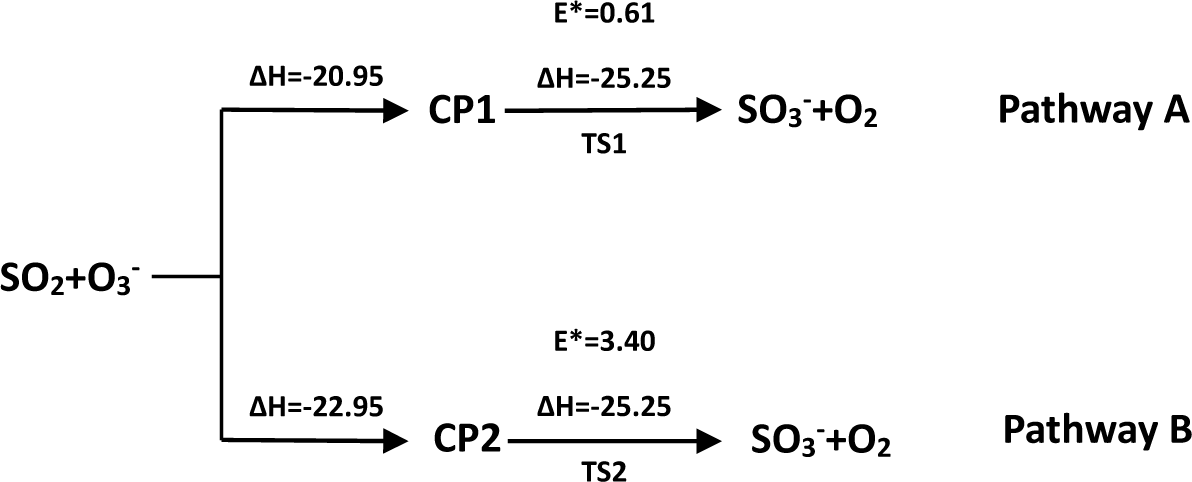
- There exist two pathways of the SO2 + O3− → SO3− + O2 reaction, pathway A and pathway B. The reaction energy is −25.25 kcal mol−1, while the activation energies for pathways A and B are 0.61 kcal mol−1 and 3.40 kcal mol−1, respectively. It is also important to note that while ab initio and ab initio-based methods predict the reaction energy in very good agreement with each other, both B3LYP/6-31G(d) and B3LYP/6-311++G(3df,2pd) underestimate the reaction energy by 6–10 kcal mol−1.
- The analysis of the reaction kinetics shows clearly that while the rate constants for pathways A and B, KA = 1.11 × 10−12exp(−2526.13/T) and KB = 2.7 × 10−14exp(−1029.25/T), differ by a factor of 2–10 only, pathway A dominates over the pathway B over the whole range of temperatures typical for aircraft engines (600–1500 K). However, at lower temperatures typical for the Earth’s atmosphere the pathway B dominates over the pathway A.
- The rate constants for both pathway A and pathway B grow with the temperature. This means that the high temperature zones, which are located near the combustor, are the sites, where most of the SO2 to SO3− conversion in the aircraft engines occurs.
- The SO2 + O3 → SO3 + O2 reaction energy [34] is close to that the energy of the SO2 + O3− → SO3− + O2 obtained in the present study. However, the barrier of the SO2 + O3 → SO3 + O2 reaction is by 9 kcal mol−1 higher than that of SO2 + O3− → SO3− + O2 reaction. This shows clearly that the O3 charging greatly reduces the barrier of the reaction of SO2 with ozone. The rate constants for the SO2 + O3− → SO3− + O2 reaction at atmosphere temperatures are much larger than those obtained by Davis et al. [32] (2 × 10−22 cm3 molecule−1 s−1 at T = 300 K) and Jiang et al. [43] (3.61 × 10−23 cm3 molecule−1 s− at T = 300 K) for the SO2 + O3 → SO3 + O2 reaction.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, R. Getting to the critical nucleus of aerosol formation. Science 2010, 328, 1366–1367. [Google Scholar]
- Almeida, J.; Schobesberger, S.; Kürten, A.; Ortega, I.K.; Kupiainen-Määttä, O.; Praplan, A.P.; Adamov, A.; Amorim, A.; Bianchi, F.; Breitenlechner, M.; et al. Molecular understanding of sulphuric acid-amine particle nucleation in the atmosphere. Nature 2013, 502, 359–363. [Google Scholar]
- Zhang, R.; Khalizov, A.F.; Wang, L.; Hu, M.; Wen, X. Nucleation and growth of nanoparticles in the atmosphere. Chem. Rev 2012, 112, 1957–2011. [Google Scholar]
- Yu, F.; Luo, G. Simulation of particle size distribution with a global aerosol model: Contribution of nucleation to aerosol and CCN number concentrations. Atmos. Chem. Phys 2009, 9, 7691–7710. [Google Scholar]
- Sipila, M.; Berndt, T.; Petaja, T.; Brus, D.; Vanhanen, J.; Stramann, F.; Patokoski, J.; Mauldin, R.L., III; Hyvarinen, A.-P.; Lihavainen, H.; et al. The role of sulfuric acid in atmospheric nucleation. Science 2010, 327, 1243–1246. [Google Scholar]
- Knaapen, A.M.; Borm, P.J.; Albrecht, C.; Schins, R.P. Inhaled particles and lung cancer. Part A: Mechanisms. Int. J. Cancer 2004, 109, 799–809. [Google Scholar]
- Saxon, A.; Diaz-Sanchez, D. Air pollution and allergy: You are what you breathe. Nature Immunol 2005, 6, 223–226. [Google Scholar]
- Zhang, R.; Suh, I.; Zhao, J.; Zhang, D.; Fortner, E.C.; Tie, X.; Molina, L.T.; Molina, M.J. Atmospheric new particle formation enhanced by organic acids. Science 2004, 304, 1487–1490. [Google Scholar]
- Xu, Y.; Nadykto, A.B.; Yu, F.; Jiang, L.; Wang, W. Formation and properties of hydrogen-bonded complexes of common organic oxalic acid with atmospheric nucleation precursors. J. Mol. Struct 2010, 951, 28–33. [Google Scholar]
- Xu, W.; Zhang, R. A theoretical study of hydrated molecular clusters of amines and dicarboxylic acids. J. Chem. Phys 2013, 139. [Google Scholar] [CrossRef]
- Xu, Y.; Nadykto, A.B.; Yu, F.; Herb, J.; Wang, W. Interaction between common organic acids and trace nucleation species in the earth’s atmosphere. J. Phys. Chem. A 2009, 114, 387–396. [Google Scholar]
- Kurten, T.; Loukonen, V.; Vehkamaki, H.; Kulmala, M. Amines are likely to enhance neutral and ion-induced sulfuric acid-water nucleation in the atmosphere more effectively than ammonia. Atmos. Chem. Phys 2008, 8, 4095–4103. [Google Scholar]
- Nadykto, A.B.; Yu, F.; Yakovleva, M.; Herb, J.; Xu, Y. Amines in the earth’s atmosphere: A DFT study of the thermochemistry of pre-nucleation clusters. Entropy 2011, 13, 554–569. [Google Scholar]
- Nadykto, A.B.; Herb, J.; Yu, F.; Xu, Y. Enhancement in the production of nucleating clusters due to dimethylamine and large uncertainties in the thermochemistry of amine-enhanced nucleation. Chem. Phys. Lett 2014, 609, 42–19. [Google Scholar]
- Yu, F.; Turco, R.P. From molecular clusters to nanoparticles: The role of ambient ionization in tropospheric aerosol formation. J. Geophys. Res 2001, 106, 4797–4814. [Google Scholar]
- Laaksonen, A.; Pirjola, L.; Kulmala, M.; Wohlfrom, K.-H.; Arnold, F.; Raes, F. Upper tropospheric SO2 conversion into sulfuric acid aerosols and cloud condensation nuclei. J. Geophys. Res. Atmos 2000, 105, 1459–1469. [Google Scholar]
- Liao, H.; Zhang, Y.; Chen, W.-T.; Raes, F.; Seinfeld, J.H. Effect of chemistry-aerosol-climate coupling on predictions of future climate and future levels of tropospheric ozone and aerosols. J. Geophys. Res 2009, 114. [Google Scholar] [CrossRef]
- Rowland, F.S. Stratospheric ozone depletion. Phil. Trans. R. Soc. Lond. B 2006, 361, 769–790. [Google Scholar]
- Fenger, J. Air pollution in the last 50 years—From local to global. Atmos. Environ 2009, 43, 13–22. [Google Scholar]
- Lelieveld, J.; Butler, T.M.; Crowley, J.N.; Dillon, T.J.; Fischer, H.; Ganzeveld, L.; Harder, H.; Lawrence, M.G.; Martinez, M.; Taraborrelli, D.; Williams, J. Atmospheric oxidation capacity sustained by a tropical forest. Nature 2008, 452, 737–740. [Google Scholar]
- Brown, R.C.; Anderson, M.R.; Miake-Lye, R.C.; Kolb, C.E.; Sorokin, A.A.; Buriko, Y.Y. Aircraft exhaust sulfur emissions. Geophys. Res. Lett 1996, 23, 3603–3606. [Google Scholar]
- Fialkov, A.B. Investigations on ions in flames. Prog. Energy Combust. Sci 1997, 23, 399–528. [Google Scholar]
- Lifshitz, C.; Wu, R.; Tiernan, T.; Terwilliger, D. Negative ion-molecule reactions of ozone and their implications on the thermochemistry of O3−. J. Chem. Phys 1978, 68, 247–260. [Google Scholar]
- Fehsenfeld, F.; Schmeltekopf, A.; Schiff, H.; Ferguson, E. Laboratory measurements of negative ion reactions of atmospheric interest. Planet. Space Sci 1967, 15, 373–379. [Google Scholar]
- Maahs, H.G. Measurements of the oxidation rate of sulfur (IV) by ozone in aqueous solution and their relevance to SO2 conversion in nonurban tropospheric clouds. Atmos. Environ. (1967) 1983, 17, 341–345. [Google Scholar]
- Möller, D. Kinetic model of atmospheric SO2 oxidation based on published data. Atmos. Environ. (1967) 1980, 14, 1067–1076. [Google Scholar]
- Bork, N.; Loukonen, V.; Vehkamäki, H. Reactions and reaction rate of atmospheric SO2 and O3−(H2O)n collisions via molecular dynamics simulations. J. Phys. Chem. A 2013, 117, 143–3148. [Google Scholar]
- Bork, N.; Kurtén, T.; Enghoff, M.B.; Pedersen, J.O.P.; Mikkelsen, K.V.; Svensmark, H. Structures and reaction rates of the gaseous oxidation of SO2 by an O3–(H2O)0–5 cluster—A density functional theory investigation. Atmos. Chem. Phys 2012, 12, 3639–3652. [Google Scholar]
- Bork, N.; Kurtén, T.; Vehkamäki, H. Exploring the atmospheric chemistry of O2SO3−; and assessing the maximum turnover number of ion-catalysed H2SO4 formation. Atmos. Chem. Phys 2013, 13, 3695–3703. [Google Scholar]
- Hoffmann, M.R. On the kinetics and mechanism of oxidation of aquated sulfur dioxide by ozone. Atmos. Environ. (1967) 1986, 20, 1145–1154. [Google Scholar]
- Mok, Y.S.; Lee, H.-J. Removal of sulfur dioxide and nitrogen oxides by using ozone injection and absorption-reduction technique. Fuel Process. Technol 2006, 87, 591–597. [Google Scholar]
- Davis, D.; Prusazcyk, J.; Dwyer, M.; Kim, P. Stop-flow time-of-flight mass spectrometry kinetics study. Reaction of ozone with nitrogen dioxide and sulfur dioxide. J. Phys. Chem 1974, 78, 1775–1779. [Google Scholar]
- Schumann, U.; Arnold, F.; Busen, R.; Curtius, J.; Kärcher, B.; Kiendler, A.; Petzold, A.; Schlager, H.; Schröder, F.; Wohlfrom, K.H. Influence of fuel sulfur on the composition of aircraft exhaust plumes: The experiments SULFUR 1–7. J. Geophys. Res. Atmos. (1984–2012) 2002, 107, 1–27. [Google Scholar]
- Starik, A.M.; Savel’ev, A.M.; Titova, N.S.; Schumann, U. Modeling of sulfur gases and chemiions in aircraft engines. Aerosp. Sci. Technol 2002, 6, 63–81. [Google Scholar]
- Ferguson, E.E. Negative ion-molecule reactions. Can. J. Chem 1969, 47, 1815–1820. [Google Scholar]
- Mok, Y.S.; Lee, H.-J. Removal of sulfur dioxide and nitrogen oxides by using ozone injection and absorption-reduction technique. Fuel Process. Technol 2006, 87, 591–597. [Google Scholar]
- Torrent-Sucarrat, M.; Francisco, J.S.; Anglada, J.M. Sulfuric acid as autocatalyst in the formation of sulfuric acid. J. Am. Chem. Soc 2012, 134, 20632–20644. [Google Scholar]
- Morokuma, K.; Muguruma, C. Ab initio molecular orbital study of the mechanism of the gas phase reaction SO3 + H2O: Importance of the second water molecule. J. Am. Chem. Soc 1994, 116, 10316–10317. [Google Scholar]
- Long, B.; Chang, C.R.; Long, Z.W.; Wang, Y.B.; Tan, X.F.; Zhang, W.J. Nitric acid catalyzed hydrolysis of SO3 in the formation of sulfuric acid: A theoretical study. Chem. Phys. Lett 2013, 581, 26–29. [Google Scholar]
- Gonzalez, J.; Torrent-Sucarrat, M.; Anglada, J.M. The reactions of SO3 with HO2 radical and H2O…HO2 radical complex. Theoretical study on the atmospheric formation of HSO5 and H2SO4. Phys. Chem. Chem. Phys 2010, 12, 2116–2125. [Google Scholar]
- Hazra, M.K.; Sinha, A. Formic acid catalyzed hydrolysis of SO3 in the gas phase: A barrierless mechanism for sulfuric acid production of potential atmospheric importance. J. Am. Chem. Soc 2011, 133, 17444–17453. [Google Scholar]
- Long, B.; Long, Z.W.; Wang, Y.B.; Tan, X.F.; Han, Y.; Long, C.; Qin, S.; Zhang, W. Formic acid catalyzed the gas phase reaction of H2O with SO3 and its reverse reaction: A theoretical study. Phys. Chem 2012, 13, 323–329. [Google Scholar]
- Jiang, S.-D.; Wang, Z.-H.; Zhou, J.-H.; Wen, Z.-C.; Cen, K.-F. A quantum chemistry study on reaction mechanisms of SO2 with O3 and H2O2. J. Zhejiang Univ. Sci. A 2009, 10, 1327–1333. [Google Scholar]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Montgomery, J., Jr; Vreven, T.; Kudin, K.; Burant, J. Gaussian 03, Revision E. 01; Gaussian Inc: Wallingford, CT, USA, 2004. [Google Scholar]
- Zhao, J.; Zhang, R. A theoretical investigation of nitrooxyalkyl peroxy radicals from NO3-initiated oxidation of isoprene. Atmos. Environ 2008, 42, 5849–5858. [Google Scholar]
- Suh, I.; Zhao, J.; Zhang, R. Unimolecular ring-cleavage of aromatic bicyclic alkoxy radicals. Chem. Phys. Lett 2006, 432, 313–320. [Google Scholar]
- Fan, J.; Zhao, J.; Zhang, R. Theoretical study of OH addition to α- and β-pinenes. Chem. Phys. Lett 2005, 411, 1–7. [Google Scholar]
- Zhang, D.; Zhang, R. Ozonolysis mechanisms of α- and β-pienes: Kinetics and mechanism. J. Chem. Phys 2005, 122, 1–12. [Google Scholar]
- Suh, I.; Zhang, R.; Molina, L.T.; Molina, M.J. Oxidation mechanism of aromatic peroxy and bicyclic radicals from OH-toluene reactions. J. Am. Chem. Soc 2003, 125, 12655–12665. [Google Scholar]
- Zhang, D.; Zhang, R.; Park, J.; North, S.W. Hydroxyperoxy nitrites and nitrates from OH initiated reactions of isoprene. J. Am. Chem. Soc 2002, 124, 9600–9605. [Google Scholar]
- Jiang, L.; Wang, W.; Xu, Y. Ab initio investigation of O3 addition to double bonds of limonene. Chem. Phys 2010, 368, 108–112. [Google Scholar]
- Lei, W.; Derecskei-Kovacs, A.; Zhang, R. Ab initio study of OH addition reaction to isoprene. J. Chem. Phys 2000, 113, 5354–5360. [Google Scholar]
- Zhang, D.; Zhang, R. Mechanism of OH formation from ozonolysis of isoprene: A quantum-chemical study. J. Am. Chem. Soc 2002, 124, 2692–2703. [Google Scholar]
- Fukui, K. The path of chemical reactions—the IRC approach. Acc. Chem. Res 1981, 14, 363–368. [Google Scholar]
- Qu, X.; Wang, H.; Zhang, Q.; Shi, X.; Xu, F.; Wang, W. Mechanistic and kinetic studies on the homogeneous gas-phase formation of PCDD/Fs from 2, 4, 5-trichlorophenol. Environ. Sci. Technol 2009, 43, 4068–4075. [Google Scholar]
- Zhang, Q.; Li, S.; Qu, X.; Shi, X.; Wang, W. A quantum mechanical study on the formation of PCDD/Fs from 2-chlorophenol as precursor. Environ. Sci. Technol 2008, 42, 7301–7308. [Google Scholar]
- Corchado, J.C.; Chuang, Y.-Y.; Fast, P.L.; Hu, W.; Liu, Y.; Lynch, G.; Nguyen, K.; Jackels, C.; Ramos, A.F.; Ellingson, B. POLYRATE, version 9.7; Computer Program for the Calculation of Chemical Reaction Rates for Polyatomics; University of Minnesota: Minneapolis, MN, USA, 2007. [Google Scholar]
- National Institute for Standards and Technology (NIST). Chemical Kinetics Database on the Web, Standard Reference Database 17. 2008. Available online: http://kinetics.nist.gov/kinetics/Detail?id=1997DEM/SAN1-266:385 (accessed on 17 November 2014).
| Method | REcp1 | REcp2 | ΔE1 | ΔE2 | RE |
|---|---|---|---|---|---|
| MP2/6-31G(d) | −24.64 | −26.23 | 2.66 | 10.17 | −28.90 |
| B3LYP/6-31G(d) | −36.38 | −37.33 | 1.48 | 12.17 | −18.65 |
| B3LYP/6-311++G(3df,2pd) | −26.59 | −28.25 | 1.37 | 11.71 | −17.77 |
| CCSD(T)/6-31G(d) | −30.75 | −32.03 | 0.72 | 3.86 | −26.13 |
| CCSD(T)/6-31G(d)+CF | −20.95 | −22.95 | 0.61 | 3.40 | −25.25 |
| G2M a | – | – | 9.68 | – | −27.45 |
| Pathway | CCSD(T)/ 6-31G(d) | CCSD(T)/ 6-31G(d)+CF | CCSD(T)/ 6-311G(d,p) | QCISD(T)/ 6-311G(d,p) |
|---|---|---|---|---|
| A | 0.72 | 0.61 | 2.41 | 2.30 |
| B | 3.86 | 3.40 | 2.53 | 4.37 |
| T(K) | Pathway A (cm3 mol−1 s−1) | Pathway B (cm3 mol−1 s−1) |
|---|---|---|
| 200 | 3.63 × 10−18 | 1.57 × 10−16 |
| 300 | 2.45 × 10−16 | 8.74 × 10−16 |
| 400 | 2.07 × 10−15 | 2.06 × 10−15 |
| 500 | 7.60 × 10−15 | 3.45 × 10−15 |
| 600 | 2.04 × 10−14 | 5.51 × 10−15 |
| 700 | 2.98 × 10−14 | 6.21 × 10−15 |
| 800 | 4.21 × 10−14 | 6.99 × 10−15 |
| 900 | 5.78 × 10−14 | 7.85 × 10−15 |
| 1000 | 7.74 × 10−14 | 8.81 × 10−15 |
| 1100 | 1.01 × 10−13 | 9.89 × 10−15 |
| 1200 | 1.30 × 10−13 | 1.11 × 10−14 |
| 1300 | 1.65 × 10−13 | 1.24 × 10−14 |
| 1400 | 2.05 × 10−13 | 1.39 × 10−14 |
| 1500 | 2.52 × 10−13 | 1.56 × 10−14 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Nadykto, A.B.; Xu, Y.; Zhang, Q.; Hu, J. Ab intio Investigation of the Thermochemistry and Kinetics of the SO2 + O3− → SO3− + O2 Reaction in Aircraft Engines and the Environment. Entropy 2014, 16, 6300-6312. https://doi.org/10.3390/e16126300
Guo X, Nadykto AB, Xu Y, Zhang Q, Hu J. Ab intio Investigation of the Thermochemistry and Kinetics of the SO2 + O3− → SO3− + O2 Reaction in Aircraft Engines and the Environment. Entropy. 2014; 16(12):6300-6312. https://doi.org/10.3390/e16126300
Chicago/Turabian StyleGuo, Xuechao, Alexey B. Nadykto, Yisheng Xu, Qingzhu Zhang, and Jingtian Hu. 2014. "Ab intio Investigation of the Thermochemistry and Kinetics of the SO2 + O3− → SO3− + O2 Reaction in Aircraft Engines and the Environment" Entropy 16, no. 12: 6300-6312. https://doi.org/10.3390/e16126300
APA StyleGuo, X., Nadykto, A. B., Xu, Y., Zhang, Q., & Hu, J. (2014). Ab intio Investigation of the Thermochemistry and Kinetics of the SO2 + O3− → SO3− + O2 Reaction in Aircraft Engines and the Environment. Entropy, 16(12), 6300-6312. https://doi.org/10.3390/e16126300




