Energy Analysis and Multi-Objective Optimization of an Internal Combustion Engine-Based CHP System for Heat Recovery
Abstract
:1. Introduction
- Model the diesel based CHP system
- Perform energy and exergy analyses and an environmental impact assessment of the system
- Determine the exergy efficiency and exergy destruction rate of each component
- Apply an optimization technique based on a code developed in the Matlab software
- Propose a new closed-form expression relating the exergy efficiency and total cost rate
- Develop an equation for the Pareto optimal points curve to provide an aid for the optimal design of the multi-generation plant
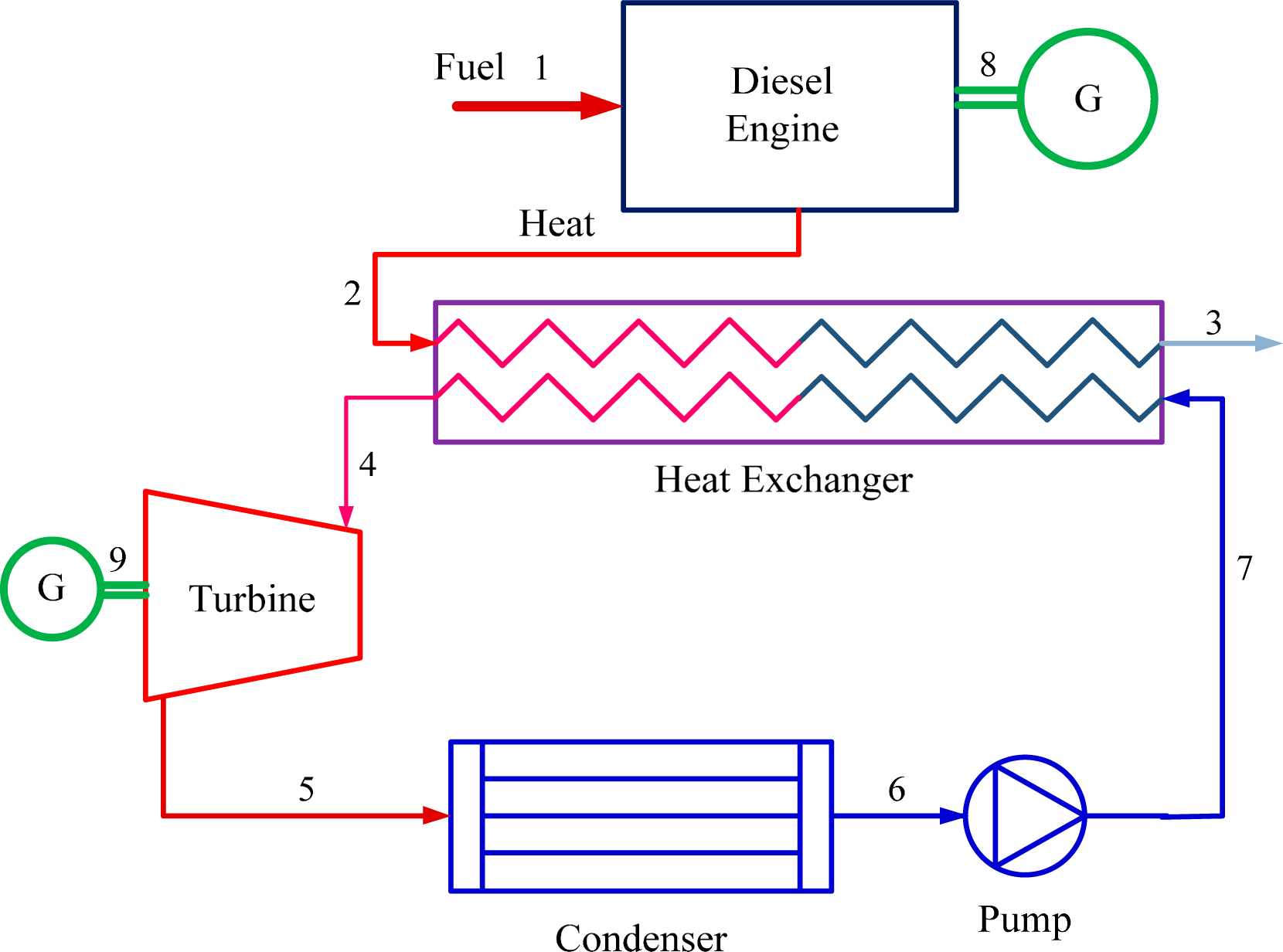
2. System Description
3. Modeling and Energy Analysis
- All processes operate at steady state
- The condenser outlet state is a saturated liquid, and its temperature is assumed to be approximately 5 °C higher than the environment temperature
- The working fluid at the evaporator outlet is a saturated vapor
- The pressure drop in the ORC cycle is negligible
- The heat loss from piping and other auxiliary components is negligible
3.1. Diesel Engine
3.2. ORC Cycle
- Heat Exchanger (evaporator)
- ORC Turbine
- ORC Condenser
- ORC Pump
4. Exergy Analysis
5. Multi-Objective Optimization
5.1. Definition of Objectives
- Exergy EfficiencyFirst objective function is selected as the exergy efficiency of the cycle. The calculation of exergy efficiency is shown in Equation (15).
- Total Cost Rate
5.2. Decision Variables
5.3. Evolutionary Algorithm: Genetic Algorithm
6. Results and Discussion
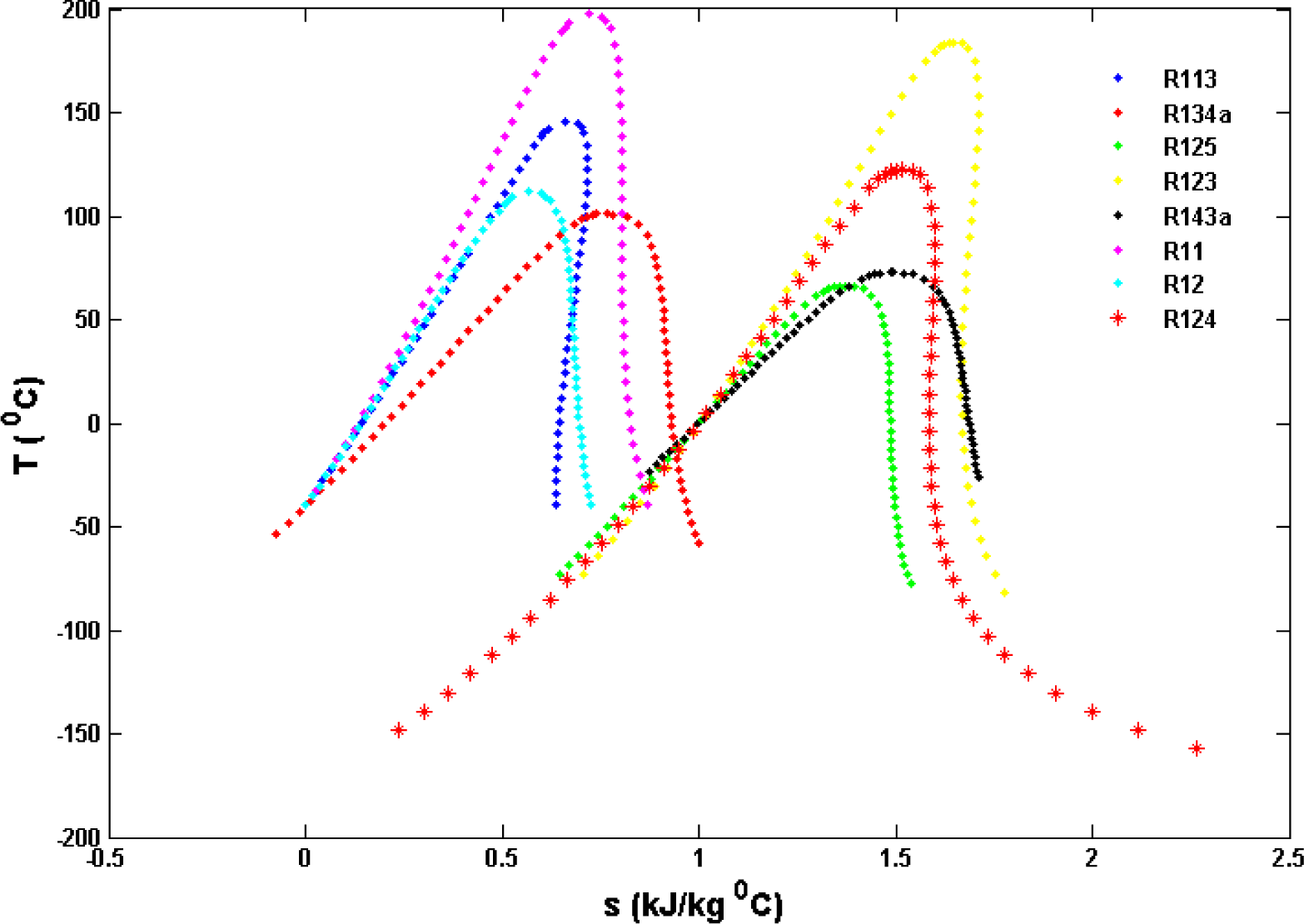
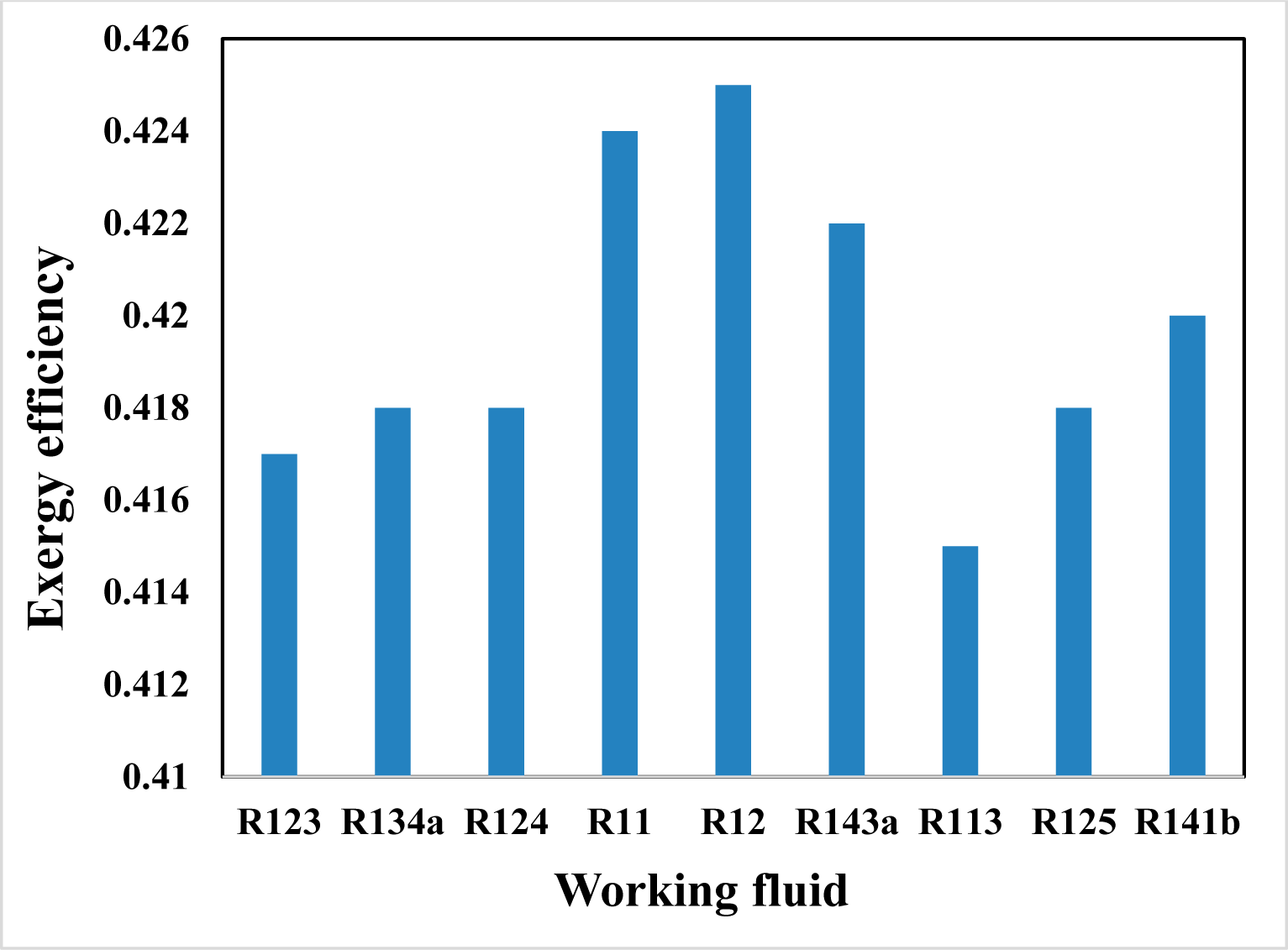
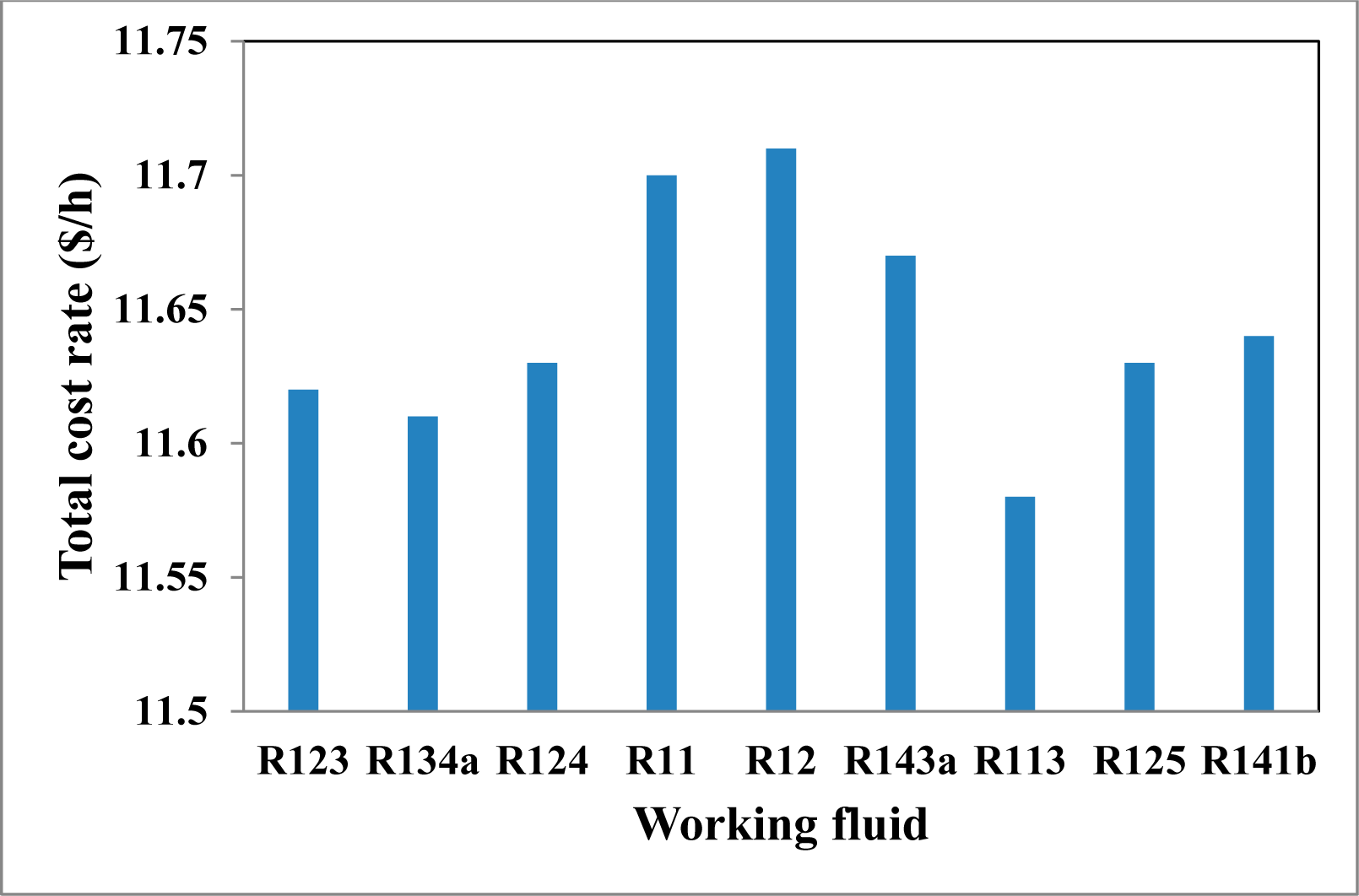
6.1. Working Fluid Selection
6.2. Exergy Analysis Results
6.3. Multi-Objective Optimization Results
7. Conclusions
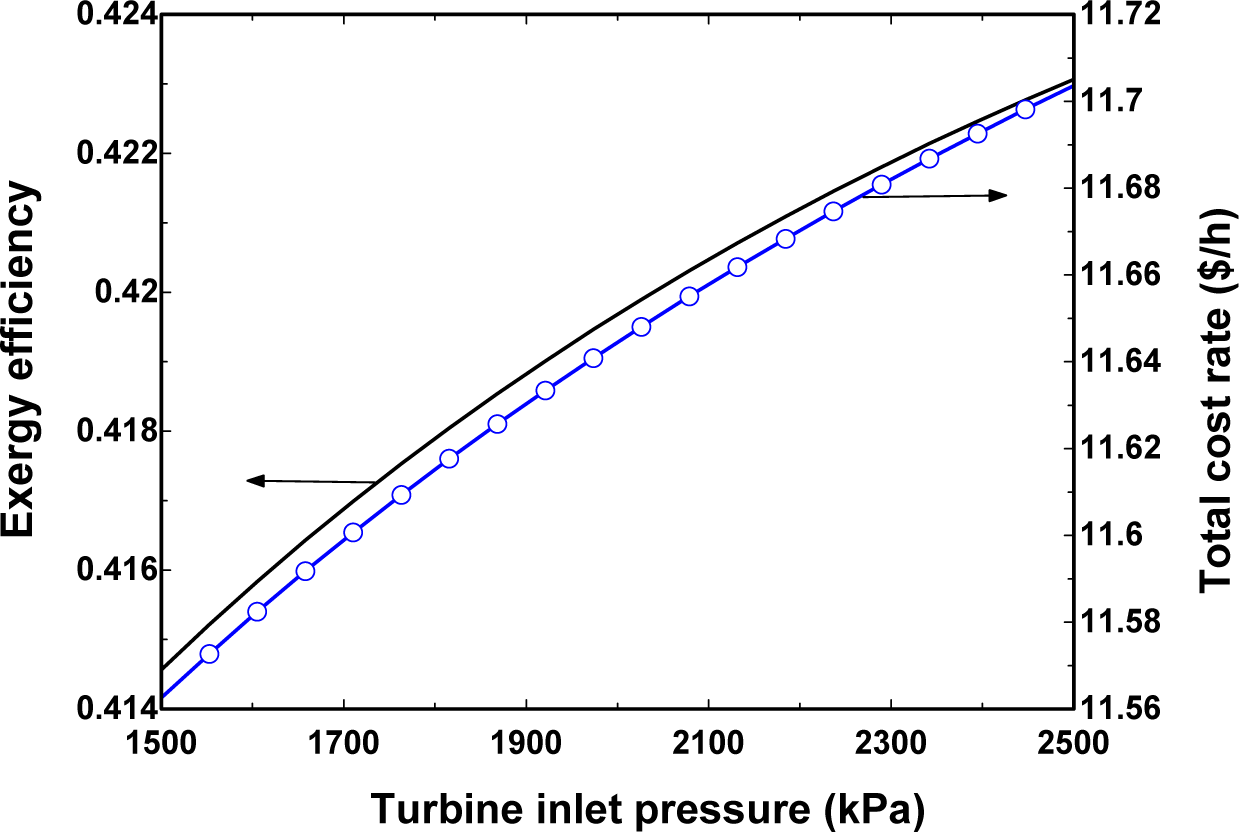
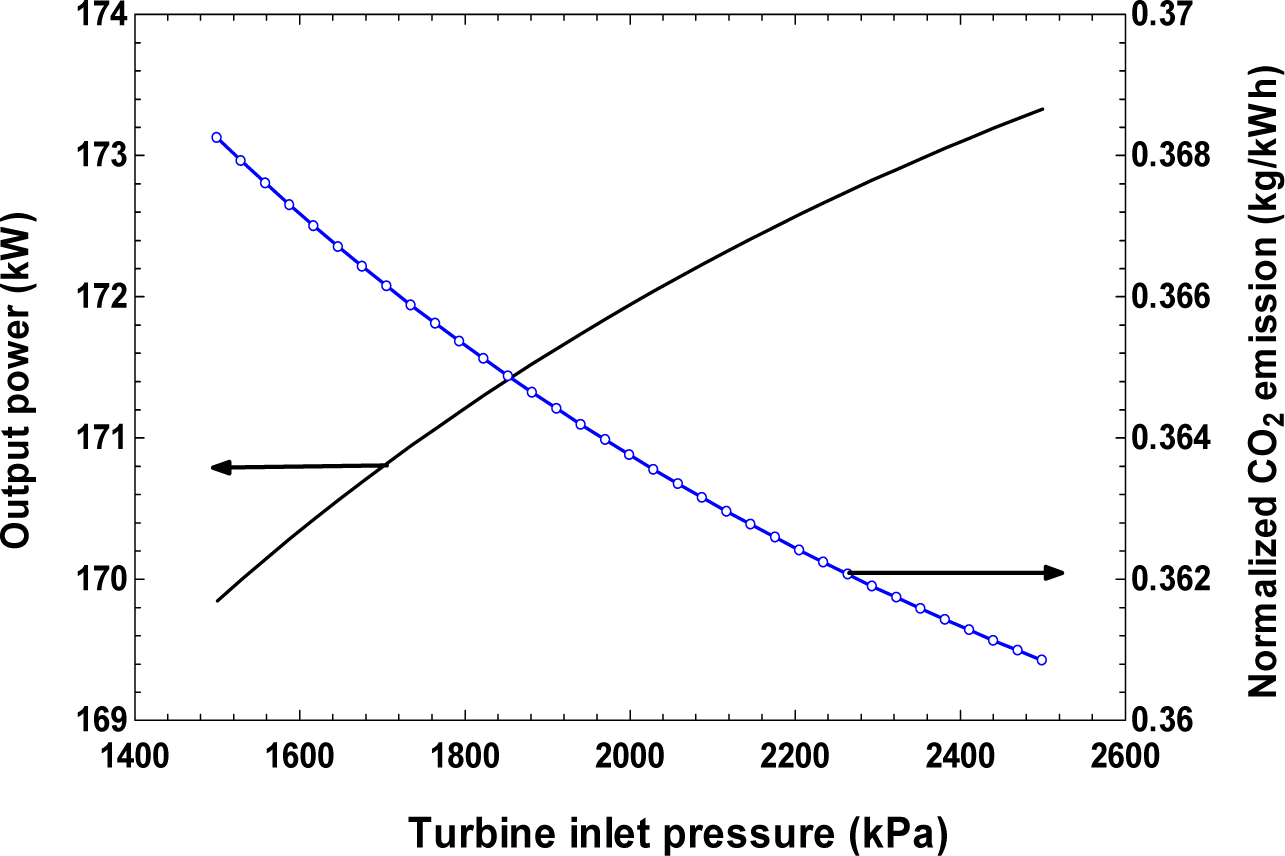
- An increase in ORC turbine inlet pressure leads to an increase in exergy efficiency of the system
- An increase in turbine inlet pressure has a negative effect on the total cost rate of the system
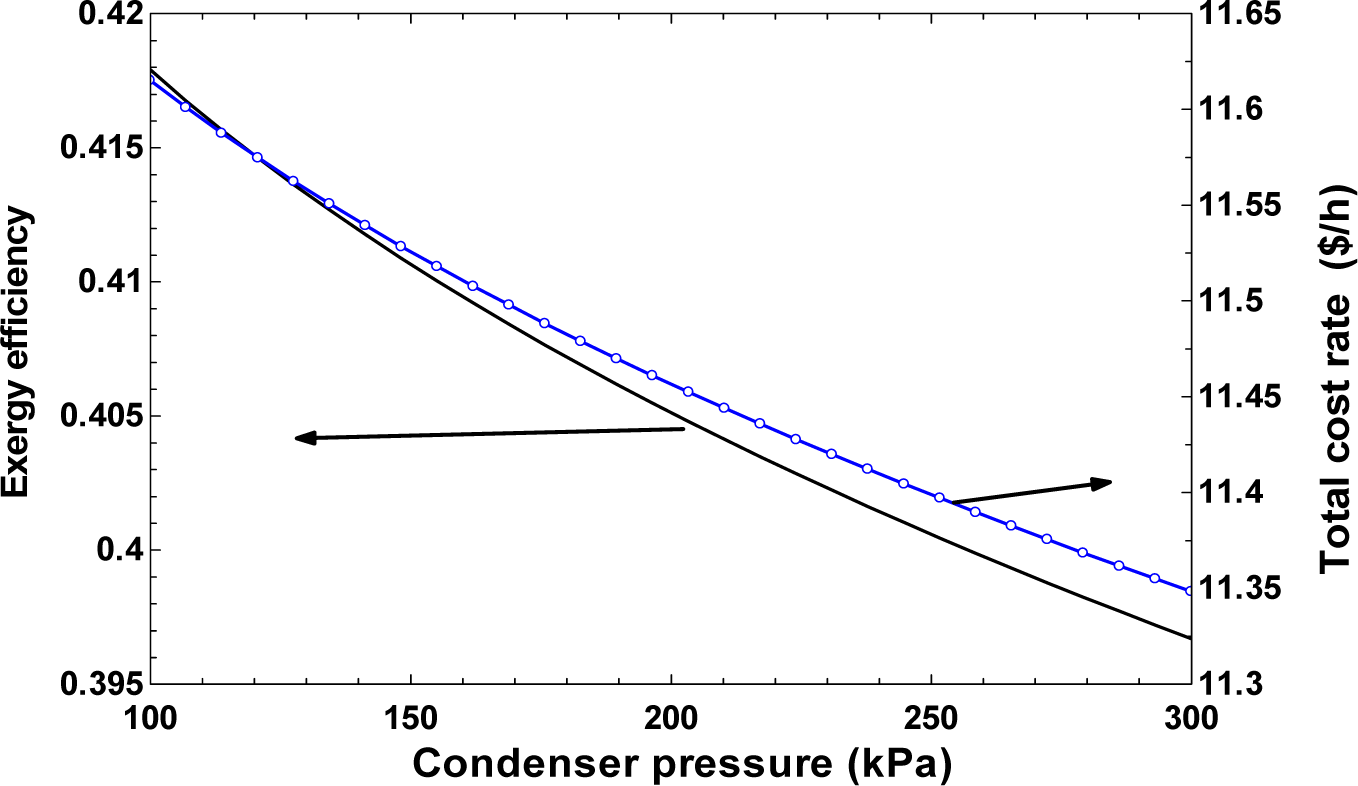
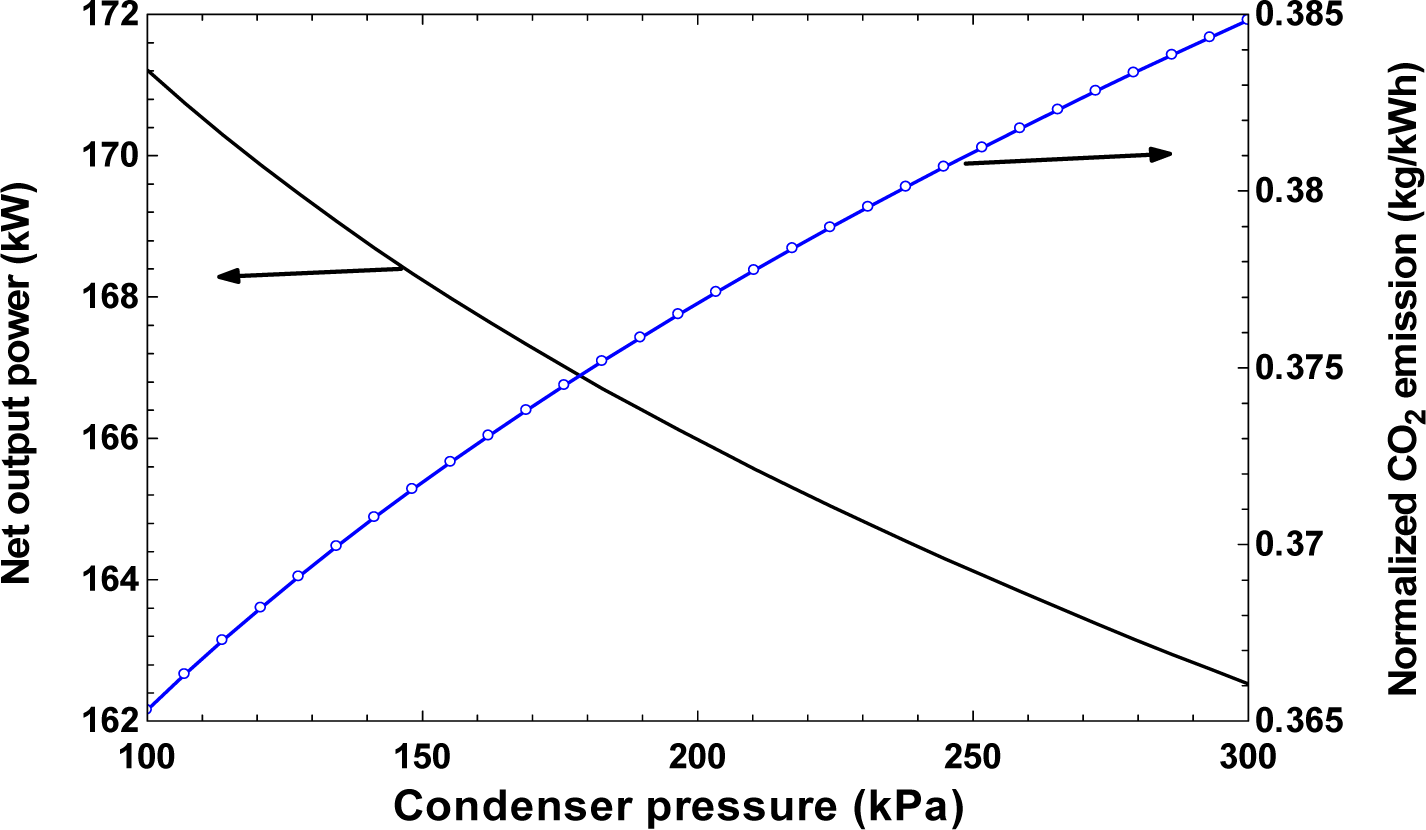
- An increase in condenser pressure decreases the exergy efficiency of the system while having a positive effect on the total cost rate of the system
- An increase in partial load of the diesel engine increases exergy efficiency of the system, net output power and the total cost rate of the system, and decreases the normalized CO2 emission of the system
Acknowledgments
Nomenclature
| C | Total cost rate, ($/h) |
| ex | specific exergy, (kJ/kg) |
exergy destruction rate, (kW) | |
| h | specific enthalpy, (kJ/kg) |
| LHV | lower heating value, (kJ/kg) |
mass flow rate, (kg/s) | |
| P | pressure, (kPa) |
| PL | partial load (%) |
heat transfer rate, (kW) | |
| R | gas constant, (kJ/kg K) |
| s | specific entropy, (kJ/kg K) |
| T | temperature, (°C) |
work rate, (kW) | |
purchase cost of each component |
| Greek Letters | |
|---|---|
| ηPump | pump isentropic efficiency, (%) |
| ηT | turbine isentropic efficiency, (%) |
| Ψ | exergy efficiency, (%) |
| Subscripts | |
|---|---|
| act | actual |
| Cond | condenser |
| Die | diesel |
| e | outlet condition |
| env | environmental |
| f | fuel |
| HEX | heat exchanger |
| i | inlet condition |
| is | isentropic |
| mix | mixture |
| nom | nominal |
| oil | oil |
| ph | physical |
| prim | |
| P | pump |
| T | turbine |
| tot | total |
| wj | water jacket |
| 0 | reference environment condition |
| Superscripts | |
|---|---|
| Ch | chemical |
| . | rate |
Author Contributions
Conflicts of Interest
References
- Teng, H.; Regner, G.; Cowland, C. Waste Heat Recovery of Heavy-Duty Diesel Engines by Organic Rankine Cycle Part I: Hybrid Energy System of Diesel and Rankine Engines; SAE Technical Paper No. 2007-01-0537; SAE International: Warrendale, PA, USA, 2007. [Google Scholar] [CrossRef]
- Teng, H.; Regner, G.; Cowland, C. Waste Heat Recovery of Heavy-Duty Diesel Engines by Organic Rankine Cycle Part II: Workingfluids for WHR-ORC; SAE Technical Paper No. 2007-01-0543; SAE International: Warrendale, PA, USA, 2007. [Google Scholar] [CrossRef]
- Ehyaei, M.A.; Ahmadi, P.; Atabi, F.; Heibati, M.R.; Khorshidvand, M. Feasibility study of applying internal combustion engines in residential buildings by exergy, economic and environmental analysis. Energy Build 2012, 55, 405–413. [Google Scholar]
- Dai, Y.; Wang, J.; Gao, L. Parametric optimization and comparative study of organic Rankine cycle (ORC) for low grade waste heat recovery. Energy Convers. Manag. 2009, 50, 576–582. [Google Scholar]
- El Chammas, R.; Clodic, D. Combined Cycle for Hybrid Vehicles; SAE Technical Paper No. 2005-01-1171; SAE International: Warrendale, PA, USA, 2005. [Google Scholar] [CrossRef]
- Liu, B.T.; Chien, K.H.; Wang, C.C. Effect of working fluids on Organic Rankine Cycle for waste heat recovery. Energy 2004, 29, 1207–1217. [Google Scholar]
- Mago, P.J.; Charma, L.M.; Srinivasan, K.; Somayaji, C. An examination of regenerative organic Rankine cycles using dry fluids. Appl. Therm. Eng. 2008, 28, 998–1007. [Google Scholar]
- Miazza, V.; Miazza, A. Unconventional working fluids in Organic Rankine cycles for waste heat recovery systems. Appl. Therm. Eng. 2001, 21, 381–390. [Google Scholar]
- Hajabdollahi, Z.; Hajabdollahi, F.; Tehrani, M.; Hajabdollahi, H. Thermo-economic environmental optimization of Organic Rankine Cycle for diesel waste heat recovery. Energy 2013, 63, 142–151. [Google Scholar]
- Drescher, U.; Bruggermann, D. Fluid selection for the Organic Rankine cycle (ORC) in biomass power and heat plants. Appl. Therm. Eng. 2007, 27, 223–228. [Google Scholar]
- Wei, D.; Lu, X.; Lu, Z.; Gu, J. Dynamic modeling and simulation of an Organic Rankine Cycle system for waste heat recovery (ORC). Appl. Therm. Eng. 2008, 28, 1216–1224. [Google Scholar]
- San, J.Y. Second-law performance of heat exchangers for waste heat recovery. Energy 2010, 35, 1936–1945. [Google Scholar]
- Saleh, B.; Koglbauer, G.; Wendland, M.; Fischer, J. Working fluids for low-temperature organic Rankine cycles. Energy 2007, 32, 1210–1221. [Google Scholar]
- Roy, J.P.; Mishra, M.K.; Misra, A. Parametric optimization and performance analysis of a waste heat recovery system using Organic Rankine Cycle. Energy 2010, 35, 5049–5062. [Google Scholar]
- Aljundi, I.H. Effect of dry hydrocarbons and critical point temperature on the efficiencies of organic Rankine cycle. Renew. Energy. 2011, 36, 1196–1202. [Google Scholar]
- Papadopoulos, A.I.; Stijepovic, M.; Linke, P. On the systematic design and selection of optimal working fluids for Organic Rankine Cycles. Appl. Therm. Eng. 2010, 30, 760–769. [Google Scholar]
- Wakui, T.; Yokoyama, R. Optimal sizing of residential gas engine cogeneration system for power interchange operation from energy-saving viewpoint. Energy 2011, 36, 3816–3824. [Google Scholar]
- Alanne, K.; Söderholm, N.; Sirén, K.; Beausoleil-Morrison, I. Techno-economic assessment and optimization of stirling engine micro-cogeneration systems in residential buildings. Energy Convers. Manag. 2010, 51, 2635–2646. [Google Scholar]
- Ren, H.; Gao, W. Economic and environmental evaluation of micro CHP systems with different operating modes for residential buildings in Japan. Energy Build 2010, 42, 853–861. [Google Scholar]
- Aussant, C.D.; Fung, A.S.; Ugursal, V.I.; Taherian, H. Residential application of internal combustion engine based cogeneration in cold climate—Canada. Energy Build 2009, 41, 1288–1298. [Google Scholar]
- Garcia-Cascales, J.R.; Vera-Garcia, F.; Gonzalvez-Macia, J.; Corberan-Salvador, J.M.; Johnson, M.W.; Kohler, G.T. Compact heat exchangers modeling: Condensation. Int. J. Refrig. 2010, 33, 135–147. [Google Scholar]
- Jung, H.C.; Krumdieck, S. Modelling of organic Rankine cycle system and heat exchanger components. Int. J. Sustain. Energy. 2014, 33, 704–721. [Google Scholar]
- Kotas, T.J. The Exergy Method of Thermal Plant Analysis; Butterworths: London, UK, 1985; p. 344. [Google Scholar]
- Ganjehkaviri, A.; Mohd Jaffar, M.N.; Tholudin, M.L.; Sharifishourabi, G. Modelling and exergoeconomic based design optimisation of combined power plants. Int. J. Exergy. 2013, 13, 141–158. [Google Scholar]
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal Design and Optimization; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Ganjehkaviri, A.; Mohd Jaafar, M.N.; Ahmadi, P.; Barzegaravval, H. Modelling and optimization of combined cycle power plant based on exergoeconomic and environmental analyses. Appl. Therm. Eng. 2014, 67, 566–578. [Google Scholar]
- Bernow, S.S.; Marron, D.B. Valuation of Environmental Externalities for Energy Planning and Operations: May 1990 Update; Tellus Institute: Boston, MA, USA, 1990. [Google Scholar]
- Bohi, D.R.; Toman, M.A. An Assessment of Energy Security Externalities; Discussion Paper ENR92-05; Resources for the Future; Washington: DC, USA, February 1992. [Google Scholar]
- Ghaffarizadeh, A.; Ahmadi, K.; Flann, N.S. Sorting unsigned permutations by reversals using multi-objective evolutionary algorithms with variable size individuals, In Proceedings of 2011 IEEE congress on evolutionary computation (CEC), New Orleans, LA, USA, 5–8, Jun 2011; pp. 292–295.
- Srinivas, N.; Deb, K. Muilti-objective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar]

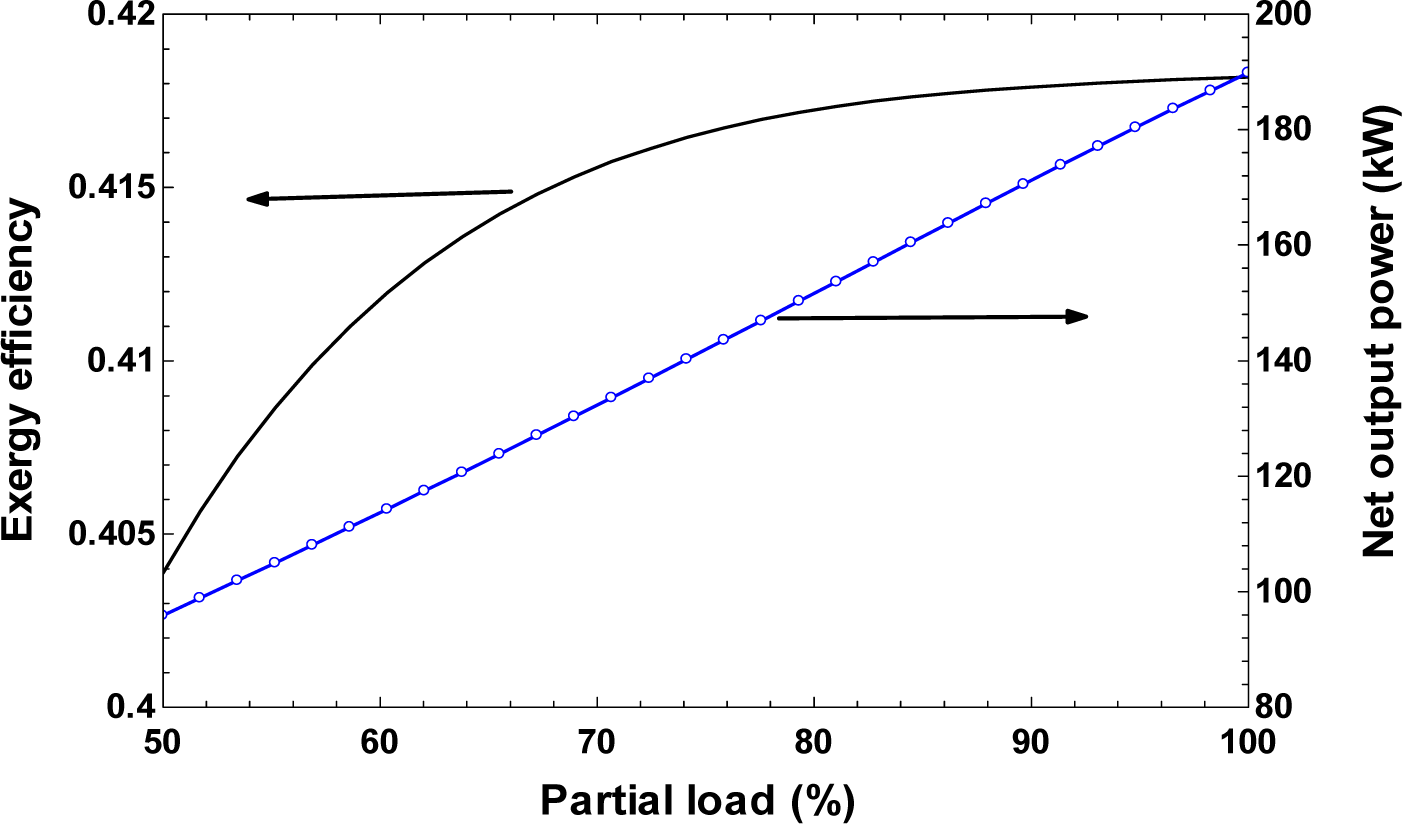
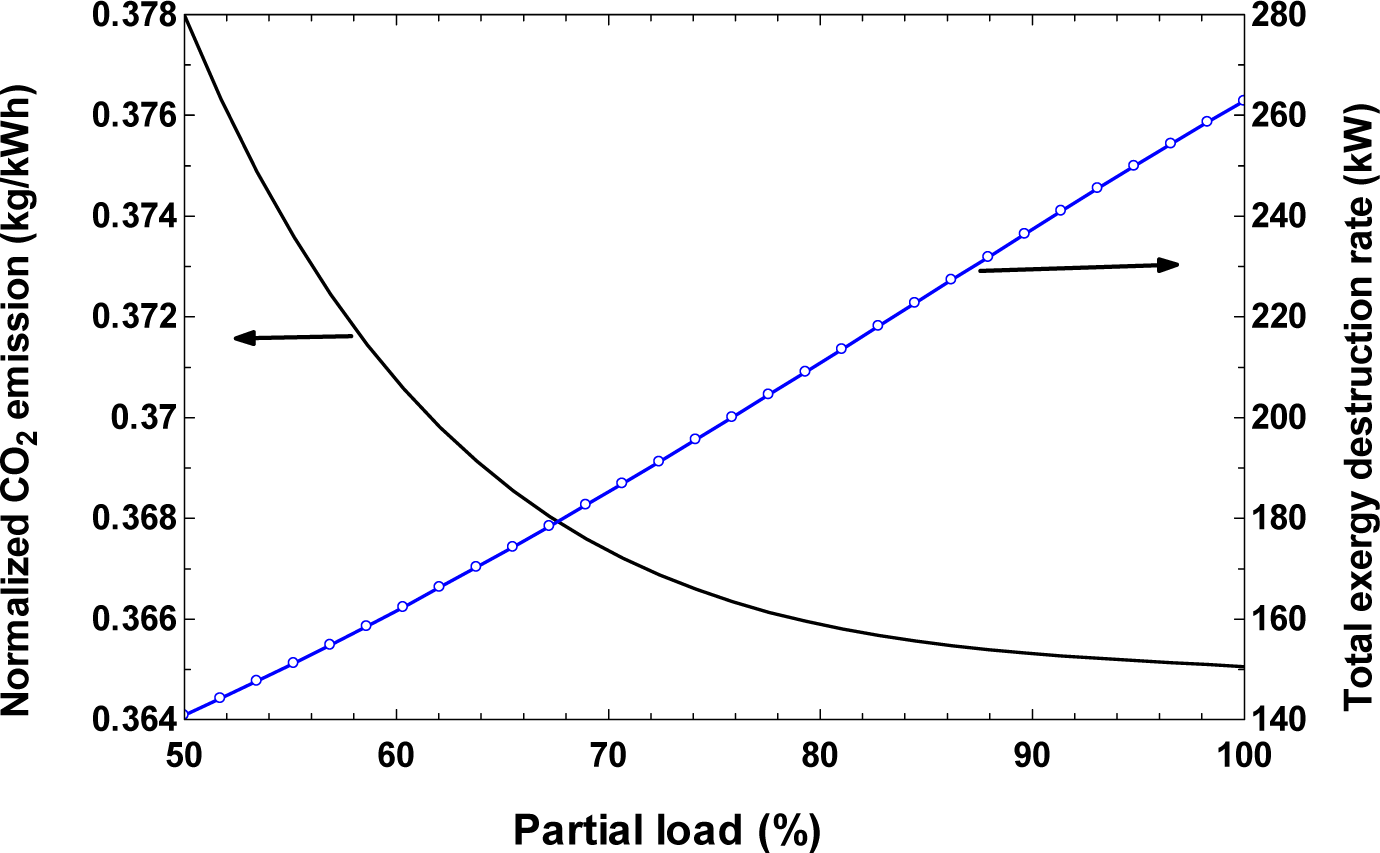

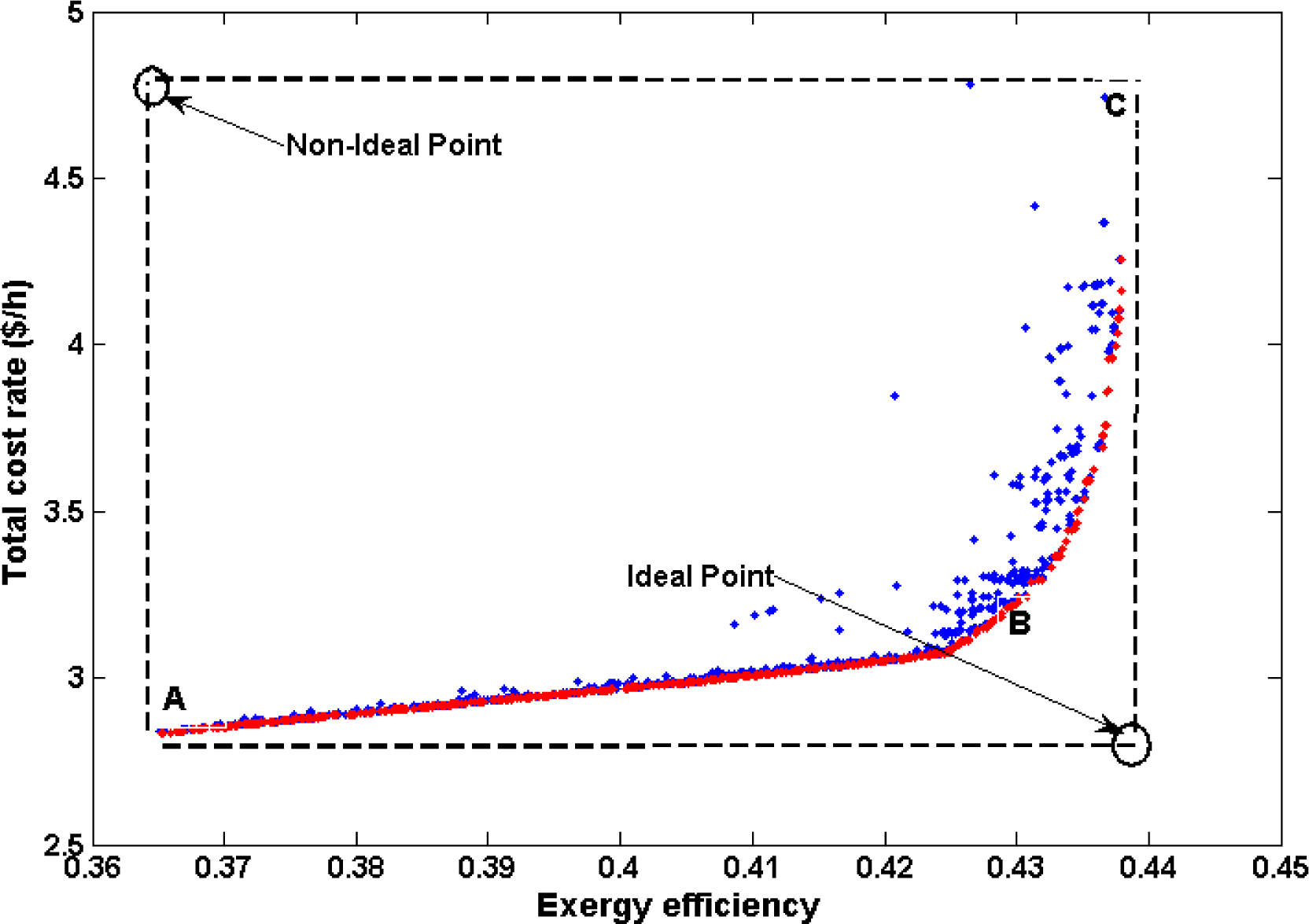
| Components | Exergy Destruction |
|---|---|
| Diesel | |
| Heat exchanger | |
| Turbine | |
| Condenser | |
| Pump |
| Components | Exergy Destruction |
|---|---|
| Diesel* | |
| Turbine | |
| Condenser | |
| Pump |
| Constraint | Reason |
|---|---|
| Diesel engine size limitation | |
| 50 < PL < 100 | Diesel engine load limitation |
| 1000 kPa < Pmain < 2500 kPa | Commercial availability |
| 50 kPa < PCond < 300 kPa | Commercial availability |
| ηT < 0.9 | Commercial availability |
| ηp < 0.9 | Commercial availability |
| Number | Substance | Molecular mass [kg/kmol] | Tba (K) | Pcrb (MPa) | Tcra (K) |
|---|---|---|---|---|---|
| 1 | R123 | 152.93 | 300.97 | 3.66 | 456.83 |
| 2 | R134a | 102.03 | 247.08 | 4.059 | 374.21 |
| 3 | R124 | 136.48 | 261.22 | 3.62 | 395.43 |
| 4 | R11 | 137.37 | 296.86 | 4.40 | 471.11 |
| 5 | R12 | 120.91 | 243.4 | 4.13 | 385.12 |
| 6 | R143a | 84.04 | 161.34 | 3.76 | 345.86 |
| 7 | R113 | 187.38 | 320.74 | 3.39 | 487.21 |
| 8 | R125 | 120.02 | 172.52 | 3.61 | 339.17 |
| 9 | R141b | 116.95 | 305.2 | 4.46 | 479.96 |
| Point | (kW) | PL (%) | P4 (kPa) | P5 (kPa) | ηTurbine(−) | ηPump(−) |
|---|---|---|---|---|---|---|
| A | 50 | 50.07 | 1004 | 28,843 | 0.7541 | 0.80 |
| B | 50 | 50 | 2496 | 63 | 0.9 | 0.84 |
| C | 54.76 | 99 | 2491 | 50.5 | 0.9 | 0.8612 |
| Point | (kW) | Ѱ (%) | (kW) | (kW) | ($/h) |
|---|---|---|---|---|---|
| A | 28.87 | 0.3635 | 45.99 | 0.42 | 2.827 |
| B | 32.55 | 0.425 | 45.06 | 0.3592 | 3.074 |
| C | 70.28 | 0.4423 | 91.71 | 0.3451 | 4.72 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ganjehkaviri, A.; Jaafar, M.N.M. Energy Analysis and Multi-Objective Optimization of an Internal Combustion Engine-Based CHP System for Heat Recovery. Entropy 2014, 16, 5633-5653. https://doi.org/10.3390/e16115633
Ganjehkaviri A, Jaafar MNM. Energy Analysis and Multi-Objective Optimization of an Internal Combustion Engine-Based CHP System for Heat Recovery. Entropy. 2014; 16(11):5633-5653. https://doi.org/10.3390/e16115633
Chicago/Turabian StyleGanjehkaviri, Abdolsaeid, and Mohammad Nazri Mohd Jaafar. 2014. "Energy Analysis and Multi-Objective Optimization of an Internal Combustion Engine-Based CHP System for Heat Recovery" Entropy 16, no. 11: 5633-5653. https://doi.org/10.3390/e16115633
APA StyleGanjehkaviri, A., & Jaafar, M. N. M. (2014). Energy Analysis and Multi-Objective Optimization of an Internal Combustion Engine-Based CHP System for Heat Recovery. Entropy, 16(11), 5633-5653. https://doi.org/10.3390/e16115633




