Progress in the Prediction of Entropy Generation in Turbulent Reacting Flows Using Large Eddy Simulation
Abstract
:1. Introduction
2. LES Formulation and Modeling
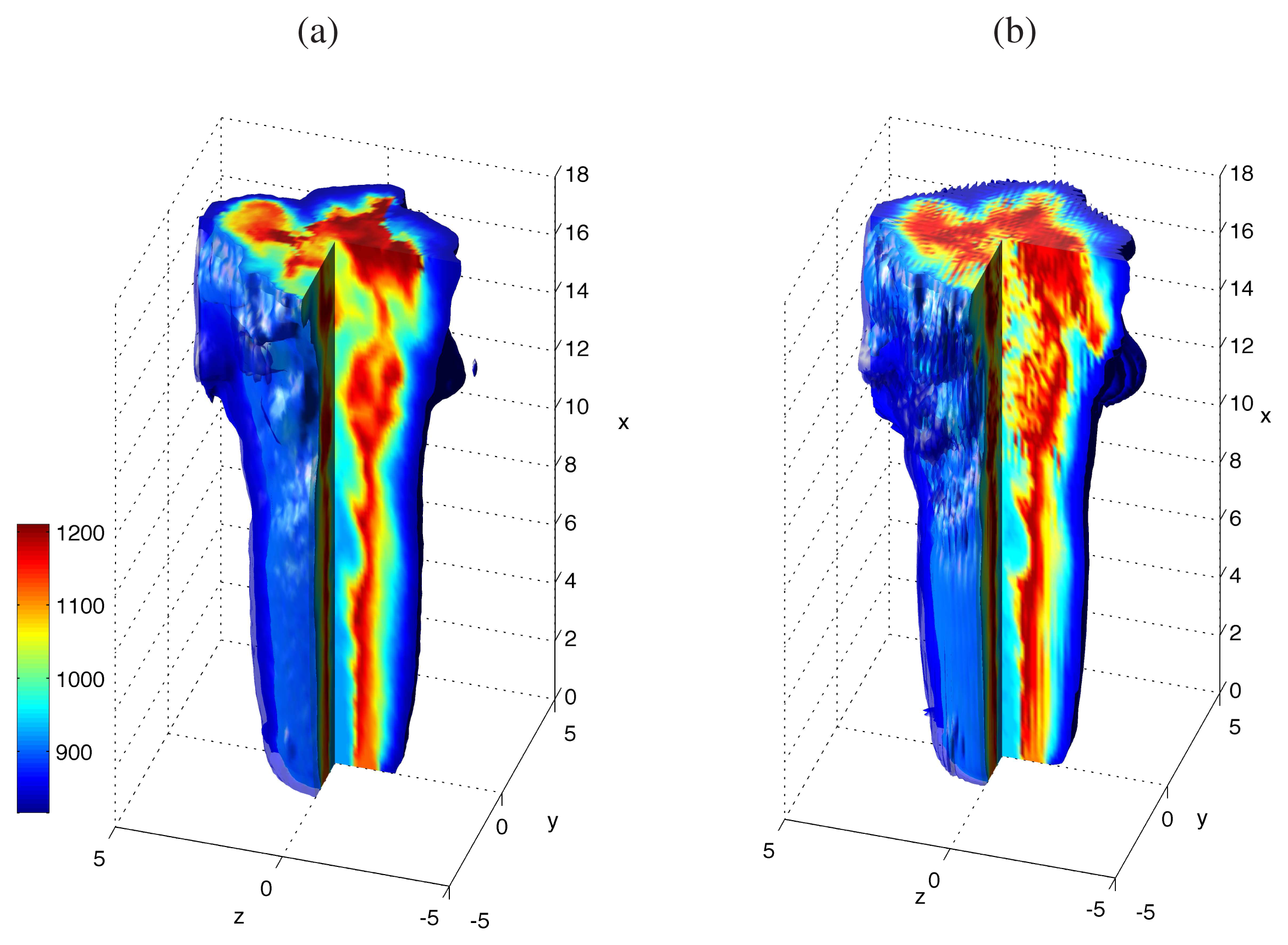
3. Simulations
4. Final Remarks
Acknowledgments
Author Contributions
References
- Keenan, J.H. Availability and Irreversibility in Thermodynamics. Br J. Appl. Phys 1951, 2, 183–192. [Google Scholar]
- Gouy, G. About Available Energy. J. Phys. II 1889, 8, 501–518. [Google Scholar]
- Stodola, A. Steam and Gas Turbines; McGraw-Hill: New York NY, USA, 1910. [Google Scholar]
- Bejan, A. Fundamentals of Exergy Analysis, Entropy Generation Minimization, and the Generation of Flow Architecture. Int. J. Energy Res 2002, 26, 545–565. [Google Scholar]
- Bejan, A. Entropy Generation Minimization: The New Thermodynamics of Finite-Size Devices and Finite-Time Processes. J. Appl. Phys 1996, 79, 1191–1218. [Google Scholar]
- Mironova, V.A.; Tsirlin, A.M.; Kazakov, V.A.; Berry, R.S. Finite-Time Thermodynamics: Exergy and Optimization of Time-Constrained Processes. J. Appl. Phys 1994, 76, 629–636. [Google Scholar]
- Andresen, B. Current Trends in Finite-Time Thermodynamics. Angew. Chem. Int. Ed 2011, 50, 2690–2704. [Google Scholar]
- Som, S.K.; Datta, A. Thermodynamic Irreversibilities and Exergy Balance in Combustion Processes. Prog. Energy Combust. Sci 2008, 34, 351–376. [Google Scholar]
- Lior, N.; Sarmiento-Darkin, W.; Al-Sharqawi, H.S. The Exergy Fields in Transport Processes: Their Calculation and Use. Energy 2006, 31, 553–578. [Google Scholar]
- Rakopoulos, C.D.; Michos, C.N. Generation of Combustion Irreversibilities in a Spark Ignition Engine Under Biogas-Hydrogen Mixtures Fueling. Int. J. Hydrog. Energy 2009, 34, 4422–4437. [Google Scholar]
- Ugarte, S.; Metghalchi, M. Evolution of Adiabatic Availability and Its Depletion through Irreversible Processes. Int. J. Exergy 2005, 2, 109–119. [Google Scholar]
- Klausner, J.F.; Li, Y.; Darwish, M.; Mei, R. Innovative Diffusion Driven Desalination Process. J. Energy Resour. Technol 2004, 126, 219–225. [Google Scholar]
- Narusawa, U. The Second-Law Analysis of Convective Pattern Change in a Rectangular Cavity. J. Fluid Mech 1999, 392, 361–377. [Google Scholar]
- Li, Z.W.; Chou, S.K.; Shu, C.; Yang, W.M. Entropy Generation During Microcombustion. J. Appl. Phys 2005, 97. [Google Scholar] [CrossRef]
- Rezac, P.; Metghalchi, H. A Brief Note on the Historical Evolution and Present State of Exergy Analysis. Int. J. Exergy 2004, 1, 426–437. [Google Scholar]
- Yilbas, B.S. Entropy Production During Laser Picosecond Heating of Copper. J. Energy Resour. Technol 2002, 124, 204–213. [Google Scholar]
- Gyftopoulos, E.P.; Beretta, G.P. Entropy Generation Rate In a Chemically Reacting System. J. Energy Resour. Technol 1993, 115, 208–212. [Google Scholar]
- Datta, A.; Som, S. Energy and Exergy Balance in a Gas Turbine Combustor. Proc. Inst. Mech. Eng. Part A 1999, 213, 23–32. [Google Scholar]
- Hutchins, T.E.; Metghalchi, M. Energy and Exergy Analyses of the Pulse Detonation Engine. J. Eng. Gas Turb. Power 2003, 125, 1075–1080. [Google Scholar]
- Jubeh, N.M. Exergy Analysis and Second Law Efficiency of a Regenerative Brayton Cycle with Isothermal Heat Addition. Entropy 2005, 7, 172–187. [Google Scholar]
- Chavannavar, P.; Caton, J. Destruction of Availability (Exergy) Due to Combustion Processes: A Parametric Study. Proc. Inst. Mech. Eng. Part A 2006, 220, 655–668. [Google Scholar]
- Sezer, I.; Altin, I.; Bilgin, A. Exergetic Analysis of Using Oxygenated Fuels in Spark-Ignition (SI) Engines. Energy Fuels 2009, 23, 1801–1807. [Google Scholar]
- Chen, S.; Li, J.; Han, H.; Liu, Z.; Zheng, C. Effects of Hydrogen Addition on Entropy Generation in Ultra-Lean Counter-Flow Methane-Air Premixed Combustion. Int. J. Hydrog. Energy 2010, 35, 3891–3902. [Google Scholar]
- Teng, H.; Kinoshita, C.M.; Masutani, S.M.; Zhou, J. Entropy Generation in Multicomponent Reacting Flows. J. Energy Resour. Technol 1998, 120, 226–232. [Google Scholar]
- Datta, A. Entropy Generation in a Confined Laminar Diffusion Flame. Combust. Sci. Technol 2000, 159, 39–56. [Google Scholar]
- Nishida, K.; Takagi, T.; Kinoshita, S. Analysis of Entropy Generation and Exergy Loss During Combustion. Proc. Combust. Inst 2002, 29, 869–874. [Google Scholar]
- Datta, A. Effects of Gravity on Structure and Entropy Generation of Confined Laminar Diffusion Flames. Int. J. Therm. Sci 2005, 44, 429–440. [Google Scholar]
- Shuja, S.Z.; Yilbas, B.S.; Khan, M. Entropy Generation in Laminar Jet: Effect of Velocity Profiles at Nozzle Exit. Heat Mass Transf 2006, 42, 771–777. [Google Scholar]
- Briones, A.M.; Mukhopadhyay, A.; Aggarwal, S.K. Analysis of Entropy Generation in Hydrogen-Enriched Methane-Air Propagating Triple Flames. Int. J. Hydrog. Energy 2009, 34, 1074–1083. [Google Scholar]
- Sciacovelli, A.; Verda, V. Entropy Generation Minimization in a Tubular Solid Oxide Fuel Cell. J. Energy Resour. Technol 2010, 132. [Google Scholar] [CrossRef]
- Jiang, D.; Yang, W.; Chua, K.J.; Ouyang, J.; Teng, J.H. Analysis of Entropy Generation Distribution in Micro-Combustors With Baffles. Int. J. Hydrog. Energy 2014, 39, 8118–8125. [Google Scholar]
- Rana, U.; Chakraborty, S.; Som, S.K. Thermodynamics of Premixed Combustion in a Heat Recirculating Micro Combustor. Energy 2014, 68, 510–518. [Google Scholar]
- Okong’o, N.; Bellan, J. Entropy Production of Emerging Turbulent Scales in a Temporal Supercritical n-Heptane/Nitrogen Three Dimensional Mixing Layer. Proc. Combust. Inst 2000, 28, 467–504. [Google Scholar]
- Okong’o, N.; Bellan, J. Direct Numerical Simulation of a Transitional Supercritical Binary Mixing Layer: Heptane and Nitrogen. J. Fluid Mech 2002, 464, 1–34. [Google Scholar]
- Okong’o, N.A.; Bellan, J. Small-Scale Dissipation in Binary-Species, Thermodynamically Supercritical, Transitional Mixing Layers. Comput. Fluids 2010, 39, 1112–1124. [Google Scholar]
- McEligot, D.M.; Nolan, K.P.; Walsh, E.J.; Laurien, E. Effects of Pressure Gradients on Entropy Generation in the Viscous Layers of Turbulent Wall Flows. Int. J. Heat Mass Transf 2008, 51, 1104–1114. [Google Scholar]
- Farran, R.; Chakraborty, N. A Direct Numerical Simulation-Based Analysis of Entropy Generation in Turbulent Premixed Flames. Entropy 2013, 15, 1540–1566. [Google Scholar]
- Ghasemi, E.; McEligot, D.M.; Nolan, K.P.; Crepeau, J.; Tokuhiro, A.; Budwig, R.S. Entropy Generation in a Transitional Boundary Layer Region Under the Influence of Freestream Turbulence Using Transitional RANS Models And DNS. Int. Commun. Heat Mass Transf 2013, 41, 10–16. [Google Scholar]
- Ghasemi, E.; McEligot, D.M.; Nolan, K.P.; Crepeau, J.; Siahpush, A.; Budwig, R.S.; Tokuhiro, A. Effects of Adverse and Favorable Pressure Gradients on Entropy Generation in a Transitional Boundary Layer Region Under the Influence of Freestream Turbulence. Int. J. Heat Mass Transf 2014, 77, 475–488. [Google Scholar]
- Stanciu, D.; Isvoranu, D.; Marinescu, M.; Gogus, Y. Second Law Analysis of Diffusion Flames. Int. J. Appl. Thermodyn 2001, 4, 1–18. [Google Scholar]
- Shuja, S.Z.; Yilbas, B.S.; Budair, M.O. Local Entropy Generation in an Impinging Jet: Minimum Entropy Concept Evaluating Various Turbulence Models. Comput. Meth. Appl. Mech. Eng 2001, 190, 3623–3644. [Google Scholar]
- Adeyinka, O.B.; Naterer, G.F. Modeling of Entropy Production in Turbulent Flows. J. Fluids Eng 2004, 126, 893–899. [Google Scholar]
- Kock, F.; Herwig, H. Local Entropy Production in Turbulent Shear Flows: A High-Reynolds Number Model with Wall Functions. Int. J. Heat Mass Transf 2004, 47, 2205–2215. [Google Scholar]
- Yapıcı, H.; Kayataş, N.; Albayrak, B.; Baştürk, G. Numerical Calculation of Local Entropy Generation in a Methane-Air Burner. Energ. Convers. Manag 2005, 46, 1885–1919. [Google Scholar]
- Herwig, H.; Kock, F. Local Entropy Production in Turbulent Shear Flows: A Tool For Evaluating Heat Transfer Performance. J. Therm. Sci 2006, 15, 159–167. [Google Scholar]
- Stanciu, D.; Marinescu, M.; Dobrovicescu, A. The Influence of Swirl Angle on the Irreversibilities in Turbulent Diffusion Flames. Int. J. Thermodyn 2007, 10, 143–153. [Google Scholar]
- Emadi, A.; Emami, M.D. Analysis of Entropy Generation in a Hydrogen-Enriched Turbulent Non-Premixed Flame. Int. J. Hydrog. Energy 2013, 38, 5961–5973. [Google Scholar]
- Givi, P. Filtered Density Function for Subgrid Scale Modeling of Turbulent Combustion. AIAA J 2006, 44, 16–23. [Google Scholar]
- Ansari, N.; Jaberi, F.A.; Sheikhi, M.R.H.; Givi, P. Filtered Density Function as a Modern CFD Tool. In Engineering Applications of CFD; Maher, R.S., Ed.; Volume 1, Fluid Mechanics and Its Applications, Chapter 1; International Energy and Environment Foundation: Al-Najaf, Iraq, 2011; pp. 1–22. [Google Scholar]
- Colucci, P.J.; Jaberi, F.A.; Givi, P.; Pope, S.B. Filtered Density Function for Large Eddy Simulation of Turbulent Reacting Flows. Phys. Fluids 1998, 10, 499–515. [Google Scholar]
- Jaberi, F.A.; Colucci, P.J.; James, S.; Givi, P.; Pope, S.B. Filtered Mass Density Function for Large Eddy Simulation of Turbulent Reacting Flows. J. Fluid Mech 1999, 401, 85–121. [Google Scholar]
- Gicquel, L.Y.M.; Givi, P.; Jaberi, F.A.; Pope, S.B. Velocity Filtered Density Function for Large Eddy Simulation of Turbulent Flows. Phys. Fluids 2002, 14, 1196–1213. [Google Scholar]
- Sheikhi, M.R.H.; Drozda, T.G.; Givi, P.; Pope, S.B. Velocity-Scalar Filtered Density Function for Large Eddy Simulation of Turbulent Flows. Phys. Fluids 2003, 15, 2321–2337. [Google Scholar]
- Sheikhi, M.R.H.; Drozda, T.G.; Givi, P.; Jaberi, F.A.; Pope, S.B. Large Eddy Simulation of a Turbulent Nonpremixed Piloted Methane Jet Flame (Sandia Flame D). Proc. Combust. Inst 2005, 30, 549–556. [Google Scholar]
- Drozda, T.G.; Sheikhi, M.R.H.; Madnia, C.K.; Givi, P. Developments in Formulation and Application of the Filtered Density Function. Flow Turbul. Combust 2007, 78, 35–67. [Google Scholar]
- Sheikhi, M.R.H.; Givi, P.; Pope, S.B. Velocity-Scalar Filtered Mass Density Function for Large Eddy Simulation of Turbulent Reacting Flows. Phys. Fluids 2007, 19. [Google Scholar] [CrossRef]
- Sheikhi, M.R.H.; Givi, P.; Pope, S.B. Frequency-Velocity-Scalar Filtered Mass Density Function for Large Eddy Simulation of Turbulent Flows. Phys. Fluids 2009, 21. [Google Scholar] [CrossRef]
- Yaldizli, M.; Mehravaran, K.; Jaberi, F.A. Large-Eddy Simulations of Turbulent Methane Jet Flames with Filtered Mass Density Function. Int. J. Heat Mass Transf 2010, 53, 2551–2562. [Google Scholar]
- Yilmaz, S.L.; Nik, M.B.; Sheikhi, M.R.H.; Strakey, P.A.; Givi, P. An Irregularly Portioned Lagrangian Monte Carlo Method for Turbulent Flow Simulation. J. Sci. Comput 2011, 47, 109–125. [Google Scholar]
- Nik, M.; Yilmaz, S.; Sheikhi, M.R.H.; Givi, P. Grid Resolution Effects on VSFMDF/LES. Flow Turbul. Combust 2010, 85, 677–688. [Google Scholar]
- Nik, M.B.; Yilmaz, S.L.; Givi, P.; Sheikhi, M.R.H.; Pope, S.B. Simulation of Sandia Flame D Using Velocity-Scalar Filtered Density Function. AIAA J 2010, 48, 1513–1522. [Google Scholar]
- Ansari, N.; Pisciuneri, P.H.; Strakey, P.A.; Givi, P. Scalar-Filtered Mass-Density-Function Simulation of Swirling Reacting Flows on Unstructured Grids. AIAA J 2012, 50, 2476–2482. [Google Scholar]
- Sheikhi, M.R.H.; Safari, M.; Metghalchi, H. Large Eddy Simulation for Local Entropy Generation Analysis of Turbulent Flows. J. Energy Resour. Technol 2012, 134. [Google Scholar] [CrossRef]
- Safari, M.; Sheikhi, M.R.H. Large Eddy Simulation for Prediction of Entropy Generation in a Nonpremixed Turbulent Jet Flame. J. Energy Resour. Technol 2014, 136. [Google Scholar] [CrossRef]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows; Springer-Verlag: New York, NY, USA, 2005. [Google Scholar]
- Geurts, B.J. Elements of Direct and Large-Eddy Simulation; R.T. Edwards, Inc: Philadelphia, PA, USA, 2004. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Haworth, D.C.; Pope, S.B. A Generalized Langevin Model for Turbulent Flows. Phys. Fluids 1986, 29, 387–405. [Google Scholar]
- Gikhman, I.I.; Skorokhod, A.V. Stochastic Differential Equations; Springer-Verlag: New York, NY, USA, 1972. [Google Scholar]
- Risken, H. The Fokker-Planck Equation, Methods of Solution and Applications; Springer-Verlag: New York, NY, USA, 1989. [Google Scholar]
- Kennedy, C.A.; Carpenter, M.H. Several New Numerical Methods for Compressible Shear-Layer Simulations. Appl. Numer. Math 1994, 14, 397–433. [Google Scholar]
- Vreman, B.; Geurts, B.; Kuerten, H. Large-Eddy Simulation of the Turbulent Mixing Layer. J. Fluid Mech 1997, 339, 357–390. [Google Scholar]
- Barlow, R.S. Sandia National Laboratories. TNF Workshop website. Available online: http://www.ca.sandia.gov/TNF/abstract.html accessed on 23 September 2014.
- Frank, J.H.; Barlow, R.S. Simultaneous Rayleigh, Raman, and LIF Measurements in Turbulent Premixed Methane-Air Flames. Proc. Combust. Inst 1998, 27, 759–766. [Google Scholar]
- Peters, N. Turbulent Combustion; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- GRI-Mech Home Page. Available online: http://www.me.berkeley.edu/gri_mech accessed on 18 September 2014.
- Poinsot, T.J.; Lele, S.K. Boundary Conditions for Direct Simulations of Compressible Viscous Flows. J. Comput. Phys 1992, 101, 104–129. [Google Scholar]

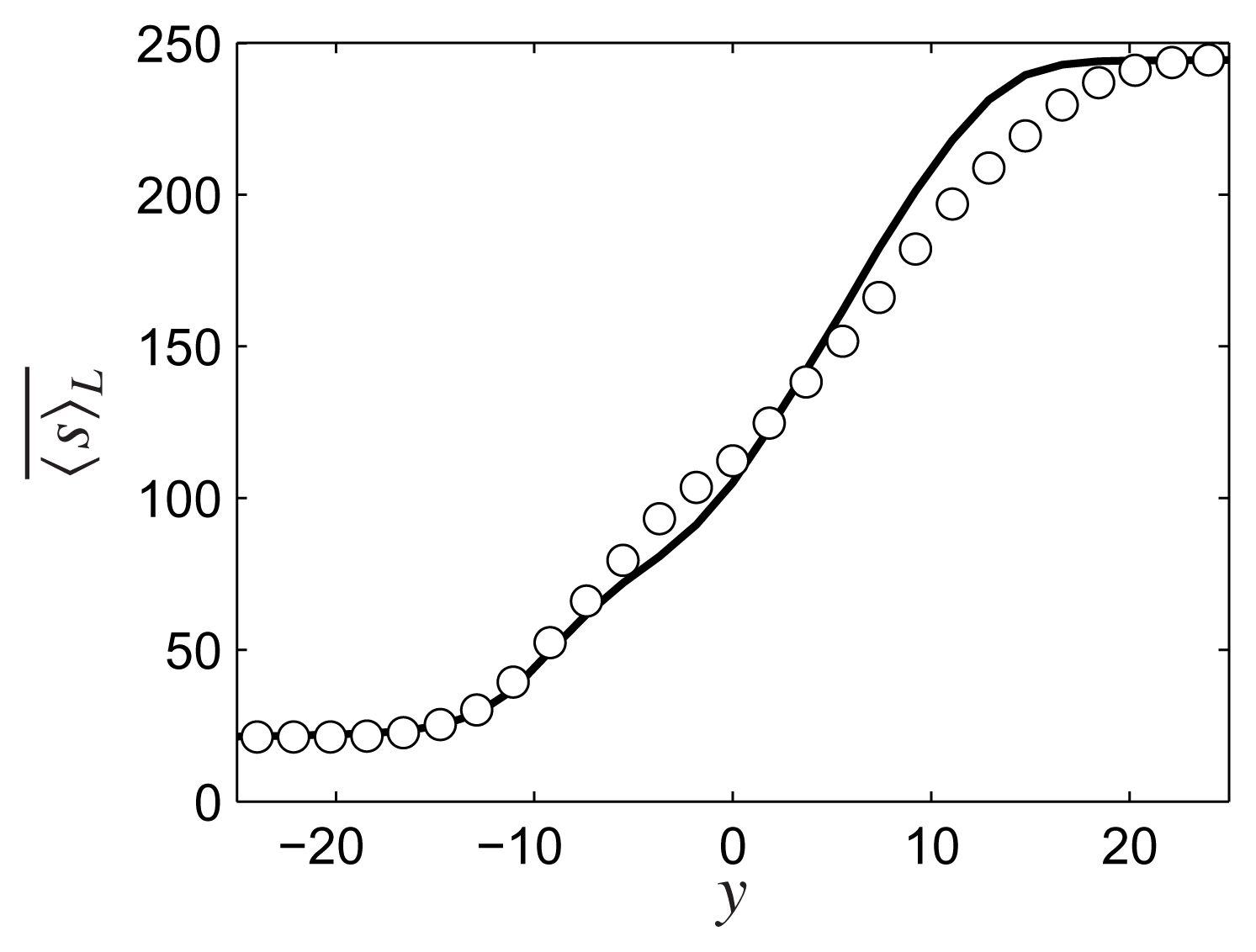
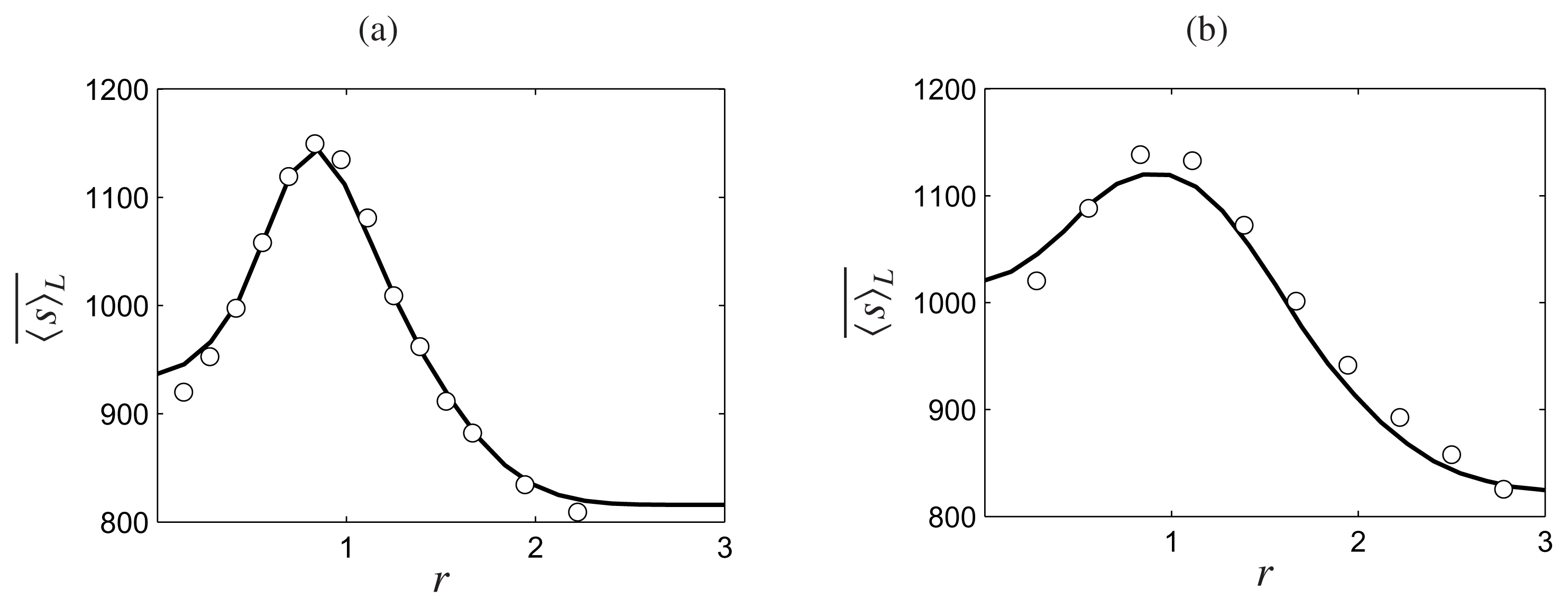

 ), x = 5 (
), x = 5 (
 ), x = 10 (
), x = 10 (
 ) and x = 15 (−).
) and x = 15 (−).
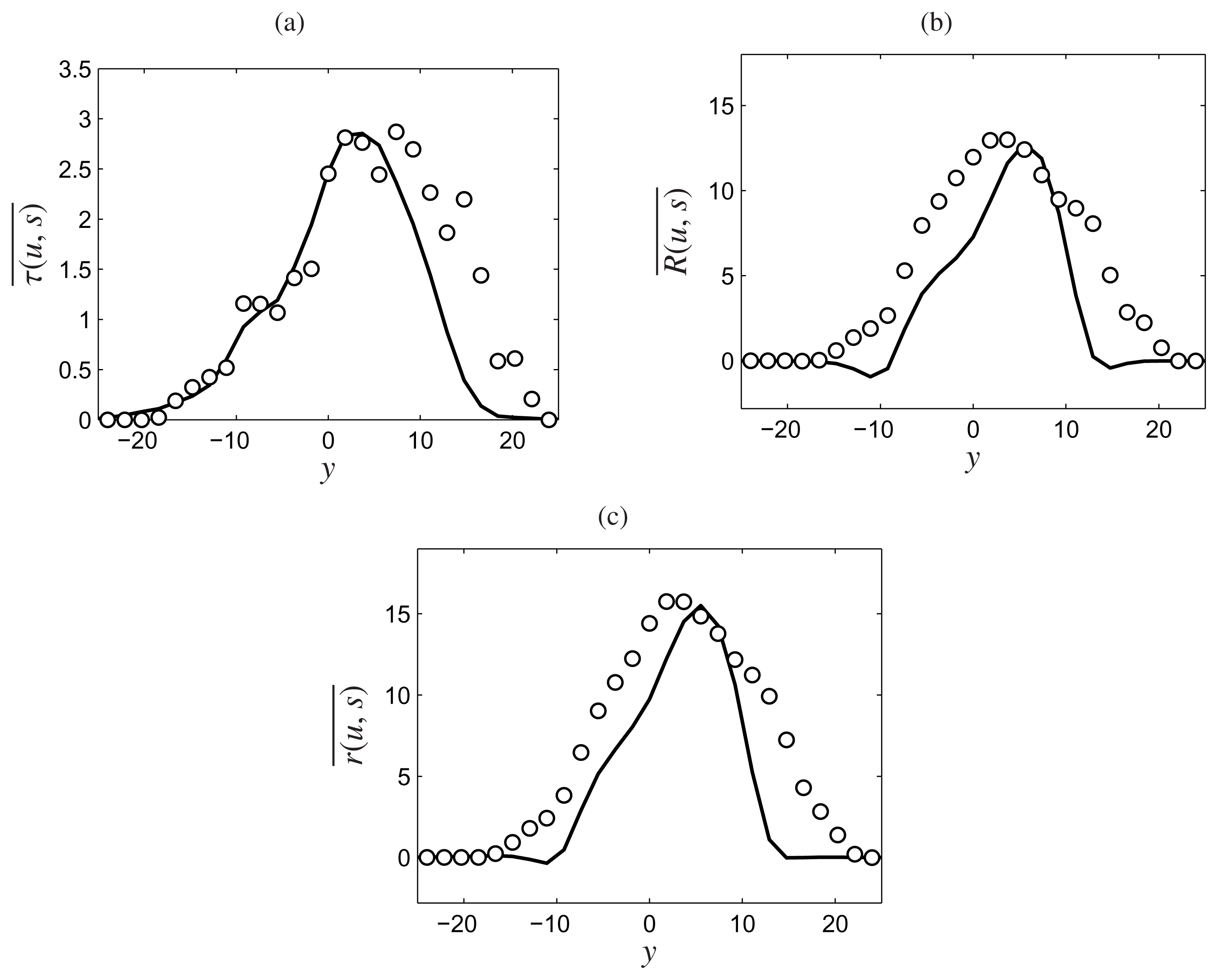
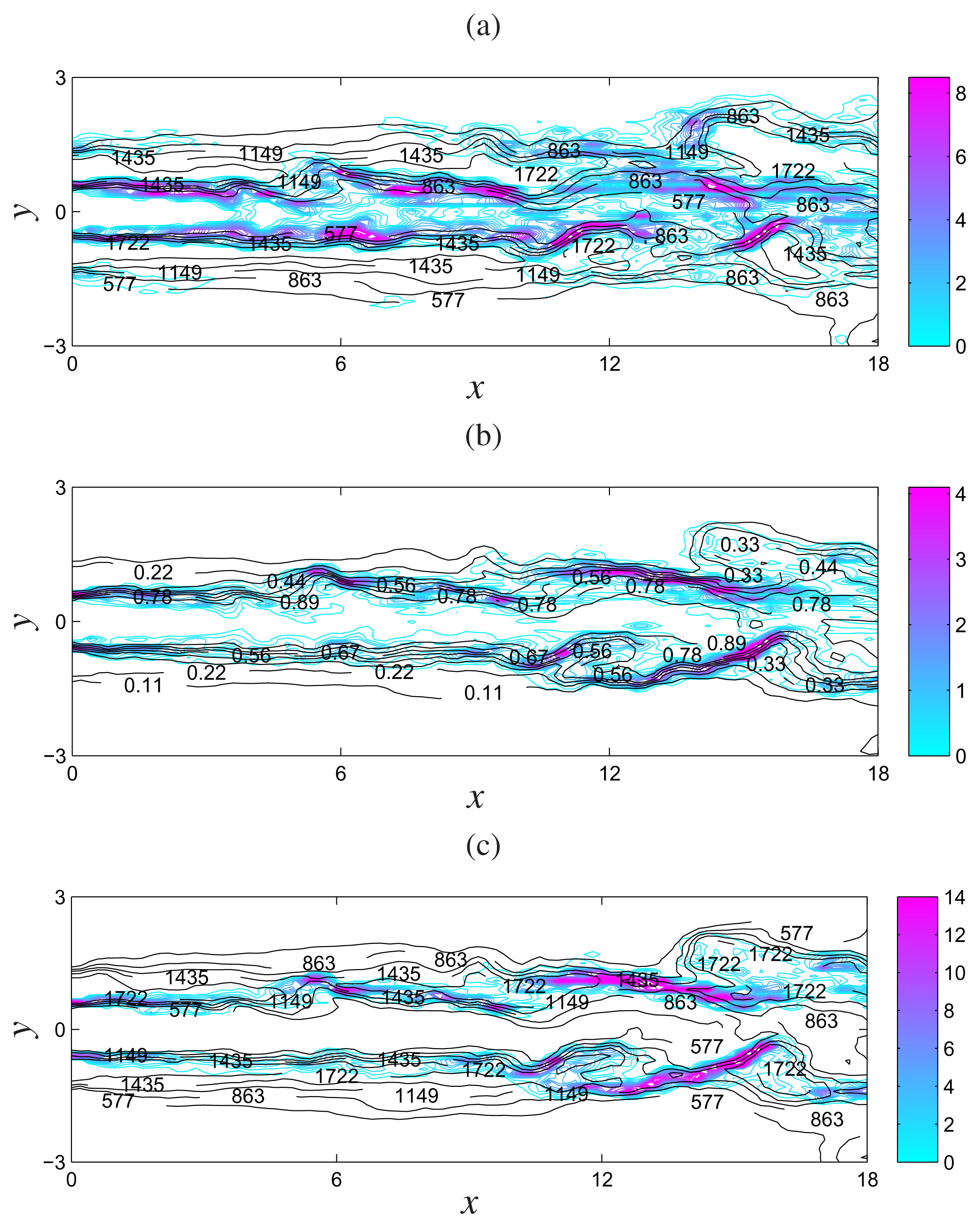
 ), x = 5 (
), x = 5 (
 ), x = 10 (
), x = 10 (
 ) and x = 15 (−).
) and x = 15 (−).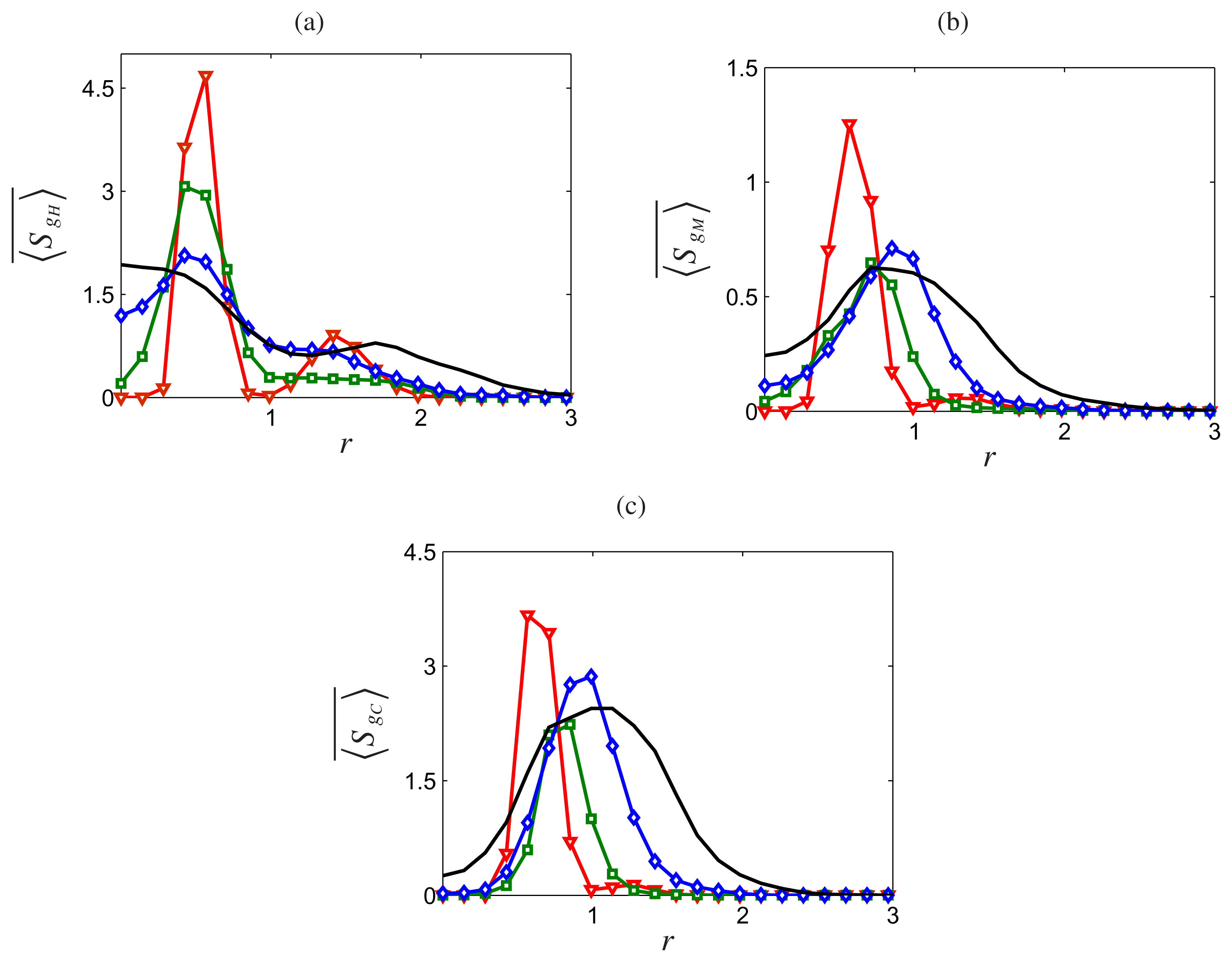
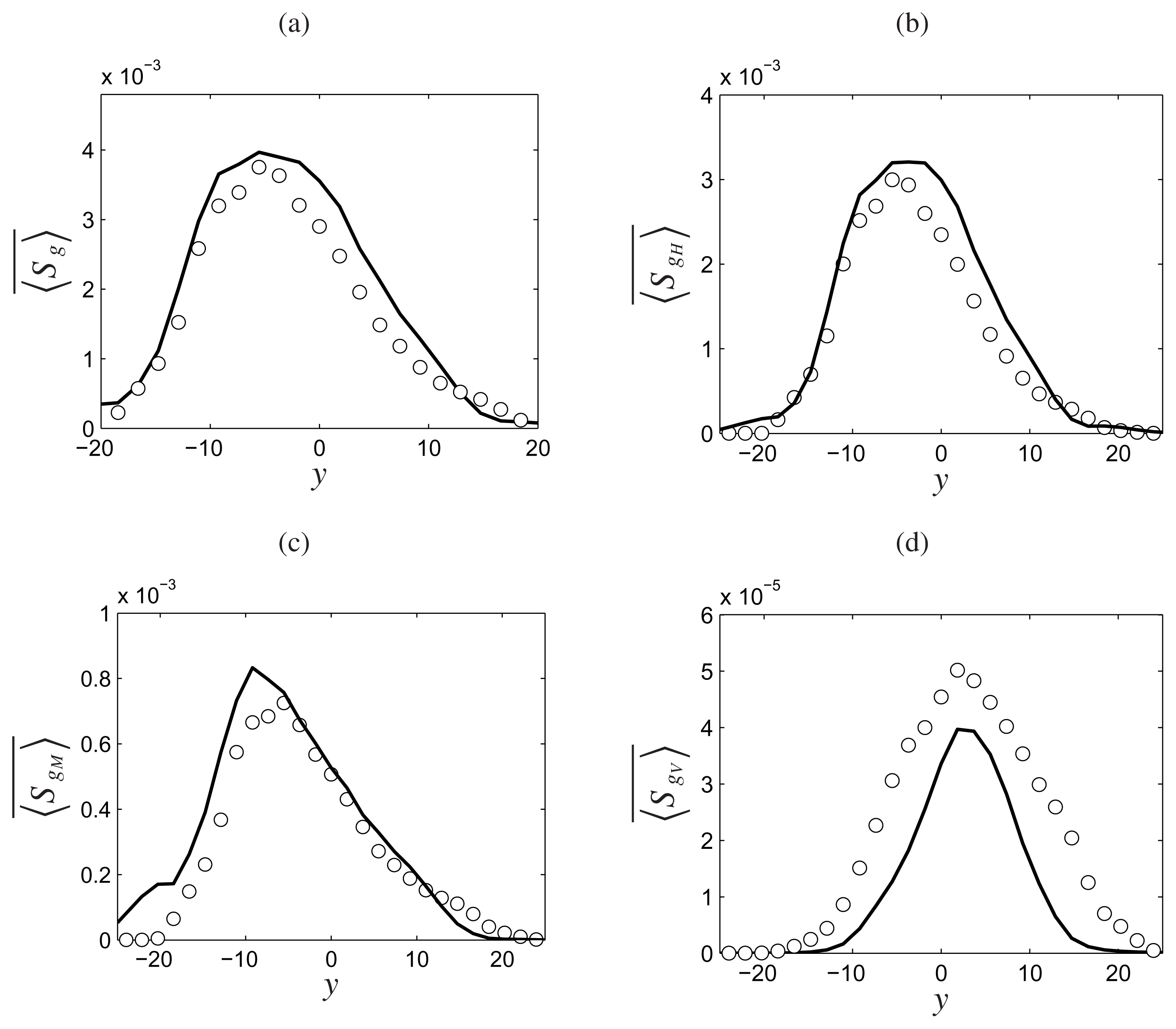
 ), mass diffusion (
), mass diffusion (
 ) and chemical reaction (−) at (a) x = 5 and (b) x = 15 in Sandia Flame D simulations.
) and chemical reaction (−) at (a) x = 5 and (b) x = 15 in Sandia Flame D simulations.
 ), mass diffusion (
), mass diffusion (
 ) and chemical reaction (−) at (a) x = 5 and (b) x = 15 in Sandia Flame D simulations.
) and chemical reaction (−) at (a) x = 5 and (b) x = 15 in Sandia Flame D simulations.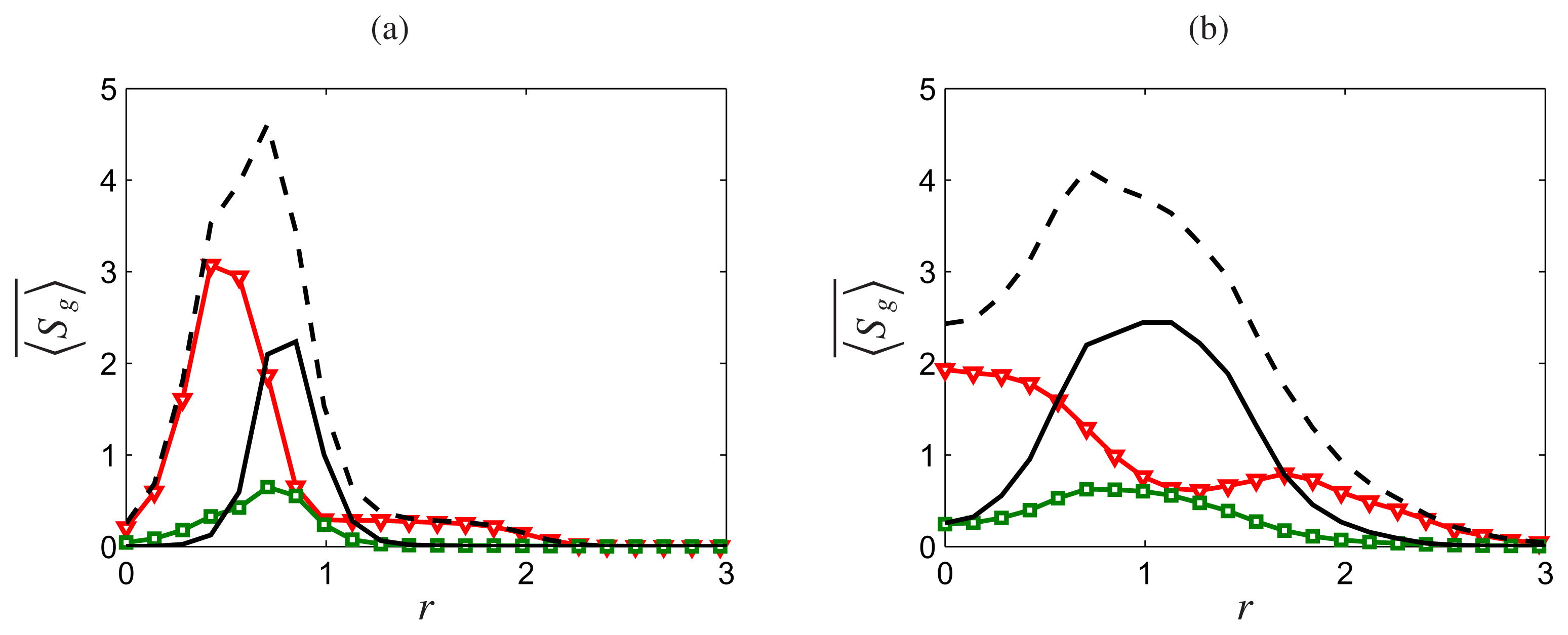
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Safari, M.; Hadi, F.; Sheikhi, M.R.H. Progress in the Prediction of Entropy Generation in Turbulent Reacting Flows Using Large Eddy Simulation. Entropy 2014, 16, 5159-5177. https://doi.org/10.3390/e16105159
Safari M, Hadi F, Sheikhi MRH. Progress in the Prediction of Entropy Generation in Turbulent Reacting Flows Using Large Eddy Simulation. Entropy. 2014; 16(10):5159-5177. https://doi.org/10.3390/e16105159
Chicago/Turabian StyleSafari, Mehdi, Fatemeh Hadi, and M. Reza H. Sheikhi. 2014. "Progress in the Prediction of Entropy Generation in Turbulent Reacting Flows Using Large Eddy Simulation" Entropy 16, no. 10: 5159-5177. https://doi.org/10.3390/e16105159
APA StyleSafari, M., Hadi, F., & Sheikhi, M. R. H. (2014). Progress in the Prediction of Entropy Generation in Turbulent Reacting Flows Using Large Eddy Simulation. Entropy, 16(10), 5159-5177. https://doi.org/10.3390/e16105159



