Permutation Complexity and Coupling Measures in Hidden Markov Models

Abstract

Recently, the duality between values (words) and orderings (permutations) has been proposed by the authors as a basis to discuss the relationship between information theoretic measures for finite-alphabet stationary stochastic processes and their permutation analogues. It has been used to give a simple proof of the equality between the entropy rate and the permutation entropy rate for any finite-alphabet stationary stochastic process and to show some results on the excess entropy and the transfer entropy for finite-alphabet stationary ergodic Markov processes. In this paper, we extend our previous results to hidden Markov models and show the equalities between various information theoretic complexity and coupling measures and their permutation analogues. In particular, we show the following two results within the realm of hidden Markov models with ergodic internal processes: the two permutation analogues of the transfer entropy, the symbolic transfer entropy and the transfer entropy on rank vectors, are both equivalent to the transfer entropy if they are considered as the rates, and the directed information theory can be captured by the permutation entropy approach.

1. Introduction

Recently, the permutation-information theoretic approach to time series analysis proposed by Bandt and Pompe [1] has become popular in various fields [2]. It has been proven that the method of permutation is easy to implement relative to the other traditional methods and is robust under the existence of noise [3,4,5,6,7]. However, if we turn our eyes to its theoretical side, few results are known for the permutation analogues of information theoretic measures, except the entropy rate.

There are two approaches to introduce permutation into dynamical systems theory [8]. The first approach is introduced by Bandt et al. [9]. Given a one-dimensional interval map, they considered permutations induced by iterations of the map. Each point in the interval is classified into one of n! permutations according to the permutation defined by n − 1 times iterations of the map starting from the point. Then, the Shannon entropy of this partition (called the standard partition) of the interval is taken and normalized by n. The quantity obtained in the limit n → ∞ is called permutation entropy if it exists. It was proven that the permutation entropy is equal to the Kolmogorov-Sinai entropy for any piecewise monotone interval map [9]. This approach based on the standard partitions was extended by Keller et al. [10,11,12,13,14].

The second approach is taken by Amigó et al. [2,15,16]. In this approach, given a measure-preserving map on a probability space, first, an arbitrary finite partition of the space is taken. This gives rise to a finite-alphabet stationary stochastic process. An arbitrary ordering is introduced on the alphabet, and the permutations of the words of finite lengths can be naturally defined (see Section 2 below). It is proven that the Shannon entropy of the occurrence of the permutations of a fixed length normalized by the length converges in the limit of the large length of the permutations. The quantity obtained is called the permutation entropy rate (also called metric permutation entropy) and is shown to be equal to the entropy rate of the process. By taking the limit of finer partitions of the measurable space, the permutation entropy rate of the measure-preserving map is defined if the limit exists. Amigó [16] proved that it exists and is equal to the Kolmogorov-Sinai entropy.

In this paper, we restrict our attention to finite-alphabet stationary stochastic processes. Thus, we follow the second approach, namely, ordering on the alphabet is introduced arbitrarily. For quantities other than the entropy rate, three results for finite-alphabet stationary ergodic Markov processes have been shown by our previous work: the equality between the excess entropy and the permutation excess entropy [17], the equality between the mutual information expression of the excess entropy and its permutation analogue [18] and the equality between the transfer entropy rate and the symbolic transfer entropy rate [19]. Whether these equalities for the permutation entropies can be extended to general finite-alphabet stationary ergodic stochastic processes is still unknown. However, for the modified permutation entropies defined by the partition of the set of words based on permutations and equalities between occurrences of symbols, which is finer than the partition obtained by permutations only, we have the corresponding equalities for general finite-alphabet stationary ergodic stochastic processes [20].

The purpose of this paper is to generalize our previous results on the permutation entropies for finite-alphabet stationary ergodic Markov processes to output processes of finite-state finite-alphabet hidden Markov models with ergodic internal processes. Upon this generalization, somewhat ad hoc proofs in our previous work for multivariate stationary ergodic Markov processes become straightforward. The key property of hidden Markov models (HMMs), which we will use repeatedly, is the following: a marginal process of the output process of a hidden Markov model with an ergodic internal process is, again, the output process of a hidden Markov model with an ergodic internal process obtained from the original hidden Markov model. In general, this property does not hold for multivariate stationary ergodic Markov processes. The generalization also makes us easily access quantities that have not been considered theoretically in the permutation approach. In this paper, we shall treat the following quantities: excess entropy [21], transfer entropy [22,23], momentary information transfer [24] and directed information [25,26]. As far as the authors are aware, the equality between the momentary information transfer and its permutation analogue and that for directed information have not been discussed anywhere. The equalities could be directly proven with some extra discussion to that in [17] for finite-alphabet multivariate stationary ergodic Markov processes. However, the equalities can be proven straightforwardly, as in [17], within the realm of HMMs with ergodic internal processes, once we show Lemma 3 below.

This paper is organized as follows: In Section 2, we briefly review our previous result on the duality between words and permutations to make this paper as self-contained as possible. In Section 3, we prove a lemma about finite-state finite-alphabet hidden Markov models. In Section 4, we show equalities between various information theoretic complexity and coupling measures and their permutation analogues that hold for output processes of finite-state finite-alphabet hidden Markov models with ergodic internal processes. In Section 5, we discuss how our results are related to the previous work in the literature.

2. The Duality between Words and Permutations

In this section, we summarize the results from our previous work [17] that will be used in this paper.

Let $A_n$ be a finite set consisting of natural numbers from one to n, called an alphabet. In this paper, $A_n$ is considered as a totally ordered set ordered by the usual “less-than-or-equal-to” relationship. When we emphasize the total order, we call $A_n$ an ordered alphabet.

Note that the results in this paper hold for every total order on $A_n$. This is because the probability of the occurrence of the permutations in a given stationary stochastic process over $A_n$ with an arbitrary total order is just a re-indexing of that with the “less-than-or-equal-to” total order.

The set of all permutations of length $L\ge 1$ is denoted by ${\mathcal{S}}_L$. Namely, ${\mathcal{S}}_L$ is the set of all bijections π on the set $\{1,2,\cdots ,L\}$. For convenience, we sometimes denote a permutation π of length L by a string $\pi (1)\pi (2)\cdots \pi (L)$. The number of descents, places with $\pi (i)>\pi (i+1)$, of $\pi \in {\mathcal{S}}_L$ is denoted by $\text{Desc}(\pi )$. For example, if $\pi \in {\mathcal{S}}_5$ is given by $\pi (1)\pi (2)\pi (3)\pi (4)\pi (5)=35,142$, then $\text{Desc}(\pi )=2$.

Let $A_n^L=\underset{L}{\underbrace{A_n\times \cdots \times A_n}}$ be the L-fold product of $A_n$. A word of length $L\ge 1$ is an element of $A_n^L$. It is denoted by $x_{1:L}:=x_1\cdots x_L:=(x_1,\cdots ,x_L)\in A_n^L$. We say that the permutation type of a word $x_{1:L}$ is $\pi \in {\mathcal{S}}_L$ if we have $x_{\pi (i)}\le x_{\pi (i+1)}$ and $\pi (i)<\pi (i+1)$ when $x_{\pi (i)}=x_{\pi (i+1)}$ for $i=1,2,\cdots ,L-1$. Namely, the permutation type of $x_{1:L}$ is the permutation of indices defined by re-ordering symbols $x_1,\cdots ,x_L$ in the increasing order. For example, the permutation type of $x_{1:5}=31,212\in A_3^5$ is $\pi (1)\pi (2)\pi (3)\pi (4)\pi (5)=24,351$, because $x_2{x}_4{x}_3{x}_5{x}_1=11,223$.

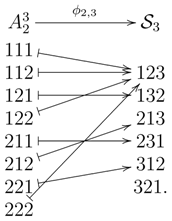Let ${\varphi }_{n,L}:A_n^L\to {\mathcal{S}}_L$ be a map sending each word, $x_{1:L}$, to its permutation type, $\pi ={\varphi }_{n,L}(x_{1:L})$. For example, the map, ${\varphi }_{2,3}:A_2^3\to {\mathcal{S}}_3$, is given by: This example illustrates the following two properties of the map, ${\varphi }_{n,L}$: first, ${\varphi }_{n,L}(A_n^L)$ can be a proper subset of ${\mathcal{S}}_L$. As one can see from Theorem 1 below, ${\varphi }_{n,L}(A_n^L)$ is a proper subset of ${\mathcal{S}}_L$, if and only if $L>n$. Second, two different words can have the same permutation type.

We define another map, ${\mu }_{n,L}:{\varphi }_{n,L}\left(A_n^L\right)\subseteq {\mathcal{S}}_L\to A_n^L$, by the following procedure:

(i)

Given a permutation, $\pi \in {\varphi }_{n,L}\left(A_n^L\right)\subseteq {\mathcal{S}}_L$, we decompose the sequence, $\pi (1)\cdots \pi (L)$, of length L into maximal ascending subsequences. A subsequence, $i_j\cdots i_{j+k}$, of a sequence, $i_1\cdots i_L$, of length L is called a maximal ascending subsequence if it is ascending, namely, $i_j\le i_{j+1}\le \cdots \le i_{j+k}$, and neither $i_{j-1}{i}_j\cdots i_{j+k}$ nor $i_j{i}_{j+1}\cdots i_{j+k+1}$ is ascending;

(ii)

If $\pi (1)\cdots \pi (i_1),\pi (i_1+1)\cdots \pi (i_2),\cdots ,\pi (i_{k-1}+1)\cdots \pi (L)$ is a decomposition of $\pi (1)\cdots \pi (L)$ into maximal ascending subsequences, then a word, $x_{1:L}\in A_n^L$, is defined by:

$$\begin{array}{c}\hfill x_{\pi (1)}=\cdots =x_{\pi (i_1)}=1,x_{\pi (i_1+1)}=\cdots =x_{\pi (i_2)}=2,\cdots ,x_{\pi (i_{k-1})+1}=\cdots =x_{\pi (L)}=k.\end{array}$$

We define ${\mu }_{n,L}(\pi )=x_{1:L}$. Note that $\text{Desc}(\pi )\le n-1$, because π is the permutation type of some word, $y_{1:L}\in A_n^L$. Thus, we have $k=\text{Desc}(\pi )+1\le n$. Hence, ${\mu }_{n,L}$ is well-defined as a map from ${\varphi }_{n,L}\left(A_n^L\right)$ to $A_n^L$.

By construction, we have ${\varphi }_{n,L}\circ {\mu }_{n,L}(\pi )=\pi$ for all $\pi \in {\varphi }_{n,L}\left(A_n^L\right)$. To illustrate the construction of ${\mu }_{n,L}$, let us consider a word, $y_{1:5}=21,123\in A_3^5$. The permutation type of $y_{1:5}$ is $\pi (1)\pi (2)\pi (3)\pi (4)\pi (5)=23,145$. The decomposition of $23,145$ into maximal ascending subsequences is 23, 145. We obtain ${\mu }_{n,L}(\pi )=x_1{x}_2{x}_3{x}_4{x}_5=21122$ by putting $x_2{x}_3{x}_1{x}_4{x}_5=11,222$.

Theorem 1 

(i) 

For every $\pi \in {\mathcal{S}}_L$,

$$|{\varphi }_{n,L}^{-1}(\pi )|=\left(\genfrac{}{}{0pt}{}{L+n-\text{Desc}(\pi )-1}{L}\right),$$

where $\left(\genfrac{}{}{0pt}{}{a}{b}\right)=0$ if $a<b$. In particular, ${\varphi }_{n,L}^{-1}(\pi )=\varnothing$, if and only if $\text{Desc}(\pi )\ge n$;

(ii) 

Let us put:

$$\begin{array}{ccc}\hfill B_{n,L}& :=& \{x_{1:L}\in A_n^L|{\varphi }_{n,L}^{-1}(\pi )=\{x_{1:L}\}\mathit{\text{for}}\mathit{\text{some}}\pi \in {\mathcal{S}}_L\},\hfill \\ \hfill C_{n,L}& :=& \{\pi \in {\mathcal{S}}_L||{\varphi }_{n,L}^{-1}(\pi )|=1\}.\hfill \end{array}$$

Then, ${\varphi }_{n,L}$ restricted on $B_{n,L}$ is a map into $C_{n,L}$ and ${\mu }_{n,L}$ restricted on $C_{n,L}$ is a map into $B_{n,L}$. They form a pair of mutually inverse maps. Furthermore, we have:

$$\begin{array}{ccc}\hfill B_{n,L}& =& \{x_{1:L}\in A_n^L|1\le \forall i\le n-1,1\le \exists j<k\le L\text{s.}\text{t.}{x}_j=i+1,x_k=i\},\hfill \\ \hfill C_{n,L}& =& \{\pi \in {\mathcal{S}}_L|\text{Desc}(\pi )=n-1\}.\hfill \end{array}$$

Proof. 

The theorem is a recasting of statements in Lemma 5 and Theorem 9 in [17].

Let $\mathbf{X}=\{X_1,X_2,\cdots \}$ be a finite-alphabet stationary stochastic process, where each stochastic variable, $X_i$, takes its value in $A_n$. By the assumed stationarity, the probability of the occurrence of any word $x_{1:L}\in A_n^L$ is time-shift invariant:

$$\begin{array}{c}\hfill \text{Pr}\{X_1=x_1,\cdots ,X_L=x_L\}=\text{Pr}\{X_{k+1}=x_1,\cdots ,X_{k+L}=x_L\}\end{array}$$

for all $k,L\ge 1$. Hence, it makes sense to define it without referring to the time to start. We denote the probability of the occurrence of a word, $x_{1:L}\in A_n^L$ by $p(x_{1:L})=p(x_1\cdots x_L)$. The probability of the occurrence of a permutation $\pi \in {\mathcal{S}}_L$ is given by $p(\pi )={\sum }_{x_{1:L}\in {\varphi }_{n,L}^{-1}(\pi )}p(x_{1:L})$.

For a finite-alphabet stationary stochastic process, $\mathbf{X}$, over the alphabet, $A_n$, we define:

$$\begin{array}{c}\hfill {\alpha }_{\mathbf{X},L}:=\sum _{\begin{array}{c}\pi \in {\mathcal{S}}_L,\\ |{\varphi }_{n,L}^{-1}(\pi )|>1\end{array}}p(\pi )=\sum _{\pi \notin C_{n,L}}p(\pi )\end{array}$$

and:

$$\begin{array}{ccc}\hfill {\beta }_{x,\mathbf{X},L}& =& \text{Pr}\{x_{1:N}\in A_n^N|x_j\ne x\text{for}\text{all}1\le j\le N\}\hfill \\ & =& \sum _{\begin{array}{c}{x}_j\ne x,\\ 1\le j\le N\end{array}}p(x_1\cdots x_N),\hfill \end{array}$$

where $L\ge 1$, $x\in A_n$, $N=\lfloor L/2\rfloor$, and $\lfloor a\rfloor$ is the largest integer not greater than a.

Lemma 2 

Let $\mathbf{X}$ be a finite-alphabet stationary stochastic process and ϵ a positive real number. If ${\beta }_{x,\mathbf{X},L}<ϵ$ for all $x\in A_n$, then we have ${\alpha }_{\mathbf{X},L}<2nϵ$.

Proof. 

The claim follows from Theorem 1 (ii). See Lemma 12 in [17] for the complete proof.

3. A Result on Finite-State Finite-Alphabet Hidden Markov Models

In this paper, we use the parametric description of hidden Markov models as given in [27].

A finite-state finite-alphabet hidden Markov model (in short, HMM) [27] is a quadruple, $(\Sigma ,A,{\{T^{(a)}\}}_{a\in A},\mu )$, where Σ and A are finite sets, called state set and alphabet, respectively, ${\{T^{(a)}\}}_{a\in A}$ is a family of $|\Sigma |\times |\Sigma |$ matrices indexed by elements of A, where $|\Sigma |$ is the size of state set Σ, and μ is a probability distribution on the set Σ. The following conditions must be satisfied:

(i)

$T_{s{s}^{\prime }}^{(a)}\ge 0$ for any $s,s^{\prime }\in \Sigma$ and $a\in A$;

(ii)

${\sum }_{s^{\prime },a}{T}_{s{s}^{\prime }}^{(a)}=1$ for any $s\in \Sigma$;

(iii)

and $\mu (s^{\prime })={\sum }_{s,a}\mu (s)T_{s{s}^{\prime }}^{(a)}$ for any $s^{\prime }\in \Sigma$.

Any probability distribution satisfying condition (iii) is called a stationary distribution. The $|\Sigma |\times |\Sigma |$ matrix $T:={\sum }_{a\in A}{T}^{(a)}$ is called a state transition matrix. The ternary, $(\Sigma ,T,\mu )$, defines the underlying Markov chain. Note that condition (iii) is equivalent to condition (iii’) $\mu (s^{\prime })={\sum }_s\mu (s)T_{s{s}^{\prime }}$.

Two finite-alphabet stationary processes are induced by a HMM $(\Sigma ,A,{\{T^{(a)}\}}_{a\in A},\mu )$. One is solely determined by the underlying Markov chain. It is called an internal process and is denoted by $\mathbf{S}=\{S_1,S_2,\cdots \}$. The alphabet for $\mathbf{S}$ is Σ. The joint probability distributions that characterize $\mathbf{S}$ is given by:

$$\text{Pr}\{S_1=s_1,S_2=s_2,\cdots ,S_L=s_L\}:=\mu (s_1)T_{s_1{s}_2}\cdots T_{s_{L-1}{s}_L}$$

for any $s_1,\cdots ,s_L\in \Sigma$ and $L\ge 1$. The other process $\mathbf{X}=\{X_1,X_2,\cdots \}$ with the alphabet, A, is defined by the following joint probability distributions:

$$\text{Pr}\{X_1=x_1,X_2=x_2,\cdots ,X_L=x_L\}:=\sum _{s,s^{\prime }}\mu (s){\left(T^{(x_1)}\cdots T^{(x_L)}\right)}_{s{s}^{\prime }}$$

for any $x_1,\cdots ,x_L\in A$ and $L\ge 1$ and is called an output process. The stationarity of the probability distribution μ ensures that of both the internal and output processes.

Symbols $a\in A$, such that $T^{(a)}=O$ occurs in the output process with a probability of zero. Hence, we obtain the equivalent output process, even if we remove these symbols. Thus, we can assume that $T^{(a)}\ne O$ for any $a\in A$ without loss of generality.

The internal process, $\mathbf{S}$, of an HMM $(\Sigma ,A,{\{T^{(a)}\}}_{a\in A},\mu )$ is called ergodic if the state transition matrix, T, is irreducible [28]: for any $s,s^{\prime }\in \Sigma$, there exists $k>0$, such that ${(T^k)}_{s{s}^{\prime }}>0$. If the internal process, $\mathbf{S}$, is ergodic, then the stationary distribution μ is uniquely determined by the state transition matrix T via condition (iii). Every finite-alphabet finite-order multivariate stationary ergodic Markov process can be described as an HMM with an ergodic internal process.

Lemma 3 

Let $\mathbf{X}$ be the output process of an HMM $(\Sigma ,A_n,{\{T^{(a)}\}}_{a\in A_n},\mu )$, where $A_n=\{1,2,\cdots ,n\}$ is an ordered alphabet. If the internal process, $\mathbf{S}$, of the HMM is ergodic, then for every $x\in A_n$, there exists $0<{\gamma }_x<1$ and $C_x>0$, such that ${\beta }_{x,\mathbf{X},L}<C_x{\gamma }_x^L$ for all $L\ge 1$.

Proof. 

Given $L\ge 1$, let us put $N:=\lfloor L/2\rfloor$. Fix an arbitrary $x\in A_n$. We have:

$$\begin{array}{ccc}\hfill {\beta }_{x,\mathbf{X},L}& =& \sum _{\begin{array}{c}{x}_j\ne x,\\ 1\le j\le N\end{array}}p(x_1\cdots x_N)\hfill \\ & =& \sum _{\begin{array}{c}{x}_j\ne x,\\ 1\le j\le N\end{array}}\sum _{s,s^{\prime }}\mu (s){\left(T^{(x_1)}\cdots T^{(x_N)}\right)}_{s{s}^{\prime }}\hfill \\ & =& \langle \mu {\left(T-T^{(x)}\right)}^N,\mathbf{1}\rangle ,\hfill \end{array}$$

where $\mathbf{1}=(1,1,\cdots ,1)$ and $\langle \cdots ,\cdots \rangle$ is the usual inner product of the $|\Sigma |$-dimensional Euclidean space, ${\mathbb{R}}^{|\Sigma |}$. The spectral radius $\rho (T_x)$ of the matrix $T_{(x)}:=T-T^{(x)}$ is less than one. Indeed, this follows immediately from the Perron-Frobenius theorem for non-negative irreducible matrices: T is a non-negative irreducible matrix with $\rho (T)=1$ by the assumption. Since $T\ge T_{(x)}\ge O$ and $T\ne T_{(x)}$, applying Theorem 1.5 (e) in [29] implies that $\rho (T_{(x)})<\rho (T)=1$. By Lemma 5.6.10 in [30], for any $ϵ>0$, there exists a matrix norm, ${\parallel \cdots \parallel }^{\prime }$, such that $\rho (T_{(x)})\le {\parallel T_{(x)}\parallel }^{\prime }<\rho (T_{(x)})+ϵ$. It follows that for any $ϵ>0$, there exists $C_{ϵ}>0$, such that for all $k\ge 1$:

$$\parallel \mu T_{(x)}^k\parallel \le C_{ϵ}{(\rho (T_{(x)})+ϵ)}^k\parallel \mu \parallel ,$$

where $\parallel \cdots \parallel$ is the Euclidean norm. Since we have $\rho (T_{(x)})<1$, we can choose $ϵ>0$, so that $\rho (T_{(x)})+ϵ<1$. If we put ${\gamma }_x:={(\rho (T_{(x)})+ϵ)}^{\frac{1}{2}}$ and $C_x:=C_{ϵ}{(\rho (T_{(x)})+ϵ)}^{-1}\parallel \mu \parallel \parallel \mathbf{1}\parallel$, then we obtain ${\beta }_{x,\mathbf{X},L}<C_x{\gamma }_x^L$ by the Cauchy-Schwartz inequality as desired.

4. Permutation Complexity and Coupling Measures

In this section, we discuss the equalities between complexity and coupling measures and their permutation analogues for the output processes of HMMs whose internal processes are ergodic.

4.1. Fundamental Lemma

Let $({\mathbf{X}}^1,\cdots ,{\mathbf{X}}^m)$ be a multivariate finite-alphabet stationary stochastic process, where each univariate process, ${\mathbf{X}}^k=\{X_1^k,X_2^k,\cdots \},k=1,2,\cdots ,m$, is defined over an ordered alphabet, $A_{n_k}$. Note that the notation for stochastic variables is different from that in [17]. Here, $X_t^k$ is the stochastic variable for the k-th component of the multivariate process at time step t.

We use the notations:

$$\begin{array}{ccc}\hfill p(x_{1:L_1}^1,\cdots ,x_{1:L_m}^m)& :=& \text{Pr}\{X_{t_1:t_1+L_1-1}^1=x_{1:L_1}^1,\cdots ,X_{t_m:t_m+L_m-1}^m=x_{1:L_m}^m\},\hfill \\ \hfill p({\pi }_1,\cdots ,{\pi }_m)& :=& \text{Pr}\{{\varphi }_{n_k,L_k}\circ X_{t_k:t_k+L_k-1}^k={\pi }_k,k=1,\cdots ,m\}\hfill \end{array}$$

and:

$$\begin{array}{c}\hfill p({\pi }_k):=\text{Pr}\{{\varphi }_{n_k,L_k}\circ X_{t_k:t_k+L_k-1}^k={\pi }_k\},\end{array}$$

where $1\le t_k,L_k$, $x_{1:L_k}^k\in A_{n_k}^{L_k}$ and ${\pi }_k\in {\mathcal{S}}_{L_k}$ for $k=1,\cdots ,m$. In general, if $m\ge 2$, then $p(x_{1:L_1}^1,\cdots ,x_{1:L_m}^m)$ and $p({\pi }_1,\cdots ,{\pi }_m)$ depend on $(t_1,\cdots ,t_m)$ and are invariant only by the simultaneous time shift $(t_1,\cdots ,t_m)\mapsto (t_1+\tau ,\cdots ,t_m+\tau )$. However, here, we make the dependence on $(t_1,\cdots ,t_m)$ implicit for notational simplicity.

Lemma 4 

Let:

$$\begin{array}{c}\hfill \Delta H:=H(X_{t_1:t_1+L_1-1}^1,\cdots ,X_{t_m:t_m+L_m-1}^m)-H^{*}(X_{t_1:t_1+L_1-1}^1,\cdots ,X_{t_m:t_m+L_m-1}^m),\end{array}$$

where:

$$\begin{array}{c}\hfill H(X_{t_1:t_1+L_1-1}^1,\cdots ,X_{t_m:t_m+L_m-1}^m)=-\sum _{x_{1:L_1}^1,\cdots ,x_{1:L_m}^m}p(x_{1:L_1}^1,\cdots ,x_{1:L_m}^m)logp(x_{1:L_1}^1,\cdots ,x_{1:L_m}^m)\end{array}$$

and:

$$\begin{array}{c}\hfill H^{*}(X_{t_1:t_1+L_1-1}^1,\cdots ,X_{t_m:t_m+L_m-1}^m)=-\sum _{{\pi }_1,\cdots ,{\pi }_m}p({\pi }_1,\cdots ,{\pi }_m)logp({\pi }_1,\cdots ,{\pi }_m)\end{array}$$

are the Shannon entropies of the joint occurrence of words $x_{1:L_1}^1,\cdots ,x_{1:L_m}^m$ and permutations ${\pi }_1,\cdots ,{\pi }_m$, respectively, and the base of the logarithm is taken as two. Then, we have:

$$\begin{array}{c}\hfill 0\le \Delta H\le \left(\sum _{k=1}^m{\alpha }_{{\mathbf{X}}^k,L_k}\right)\left(\sum _{k=1}^m{n}_{k}log(L_k+n_k)\right).\end{array}$$

Proof. 

We have:

$$\begin{array}{ccc}\hfill \Delta H& =& H(X_{t_1:t_1+L_1-1}^1,\cdots ,X_{t_m:t_m+L_m-1}^m)-H^{*}(X_{t_1:t_1+L_1-1}^1,\cdots ,X_{t_m:t_m+L_m-1}^m)\hfill \\ & =& \sum _{\begin{array}{c}{\pi }_1,\cdots ,{\pi }_m,\\ p({\pi }_1,\cdots ,{\pi }_m)>0\end{array}}p({\pi }_1,\cdots ,{\pi }_m)\hfill \\ & & \times \left(-\sum _{\begin{array}{c}{x}_{1:L_k}^k\in {\varphi }_{n_k,L_k}^{-1}({\pi }_k),\\ 1\le k\le m\end{array}}\frac{p(x_{1:L_1}^1,\cdots ,x_{1:L_m}^m)}{p({\pi }_1,\cdots ,{\pi }_m)}log\frac{p(x_{1:L_1}^1,\cdots ,x_{1:L_m}^m)}{p({\pi }_1,\cdots ,{\pi }_m)}\right).\hfill \end{array}$$

By Theorem 1 (i), it holds that:

$$\begin{array}{ccc}\hfill 0& \le & -\sum _{\begin{array}{c}{x}_{1:L_k}^k\in {\varphi }_{n_k,L_k}^{-1}({\pi }_k),\\ 1\le k\le m\end{array}}\frac{p(x_{1:L_1}^1,\cdots ,x_{1:L_m}^m)}{p({\pi }_1,\cdots ,{\pi }_m)}log\frac{p(x_{1:L_1}^1,\cdots ,x_{1:L_m}^m)}{p({\pi }_1,\cdots ,{\pi }_m)}\hfill \\ & \le & log\left(\prod _{k=1}^m\left(\genfrac{}{}{0pt}{}{L_k+n_k-\text{Desc}({\pi }_k)-1}{L_k}\right)\right)\hfill \\ & \le & log\left(\prod _{k=1}^m{(L_k+n_k)}^{n_k}\right)\hfill \\ & =& \sum _{k=1}^m{n}_{k}log(L_k+n_k)\hfill \end{array}$$

for $({\pi }_1,\cdots ,{\pi }_m)\in {\mathcal{S}}_{L_1}\times \cdots \times {\mathcal{S}}_{L_k}$ such that $p({\pi }_1,\cdots ,{\pi }_m)>0$.

If $|{({\varphi }_{n_1,L_1}\times \cdots \times {\varphi }_{n_m,L_m})}^{-1}({\pi }_1,\cdots ,{\pi }_m)|=1$ then:

$$\begin{array}{c}\hfill -\sum _{\begin{array}{c}{x}_{1:L_k}^k\in {\varphi }_{n_k,L_k}^{-1}({\pi }_k),\\ 1\le k\le m\end{array}}\frac{p(x_{1:L_1}^1,\cdots ,x_{1:L_m}^m)}{p({\pi }_1,\cdots ,{\pi }_m)}log\frac{p(x_{1:L_1}^1,\cdots ,x_{1:L_m}^m)}{p({\pi }_1,\cdots ,{\pi }_m)}=0.\end{array}$$

On the other hand, we have:

$$\begin{array}{ccc}\hfill \sum _{\begin{array}{c}{\pi }_1,\cdots ,{\pi }_m,\\ \exists k\text{s.t.}|{\varphi }_{n_k,L_k}^{-1}({\pi }_k)|>1\end{array}}p({\pi }_1,\cdots ,{\pi }_m)& \le & \sum _{k=1}^m\sum _{\begin{array}{c}{\pi }_k,\\ |{\varphi }_{n_k,L_k}^{-1}({\pi }_k)|>1\end{array}}p({\pi }_k)\hfill \\ & =& \sum _{k=1}^m{\alpha }_{{\mathbf{X}}^k,L_k}.\hfill \end{array}$$

This completes the proof of the inequality.

4.2. Excess Entropy

Let $\mathbf{X}$ be a finite-alphabet stationary stochastic process. Its excess entropy is defined by [21]:

$$\begin{array}{ccc}\hfill \mathbf{E}(\mathbf{X})& =& \underset{L\to \infty }{lim}\left(H(X_{1:L})-h(\mathbf{X})L\right)\hfill \\ & =& \sum _{L=1}^{\infty }\left(H(X_L|X_{1:L-1})-h(\mathbf{X})\right),\hfill \end{array}$$

if the limit on the right-hand side exists, where $h(\mathbf{X})={lim}_{L\to \infty }H(X_{1:L})/L$ is the entropy rate of $\mathbf{X}$, which exists for any finite-alphabet stationary stochastic process [31].

The excess entropy has been used as a measure of complexity [32,33,34,35,36,37]. Actually, it quantifies global correlations present in a given stationary process in the following sense. If $\mathbf{E}(\mathbf{X})$ exists, then it can be written as the mutual information between the past and future:

$$\begin{array}{c}\hfill \mathbf{E}(\mathbf{X})=\underset{L\to \infty }{lim}I(X_{1:L};X_{L+1:2L}).\end{array}$$

It is known that if $\mathbf{X}$ is the output process of an HMM, then $\mathbf{E}(\mathbf{X})$ exists [38].

When the alphabet of $\mathbf{X}$ is an ordered alphabet $A_n$, we define the permutation excess entropy of $\mathbf{X}$ by [17]:

$$\begin{array}{ccc}\hfill {\mathbf{E}}^{*}(\mathbf{X})& =& \underset{L\to \infty }{lim}\left(H^{*}(X_{1:L})-h^{*}(\mathbf{X})L\right)\hfill \\ & =& \sum _{L=1}^{\infty }\left(H^{*}(X_L|X_{1:L-1})-h^{*}(\mathbf{X})\right),\hfill \end{array}$$

if the limit on the right-hand side exists, where $h^{*}(\mathbf{X})={lim}_{L\to \infty }{H}^{*}(X_{1:L})/L$ is the permutation entropy rate of $\mathbf{X}$, which exists for any finite-alphabet stationary stochastic process and is equal to the entropy rate $h(\mathbf{X})$ [2,15,16, $H^{*}(X_L|X_{1:L-1}):=H^{*}(X_{1:L})-H^{*}(X_{1:L-1})$, and $H^{*}(X_{1:L})$ and $H^{*}(X_{1:L-1})$ are as defined in the statement of Lemma 4.

The following proposition is a generalization of our previous results in [17,18].

Proposition 5 

Let $\mathbf{X}$ be the output process of an HMM $(\Sigma ,A_n,{\{T^{(a)}\}}_{a\in A_n},\mu )$ with an ergodic internal process. Then, we have:

$$\mathbf{E}(\mathbf{X})={\mathbf{E}}^{*}(\mathbf{X})=\underset{L\to \infty }{lim}{I}^{*}(X_{1:L};X_{L+1:2L}),$$

where $I^{*}(X_{1:L};X_{L+1:2L}):=H^{*}(X_{1:L})+H^{*}(X_{L+1:2L})-H^{*}(X_{1:L},X_{L+1:2L})=2H^{*}(X_{1:L})-H^{*}(X_{1:L},X_{L+1:2L})$.

Proof. 

Let $L\ge 1$. We have:

$$\begin{array}{ccc}\hfill |\left(H(X_{1:L})-h(\mathbf{X})L\right)-\left(H^{*}(X_{1:L})-h^{*}(\mathbf{X})L\right)|& =& |H(X_{1:L})-H^{*}(X_{1:L})|\hfill \\ & \le & {\alpha }_{\mathbf{X},L}nlog(L+n)\hfill \\ & \le & 2C{n}^{2}log(L+n){\gamma }^L,\hfill \end{array}$$

where $C:={max}_{x\in A_n}\{C_x\}$, $\gamma :={max}_{x\in A_n}\{{\gamma }_x\}<1$, and we have used $h(\mathbf{X})=h^{*}(\mathbf{X})$ for the first equality, Lemma 4 for the second inequality and Lemma 2 and Lemma 3 for the last inequality. By taking the limit, $L\to \infty$, we obtain $\mathbf{E}(\mathbf{X})={\mathbf{E}}^{*}(\mathbf{X})$.

To prove ${lim}_{L\to \infty }I(X_{1:L};X_{L+1:2L})={lim}_{L\to \infty }{I}^{*}(X_{1:L};X_{L+1:2L})$, it is sufficient to show that $|H(X_{1:L},X_{L+1:2L})-H^{*}(X_{1:L},X_{L+1:2L})|\to 0$ as $L\to \infty$. This is because we have:

$$\begin{array}{ccc}& & |I(X_{1:L};X_{L+1:2L})-I^{*}(X_{1:L};X_{L+1:2L})|\hfill \\ & \le & 2|H(X_{1:L})-H(X_{1:L})|+|H(X_{1:L},X_{L+1:2L})-H^{*}(X_{1:L},X_{L+1:2L})|.\hfill \end{array}$$

However, this can be shown similarly with the above discussion by applying Lemma 4 to the bivariate process $({\mathbf{X}}^1,{\mathbf{X}}^2):=(\mathbf{X},\mathbf{X})$ and, then, using Lemma 2 and Lemma 3.

4.3. Transfer Entropy and Momentary Information Transfer

In this subsection, we consider two information rates that are measures of coupling direction and strength between two jointly distributed processes and discuss the equalities between them and their permutation analogues. One is the rate of the transfer entropy [22], and the other is the rate of the momentary information transfer [24]. Both are particular instances of the conditional mutual information [39].

Let $(\mathbf{X},\mathbf{Y})$ be a bivariate finite-alphabet stationary stochastic process. We assume that the alphabets of $\mathbf{X}$ and $\mathbf{Y}$ are ordered alphabets, $A_n$ and $A_m$, respectively. For $\tau =1,2,\cdots$, we define the τ-step transfer entropy rate from $\mathbf{Y}$ to $\mathbf{X}$ by:

$$\begin{array}{ccc}\hfill t_{\tau }(\mathbf{Y}\to \mathbf{X})& =& \underset{L\to \infty }{lim}\left[H(X_{L+1:L+\tau }|X_{1:L})-H(X_{L+1:L+\tau }|X_{1:L},Y_{1:L})\right]\hfill \\ & =& \underset{L\to \infty }{lim}\left[H(X_{1:L+\tau })-H(X_{1:L})-H(X_{1:L+\tau },Y_{1:L})+H(X_{1:L},Y_{1:L})\right].\hfill \end{array}$$

When $\tau =1$, $t_1(\mathbf{Y}\to \mathbf{X})$ is called just the transfer entropy rate [40] from $\mathbf{Y}$ to $\mathbf{X}$ and simply denoted by $t(\mathbf{Y}\to \mathbf{X})$.

If we introduce the τ-step entropy rate of $\mathbf{X}$ by:

$$h_{\tau }(\mathbf{X})=\underset{L\to \infty }{lim}H(X_{L+1:L+\tau }|X_{1:L})$$

and the τ-step conditional entropy rate of $\mathbf{X}$ given $\mathbf{Y}$ by:

$$h_{\tau }(\mathbf{X}|\mathbf{Y})=\underset{L\to \infty }{lim}H(X_{L+1:L+\tau }|X_{1:L},Y_{1:L})$$

then we can write:

$$t_{\tau }(\mathbf{Y}\to \mathbf{X})=h_{\tau }(\mathbf{X})-h_{\tau }(\mathbf{X}|\mathbf{Y})$$

because both $h_{\tau }(\mathbf{X})$ and $h_{\tau }(\mathbf{X}|\mathbf{Y})$ exist. We call $h_1(\mathbf{X}|\mathbf{Y})$ the conditional entropy rate and denote it by $h(\mathbf{X}|\mathbf{Y})$. Note that the conditional entropy rate here is slightly different from that found in the literature. For example, in [41], the conditional entropy rate (called the conditional uncertainty) is defined by ${lim}_{L\to \infty }H(X_{L+1}|X_{1:L},Y_{1:L+1})$. The difference from the conditional entropy rate defined here is in whether the conditioning on $Y_{L+1}$ is involved or not.

$h_{\tau }(\mathbf{X})$ is additive, namely, we always have:

$$h_{\tau }(\mathbf{X})=\tau h_1(\mathbf{X})=\tau h(\mathbf{X}).$$

However, for the τ-step conditional entropy rate, the additivity cannot hold in general. It is at most super-additive: we only have the inequality:

$$h_{\tau }(\mathbf{X}|\mathbf{Y})\ge \tau h(\mathbf{X}|\mathbf{Y})$$

in general. Indeed, we have:

$$\begin{array}{ccc}\hfill h_{\tau }(\mathbf{X}|\mathbf{Y})& =& \underset{L\to \infty }{lim}H(X_{L+1:L+\tau }|X_{1:L},Y_{1:L})\hfill \\ & =& \underset{L\to \infty }{lim}\sum _{{\tau }^{\prime }=1}^{\tau }H(X_{L+{\tau }^{\prime }}|X_{1:L+{\tau }^{\prime }-1},Y_{1:L})\hfill \\ & \ge & \underset{L\to \infty }{lim}\sum _{{\tau }^{\prime }=1}^{\tau }H(X_{L+{\tau }^{\prime }}|X_{1:L+{\tau }^{\prime }-1},Y_{1:L+{\tau }^{\prime }-1})\hfill \\ & =& \tau h(\mathbf{X}|\mathbf{Y}).\hfill \end{array}$$

This leads to the sub-additivity of the τ-step transfer entropy rate:

$$t_{\tau }(\mathbf{Y}\to \mathbf{X})\le \tau t(\mathbf{Y}\to \mathbf{X}).$$

An example with the strict inequality can be easily given. Let $\mathbf{Y}$ be an independent and identically distributed (i.i.d.) process and $\mathbf{X}$ defined by $X_1=Y_1$ and $X_{i+1}=Y_i$. We have $h(\mathbf{X})=h(\mathbf{Y})=H(Y_1)$ and $h_{\tau }(\mathbf{X}|\mathbf{Y})=(\tau -1)H(Y_1)$. Hence, $t_{\tau }(\mathbf{Y}\to \mathbf{X})=H(Y_1)$ for all $\tau =1,2,\cdots$.

There are two permutation analogues of the transfer entropy. One is called the symbolic transfer entropy (STE) [42], and the other is called the transfer entropy on rank vector (TERV) [43]. Here, we introduce their rates as follows: the rate of STE from $\mathbf{Y}$ to $\mathbf{X}$ is defined by:

$$\begin{array}{c}\hfill t_{\tau }^{**}(\mathbf{Y}\to \mathbf{X})=\underset{L\to \infty }{lim}\left[H^{*}(X_{1:L},X_{1+\tau :L+\tau })-H^{*}(X_{1:L})-H^{*}(X_{1:L},X_{1+\tau :L+\tau },Y_{1:L})+H^{*}(X_{1:L},Y_{1:L})\right]\end{array}$$

if the limit on the right-hand side exists. The rate of TERV from $\mathbf{Y}$ to $\mathbf{X}$ is defined by:

$$\begin{array}{c}\hfill t_{\tau }^{*}(\mathbf{Y}\to \mathbf{X})=\underset{L\to \infty }{lim}\left[H^{*}(X_{1:L+\tau })-H^{*}(X_{1:L})-H^{*}(X_{1:L+\tau },Y_{1:L})+H^{*}(X_{1:L},Y_{1:L})\right].\end{array}$$

if the limit on the right-hand side exists. If ${\mathbf{E}}^{*}(\mathbf{X})$ exists, then, by the definition of the permutation excess entropy, we have:

$$\begin{array}{c}\hfill h^{*}(\mathbf{X})=\underset{L\to \infty }{lim}\left(H^{*}(X_{1:L+1})-H^{*}(X_{1:L})\right).\end{array}$$

In this case, $t_1^{*}(\mathbf{Y}\to \mathbf{X})$ coincides with a quantity called the symbolic transfer entropy rate, introduced in [19].

Proposition 6 

Let $(\mathbf{X},\mathbf{Y})$ be the output process of an HMM $(\Sigma ,A_n\times A_m,{\{T^{(a,b)}\}}_{(a,b)\in A_n\times A_m},\mu )$ with an ergodic internal process. Then, we have:

$$t_{\tau }(\mathbf{Y}\to \mathbf{X})=t_{\tau }^{*}(\mathbf{Y}\to \mathbf{X})=t_{\tau }^{**}(\mathbf{Y}\to \mathbf{X}).$$

Proof. 

Since both $\mathbf{X}$ and $\mathbf{Y}$ are the output processes of appropriate HMMs with ergodic internal processes, the equalities follow from the similar discussion with that in the proof of Proposition 5. Indeed, for example, $\mathbf{X}$ is the output process of the HMM $(\Sigma ,A_n,{\{T^{(a)}\}}_{a\in A_n},\mu )$, where $T^{(a)}:={\sum }_{b\in A_m}{T}^{(a,b)}$.

A different instance of conditional mutual information, called momentary information transfer, is considered in [24]. It was proposed to improve the ability to detect coupling delays, which is lacking in the transfer entropy. Here, we consider its rate: the momentary information transfer rate is defined by:

$$\begin{array}{ccc}\hfill m_{\tau }(\mathbf{Y}\to \mathbf{X})& =& \underset{L\to \infty }{lim}\left[H(X_{L+\tau }|X_{1:L+\tau -1},Y_{1:L-1})-H(X_{L+\tau }|X_{1:L+\tau -1},Y_{1:L})\right]\hfill \\ & =& \underset{L\to \infty }{lim}[H(X_{1:L+\tau },Y_{1:L-1})-H(X_{1:L+\tau -1},Y_{1:L-1})\hfill \\ & & -H(X_{1:L+\tau },Y_{1:L})+H(X_{1:L+\tau -1},Y_{1:L})].\hfill \end{array}$$

Its permutation analogue, called the momentary sorting information transfer rate, is defined by:

$$\begin{array}{ccc}\hfill m_{\tau }^{*}(\mathbf{Y}\to \mathbf{X})& =& \underset{L\to \infty }{lim}[H^{*}(X_{1:L+\tau },Y_{1:L-1})-H^{*}(X_{1:L+\tau -1},Y_{1:L-1})\hfill \\ & & -H^{*}(X_{1:L+\tau },Y_{1:L})+H^{*}(X_{1:L+\tau -1},Y_{1:L})].\hfill \end{array}$$

By a similar discussion with that in the proof of Proposition 6, we obtain the following equality:

Proposition 7 

Let $(\mathbf{X},\mathbf{Y})$ be the output process of an HMM $(\Sigma ,A_n\times A_m,{\{T^{(a,b)}\}}_{(a,b)\in A_n\times A_m},\mu )$ with an ergodic internal process. Then, we have:

$$m_{\tau }(\mathbf{Y}\to \mathbf{X})=m_{\tau }^{*}(\mathbf{Y}\to \mathbf{X}).$$

4.4. Directed Information

Directed information is a measure of coupling direction and strength based on the idea of causal conditioning [26,44]. Since it is not a particular instance of conditional mutual information, here, we treat it separately. In the following presentation, we make use of terminologies from [40,45].

Let $(\mathbf{X},\mathbf{Y})$ be a bivariate finite-alphabet stationary stochastic process. The alphabets of $\mathbf{X}$ and $\mathbf{Y}$ are ordered alphabets, $A_n$ and $A_m$, respectively. The directed information rate from $\mathbf{Y}$ to $\mathbf{X}$ is defined by:

$$\begin{array}{c}\hfill I_{\infty }(\mathbf{Y}\to \mathbf{X})=\underset{L\to \infty }{lim}\frac{1}{L}I(Y_{1:L}\to X_{1:L})\end{array}$$

where:

$$\begin{array}{ccc}\hfill I(Y_{1:L}\to X_{1:L})& =& \sum _{i=1}^{L}I(X_i,Y_{1:i}|X_{1:i-1})\hfill \\ & =& H(X_{1:L})-\sum _{i=1}^{L}H(X_i|X_{1:i-1},Y_{1:i}).\hfill \end{array}$$

Note that if $Y_{1:i}$ in the above expression on the right-hand side is replaced by $Y_{1:L}$, then we obtain the mutual information between $X_{1:L}$ and $Y_{1:L}$:

$$\begin{array}{c}\hfill I(X_{1:L};Y_{1:L})=H(X_{1:L})-\sum _{i=1}^{L}H(X_i|X_{1:i-1},Y_{1:L}).\end{array}$$

Thus, conditioning on $Y_{1:i}$ for $i=1,\cdots ,L$, not on $Y_{1:L}$, distinguishes the directed information from the mutual information. Following [44], we write:

$$\begin{array}{c}\hfill H(X_{1:L}||Y_{1:L}):=\sum _{i=1}^{L}H(X_i|X_{1:i-1},Y_{1:i})\end{array}$$

and call the quantity causal conditional entropy. By using this notation, we have:

$$I(Y_{1:L}\to X_{1:L})=H(X_{1:L})-H(X_{1:L}||Y_{1:L}).$$

The permutation analogue of the directed information rate, which we call the symbolic directed information rate is defined by:

$$\begin{array}{c}\hfill I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X})=\underset{L\to \infty }{lim}\frac{1}{L}{I}^{*}(Y_{1:L}\to X_{1:L})\end{array}$$

if the limit on the right-hand side exists, where:

$$\begin{array}{c}\hfill I^{*}(Y_{1:L}\to X_{1:L}):=H^{*}(X_{1:L})-\sum _{i=1}^L\left(H^{*}(X_{1:i},Y_{1:i})-H^{*}(X_{1:i-1},Y_{1:i})\right).\end{array}$$

If we write:

$$I^{*}(X_i;Y_{1:i}|X_{1:i-1}):=H^{*}(X_{1:i})-H^{*}(X_{1:i-1})-H^{*}(X_{1:i},Y_{1:i})+H^{*}(X_{1:i-1},Y_{1:i})$$

and:

$$\begin{array}{c}\hfill H^{*}(X_{1:L}||Y_{1:L}):=\sum _{i=1}^L\left(H^{*}(X_{1:i},Y_{1:i})-H^{*}(X_{1:i-1},Y_{1:i})\right)\end{array}$$

then we have the expressions:

$$I^{*}(Y_{1:L}\to X_{1:L})=\sum _{i=1}^L{I}^{*}(X_i;Y_{1:i}|X_{1:i-1})=H^{*}(X_{1:L})-H^{*}(X_{1:L}||Y_{1:L}).$$

Proposition 8 

Let $(\mathbf{X},\mathbf{Y})$ be the output process of an HMM $(\Sigma ,A_n\times A_m,{\{T^{(a,b)}\}}_{(a,b)\in A_n\times A_m},\mu )$ with an ergodic internal process. Then, we have:

$$I_{\infty }(\mathbf{Y}\to \mathbf{X})=I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X}).$$

Proof. 

We have:

$$\begin{array}{ccc}& & |I(Y_{1:L}\to X_{1:L})-I^{*}(Y_{1:L}\to X_{1:L})|\hfill \\ & \le & |H(X_{1:L})-H^{*}(X_{1:L})|+\sum _{i=1}^L|H(X_{1:i},Y_{1:i})-H^{*}(X_{1:i},Y_{1:i})|\hfill \\ & & +\sum _{i=1}^L|H(X_{1:i-1},Y_{1:i})-H^{*}(X_{1:i-1},Y_{1:i})|.\hfill \end{array}$$

We know that the first term on the right-hand side in the above inequality goes to zero as $L\to \infty$. Let us evaluate the second sum. By Lemma 4, it holds that:

$$\begin{array}{c}\hfill \sum _{i=1}^L|H(X_{1:i},Y_{1:i})-H^{*}(X_{1:i},Y_{1:i})|\le \sum _{i=1}^L\left({\alpha }_{\mathbf{X},i}+{\alpha }_{\mathbf{Y},i}\right)\left(nlog(i+n)+mlog(i+m)\right)\end{array}$$

By Lemma 2 and Lemma 3, we have:

$$\begin{array}{c}\hfill \sum _{i=1}^L{\alpha }_{\mathbf{X},i}nlog(i+n)\le 2C{n}^2\sum _{i=1}^L{\gamma }^{i}log(i+n),\end{array}$$

where $C:={max}_{x\in A_n}\{C_x\}$ and $\gamma :={max}_{x\in A_n}\{{\gamma }_x\}<1$. It is elementary to show that ${lim}_{L\to \infty }{\sum }_{i=1}^L{\gamma }^{i}log(i+n)$ is finite. The limits of the other terms are also shown to be finite similarly. Thus, we can conclude that the limit of the second sum is bounded. Similarly, the limit of the third sum is also bounded. The equality in the claim follows immediately.

For output processes of HMMs with ergodic internal processes, properties on the directed information rate can be transferred to those on the symbolic directed information rate. Since proofs of them can be given by the same manner as those of the above propositions, here, we list some of them without proofs. For the proofs of the properties on the directed information rate, we refer to [44,45].

Let $(\mathbf{X},\mathbf{Y})$ be the output process of an HMM $(\Sigma ,A_n\times A_m,{\{T^{(a,b)}\}}_{(a,b)\in A_n\times A_m},\mu )$ with an ergodic internal process. Then, we have:

(i)

$$I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X})=\underset{L\to \infty }{lim}{I}^{*}(X_L;Y_{1:L}|X_{1:L-1}).$$

This is the permutation analogue of the equality:

$$I_{\infty }(\mathbf{Y}\to \mathbf{X})=\underset{L\to \infty }{lim}I(X_L;Y_{1:L}|X_{1:L-1});$$

(ii)

$$\begin{array}{c}\hfill I_{\infty }(D\mathbf{Y}\to \mathbf{X})=I_{\infty }^{*}(D\mathbf{Y}\to \mathbf{X})=\underset{L\to \infty }{lim}{I}^{*}(X_L;Y_{1:L-1}|X_{1:L-1}).\end{array}$$

Here:

$$\begin{array}{c}\hfill I_{\infty }(D\mathbf{Y}\to \mathbf{X}):=\underset{L\to \infty }{lim}\frac{1}{L}I(D{Y}_{1:L}\to X_{1:L})\end{array}$$

and:

$$\begin{array}{c}\hfill I(D{Y}_{1:L}\to X_{1:L}):=\sum _{i=1}^{L}I(X_i;Y_{1:i-1}|X_{1:i-1}).\end{array}$$

The symbol, D, denotes the one-step delay. $I_{\infty }^{*}(D\mathbf{Y}\to \mathbf{X})$ is the corresponding permutation analogue. The second equality is the permutation analogue of the equality $I_{\infty }(D\mathbf{Y}\to \mathbf{X})={lim}_{L\to \infty }I(X_L;Y_{1:L-1}|X_{1:L-1})$. Since $I_{\infty }(D\mathbf{Y}\to \mathbf{X})$ coincides with the transfer entropy rate, the first equality is just the equality between the transfer entropy rate and the symbolic transfer entropy rate (or the rate of one-step TERV) proven in Proposition 6, given the second equality;

(iii)

$$\begin{array}{c}\hfill I_{\infty }(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y})=I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y})=\underset{L\to \infty }{lim}{I}^{*}(X_L;Y_L|X_{1:L-1},Y_{1:L-1}),\end{array}$$

where $I_{\infty }(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y})$ is called the instantaneous information exchange rate and is defined by:

$$\begin{array}{c}\hfill I_{\infty }(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y}):=\underset{L\to \infty }{lim}\frac{1}{L}I(Y_{1:L}\to X_{1:L}||D{Y}_{1:L})\end{array}$$

and:

$$\begin{array}{ccc}\hfill I(Y_{1:L}\to X_{1:L}||D{Y}_{1:L})& =& H(X_{1:L}||D{Y}_{1:L})-H(X_{1:L}||Y_{1:L},D{Y}_{1:L})\hfill \\ & =& \sum _{i=1}^{L}I(X_i;Y_{1:i}|X_{1:i-1},Y_{1:i-1})\hfill \\ & =& \sum _{i=1}^{L}I(X_i;Y_i|X_{1:i-1},Y_{1:i-1}).\hfill \end{array}$$

From the last expression of $I(Y_{1:L}\to X_{1:L}||D{Y}_{1:L})$, we can obtain:

$$\begin{array}{c}\hfill I_{\infty }(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y})=\underset{L\to \infty }{lim}I(X_L;Y_L|X_{1:L-1},Y_{1:L-1}).\end{array}$$

$I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y})$ is the corresponding permutation analogue and called the symbolic instantaneous information exchange rate;

(iv)

$$\begin{array}{c}\hfill I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X})=I_{\infty }^{*}(D\mathbf{Y}\to \mathbf{X})+I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y}).\end{array}$$

Namely, the symbolic directed information rate decomposes into the sum of the symbolic transfer entropy rate and the symbolic instantaneous information exchange rate. This follows immediately from (ii), (iii) and the equality saying that the directed information rate decomposes into the sum of the transfer entropy rate and the instantaneous information exchange rate:

$$\begin{array}{c}\hfill I_{\infty }(\mathbf{Y}\to \mathbf{X})=I_{\infty }(D\mathbf{Y}\to \mathbf{X})+I_{\infty }(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y});\end{array}$$

(v)

$$\begin{array}{c}\hfill I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X})+I_{\infty }^{*}(D\mathbf{X}\to \mathbf{Y})=I_{\infty }^{*}(\mathbf{X};\mathbf{Y}).\end{array}$$

This is the permutation analogue of the equality saying that the mutual information rate between $\mathbf{X}$ and $\mathbf{Y}$ is the sum of the directed information rate from $\mathbf{Y}$ to $\mathbf{X}$ and the transfer entropy rate from $\mathbf{X}$ to $\mathbf{Y}$:

$$\begin{array}{c}\hfill I_{\infty }(\mathbf{Y}\to \mathbf{X})+I_{\infty }(D\mathbf{X}\to \mathbf{Y})=I_{\infty }(\mathbf{X};\mathbf{Y}),\end{array}$$

where:

$$\begin{array}{c}\hfill I_{\infty }(\mathbf{X};\mathbf{Y}):=\underset{L\to \infty }{lim}\frac{1}{L}I(X_{1:L};Y_{1:L})\end{array}$$

is the mutual information rate and $I_{\infty }^{*}(\mathbf{X};\mathbf{Y})$ is its permutation analogue, called the symbolic mutual information rate. It is known that they are equal for any bivariate finite-alphabet stationary stochastic process [19]. Thus, the symbolic mutual information rate between $\mathbf{X}$ and $\mathbf{Y}$ is the sum of the symbolic directed information rate from $\mathbf{Y}$ to $\mathbf{X}$ and the symbolic transfer entropy rate from $\mathbf{X}$ to $\mathbf{Y}$.

We can also introduce the permutation analogue of the causal conditional directed information rate and prove the corresponding properties. To be precise, let us consider a multivariate finite-alphabet stationary stochastic process $(\mathbf{X},\mathbf{Y},{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)$ with the alphabet, $A_n\times A_m\times A_{l_1}\times \cdots \times A_{l_k}$. The causal conditional directed information rate from $\mathbf{Y}$ to $\mathbf{X}$ given $({\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)$ is defined by:

$$\begin{array}{c}\hfill I_{\infty }(\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k):=\underset{L\to \infty }{lim}\frac{1}{L}I(Y_{1:L}\to X_{1:L}||Z_{1:L}^1,\cdots ,Z_{1:L}^k)\end{array}$$

where:

$$\begin{array}{ccc}\hfill I(Y_{1:L}\to X_{1:L}||Z_{1:L}^1,\cdots ,Z_{1:L}^k)& =& H(X_{1:L}||Z_{1:L}^1,\cdots ,Z_{1:L}^k)-H(X_{1:L}||Y_{1:L},Z_{1:L}^1,\cdots ,Z_{1:L}^k)\hfill \\ & =& \sum _{i=1}^{L}I(X_i;Y_{1:i}|X_{1:i-1},Z_{1:L}^1,\cdots ,Z_{1:L}^k).\hfill \end{array}$$

Corresponding to Proposition 8, we have the following equality if $(\mathbf{X},\mathbf{Y},{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)$ is the output process of an HMM with an ergodic internal process:

$$\begin{array}{c}\hfill I_{\infty }(\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)=I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k),\end{array}$$

where $I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)$ is the symbolic causal conditional directed information rate, which is defined in the same manner as the symbolic directed information rate. The following properties also hold: assume that $(\mathbf{X},\mathbf{Y},{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)$ is the output process of an HMM with an ergodic internal process. Then, we have:

(i’)

$$I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)=\underset{L\to \infty }{lim}{I}^{*}(X_L;Y_{1:L}|X_{1:L-1},Z_{1:L}^1,\cdots ,Z_{1:L}^k).$$

This is the permutation analogue of the equality:

$$I_{\infty }(\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)=\underset{L\to \infty }{lim}I(X_L;Y_{1:L}|X_{1:L-1},Z_{1:L}^1,\cdots ,Z_{1:L}^k);$$

(ii’)

$$\begin{array}{ccc}\hfill I_{\infty }(D\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)& =& I_{\infty }^{*}(D\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)\hfill \\ & =& \underset{L\to \infty }{lim}{I}^{*}(X_L;Y_{1:L-1}|X_{1:L-1},Z_{1:L}^1,\cdots ,Z_{1:L}^k).\hfill \end{array}$$

The second equality is the permutation analogue of the equality:

$$\begin{array}{c}\hfill I_{\infty }(D\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)=\underset{L\to \infty }{lim}I(X_L;Y_{1:L-1}|X_{1:L-1},Z_{1:L}^1,\cdots ,Z_{1:L}^k);\end{array}$$

The quantities, $I_{\infty }(D\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)$ and $I_{\infty }^{*}(D\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)$, are called the causal conditional transfer entropy rate and the symbolic causal conditional transfer entropyrate, respectively.

(iii’)

$$\begin{array}{ccc}\hfill I_{\infty }(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y},{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)& =& I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y},{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)\hfill \\ & =& \underset{L\to \infty }{lim}{I}^{*}(X_L;Y_L|X_{1:L-1},Y_{1:L-1},Z_{1:L}^1,\cdots ,Z_{1:L}^k),\hfill \end{array}$$

where $I_{\infty }(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y},{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)$ is called the causal conditional instantaneous information exchange rate. The second equality is the permutation analogue of the equality:

$$\begin{array}{c}\hfill I_{\infty }(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y},{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)=\underset{L\to \infty }{lim}I(X_L;Y_L|X_{1:L-1},Y_{1:L-1},Z_{1:L}^1,\cdots ,Z_{1:L}^k).\end{array}$$

$I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y},{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)$ is the permutation analogue and is called the symbolic causal conditional instantaneous information exchange rate;

(iv’)

$$\begin{array}{c}\hfill I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)=I_{\infty }^{*}(D\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)+I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y},{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k).\end{array}$$

This is the permutation analogue of the following equality:

$$\begin{array}{c}\hfill I_{\infty }(\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)=I_{\infty }(D\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)+I_{\infty }(\mathbf{Y}\to \mathbf{X}||D\mathbf{Y},{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k);\end{array}$$

(v’)

$$\begin{array}{c}\hfill I_{\infty }^{*}(\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)+I_{\infty }^{*}(D\mathbf{X}\to \mathbf{Y}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)=I_{\infty }^{*}(\mathbf{X};\mathbf{Y}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k).\end{array}$$

This is the permutation analogue of the equality:

$$\begin{array}{c}\hfill I_{\infty }(\mathbf{Y}\to \mathbf{X}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)+I_{\infty }(D\mathbf{X}\to \mathbf{Y}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)=I_{\infty }(\mathbf{X};\mathbf{Y}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k),\end{array}$$

where:

$$\begin{array}{ccc}\hfill I_{\infty }(\mathbf{X};\mathbf{Y}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)& :=& \underset{L\to \infty }{lim}\frac{1}{L}(H(X_{1:L}||Z_{1:L}^1,\cdots ,Z_{1:L}^k)\hfill \\ & & +H(Y_{1:L}||Z_{1:L}^1,\cdots ,Z_{1:L}^k)-H(X_{1:L},Y_{1:L}||Z_{1:L}^1,\cdots ,Z_{1:L}^k))\hfill \end{array}$$

is the causal conditional mutual information rate and $I_{\infty }^{*}(\mathbf{X};\mathbf{Y}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)$ is its permutation analogue, called the symbolic causal conditional mutual information rate. It can be shown that:

$$\begin{array}{c}\hfill I_{\infty }(\mathbf{X};\mathbf{Y}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)=I_{\infty }^{*}(\mathbf{X};\mathbf{Y}||{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)\end{array}$$

if $(\mathbf{X},\mathbf{Y},{\mathbf{Z}}^1,\cdots ,{\mathbf{Z}}^k)$ is the output process of an HMM with an ergodic internal process.

5. Discussion

In this section, we discuss how our theoretical results in this paper are related to the previous work in the literature.

Being confronted with real-world time series data, we cannot take the limit of a large length of words. Hence, we have to estimate information rates with a finite length of words. In such a situation, one permutation method could have some advantages over the other permutation methods. As a matter of fact, TERV was originally proposed as an improved analogue of STE [43]. However, it has been unclear whether they coincide in the limit of a large length of permutations. In this paper, we provide a partial answer to this question: the two permutation analogues of the transfer entropy rate, the rate of STE and the rate of TERV, are equivalent to the transfer entropy rate for bivariate processes generated by HMMs with ergodic internal processes.

The Granger causality graph [46] is a model of causal dependence structure in multivariate stationary stochastic processes. Given a multivariate stationary stochastic process, nodes in a Granger causality graph are components of the process. There are two types of edges: one is directed, and the other is undirected. The absence of a directed edge from one node to another node indicates the lack of the Granger cause from the former to the latter relative to the other remaining processes. Similarly, the absence of an undirected edge between two nodes indicates the lack of the instantaneous cause between them relative to the other remaining processes. Amblard and Michel [40,45] proposed that the Granger causality graph can be constructed based on directed information theory: let $\mathcal{X}=({\mathbf{X}}^1,{\mathbf{X}}^2,\cdots ,{\mathbf{X}}^m)$ be a multivariate finite-alphabet stationary stochastic process with the alphabet, $A_{n_1}\times A_{n_2}\times \cdots \times A_{n_m}$, and $(V,E_d,E_u)$, the Granger causality graph of the process, $\mathcal{X}$, where $V=\{1,2,\cdots ,m\}$ is the set of nodes, $E_d$ is the set of directed edges and $E_u$ is the set of undirected edges. Their proposal is that:

(i)

for any $i,j\in V$, $(i,j)\notin E_d$, if and only if $I_{\infty }(D{\mathbf{X}}^i\to {\mathbf{X}}^j||\mathcal{X}\setminus \{{\mathbf{X}}^i,{\mathbf{X}}^j\})=0$;

(ii)

for any $i,j\in V$, $(i,j)\notin E_u$, if and only if $I_{\infty }({\mathbf{X}}^i\to {\mathbf{X}}^j||D{\mathbf{X}}^i,\mathcal{X}\setminus \{{\mathbf{X}}^i,{\mathbf{X}}^j\})=0$.

Thus, in the Granger causality graph construction proposed in [40], the causal conditional transfer entropy rate captures the Granger cause from one process to another process relative to the other remaining processes. On the other hand, the causal conditional instantaneous information exchange rate captures the instantaneous cause between two processes relative to the other remaining processes.

Now, let us consider the case when $\mathcal{X}$ is an output process of an HMM with an ergodic internal process. Then, from the results of Section 4.4, we have:

(i’)

for any $i,j\in V$, $(i,j)\notin E_d$, if and only if $I_{\infty }^{*}(D{\mathbf{X}}^i\to {\mathbf{X}}^j||\mathcal{X}\setminus \{{\mathbf{X}}^i,{\mathbf{X}}^j\})=0$;

(ii’)

for any $i,j\in V$, $(i,j)\notin E_u$, if and only if $I_{\infty }^{*}({\mathbf{X}}^i\to {\mathbf{X}}^j||D{\mathbf{X}}^i,\mathcal{X}\setminus \{{\mathbf{X}}^i,{\mathbf{X}}^j\})=0$.

Thus, the Granger causality graphs in the sense of [40,45] for multivariate processes generated by HMMs with ergodic internal processes can be captured by the language of the permutation entropy: the symbolic causal conditional transfer entropy rate and the symbolic instantaneous information exchange rate. This statement opens up a possibility of the permutation approach to the problem of assessing the causal dependence structure of multivariate stationary stochastic processes. However, of course, the details of the practical implementation should be an issue of further study.

Real-world time series data are often multivariate. However, it seems that univariate analysis is still main stream in the field of ordinal pattern analysis (see, for example, the papers in [47]). We hope that this work stimulates multivariate analysis of real-world time series data.