SpaGrOW—A Derivative-Free Optimization Scheme for Intermolecular Force Field Parameters Based on Sparse Grid Methods
Abstract
:1. Introduction
1.1. Force Field Parameterization
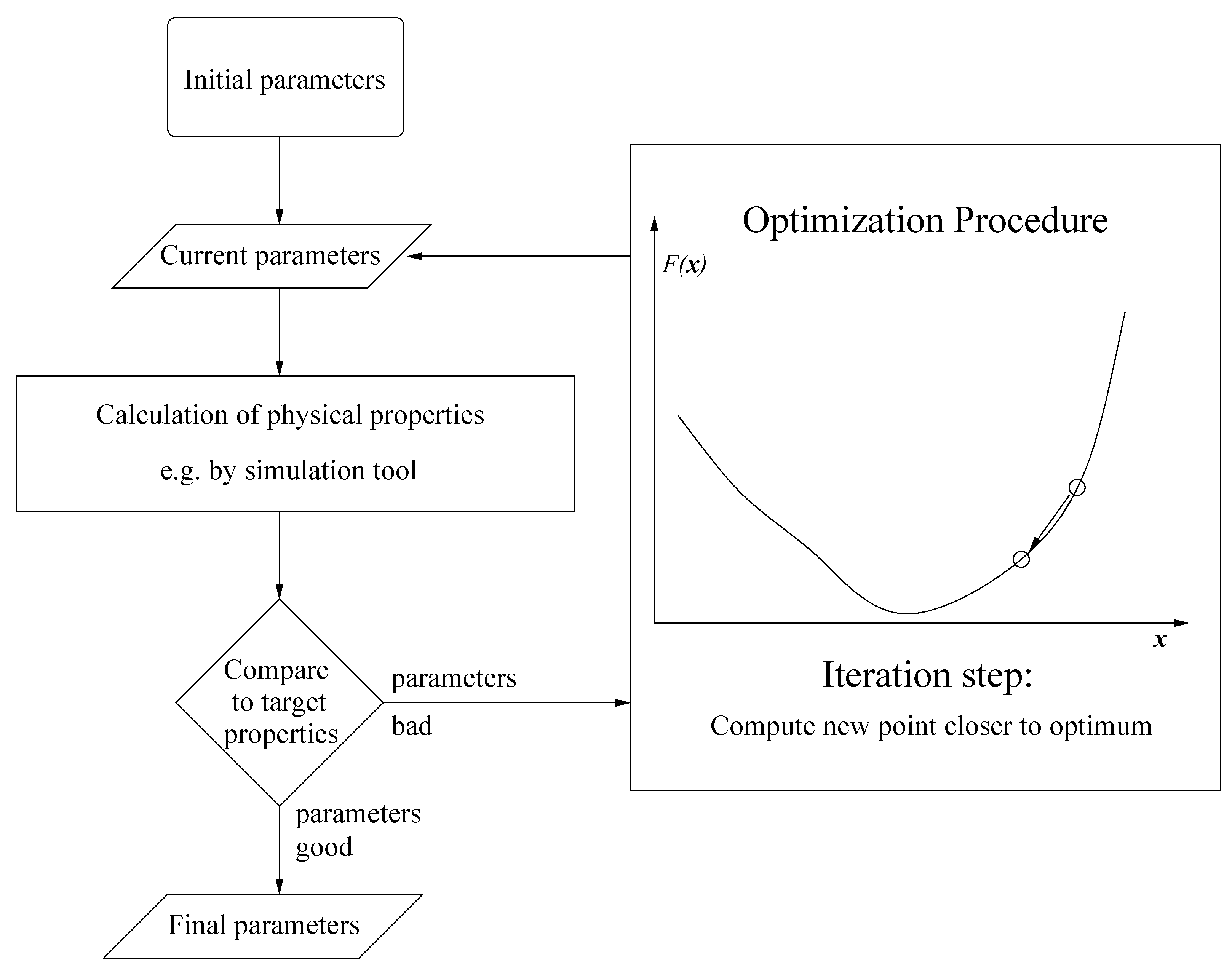
1.2. Drawbacks of Gradient-Based Methods
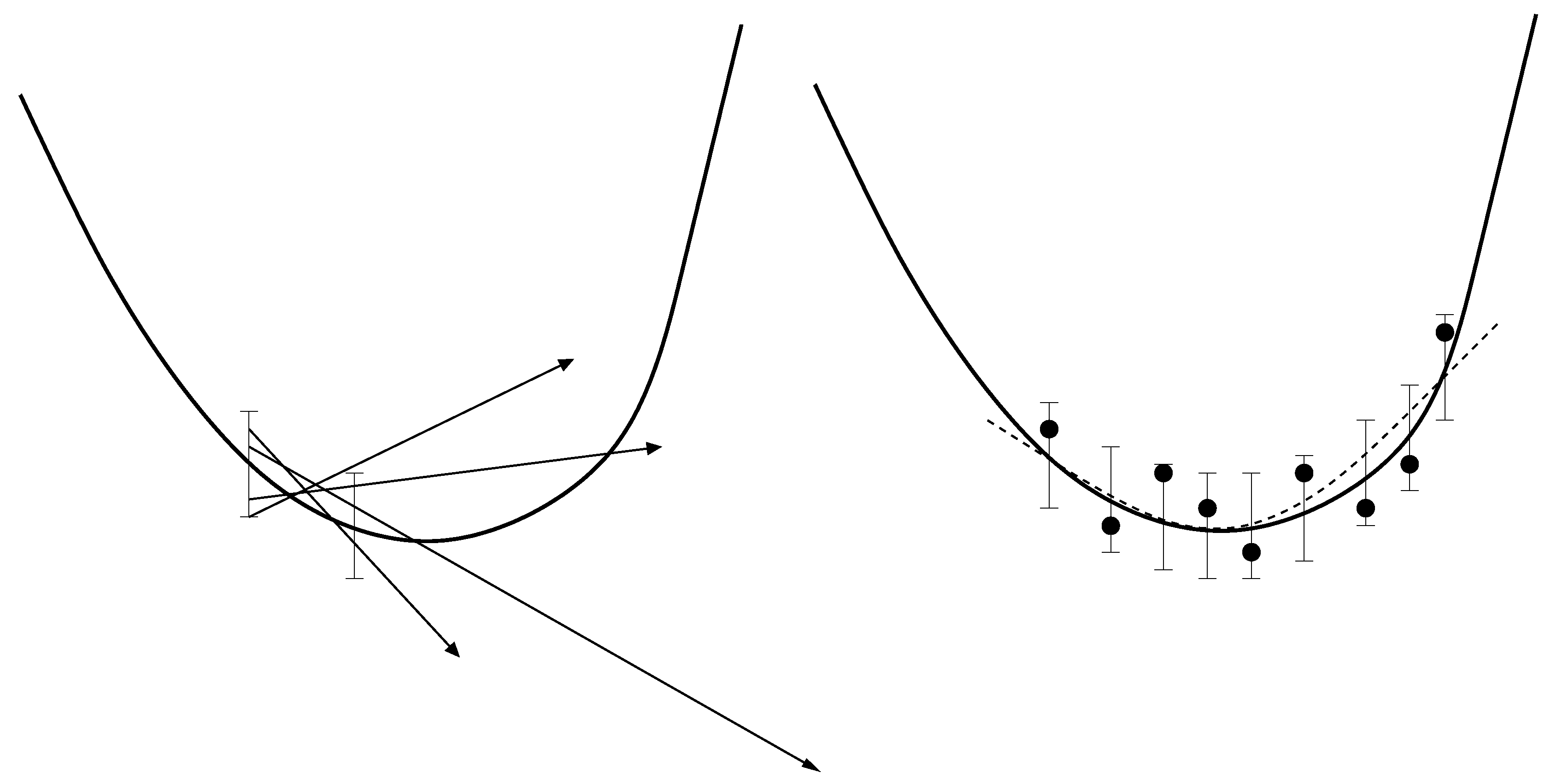
- Due to the statistical noise in the simulation data, the accuracy of a gradient is always limited. It can only predict the decreasing trend of the loss function. As motivated above, this becomes problematic close to the minimum. Theoretically, it is possible to counteract this problem by a suitable discretization for the calculation of the finite differences. However, optimizing the distance of two adjacent points would lead to much more computational effort. Moreover, even if the direction of the gradient can be calculated accurately, the step length control algorithm will only deliver insignificantly small improvements compared to the higher amount of computation time. This is a drawback of the Armijo step length control, but the application of more efficient step length control mechanisms would lead to more computational effort again.
- Whenever a descent direction is incorrect, a point with a smaller loss function value can only be found by chance, because there is no possibility to change the direction. In contrast to descent methods, Trust Region methods decrease the step length in order to find a new, maybe more suitable descent direction of the loss function. This is why these methods are able to get closer to the minimum. However, the Trust Region method applied in previous work requires a Hessian matrix, which leads to significantly more loss function evaluations.
- The amount of simulations is still quite high for gradient- and especially Hessian-based optimization algorithms. At each iteration, a gradient or, additionally, a Hessian have to be computed, which leads to N or, even, loss function evaluations. Furthermore, the Armijo step length control algorithm requires additional functional evaluations.
2. SpaGrOW Methodology: The Main Elements
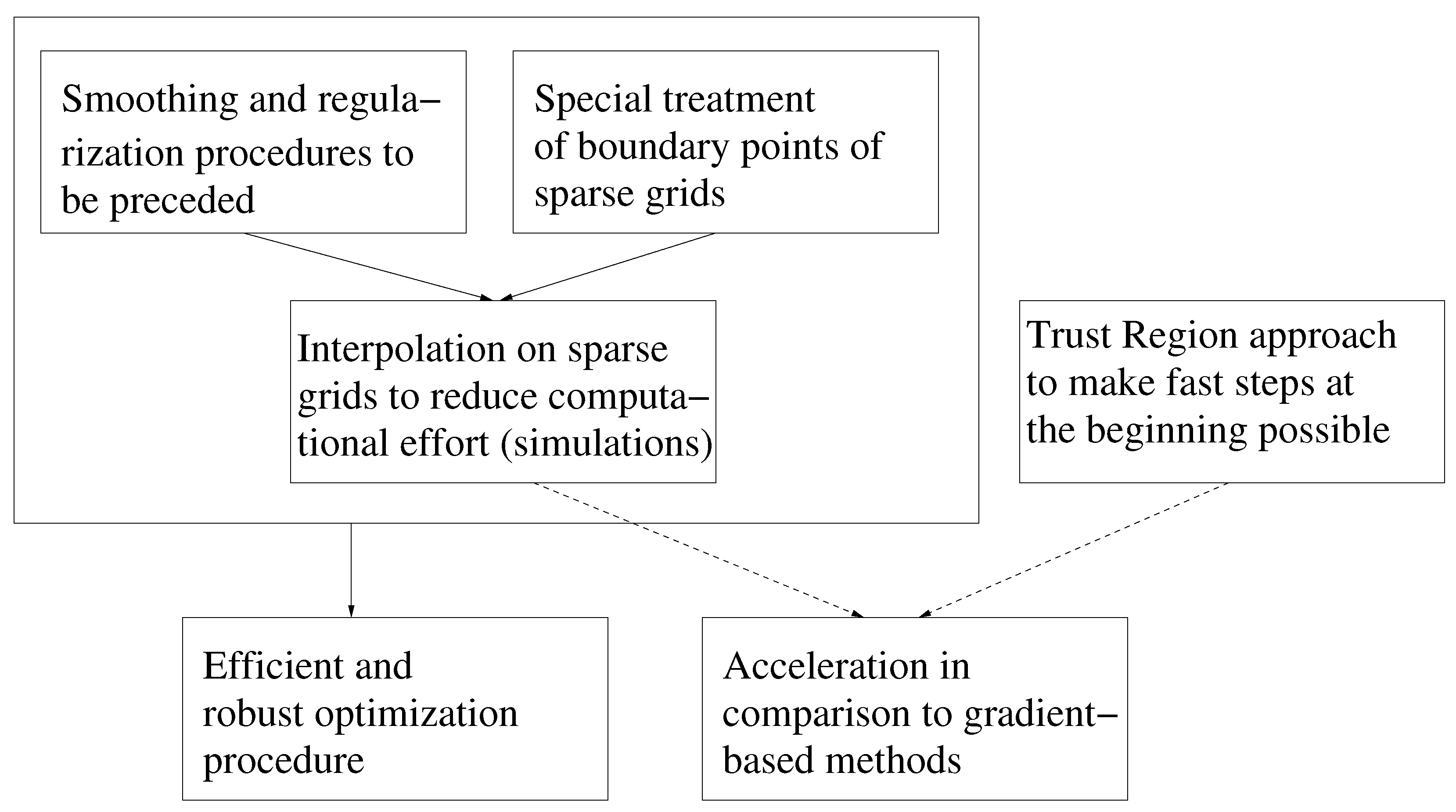
2.1. Interpolation on Sparse Grids
2.1.1. Idea of Sparse Grids
| Level | ||||
|---|---|---|---|---|
| 1 | 3 → 3 | 9 → 9 | 27 → 27 | 81 → 81 |
| 2 | 5 → 5 | 25 → 21 | 125 → 81 | 625 → 393 |
| 3 | 9 → 9 | 81 → 49 | 729 → 225 | 6561 → 1329 |
| 4 | 17 → 17 | 289 → 113 | 4913 → 593 | 83521 → 3921 |
| 10 | 1025 → 1025 | 1.05 9217 | 1.07 47103 | 1.1 1.78 |

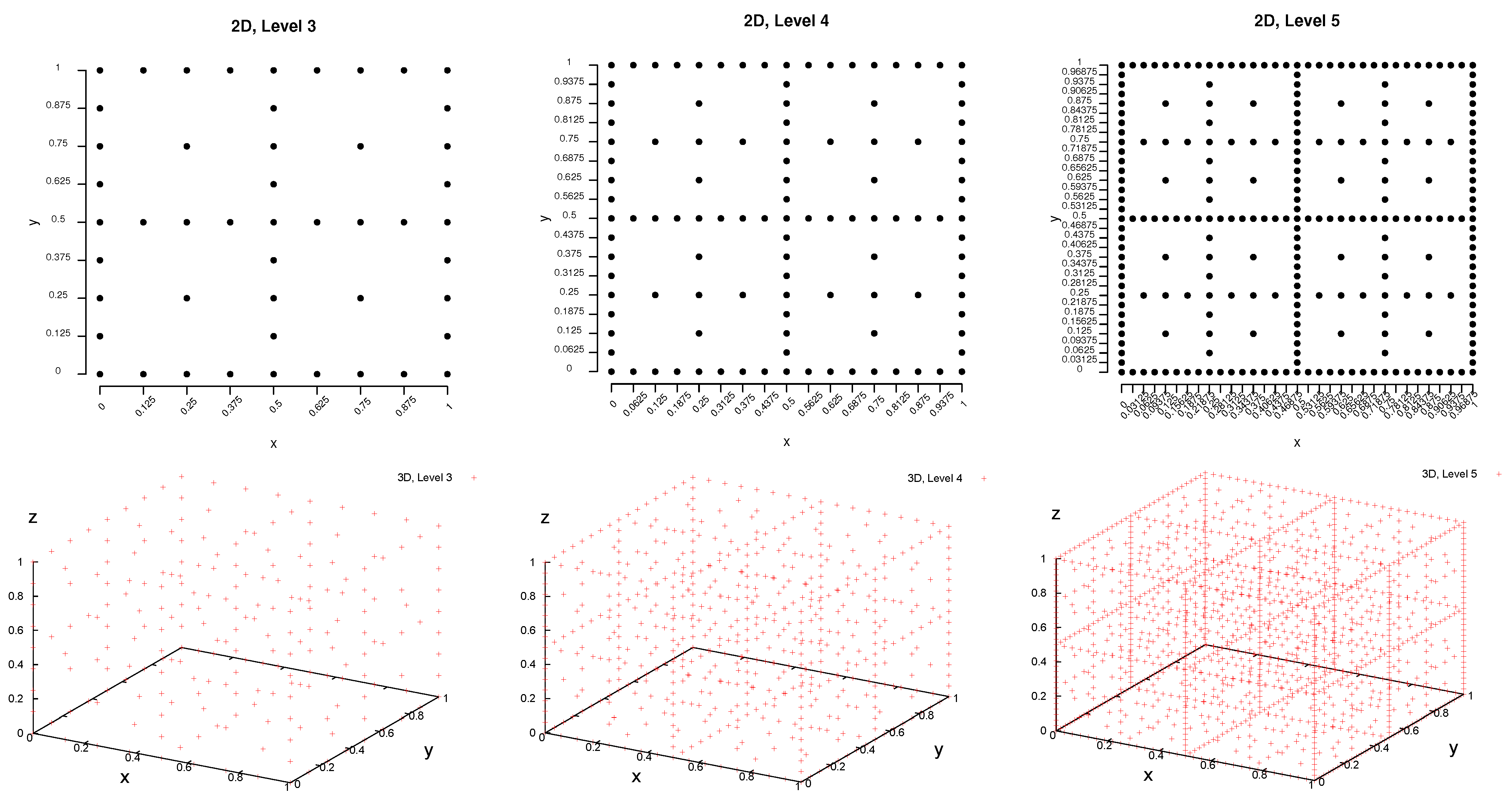
2.1.2. Combination Technique
2.2. Smoothing Procedures
2.2.1. Effects of Statistical Noise on Piecewise-linear Interpolation

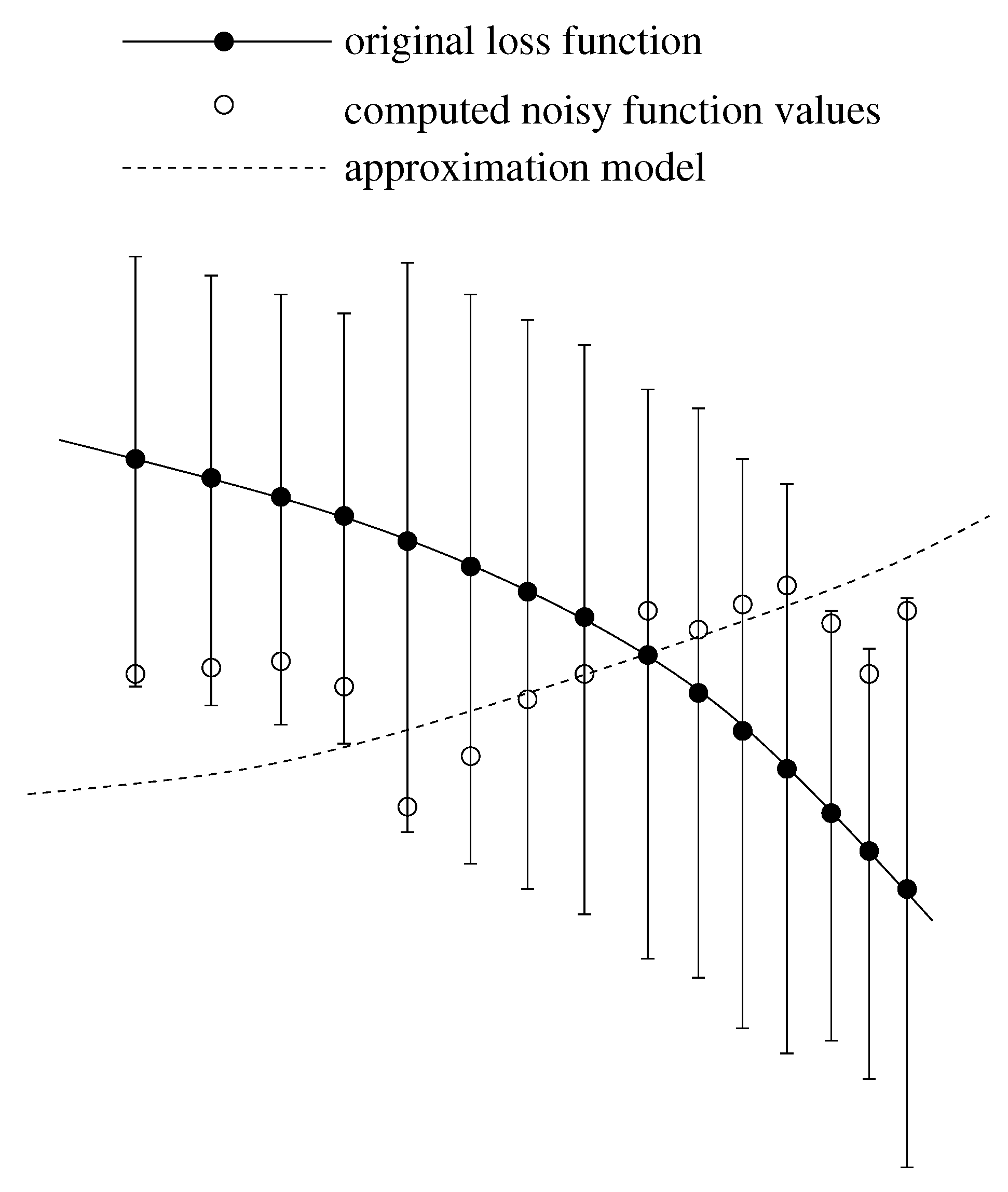
2.2.2. Smoothing Functions

2.2.3. Regularization Algorithms
- (1)
- Due to its high variance, the probability of overfitting is always high.
- (2)
- The euclidean norm, , is, in general, high, as well.
- (3)
- There is no variable selection, i.e., none of the coefficients of can be zero. Hence, correlated variables have always an influence within the model, even if they do not have any impact on the loss function.
- (4)
- If the dimension is greater than the number of data points, the least square method does not have a solution. However, due to , this is not important in the present case.
2.2.4. Selection of Smoothing Procedures: Theoretical Considerations
3. The SpaGrOW Algorithm
3.1. Ingredients of the Algorithm
3.1.1. Local and Global Consideration
- Comparison of the total errors:
- −
- In the global consideration, the total errors were significantly higher than in the local consideration with respect to both the - and the -norm.
- −
- The smoothing error is considerably higher in the global case than in the local one, i.e., the function cannot be reproduced accurately. This was also the case when the function was not affected with statistical noise.
- Convergency analysis:
- −
- Without artificial uncertainties, the global variant of SpaGrOW only led to the minimum when the minimum was a grid point. Otherwise, the minimum could only be determined within the accuracy of the discretization.
- −
- With artificial uncertainties, both discretization and approximation error had a negative effect on the convergency. The resulting approximated minimum was far away from the real one.
3.1.2. Combination with the Trust Region Approach
- —in this case, the model is consistent with F, and the minimum, , is taken as a new iteration: .
- —then, is taken as a new iteration, as well, and at the same time, the trust region is increased in order to accelerate the convergency: .
- —in this case, the model is not consistent with F, and a better model has to be determined by decreasing the trust region: .
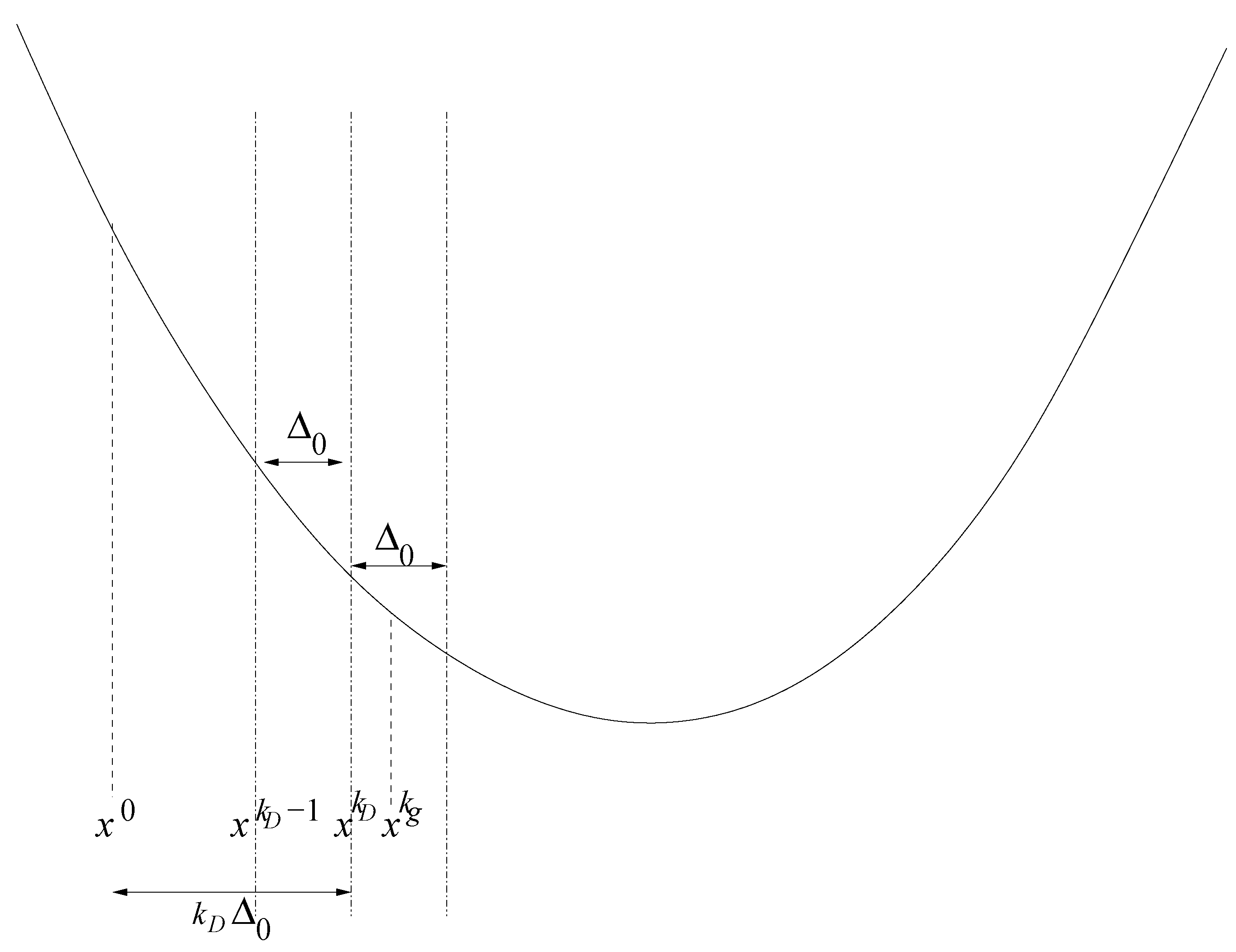
3.1.3. Treatment of Boundary Points
3.2. The Full Algorithm
3.2.1. Structure
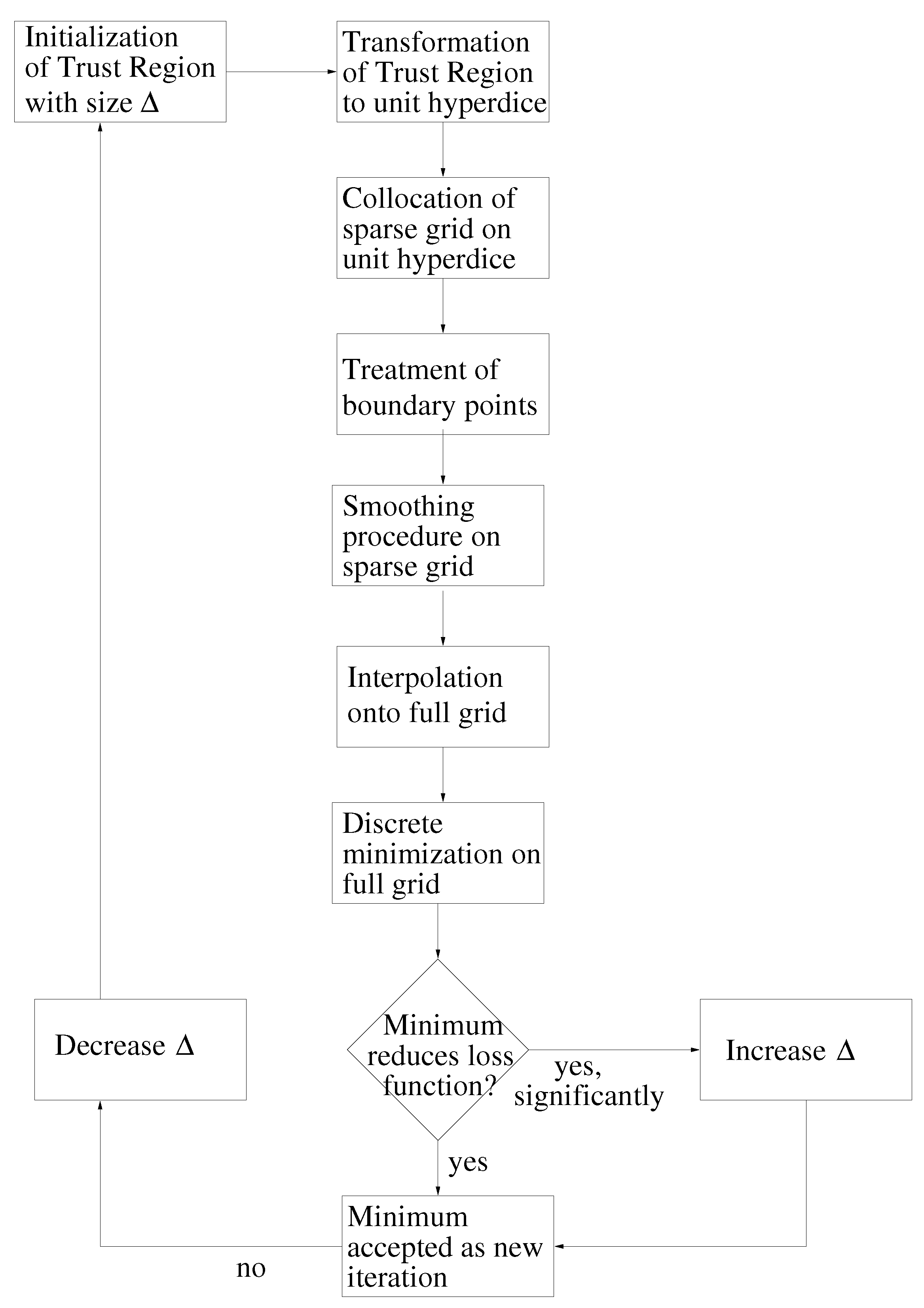
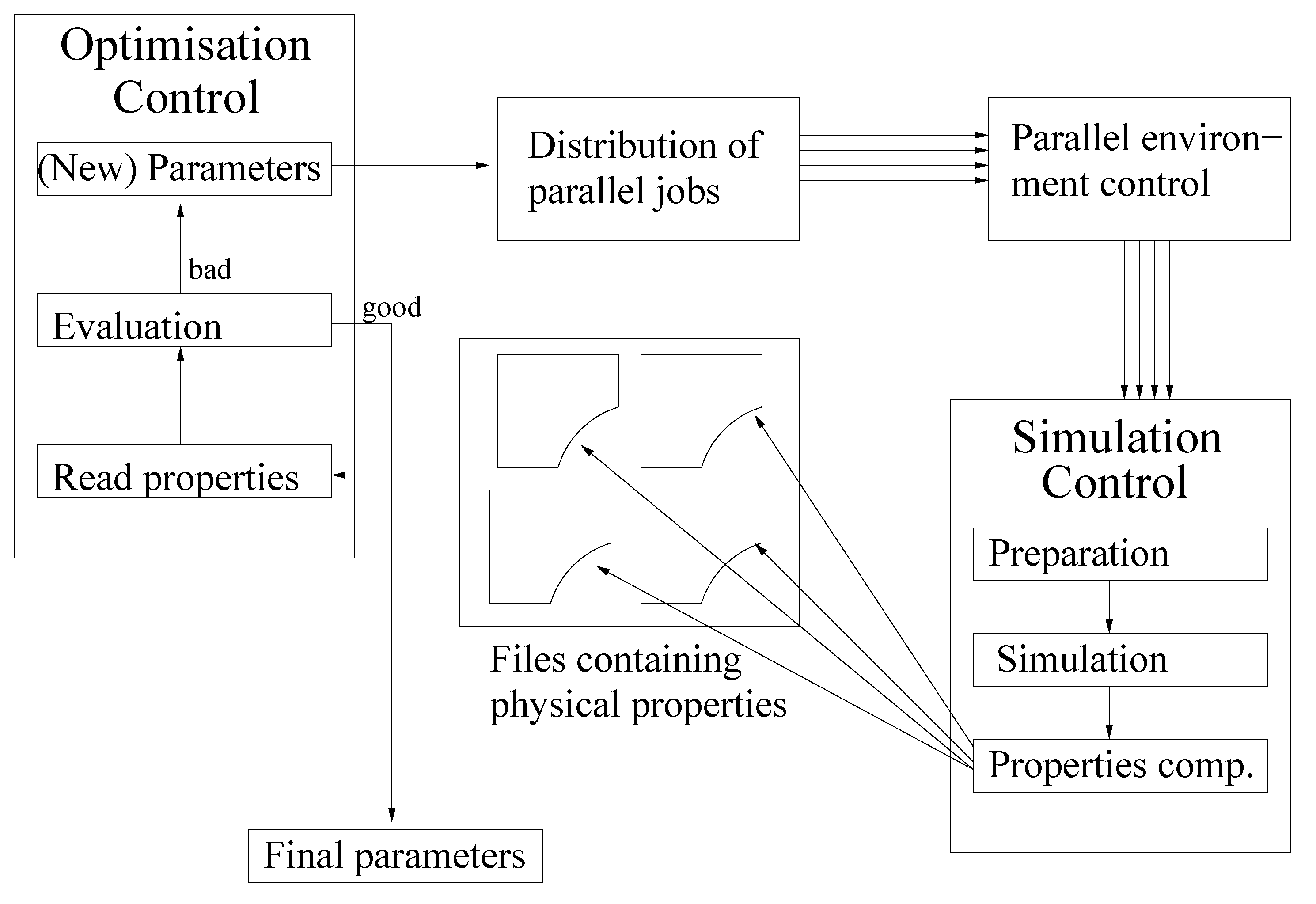
- Initialization: Choose an initial vector, , and an initial step length, , so that:Thereby, is the feasible interval for the ith force field parameter. The maximal step length possible, , is computed at the beginning, and , as well as a minimal step length, , are set in relation to it. Please note that on the one hand, must not be too small, due to the noise, and that, on the other hand, it must not be too large, so that the problematic described in Section 3.1.1. is not faced.Let .Figure 9. Overview of the SpaGrOW algorithm, i.e., the inner iteration of the optimization procedure visualized in Figure 1. The Trust Region size, Δ, is increased or decreased, depending on the quality of the approximation model on the sparse grid.Figure 9. Overview of the SpaGrOW algorithm, i.e., the inner iteration of the optimization procedure visualized in Figure 1. The Trust Region size, Δ, is increased or decreased, depending on the quality of the approximation model on the sparse grid.
- Transformation: Via the transformation:the initial vector, , is mapped from the hyperdice of the size, , into the unit hyperdice. Thereby, and are the components of the vector, .Please note that only the back-transformation obtained by the inverse function:is important, because, first, a sparse grid is simply collocated in . Then, the grid points are back-transformed into the force field parameter space via , so that molecular simulations can be executed.
- Sparse grid: A sparse grid, , is determined within . Note that the transformation, ξ, has not to be applied explicitly. As the combination technique is used, the grid points of the sparse grid are determined hierarchically from the required subgrids, cf. Equation (11). Let be a point of the subgrids of the level, , and position, , which is, at the same time, a non-boundary point of the sparse grid. For each of these points, the loss function value, , is computed.
- Boundary: By multiplying F with a sine term:homogeneous Dirichlet boundary conditions are realized in order to reduce the computational effort significantly. The function, , is applied to each point, , of the sparse grid.
- Smoothing: As the function to be minimized is affected with statistical noise, the function, , is smoothed and regularized by the methods indicated in Section 2.2.2. Hence, for each point, , of the sparse grid, a value, , of the approximating function is obtained.
- Interpolation: The function, G, is interpolated from the sparse grid, , on the full grid, , by the combination technique. Hence, an interpolation model, , is obtained for each point, .As the smoothing and interpolation procedures have been executed for , the following division has to be applied for each non-boundary point of the full grid:The interpolation model, q, is only valid for all .
- Discrete minimization: Determine:
- Iteration step : The ratio:is determined, and the following three cases are differentiated:
- −
- .
- −
- −
- .
Thereby, and are global parameters.Let , and go to step 2. - Stopping criteria: The general stopping criterion is:where . However, an additional criterion is that the minimum is situated within the hyperdice and not at its boundary. In total, the following three stopping criteria are considered:
- (i)
- (ii)
- (iii)
- .
Thereby:Moreover, , where .If the stopping criteria, (i) and (ii), are fulfilled, then SpaGrOW has converged successfully. Due to , it is excluded, as well, that the minimum is situated at the boundary of the grid, where the interpolation model, q, is valid. Stopping criterion (ii) contains the additional condition, , excluding that improvements can be achieved by local refinements. Hence, this is the ideal stopping criterion.Stopping criterion (iii) means that SpaGrOW has not led to success, i.e., even by decreasing the trust region, no accurate model, q, can be found. In particular, this is the case when the assumptions for the application of the combination technique are not fulfilled, which may be caused by an inaccurate smoothing procedure, wherein the noise has not been filtered out in a sufficient way.
3.2.2. Complexity
- Initialization: The effort is only caused by the allocation of the initial variables, like the initial force field parameters, their upper and lower bounds, as well as the maximal, initial and minimal step length.
- Transformation: The transformation is performed in an imaginary way only. The sparse grid is constructed directly in step 3. Only the execution of the back-transformation, , requires a small computational effort.
- Sparse grid: The complexity to obtain a sparse grid of the level, , is , which is still exponential in the dimension, but especially in the case of higher dimensions, it is significantly lower than for a full grid of the same level. The computational effort does not only concern the number of grid points to be computed, but in the first instance, the number of loss function evaluations, i.e., simulations.
- Boundary: Setting the loss function values to zero at the boundary of the sparse grid does not mean any computational effort. For all other grid points, () multiplications have to be performed, cf. Equation (35). Furthermore, there are N sine evaluations. The number of boundary points of an N-dimensional sparse grid of the level, , is . Thereby, is the number of edges of an N-dimensional hyperdice. Hence, the number of simulations to be executed is reduced to:This number multiplied by is the number of required multiplications and multiplied by N, the number of sine evaluations required. The reduction of molecular simulations is achieved at the expense ofmultiplications and sine evaluations, a computational effort that can be neglected, if the high amount of computation time for a simulation is opposed.
- Smoothing: In the case of most approximation methods, a multivariate linear regression has to be performed with complexity , where m is the number of data points and M, the number of basis functions (e.g., for RBFs). However, this complexity can often be reduced to or, even, to by smart numerical methods, e.g., by a Cholesky factorization, in the case of positive definiteness. In contrast to simulations, the computational effort required for a smoothing procedure is negligible, as well. However, one has to consider that m and M must be large enough, on the one hand, in order to achieve an approximation as accurate as possible, and also small enough, on the other hand, in order to keep the computational effort low and to avoid overfitting. Additional effort appears due to the selection of centroids by the k-means algorithm, whose convergency speed always depends on the random choice of the initial centroids. The evaluation of the model function is done by a summation of the centroids only.Furthermore, the regularization methods require some amount of computational effort, in particular, due to the application of Newton-Lagrange algorithms for the constrained optimization. Please note that most of them have been parameterized, as well, e.g., by cross validation.
- Interpolation: In the multilinear interpolation, all adjacent points have to be considered for each grid point. Hence, the interpolation is in .After the multilinear interpolation, a division by a sine term has to be executed for each point situated inside the unit hyperdice. As the sine term has already been calculated for each point of the sparse grid, only:multiplications and:sine evaluations have to be performed. The number of required divisions is equal to . Please note that the divisions have to be performed for each inner point of the sparse grid, as well, because only the approximating function, G, coincides with the interpolation model, but not .
- Discrete minimization For the minimization of q, a maximal function value of is supposed. For each point on the full grid, a comparison has to be performed, in total, comparisons.
- Iteration step: Only a few small operations are necessary in order to perform an iteration step, i.e., simple subtractions, divisions, multiplications and comparisons.
- Stopping criteria: Only comparisons have to be performed in order to check the stopping criteria. The decision whether a vector is situated in or not is made by comparing the components of y with the values zero, one, h and . If one component coincides with one of these four values, the procedure is stopped, and is observed.
3.3. Convergency
3.3.1. Interpolation Error
3.3.2. Smoothing Error
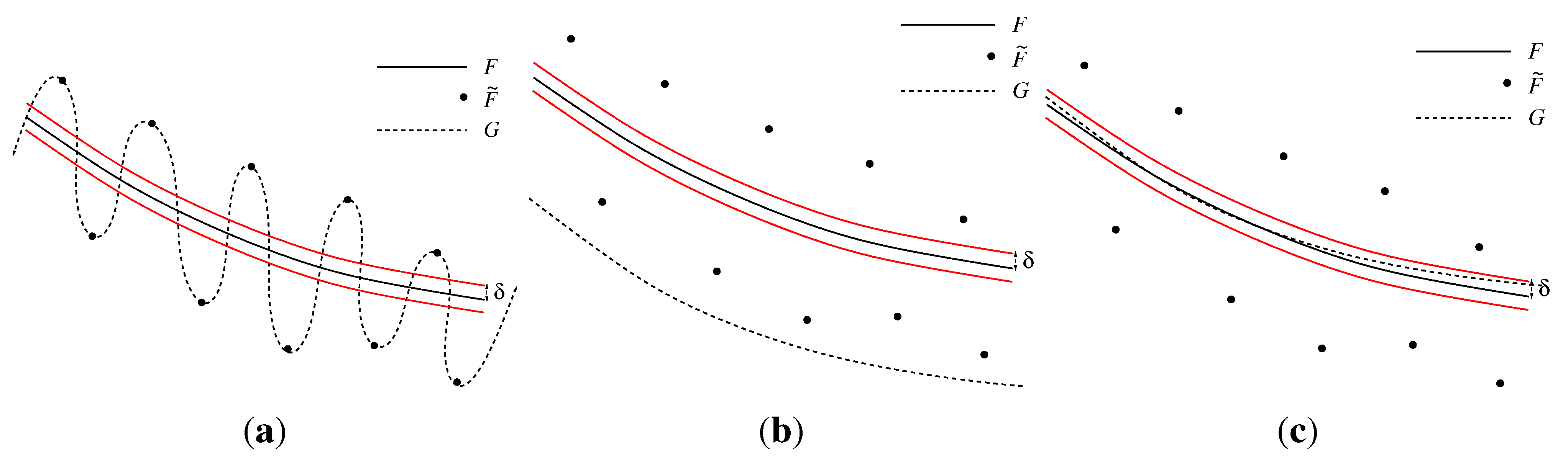
3.4. Speed of Convergency Compared to Gradient-Based Methods
4. Practical Evaluation and Results
- Which smoothing and regularization procedure are most suitable?
- Is SpaGrOW capable of saving simulations in comparison to gradient-based methods?
- How close does SpaGrOW get to the minimum?
4.1. Selection of Smoothing and Regularization Methods
| Smoothing procedures | Regularization procedures |
|---|---|
| Radial Basis Functions | Least squares |
| Naive Elastic Nets (NENs) | |
| : Least Absolute Shrinkage and Selection Operator (LASSO) | |
| : Ridge Regression | |
| Linear property approximation (Lipra) | Multivariate Adaptive Regression Splines (MARS) |
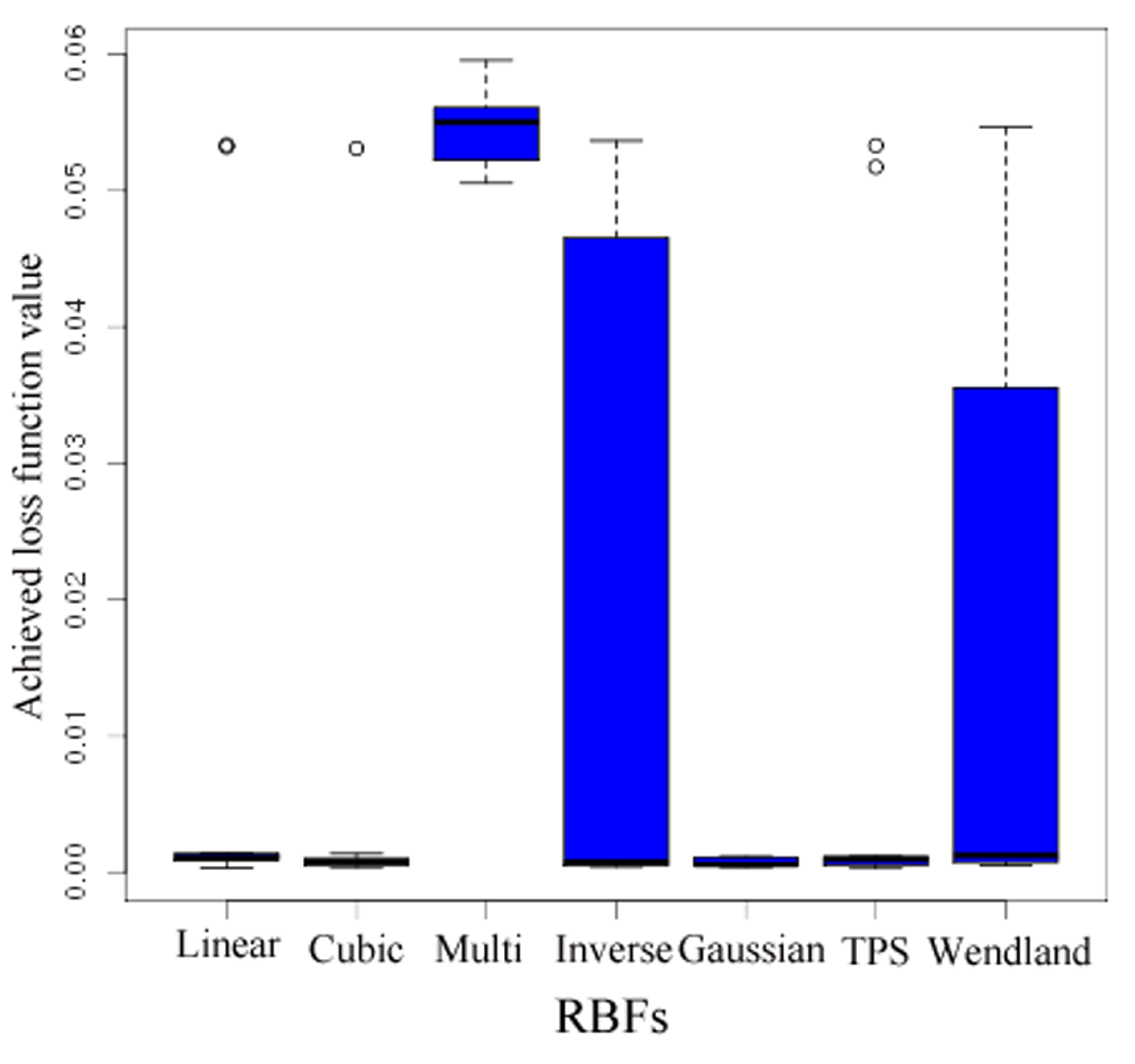
- No outliers were detected.
- A more accurate analysis of the approximation error has shown that the smoothing procedures based on cubic and thin plate spline RBFs reproduced the function, , cf. Section 3.2.1, worse than the one based on Gaussian RBFs. Figure 14 depicts the results for the Gaussian RBFs (Figure 14a) and the thin plate spline RBFs (Figure 14b) for the two-dimensional case: The approximating function and the original function values of , cf. Equation (35), on a sparse grid of the level 2 are plotted versus and , cf. Equation (39). The LJ parameters, σ and ε, were fixed. As can be seen, a smoothing procedure based on thin plate spline RBFs reproduced at the boundary of the unit square in a very bad fashion, whereas Gaussian RBFs delivered a good approximation on the complete unit square.
- The Gaussian RBF is the only of the four RBFs mentioned above that is positive definite, i.e., the selection of Gaussian RBFs is also founded theoretically according to the considerations in Section 2.2.4.
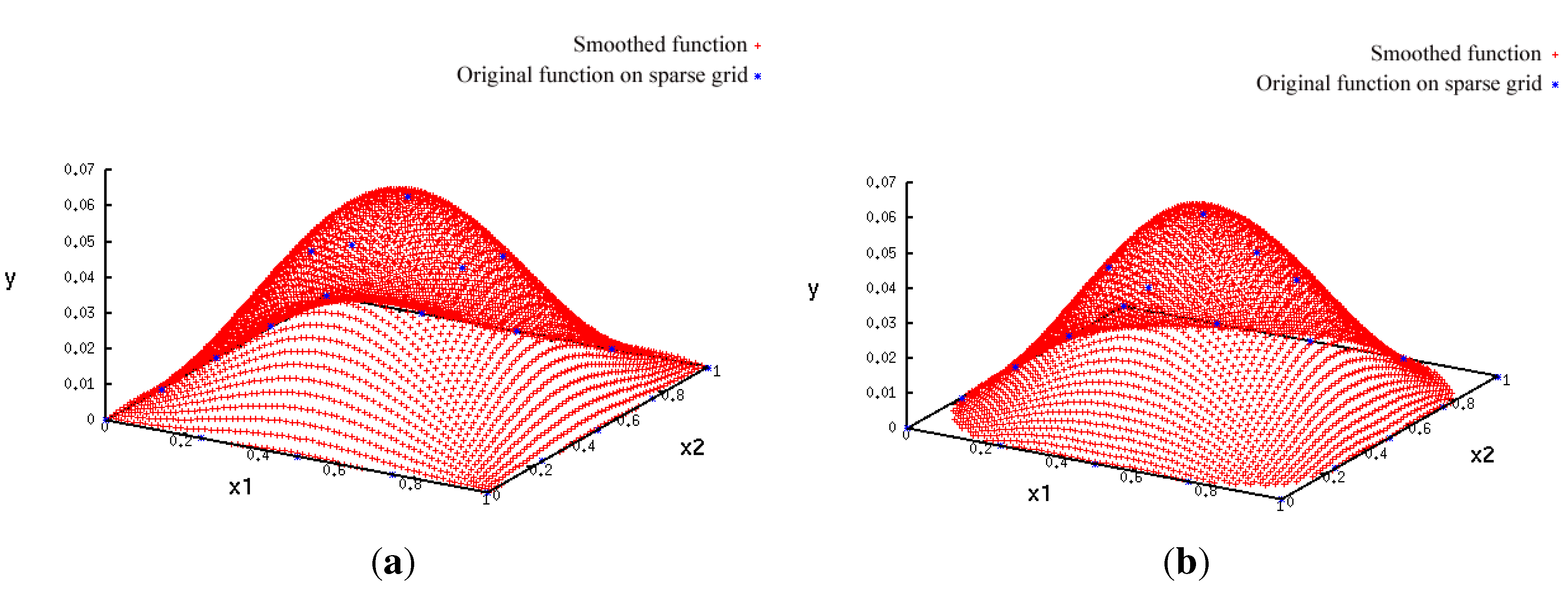
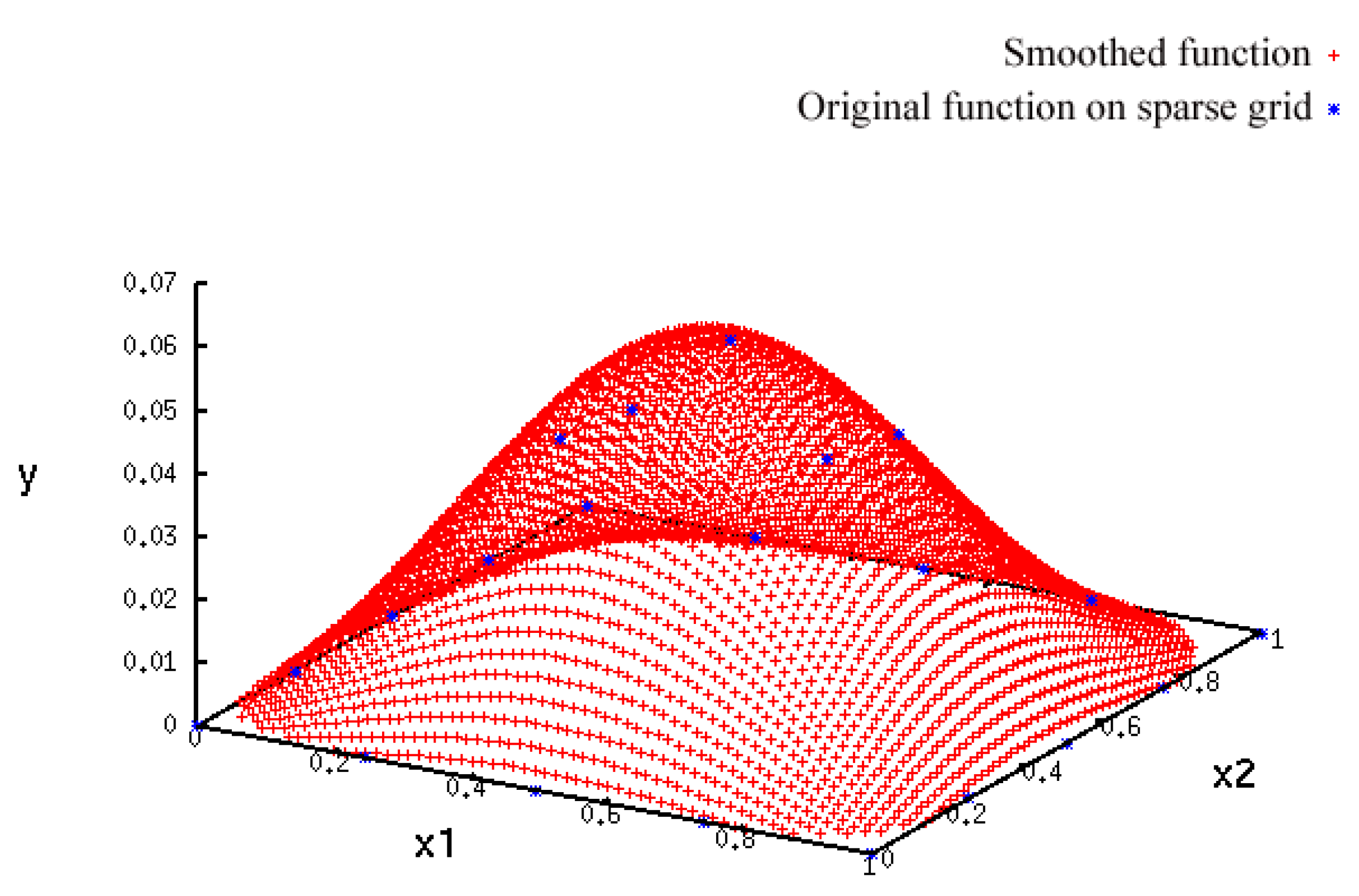
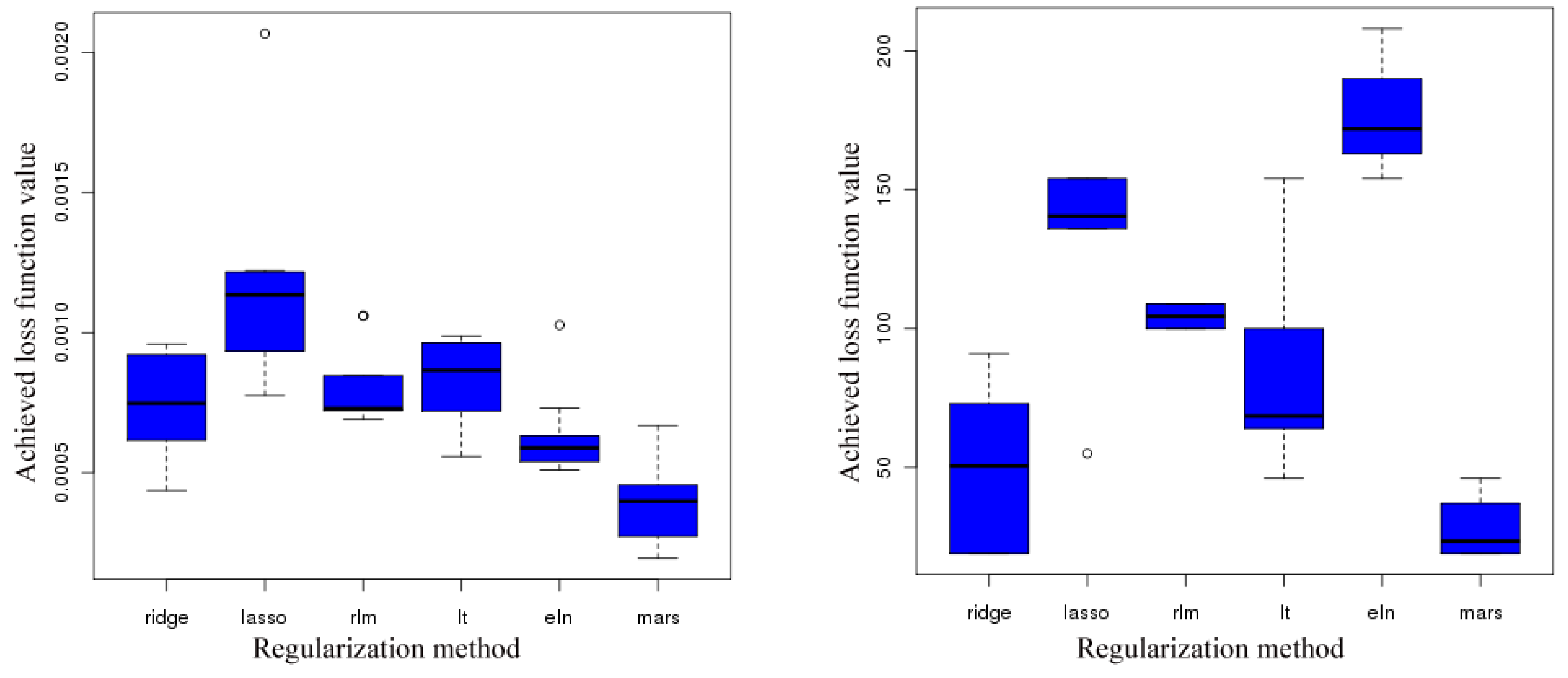
4.2. Application of SpaGROW to Molecular Simulations
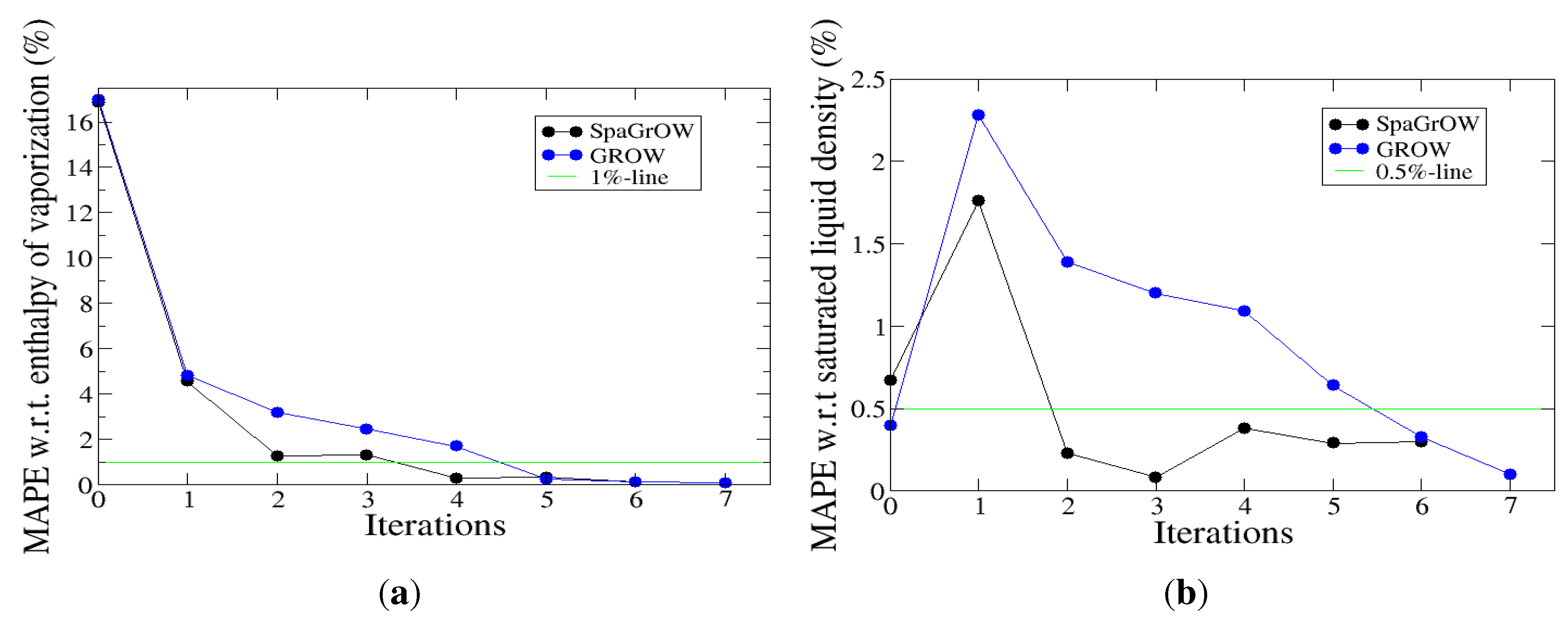
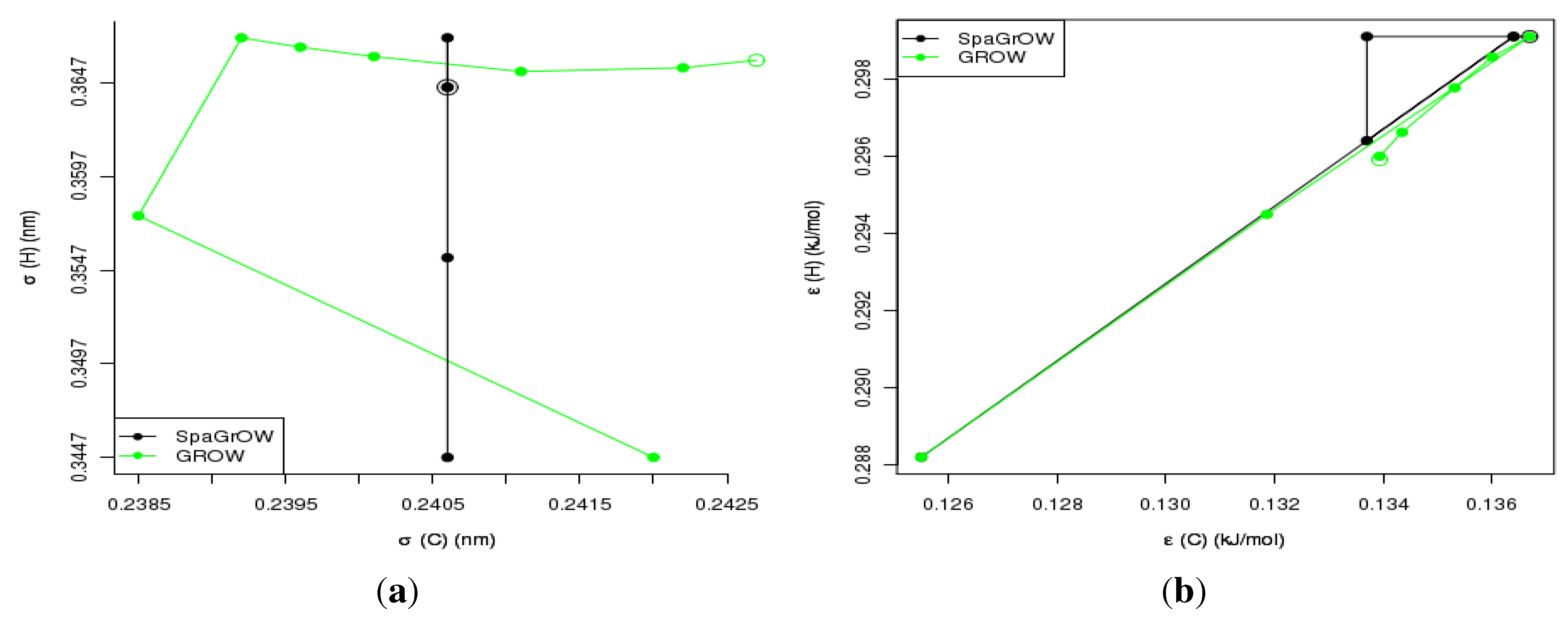
4.2.1. Comparison to Gradient-Based Methods with Respect to Computation Time: Benzene and Ethylene Oxide
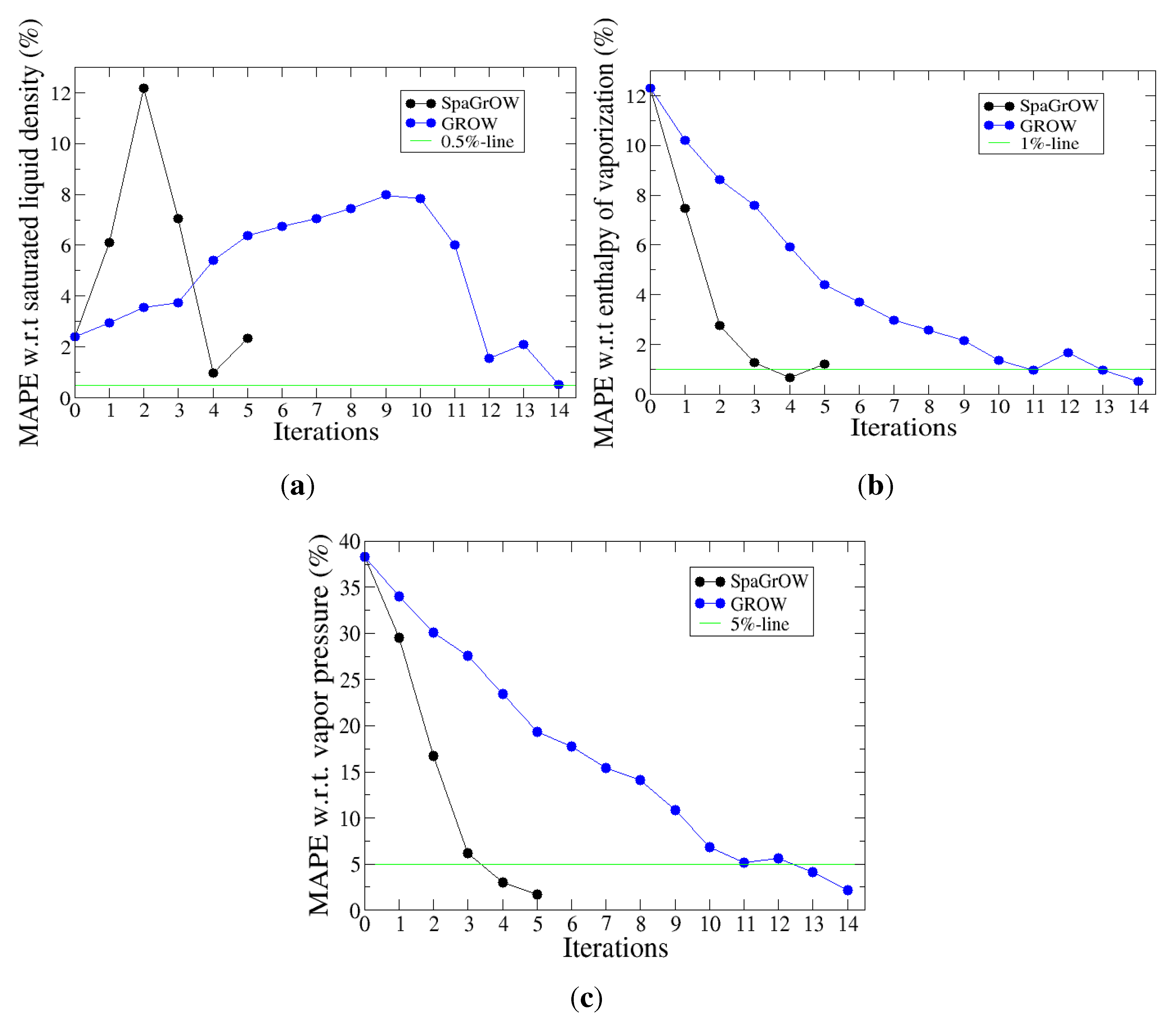
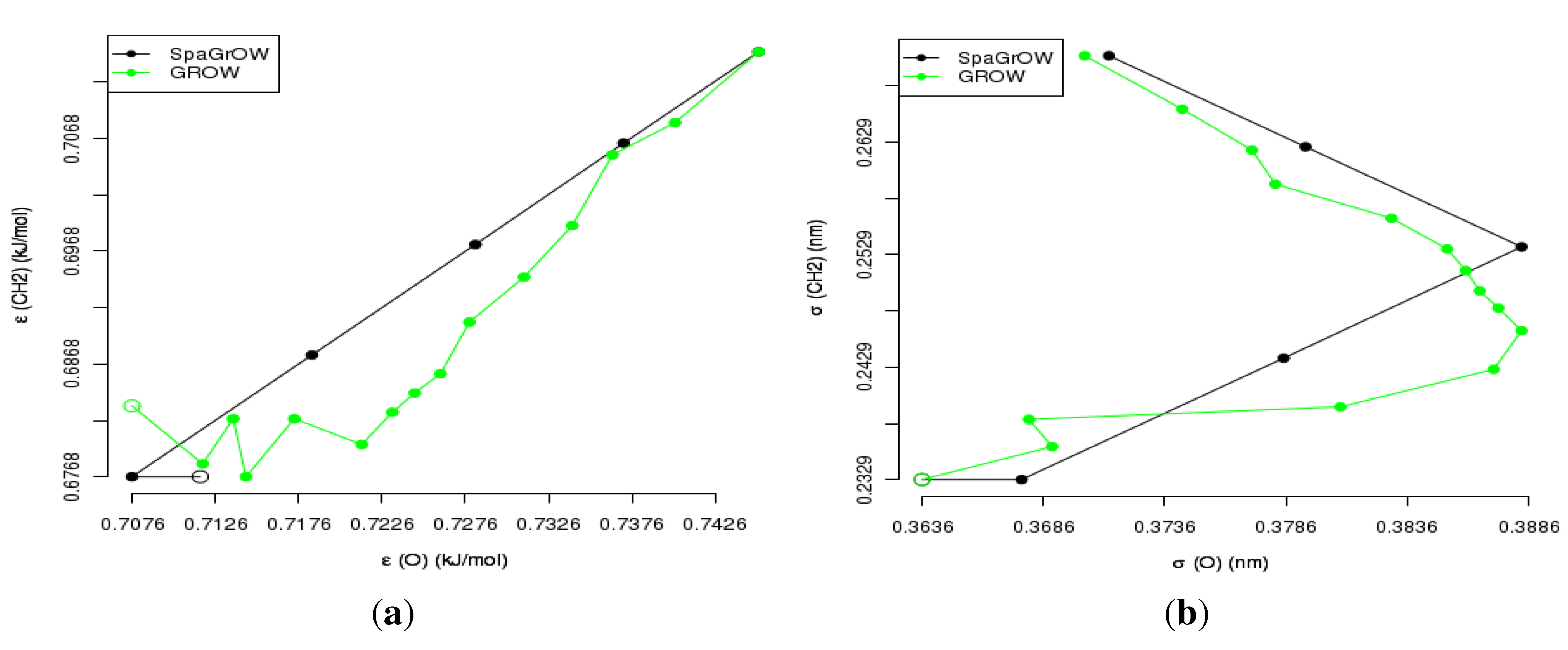
4.2.2. Comparison to Gradient-Based Methods Close to the Minimum: Dipropylene Glycol Dimethyl Ether
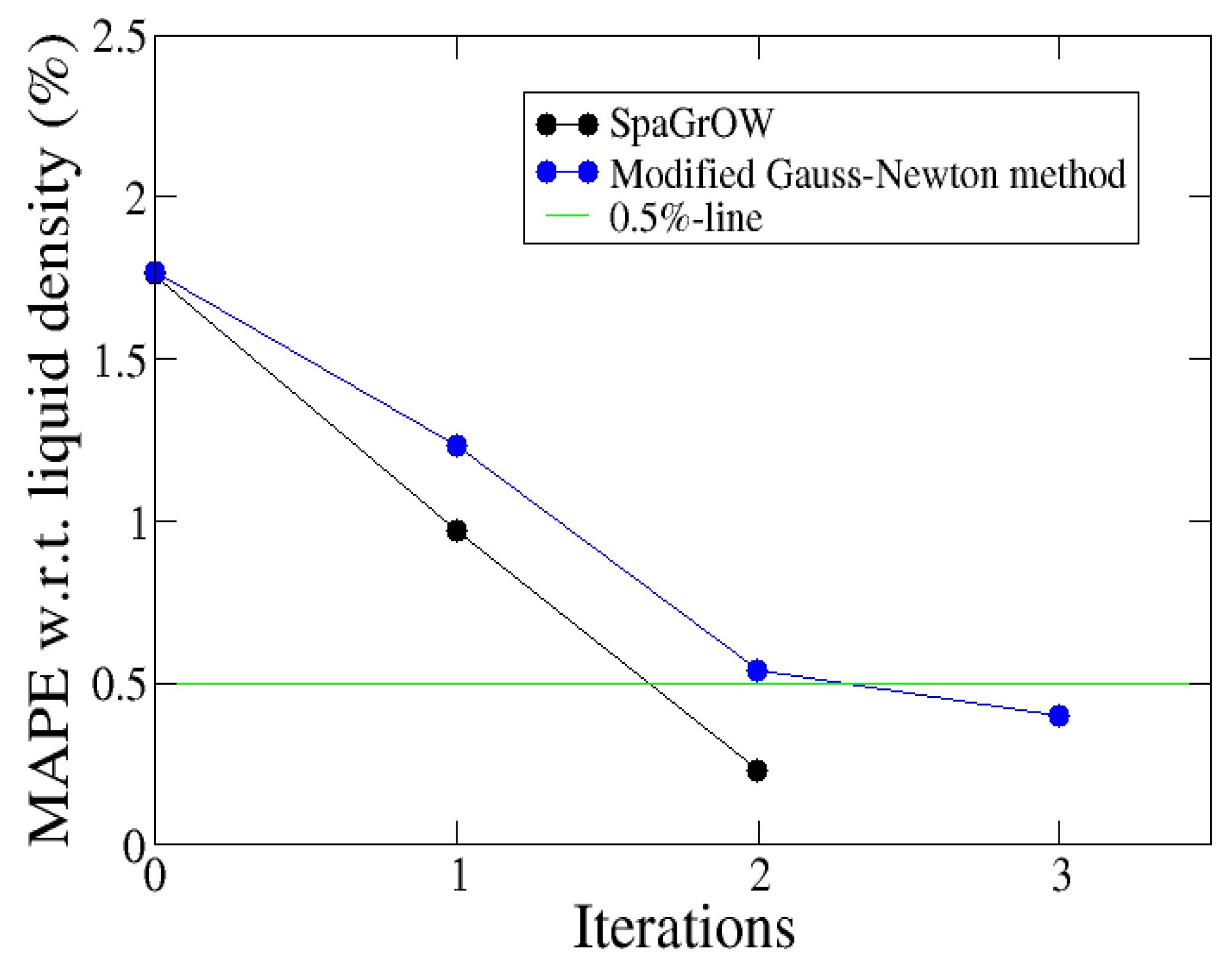
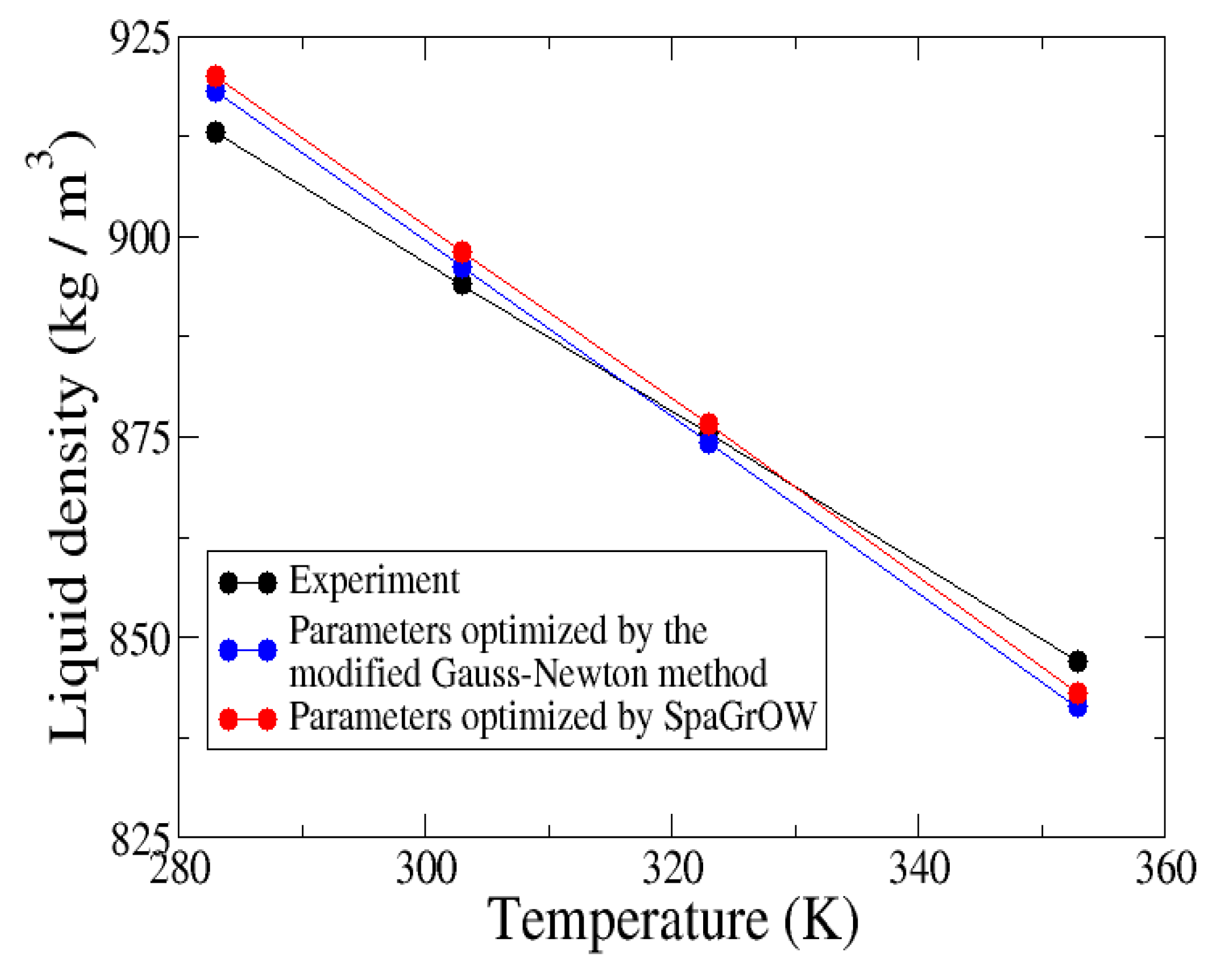
5. Conclusions
- Speed of convergency: Whenever is chosen properly, SpaGrOW often requires only half of the number of simulations than gradient-based methods. The speed of convergency was also higher, i.e., the number of iterations was significantly lower.The choice, , was suitable in most cases, i.e., the parameterization of SpaGrOW is not critical at the beginning of the optimization.
- Local refinements: SpaGrOW is capable of getting closer to the minimum than GROW. However, the choice of Δ becomes critical, which reduces the robustness of SpaGrOW: If Δ is too high, the smoothing and interpolation algorithms cannot deliver a reliable model for the loss functions. If it is too small, only noise can be reproduced. A modified Gauss-Newton method turned out to be more efficient and close to the minimum, if the associated gradients can be computed correctly. An important advantage of SpaGrOW is the fact that the step length can be modified by the Trust Region steps, leading to different descent directions, which is not possible for gradient-based methods first determining the descent direction and, then, searching for a reliable step length.
- Robustness: SpaGrOW exhibits a slightly lower robustness than the gradient-based methods. Due to an inappropriate choice of Δ, the minimum of the model can be transferred under certain conditions, and the course of the algorithm can be modified. The variable must be chosen, so that a decreasing trend of the loss function is present within the actual trust region. However, this is not trivial here, because the shape of the loss function is not known a priori.
Acknowledgements
Conflicts of Interest
References
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: Waltham, MA, USA, 2006. [Google Scholar]
- Schrödinger, E. Quantisierung als eigenwertproblem. Ann. Phys. 1926, 79, 361–367. [Google Scholar] [CrossRef]
- Jensen, F. Introduction to Computational Chemistry; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Guevara-Carrion, G.; Hasse, H.; Vrabec, J. Multiscale Molecular Methods in Applied Chemistry; Kirschner, B., Vrabec, J., Eds.; Series: Topics in Current Chemistry; Volume 307, Springer: Berlin/Heidelberg, Germany, 2012; pp. 201–249. [Google Scholar]
- Weiner, S.J.; Kollman, P.A.; Case, D.A.; Singh, U.C.; Ghio, C.; Alagona, G.; Profeta, S.; Weiner, P. A new force field for molecular mechanical simulation of nucleic acids and proteins. J. Am. Chem. Soc. 1984, 106, 765–784. [Google Scholar] [CrossRef]
- Berendsen, H.J.; van Gunsteren, W.F. GROMOS87 Manual; Library Manual; Biomos AG: Groningen, The Netherlands, 1987. [Google Scholar]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Duan, Y.; Wu, C.; Chowdhury, S.; Lee, M.C.; Xiong, G.; Zhang, W.; Yang, R.; Cieplak, P.; Luo, R.; Lee, T.; et al. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechancical calculations. J. Comput. Chem. 2003, 24, 1999–2012. [Google Scholar] [CrossRef] [PubMed]
- Reith, D.; Kirschner, K.N. A modern workflow for force-field development—bridging quantum mechanics and atomistic computational models. Comput. Phys. Commun. 2011, 182, 2184–2191. [Google Scholar] [CrossRef]
- Kräemer-Fuhrmann, O.; Neisius, J.; Gehlen, N.; Reith, D.; Kirschner, K.N. Wolf2Pack—Portal based atomistic force-field development. J. Chem. Inf. Mod. 2013, 53, 802–808. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Madura, J.D.; Swensen, C.J. Optimized intermolecular potential functions for liquid hydrocarbons. J. Am. Chem. Soc. 1984, 106, 6638–6646. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 1998, 102, 2567–2577. [Google Scholar] [CrossRef]
- Eckl, B.; Vrabec, J.; Hasse, H. On the application of force fields for predicting a wide variety of properties: Ethylene oxide as an example. Fluid Phase Equilib. 2008, 274, 16–26. [Google Scholar] [CrossRef]
- Peguin, R.P.S.; Kamath, G.; Potoff, J.J.; da Rocha, S.R.P. All-atom force field for the prediction of vapor–liquid equilibria and interfacial properties of HFA134a. J. Phys. Chem. B 2009, 113, 178–187. [Google Scholar] [CrossRef] [PubMed]
- Faller, R.; Schmitz, H.; Biermann, O.; Müller-Plathe, F. Automatic parameterization of force fields liquids by simplex optimization. J. Comput. Chem. 1999, 20, 1009–1017. [Google Scholar] [CrossRef]
- Ungerer, P.; Beauvais, C.; Delhommelle, J.; Boutin, A.; Rousseau, B.; Fuchs, A.H. Optimization of the anisotropic united atoms intermolecular potential for n-alkanes. J. Comput. Phys. 1999, 112, 5499–5510. [Google Scholar] [CrossRef]
- Bourasseau, E.; Haboudou, M.; Boutin, A.; Fuchs, A.H.; Ungerer, P. New optimization method for intermolecular potentials: Optimization of a new anisotropic united atoms potential for Olefins: Prediction of equilibrium properties. J. Chem. Phys. 2003, 118, 3020–3034. [Google Scholar] [CrossRef]
- Stoll, J.; Vrabec, J.; Hasse, H. A set of molecular models for carbon monoxide and halogenated hydrocarbons. J. Chem. Phys. 2003, 119, 11396–11407. [Google Scholar] [CrossRef]
- Sun, H. Prediction of fluid densities using automatically derived VDW parameters. Fluid Phase Equilib. 2004, 217, 59–76. [Google Scholar] [CrossRef]
- Hülsmann, M.; Köddermann, T.; Vrabec, J.; Reith, D. GROW: A gradient-based optimization workflow for the automated development of molecular models. Comput. Phys. Commun. 2010, 181, 499–513. [Google Scholar] [CrossRef]
- Hülsmann, M.; Vrabec, J.; Maaß, A.; Reith, D. Assessment of numerical optimization algorithms for the development of molecular models. Comput. Phys. Commun. 2010, 181, 887–905. [Google Scholar] [CrossRef]
- Hülsmann, M.; Müller, T.J.; Köddermann, T.; Reith, D. Automated force field optimisation of small molecules using a gradient-based workflow package. Mol. Simul. 2011, 36, 1182–1196. [Google Scholar] [CrossRef]
- Griebel, M.; Schneider, M.; Zenger, C. A Combination Technique for the Solution of Sparse Grid Problems; Technical Report; Institut für Informatik, Technische Universität München: Munich, Germany, 1990. [Google Scholar]
- Moré, J.J. Mathematical Programming: The State of the Art; Bachem, A., Grötschel, M., Korte, B., Eds.; Springer: Berlin/Heidelberg, Germany, 1983; pp. 258–287. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Mangasarian, O.L.; Rosen, J.B.; Thompson, M.E. Global minimization via piecewise-linear underestimation. J. Glob. Optim. 2004, 32, 1–9. [Google Scholar] [CrossRef]
- Smolyak, S.A. Quadrature and interpolation formulas for tensor products of certain classes of functions. Sov. Math. Doklady 1963, 4, 240–243. [Google Scholar]
- Zenger, C. Parallel Algorithms for Partial Differential Equations, Notes on Numerical Fluid Mechanics; Hackbusch, W., Ed.; Vieweg: Wiesbaden, Germany, 1991; Volume 31, pp. 241–251. [Google Scholar]
- Bungartz, H.-J. Iterative Methods in Linear Algebra. In Proceedings of the IMACS International Symposium, Brüssel, Belgium, April 1991; de Groen, P., Beauwens, R., Eds.; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1992; pp. 293–310. [Google Scholar]
- Powell, M. Algorithms for Approximation; Mason, J.C., Cox, M.G., Eds.; Clarendon Press: Oxford, UK, 1987; pp. 143–167. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Series: Information Science and Statistics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- MacQueen, J.B. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, June/July 1965; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. Roy. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. Roy. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Wendland, H. Scattered Data Approximation; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Wendland, H. Konstruktion und Untersuchung radialer Basisfunktionen mit kompaktem Träger. Ph.D. Thesis, Universität Göttingen, Göttingen, Germany, 1996. [Google Scholar]
- Hülsmann, M. Effiziente und neuartige Verfahren zur Optimierung von Kraftfeldparametern bei atomistischen Molekularen Simulationen kondensierter Materie. Ph.D. Thesis, Universität zu Köln, Cologne, Germany, 2012. [Google Scholar]
- Conn, A.R.; Scheinberg, K.; Toint, P.L. On the Convergence of Derivative-free Methods for Unconstrained Optimization; Iserles, A., Buhmann, M., Eds.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- The R Project for Statistical Computing. Available online: http://www.r-project.org/ (accessed on 14 February 2013).
- Stoll, J.; Vrabec, J.; Hasse, H.; Fischer, J. Comprehensive study of the vapour-liquid equilibria of the pure two-centre Lennard-Jones plus pointquadrupole fluid. Fluid Phase Equilib. 2001, 179, 339–362. [Google Scholar] [CrossRef]
- Yoshida, K.; Matubayasi, N.; Nakahara, M. Self-diffusion coefficients for water and organic solvents at high temperatures along the coexistence curve. J. Chem. Phys. 2008, 129, 214501–214509. [Google Scholar] [CrossRef] [PubMed]
- NIST Chemistry Webbook. Available online: http://webbook.nist.gov/chemistry/ (accessed on 14 February 2013).
- GROMACS Molecular Simulation Tool. Available online: http://www.gromacs.org/ (accessed on 14 February 2013).
- Moscito Molecular Simulation Tool. Available online: http://ganter.chemie.uni-dortmund.de/MOSCITO/ (accessed on 14 February 2013).
- Buckles, C.; Chipman, P.; Cubillas, M.; Lakin, M.; Slezak, D.; Townsend, D.; Vogel, K.; Wagner, M. Ethylene Oxide User’s Guide; Online Manual, Publisher; American Chemistry Council, 1999; Available online: http://www.ethyleneoxide.com (accessed on 14 February 2013).
- Olson, J.D.; Wilson, L.C. Benchmarks for the fourth industrial fluid properties simulation Challenge. Fluid Phase Equilib. 2008, 274, 10–15. [Google Scholar] [CrossRef]
- Müller, T.J.; Roy, S.; Zhao, W.; Maaß, A.; Reith, D. Economic simplex optimization for broad range property prediction: Strengths and weaknesses of an automated approach for tailoring of parameters. Fluid Phase Equilib. 2008, 274, 27–35. [Google Scholar] [CrossRef]
- Maaß, A.; Nikitina, L.; Clees, T.; Kirschner, K.N.; Reith, D. Multiobjective optimisation on the basis of random models for ethylene oxide. Mol. Simul. 2010, 36, 1208–1218. [Google Scholar] [CrossRef]
- ms2 Molecular Simulation Tool. Available online: http://www.ms-2.de/ (accessed on 14 February 2013).
- The Industrial Fluid Property Simulation Challenge. 2010. Available online: http://www.ifpsc.com (accessed on 14 February 2013).
- Esteve, X.; Conesa, A.; Coronas, A. Liquid densities, kinematic viscosities, and heat capacities of some alkylene glycol dialkyl ethers. J. Chem. Eng. Data 2003, 48, 392–397. [Google Scholar] [CrossRef]
- Köddermann, T.; Kirschner, K.N.; Vrabec, J.; Hülsmann, M.; Reith, D. Liquid-liquid equilibria of dipropylene glycol dimethyl ether and water by molecular dynamics. Fluid Phase Equilib. 2011, 310, 25–31. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hülsmann, M.; Reith, D. SpaGrOW—A Derivative-Free Optimization Scheme for Intermolecular Force Field Parameters Based on Sparse Grid Methods. Entropy 2013, 15, 3640-3687. https://doi.org/10.3390/e15093640
Hülsmann M, Reith D. SpaGrOW—A Derivative-Free Optimization Scheme for Intermolecular Force Field Parameters Based on Sparse Grid Methods. Entropy. 2013; 15(9):3640-3687. https://doi.org/10.3390/e15093640
Chicago/Turabian StyleHülsmann, Marco, and Dirk Reith. 2013. "SpaGrOW—A Derivative-Free Optimization Scheme for Intermolecular Force Field Parameters Based on Sparse Grid Methods" Entropy 15, no. 9: 3640-3687. https://doi.org/10.3390/e15093640
APA StyleHülsmann, M., & Reith, D. (2013). SpaGrOW—A Derivative-Free Optimization Scheme for Intermolecular Force Field Parameters Based on Sparse Grid Methods. Entropy, 15(9), 3640-3687. https://doi.org/10.3390/e15093640