Abstract
A quantum entropy space is suggested as the fundamental arena describing the quantum effects. In the quantum regime the entropy is expressed as the superposition of many different Boltzmann entropies that span the space of the entropies before any measure. When a measure is performed the quantum entropy collapses to one component. A suggestive reading of the relational interpretation of quantum mechanics and of Bohm’s quantum potential in terms of the quantum entropy are provided. The space associated with the quantum entropy determines a distortion in the classical space of position, which appears as a Weyl-like gauge potential connected with Fisher information. This Weyl-like gauge potential produces a deformation of the moments which changes the classical action in such a way that Bohm’s quantum potential emerges as consequence of the non classical definition of entropy, in a non-Euclidean information space under the constraint of a minimum condition of Fisher information (Fisher Bohm- entropy). Finally, the possible quantum relativistic extensions of the theory and the connections with the problem of quantum gravity are investigated. The non classical thermodynamic approach to quantum phenomena changes the geometry of the particle phase space. In the light of the representation of gravity in ordinary phase space by torsion in the flat space (Teleparallel gravity), the change of geometry in the phase space introduces quantum phenomena in a natural way. This gives a new force to F. Shojai’s and A. Shojai’s theory where the geometry of space-time is highly coupled with a quantum potential whose origin is not the Schrödinger equation but the non classical entropy of a system of many particles that together change the geometry of the phase space of the positions (entanglement). In this way the non classical thermodynamic changes the classical geodetic as a consequence of the quantum phenomena and quantum and gravity are unified. Quantum affects geometry of multidimensional phase space and gravity changes in any point the torsion in the ordinary four-dimensional Lorenz space-time metric.
1. Introduction
The advantage of a geometric representation of physical phenomena is not only the elegance, but also and above all the immediate visualization of processes. In the first part of the article, we will consider the entropy of a quantum system as a vector of the superposition of many different entropies whose values are conditioned by the observer and will provide a new suggestive reading to Rovelli’s relational quantum mechanics. Any observer makes the system in superposition collapse to a classical value of entropy, i.e., he/she fixes classical information by a measurement. When the observer does not interact with a quantum system, the composed system given by the quantum microsystem + observer is in an entangled state. When the observer interacts with the microsystem under consideration thus becoming an active element, the composed system given by the quantum microsystem + observer is in a pure state and follows the non classical thermodynamics defined by a quantum multidimensional space of entropies.
In the second part of the article, fixed the background of the rectangular coordinates of the entropy, we will show that the non linear relation of the average values of the phase space with the different observed entropy generates an information manifold of the phase space with Fisher metric. By the covariant derivatives in a general form represented by the Morphogenetic system illustrated in the mathematical appendix, the Bohm quantum potential by a minimum principle of the average action is obtained as Fisher metric or information metric in the phase space. In this approach, the Bohm quantum potential emerges as a consequence of the classical equilibrium condition in the quantum entropy space. Fisher information metric in the curved phase space can be considered as an information medium whose deformation or curvature justify the usual quantum phenomena. In the non classical entropic picture the curvature of space indicates the Weyl-like gauge potential connected with Fisher metric. Because Bohm’s quantum potential is a consequence of the Schrödinger equation and vice versa, one can give a thermodynamic justification of the quantum mechanics modeled by Schrödinger equation. In this approach, we will also unify quantum and gravity theories for Bohm’s representation in general relativity. All the quantum phenomena disappear when the vacuum curvature in phase space is zero, the Fisher metric is the Euclidean metric and the Weyl-like gauge potential that is function of all particles’ positions is zero.
2. Quantum Mechanics from Vector of Boltzmann Entropies
In his paper The Statistic Origin of Quantum Mechanics Klein [1] takes into consideration three different levels of the role played by probability in Physics passing from the classical scenario to the quantum one: “With regard to the role of probability, three types of physical theories may be distinguished:
- Theories of type 1 are deterministic. Single events are completely described by their known initial values and deterministic laws (differential equations). Classical mechanics is obviously such a theory. We include this type of theory, where probability does not play any role, in our classification scheme because it provides a basis for the following two types of theories. Theories of type 2 have deterministic laws but the initial values are unknown. Therefore, no predictions on individual events are possible, despite the fact that deterministic laws describing individual events are valid. In order to verify a prediction of a type 2 theory a large number of identically prepared experiments must be performed. We have no problems to understand or to interpret such a theory because we know it is just our lack of knowledge which causes the uncertainty. An example is given by classical statistical mechanics. Of course, in order to construct a type 2 theory one needs a type 1 theory providing the deterministic laws.
- It is possible to go one step further in this direction increasing the relative importance of probabilityeven more. We may not only work with unknown initial values but with unknown laws as well. In the type 3 theories there are no deterministic laws describing individual events, only probabilities can be assigned. There is no need to mention initial values for particle trajectories any more (initial values for probabilistic dynamical variables are still required).”
In the type 3 theories we have unknown laws so the entropy is dependent on the observer. Any observer by a measure can see only one of the possible values of the vector of entropies. While in classical thermodynamics the entropy has the same value and structure for any observer and the observer cannot change the physical form of the entropy, in the quantum regime before any measure the entropy is the superposition of many different possible entropies that span the space of the entropies or quantum entropy space. When a measure is performed the quantum entropy space given by the superposition of different Boltzmann entropies collapses to one component. The vector of the entropies one for any observer can be expressed as follows:
where
and where k is the Boltzmann constant, x and θ are the phase space positions of the particles and parameters (such as average of the positions) of the probability distribution respectively. One has to remark here that the parameters’ distributions can differ one from another also as regards the number of parameters characterizing them and that the distributions can be characterized by many different parameters, including the average coordinates, but not limited only to these ones. For the equilibrium condition the probability for any observer is equal in any position x and is function only of the parameters. So we have:
and:
where W are the number of the microstates for the same parameters θ as temperatures, pressures etc. In this case S is a vector of Boltzmann entropies one for any observer in the non classical space of entropies ( S1 , S2,….,Sn ). Now we have:
where J is a rectangular metric. For the mathematical appendix A we have the metric in the parameter space of the average position of the particles in the curved phase space in this way:
where F is the quadratic and symmetric Fisher metric [2,3]. We have also that:
where ∑ is the covariant matrix of the Cramer Rao lower bound.
The interpretation of quantum mechanics from a vector of Boltzmann entropies whose values are conditioned by the observer can be considered as a new elegant and suggestive way to formulate relational quantum mechanics. The central tenet of relational quantum mechanics [4,5,6,7] is that there is no meaning in saying that a certain quantum event has happened or that a variable of the system S has taken the value q: rather, there is meaning in saying that the event q has happened or the variable has taken the value q with respect to another system O. The apparent contradiction between the two statements that a variable has or has not a value is resolved by indexing the statements with the different systems with which the system in question interacts. Quantum events only happen in interactions between systems, and the fact that a quantum event has happened is only true with respect to the systems involved in the interaction. The unique account of the state of the world of the classical theory is thus fractured into a multiplicity of accounts, one for each possible “observing” physical system. On the basis of the mathematical formalism developed in this section, one can say that the non classical space of the entropies (whose values are conditioned by the observer) is the fundamental entity that explains in what sense, when a quantum event happens, it happens only with respect a peculiar observing physical system. In quantum mechanics, one can say that a variable of a quantum system takes the value q because the vector of different Boltzmann entropies collapses to one specific entropy which corresponds with the value q of the variable under consideration: an interaction between the quantum system and an observer happens which produces the collapse of the quantum vector of entropies into one specific entropy and the observer involved in this interaction measures just the value q of the variable under consideration.
3. From Vector of Boltzmann Entropies to Bohm’s Quantum Potential
In Section 2, we have shown that a non classical entropy space can lead to a new interesting reading of Rovelli’s relational quantum mechanics. However, as is known, Rovelli’s relational quantum mechanics points towards the reconciliation between irreversibility (collapse of the wave function and thus the standard interpretation of quantum mechanics) with the reversibility of the Lorentzian observers. Rovelli’s approach indeed continuously turns each question on the collapse of the wave function. So, the wave function collapse remains the “fifth postulate” of quantum mechanics and diffuses the Von Neumann chain hidden dangers in a network of observers. In this regard, from the viewpoint of the standard interpretation of quantum mechanics and somewhat also of relational quantum mechanics, one can say that no collapse has happened until the information about the interaction between the quantum microsystem under consideration and the observer has arrived in this observer’s brain. If an observer A has the information that the measurement has happened but an observer B has not had an interaction with the microsystem under consideration and thus has the information that the measurement has not happened, this implies that for the observer B the measured system and the brain of the first observer (A) have both remained in a superposition. This leads to the conclusion that “subjectively” a collapse of the wave function has occurred relative only to a peculiar observer’s consciousness state, but “objectively” there is no collapse [8].
Let us pose the following example: before an observer A measures the spin of an electron S, it is in a superposition state. Before this observer A has any contact with the electron, the apparatus O, or their environment, they are altogether in a superposition state. After looking at the apparatus, there is no longer superposition relative to his/her consciousness. However, relative to another observer B the combined state of the electron S, the apparatus O and the brain of the observer A can remain in superposition until B himself gets in contact with A, O, S, or the environment of S, O and A. As a consequence it seems legitimate to argue that a wave function is always relative to something, or, better, to somebody. There can be no “objective” wave function. In the standard interpretation of quantum mechanics, and consequently in relational quantum mechanics too, a wave function can be always considered as relative to some observer. Thus the collapse of the wave function can be always considered as a subjective collapse. Relative to a given observer A, a wave function is collapsing all the time: whenever the information (direct or indirect — through the environmental degrees of freedom) about the outcome of measurement reaches the observer A. Instead, there is no collapse if we contemplate other observers B, C, D, … performing their experiments. On the basis of these considerations, according to the authors of this article, it seems legitimate to conclude that—since an observer can always be defined for everything is in a superposition state—the quantum superposition and the quantum entanglement between given systems can be considered as the fundamental reality of the universe. But such aspect has not at all to be considered as “subjective”: at the origin of the universe there were no observers; in a double-slit experiment the electrons’ pattern does not depend on an observer!
What we mean to say is that the wave-function is not a mysterious ghost who vanishes when the measurement arrives, but something which acts on the matter and determines the conditions of the measurement itself [9]. Quantum mechanics pictures the world also without observers: it is possible to eliminate the mystery of the collapse in a realistic picture by recognizing the contextual nature of the quantum measurement. In this chapter, by making use of the non classical space of the entropies we will provide a new interesting reading of Bohm’s version of quantum mechanics in which the quantum potential emerges as a deformation of the information medium determined by the vector of the space of Boltzmann entropies [10,11]. Finally, remember that these “strange problems” of QM arise from the fact that-contrary to what is being said-it is not a “fundamental” theory (or “complete”, in the Einstein’s sense). A clarification of the problems of wave/particle duality require a rethinking in terms of Quantum Field Theory, maybe the only “realistic” interpretation of quantum mechanics, which is beyond our goals [12,13]
In virtue of the formalism developed in the mathematical appendix A we have:
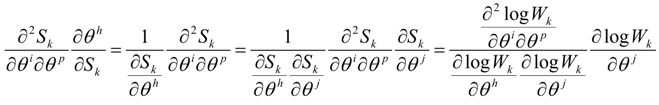 which, if:
which, if:
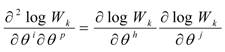 leads to the following equation:
leads to the following equation:
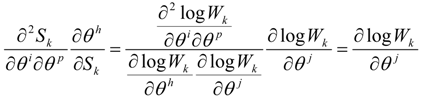
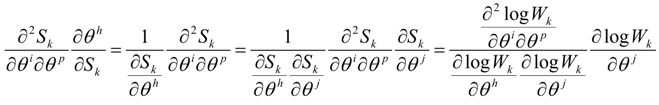
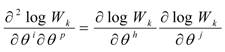
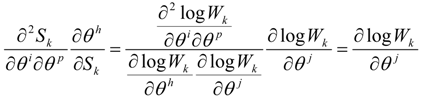
Thus one obtains a deformation of the derivative for the non Euclidean geometry which is given by the relation:
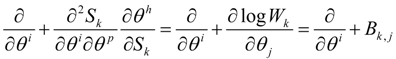 where:
where:
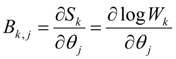 is a Weyl-like gauge potential [14,15,16].
is a Weyl-like gauge potential [14,15,16].
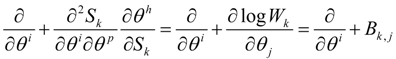
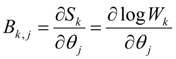
Now in the classical mechanics the equation of average motion can be expressed, by the definition of the action A, in this way:
In quantum mechanics we have non-local correlations of momenta and thus the change of the geometry of the action:
which gives:
namely:
namely:
The Fisher information (quantum action) assumes the minimum value when
under Euler Lagrange condition:
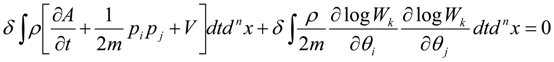 and thus:
where Q is the Bohm quantum potential (in the next equations, for simplicity we are going to denote the generic function
[defined by Equations (3)] with W ) [17]:
and thus:
where Q is the Bohm quantum potential (in the next equations, for simplicity we are going to denote the generic function
[defined by Equations (3)] with W ) [17]:
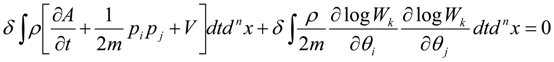
It is of great physical interest to note that the Equation (20) connects the Bohm potential to W, number of microstates of the system, thus providing a vivid picture of how non-locality modifies the probability distribution. In other words, according to Bohm-Hiley “active information” [18], the quantum Potential emerges as an informational channel given by the functions W in the non Euclidean space of the entropies with Fisher metric. Even the metric assumes here a direct physical meaning, i.e., distance as distinguishability between W micro-states.
The approach of the quantum potential expressed by Equations (12)–(21), which we will call Fisher-Bohm Entropy, may be put in comparison with another entropic approach, developed recently in the papers [19,20] according to which the space-temporal distribution of the ensemble of particles describing the physical system under consideration is assumed to generate a modification of the geometry described by a quantum entropy given by equation:
In the Sbitnev and Fiscaletti papers it was demonstrated that, by starting from the quantum entropy in Equation (22)—which was introduced as the degree of order and chaos of the vacuum supporting the density of the ensemble of particles associated with the wave function—a new picture of non-relativistic de Broglie-Bohm theory emerges in which the quantum potential can be expressed as:
namely as a sum of two quantum corrector terms: the term
which can be interpreted as the quantum corrector of the kinetic energy
of the particle and the term
which can be interpreted as the quantum corrector of the potential energy. Therefore, by equating Equations (21) and (23) one obtains:
which tells us that the two quantum corrector terms of the energy of the particle
and
correspond with two terms depending on the functions W defining the number of the microstates of the physical system, namely
and
respectively:
Thus, on the basis of Equations (25) and (26), one can say that the functions W appearing in the vector of the superposed Boltzmann entropies Equation (3) are linked with the quantity Equation (22) and thus with the density of the particles associated with the wave function under consideration. Moreover, introducing the two quantum correctors of the energy given by Equations (25) and (26), the quantum Hamilton-Jacobi equation of non-relativistic Bohmian mechanics reads as:
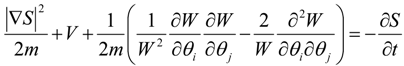
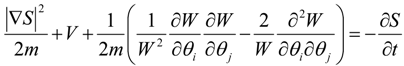
Equation (27) provides an energy conservation law in non-relativistic quantum mechanics in the space of parameters where the two quantum corrector terms given by relations Equation (25) and (26) can be interpreted as a sort of modification of the geometry of the parameter space determined by the density of the ensemble of particles associated with the wave function under consideration.
Finally, in non-relativistic Bohmian mechanics, the quantum potential contains a global information on the environment and at the same time it is a dynamical entity derives just from the functions—linked with the density of the ensemble of particles associated with the wave function under consideration on the basis of Equations (25) and (26). The functions W emerge just as informational lines of the quantum potential. It has to be mentioned here another advantage of Bohm’s theory. What is usually defined as “background space” in quantum mechanics is nothing but an “open door” on a typical level of quantum field theory; it is possible to show that the Feynman integral paths can be correlated with Bohm’s quantum potential and the same classic concept of “trajectory” emerges from the dynamics of quantum fields [21,22,23,24].
If we consider, for example, the double slit experiment, the quantum potential is an information potential, namely brings a global, instantaneous (in classical language) and active information (in Bohm-Hiley acception [18]) on the process and its environment (in fact, it turns out to depend on the width of the slits, their distance apart and the momentum of the particle and turns out to modify the behaviour of the particle itself), because it is determined by the functions W and its geometric properties, which represent its informational lines, and thus by the quantum entropy space. So, if one of the two slits is closed the quantum potential changes just because its informational lines represented by the functions W geometry change contextually.
In conclusion from classical entropy without the introduction of the wave function we have built for the different observers a non classical definition of the entropy space whose geometry gives us the non local quantum effects. Any component of this entropic space is classic (after “collapse”) but the multidimensional space is not classic. This entropy space can be considered as the original entity from which we can obtain Bohm’s potential as an intermediate entity to obtain a physical justification of the wave representation of the quantum phenomena with the entanglement.
4. Curved Space-Time Embedded in Phase Space with Fisher Metric as Fusion of Quantum with Gravity
Soon after General Relativity was given its final presentation as a new theory for the gravitational field, an attempt to unify gravitation and electromagnetism was made by Weyl in 1918 [25]. His proposal did not succeed, but introduced for the first time the notions of gauge transformations and gauge invariance. Another attempt in the same direction was made by A. Einstein, about ten years later. This attempt was based on the mathematical structure of teleparallelism, also referred to as distant or absolute parallelism. Roughly speaking, the idea was the introduction of a tetrad field, a field of orthonormal bases on the tangent spaces at each point of the four-dimensional spacetime. The tetrad has sixteen components, whereas the gravitational field, represented by the spacetime metric, has only ten. According to this approach, General Relativity as a theory that involves only curvature was supplemented by Teleparallel Gravity [23], a theory that involves only torsion. This theory, called New General Relativity, represented a new way of including torsion in General historical account of the teleparallelism. Teleparallel Gravity is found to be completely equivalent to General Relativity. In this case it is sometimes referred to as the Teleparallel Equivalent of General Relativity. Although frequently reserved for the three-parameter theory, the name Teleparallel Gravity will be used here as a synonymous for the teleparallel equivalent of General Relativity. A fundamental property embodied in Teleparallel Gravity is that, due to the equivalence with General Relativity, curvature and torsion are able to provide equivalent descriptions of the gravitational interaction. In General Relativity, curvature is used to geometrize the gravitational interaction. That is to say, geometry replaces the concept of gravitational force, and the trajectories are determined, not by force equations, but by geodesics.
Teleparallel Gravity, on the other hand, attributes gravitation to torsion, but not through a geometrization: it acts as a force. In consequence, there are no geodesics in Teleparallel Gravity, only force equations quite analogous to the Lorentz force equation of electrodynamics. The reason for gravitation to present two equivalent descriptions lies in its most peculiar property: universality. Like the other fundamental interactions of Nature, gravitation can be described in terms of a gauge theory. In fact, Teleparallel Gravity is a gauge theory for the translation group. Universality of free fall, on the other hand, makes it possible a second, geometrized description, based on the equivalence principle, just General Relativity. As the sole universal interaction, it is the only one to allow also a geometrical interpretation, and hence two alternative descriptions. From this point of view, curvature and torsion are simply alternative ways of representing the same gravitational interaction.
The next important step is to see what happens to the quantum potential Equation (21) in a relativistic version of Bohm’s theory in curved space-time. When we use the teleparallel model of gravity with forces in the flat space time, flat space with torsion can be enriched by the quantum phenomena that is represented without any forces by the Fisher information metric in the space of the particles’ positions (configuration space). To connect the Fisher information to Bohm’s theory we introduce new type of forces or gauge potential in Equation (12) for gauge translation in the configuration space. The new forces are not function of the space-time point but are function of all points of the space where the particles are located in the universe. The forces in the teleparallel model of gravity are similar to Lorenz forces, but the forces in the dependent observers entropies in Equation (12) are global forces that are defined by all particles together (entanglement). So the movement in this quantum gravity system is not a geodetic but we have a deviation for the deformation of the phase space due to the entropic distribution for any observer of the particles’ positions (entanglement). All the previous quantum gravity effects can be studied by taking under consideration the bohmian approach to Klein-Gordon equation developed by F. Shojai and A. Shojai in [26,27], which has the merit to provide a geometrodynamic interpretation of relativistic Bohm theory characterized by a significant unification of the quantum and gravitational behaviours of matter in a geometric picture. In F. Shojai’s and A. Shojai’s model, the quantum Hamilton-Jacobi equation which derives from the decomposition of the wave function in its polar form
has the following form:
which is Poincarè invariant and has the correct non-relativistic limit and where the quantum potential is defined as:
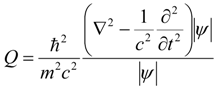
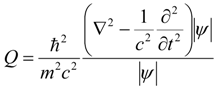
According to the view suggested in this chapter, on the basis of Equation (21), the space-temporal distribution of the ensemble of particles describing the individual physical system under consideration is assumed to generate a modification of the geometry, and thus a degree of chaos, of the background space linked with the functions W and thus with the quantum Entropy in Equation (3).
This modification of the geometry of the parameter space defined by the functions W determines a quantum potential which, taking account of F. Shojai’s and A.Shojai’s model, produces a quantum mass given by equation:
namely:
Moreover, F. Shojai and A. Shojai showed that, as regards Bohm’s version of Klein-Gordon equation, by changing the ordinary differentiating ∂μ with the covariant derivative ∇μ and by changing the Lorentz metric with the curved metric gμν inside Equations (28) and (29), it is possible to combine the Bohm quantum theory of motion and gravity and to interpret the quantum potential as the conformal degree of freedom of the space–time metric. In this picture, the quantum Hamilton-Jacobi equation of motion for a particle (of spin 0) in a curved background is the following:
where:
is the quantum potential. By utilizing a fruitful observation of de Broglie [28], that the quantum theory of motion for relativistic spinless particles is very similar to the classical theory of motion in a conformally flat space-time in which the conformal factor is related to Bohm’s quantum potential, the quantum Hamilton-Jacobi Equation (32) can be written as:
From Equation (34) one can conclude that the quantum effects are equivalent to the change of the space-time metric from gμν to:
which is a conformal transformation. In this way Equation (34) can be written as:
where
represents the covariant differentiation with respect to the metric
.
In F. Shojai’s and A. Shojai’s model, the important conclusion is thus that the presence of the quantum potential is equivalent to a curved space-time with its metric being given by Equation (35), i.e., we have obtained that there is a geometrization of the quantum aspects of matter. It seems that there is a dual aspect to the role of geometry in physics. The space-time geometry sometimes looks like what we call gravity and sometimes looks like what we understand as quantum behaviours. In other words, in F. Shojai’s and A. Shojai’s model, the effects of gravity on geometry and the quantum effects on the geometry of space-time are highly coupled, the geometric properties which are expressed by the quantum potential and which determine the behaviour of a particle of spin zero are linked with the curved space-time: the particles determine the curvature of space-time and at the same time the spacetime metric is linked with the quantum potential which influences the behaviour of the particles [29]. Now, in the approach suggested in this chapter based on the definition Equation (21) of the quantum potential as physical entity characterized by information lines linked with the functions W namely with the quantum entropy, one can interpret in a clear way why and in what sense the quantum potential is the conformal degree of freedom of the space-time metric, why and in what sense the effects of gravity on geometry and the quantum effects on the geometry of space-time are highly coupled: the key of explanation of these results lies just in the functions W, and thus in the quantum entropy, corresponding with the degree of chaos, with the modification of the geometry of the parameter space determined by the ensemble of particles associated with the wave function under consideration. The space-time which characterizes a relativistic curved space-time (in the presence of a particle of spin 0) has a conformal metric which is determined by the functions W (and thus is also linked with the quantum entropy) on the basis of equation:
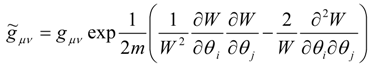 and the quantum Hamilton-Jacobi equation of motion Equation (36) in this background becomes:
and the quantum Hamilton-Jacobi equation of motion Equation (36) in this background becomes:
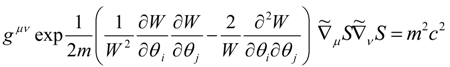
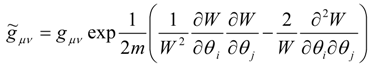
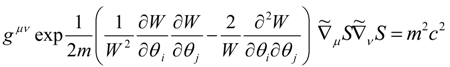
The dual role of the geometry in physics expected by F. Shojai’s and A. Shojai’s model receives therefore a new suggestive reading: the real key of reading of the link between gravity and quantum behaviours lies just in the functions W, namely in the quantum entropy Equation (3). The effects of gravity on geometry and the quantum effects on the geometry of space-time are highly coupled because they are both determined by the background space described by the quantum entropy, and thus by the functions W. Moreover, in the context of an entropic approach of F.Shojai’s and A. Shojai’s model based on a quantum entropy given by Equation (22), it was demonstrated that Bohm’s quantum potential for a spinless particle in a curved relativistic space-time is:
and that the conformal metric Equation (35) is [19]:
As a consequence, by equating Equations (37) and (40) one obtains:
which tells us that the functions W defining the number of the microstates of the spinless system is linked with the density of the ensemble of particles associated with the wave function of the system through equations:
On the basis of the picture proposed in this chapter, one can say that the quantum particles determine the curvature of space-time and at the same time the space-time metric is linked with the functions W indicating the informational lines of the motion of the particles. The functions W, the informational lines of the quantum potential, and thus the quantum entropy given by the superposition of different Boltzmann entropies, appear indeed as real intermediaries between gravitational and quantum effects of matter. The functions W, and thus the quantum entropy generates itself a curvature which may have a large influence on the classical contribution to the curvature of the space-time.
5. Conclusions
In this paper we have provided a new suggestive reading of quantum mechanics by starting from the superposition of different Boltzmann entropies one for any observer. In the first part of the article, we have seen that, while in classical thermodynamics entropy is defined independently from the observer, in quantum mechanics a system can be defined by its entropy whose value is conditioned by an observer. The collapse of the vector given by a superposition of different Boltzmann entropies into a specific entropy as a consequence of an interaction with an observer introduces a new reading of Rovelli’s relational interpretation of quantum mechanics. All this happens because the non-locality can be seen as “active information” inaccessible to the classical observer. In the second part of the article, given the relation between the number of the microstates W which are functions of the macrostates and given the entropies S as Cartesian coordinates, one can move from Euclidean coordinates of the entropies, in which the observers are independent, to a non Euclidean space of the parameters (average positions). In this background we compute covariant derivatives (Appendix A) in the parameter space and we can obtain by entropy the Bohm quantum potential and the quantum effects. So we can show that Bohm’s quantum potential is not consequence of the Schrödinger equation but is obtained by a non classical entropy of a many particles’ system. From non classical entropy space we can rebuilt the Schrödinger equation. The approach suggested in this background leads to the idea that non classical entropy and Fisher information are the origin of Bohm’s quantum potential. This approach has also the merit that, in a relativistic curved space-time or teleparallel gravity, the informational quantum entropy appears as the real link between gravitational and quantum effects of matter, determining a high coupling between the effects of gravity on geometry and the information quantum effects of change of the phase space position of the particles. The informational lines associated with the quantum entropy introduce a research line which is still widely unexplored, but very promising for the problem of quantum gravity.
Appendix A
A.1. Tensor, Covariant and Contravariant Derivatives and Morphogenetic System
In this chapter we rewrite by the morphogenetic theory the classical tensor calculus with possible extensions. We will show in short that classical tensor calculus is part of a more general theory denoted morphogenetic theory. The aim of this chapter is to prepare the mathematical instruments to create the relation between Fisher information, Bohm’s quantum potential and Boltzmann entropy with a possible new interpretation of the field theory [30,31,32].
Given the transformation:
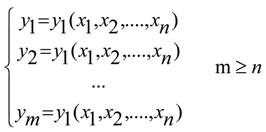 we have:
we have:
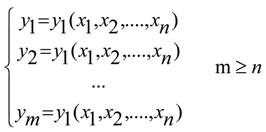
For the Jacobian matrix:
we have:
In the ordinary tensor calculus we have the tensor relations:
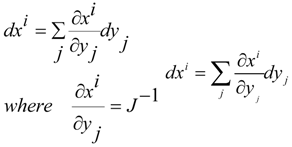 where:
and:
where:
where y are the Cartesian coordinates and x are the general coordinates. Moreover, we have:
where:
and:
where:
where y are the Cartesian coordinates and x are the general coordinates. Moreover, we have:
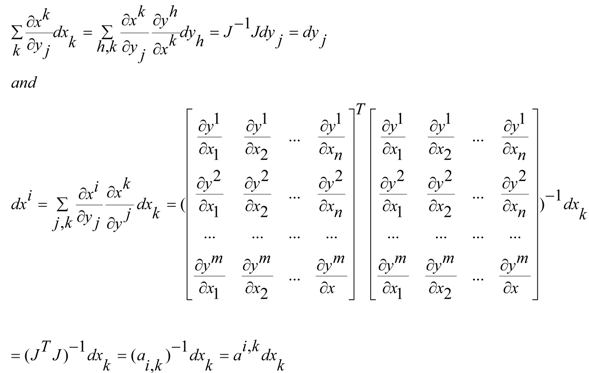 where the metric tensor a is calculated by the Jacobian matrix. Now we can write the previous expressions in a more general way:
where the metric tensor a is calculated by the Jacobian matrix. Now we can write the previous expressions in a more general way:
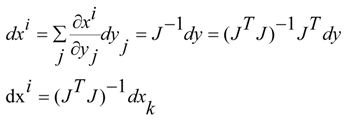
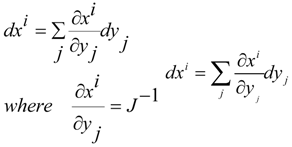

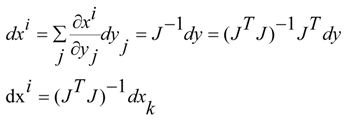
And in general way for the relation between covariant and contravariant components we have:
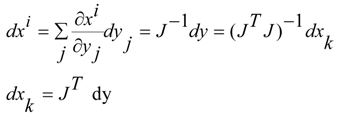 in the morphogenetic system because J is a rectangular matrix we have:
in the morphogenetic system because J is a rectangular matrix we have:
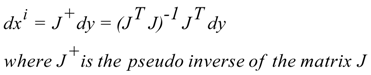
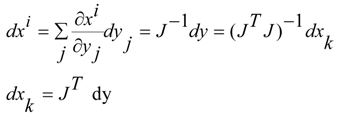
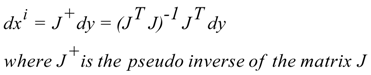
A.2. Commutators in Morphogenetic System and Tensor Derivative
Given the differential operator D and the vector V whose covariant components are:
We have:
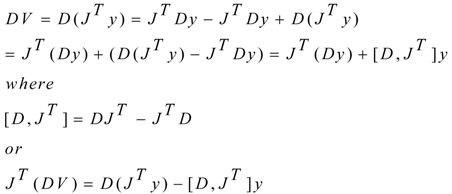
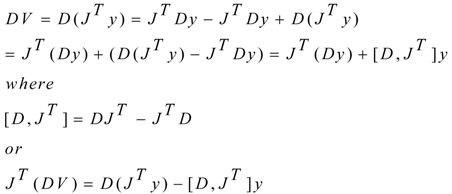
For example, in the classical tensor calculus we have:
These are the Christoffel elements for covariant and contravariant derivatives. We can repeat the same process for the contravariant components of the vector V.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Klein, U. The statistical origins of quantum mechanics. 2011; arXiv 0810.2394v4. [Google Scholar]
- Braunstein, S.L.; Caves, C.M. Statistical distance and the geometry of quantum States. Phys. Rev. Lett. 1994, 72, 3439–3443. [Google Scholar] [CrossRef] [PubMed]
- Garbaczewski, P. Random dynamics, entropy production and fisher information. Acta Phys. Pol. B 2003, 34, 3555–3568. [Google Scholar]
- Rovelli, C. Relational quantum mechanics. Int. J. Theor. Phys. 1996, 35, 1637–1678. [Google Scholar] [CrossRef]
- Rovelli, C. Half way through the woods. In The Cosmos of Science; Earman, J., Norton, J.D., Eds.; University of Pittsburgh Press: Pittsburgh, PA, USA, 1997. [Google Scholar]
- Van Fraassen, B. Rovelli’s World. Found. Phys. 2008, 40, 390–417. [Google Scholar] [CrossRef]
- Bitbol, M. Physical relations or functional relations? A non-metaphysical construal of Rovelli’s relational quantum mechanics. Available online: http://www.academia.edu/839181/Physical_Relations_or_Functional_Relations_A_non metaphysical_construal_of_Rovellis_Relational_Quantum_Mechanics (accessed on 4 May 2013).
- Pavsic, M. The Landscape of Theoretical Physics: A Global View; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Cini, M.; Levy Leblond, J.M. Quantum Theory without Reduction; IOP: London, UK, 1990. [Google Scholar]
- Licata, I. Emergence and Information at the Edge of Classical and Quantum Systems. In Physics of Emergence and Organization; Licata, I., Sakaji, A., Eds.; World Scientific: Singapore, Singapore, 2008. [Google Scholar]
- Licata, I. Effective physical processes and active information in quantum computing. Quant. BioSys. 2007, 1, 51–65. [Google Scholar]
- Preparata, G. An Introduction to a Realistic Quantum Physics; World Scientific: Singapore, Singapore, 2002. [Google Scholar]
- Blasone, M.; Jizba, P.; Vitiello, G. Quantum Field Theory and Its Macroscopic Manifestations; Imperial College Press: London, UK, 2011. [Google Scholar]
- Castro, C.; Mahecha, J. On nonlinear quantum mechanics, Brownian motion, Weyl geometry and Fisher information. Prog. Phys. 2006, 1, 38–45. [Google Scholar]
- Falciano, F.T.; Novello, M.; Salim, J.M. Geometrizing relativistic quantum mechanics. Found. Phys. 2010, 40, 1885–1901. [Google Scholar] [CrossRef]
- Novello, M.; Salim, J.M.; Falciano, F.T. On a Geometrical description of quantum mechanics. Int. J. Geom. Meth. Mod. Phys. 2011, 8, 87–98. [Google Scholar] [CrossRef]
- Fiscaletti, D.; Licata, I. Weyl geometries, Fisher information and quantum entropy in quantum mechanics. Int. J. Theor. Phys. 2012, 51, 3587–3595. [Google Scholar]
- Bohm, D.; Hiley, B.J. Measurement understood through the quantum potential approach. Found. Phys. 1984, 14, 255–274. [Google Scholar]
- Sbitnev, V.I. Bohmian split of the Schrödinger equation onto two equations describing evolution of real functions. Kvantovaya Magiya 2008, 5, 1101–1111. [Google Scholar]
- Fiscaletti, D. The quantum entropy as an ultimate visiting card of the de Broglie-Bohm theory. Ukr. J. Phys. 2012, 57, 947–963. [Google Scholar]
- Durr, D.; Teufel, S. Bohmian Mechanics: The Physics and Mathematics of Quantum Theory; Springer: Berlin, Germay, 2009. [Google Scholar]
- Vigier, J.P. Real physical paths in quantum mechanics. Equivalence of the Einstein-de Broglie and Feynman points of view on quantum particle behaviour. In Proceedings of Third International Symposium Foundations of Quantum Mechanics, Tokyo, Japan, 28–31 August 1989; Physical Society of Japan: Tokyo, Japan, 1990. [Google Scholar]
- Fiscaletti, D. Bohmian quantum potential and Feynman’s path integrals: Considerations about the foundations. In Vision of Oneness: A Journey in Matter; Licata, I., Sakaji, A., Eds.; Aracne Publ.: Rome, Italy, 2011. [Google Scholar]
- Vitiello, G. Classical trajectories and quantum field theory. Braz. J. Phys. 2005, 35, 351–358. [Google Scholar] [CrossRef]
- Weyl, H. Space, Time, Matter; Methuen&Co.: London, UK, 1922. [Google Scholar]
- Aldrovandi, R.; Pereira, J.G. Teleparallel Gravity: An Introduction; Springer: Berlin, Germany, 2013. [Google Scholar]
- Shojai, F.; Shojai, A. Constraint algebra and equations of motion in the Bohmian interpretation of quantum gravity. Classical Quant. Grav. 2004, 21, 1–9. [Google Scholar] [CrossRef]
- Shojai, F.; Shojai, A. Understanding quantum theory in terms of geometry. 2004; arXiv:grqc/0404102 v1. [Google Scholar]
- De Broglie, L. Non-linear Wave Mechanics: A Causal Interpretation; Elsevier: Amsterdam, The Netherlands, 1960. [Google Scholar]
- Fiscaletti, D. The geometrodynamic nature of the quantum potential. Ukr. J. Phys. 2012, 57, 560–572. [Google Scholar]
- Resconi, G.; Nikravesh, M. Morphic computing: Concepts and foundation. In Forging the New Frontiers: Fuzzy Pioneers I; Springer Series Studies in Fuzziness and Soft Computing; Nikravesh, M., Zadeh, L.A., Kacprzyk, J., Eds.; Springer: Berlin, Germany, 2007. [Google Scholar]
- Resconi, G.; Nikravesh, M. Morphic computing: Quantum and field. In Forging the New Frontiers: Fuzzy Pioneers II; Springer Series Studies in Fuzziness and Soft Computing; Nikravesh, M., Zadeh, L.A., Kacprzyk, J., Eds.; Springer: Berlin, Germany, 2007. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).