Low-Temperature Behaviour of Social and Economic Networks
Abstract
:1. Introduction
2. Temperature-Dependent Ensembles of Graphs
2.1. General Formalism
2.2. Networks with Finite Energy Per Link
3. Random Graphs: Vanishing of the Percolation Threshold at Zero Temperature
3.1. Critical Percolation Temperature
3.2. Large and Sparse Graphs Have Low Temperature
4. Fitness Models: Random Graphs at High Temperature, Scale-Free Networks at Low Temperature
4.1. High-Temperature Regime ()
4.2. Finite-Temperature Regime ()
4.3. Zero-Temperature Regime ()
4.4. The Temperature of Real Binary Networks
5. More General Models
6. A Temperature-Driven Small-World Model
6.1. Non-Scale-Free Small-Worlds
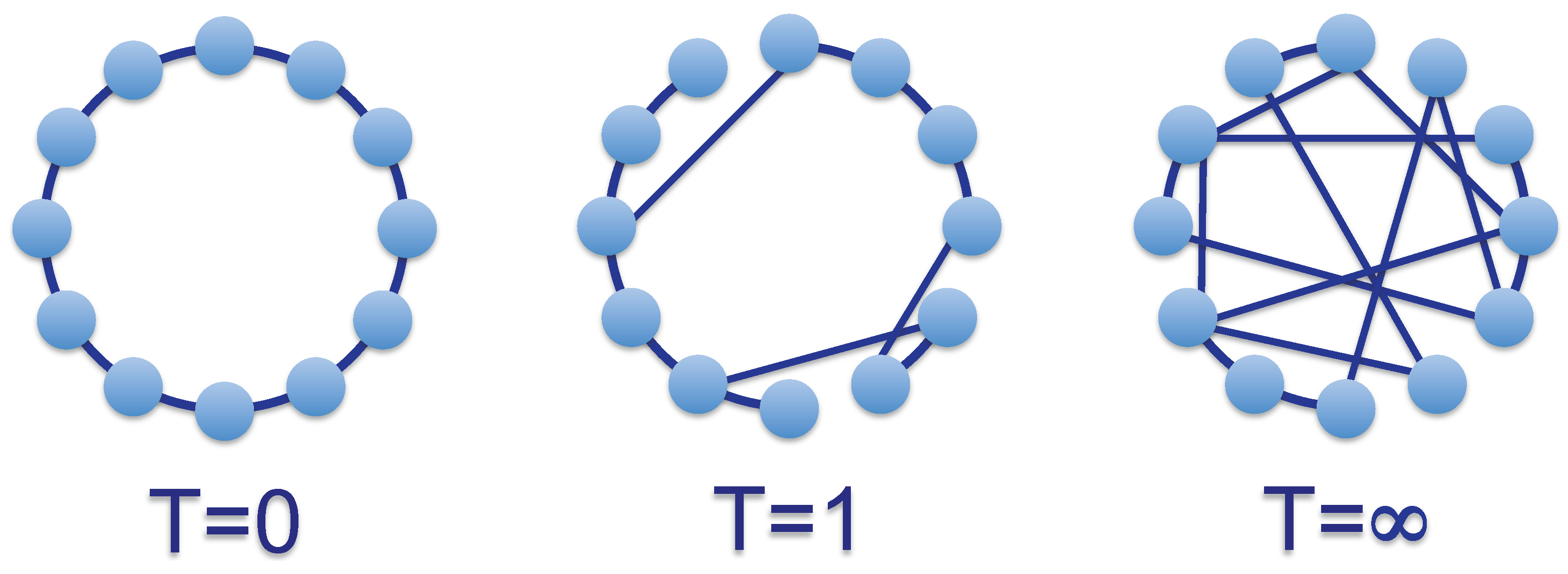
6.2. Scale-Free Small-Worlds
7. A Model of Networks with Low-Temperature Community Structure
7.1. Ultrametric Small-World Model

7.2. Ultrametric Scale-Free Model
8. Weighted Networks as Temperature-Dependent Ensembles of Binary Graphs
8.1. The Temperature of Real Weighted Networks
| Network | α | Ref. | |
|---|---|---|---|
| Metabolic flux networks | [29] | ||
| Interbank network | [30] | ||
| Erdős collaboration network | 2 | 1 | [31] |
| Chaos control & synchron. co-authorship | [31] | ||
| Financial cross-correlations | [32] | ||
| Financial cross-correlations | [33] | ||
| Financial cross-correlations | [33] | ||
| Mollusk research co-authorship | [31] | ||
| Binary graphs |
8.2. Filtering of Weighted Networks as the Zero-Temperature Limit
9. Conclusions
Acknowledgments
Conflict of Interest
References
- Albert, R.; Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002. [Google Scholar] [CrossRef]
- Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Granovetter, M. S. The strength of weak ties. Am. J. Sociol. 1973, 1360–1380. [Google Scholar] [CrossRef]
- Karsai, M.; Kivela, M.; Pan, R. K.; Kaski, K.; Kertész, J.; Barabási, A. L.; Saramaki, J. Small but slow world: How network topology and burstiness slow down spreading. Phys. Rev. E 2011, 83, 025102. [Google Scholar] [CrossRef] [PubMed]
- Holland, P. W.; Leinhardt, S. An exponential family of probability distributions for directed graphs. J. Am. Stat. Assoc. 1981, 76, 33–50. [Google Scholar] [CrossRef]
- Park, J.; Newman, M.E.J. Statistical mechanics of networks. Phys. Rev. E 2004, 70, 066117. [Google Scholar] [CrossRef] [PubMed]
- Berg, J.; Lässig, M. Correlated random networks. Phys. Rev. Lett. 2002, 89, 228701. [Google Scholar] [CrossRef] [PubMed]
- Burda, Z.; Jurkiewicz, J.; Krzywicki, A. Perturbing general uncorrelated networks. Phys. Rev. E 2004, 69, 026106. [Google Scholar] [CrossRef] [PubMed]
- Garlaschelli, D.; Loffredo, M.I. Multispecies grand-canonical models for networks with reciprocity. Phys. Rev. E 2006, 73, 015101(R). [Google Scholar] [CrossRef] [PubMed]
- Garlaschelli, D.; Loffredo, M.I. Generalized bose-fermi statistics and structural correlations in weighted networks. Phys. Rev. Lett. 2009, 102, 038701. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, G. Entropy of network ensembles Phys. Rev. E 2009, 79, 036114. [Google Scholar]
- Squartini, T.; Garlaschelli, D. Analytical maximum-likelihood method to detect patterns in real networks. New J. Phys. 2011, 13, 083001. [Google Scholar] [CrossRef]
- Squartini, T.; Picciolo, F.; Ruzzenenti, F.; Garlaschelli, D. Reciprocity of weighted networks. Physics 2012. [Google Scholar] [CrossRef] [PubMed]
- Squartini, T.; Garlaschelli, D. Triadic Motifs and Dyadic Self-organization in the World Trade Network. In Self-Organizing Systems; Kuipers, F.A., Heegaard, P.E., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 24–35. [Google Scholar]
- Picciolo, F.; Ruzzenenti, F.; Basosi, R.; Squartini, T.; Garlaschelli, D. The Role of Distances in the World Trade Web. In Proceedings of the Eighth International Conference on Signal Image Technology and Internet Based Systems (SITIS), Naples, Italy, 25–29 Nov. 2012; pp. 784–792.
- Newman, M.E.J.; Strogatz, S.H.; Watts, D.J. Random graphs with arbitrary degree distributions and their applications. Phys. Rev. E 2001, 64, 026118. [Google Scholar] [CrossRef] [PubMed]
- Caldarelli, G.; Capocci, A.; De Los Rios, P.; Muñoz, M.A. Scale-free networks from varying vertex intrinsic fitness. Phys. Rev. Lett. 2002, 89, 258702. [Google Scholar] [CrossRef] [PubMed]
- Boguñá, M.; Pastor-Satorras, R. Class of correlated random networks with hidden variables. Phys. Rev. E 2003, 68, 036112. [Google Scholar]
- Ahnert, S.E.; Garlaschelli, D.; Fink, T.M.; Caldarelli, G. Ensemble approach to the analysis of weighted networks. Phys. Rev. E 2007, 76, 016101. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Newman, M.E.J. Origin of degree correlations in the Internet and other networks. Phys. Rev. E 2003, 68, 026112. [Google Scholar] [CrossRef] [PubMed]
- Gabrielli, A.; Caldarelli, G.; Pietronero, L. Invasion percolation with temperature and the nature of self-organized criticality in real systems. Phys. Rev. E 2000, 62, 7638–7641. [Google Scholar] [CrossRef]
- Garlaschelli, D.; Loffredo, M.I. Fitness-dependent topological properties of the world trade web. Phys. Rev. Lett. 2004, 93, 188701. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of small-world-networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- Ruzzenenti, F.; Picciolo, F.; Basosi, R.; Garlaschelli, D. Spatial effects in real networks: Measures, null models, and applications. Phys. Rev. E 2012, 86, 066110. [Google Scholar] [CrossRef] [PubMed]
- Krioukov, D.; Papadopoulos, F.; Vahdat, A.; Boguna, M. Curvature and temperature of complex networks. Phys. Rev. E 2009, 80, 035101(R). [Google Scholar] [CrossRef] [PubMed]
- Krioukov, D.; Papadopoulos, F.; Kitsak, M.; Vahdat, A.; Boguna, M. Hyperbolic geometry of complex networks. Phys. Rev. E 2010, 82, 036106. [Google Scholar] [CrossRef] [PubMed]
- Valori, L.; Picciolo, F.; Allansdottir, A.; Garlaschelli, D. Reconciling long-term cultural diversity and short-term collective social behavior. Proc. Natl. Acad. Sci. USA 2012, 109, 1068–1073. [Google Scholar] [CrossRef] [PubMed]
- Almaas, E.; Kovács, B.; Vicsek, T.; Oltvai, Z.N.; Barabási, A.-L. Global organization of metabolic fluxes in the bacterium Escherichia coli. Nature 2004, 427, 839–843. [Google Scholar] [CrossRef] [PubMed]
- Boss, M.; Elsinger, H.; Summer, M.; Thurner, S. Network topology of the interbank market. Quant. Financ. 2004, 4, 677–684. [Google Scholar] [CrossRef]
- Li, C.; Chen, G. Network connection strengths: Another power-law? Cond. Mat. 2003. [Google Scholar]
- Kim, H.-J.; Lee, Y.; Kahng, B.; Kim, I.-M. Weighted scale-free network in financial correlations. J. Phys. Soc. Jpn. 2002, 71, 2133–2136. [Google Scholar] [CrossRef]
- Burda, Z.; Jurkiewicz, J.; Nowak, M.A.; Papp, G.; Zahed, I. Levy matrices and financial covariances. Acta Phys. Polonica B 2003, 34, 4747–4763. [Google Scholar]
- Onnela, J.-P.; Kaski, K.; Kertesz, J. Clustering and information in correlation based financial networks. Eur. Phys. J. B 2004, 38, 353–362. [Google Scholar] [CrossRef]
- Garlaschelli, D.; Caldarelli, G.; Pietronero, L. Universal scaling relations in food webs. Nature 2003, 423, 165–168. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Garlaschelli, D.; Ahnert, S.E.; Fink, T.M.A.; Caldarelli, G. Low-Temperature Behaviour of Social and Economic Networks. Entropy 2013, 15, 3148-3169. https://doi.org/10.3390/e15083238
Garlaschelli D, Ahnert SE, Fink TMA, Caldarelli G. Low-Temperature Behaviour of Social and Economic Networks. Entropy. 2013; 15(8):3148-3169. https://doi.org/10.3390/e15083238
Chicago/Turabian StyleGarlaschelli, Diego, Sebastian E. Ahnert, Thomas M. A. Fink, and Guido Caldarelli. 2013. "Low-Temperature Behaviour of Social and Economic Networks" Entropy 15, no. 8: 3148-3169. https://doi.org/10.3390/e15083238
APA StyleGarlaschelli, D., Ahnert, S. E., Fink, T. M. A., & Caldarelli, G. (2013). Low-Temperature Behaviour of Social and Economic Networks. Entropy, 15(8), 3148-3169. https://doi.org/10.3390/e15083238





