1. Introduction
Let , and let . Consider the shift map, , given by . Let be a matrix, where the are or for any . A subshift of finite type (SFT in short) is the restriction of σ to the set, . Note that is compact and metrizable and , that is, is invariant by σ.
Let
X be a metric space and consider continuous maps,
. Let
be the skew-product map given by:
Recently, this class of skew-product maps has been studied by several authors (see [
1,
2,
3,
4,
5]). The interest for studying systems that are generated by alternative iterations of a finite number of maps comes from several fields, like population dynamics (see, e.g., [
6,
7]) and economic dynamics (see, e.g., [
8,
9]), where the systems are generated by SFT with many finite elements. For SFT with infinitely many elements, the term crazy dynamics was introduced in [
1]. Let us also point out that this kind of skew-product has been useful for analyzing difference inclusions used in discrete control systems (see, e.g., [
10]).
Recently, in [
2], the topological entropy of
φ was analyzed when
and
, proving that when
and
belong to a family of contractive homeomorphisms on the real line, the topological entropy of some invariant set agrees with that of the full shift,
. Additionally, in [
3], they extend their results to homeomorphisms on higher dimension spaces. The aim of this paper is to analyze the same question under different conditions. Let
and
denote the topological entropy and a variant valid for non-compact spaces introduced in
Section 2. The main aim of this paper is to state the following results.
Theorem 1 Let be homeomorphisms on , or . Let , be the skew-product map defined in Equation (1). Then:- (a)
If or , then .
- (b)
If , then . If there exists a compact subset, , such that , then .
Note that homeomorphisms on the circle, the compact interval and the real line have zero topological entropy, and therefore, one might wonder whether the above result remains true for simple maps, that is, for zero entropy maps. The next result, in the spirit of the dynamic Parrondo paradox (see, e.g., [
11,
12,
13,
14]), shows that this is not true in general.
Theorem 2 Let , be the skew-product map defined in Equation (1). Then, there are zero topological entropy continuous maps, , such that . The maps used in the proof of Theorem 2 are constructed by gluing different continuous interval maps, which usually do not appear in discrete models from natural or social sciences. The next result shows that a similar result holds for a well-known one-parameter family of interval maps.
Theorem 3 Let , and . Fix , and let , be the skew-product map defined in Equation (1) with and . Then, there are parameter values, , such that and for a suitable SFT. Let us remark that there are a wide ranges of parameters, , satisfying Theorem 3. However, we can give some positive results if we strengthen our hypothesis. Recall that a continuous interval map is piecewise monotone if there are , such that is monotone for . Recall that two maps, and , commute if . Then, we can prove the following result, which gives a partial positive answer to our previous question.
Theorem 4 Let be commuting continuous piecewise monotone with zero topological entropy. Let , be the skew-product map defined in Equation (1). Then, . Remark 1 Theorem 4 is not true in general if both maps, and , are not piecewise monotone. Namely, in [15], two commuting maps, and , with zero topological entropy are constructed, such that , and so, following the proof of Theorem 3, we can conclude that . The paper is organized as follows. The next section is devoted to introduce basic notation and useful definitions. Then, we give a proof of Theorem 1. The last section is devoted to proving Theorems 2–4.
2. Basic Definitions
Firstly, we will introduce Bowen’s definition of topological entropy (see [
16]). Let
X be a compact metric space with metric
d, and let
be a continuous map. Let
K be a compact subset of
X, and fix
and
. A subset,
, is said to be
-separated if for any
,
, there is
, such that
. Denote by
the cardinality of an
-separated set with maximal cardinality. The topological entropy is defined as:
We say that a continuous map,
f, is topologically chaotic if
. In particular, topologically chaotic maps are chaotic in the sense of Li and Yorke (see [
17,
18]), which is one of the most accepted notions of chaos. In addition, the topological entropy of the skew-product map,
φ, defined in Equation (
1), satisfies the following Bowen’s inequalities:
where for any
:
which can be meant as the topological entropy of the non-autonomous discrete system given by the sequence of maps,
(see [
19] for the definition).
When
X is not compact, the above definition of topological entropy makes sense when
f is uniformly continuous. Then, we need to add a new limit in the definition as follows:
We stress the metric,
d, now, because this definition is metric-dependent. However, it is known (see, e.g., [
20]) that, although the dynamics of the map,
,
, is simple, we have that
for the standard Euclidean metric on
. To solve this problem, in [
21], a notion of topological entropy for non-compact spaces has been introduced, such that it can be computed for any continuous map and keeps the above property, that positive entropy maps have a complicated dynamic behavior. Denote by
the family of compact subsets,
K of
X, such that
, and define:
Note that, clearly,
, and for
, we easily see that
, because the only invariant compact subset is
. Additionally,
when
.
Now, we concentrate our efforts in proving our main results.
3. Proof of Theorem 1
Proof of case (a). Let
be a sequence of homeomorphisms with
or
. It can be seen in [
19] that if we denote by
the sequence of maps,
, then
. To finish the proof, we apply Bowen’s inequality (
2) to conclude that, since:
we have that
.
When , we cannot apply Bowen’s inequality, and therefore, the proof requires extra work.
Proof of case (b). Note that
. We add two symbols to
and construct the compact space,
, which is homeomorphic to a compact interval. Since
and
are homeomorphisms, we can extend them continuously and construct maps,
, such that
,
. Note that
and
are homeomorphisms, as well, and therefore:
for all
.
On the other hand, we consider the continuous extension of
φ:
given by:
Since any compact subset of
is a compact subset of
, we conclude that:
Applying Bowen’s inequality to
, we conclude that:
and since:
we conclude that:
Now, we assume that there exists a compact set,
, such that
. Applying Bowen’s inequality to
, we conclude that:
which concludes the proof.
Remark 2 The existence of compact subsets, K, holding the conditions of Theorem 1 (b) can be seen in [2,10]. The following example shows that the equality, , is not true in general when such compact subsets do not exist. We just consider the real maps, , , and construct the map, φ. Clearly , which implies that . If we take as a base map, , with positive topological entropy, then we find that . 4. Proof of Theorems 2–4
Proof of Theorem 2. Let
, and define the maps,
and
, as follows:
and:
where
,
and
,
, and
t is the standard tent map,
,
, which holds that
.
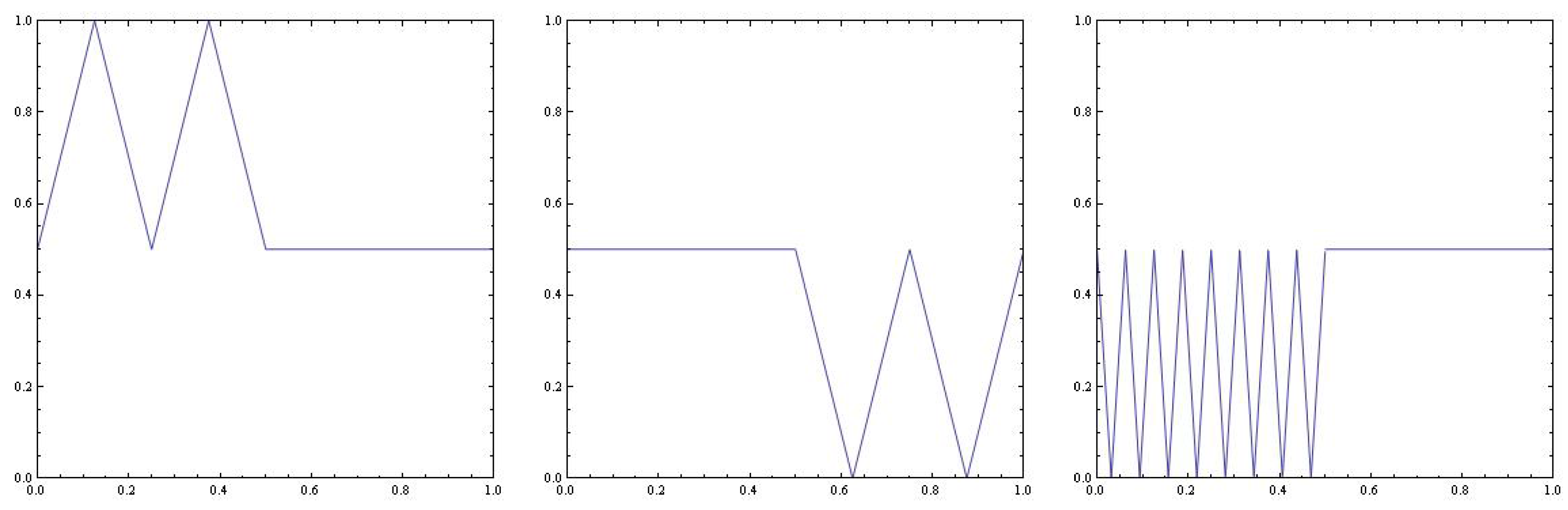
Figure 1 shows the graph of
and
on the interval,
.
Figure 1.
We show the graphic on of maps (left), (center) and (right), defined in the proof of Theorem 2.
Figure 1.
We show the graphic on of maps (left), (center) and (right), defined in the proof of Theorem 2.
Note that
,
, and thus,
. Let
, and note that, by [
19]:
On the other hand, we have that:
whose graphic can be seen in
Figure 1. By [
22],
. By Bowen’s inequalities:
and the proof concludes.
Proof of Theorem 3. Let
,
and
. It is well-known that
increases when
a increases (see, e.g., [
23]), and it is positive for
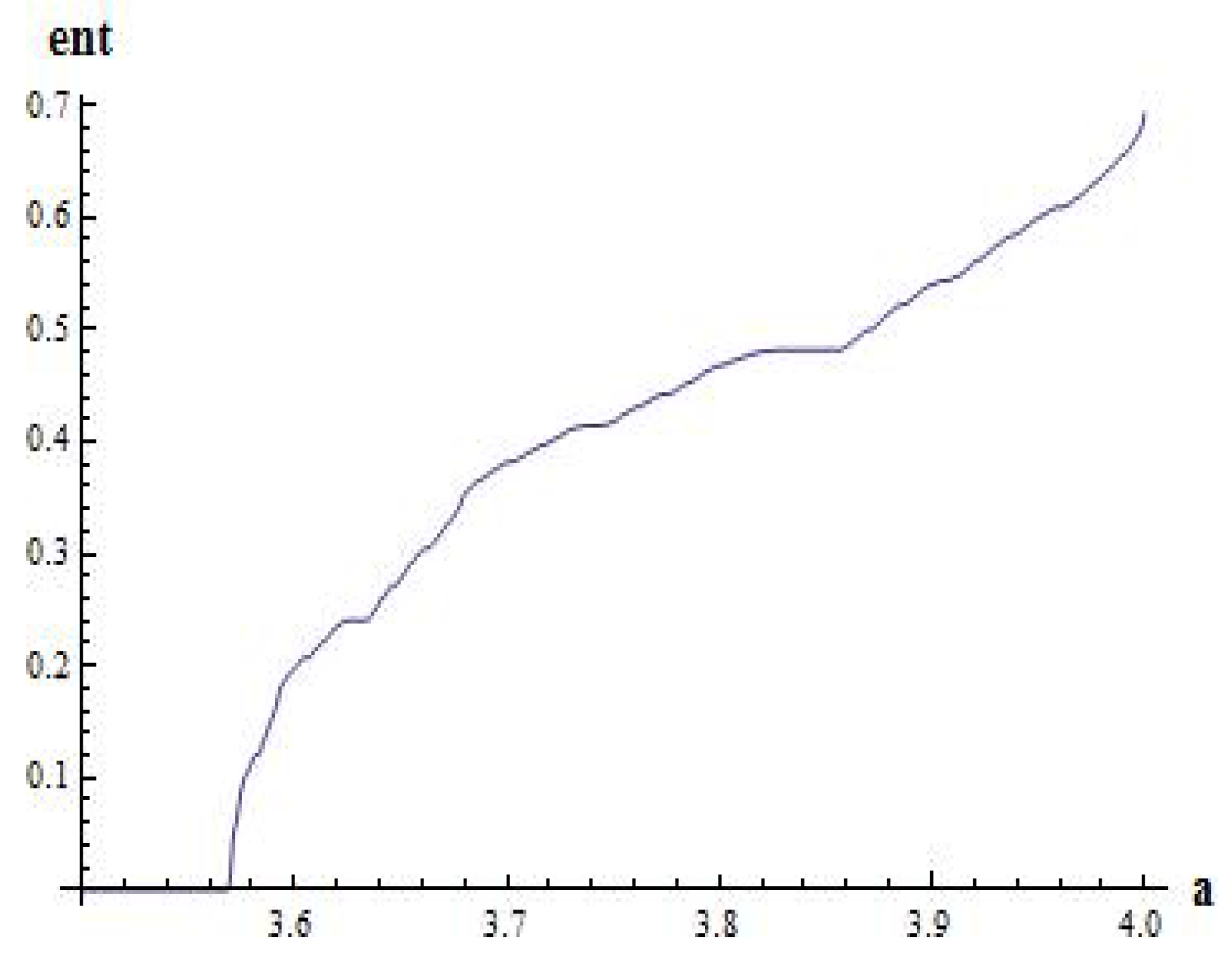
Figure 2 shows the computation of
with accuracy
by using an algorithm from [
24]. However, for
,
, the computation of topological entropy with prescribed accuracy is more complicated. For doing it, we use the recently developed algorithm from [
25].
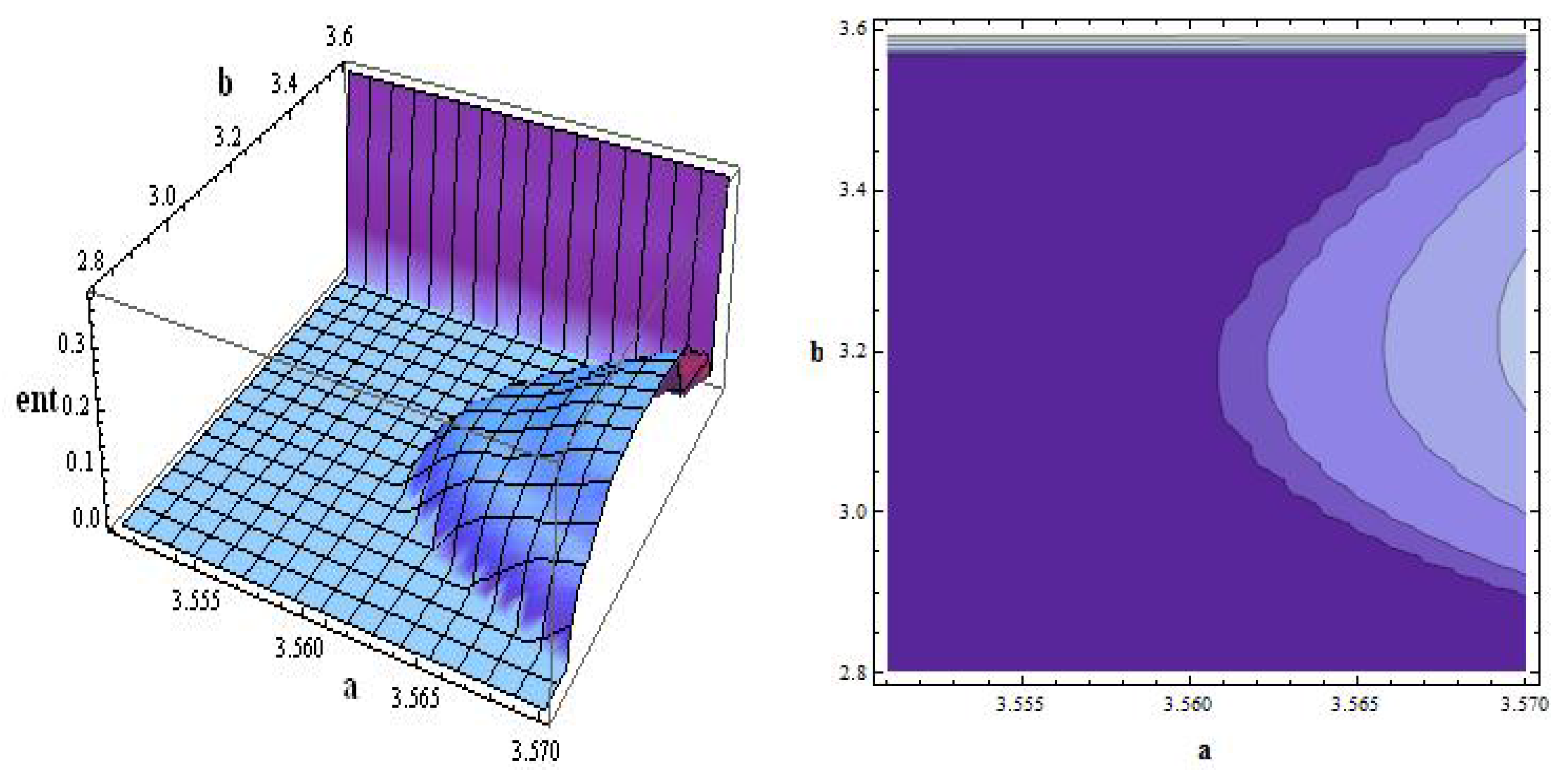
Figure 3 shows the entropy computations with prescribed accuracy,
. From the shown computations, we may find parameter values,
a and
b, a bit smaller than
with zero topological entropy for maps
and
, such that
is positive (for instance,
and
gives positive values of
).
Figure 2.
We compute the topological entropy (ent in the figure) for with accuracy, . We note that the first parameter value providing positive topological entropy is
Figure 2.
We compute the topological entropy (ent in the figure) for with accuracy, . We note that the first parameter value providing positive topological entropy is
Figure 3.
We compute the topological entropy (ent in the figure) for and with accuracy, . The darker region represents those parameter values providing zero topological entropy.
Figure 3.
We compute the topological entropy (ent in the figure) for and with accuracy, . The darker region represents those parameter values providing zero topological entropy.
Now, we consider the matrix:
and notice that the SFT,
, generated by
A is composed of two periodic sequences,
and
, which implies that
. On the other hand, if
and
, notice that:
It is easy to check that:
which concludes the proof.
Proof of Theorem 4. Let
denote the number of monotonicity pieces of a piecewise monotone map,
f. By the Misiurewicz-Szlenk (see [
22]) formula:
Fix
and note that:
where
. Since the sequence,
, contains two maps, it is equicontinuous, and then, the Misiurewicz-Szlenk formula is valid in this setting (see [
26]). Thus:
and since
, we find that for any
, we have that
. By Bowen’s inequality:
Since the inequality,
, also holds, we conclude the proof.