Zero Delay Joint Source Channel Coding for Multivariate Gaussian Sources over Orthogonal Gaussian Channels
Abstract
:1. Introduction
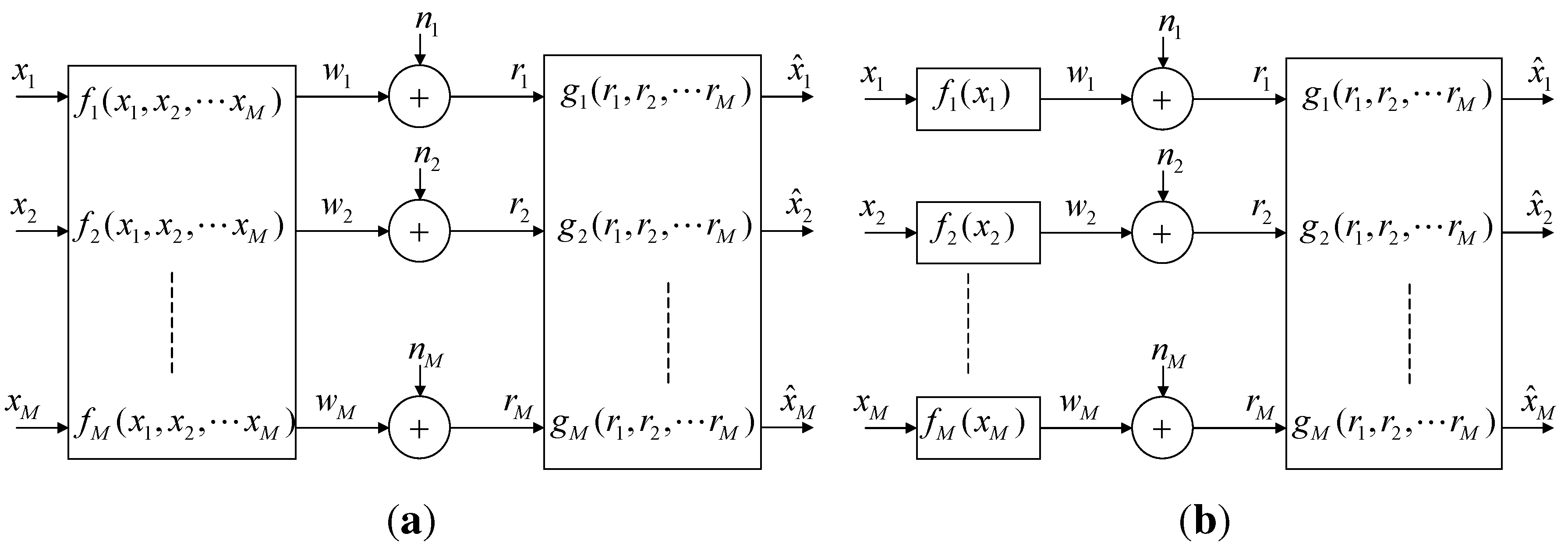
2. Problem Formulation and Performance Bounds
2.1. Distortion Bounds
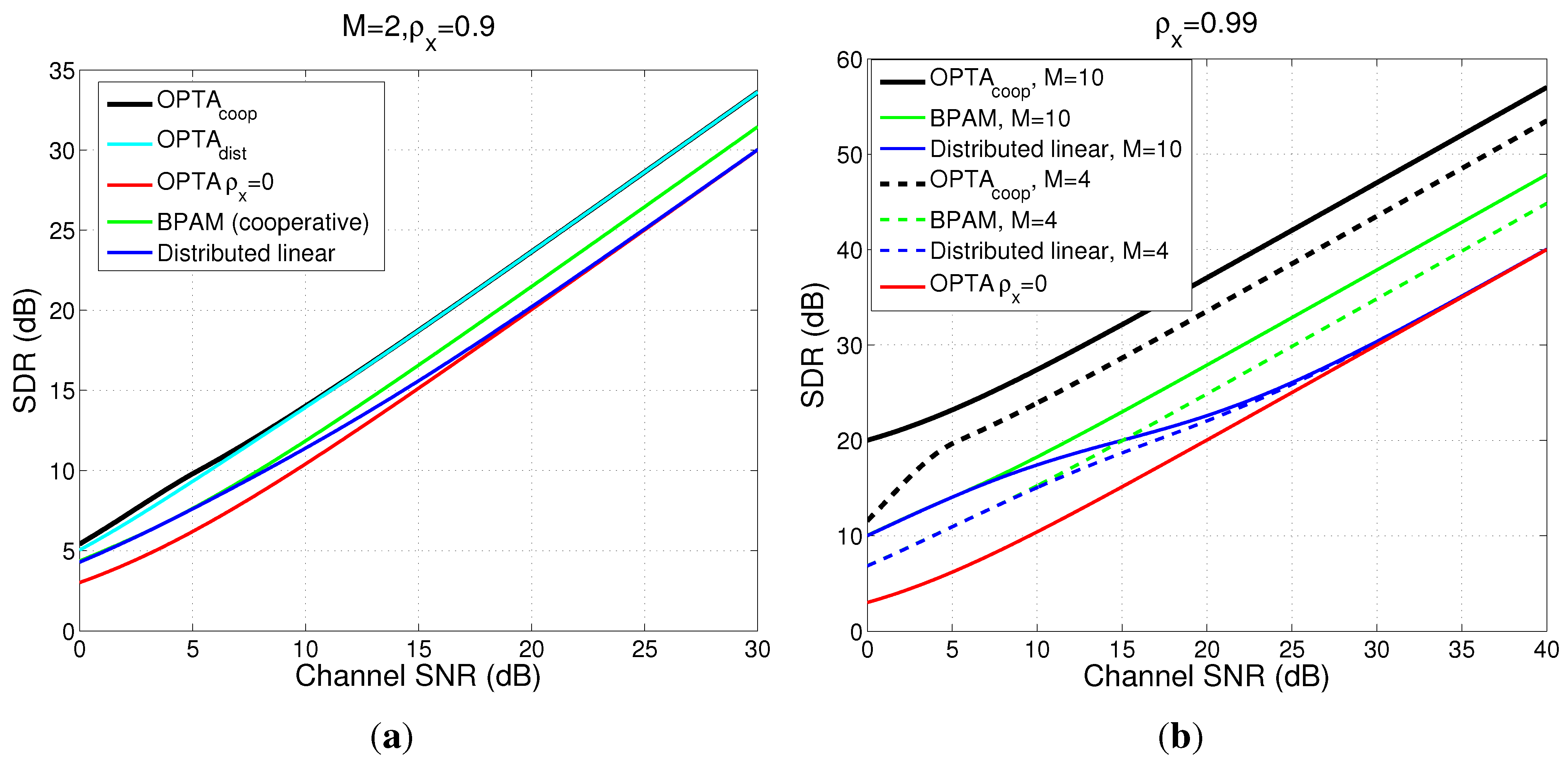
3. Optimal Linear Mappings
3.1. Distributed Linear Mapping
3.2. Cooperative Linear Mapping
4. Nonlinear Mappings
4.1. Special Case
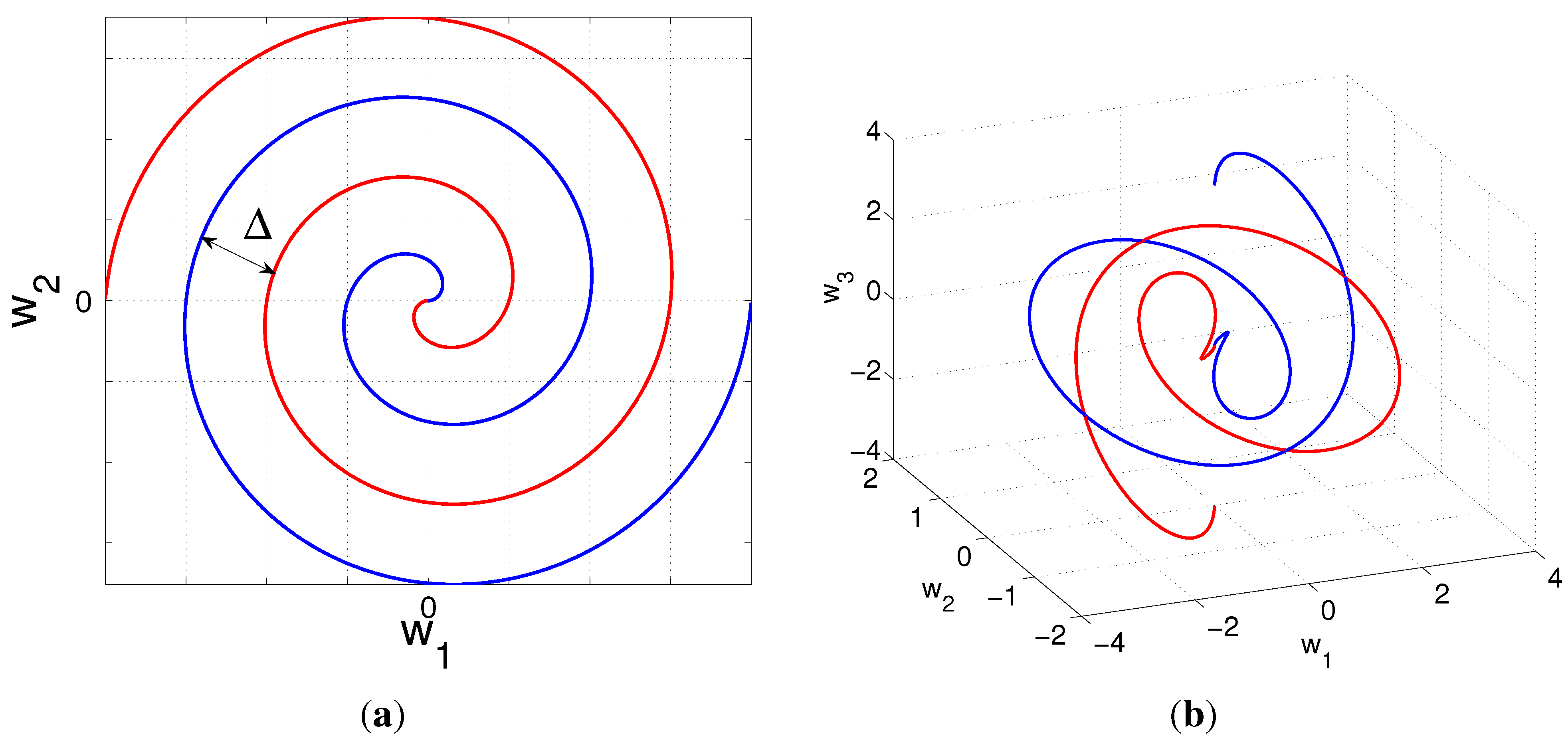
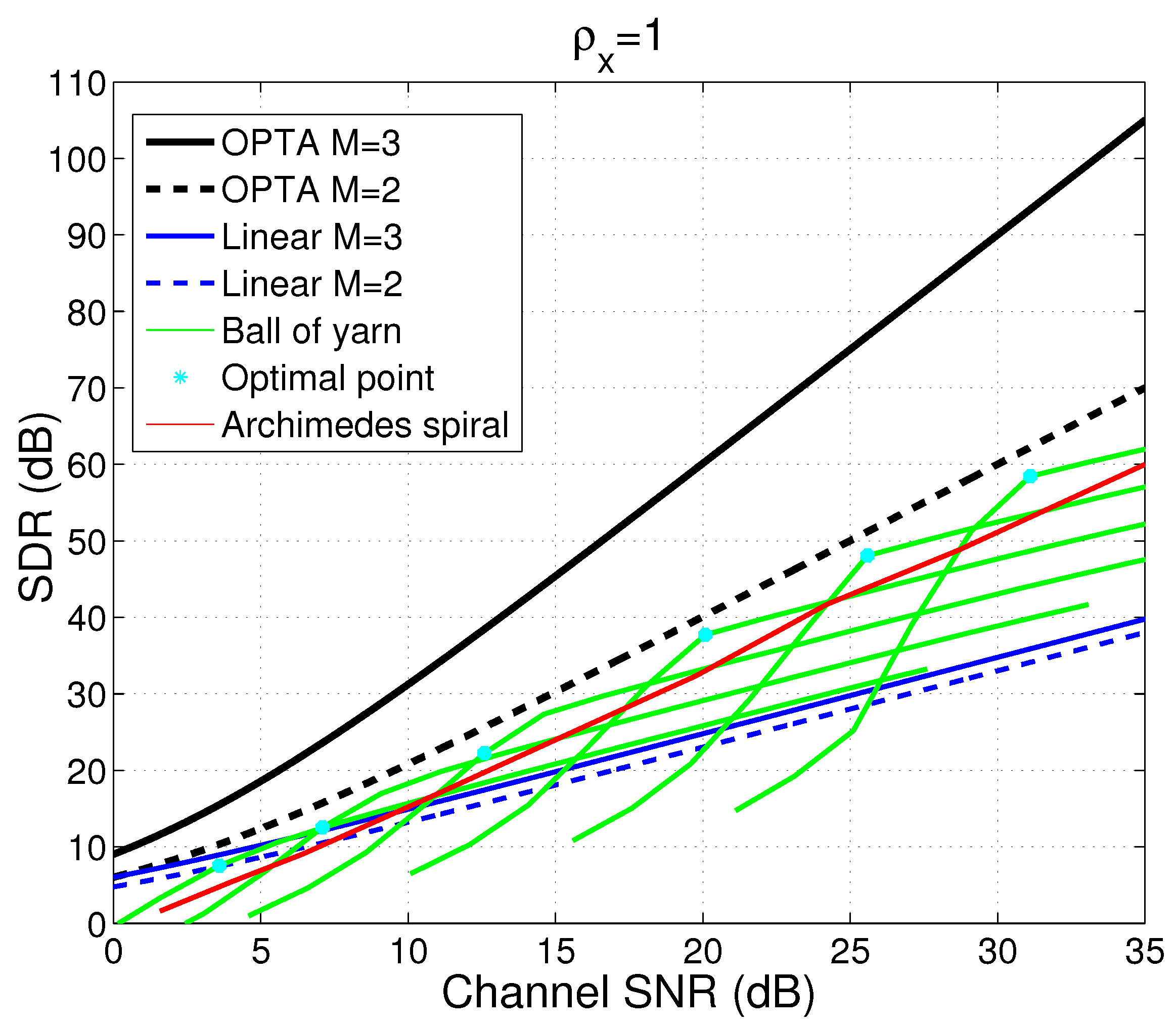

4.2. Nonlinear Mappings for
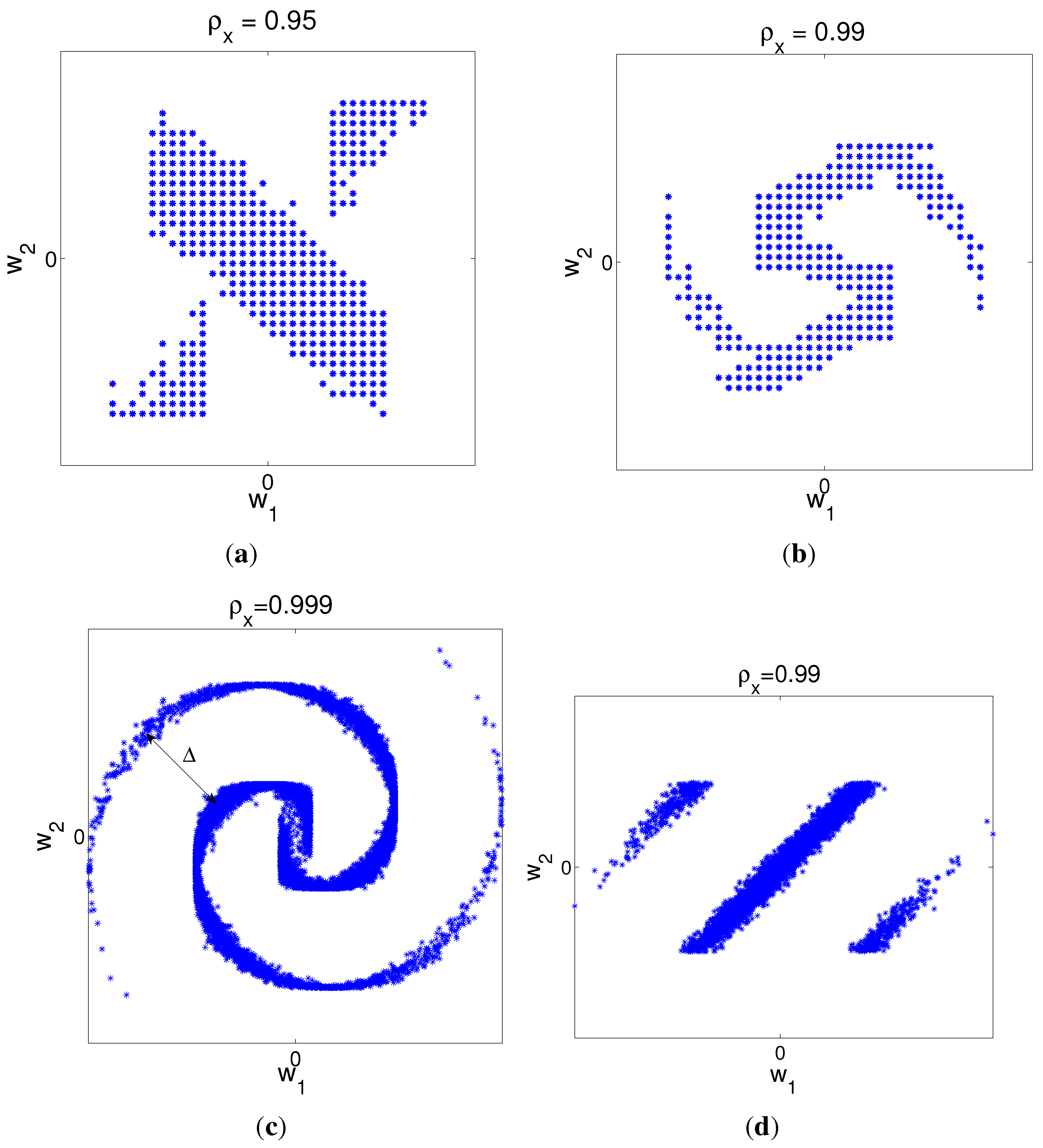
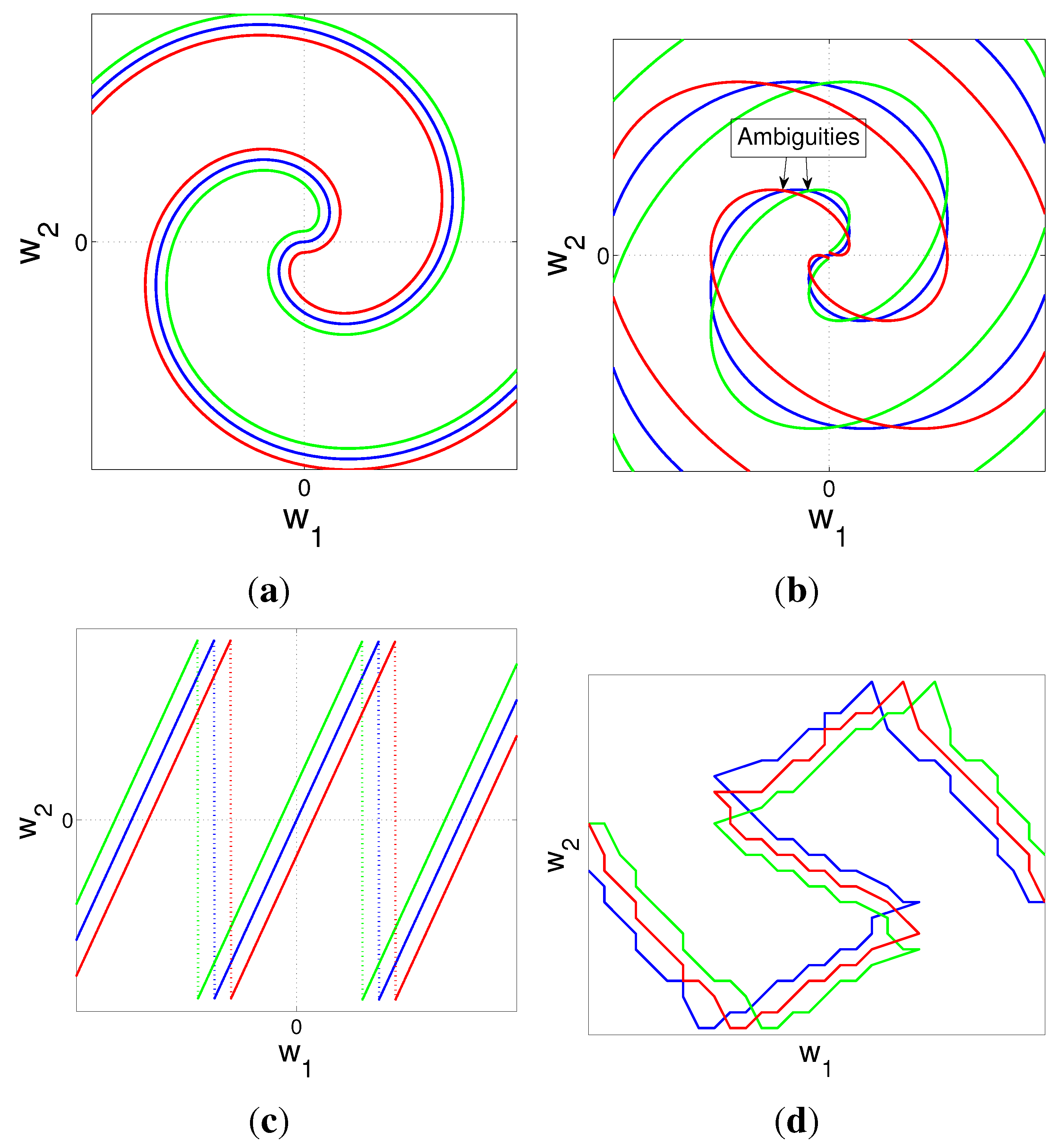
4.3. Power and Distortion Formulation: Collaborative Encoders
4.3.1. Reconstruction of Common Information
4.3.2. Reconstruction of Common Information and Individual Contributions
4.4. Distributed Encoders:
4.4.1. Reconstruction of Common Information
4.4.2. Reconstruction of Common Information and Individual Contributions
4.5. Examples for the Case When
4.5.1. Power and Distortion Calculation for Collaborating Encoders

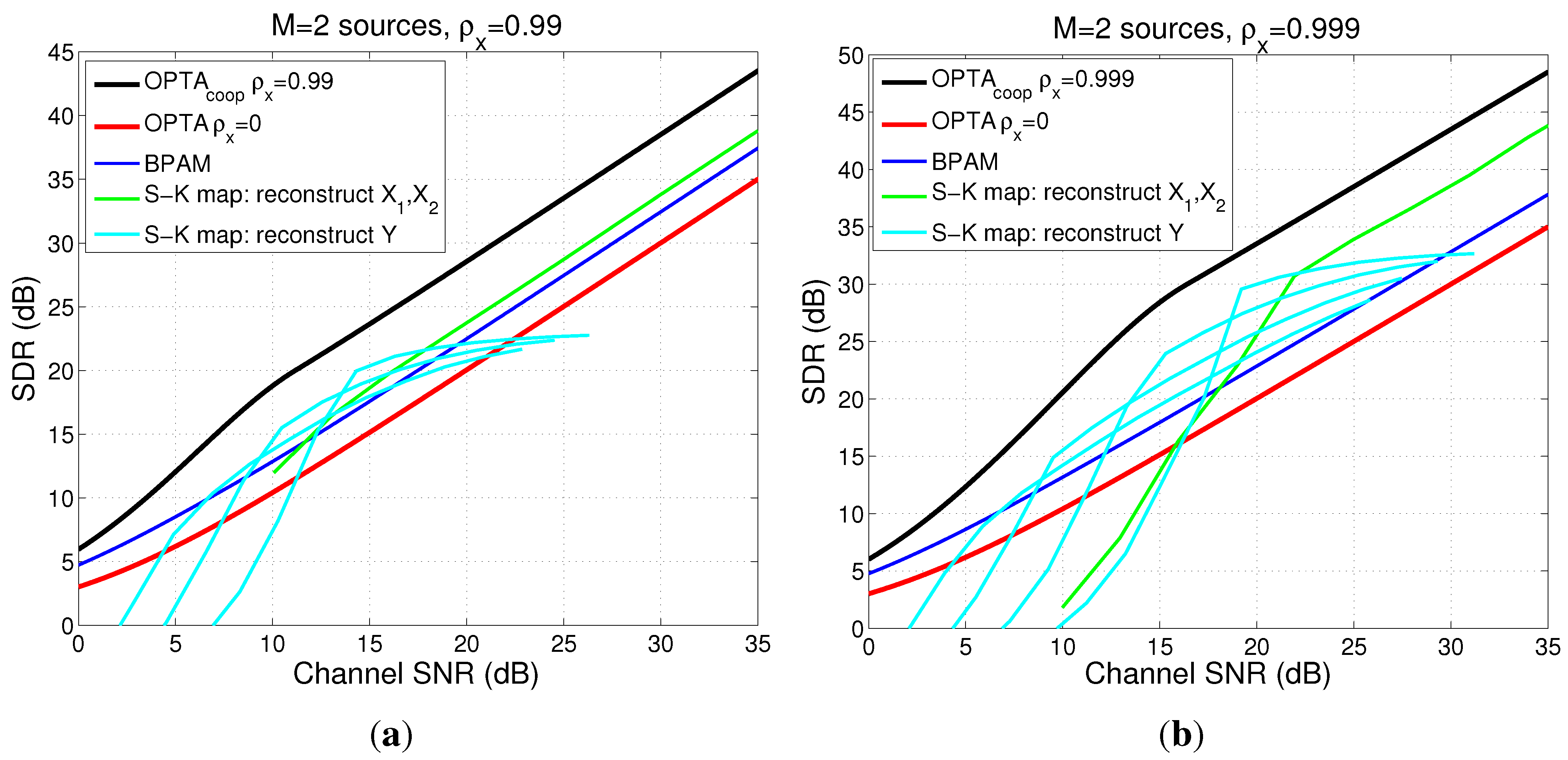
4.5.2. Power and Distortion Calculation for Distributed Encoders

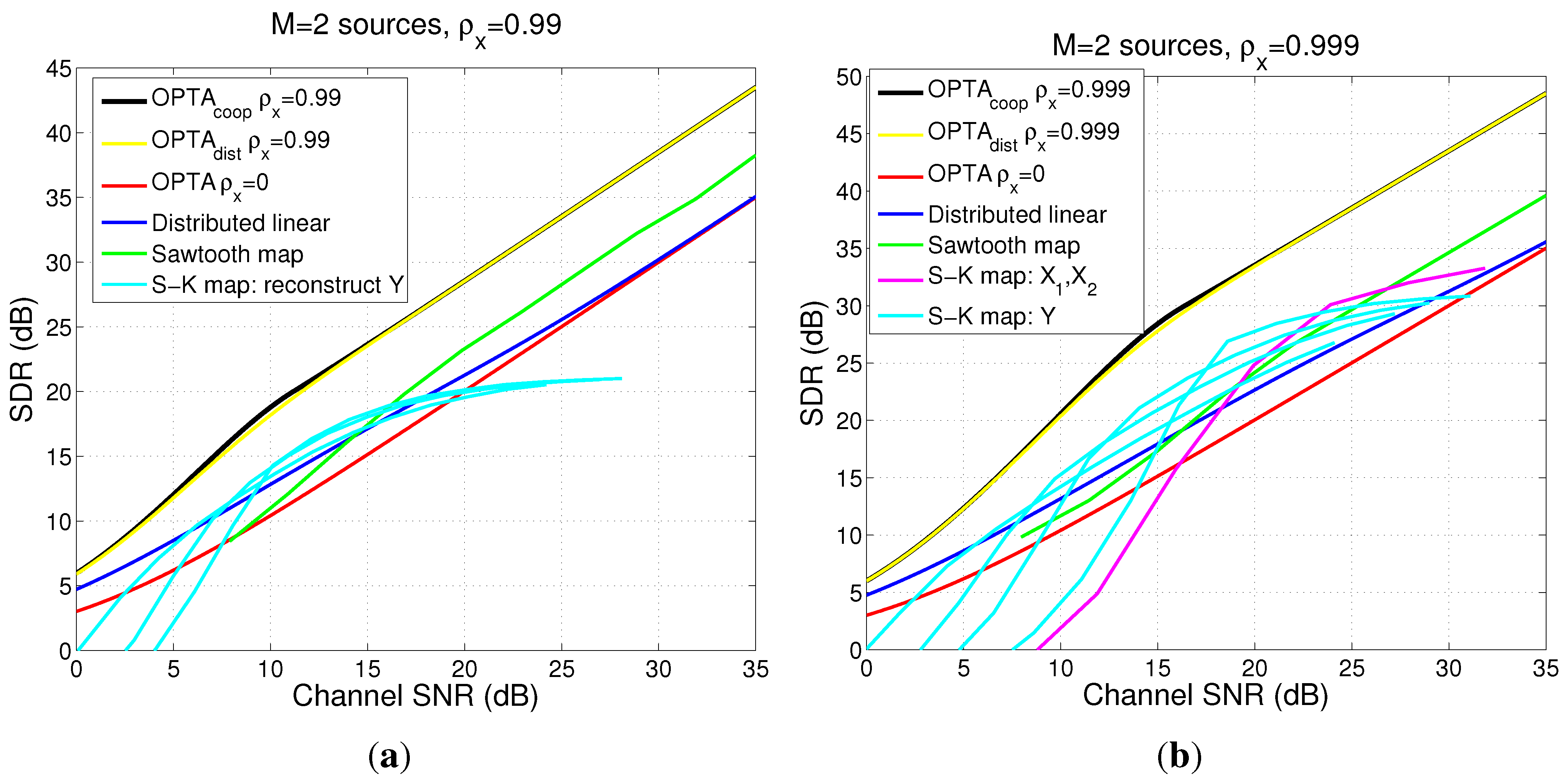
4.5.3. Comparison Between Collaborative Case, Distributed Case and DQ

4.6. Extensions
5. Summary, Conclusions and Future Work
Acknowledgments
Appendix
A. Normal Vector for Archimedes Spiral
B. Metric Tensor
References
- Slepian, D.; Wolf, J.K. Noiseless coding of correlated information sources. IEEE Trans. Inf. Theory 1973, 19, 471–480. [Google Scholar] [CrossRef]
- Berger, T. Rate Distortion Theory: A Mathematical Basis for Data Compression; Prentice-Hall: Englewood Cliffs, NJ, USA, 1971. [Google Scholar]
- Oohama, Y. The rate-distortion function for the quadratic Gaussian CEO problem. IEEE Trans. Inf. Theory 1998, 44, 1057–1070. [Google Scholar] [CrossRef]
- Oohama, Y. Gaussian multiterminal source coding. IEEE Trans. Inf. Theory 1997, 43, 1912–1923. [Google Scholar] [CrossRef]
- Wagner, A.B.; Tavildar, S.; Viswanath, P. Rate region of the quadratic Gaussian two-encoder source-coding problem. IEEE Trans. Inf. Theory 2008, 54, 1938–1961. [Google Scholar] [CrossRef]
- Oohama, Y. Distributed source coding for correlated memoryless Gaussian sources. 2010; arXiv:0908.3982v4 [cs.IT]. [Google Scholar]
- Ray, S.; Medard, M.; Effros, M.; Kotter, R. On separation for multiple access channel. In Proceedings of IEEE Information Theory Workshop, Chengdu, China, 22–26 October 2006; pp. 399–403.
- Wernersson, N.; Skoglund, M. Nonlinear coding and estimation for correlated data in wireless sensor networks. IEEE Trans. Commun. 2009, 57, 2932–2939. [Google Scholar] [CrossRef]
- Wernersson, N.; Karlsson, J.; Skoglund, M. Distributed quantization over noisy channels. IEEE Trans. Commun. 2009, 57, 1693–1700. [Google Scholar] [CrossRef]
- Karlsson, J.; Skoglund, M. Lattice-based source-channel coding in wireless sensor networks. In Proceedings of IEEE International Conferece on Communications, Kyoto, Japan, 5–9 June 2011; pp. 1–5.
- Akyol, E.; Rose, K.; Ramstad, T.A. Optimized analog mappings for distributed source-channel coding. In Proceedings of IEEE Data Compression Conference, Snowbird, Utah, USA, 24–26 March 2010; pp. 159–168.
- Gastpar, M.; Dragotti, P.L.; Vetterli, M. The distributed Karhunen-Loeve transform. IEEE Trans. Inf. Theory 2006, 52, 5177–5196. [Google Scholar] [CrossRef]
- Rajesh, R.; Sharma, N. Correlated Gaussian sources over orthogonal Gaussian channels. In Proceedings of International Symposium on Information Theory and its Applications, Auckland, New Zealand, 7–10 December 2008; pp. 1–6.
- Lapidoth, A.; Tinguely, S. Sending a bi-variate Gaussian over a Gaussian MAC. IEEE Trans. Inf. Theory 2010, 60, 2714–2752. [Google Scholar] [CrossRef]
- Floor, P.A.; Kim, A.; Wernersson, N.; Ramstad, T.; Skoglund, M.; Balasingham, I. Zero-delay joint source-channel coding for a bi-variate Gaussian on a Gaussian MAC. IEEE Trans. Commun. 2012, 60, 3091–3102. [Google Scholar] [CrossRef]
- Vaishampayan, V.A. Combined source-channel coding for bandlimited waveform channels. Ph.D. dissertation, University of Maryland, MD, USA, 1989. [Google Scholar]
- Shannon, C.E. Communication in the presence of noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Kotel’nikov, V.A. The Theory of Optimum Noise Imunity; McGraw-Hill Book Company: New York, NY, USA, 1959. [Google Scholar]
- Goblick, T.J. Theoretical limitations on the transmission from analog sources. IEEE Trans. Inf. Theory 1965, 11, 558–567. [Google Scholar] [CrossRef]
- McRae, D. Performance evaluation of a new modulation technique. IEEE Trans. Inf. Theory 1970, 16, 431–445. [Google Scholar] [CrossRef]
- Timor, U. Design of signals for analog communication. IEEE Trans. Inf. Theory 1970, 16, 581–587. [Google Scholar] [CrossRef]
- Thomas, C.; May, C.; Welti, G. Hybrid amplitude-and-phase modulation for analog data transmission. IEEE Trans. Commun. 1976, 23, 634–645. [Google Scholar] [CrossRef]
- Lee, K.H.; Petersen, D.P. Optimal linear coding for vector channels. IEEE Trans. Commun. 1976, 24, 1283–1290. [Google Scholar]
- Fuldseth, A.; Ramstad, T.A. Bandwidth compression for continuous amplitude channels based on vector approximation to a continuous subset of the signal space. In Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, Atlanta, GA, USA, 21–24 April 1997; pp. 3093–3096.
- Coward, H.; Ramstad, T.A. Quantizer optimization in hybrid digital-analog transmission of analog source signals. In Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 5–9 June 2000; pp. 2637–2640.
- Chung, S.Y. On the construction of some capacity-approaching coding schemes. Ph.D. dissertation, Massachusetts Institute of Technology, MA, USA, 2000. [Google Scholar]
- Ramstad, T.A. Shannon mappings for robust comunication. Telektronikk 2002, 98, 114–128. [Google Scholar]
- Mittal, U.; Phamdo, N. Hybrid digital-analog (HDA) joint source-chanel codes for broadcasting and robust communications. IEEE Trans. Inf. Theory 2002, 48, 1082–1102. [Google Scholar] [CrossRef]
- Gastpar, M.; Rimoldi, B.; Vetterli, M. To code, or not to code: Lossy source-channel communication revisited. IEEE Trans. Inf. Theory 2003, 49, 1147–1158. [Google Scholar] [CrossRef]
- Skoglund, M.; Phamdo, N.; Alajaji, F. Hybrid digital-analog source-chanel coding for bandwidth compression/expansion. IEEE Trans. Inf. Theory 2006, 52, 3757–3763. [Google Scholar] [CrossRef]
- Hekland, F.; Floor, P.A.; Ramstad, T.A. Shannon-Kotel’nikov mappings in joint source-channel coding. IEEE Trans. Commun. 2009, 57, 94–105. [Google Scholar] [CrossRef]
- Floor, P.A.; Ramstad, T.A. Optimality of dimension expanding Shannon-Kotel’nikov mappings. In Proceedings of IEEE Information Theory Workshop, Tahoe City, CA, USA, 2–6 September 2007; pp. 289–294.
- Cai, X.; Modestino, J.W. Bandwidth expansion Shannon mapping for analog error-control coding. In Proceedings of IEEE Conference on Information Sciences and Systems, Princeton University, Princeton, NJ, USA, 22–24 March 2006; pp. 1709–1712.
- Akyol, E.; Rose, K.; Ramstad, T.A. Optimal mappings for joint source channel coding. In Proceedings of IEEE Information Theory Workshop, Dublin, Ireland, 30 August–3 September 2010; pp. 1–5.
- Hu, Y.; Garcia-Frias, J.; Lamarca, M. Analog joint source-channel coding using non-linear curves and MMSE decoding. IEEE Trans. Commun. 2011, 59, 3016–3026. [Google Scholar] [CrossRef]
- Erdozain, A.; Crespo, P.M.; Beferull-Lozano, B. Multiple description analog joint source-chanel coding to exploit the diversity in parallel channels. IEEE Trans. Signal Proc. 2012, 60, 5880–5892. [Google Scholar] [CrossRef]
- Kochman, Y.; Zamir, R. Analog matching of colored sources to colored channels. IEEE Trans. Inf. Theory 2011, 57, 3180–3195. [Google Scholar] [CrossRef]
- Floor, P.A.; Ramstad, T.A. Shannon-Kotel’nikov mappings for analog point-to-point communications. 2012; arXiv:1101.5716v2 [cs.IT]. [Google Scholar]
- Kim, A.; Floor, P.A.; Ramstad, T.A.; Balasingham, I. Delay-free joint source-channel coding for Gaussian network of multiple sensors. In Proceedings of IEEE International Conferece on Communications, Kyoto, Japan, 5–9 June 2011; pp. 1–6.
- Wozencraft, J.M.; Jacobs, I.M. Principles of Communication Engineering; John Wiley & Sons: New York, NY, USA, 1965. [Google Scholar]
- Floor, P.A.; Ramstad, T.A. Dimension reducing mappings in joint source-channel coding. In Proceedings of IEEE Nordic Signal Processing Symposium, Reykjavik, Iceland, 7–9 June 2006; pp. 282–285.
- Saleh, A.A.; Alajaji, F.; Chan, W.Y. Hybrid digital-analog source-channel coding with one-to-three bandwidth expansion. In Proceedings of IEEE Canadian Workshop in Information Theory, Kelowna, Canada, 17–20 May 2011; pp. 70–73.
- Merhav, N. Threshold effects in parameter estimation as phase transitions in statistical mechanics. IEEE Trans. Inf. Theory 2011, 57, 7000–7010. [Google Scholar] [CrossRef]
- Cramér, H. Mathematical Methods of Statistics; Princeton University Press: Princeton, NJ, USA, 1951. [Google Scholar]
- Cover, T.A.; Thomas, J.A. Elements of Information Theory; John Wiely & Sons: New York, NY, USA, 1991. [Google Scholar]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables and Stochastic Processes; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Gasquet, C.; Witomski, P. Fourier Analysis and Applications; Springer-Verlag: New York, NY, USA, 1999. [Google Scholar]
- Sakrison, D.J. Communication Theory: Transmission of Waveforms and Digital Infromation; John Wiley & Sons: New York, NY, USA, 1968. [Google Scholar]
- Edwards, C.H.; Penney, D.E. Calculus with Analytic Geometry; Prentice Hall International Inc.: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Spivak, M. A Comprehensive Introduction to Differential Geometry; Publish or Perish: Huston, TX, USA, 1999. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Floor, P.A.; Kim, A.N.; Ramstad, T.A.; Balasingham, I. Zero Delay Joint Source Channel Coding for Multivariate Gaussian Sources over Orthogonal Gaussian Channels. Entropy 2013, 15, 2129-2161. https://doi.org/10.3390/e15062129
Floor PA, Kim AN, Ramstad TA, Balasingham I. Zero Delay Joint Source Channel Coding for Multivariate Gaussian Sources over Orthogonal Gaussian Channels. Entropy. 2013; 15(6):2129-2161. https://doi.org/10.3390/e15062129
Chicago/Turabian StyleFloor, Pål Anders, Anna N. Kim, Tor A. Ramstad, and Ilangko Balasingham. 2013. "Zero Delay Joint Source Channel Coding for Multivariate Gaussian Sources over Orthogonal Gaussian Channels" Entropy 15, no. 6: 2129-2161. https://doi.org/10.3390/e15062129
APA StyleFloor, P. A., Kim, A. N., Ramstad, T. A., & Balasingham, I. (2013). Zero Delay Joint Source Channel Coding for Multivariate Gaussian Sources over Orthogonal Gaussian Channels. Entropy, 15(6), 2129-2161. https://doi.org/10.3390/e15062129



