Entanglement Structure in Expanding Universes
Abstract
:1. Introduction
2. Detector Model
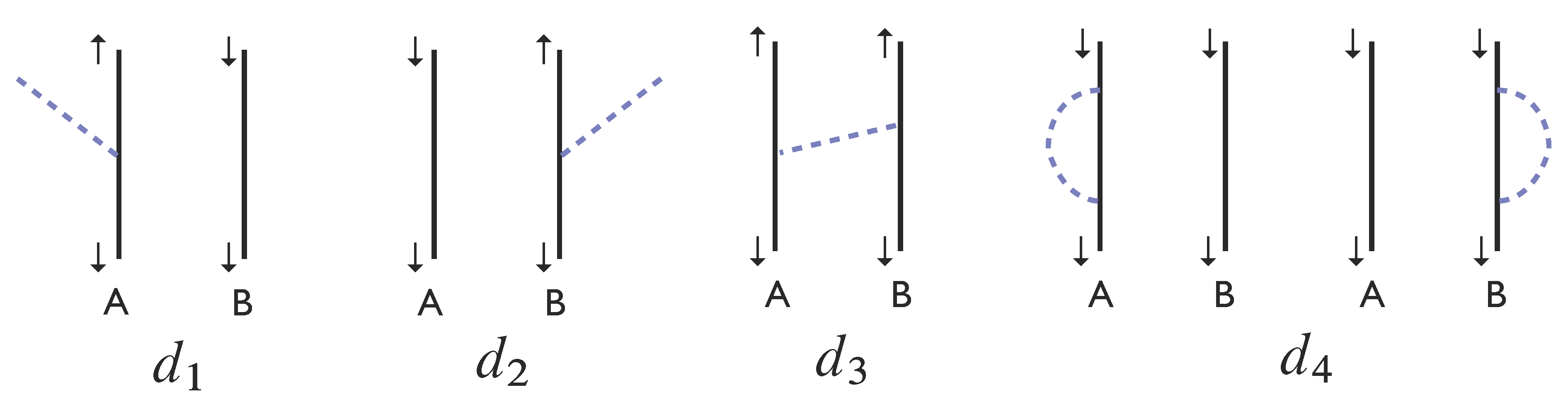
3. Scalar Fields and Wightman Functions
3.1. Minkowski Vacuum and Thermal State
3.2. Conformal Vacuum
3.3. Minimal Scalar
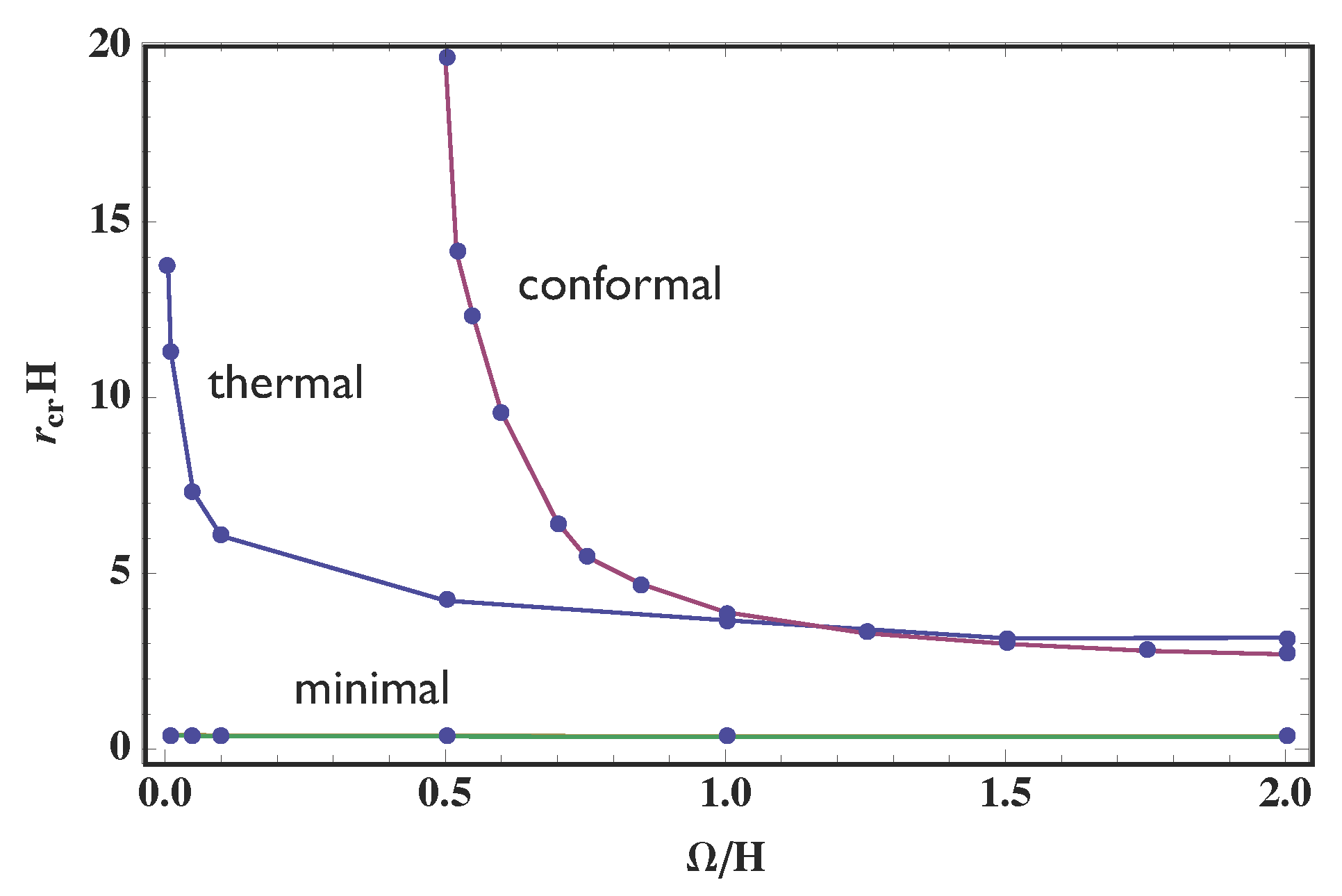
4. Behavior of the Negativity
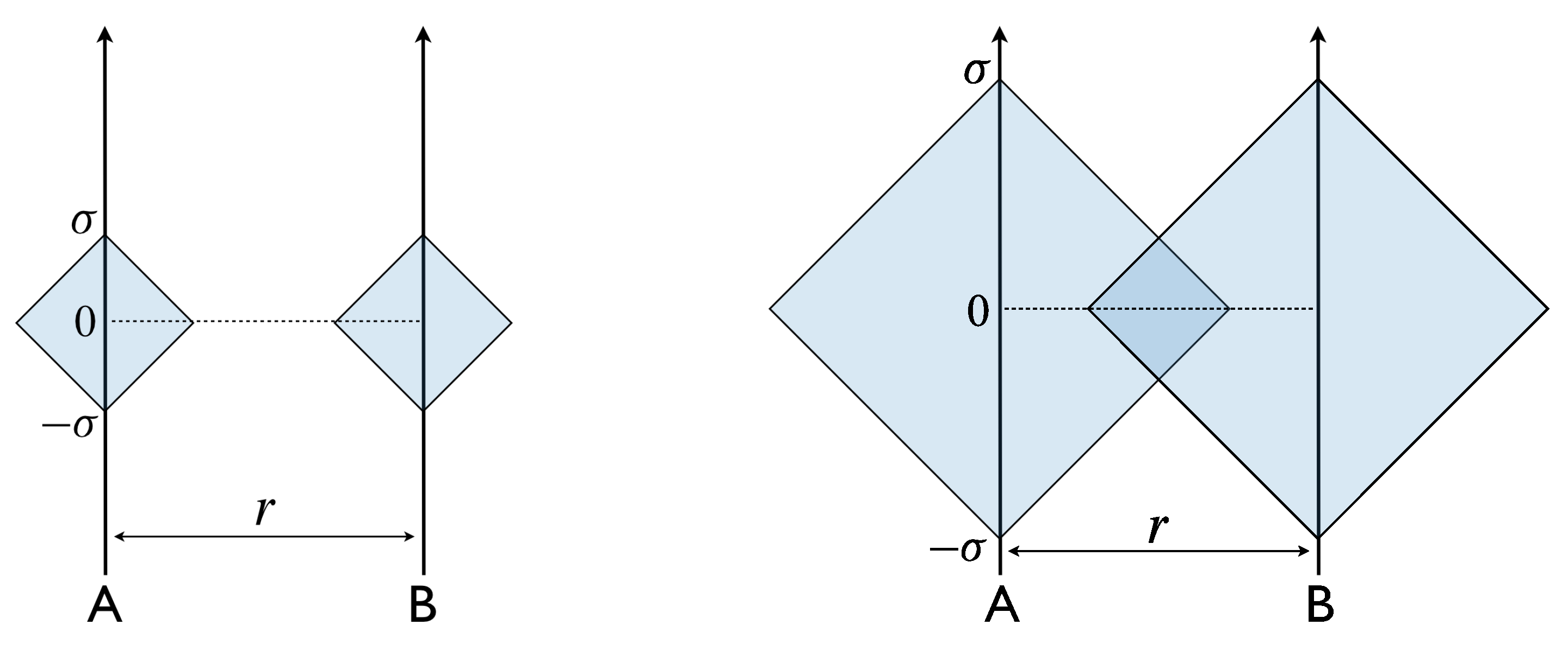
4.1. Causal Structure
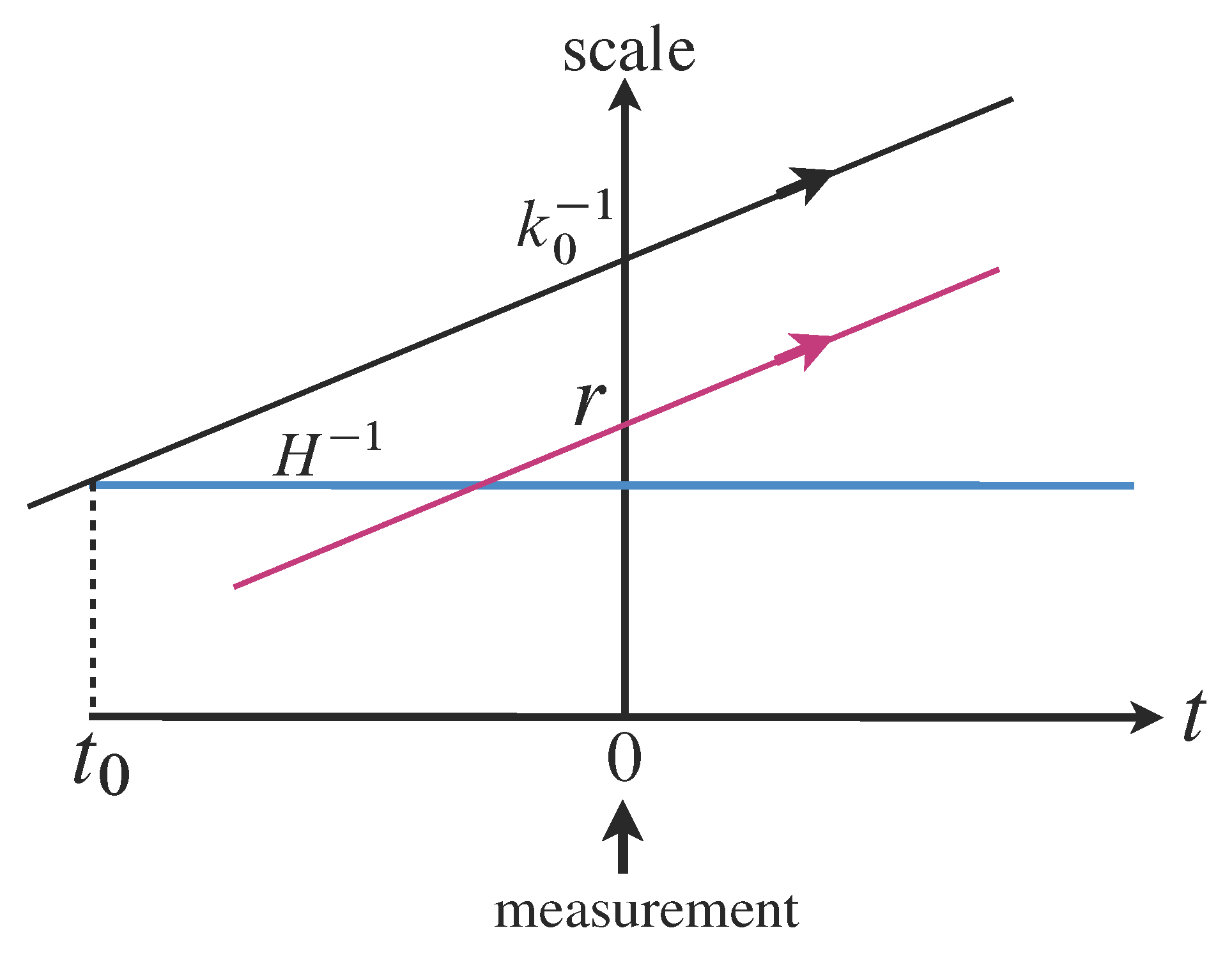
4.2. X and E
4.2.1. Minkowski Vacuum and Thermal State
4.2.2. De Sitter
4.3. Asymptotic Analysis
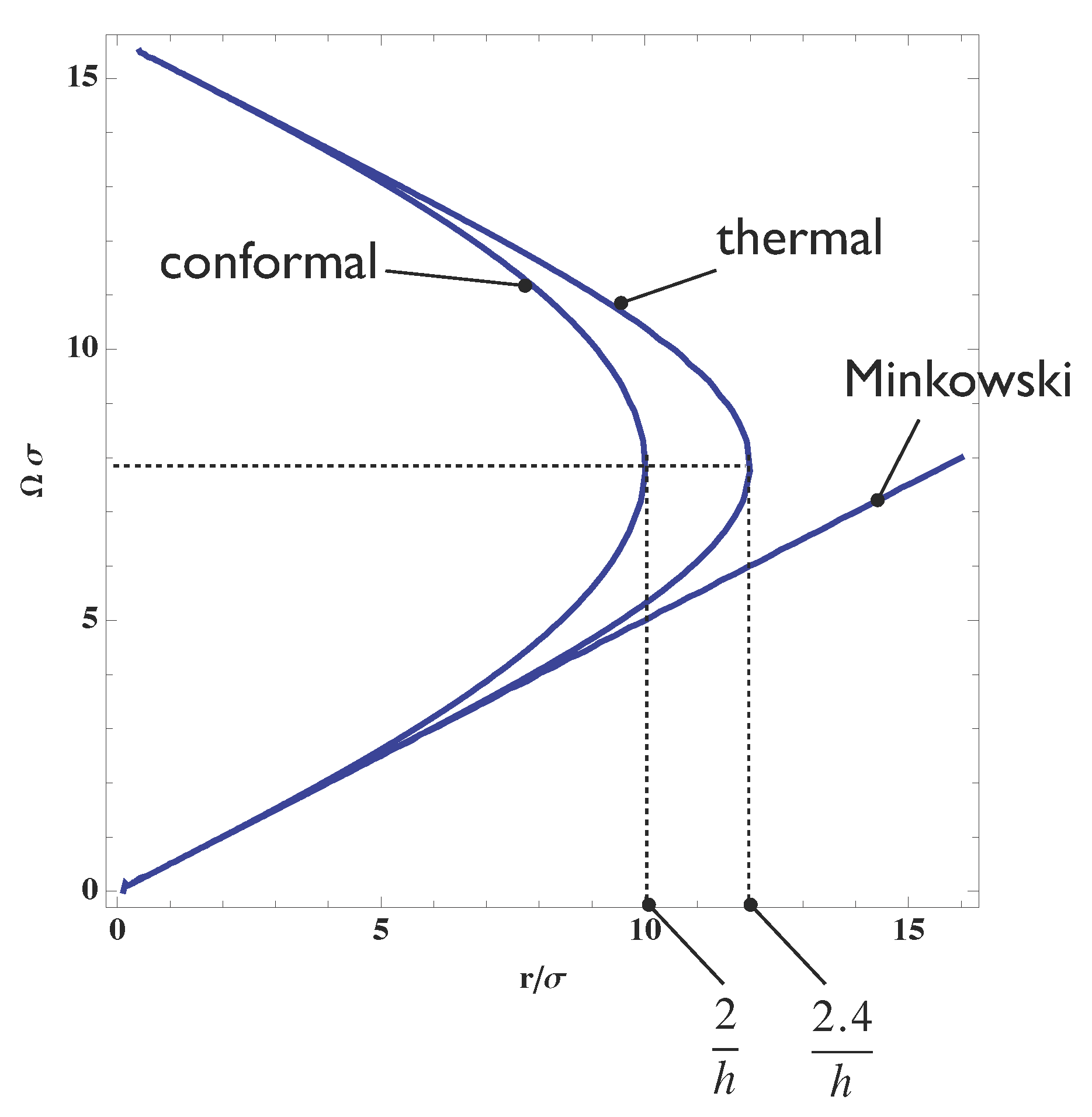
5. Numerical Evaluation of Negativity
5.1. Thermal State
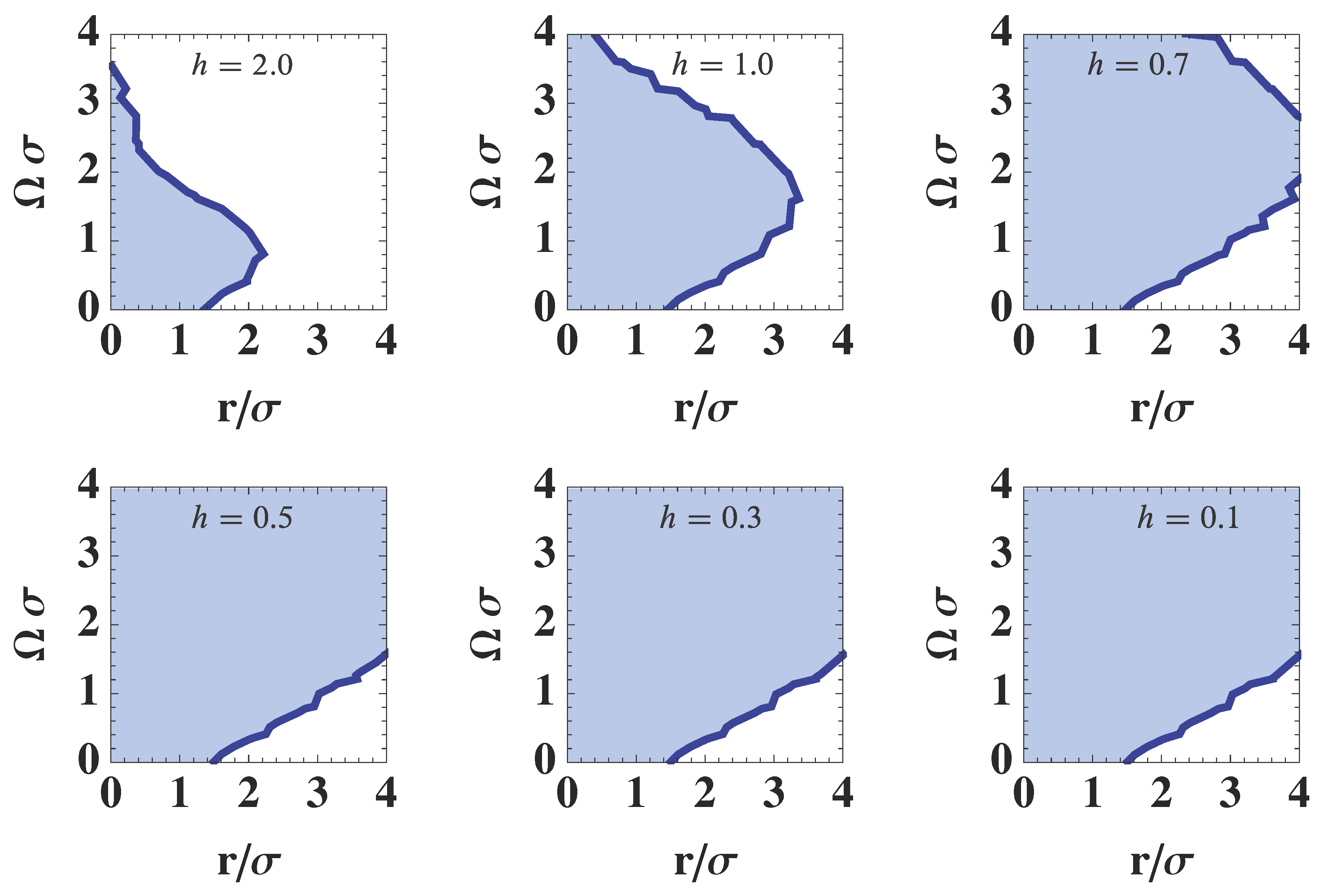
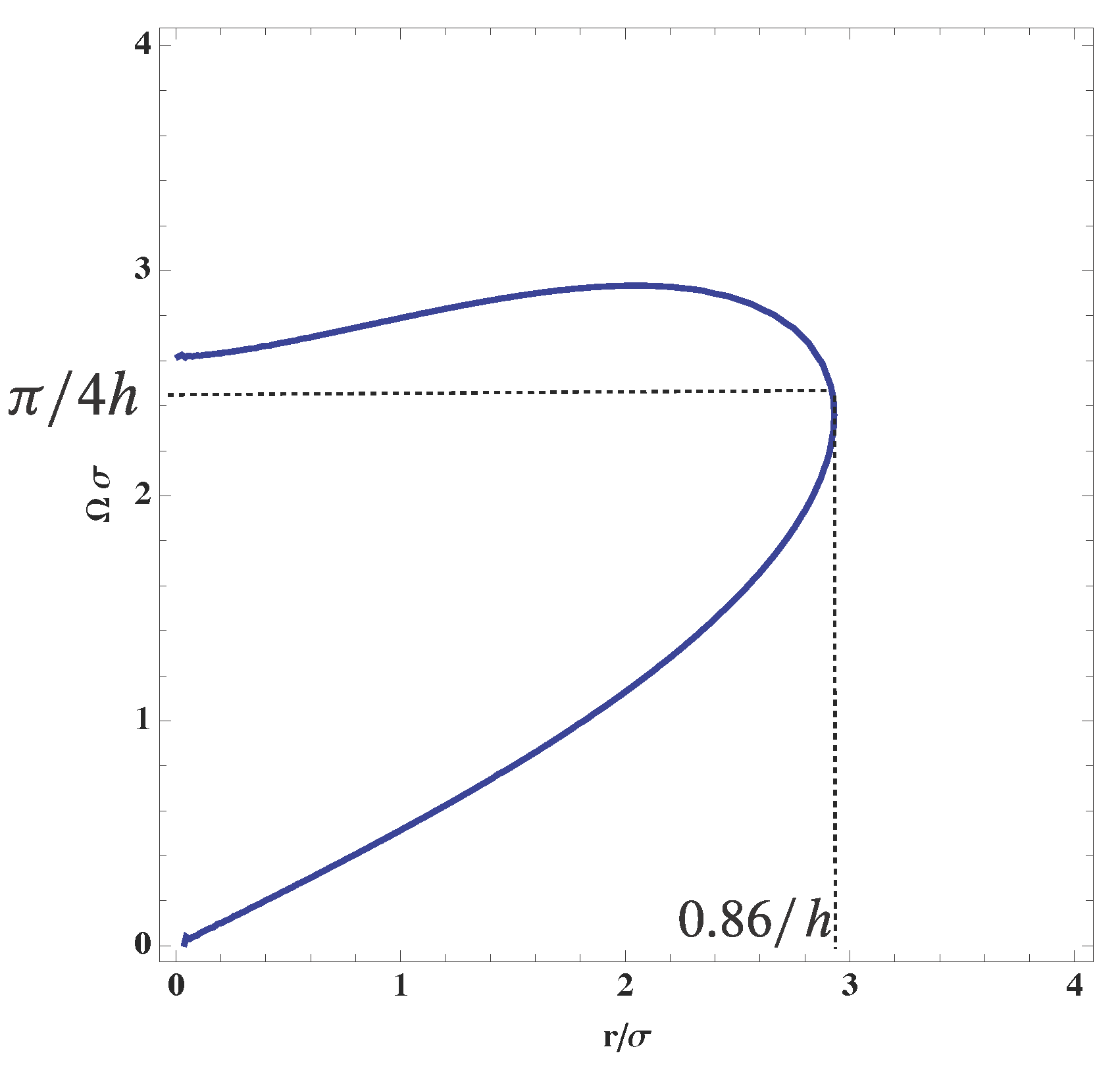
5.2. De Sitter

- For , it is possible to detect entanglement of the scalar field for . For larger separation , the detectors are separable; however, this does not imply the scalar field is separable. Because the initial separable state evolves to the final separable state and we cannot say anything about the separability of the scalar field in this case.
- For sufficiently large value of , two detectors can be entangled for any value of spatial separation (Figure 8). In this parameter regime, the maximal spatial size of the entangled region becomes infinite for . For , the causal diamonds of two detectors can have overlap even for and two detectors are causally connected. Hence the entanglement between two detectors in this case does not mean non-local quantum correlation. The entanglement between detectors is established via causal contact between detectors.
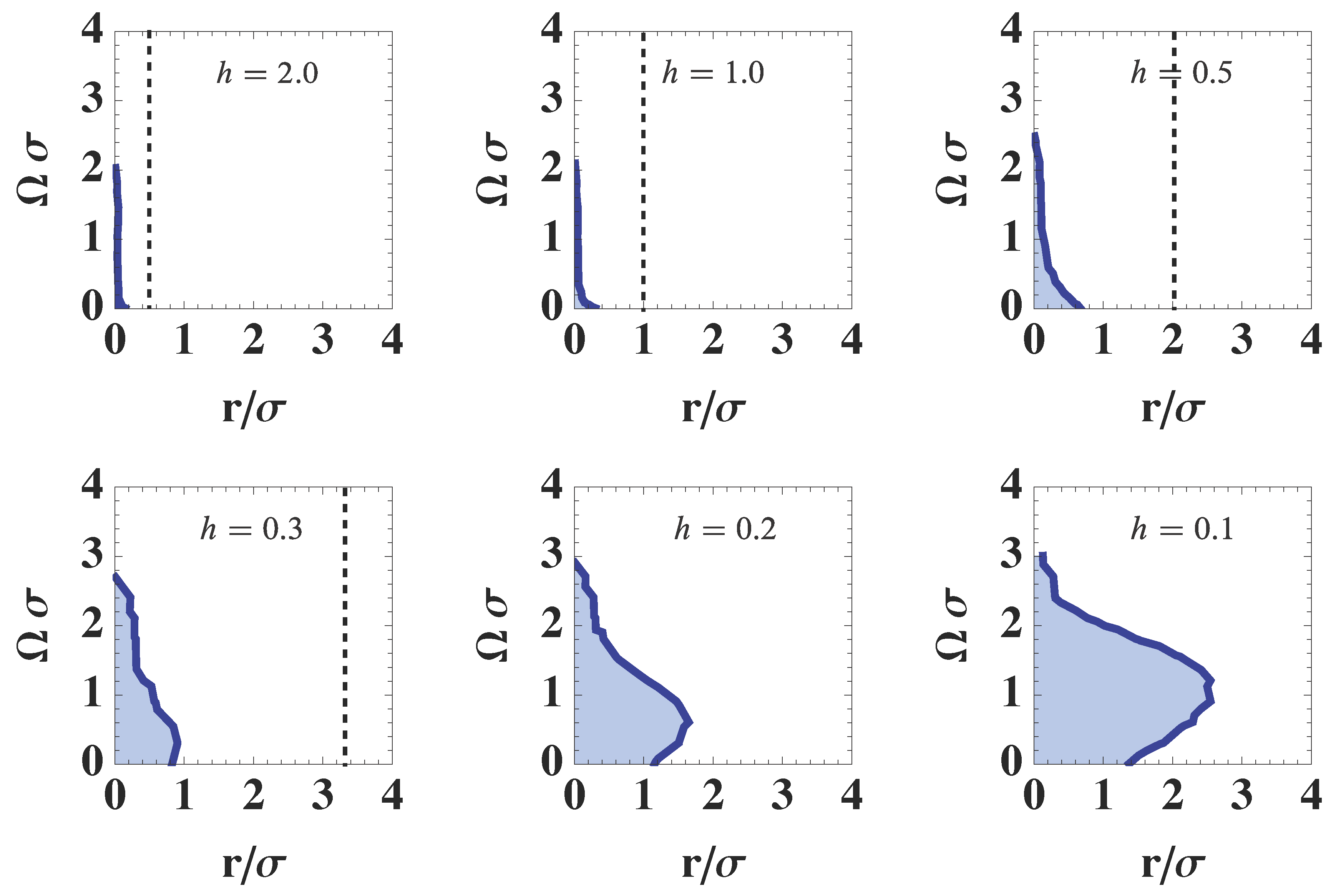
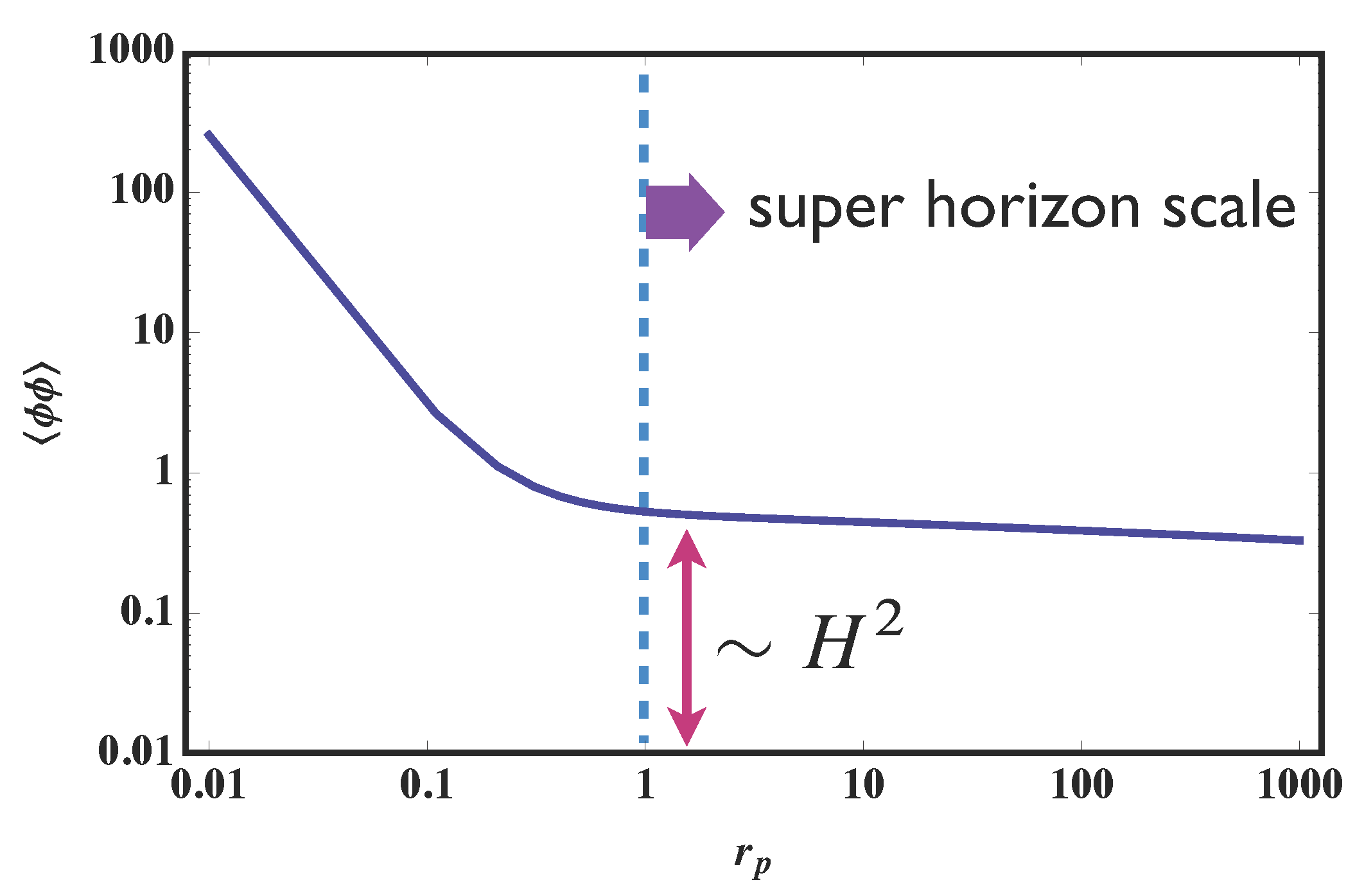
- The critical value is always about and it is not possible to find out detector’s parameters with which the two detectors are entangled beyond this scale. This result implies that the Bunch–Davies vacuum state for the massless minimal scalar field is not entangled for the large scale .
- Our numerical evaluation of the negativity for the minimal scalar field strongly suggests that the minimal scalar field does not have the entanglement for the super-horizon scale. This is precisely our expected feature for classical behavior of the scalar field in the inflationary universe.
6. Strength of Observable Correlation
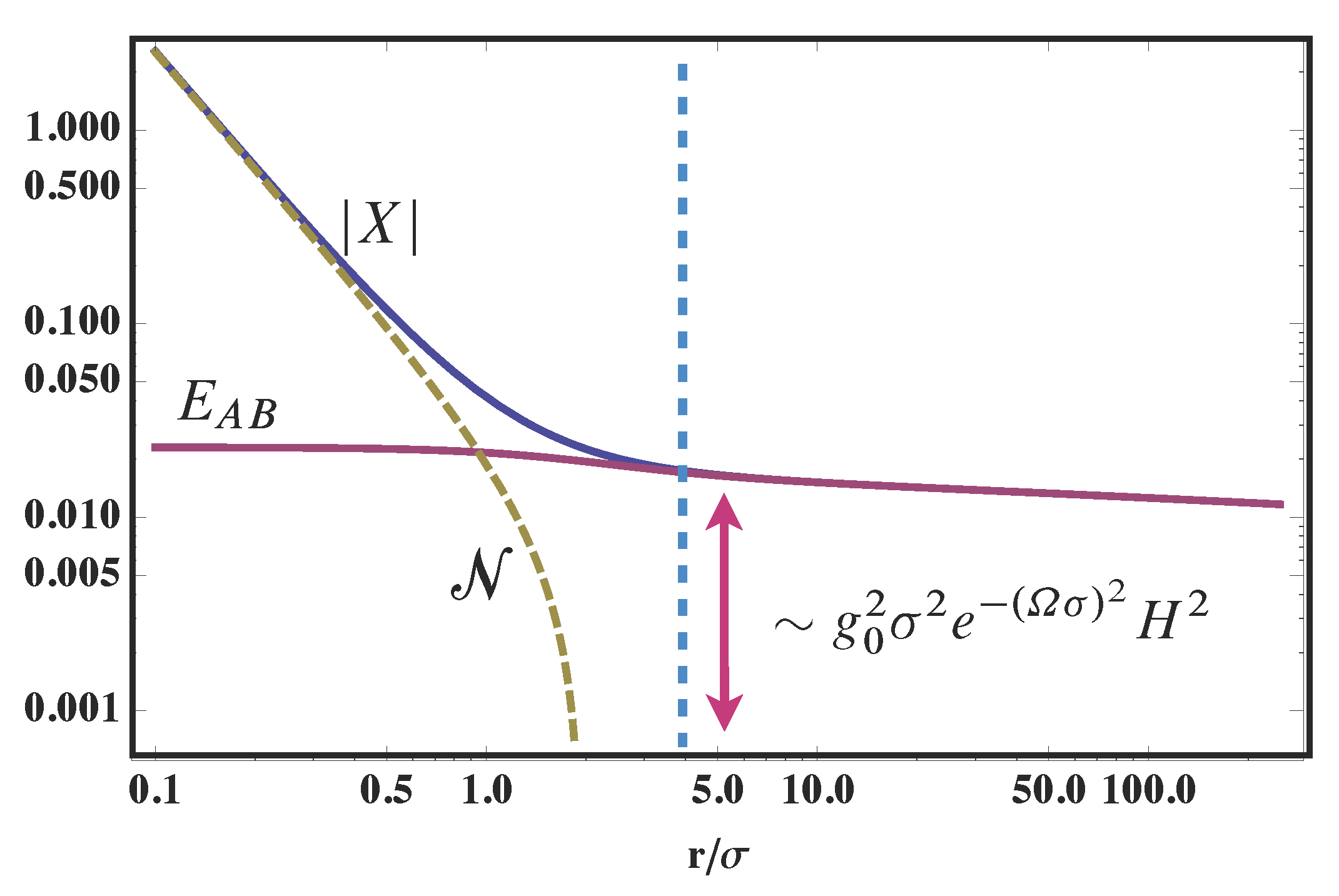
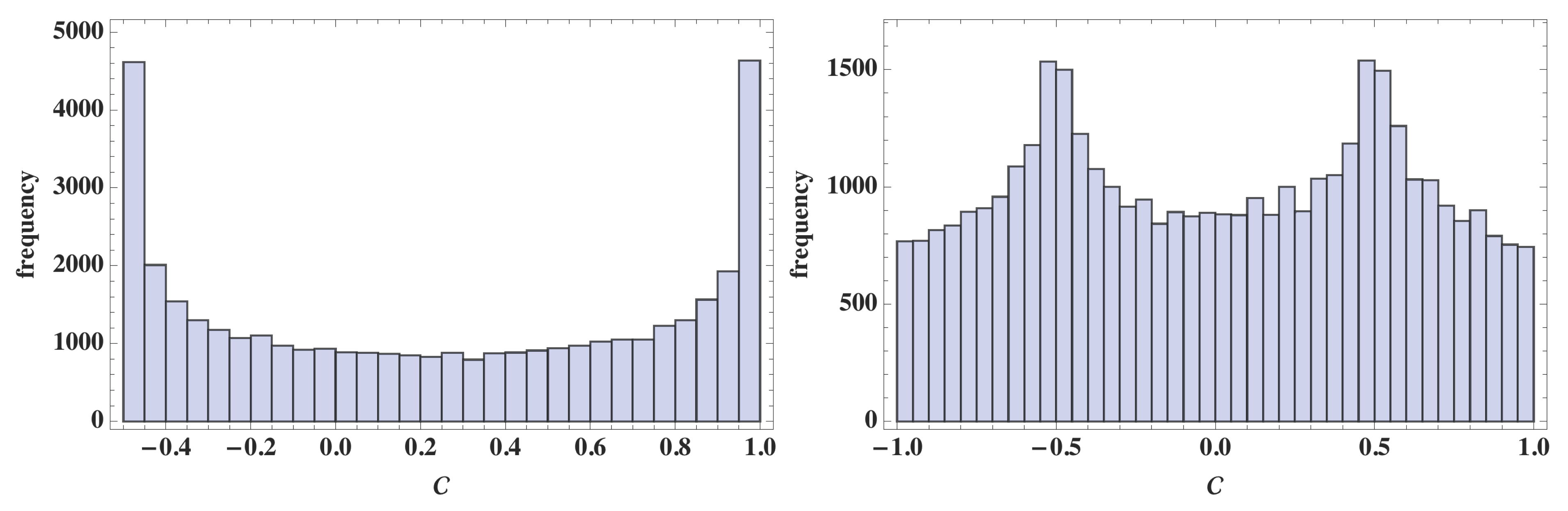
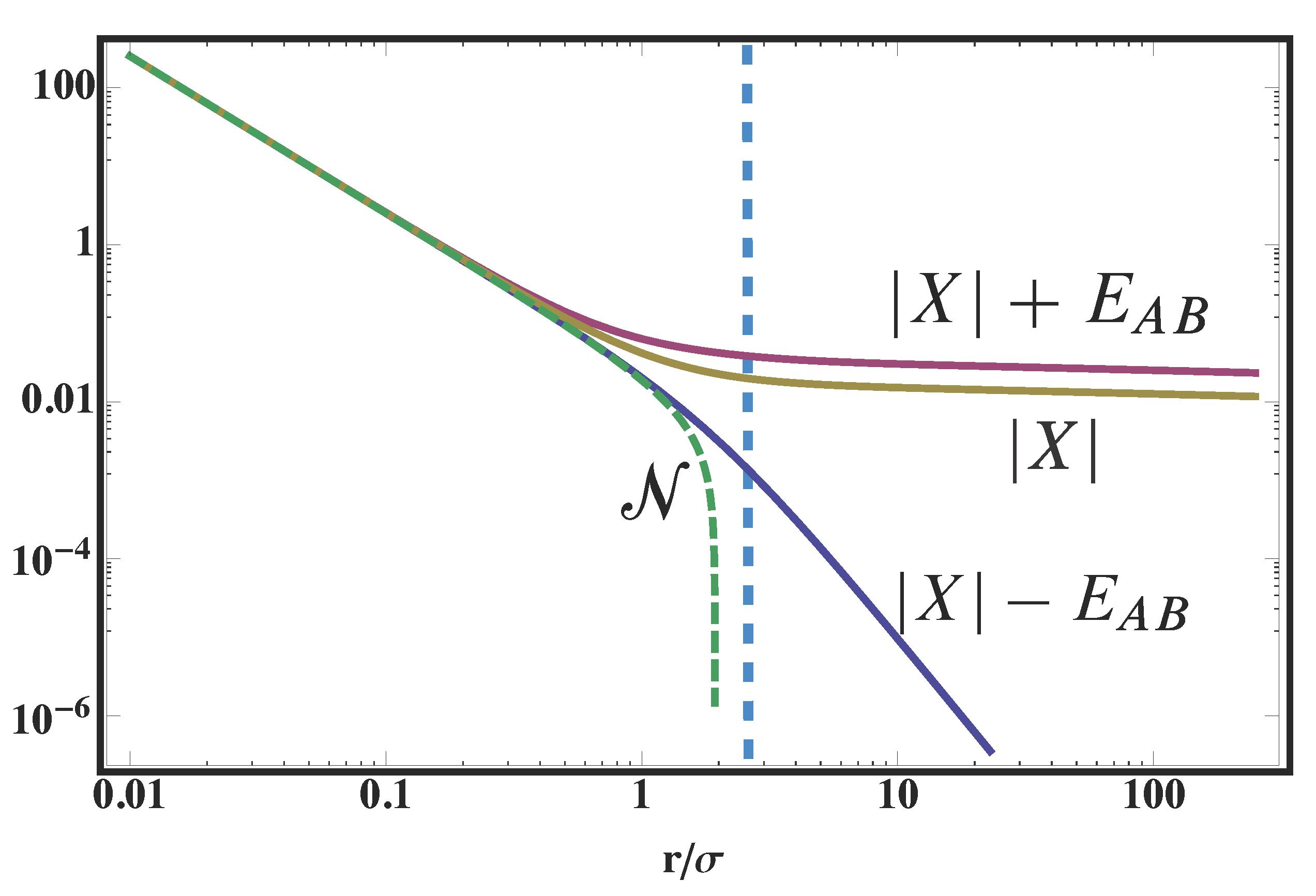
7. Summary
Acknowledgments
Appendix
A. Contour Integration
A.1. Minkowski vacuum
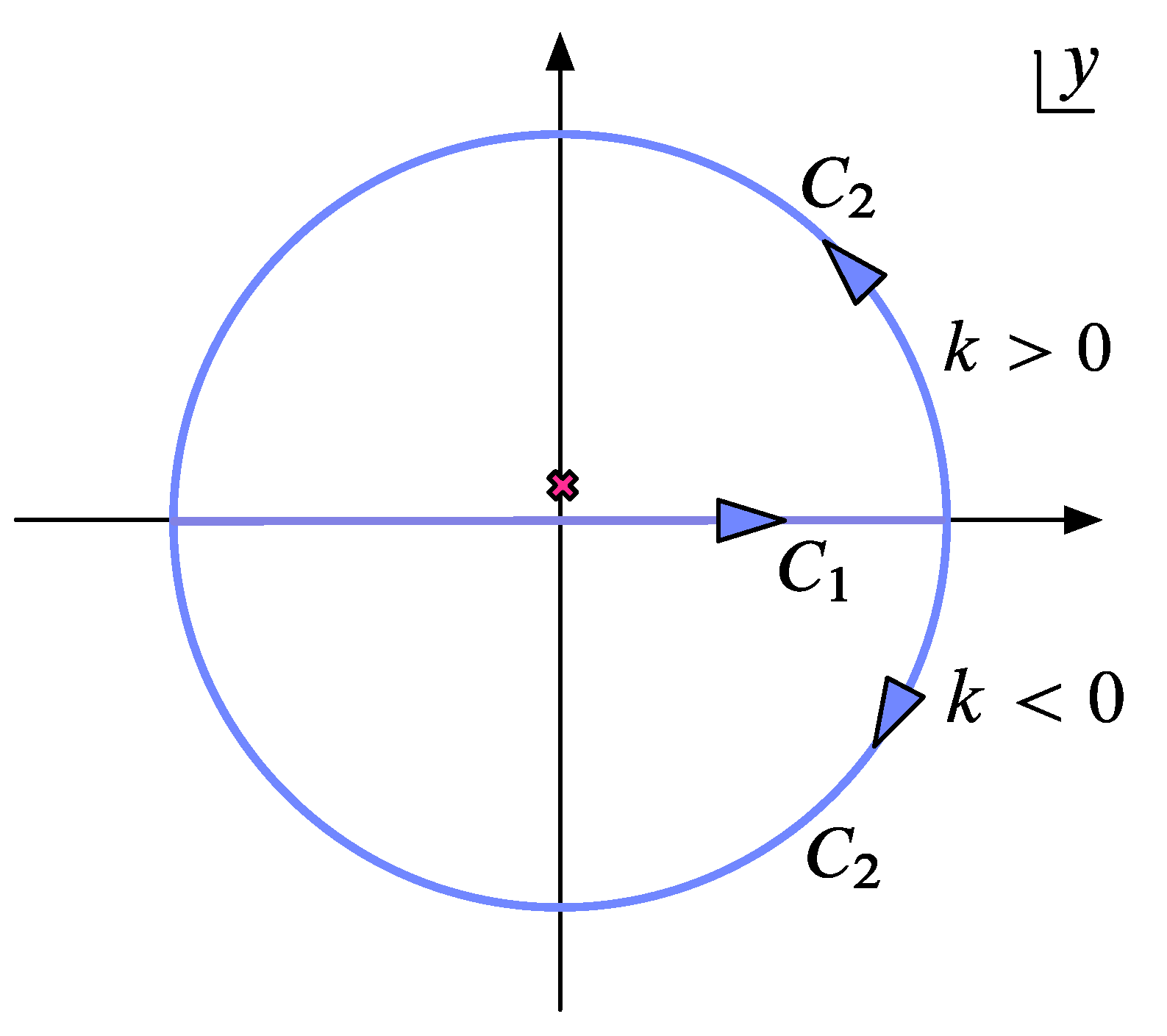
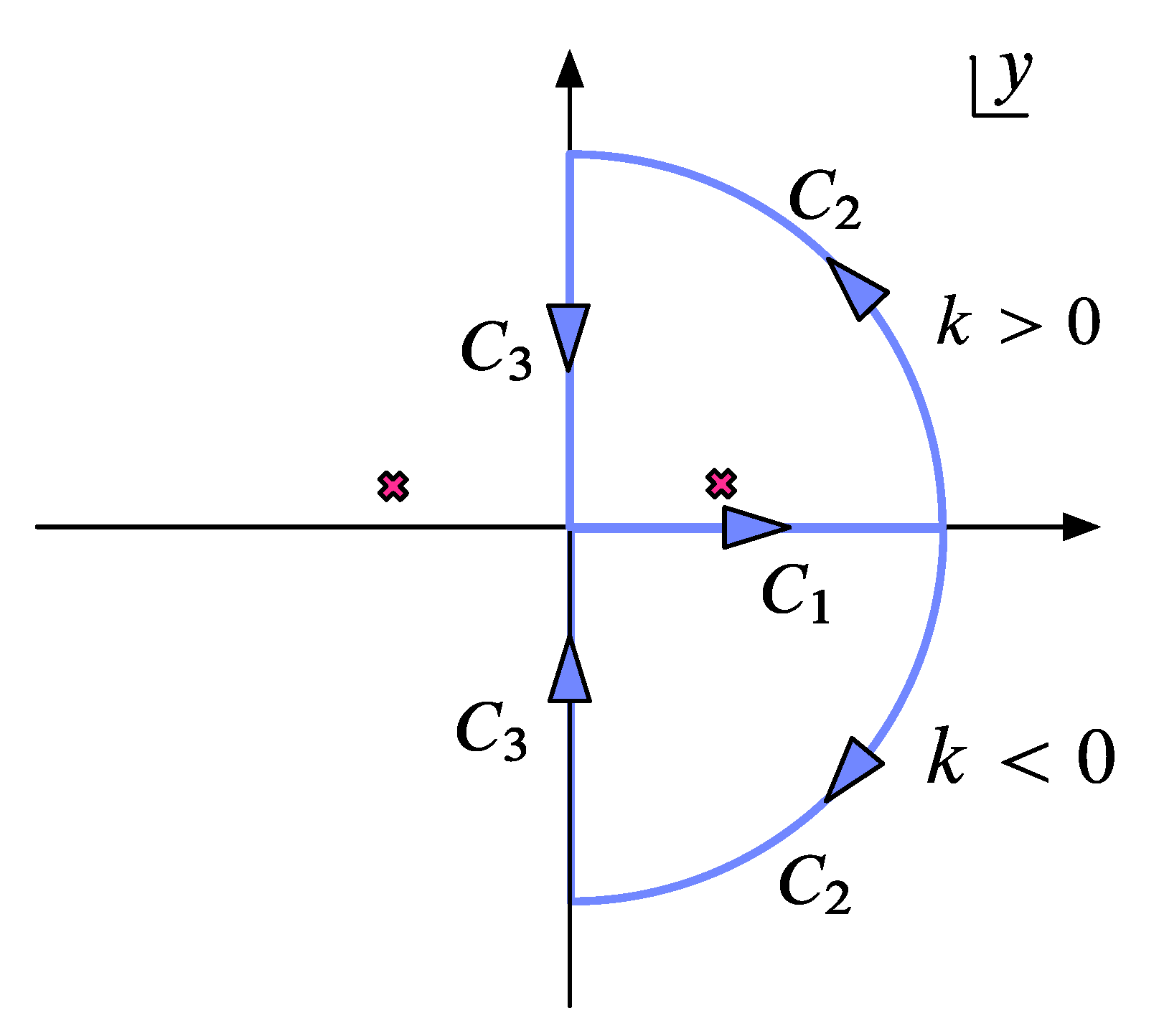
A.2. The Thermal State
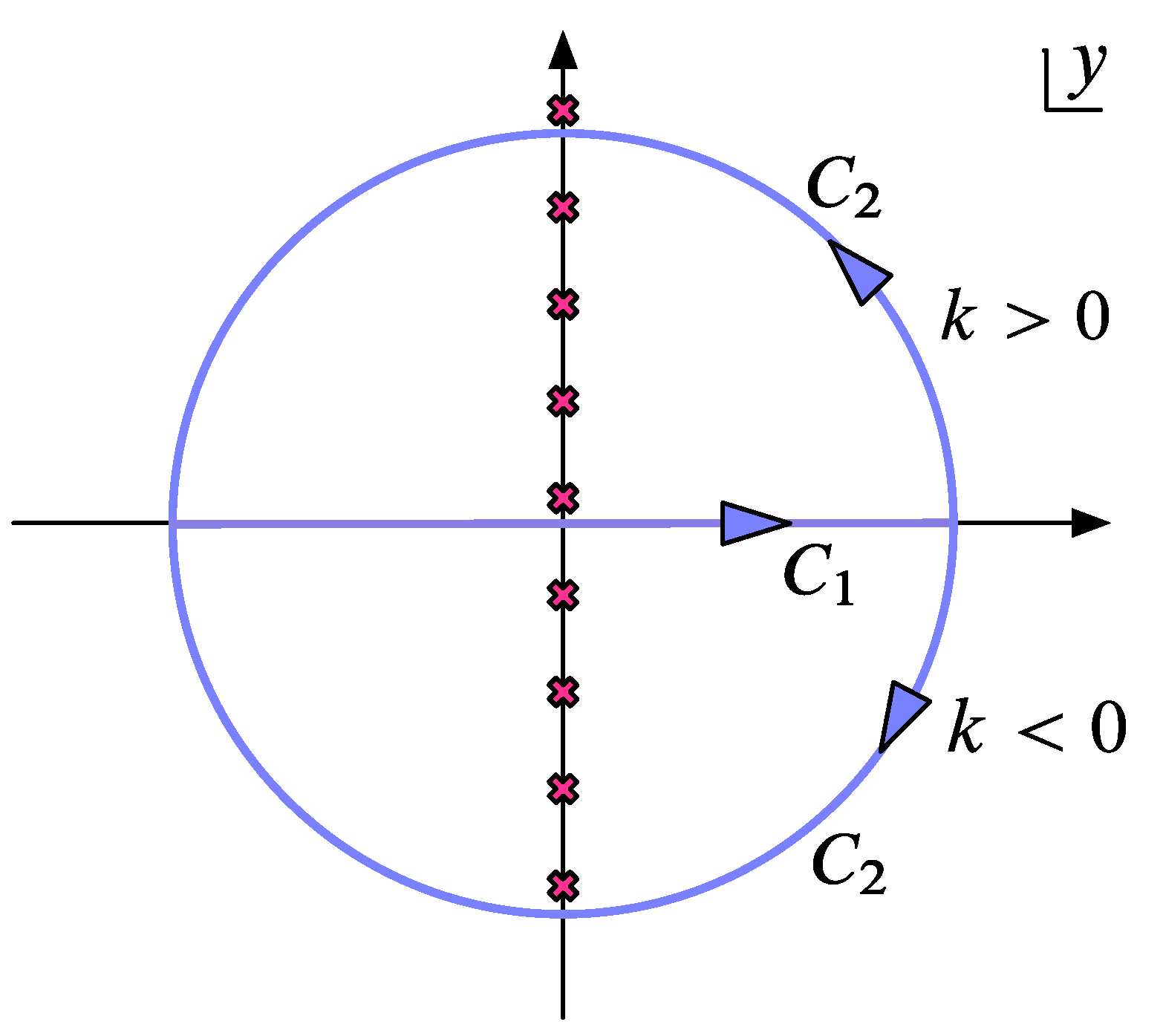
A.3. The Conformal Scalar Field
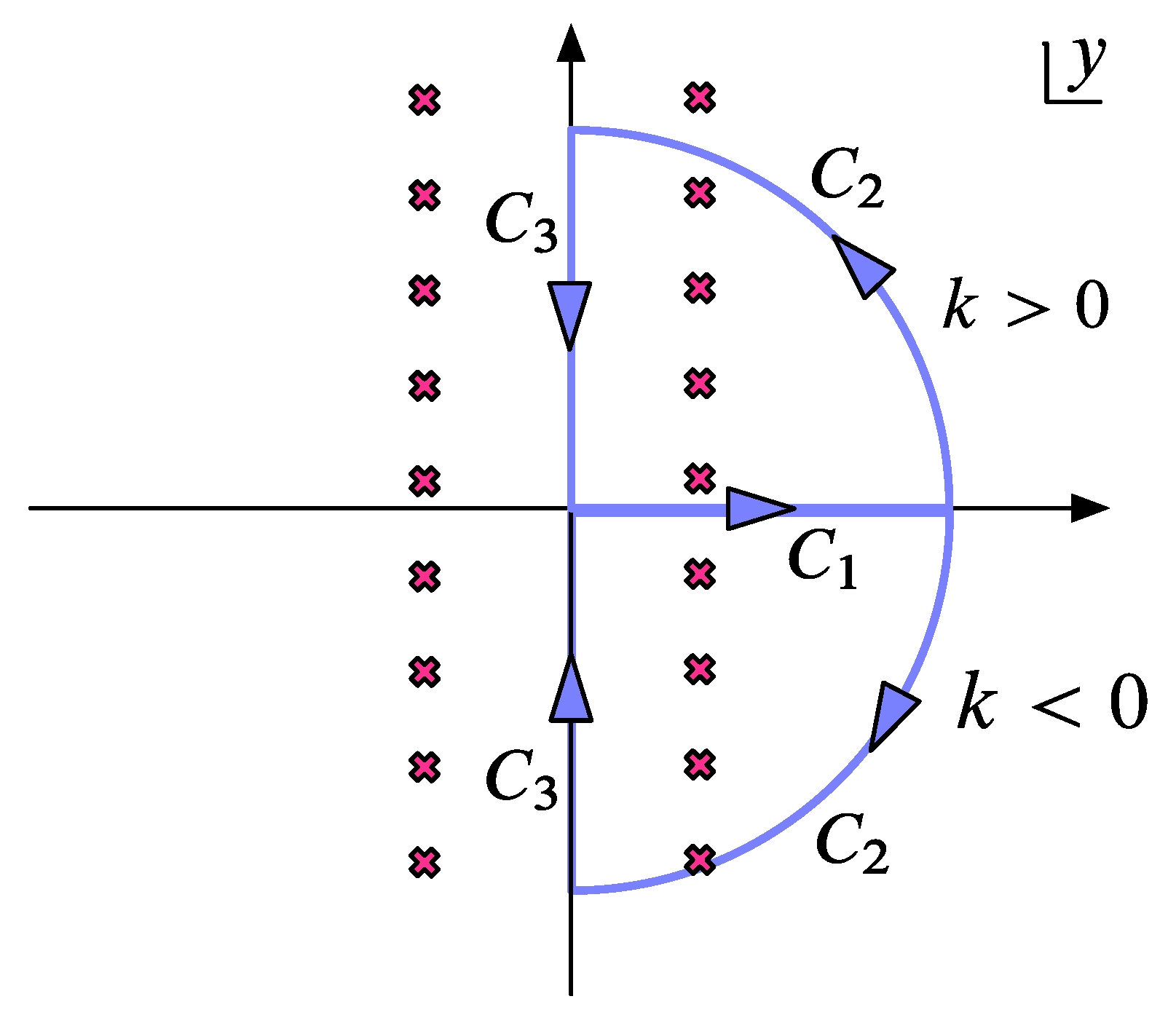
References
- Kiefer, C.; Polarski, D. Why do cosmological perturbations look classical to us? Adv. Sci. Lett. 2009, 2, 164–173. [Google Scholar] [CrossRef]
- Genovese, M. Cosmology and entanglement. Adv. Sci. Lett. 2009, 2, 303–309. [Google Scholar] [CrossRef]
- Ball, J.L.; F-Schuller, I.; Schuller, F.P. Entanglement in an expanding spacetime. Phys. Lett. A 2006, 359, 550–554. [Google Scholar] [CrossRef]
- Fuentes, I.; Mann, R.B.; Martín-Martínez, E.; Moradi, S. Entanglement of Dirac fields in an expanding spacetime. Phys. Rev. D 2010, 83, 045030. [Google Scholar] [CrossRef]
- Nambu, Y. Entanglement of qauntum fluctuations in the inflationary universe. Phys. Rev. D 2008, 78, 044023. [Google Scholar] [CrossRef]
- Nambu, Y.; Ohsumi, Y. Entanglement of coarse grained quantum field in the expanding universe. Phys. Rev. D 2009, 80, 124031. [Google Scholar] [CrossRef]
- Nambu, Y.; Ohsumi, Y. Classical and quantum correlations of scalar field in the inflationary universe. Phys. Rev. D 2011, 84, 044028. [Google Scholar] [CrossRef]
- Simon, R. Peres-horodecki separability criterion for continuous variable system. Phys. Rev. Lett. 2000, 84, 2726–2729. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.; Giedke, G.; Cirac, J.I.; Zoller, P. Inseparability criterion for continuous variable systems. Phys. Rev. Lett. 2000, 84, 2722–2725. [Google Scholar] [CrossRef] [PubMed]
- Unruh, W.G. Notes on black-hole evapolation. Phys. Rev. D 1976, 14, 870–892. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davis, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Peres, A. Separability criterion for density matrices. Phys. Rev. Lett. 1996, 77, 1413–1415. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1–8. [Google Scholar] [CrossRef]
- Reznik, B. Entanglement from the vacuum. Found. Phys. 2003, 33, 167–176. [Google Scholar] [CrossRef]
- Reznik, B.; Retzker, A.; Silman, J. Violating Bell’s inequalities in vacuum. Phys. Rev. A 2005, 71, 042104. [Google Scholar] [CrossRef]
- Cliche, M.; Kempf, A. Relativistic quantum channel of communication through field quanta. Phys. Rev. A 2010, 81, 012330. [Google Scholar] [CrossRef]
- Steeg, G.V.; Menicucci, N.C. Entangling power of an expanding universe. Phys. Rev. D 2009, 79, 044027. [Google Scholar] [CrossRef]
- Martín-Martínez, E.; Menicucci, N.C. Cosmological quantum entanglement. Class. Quantum Grav. 2012, 29, 224003. [Google Scholar] [CrossRef]
- Sabín, C.; Peropadre, B.; del Rey, M.; Martín-Martínez, E. Extracting past-future vacuum correlations using circuit QED. Phys. Rev. Lett. 2012, 109, 033602. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, P. Separability criterion and inseparable mixed states with positive partial transposition. Phys. Lett. A 1997, 232, 333–339. [Google Scholar] [CrossRef]
- Vidal, G.; Werner, R.F. Computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar] [CrossRef]
- Marcovitch, S.; Retzker, A.; Plenio, M.B.; Reznik, B. Critical and noncritical long-range entanglement in Klein-Gordon fields. Phys. Rev. A 2009, 80, 012325. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Barceló, C.; Liberati, S.; Visser, M. Anologue gravity. Living Rev. Relativ. 2005, 8, 1–113. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Nambu, Y. Entanglement Structure in Expanding Universes. Entropy 2013, 15, 1847-1874. https://doi.org/10.3390/e15051847
Nambu Y. Entanglement Structure in Expanding Universes. Entropy. 2013; 15(5):1847-1874. https://doi.org/10.3390/e15051847
Chicago/Turabian StyleNambu, Yasusada. 2013. "Entanglement Structure in Expanding Universes" Entropy 15, no. 5: 1847-1874. https://doi.org/10.3390/e15051847
APA StyleNambu, Y. (2013). Entanglement Structure in Expanding Universes. Entropy, 15(5), 1847-1874. https://doi.org/10.3390/e15051847



