This section details MEM numerical calculation results. Particular attention is paid to the number of measured data points and noise because they are very important elements for experiments. In addition, as described above, the assumed default function, m, might affect the results and thus has to be considered. The computing time also largely depends on m and the users might need to choose the appropriate m before performing the MEM calculations. Therefore, m was also examined.
2.2.1. ARXPS Case
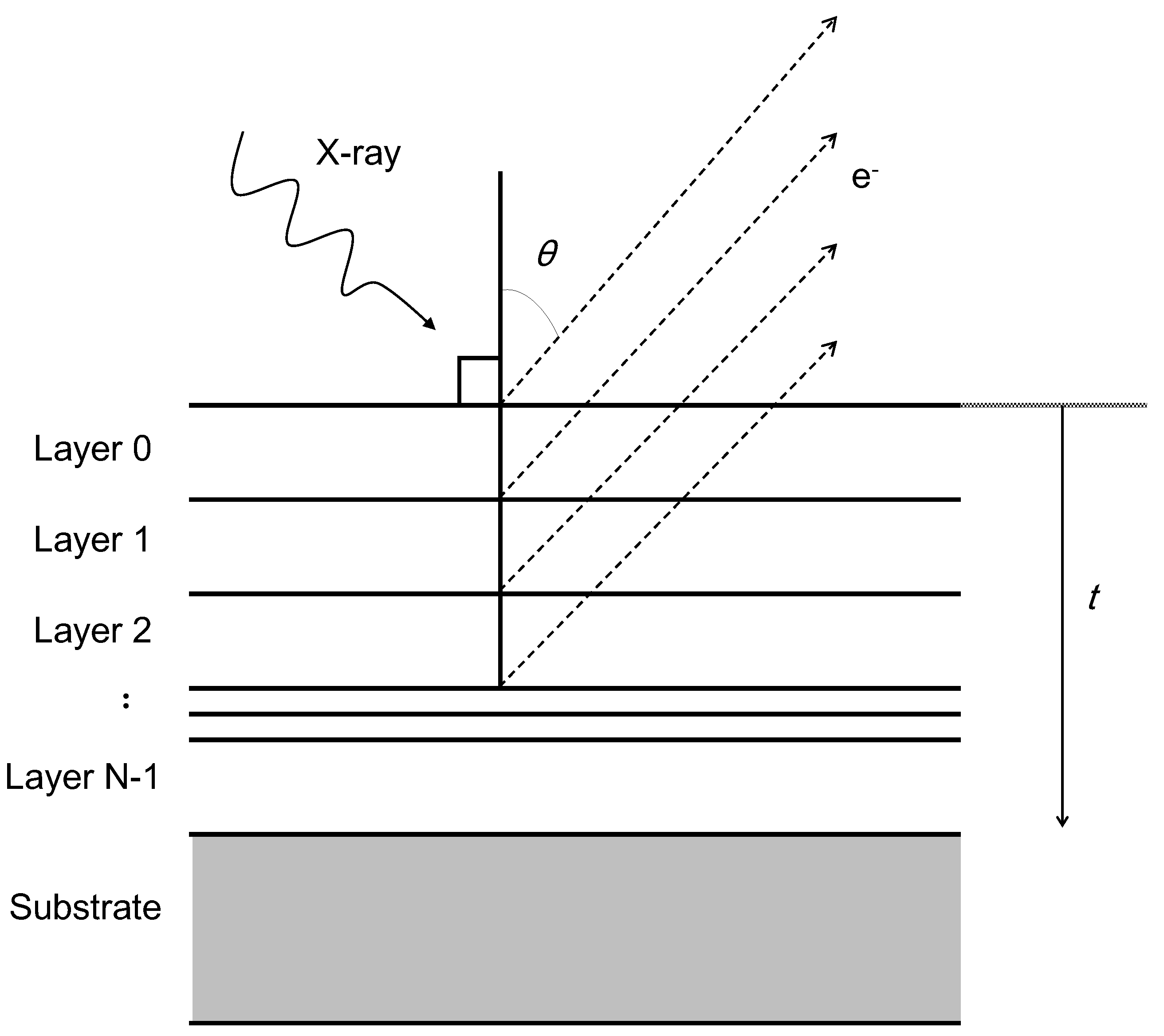
The assumed structure for ARXPS calculation is SiO
2 film on Si substrate, and C and N are distributed inside the film shown in
Figure 4a.
λ for C, N, Si and O are 3.37, 3.15, 3.80 and 2.80 Å [
27], and Al
Kα X-ray source was assumed. Generally, thin film thickness in semiconductor engineering is known in advance or can be easily determined by using spectroscopic ellipsometry, X-ray reflectivity, or XPS methods, and the Si concentration of the substrate is 100%. In this case, it is enough to perform MEM calculations under the assumption that the depth beyond the film thickness is uniform, Si = 100%, which reduces the computing time. Therefore, the composition in the region deeper than 5 nm from the surface was fixed to be Si 100%. Note that even when this assumption is not used, the obtained results are coincident within a few percent (figures not shown), though the computing time significantly varies.
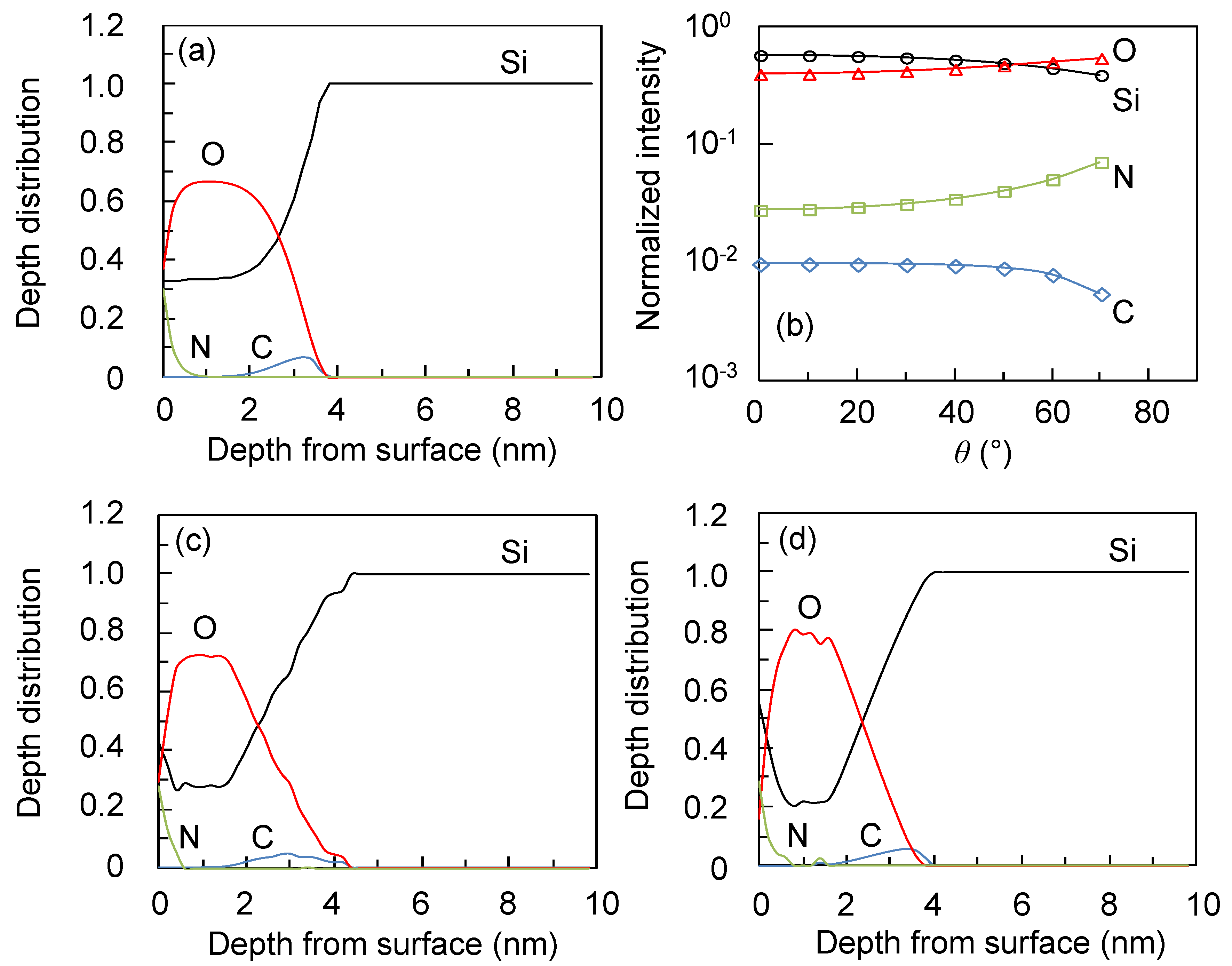
First,
mA(
t) (A = O, Si, N, and C) dependence was examined. The ARXPS signal intensities calculated as a function of
θ (0, 10, 20, ..., and 70°; total = 8 points) without noises are shown in
Figure 4b. The MEM calculations were performed for two sets of
mA(
t) where
mA(
t) is set to be atomic percent determined from the intensity ratio at
θ = 0°,
i.e., C, N, Si, and O = 1%, 3%, 57%, and 39%, and
mA(
t) for all elements is equal and uniform, that is, 0.25. The MEM calculations reproduce well the calculated ARXPS intensities and the assumed depth distributions as shown in
Figure 4(b)–(d). In this study little
mA(
t) dependence is present, but it might appear when using other calculation routines and/or the assumed depth distribution. It may also be observed if a significantly different
mA(
t) is used. To confirm this, I carried out the MEM calculations for different assumed atom distribution systems with various
mA(
t), but only negligible dependence was observed. From these results, I think that
mA(
t) is to a considerable extent arbitrary. On the other hand, the computing time significantly depends on
mA(
t), and
mA(
t) determined by the values at
θ = 0° led to the shortest computing time in
mA(
t) that was tried. I therefore used the values below. If structural data determined by using methods such as Rutherford backscattering is available, one can use it as
mA(
t),
i.e., prior knowledge, leading to more precise and faster determination.
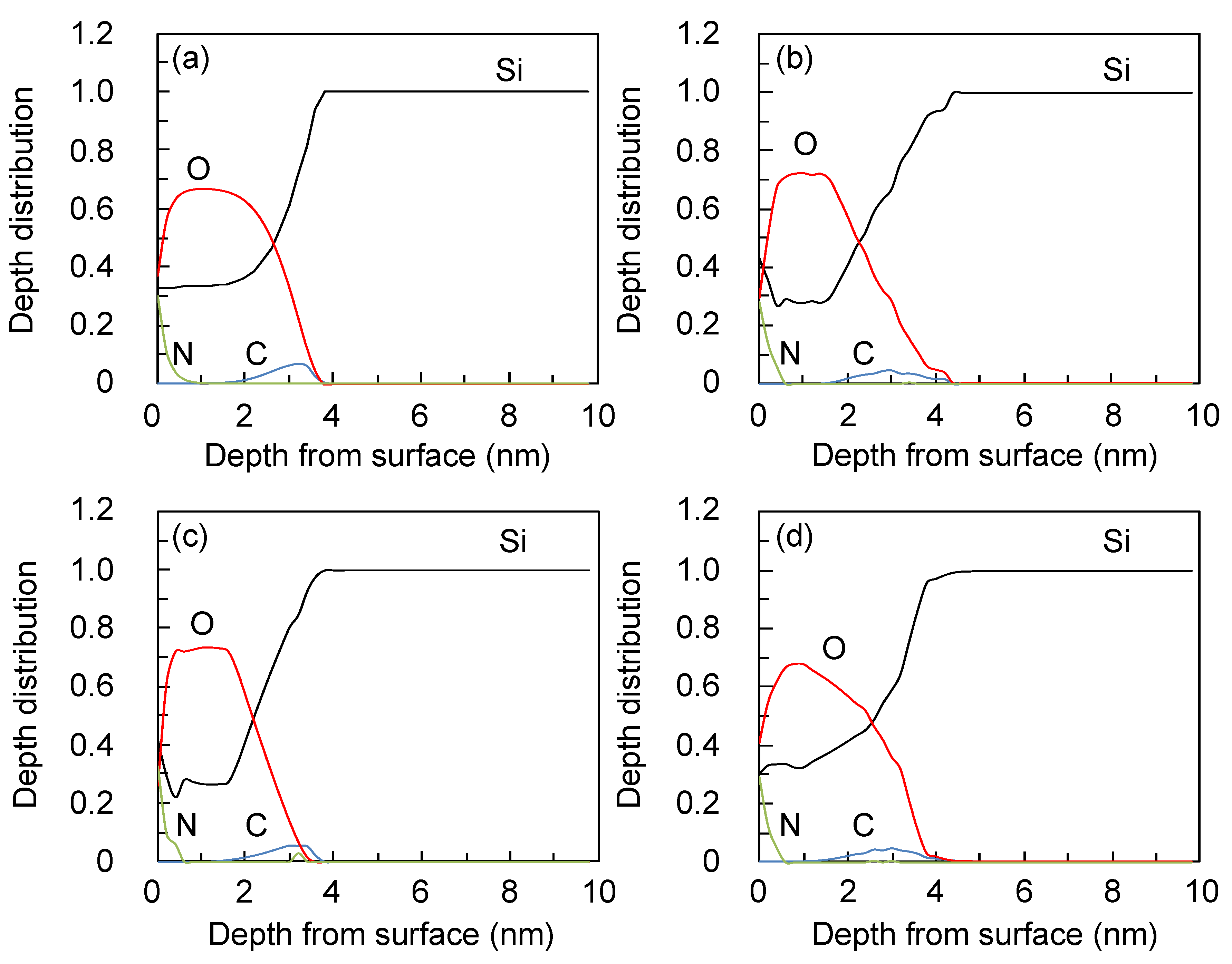
Figure 4.
The mA(t) dependence of the MEM calculation results for ARXPS (θ = 0, 10, 20, …, 70° and the no noise case). (a): Assumed depth distribution of C, N, Si, and O atoms for ARXPS-MEM calculations. (b): Normalized ARXPS intensity as a function of θ calculated from Equations (11), (12), and the depth distribution shown in (a) (symbols). The lines are the MEM calculation results with mA(t) determined by θ = 0° values. (c) and (d): Reconstructed depth distribution from ARXPS normalized intensity (symbols in (b)) using MEM with mA(t) determined respectively by θ = 0° values (c) and mA(t) = 0.25 (d) for all atoms.
Figure 4.
The mA(t) dependence of the MEM calculation results for ARXPS (θ = 0, 10, 20, …, 70° and the no noise case). (a): Assumed depth distribution of C, N, Si, and O atoms for ARXPS-MEM calculations. (b): Normalized ARXPS intensity as a function of θ calculated from Equations (11), (12), and the depth distribution shown in (a) (symbols). The lines are the MEM calculation results with mA(t) determined by θ = 0° values. (c) and (d): Reconstructed depth distribution from ARXPS normalized intensity (symbols in (b)) using MEM with mA(t) determined respectively by θ = 0° values (c) and mA(t) = 0.25 (d) for all atoms.
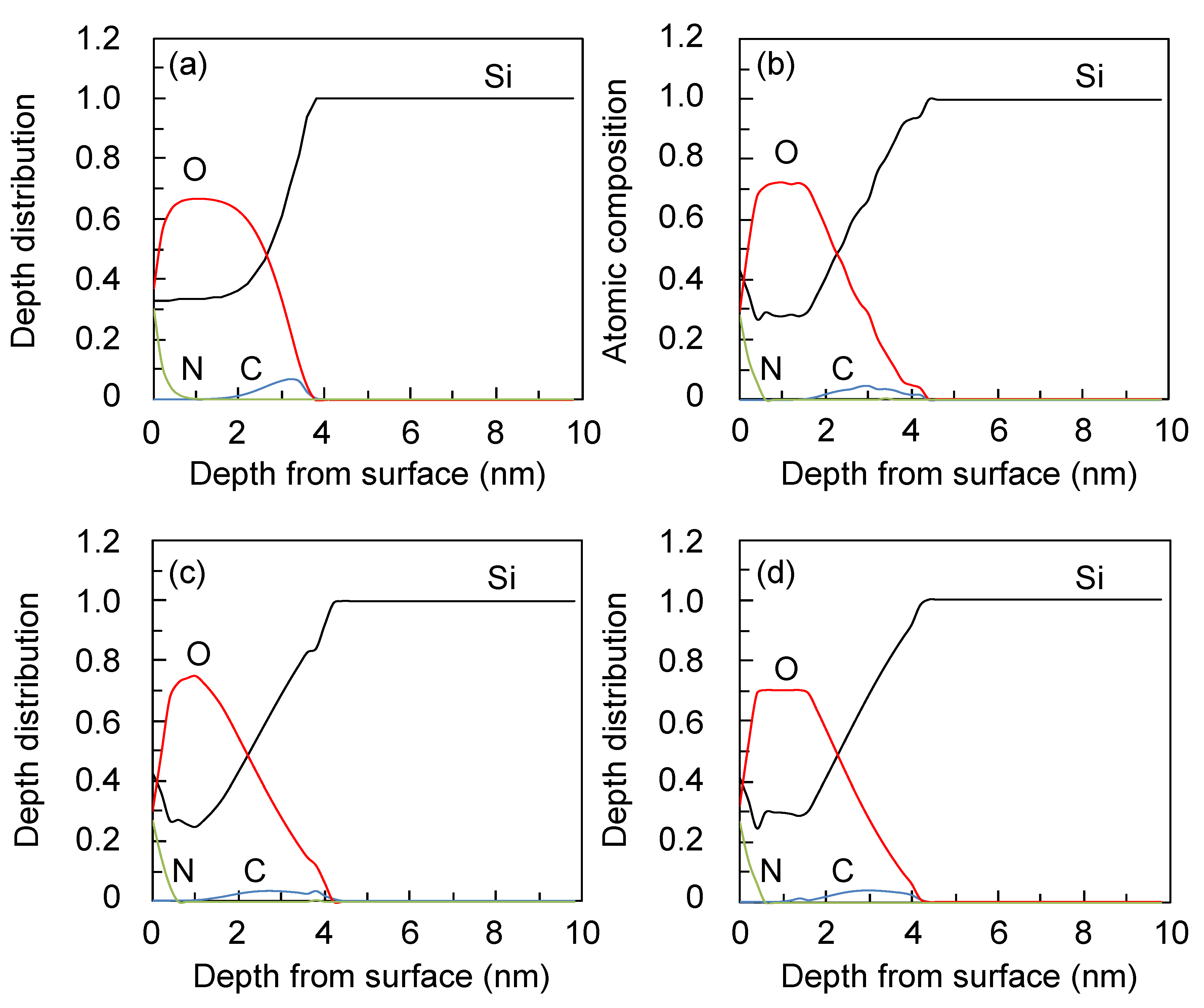
Figure 5 shows the effect of the number of data points,
i.e., 5, 8, or 15 points (
θ = 0, 17, 34, 51, 68° for 5 points,
θ = 0, 10, 20, …, 70° for 8 points, and
θ = 0, 5, 10, …, 70° for 15 points). Intuitively, it would appear that more data points gives more precise results,
i.e., MEM can reproduce the assumed distribution better. However, the dependence on the number of data points is insignificant. Even with only five data points, the MEM results reproduce the assumed distribution relatively well. I think that measuring the data points at eight angles is sufficient in general cases. Livesey
et al. pointed out that the data measured at angles above 70° has negligible impact on the MEM calculations [
16]. They also pointed out that the absolute ARXPS signal intensity becomes considerably weaker at such angles. Therefore, in many cases it is sufficient to measure the eight data points at angles under 70°. Next, the MEM tolerance to noise was examined. The MEM calculation results with ARXPS signals including artificial Gaussian noise (0%, 5%, 10%) are shown in
Figure 6. It should be noted that even in the 10% case, the overall shapes of the assumed distribution are reproduced though they become somewhat distorted. This proves the validity of MEM and is very helpful for practical use.
Figure 5.
Dependence of the MEM calculation results on the number of data points for ARXPS (mA(t) determined by θ = 0° values, and the no noise case). (a): Assumed depth distribution of C, N, Si, and O atoms for ARXPS-MEM calculations. (b)–(d): Reconstructed depth distribution from ARXPS normalized intensity using MEM respectively for θ = 0, 10, 20, …, 70° (8 points), θ = 0, 17, 34, 51, 68° (5 points), and θ = 0, 5, 10, …, 70° (15 points) cases.
Figure 5.
Dependence of the MEM calculation results on the number of data points for ARXPS (mA(t) determined by θ = 0° values, and the no noise case). (a): Assumed depth distribution of C, N, Si, and O atoms for ARXPS-MEM calculations. (b)–(d): Reconstructed depth distribution from ARXPS normalized intensity using MEM respectively for θ = 0, 10, 20, …, 70° (8 points), θ = 0, 17, 34, 51, 68° (5 points), and θ = 0, 5, 10, …, 70° (15 points) cases.
Figure 6.
Noise dependence of the MEM calculation results for ARXPS (θ = 0, 10, 20, …, 70° and mA(t) determined by θ = 0° values case). (a): Assumed depth distribution of C, N, Si, and O atoms for ARXPS-MEM calculations. (b)–(d): Reconstructed depth distribution from ARXPS normalized intensity respectively using MEM for artificially introduced Gaussian noise = 0%, 5%, and 10% cases.
Figure 6.
Noise dependence of the MEM calculation results for ARXPS (θ = 0, 10, 20, …, 70° and mA(t) determined by θ = 0° values case). (a): Assumed depth distribution of C, N, Si, and O atoms for ARXPS-MEM calculations. (b)–(d): Reconstructed depth distribution from ARXPS normalized intensity respectively using MEM for artificially introduced Gaussian noise = 0%, 5%, and 10% cases.
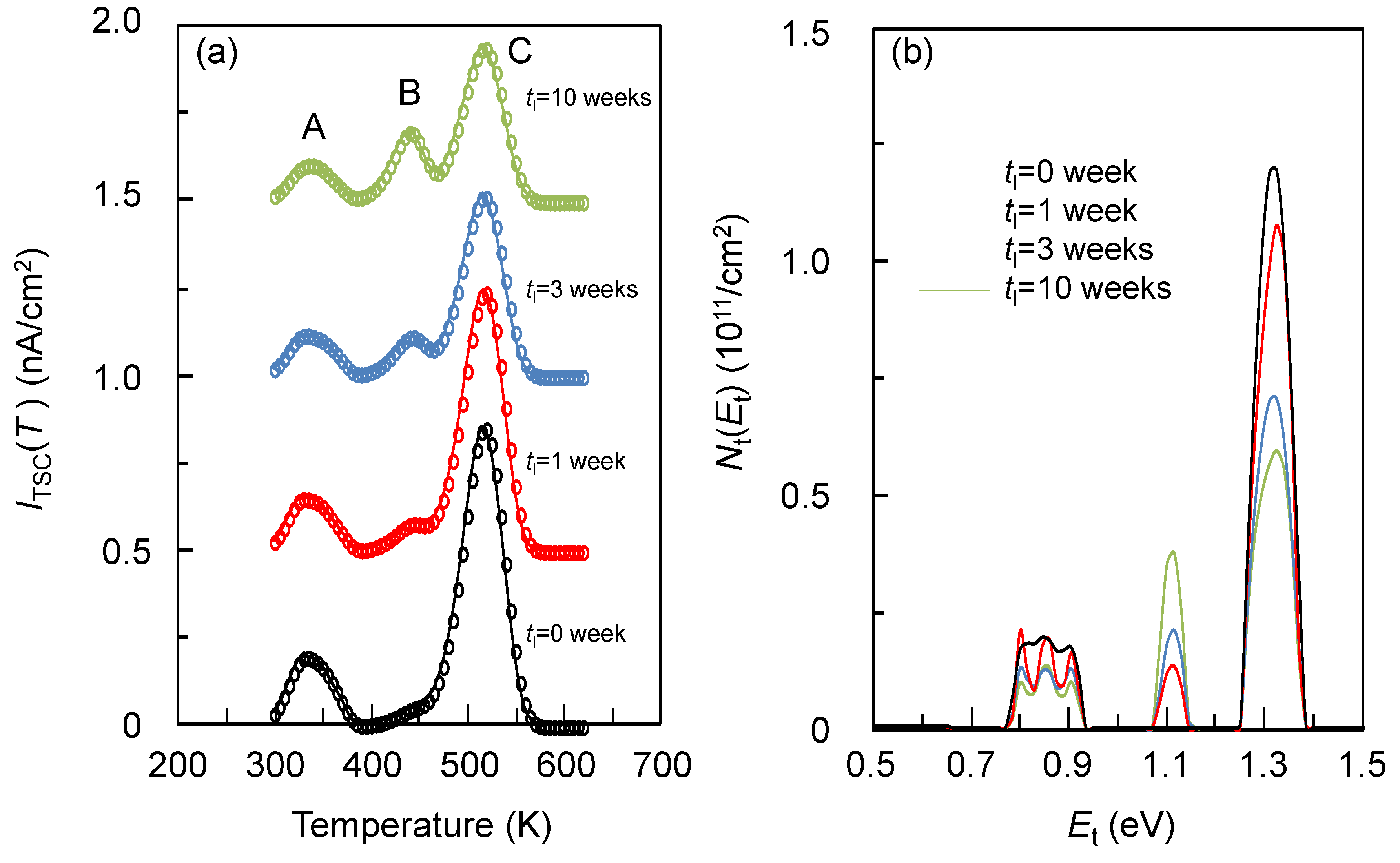
2.2.2. TSC Case
For this case
β = 20 K/min and
ν = 10
11 /s were assumed [
22,
23,
24]. The assumed
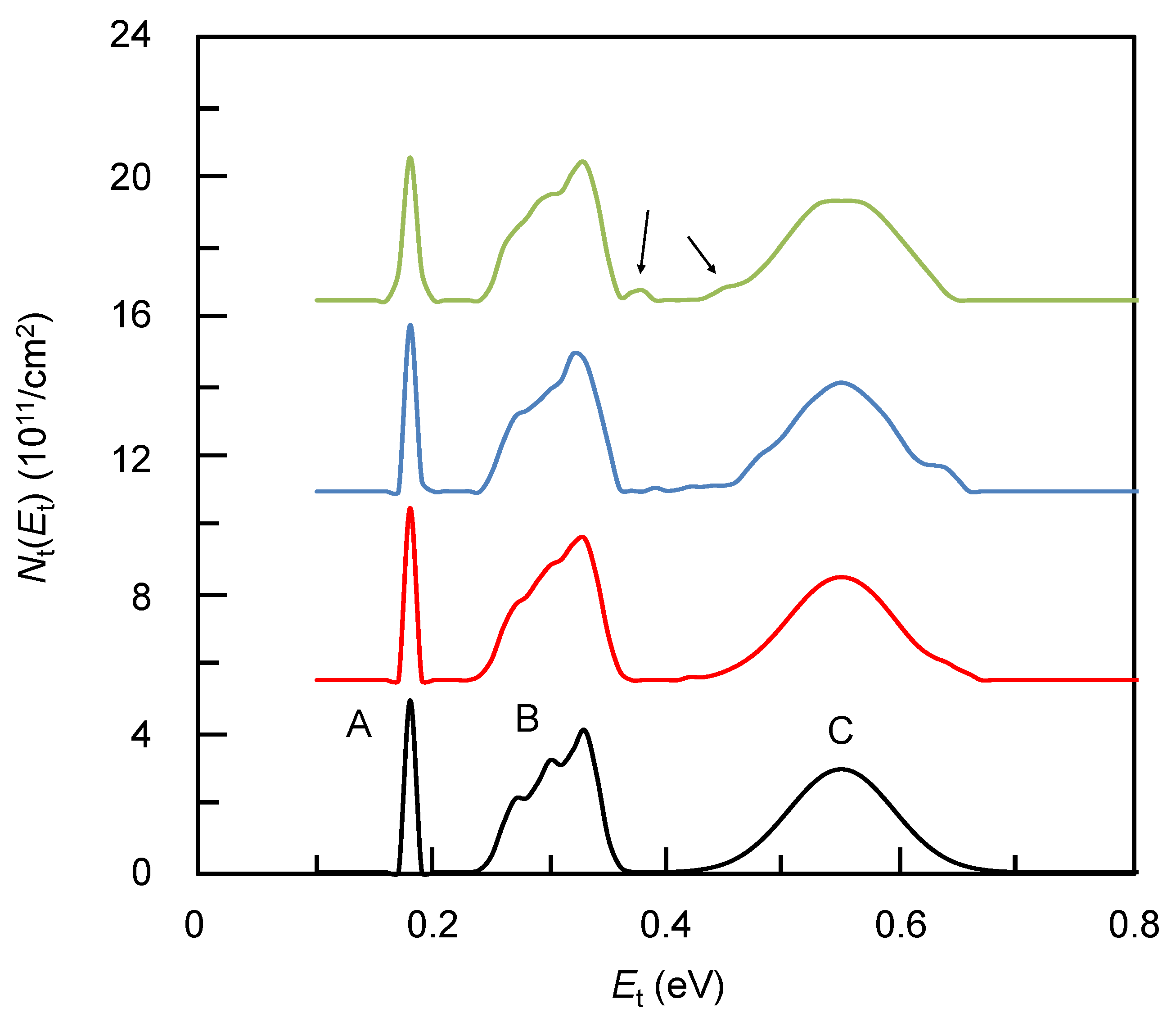
Nt(
Et) distribution is shown in
Figure 7a (peaks A, B, and C). The corresponding TSC spectra calculated with Equation (16) is plotted in
Figure 7b. The MEM calculation results are plotted in
Figure 7a,b. Constant
m(
Et) was used in this calculation. The MEM results well reproduce the assumed
Nt(
Et) distribution, which demonstrates that MEM can be applied to arbitrary
Et distribution. The MEM calculations were also performed with exponential or Gaussian
m(
Et) and almost the same results were obtained [
24]. However, the computing time significantly depended on
m(
Et). It becomes shorter when
m(
Et) is closer to the assumed
Nt(
Et). Thus, for practical use, one should chose
m(
Et) carefully. Fortunately, the appropriate
m(
Et) can be obtained from the equations [
28]
and
These equations give
Nt(
Et) shown in
Figure 7a. They cannot reproduce all the peaks because they directly convert
to
Nt(
Et) and the obtained
Nt(
Et) trails
. The broad peak C is reproduced very well but the A and B peaks are not. From this, one can conclude that although Equations (41) and (42) are easy to use, they reproduce only widely distributed
. However, this can be used as
m(
Et) to reduce the computing time.
Figure 7.
Assumed Nt(Et), and MEM results. (a): From bottom to top, assumed Nt(Et), MEM reconstructed results, and Nt(Et) calculated from Equations (41), (42) and . (b): calculated from assumed Nt(Et) (lower) and MEM result (upper). MEM was performed without noise and with constant m(Et).
Figure 7.
Assumed Nt(Et), and MEM results. (a): From bottom to top, assumed Nt(Et), MEM reconstructed results, and Nt(Et) calculated from Equations (41), (42) and . (b): calculated from assumed Nt(Et) (lower) and MEM result (upper). MEM was performed without noise and with constant m(Et).
The number of data points in TSC spectra is usually enough, typically more than 1000, and one does not need to be concerned about this point for MEM calculations.
Regarding noise, the MEM calculation is slightly affected by noises in
ITSC(
T). The MEM calculation results with artificial Gaussian noises are shown in
Figure 8. For larger noise, the peaks become gradually distorted. Moreover, a ghost shoulder and peak (indicated by arrows) appear. However, their effect is very slight. Note that this is an extreme case and that the usual
ITSC(
T) is not so noisy (see [
22,
23]) except for the region where
ITSC(
T) is extremely low (in the order of 10
−15 A). Therefore, in practical use, it is thought that the noise has much less impact on the MEM calculation.
Figure 8.
Noise dependence of the MEM calculation results for TSC (constant m(Et) case). From bottom to top, assumed Nt(Et), MEM results for artificially introduced Gaussian noise = 0%, 5%, and 10% cases. The arrows indicate a ghost shoulder and peak.
Figure 8.
Noise dependence of the MEM calculation results for TSC (constant m(Et) case). From bottom to top, assumed Nt(Et), MEM results for artificially introduced Gaussian noise = 0%, 5%, and 10% cases. The arrows indicate a ghost shoulder and peak.
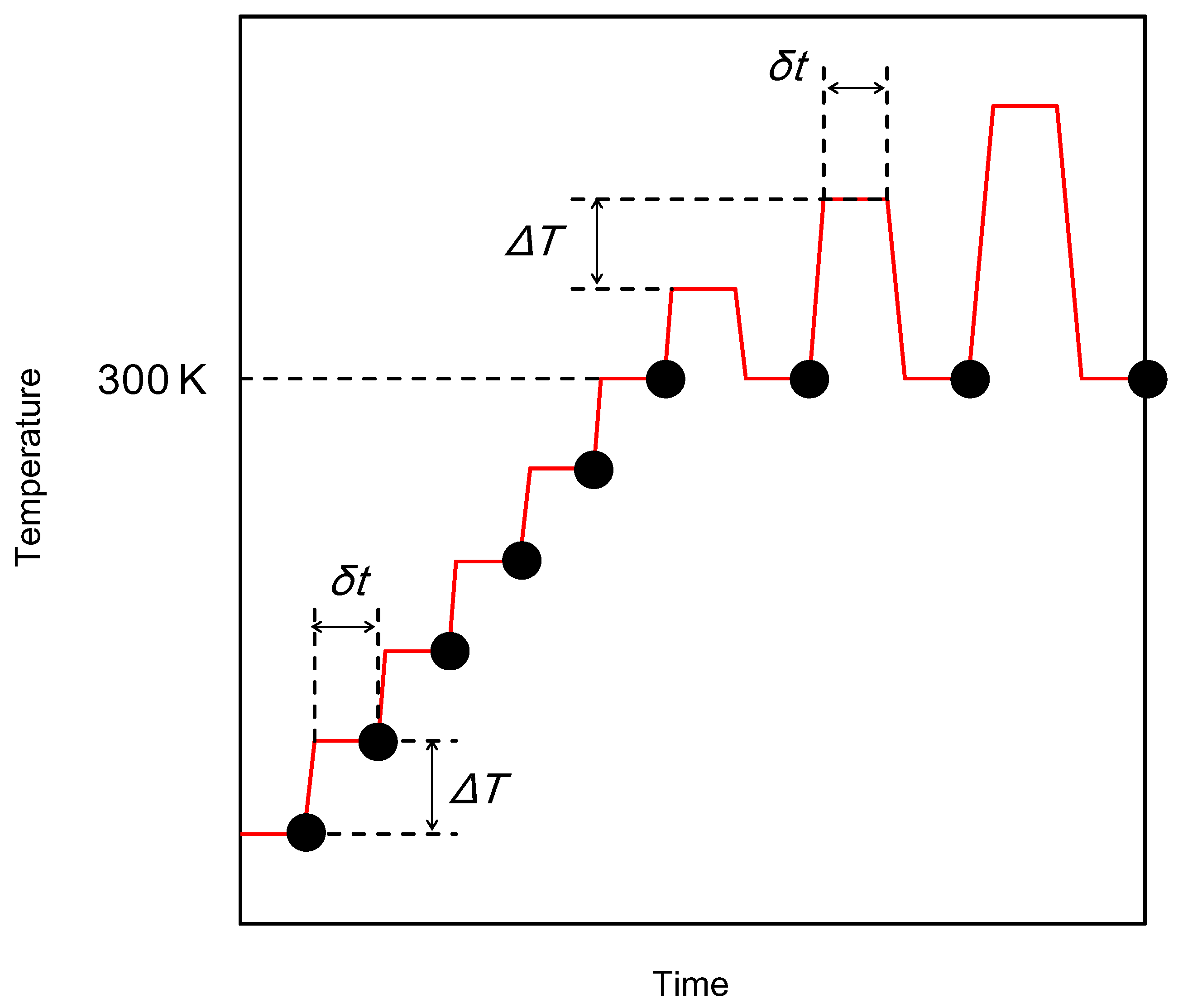
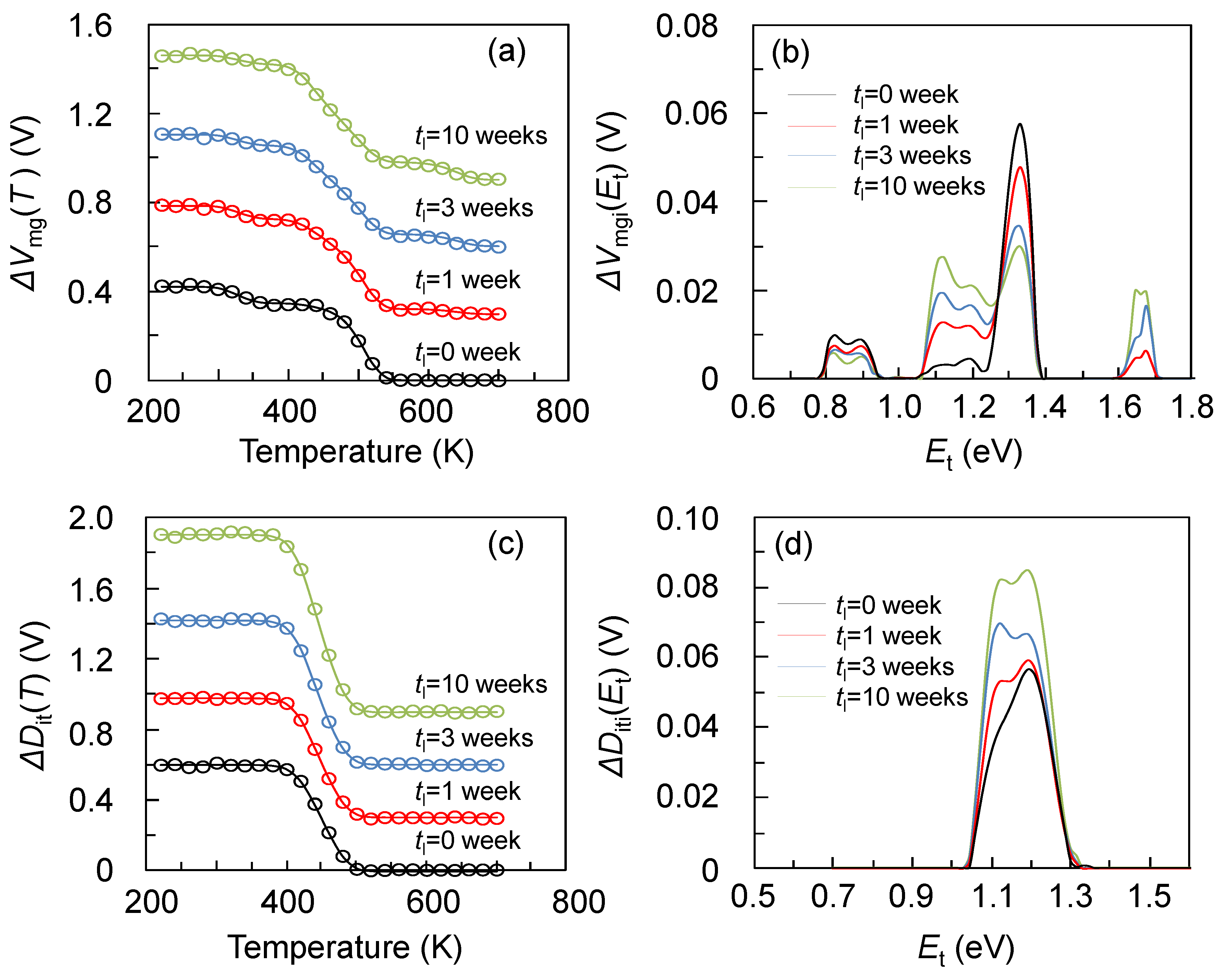
2.2.3. IA Case
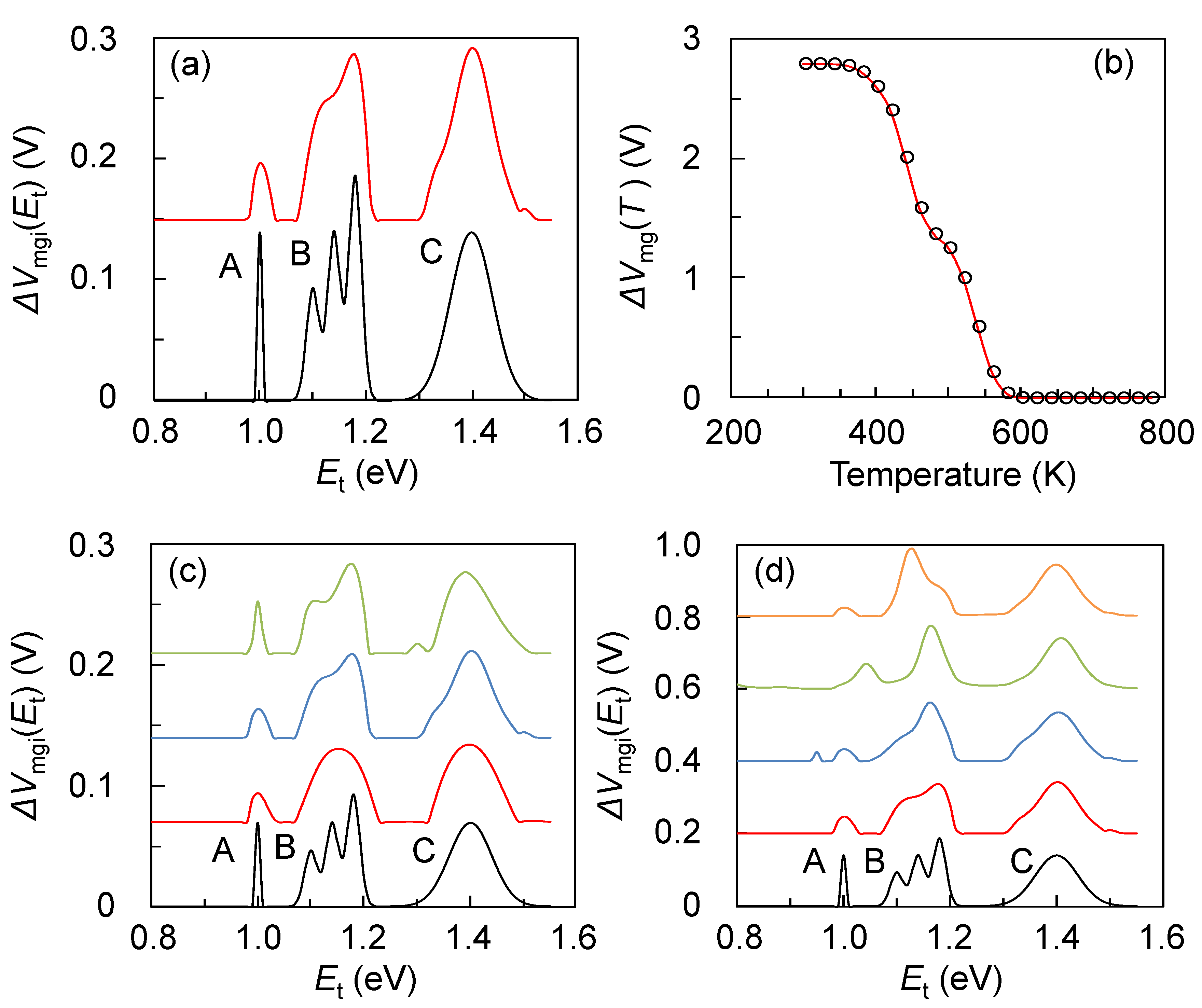
For this case, the Δ
Vmgi(
Et) distribution shown in
Figure 9a and
ν = 10
11 /s were assumed [
22,
23,
24]. From this distribution, the corresponding Δ
Vmg(
T) values were calculated as shown in
Figure 9b. Here the calculations were performed with Δ
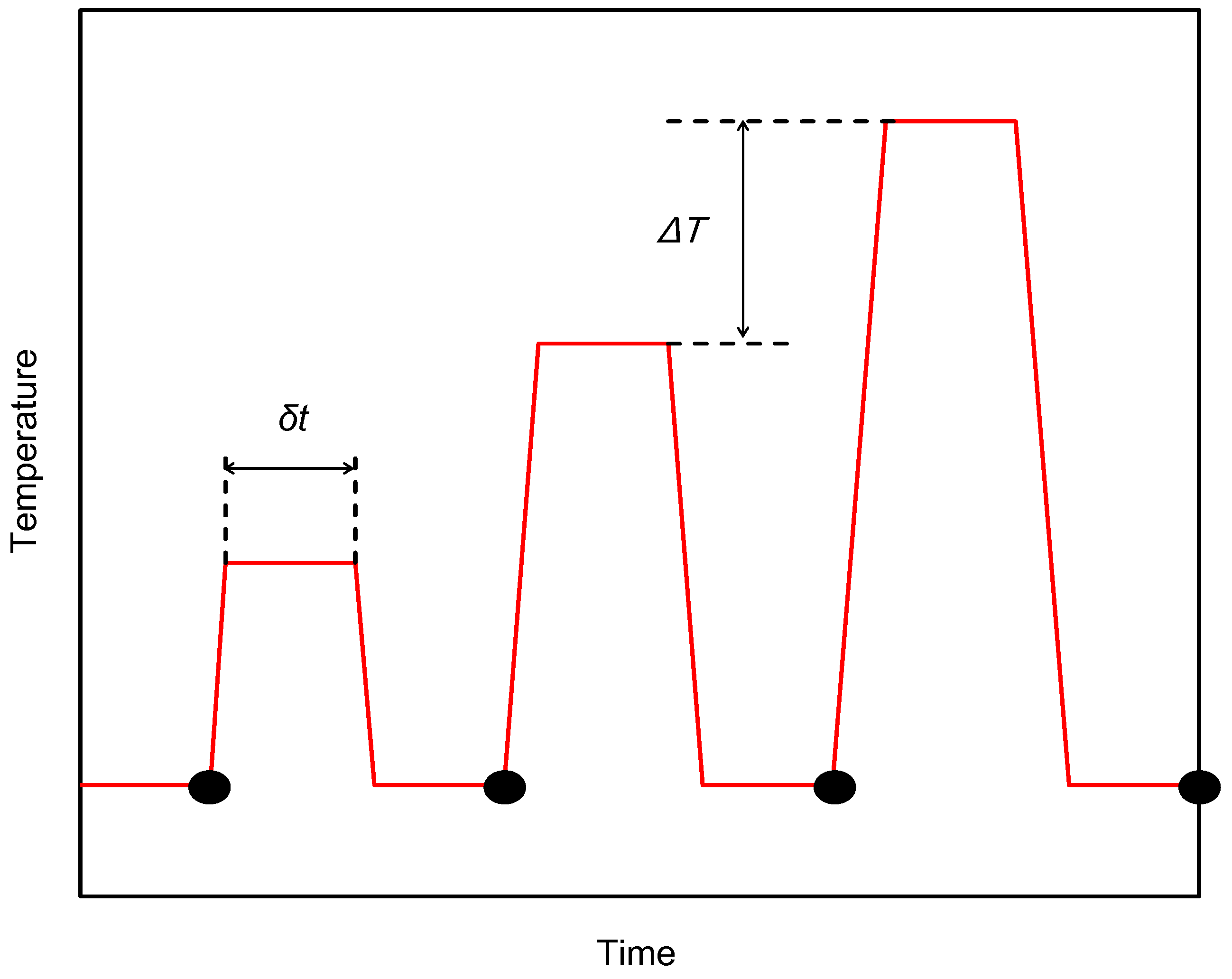
T = 20 K and
δt = 600 s. The MEM calculation results obtained with constant
m(
Ea) are shown in
Figure 9a,b. Exponential or Gaussian
m(
Ea) were examined with respect to
m(
Ea) dependence. However, the obtained results remain almost unchanged, which means that the MEM calculations are hardly affected by the assumed
m(
Ea). Unfortunately, unlike the TSC case, no appropriate
m(
Ea) is obtainable prior to the MEM calculations and it is difficult to even predict the Δ
Vmgi(
Ea) curves from experimental data, Δ
Vmg(
T). Therefore, it was considered that there was no choice but to use the constant
m(
Ea) although the computing time might be longer than the case where the appropriate
m(
Ea) (closer to the Δ
Vmgi(
Et)) is used.
With respect to the obtained Δ
Vmgi(
Et) shown in
Figure 9a, the overall shape is reproduced but there is a large deviation between the assumed distribution and the MEM results. The intensity ratio between peaks is different and the peaks are smoothed, especially peaks A and B. This is because Δ
T is somewhat large and the fine structures are not reflected in Δ
Vmg(
T) sufficiently. The Δ
T value is limited by the temperature control precision of the annealing furnace. As a result, the number of data points is limited and the information in Δ
Vmg(
T) is averaged in comparison with the above TSC case, which degrades the precision of the MEM result. Actually, when more (less) data points,
i.e., Δ
T is 10 K (30 K), are assumed, the reproducibility is slightly improved (degraded) as shown in
Figure 9(c). Therefore, the number of data points has to be taken into consideration when MEM is used. It should be noted that although its accuracy is lower than that of TSC, IA has three distinct advantages,
i.e., it can be applied to devices, can observe very deep traps while TSC can detect only traps with
Et up to ≈ 1.5 eV, and can determine
Diti(
Ea).
Figure 9.
The dependence of the MEM calculation results on the number of points (i.e., ΔT) and noise for the IA (constant m(Ea) case). (a): Assumed ΔVmgi(Et) (lower) and the MEM results with ΔT = 20 K and without noise (upper). (b): Calculated ΔVmg(T) from Equation (26) and (a) with ΔT = 20 K and without noise (symbol). The line corresponds to the MEM result. (c): From bottom to top, assumed ΔVmgi(Et), the MEM results without noise and with ΔT = 30, 20, and 10 K, respectively. (d): From bottom to top, assumed ΔVmgi(Et), the MEM results with ΔT = 20 K and with artificially introduced Gaussian noise = 0%, 5%, 8%, and 10%, respectively.
Figure 9.
The dependence of the MEM calculation results on the number of points (i.e., ΔT) and noise for the IA (constant m(Ea) case). (a): Assumed ΔVmgi(Et) (lower) and the MEM results with ΔT = 20 K and without noise (upper). (b): Calculated ΔVmg(T) from Equation (26) and (a) with ΔT = 20 K and without noise (symbol). The line corresponds to the MEM result. (c): From bottom to top, assumed ΔVmgi(Et), the MEM results without noise and with ΔT = 30, 20, and 10 K, respectively. (d): From bottom to top, assumed ΔVmgi(Et), the MEM results with ΔT = 20 K and with artificially introduced Gaussian noise = 0%, 5%, 8%, and 10%, respectively.
Regarding noise, I examined the noise dependent MEM calculations and the results are shown in
Figure 9d. The noise significantly affects the obtained spectra, especially on peak A. This peak is very sharp and its recovery occurs in a very narrow temperature range,
i.e., Δ
Vmg(
T) drops very sharply with temperature. As a result, the drop is included in only a few data points and it is susceptible to noise. This even shifts the peak A position. Similarly, peak B is considerably distorted. Meanwhile, the broad peak C is less susceptible to noise as expected from the above argument. This means that one should obtain high signal-to-noise ratio data for the MEM calculations.
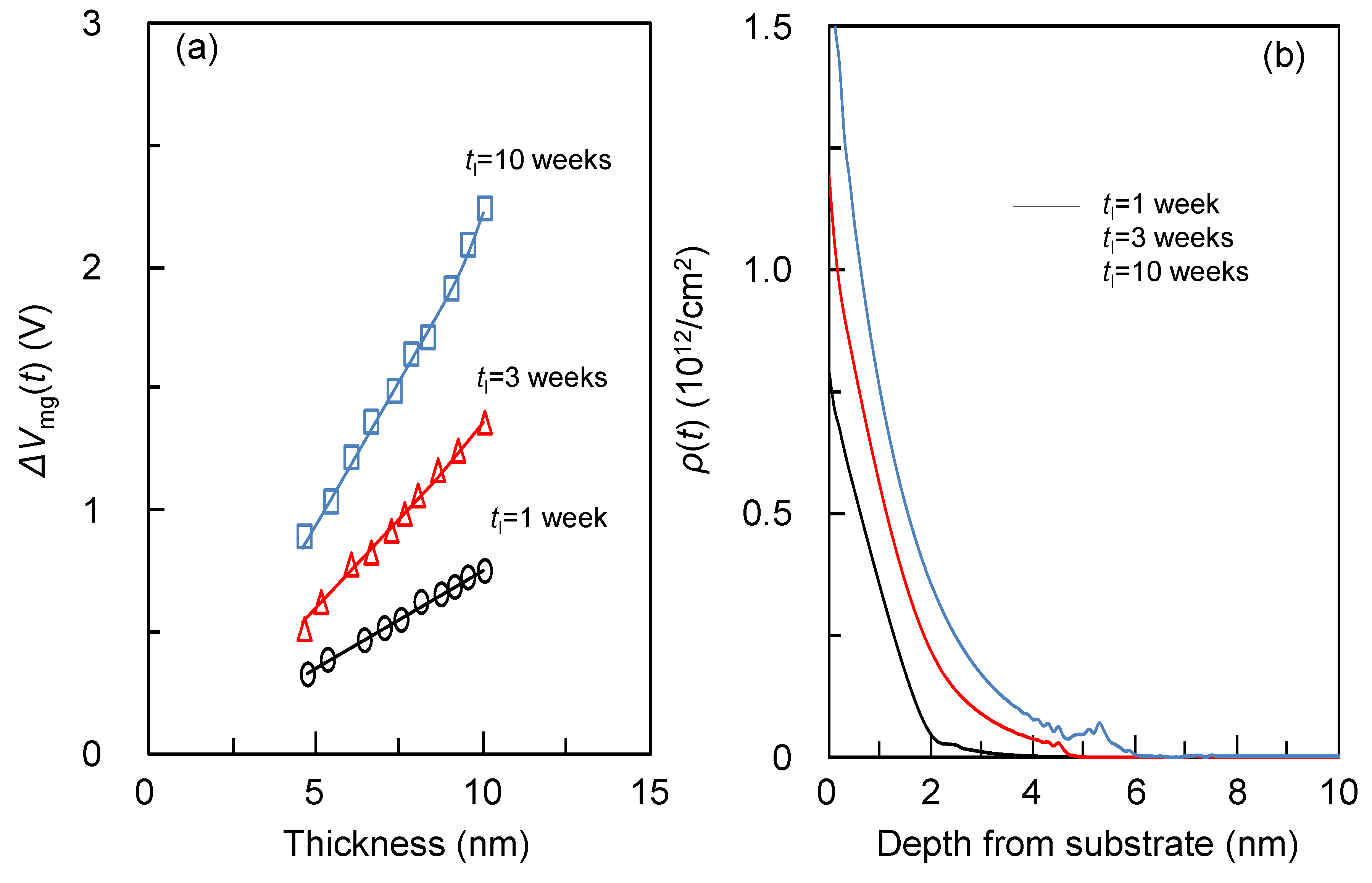
2.2.4. TDCV Case
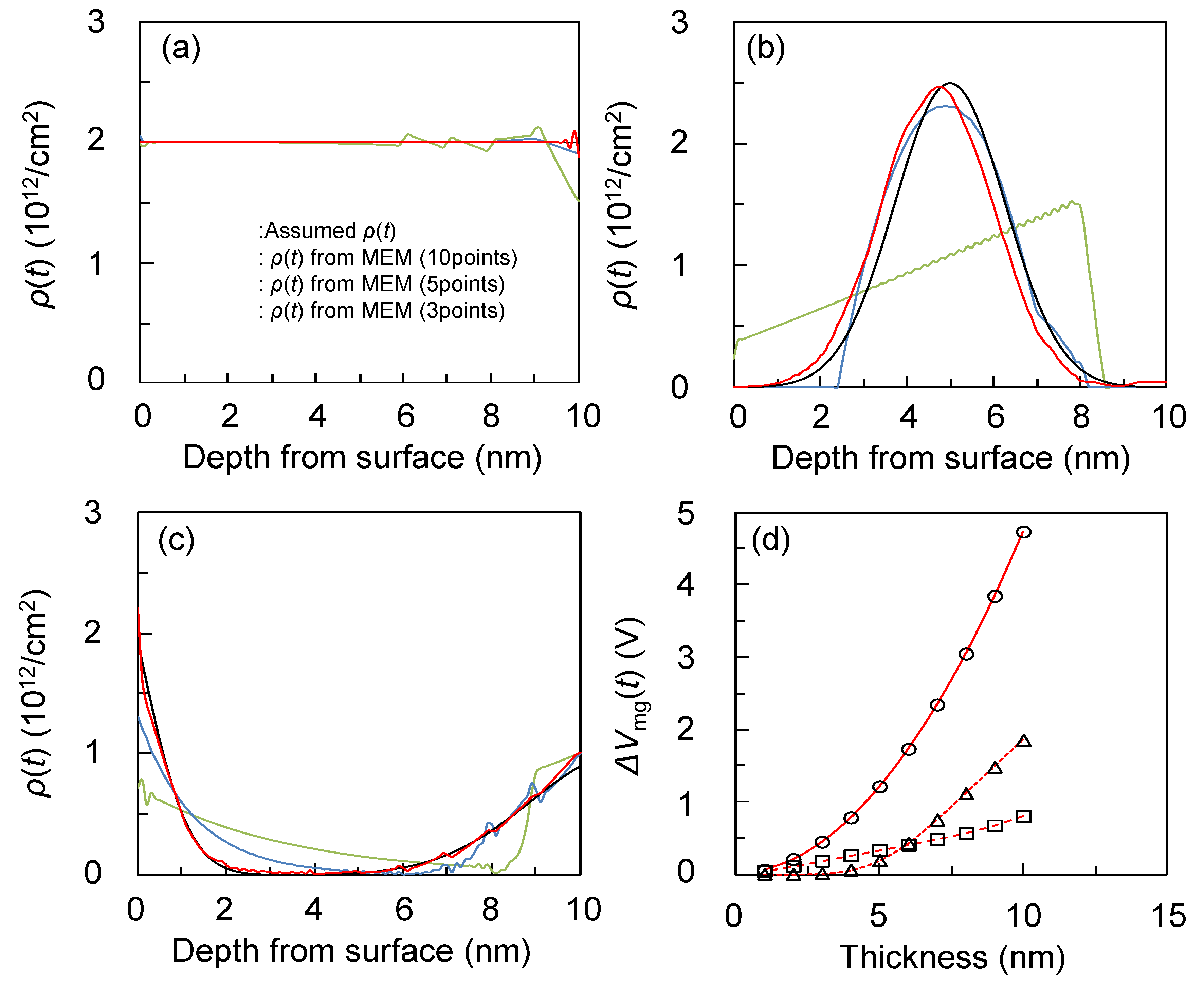
I assumed a SiO
2(10 nm)/Si system with the three fixed charge distributions,
ρ(
t), shown in
Figure 10a–c. The Δ
Vmg(
t) calculated from each
ρ(
t) and the corresponding MEM results are plotted in
Figure 10(a)–(d). The
m(
kn) value is impossible to deduce before MEM calculation. If
ρ(
t) is proportional to thickness, the distribution is localized at the interface. On the other hand, the distribution is uniform inside a film when
ρ(
t)
2 is proportional to the thickness. From these, one can deduce
m(
kn); however, this estimation is insufficient in many cases. Therefore, a constant
m(
kn) value was assumed although the computing time might be longer. Since this assumption seems to work well (see the results for the 10 point case), one can conclude that the constant
m(
kn) can be used when deducing its value is difficult.
Figure 10.
Assumed fixed charge distribution and the number of points dependence of the MEM calculation results for TDCV (constant m(kn) and the no noise case). (a)–(c): The black lines are the assumed rho(t). The colored lines are the MEM calculated results with the number of points = 10, 5, and 3. (d): The circles, triangles, and squares are calculated ΔVmg(t) for the assumed distribution rho(t) in (a)–(c), respectively. The lines are the corresponding MEM calculation results.
Figure 10.
Assumed fixed charge distribution and the number of points dependence of the MEM calculation results for TDCV (constant m(kn) and the no noise case). (a)–(c): The black lines are the assumed rho(t). The colored lines are the MEM calculated results with the number of points = 10, 5, and 3. (d): The circles, triangles, and squares are calculated ΔVmg(t) for the assumed distribution rho(t) in (a)–(c), respectively. The lines are the corresponding MEM calculation results.
In addition, the number of the corresponding Δ
Vmg(
t) data points are set to be 10, 5, and 3 to confirm the dependence of the MEM calculation accuracy on the number of data points. The obtained MEM results are plotted in
Figure 10a–c. It would intuitively seem that fewer data points would result in less accurate results, as expected from the IA case. This was found to be the case; the MEM results significantly depend on the number of data points. When it is 10, MEM reproduces the assumed distributions well, while a slight (significant) deviation is seen for the 5 (3) point case. Therefore, one can conclude that at when MEM is applied to TDCV, at least 10 points are required to obtain satisfactory results.
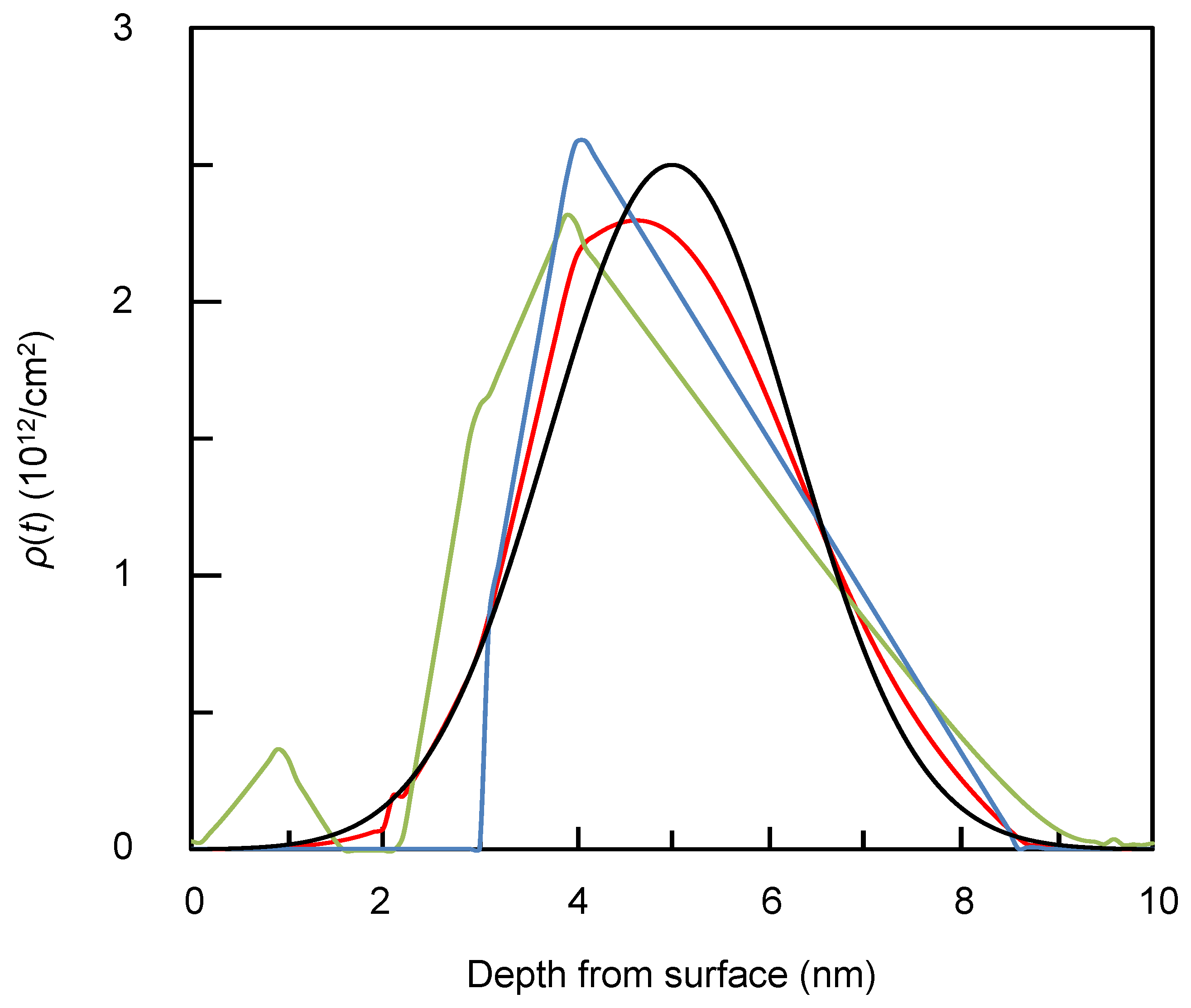
Noise was found to have a considerable impact on the MEM calculation results (
Figure 11). In particular, a large deviation from the assumed
ρ(
t) appears when the noise exceeds 5%. The peak becomes distorted and even a ghost shoulder and peak are present in the 10% case. However, one does not need to take noise into consideration since in general cases the CV measurement accuracy is less than 5%.
In concluding this section, I can state that MEM can analyze the data accurately without any prior knowledge regarding the results. In the next section, I will explain an example of application results to assist readers’ understanding of the validity of MEM.
Figure 11.
Noise dependence of the MEM calculation results for TDCV (constant m(kn) and the 10 point case). The black line is the assumed ρ(t). The red, blue, and green lines correspond to the artificially introduced Gaussian noise = 3%, 5%, and 10% cases, respectively.
Figure 11.
Noise dependence of the MEM calculation results for TDCV (constant m(kn) and the 10 point case). The black line is the assumed ρ(t). The red, blue, and green lines correspond to the artificially introduced Gaussian noise = 3%, 5%, and 10% cases, respectively.