Genetic Algorithm-Based Identification of Fractional-Order Systems
Abstract
:1. Introduction
2. Fractional-Order System Model
2.1. The Definition of Fractional Calculus
2.2. Fractional-Order Systems
2.3. Common Parameter Identification Methods
3. Fractional-Order System Identification Based on GA
3.1. Fractional-Order Benchmark Model
3.2. Fitness Function of Optimization
3.3. Evaluation Index of Fitness Function
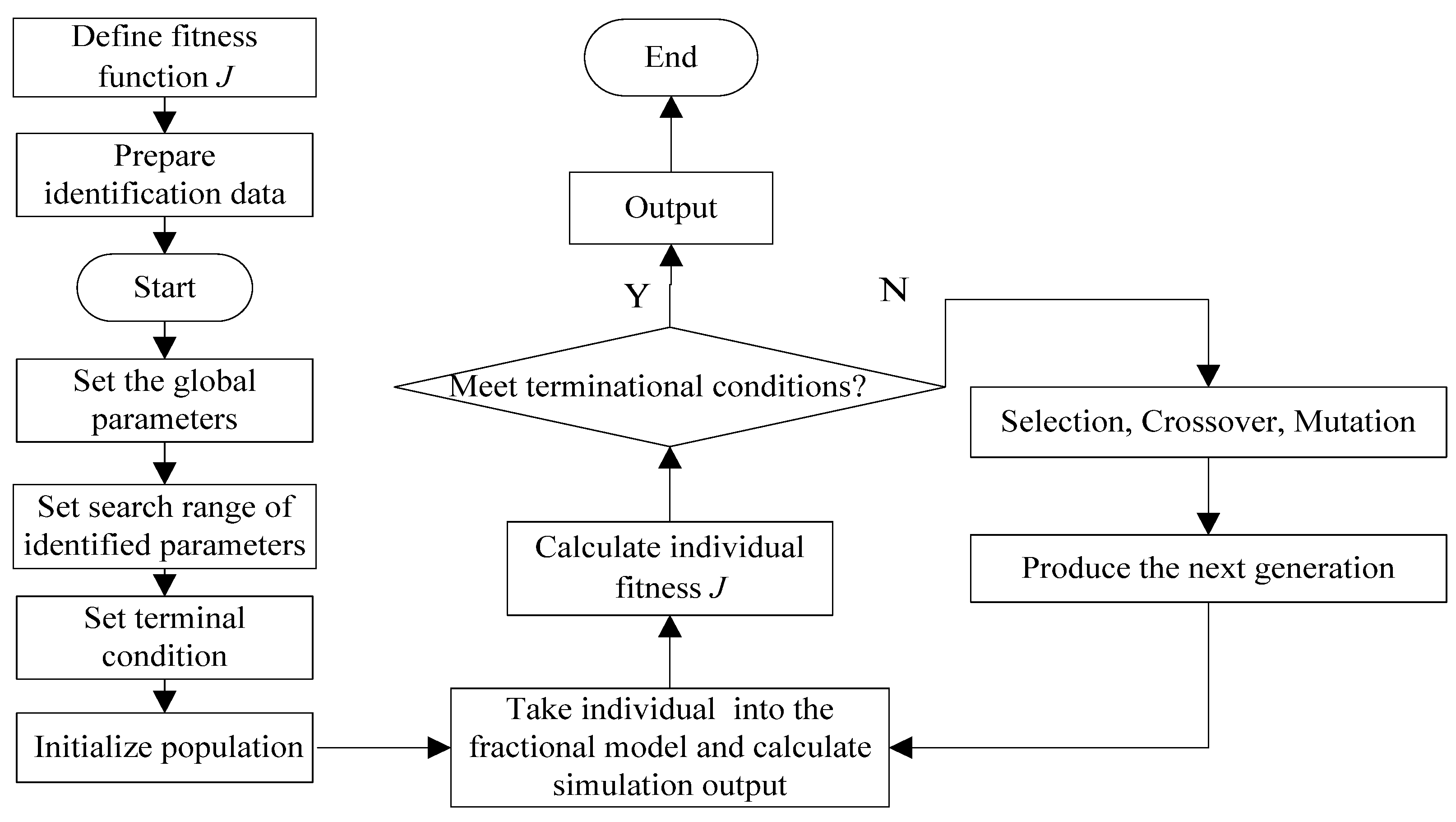
3.4. The Identification Process Based on Genetic Algorithm
4. Numerical Simulation and Results
4.1. Excitation Signals
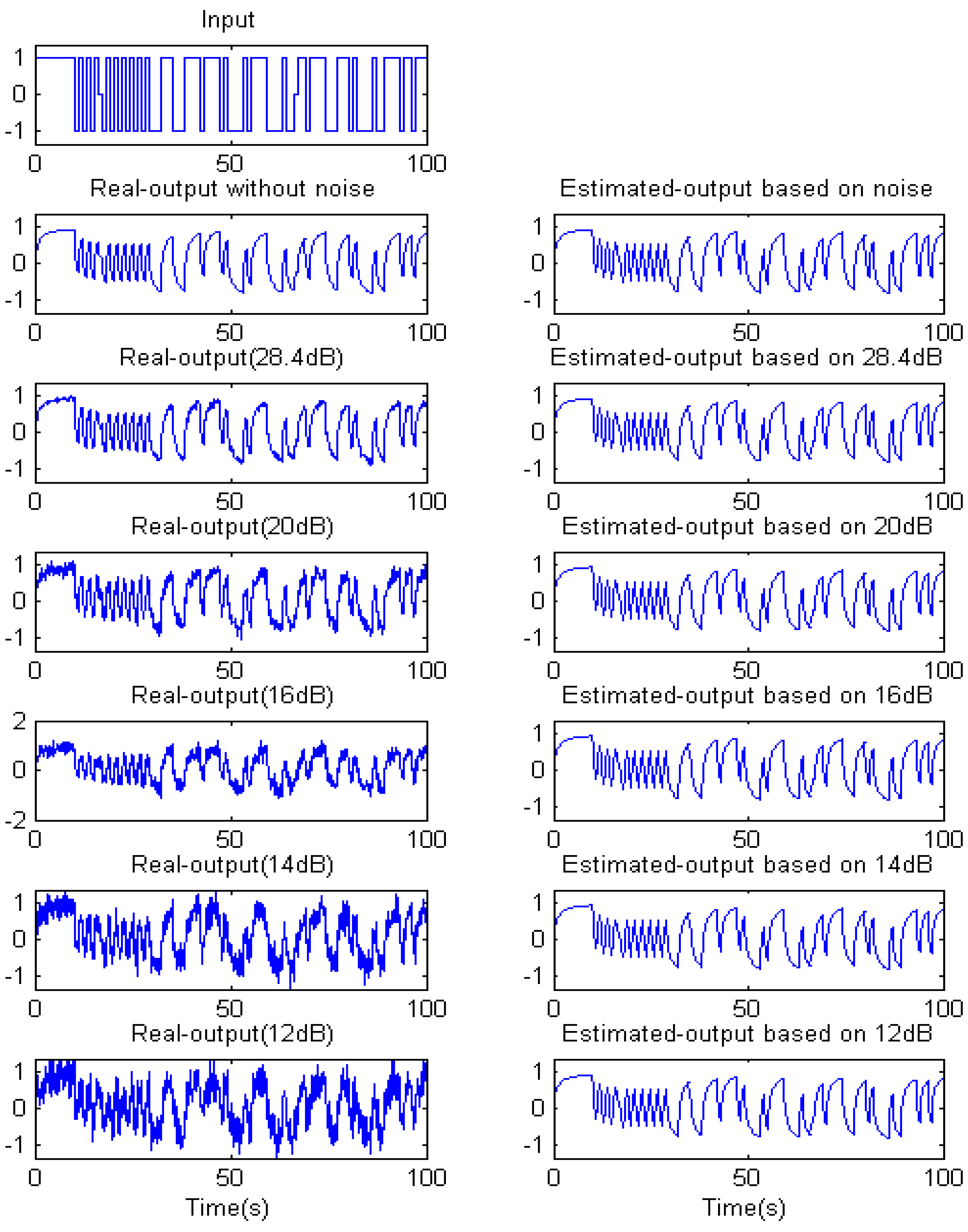
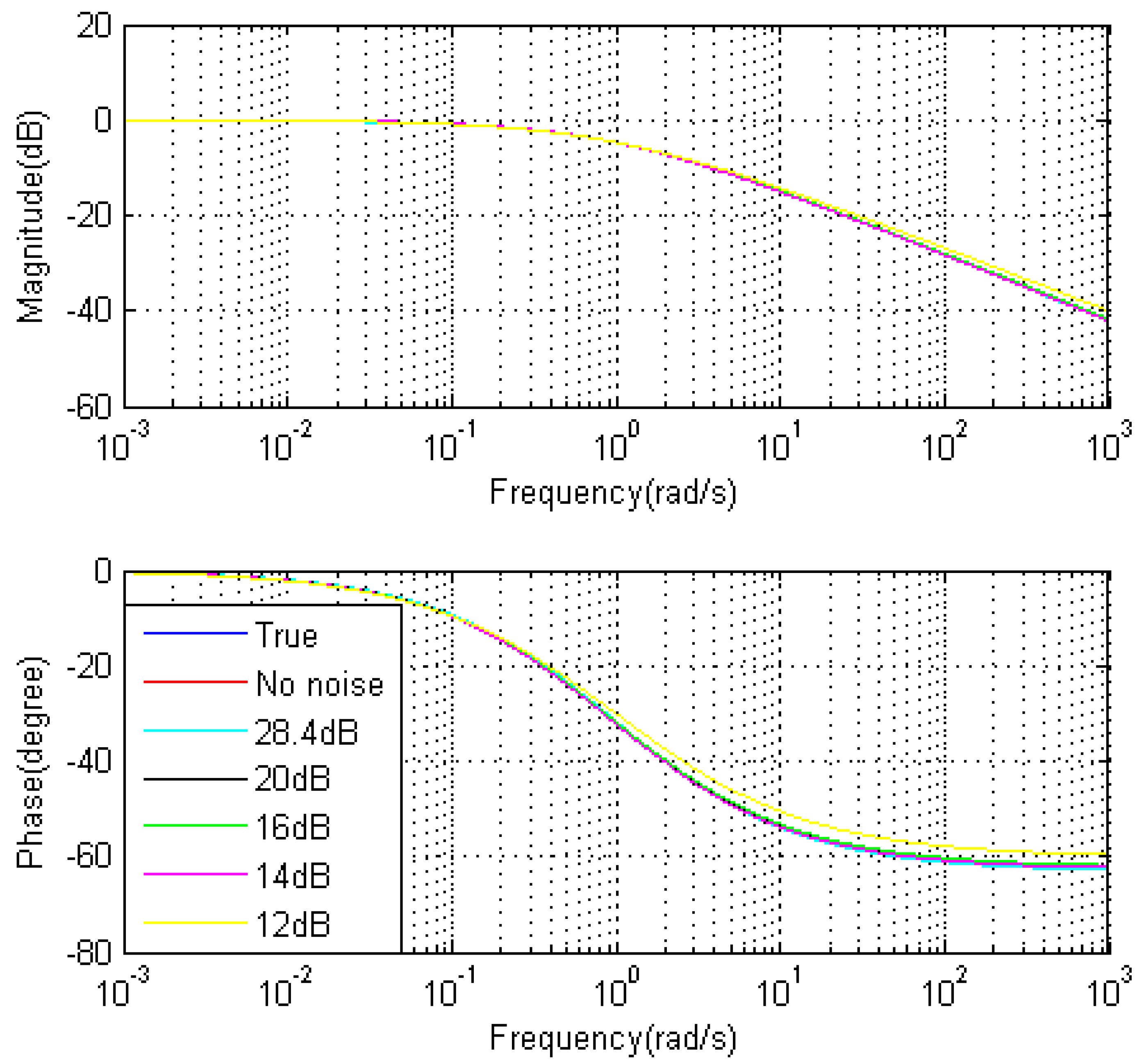
4.2. The Effect of Noise Level
| Excitation | A | /10−5 | b | /10−5 | v | /10−5 | fit |
|---|---|---|---|---|---|---|---|
| True | 1 | 1 | 0.7 | ||||
| No noise | 1.000034 | 0.960063 | 1.000018 | 0.869508 | 0.700011 | 0.508406 | 99.9997% |
| 28.4 dB | 1.006228 | 2.725825 | 0.999772 | 1.416844 | 0.701493 | 0.806250 | 99.58% |
| 20 dB | 0.976071 | 2.339170 | 0.988563 | 1.339580 | 0.696444 | 0.713023 | 99.35% |
| 16 dB | 0.972494 | 2.847766 | 0.988270 | 1.71262 | 0.696197 | 0.711188 | 99.18% |
| 14 dB | 0.958144 | 0.695666 | 0.972546 | 0.305697 | 0.696120 | 0.478331 | 98.76% |
| 12 dB | 1.007271 | 3.584513 | 1.016610 | 1.986676 | 0.667246 | 1.086456 | 97.09% |
| Error types | No noise | 28.4 dB | 20 dB | 16 dB | 14 dB | 12 dB |
|---|---|---|---|---|---|---|
| Maximum error of Magnitude(dB) | 5.8848 × 10−5 | −0.0205 | 0.1131 | 0.1376 | 0.1269 | 2.0961 |
| Maximum error of Phase(degree) | 4.3329 × 10−4 | 0.0793 | 0.3190 | 0.3404 | 0.3416 | 3.3482 |
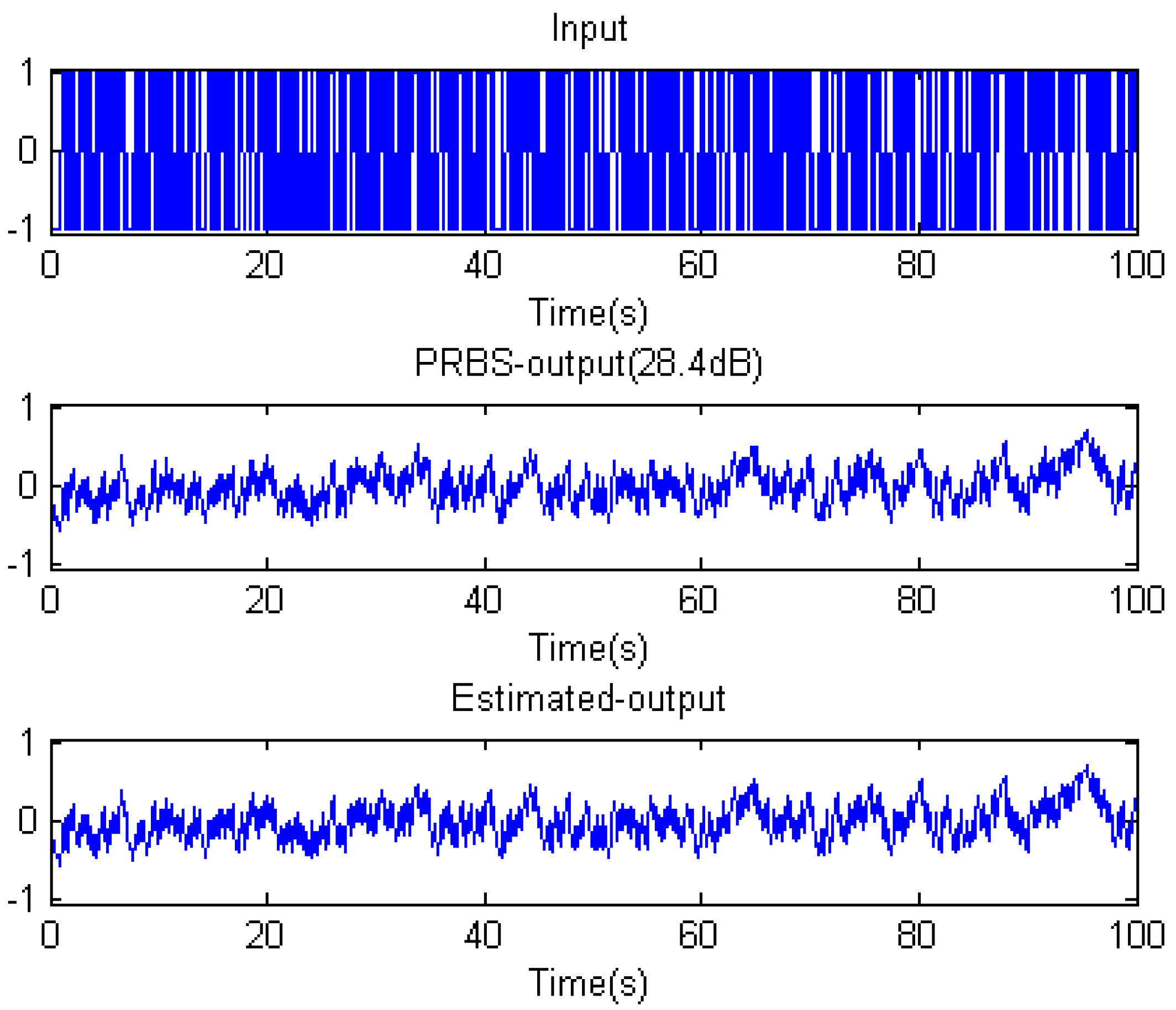
4.3. The Effect of Excitation Signals
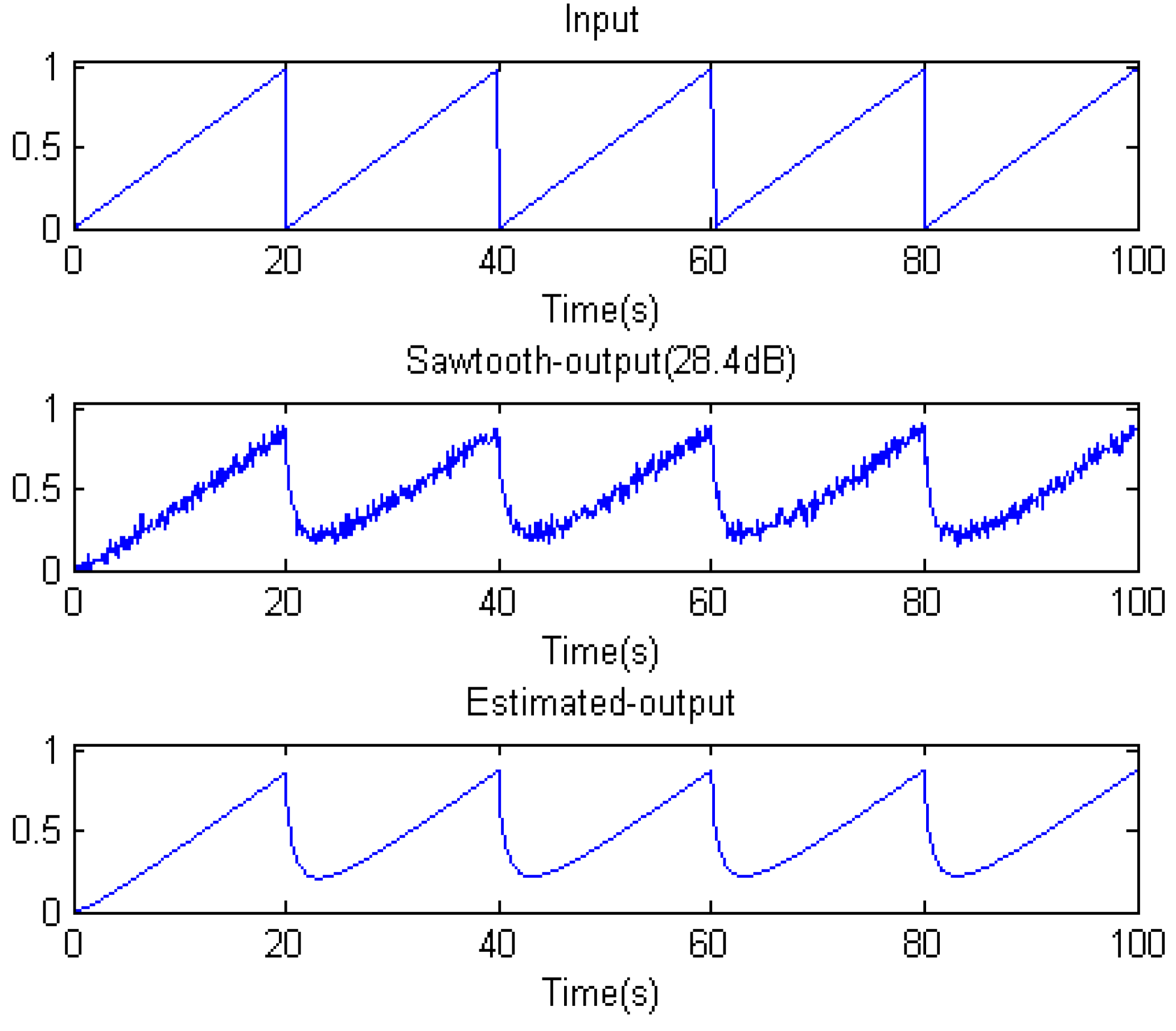
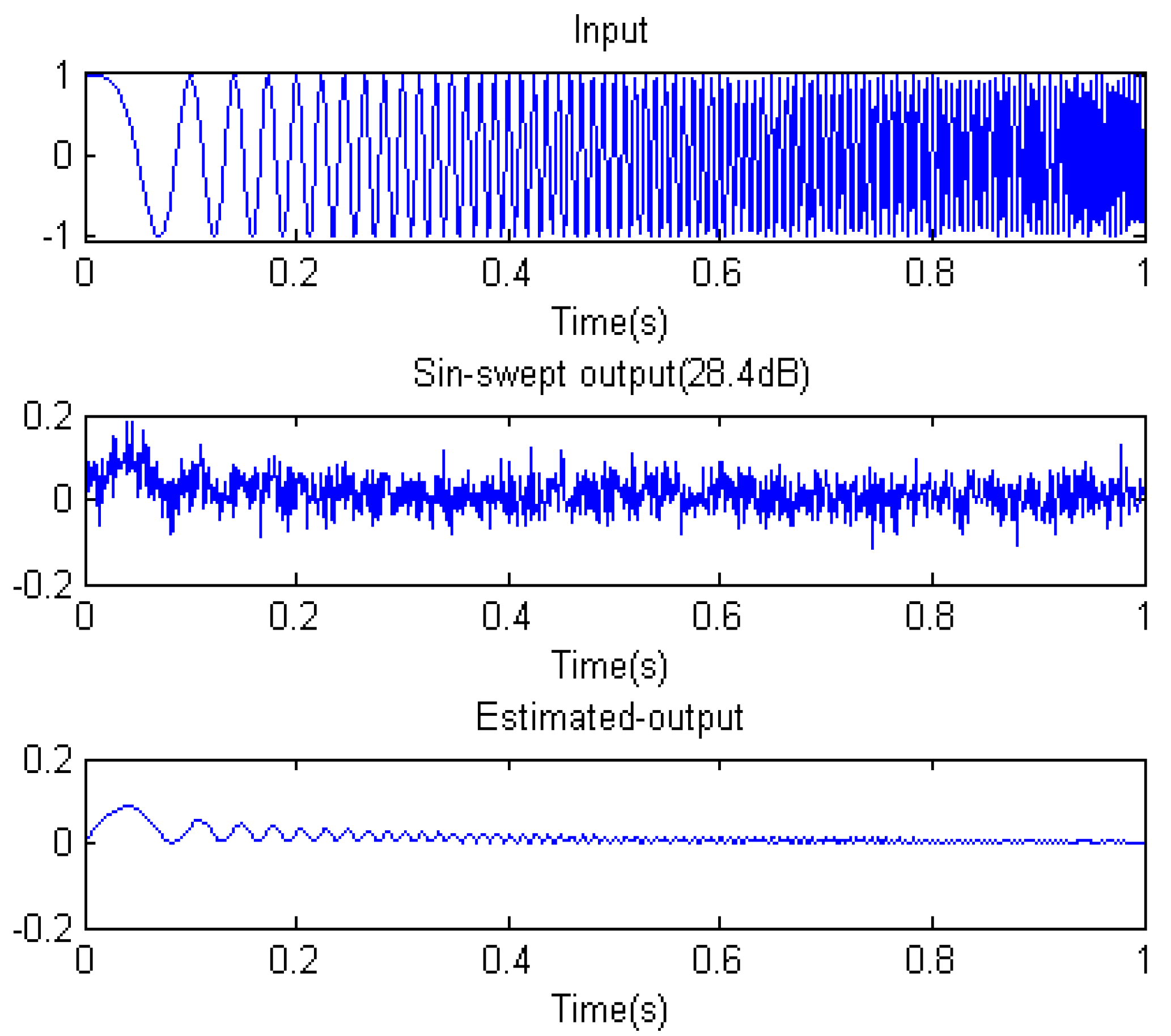
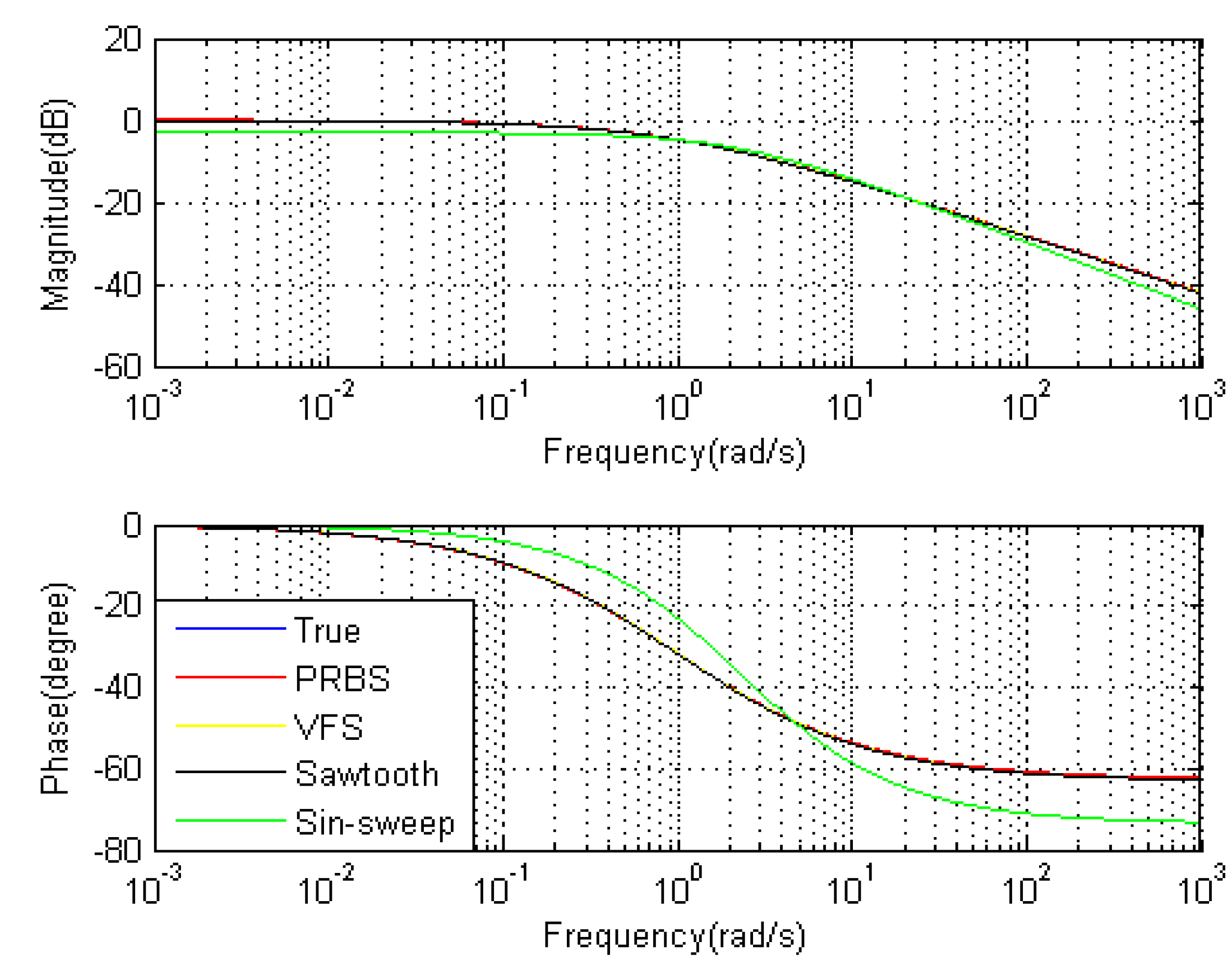
| Excitation | a | /10−5 | b | /10−5 | v | /10−5 | fit |
|---|---|---|---|---|---|---|---|
| True | 1 | 1 | 0.7 | ||||
| PRBS | 0.985850 | 5.757508 | 0.995380 | 2.927489 | 0.696537 | 1.187264 | 99.51% |
| VFS | 1.006228 | 2.725825 | 0.999772 | 1.416844 | 0.701493 | 0.806250 | 99.58% |
| Sawtooth | 0.996426 | 1.329199 | 0.992339 | 1.266606 | 0.711274 | 0.222961 | 98.67% |
| Sin-sweep | 1.999999 | 0.000415 | 1.427971 | 0.042450 | 0.817042 | 0.008724 | 81.59% |
| Error types | PRBS | VFS | Sawtooth | Sin-sweep |
|---|---|---|---|---|
| Maximum error of Magnitude(dB) | 0.1669 | −0.0205 | 0.0232 | 0.9075 |
| Maximum error of Phase(degree) | 0.3146 | 0.0793 | 0.1052 | 9.2118 |
4.4. Identification of General Non-Commensurate Rate Fractional-Order System
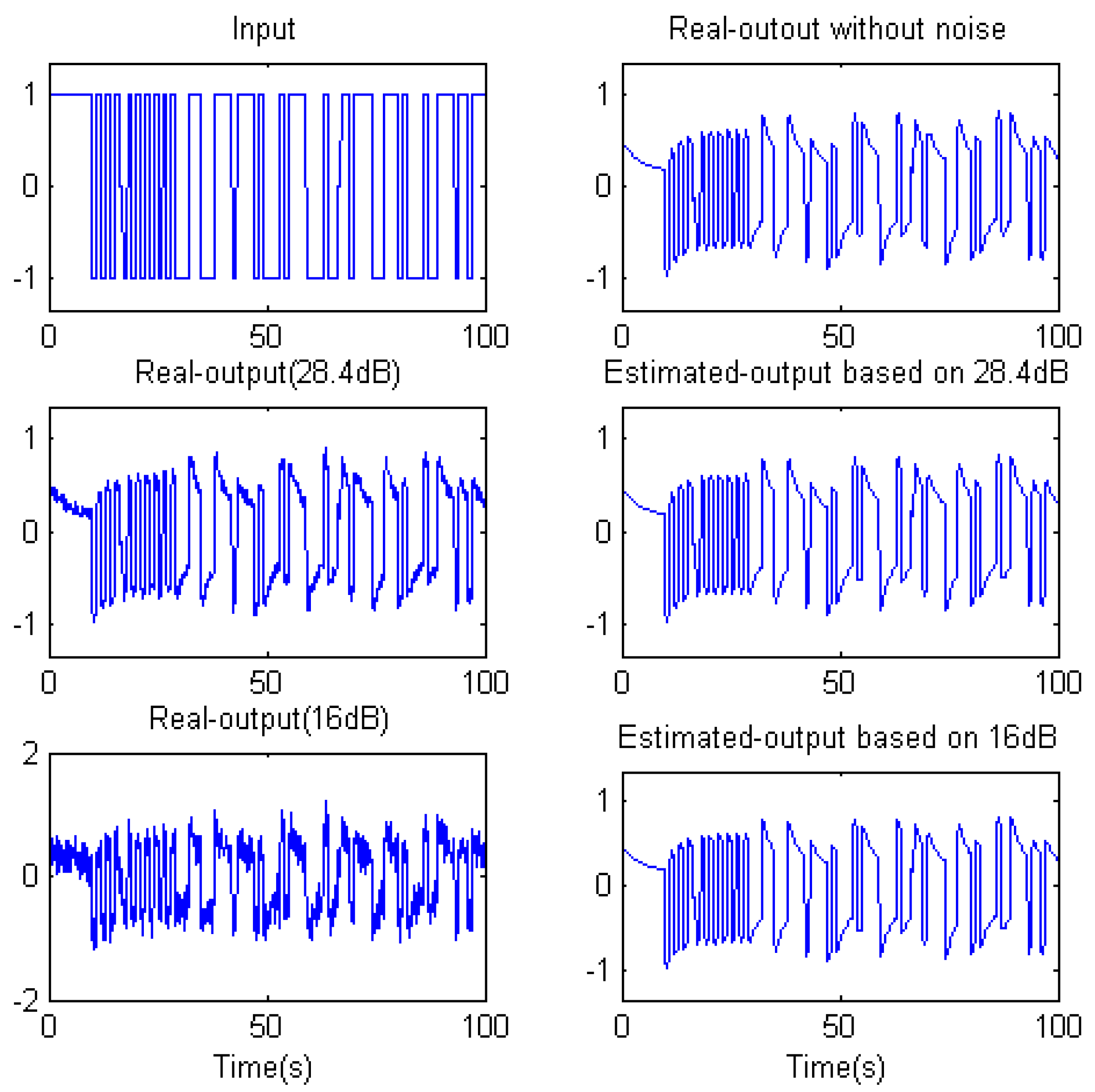

5. Conclusions
Acknowledgements
References
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and applications; Gordon and Breach Science Publisher: New York, NY, USA, 1993. [Google Scholar]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: characterization and synthesis. IEEE Trans. Circuits and Systems I Fund. Theory Appl. 2000, 47, 25–40. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Miller, K.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley-Blackwell: New York, NY, USA, 1993. [Google Scholar]
- Vinagre, B.M.; Feliú, V.; Feliú, J.J. Frequency domain identification of a flexible structure with piezoelectric actuators using irrational transfer function models. In Proceedings of the 37th IEEE Conference on Decision and Control, Tampa, FL, USA, 16–18 December 1998; pp. 1278–1280.
- Lewandowski, R.; Chorazyczewski, B. Identification of the parameters of the Kelvin–Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers. Comput. Struct. 2010, 88, 1–17. [Google Scholar] [CrossRef]
- Dzielinski, A.; Sierociuk, D. Ultracapacitor modelling and control using discrete fractional order state-space model. Acta Montan. Slovaca 2008, 13, 136–145. [Google Scholar]
- Sabatier, J.; Aoun, M.; Oustaloup, A.; Grégoire, G.; Ragot, F.; Roy, P. Fractional system identification for lead acid battery state of charge estimation. Signal Process. 2006, 86, 2645–2657. [Google Scholar] [CrossRef]
- Suchorsky, M.K.; Rand, R.H. A pair of van der Pol oscillators coupled by fractional derivatives. Nonlinear Dynamics 2012, 69, 313–324. [Google Scholar] [CrossRef]
- Cao, J.Y.; Ma, C.B.; Xie, H.; Jiang, Z.D. Nonlinear dynamics of duffing system with fractional order damping. ASME J. Comput. Nonlinear Dyn. 2010, 5, 041012–041018. [Google Scholar] [CrossRef]
- Diethelm, K. A fractional calculus based model for the simulation of an outbreak of dengue fever. Nonlinear Dyn. 2013, 71, 613–619. [Google Scholar] [CrossRef]
- Yang, J.H.; Zhu, H. Vibrational resonance in Duffing systems with fractional-order damping. Chaos 2012, 22, 013112:1–013112:9. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhang, X.D.; Cai, X. A study on modified Szabo’s wave equation modeling of frequency-dependent dissipation in ultrasonic medical imaging. Phys. Scripta 2009, T136, 014014. [Google Scholar] [CrossRef]
- Machado, J.T.; Galhano, A.S. Statistical fractional dynamics. J. Comput.Nonlinear Dyn. 2008, 3, 021201:1–021201:5. [Google Scholar] [CrossRef]
- Ubriaco, M.R. Entropies based on fractional calculus. Phys. Lett. A 2009, 373, 2516–2519. [Google Scholar] [CrossRef]
- Machado, J.A.T. Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn. 2010, 62, 371–378. [Google Scholar]
- Hoffmann, K.H.; Essex, C.; Schulzky, C. Fractional diffusion and entropy production. J. Non-Equilib. Thermodyn. 1998, 23, 166–175. [Google Scholar] [CrossRef]
- Essex, C.; Schulzky, C.; Franz, A.; Hoffmann, K.H. Tsallis and Rényi entropies in fractional diffusion and entropy production. Phys. Stat. Mech. Appl. 2000, 284, 299–308. [Google Scholar] [CrossRef]
- Prehl, J.; Essex, C.; Hoffmann, K.H. The super diffusion entropy production paradox in the space-fractional case for extended entropies. Phys. Stat. Mech. Appl. 2010, 389, 215–224. [Google Scholar] [CrossRef]
- Li, H.; Haldane, F.D.M. Entanglement spectrum as a generalization of entanglement entropy: identification of topological order in non-abelian fractional quantum hall effect states. Phys. Rev. Lett. 2008, 101, 010504. [Google Scholar] [CrossRef] [PubMed]
- Rossikhin, Y.A.; Shitikova, M.V. Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results. J. Appl. Mech. Rev. 2010, 63, 1–52. [Google Scholar] [CrossRef]
- Baleanu, D.; Güvenç, Z.B.; Machado, J.A.T. New Trends in Nanotechnology and Fractional Calculus Applications; Springer-Verlag: New York, NY, USA, 2010. [Google Scholar]
- Sabatier, J.; Agrawal, O.P.; Machado, J.A.T. Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering; Springer-Verlag: New York, NY, USA, 2007. [Google Scholar]
- Mathieu, B.; Melchior, P.; Oustaloup, A.; Ceyral, C. Fractional differentiation for edge detection. Signal Process. 2003, 83, 2421–2432. [Google Scholar] [CrossRef]
- Takayasu, H. Fractals in the Physical Sciences; St. Martin’s Press: New York, NY, USA, 1990. [Google Scholar]
- Fisher, Y. Fractal Image Compression: Theory and Application; Springer-Verlag: New York, NY, USA, 1995. [Google Scholar]
- Gabano, J.D.; Poinot, T.; Kanoun, H. Identification of a thermal system using continuous linear parameter-varying fractional modeling. Control Theory Appl. 2011, 5, 889–899. [Google Scholar] [CrossRef]
- Victor, S.; Melchior, P.; Nelson-Gruel, D.; Oustaloup, A. Flatness control for linear fractional MIMO systems: thermal application. In Proceedings of 3rd IFAC Workshop on Fractional Differentiation and Its Application, Ankara, Turkey, 5–7 November 2008; pp. 5–7.
- Ionescu, C.-M.; Hodrea, R.; de Keyser, R. Variable time-delay estimation for anesthesia control during intensive care. IEEE Trans. Biomed. Eng. 2011, 58, 363–369. [Google Scholar] [CrossRef] [PubMed]
- Sommacal, L.; Melchior, P.; Dossat, A.; Petit, J.; Cabelguen, J.-M.; Oustaloup, A.; Ijspeert, A.J. Improvement of the muscle fractional multimodel for low-rate stimulation. Biomed. Signal Process. Control 2007, 2, 226–233. [Google Scholar] [CrossRef]
- Sommacal, L.; Melchior, J.; Cabelguen, J.-M.; Oustaloup, A.; Ijspeert, A.J. Fractional Multi-Models of the Gastrocnemius Frog Muscle. J. Vib. Control 2008, 14, 1415–1430. [Google Scholar] [CrossRef]
- Oustaloup, A.; Sabatier, J.; Lanusse, P. From fractal robustness to the Crone control. Fract. Calc. Appl. Anal. 1999, 2, 1–30. [Google Scholar]
- Machado, J.A.T. Discrete-time fractional-order controllers. Fract. Calc. Appl. Anal. 2001, 4, 47–66. [Google Scholar]
- Monje, C.A.; Vinagre, B.M.; Feliu, V.; Chen, Y.Q. Tuning and auto-tuning of fractional order controllers for industry applications. Control Eng. Pract. 2008, 16, 798–812. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Ahn, H.S.; Podlubny, I. Robust stability check of fractional order linear time invariant systems with interval uncertainties. Signal Process. 2006, 86, 2611–2618. [Google Scholar] [CrossRef]
- Zhao, M.C.; Wang, J.W. Outer synchronization between fractional-order complex networks: A non-fragile observer-based control scheme. Entropy 2013, 15, 1357–1374. [Google Scholar] [CrossRef]
- Barbosa, R.S.; Machado, J.A.T.; Silva, M.F. Time domain design of fractional differ integrators using least-squares. Signal Process. 2006, 86, 2567–2581. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.A.T. Fractional signal processing and applications. Signal Process. 2003, 83, 2285–2286. [Google Scholar] [CrossRef]
- Melchior, P.; Orsoni, B.; Lavialle, O.; Poty, A.; Oustaloup, A. Consideration of obstacle danger level in path planning using A* and fast-marching optimisation: Comparative study. Signal Process. 2003, 83, 2387–2396. [Google Scholar] [CrossRef]
- Yousfi, N.; Melchior, P.; Rekik, C.; Derbel, N.; Oustaloup, A. Design of centralized CRONE controller combined with MIMO-QFT approach applied to non-square multivariable systems. Int. J. Comput. Appl. 2012, 45, 6–14. [Google Scholar]
- Yousfi, N.; Melchior, P.; Rekik, C.; Derbel, N.; Oustaloup, A. Path tracking design by fractional prefilter using a combined QFT/H∞ design for TDOF uncertain feedback systems. Nonlinear Dyn. 2013, 71, 701–712. [Google Scholar] [CrossRef]
- Ferreira, N.M.F.; Machado, J.A.T. Fractional-order hybrid control of robotic manipulators. In Proceedings of ICAR 2003, the 11th International Conference on Advanced Robotics, Coimbra, Portugal, 30 June–3 July 2003.
- Silva, M.F.; Machado, J.A.T.; Lopes, A.M. Fractional order control of a hexapod robot. Nonlinear Dyn. 2004, 38, 417–433. [Google Scholar] [CrossRef]
- Gaul, L.; Klein, P.; Kemple, S. Damping description involving fractional operators. Mech. Syst. Signal Process. 1991, 5, 81–88. [Google Scholar] [CrossRef]
- Cugnet, M.; Sabatier, J.; Laruelle, S.; Grugeon, S.; Sahut, B.; Oustaloup, A.; Tarascon, J.-M. Lead-acid battery fractional modeling associated to a model validation method for resistance and cranking capability estimation. IEEE Trans. Ind. Electron. 2010, 57, 909–917. [Google Scholar] [CrossRef]
- Sabatier, J.; Cugnet, M.; Laruelle, S.; Grugeon, S.; Sahut, B.; Oustaloup, A.; Tarascon, J.M. A fractional order model for lead-acid battery crankability estimation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1308–1317. [Google Scholar] [CrossRef]
- Baleanu, D.; Golmankhaneh, A.K.; Nigmatulli, R.; Golmankhaneh, A.K. Fractional Newtonian mechanics. Cent. Eur. J. Phys. 2010, 8, 120–125. [Google Scholar] [CrossRef]
- Herallah, M.A.E.; Baleanu, D. Fractional-order Euler–Lagrange equations and formulation of Hamiltonian equations. Nonlinear Dyn. 2009, 58, 385–391. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, W.; Chen, Y.Q. Variable-order fractional differential operators in anomalous diffusion modeling. Phys. Stat. Mech. Appl. 2009, 388, 4586–4592. [Google Scholar] [CrossRef]
- Chen, W.; Ye, L.J.; Sun, H.G. Fractional diffusion equations by the Kansa method. Comput. Math. Appl. 2010, 59, 1614–1620. [Google Scholar] [CrossRef]
- Li, C.P.; Peng, G.J. Chaos in Chen’s system with a fractional order. Chaos Soliton. Fract. 2007, 32, 443–450. [Google Scholar] [CrossRef]
- Yan, J.P.; Li, C.P. On chaos synchronization of fractional differential equations. Chaos Soliton. Fract. 2007, 32, 725–735. [Google Scholar] [CrossRef]
- Poinot, T.; Trigeassou, J.-C. Identification of fractional systems using an output-error technique. Nonlinear Dyn. 2004, 38, 133–154. [Google Scholar] [CrossRef]
- Cois, O.; Oustaloup, A.; Battaglia, E.; Battaglia, J.-L. Non integer model from modal decomposition for time domain system identification. In Proceedings of the 12th IFAC Symposium on System Identification, Santa Barbara, CA, USA, 21–23 June 2000; pp. 989–994.
- Lin, J.; Poinot, T.; Li, S.T.; Trigeassou, J.-C. Identification of non-integer-order systems in frequency domain. J. Control Theory Appl. 2008, 25, 517–520. [Google Scholar]
- Valério, D.; Costa, J.S.D. Identifying digital and fractional transfer functions from a frequency response. Int. J. Control 2011, 84, 445–457. [Google Scholar] [CrossRef]
- Poinot, T.; Trigeassou, J.-C. A method for modeling and simulation of fractional systems. Signal Process. 2003, 83, 2319–2333. [Google Scholar] [CrossRef]
- Hartley, T.T.; Lorenzo, C.F. Fractional-order system identification based on continuous order-distributions. Signal Process. 2003, 83, 2287–2300. [Google Scholar] [CrossRef]
- Nyikos, L.; Pajkossy, T. Fractal dimension and fractional power frequency-dependent impedance of blocking electrodes. Electrochim. Acta 1985, 30, 1533–1540. [Google Scholar] [CrossRef]
- Liu, D.H.; Cai, Y.W.; Su, Y.Z.; Yi, Y.X. Optimization method of parameter identification. In System Identification and Its Application, 1st ed.; Zhao, X.G., Yu, X.H., Eds.; National Defense Industry Press: Beijing, China, 2010; Volume 1, pp. 101–106. [Google Scholar]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Grefenstette, J.J. Optimization of control parameters for genetic algorithms. Syst. IEEE Trans. Man Cybern. 1986, 16, 122–128. [Google Scholar] [CrossRef]
- Harik, G.; Cantú-Paz, E.; Goldberg, D.E.; Miller, B.L. The gambler’s ruin problem, genetic algorithms, and the sizing of populations. In Proceedings of the IEEE International Conference on Evolutionary Computation, Ann Arbor, MI, USA, 13–16 April 1997; pp. 231–253.
- Miller, B.L.; Goldberg, D.E. Genetic algorithms, selection schemes, and the varying effects of noise. Evol. Comput. 1996, 4, 113–131. [Google Scholar] [CrossRef]
- Vale´rio, D.; Costa, J.S.D. Time-domain implementati on of fractional order controllers. IEEE Proc. Control Theory Appl. 2005, 152, 539–552. [Google Scholar] [CrossRef]
- Haber, R.; Keviczky, L. Nonlinear System Identification: Input-Output Modeling Approach; Springer-Verlag: New York, NY, USA, 1999. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhou, S.; Cao, J.; Chen, Y. Genetic Algorithm-Based Identification of Fractional-Order Systems. Entropy 2013, 15, 1624-1642. https://doi.org/10.3390/e15051624
Zhou S, Cao J, Chen Y. Genetic Algorithm-Based Identification of Fractional-Order Systems. Entropy. 2013; 15(5):1624-1642. https://doi.org/10.3390/e15051624
Chicago/Turabian StyleZhou, Shengxi, Junyi Cao, and Yangquan Chen. 2013. "Genetic Algorithm-Based Identification of Fractional-Order Systems" Entropy 15, no. 5: 1624-1642. https://doi.org/10.3390/e15051624
APA StyleZhou, S., Cao, J., & Chen, Y. (2013). Genetic Algorithm-Based Identification of Fractional-Order Systems. Entropy, 15(5), 1624-1642. https://doi.org/10.3390/e15051624







