A Novel Nonparametric Distance Estimator for Densities with Error Bounds

Abstract

The use of a metric to assess distance between probability densities is an important practical problem. In this work, a particular metric induced by an α-divergence is studied. The Hellinger metric can be interpreted as a particular case within the framework of generalized Tsallis divergences and entropies. The nonparametric Parzen’s density estimator emerges as a natural candidate to estimate the underlying probability density function, since it may account for data from different groups, or experiments with distinct instrumental precisions, i.e., non-independent and identically distributed (non-i.i.d.) data. However, the information theoretic derived metric of the nonparametric Parzen’s density estimator displays infinite variance, limiting the direct use of resampling estimators. Based on measure theory, we present a change of measure to build a finite variance density allowing the use of resampling estimators. In order to counteract the poor scaling with dimension, we propose a new nonparametric two-stage robust resampling estimator of Hellinger’s metric error bounds for heterocedastic data. The approach presents very promising results allowing the use of different covariances for different clusters with impact on the distance evaluation.

1. Introduction

Distances measures between two probability densities have been extensively studied in the last century [1]. These measures address two important main objectives: how difficult it is to distinguish between one pair of densities in the context of others and to assess the closeness of two densities, compared to others [2]. In learning scenarios essentially associated with the test of a single hypothesis, the use of a divergence to represent the notion of distance is efficient. However, in scenarios involving multiple hypotheses, such as clustering, image retrieval, or pattern recognition and signal detection, for instance, the non-symmetric and non-metric nature of divergences becomes problematic [3]. When deciding the closest or the farthest among three or more clusters, the use of a metric is important. In this work, a novel nonparametric metric estimator for densities with error bounds is presented. Shannon’s entropy has a central role in information-theoretic studies. However, the concept of information is so rich that perhaps there is no single definition that will be able to quantify information properly [4]. The idea of using information theory functional, such as entropies or divergences, in statistical inference is not new. In fact, the so-called statistical information theory has been the subject of much research over the last half century [5]. How to measure the distance between two densities is an open problem with several proposals since the work of Hellinger in 1909 with Hellinger’s distance [1], Kullback and Leibler (1951), with Kullback-Leibler’s divergence [6], Bregman (1967) with the Bregman’s divergence [7], Jeffreys (1974) with J-distance [8], RAO (1985) and Jianhua Lin (1991) with Jensen-Shannon’s divergence [9,10], Menéndez et al. (1997) with (h, Φ)-entropy differential metric [11], Seth and Principe (2008) with correntropy [12], among others. This work looks into Hellinger’s metric that is the preferred [13,14] or natural model metric [15]. In 2007 Puga found that Hellinger’s metric is one particular α-divergence [16]. Here, we propose a new measure change to solve the nonparametric metric estimation and a two stage robust estimator with error bounds.

2. Theory Background

Following Hartley’s (1928) and Shannon’s (1948) works [17,18], Alfred Rényi introduced in 1960 the generalized α-entropy [19] of probability density function $f\left(x\right)$:

$$R_{\alpha }\left(f\right)=\frac{1}{1-\alpha }\ln {\displaystyle \int f{\left(x\right)}^{\alpha }dx}, \alpha >0$$

(1)

The corresponding generalized differential divergence between two densities $f_1\left(x\right)$ and $f_2\left(x\right)$ is:

$$D_{\alpha }^R\left(f_1,f_2\right)=\frac{1}{\alpha -1}\ln {\displaystyle \int \frac{f_1{\left(x\right)}^{\alpha }}{f_2{\left(x\right)}^{\alpha -1}}dx}$$

(2)

Gell-Mann and Tsallis considered another family of α-entropies [20]:

$$T_{\alpha }\left(f\right)=\frac{1}{\alpha -1}\left[1-{\displaystyle \int f{\left(x\right)}^{\alpha }dx}\right]$$

(3)

being the corresponding α-divergences given as:

$$D_{\alpha }^T\left(f_1,f_2\right)=\frac{1}{1-\alpha }\left[1-{\displaystyle \int \frac{f_1{\left(x\right)}^{\alpha }}{f_2{\left(x\right)}^{\alpha -1}}dx}\right]$$

(4)

Making $\alpha \to 1$, one easily can conclude that:

$$\underset{\alpha \to 1}{\lim }{R}_{\alpha }\left(f\right)=\underset{\alpha \to 1}{\lim }{T}_{\alpha }\left(f\right)=H_S\left(f\right)$$

(5)

and:

$$\underset{\alpha \to 1}{\lim }{D}_{\alpha }^R\left(f_1,f_2\right)=\underset{\alpha \to 1}{\lim }{D}_{\alpha }^T\left(f_1,f_2\right)=D_{KL}\left(f_1,f_2\right)$$

(6)

where:

$$H_S\left(f\right)=-{\displaystyle \int f\left(x\right)\ln f\left(x\right)dx}$$

(7)

is Shannon’s differential entropy and:

$$D_{KL}\left(f_1,f_2\right)={\displaystyle \int f_1\left(x\right)\ln \frac{f_1\left(x\right)}{f_2\left(x\right)}dx}$$

(8)

is Kulback-Leibler’s divergence.

Another member of these families is the Rényi’s quadratic entropy (α=2) that is defined as:

$$R_2\left(f\right)=-\ln {\displaystyle \int f{\left(x\right)}^{2}dx}$$

(9)

while the respective divergence is:

$$D_2^R\left(f_1,f_2\right)=\ln {\displaystyle \int \frac{f_1{\left(x\right)}^2}{f_2\left(x\right)}dx}$$

(10)

Rényi’s quadratic entropy, given by Equation (9), is particularly interesting because it accepts a close form nonparametric estimator, saving computational time compared to numerical integration or resampling [21,22].

α-Entropy families given by Equations (1) and (3) are monotonically coupled (Ramshaw [23]) through:

$$T_{\alpha }=\left(e^{\left(1-\alpha \right)R_{\alpha }}-1\right)/\left(1-\alpha \right)$$

(11)

Therefore, an optimization in one family has equivalence in the other.

2.1. Square-Root Entropy

Let us consider $\alpha =1/2$ in Equations (1)–(4). Then, the square-root entropy in the form of Tsallis is:

$$T_{1/2}\left(f\right)=2{\displaystyle \int \sqrt{f\left(x\right)}dx-2}$$

(12)

with the corresponding divergence given as:

$$D_{1/2}^T\left(f_1,f_2\right)=2-2{\displaystyle \int \sqrt{f_1\left(x\right)f_2\left(x\right)}dx}$$

(13)

In Rényi’s form one finds, respectively, the entropy:

$$R_{1/2}\left(f\right)=2\ln {\displaystyle \int \sqrt{f\left(x\right)}dx},$$

(14)

and the divergence:

$$D_{1/2}^R\left(f_1,f_2\right)=-2\ln {\displaystyle \int \sqrt{f_1\left(x\right)f_2\left(x\right)}dx}$$

(15)

It should be noted that, from Equation (13), one obtains:

$$\sqrt{D_{1/2}^T\left(f_1,f_2\right)}=\sqrt{{\displaystyle \int {\left(\sqrt{f_1\left(x\right)}-\sqrt{f_2\left(x\right)}\right)}^{2}dx}}=M\left(f_1,f_2\right)$$

(16)

where $M\left(f_1,f_2\right)$ is a information theoretic derived metric that, among other properties, verifies the triangular inequality. This particular α-divergence, by means of a monotonous transformation, induces the Hellinger’s distance, which is a metric [13,14,24]:

$$M\left(f_1,f_2\right)=\sqrt{2-2I(f_1,f_2)}$$

(17)

On the other hand, information theoretic derived metrics given by Equations (15) and (16) are also related with Hellinger’s affinity or Bhattacharya’s coefficient ($0\le I\left(f_1,f_2\right)\le 1$):

$$I\left(f_1,f_2\right)={\displaystyle \int \sqrt{f_1\left(x\right)f_2\left(x\right)}dx}.$$

(18)

Considering the expected cross-value of two probability density functions $C\left(f_1,f_2\right)$:

$$C\left(f_1,f_2\right)=E_{f_1}\left(f_2\right)=E_{f_2}\left(f_1\right)={\displaystyle \int f_1\left(x\right)}{f}_2\left(x\right)dx$$

(19)

the Hellinger’s affinity given by Equation (18) can be then written as:

$$I\left(f_1,f_2\right)=\sqrt{C\left(f_1,f_2\right)}{\displaystyle \int \sqrt{f_{\mathrm{\Omega }}\left(x\right)}dx}=\sqrt{C\left(f_1,f_2\right)}H\left(f_{\mathrm{\Omega }}\right)$$

(20)

where $f_{\mathrm{\Omega }}\left(x\right)$ is the normalized product density:

$$f_{\mathrm{\Omega }}\left(x\right)=\frac{f_1\left(x\right)f_2\left(x\right)}{C\left(f_1,f_2\right)}$$

(21)

and $H\left(f_{\mathrm{\Omega }}\right)$ the corresponding entropy of the information theoretic derived metric.

This metric has bounds that can be directly computed from the samples as shown by Puga [16]. These bounds often present overlapping hypothesis intervals, and resampling estimation is a necessary tool to remove ambiguities and access distances between densities.

2.2. Nonparametric Hellinger’s Affinity Estimation

Let us focus on the application of the previous measures on two Parzen’s nonparametric densities [25] from two data clusters $C{l}^{(1)}=\left\{{x_1}^{\left(1\right)},{x_2}^{\left(1\right)},\mathrm{...},{x_{N_1}}^{\left(1\right)}\right\}$ and $C{l}^{(2)}=\left\{{x_1}^{\left(2\right)},{x_2}^{\left(2\right)},\mathrm{...},{x_{N_2}}^{\left(2\right)}\right\}$:

$$f_1\left(x\right)=\frac{1}{N_1}{\displaystyle \sum _{j=1}^{N_1}G\left(x,{\sigma }_1,{x_j}^{\left(1\right)}\right)}$$

(22)

and:

$$f_2\left(x\right)=\frac{1}{N_2}{\displaystyle \sum _{j=1}^{N_2}G\left(x,{\sigma }_2,{x_j}^{\left(2\right)}\right)}$$

(23)

where $G\left(x,\sigma ,\mu \right)$ is the Parzen’s Gaussian kernel, also known as kernel bandwidth, with the approximation of covariance ${\sigma }^{2}I$, and mean $\mu$ given as:

$$G\left(x,\sigma ,\mu \right)={\displaystyle \prod _{i=1}^{\aleph }\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{{\left(x\left(i\right)-\mu (i)\right)}^2}{2{\sigma }^2}}}$$

(24)

where $\aleph$ is the dimension. Notice that the two clusters in Equations (22) and (23) may have two different Gaussian kernel covariances. The kernel covariance may be obtained directly from the a priori knowledge of the instruments used to produce the data; for instance, two different instruments with different precisions may produce the same data, but the densities should reflect the measurements error through the bandwidth, (covariances). To estimate the bandwidth without instrumental apriori knowledge it is possible to estimate the kernel bandwidth with a suitable method, such as k-Nearest Neighbor (k-NN), Silverman [25] or Scott [26].

Now, let us adopt the summing convention ${\displaystyle \sum _{i,j}\equiv }{\displaystyle \sum _{i=1}^{N_1}{\displaystyle \sum _{j=1}^{N_2}}}$ and define the following auxiliary variables:

$${\sigma }^2=\left({\sigma }_1^2+{\sigma }_2^2\right)/2$$

(25)

$${\sigma }_{*}^2={\sigma }_1^2{\sigma }_2^2/2{\sigma }^2$$

(26)

$$s_{i,j}=\left({\sigma }_2^2{x}_i^{\left(1\right)}+{\sigma }_1^2{x}_j^{\left(2\right)}\right)/2{\sigma }^2$$

(27)

$$d_{i,j}=\left(x_i^{\left(1\right)}-x_j^{\left(2\right)}\right)/2$$

(28)

and:

$$F_D\left(d_{i,j}\right)=e^{-\frac{{\Vert d_{i,j}\Vert }^2}{{\sigma }^2}}/{\displaystyle \sum _{k,l}{e}^{-\frac{{\Vert d_{k,l}\Vert }^2}{{\sigma }^2}}}$$

(29)

The nonparametric estimator ${\widehat{f}}_{\mathrm{\Omega }}\left(\omega \right)$ results in:

$${\widehat{f}}_{\mathrm{\Omega }}\left(\omega \right)={\displaystyle \sum _{i,j}{F}_D\left(d_{i,j}\right)G\left(\omega ,{\sigma }_{*}^2,s_{i,j}\right)}$$

(30)

2.3. The Resampling Estimator

The bootstrap resampling is reached through the distribution of probability given by Equation (30) combined with the random generation of samples $\left({\omega }_k\right)$ from nonparametric Parzen’s density with diagonal covariance, which is a well-established as well as a computationally efficient procedure [27]. Then, the synthesized samples are directly usable in the estimator:

$$\begin{array}{ll}H\left(f_{\mathrm{\Omega }}\right)& ={\displaystyle \int \sqrt{f_{\mathrm{\Omega }}\left(\omega \right)}}d\omega ={\displaystyle \int \frac{f_{\mathrm{\Omega }}\left(\omega \right)}{\sqrt{f_{\mathrm{\Omega }}\left(\omega \right)}}}d\omega \\ & =E_{f_{\mathrm{\Omega }}}\left[\frac{1}{\sqrt{f_{\mathrm{\Omega }}\left(\omega \right)}}\right]=\underset{K\to \infty }{\lim }{\tilde{H}}_K\left(f_{\mathrm{\Omega }}\right)=\underset{K\to \infty }{\lim }\frac{1}{K}{\displaystyle \sum _{k=1}^K\frac{1}{\sqrt{{\widehat{f}}_{\mathrm{\Omega }}\left({\omega }_k\right)}}}\end{array}$$

(31)

with ${\omega }_k\underset{i.i.d.}{~}{f}_{\mathrm{\Omega }}$.

However, the use of Equation (31) is associated with serious practical difficulties because the second moment:

$${\displaystyle \int d\omega }-H{\left(f_{\mathrm{\Omega }}\right)}^2=\infty$$

(32)

has infinite variance, which is a condition where the central limit theorem is not valid. In this work, we use measure theory and propose the following change of measure:

$$z=f_{\mathrm{\Omega }}\left(\omega \right)$$

(33)

with the associated density $f_Z(z)$:

$$E_{f_{\mathrm{\Omega }}}\left[\frac{1}{\sqrt{f_{\mathrm{\Omega }}\left(\omega \right)}}\right]=E_{f_Z}\left[\frac{1}{\sqrt{z}}\right]=\underset{K\to \infty }{\lim }{\displaystyle \sum _0^{z_k^{\max }}\frac{1}{\sqrt{z_k}}{\widehat{f}}_z(z_k)dz} \mathrm{with} z_k\underset{i.i.d.}{~}{f}_Z$$

(34)

This new density presents a finite second moment:

$${\displaystyle \underset{0}{\overset{z^{\max }}{\int }}\frac{1}{z}{f}_z(z)dz}-H{\left(f_{\mathrm{\Omega }}\right)}^2$$

(35)

having $f_z$ a limited support between 0 (zero) and $z^{\max }$. This is a density with an abrupt jump in $z^{\max }$ end of the density. However, the approximation properties of a histogram are not affected by a simple jump at the end of the density [26], hence the histogram estimator was used to estimate ${\widehat{f}}_Z(z_k)$ with $z_k={\widehat{f}}_{\mathrm{\Omega }}({\omega }_k)$.

The product probability density function $\left(f_z\right)$ must be estimated from the random variable $z=f_{\mathrm{\Omega }}\left(\omega \right)$, but it ensures finite variance, which is a requisite of the central limit theorem and the t-student confidence interval may be used Equation (39).

Figure 1. A logarithmic scale for the ${\sigma }_1/{\sigma }_2$ coefficient variation and metric measure change between the two respective densities $\left(f_1,f_2\right)$.

Figure 1. A logarithmic scale for the ${\sigma }_1/{\sigma }_2$ coefficient variation and metric measure change between the two respective densities $\left(f_1,f_2\right)$.

To test the algorithm, we consider the simplest case of Hellinger’s metric (17) associated with the nonparametric densities of Equations (22) and (23). In this particular case, we have access to the analytical value of Hellinger’s metric:

$$\tilde{M}\left(f_1,f_2\right)=\sqrt{2-2{\left(\frac{2{\sigma }_1{\sigma }_2}{{\sigma }_1^2+{\sigma }_2^2}\right)}^{\frac{\aleph }{2}}{e}^{-\frac{{\Vert d_{1,2}\Vert }^2}{{\sigma }^2}}}$$

(36)

Using Equations (34) and (36), we can quantify the computational behavior of the resampling estimator. Let us first consider the behavior of the Parzen’s density estimator with two distinct kernel sizes: ${\sigma }_1,{\sigma }_2$. In the simplest case with only two kernels, located at the same coordinates, despite the same location, different Parzen’s windows in Equation (36) provide different distances, as can be observed in Figure 1. It is possible to verify the symmetric behavior of the distance estimator and realize that the bandwidth of the Parzen’s kernel is important to access the distance between clusters. This is a relevant characteristic, especially when the experimental data have different instrumental origins with different measurement precisions; the use of different bandwidths in the Parzen’s kernels may reflect this importance feature of the density, and this implies that the data is heterocedastic.

To quantify the error bounds estimation performance, we propose the generation of N₁ distance samples ${\tilde{M}}_m$ from resampling the density of Equation (34), and to estimate ${\tilde{f}}_Z$ we use a discrete histogram with N₁ bins, obtaining the ordered $z_k$ and ${\tilde{f}}_{Z_k}$. As such, the metric $\tilde{M}$ estimator becomes:

$${\tilde{M}}_m={\left\{\sqrt{2-2\sqrt{C\left(f_1,f_2\right)}\frac{1}{\sqrt{z_k}}{\tilde{f}}_Z(z_k)\Delta z}\right\}}_{m=\mathrm{1...}{N}_1}$$

(37)

which can be written as:

$$\tilde{M}=\sqrt{2-2\sqrt{C\left(f_1,f_2\right)}{\displaystyle \sum _0^{z_k^{\max }}\frac{1}{\sqrt{z_k}}{\tilde{f}}_Z(z_k)\Delta z}}$$

(38)

To assess the error bounds estimation, we use the t-student 95% confidence interval (39), which is a maximum entropy distribution [28,29] and provides a parametric approach to robust statistics [30], and allows the following calculation of the confidence limits:

$$\left[L,U\right]=\tilde{M}\pm t_{N_1-1,0.5+0.95/2}\sqrt{\frac{1}{N_1(N_1-1)}{\displaystyle \sum _{k=1}^{N_1}{\left({\tilde{M}}_m-\tilde{M}\right)}^2}}$$

(39)

We calculate the 95% confidence limits, the upper ($U$) and the lower ($L$) for the respective density resampling. The variance of this new estimator is well controlled in one dimension. The unexpected drawback of this estimator is its poor scaling performance with increased dimension, as depicted in Figure 2.

The new variable $z=f_{\mathrm{\Omega }}\left(\omega \right)$ may be seen as a projection of the multidimensional Parzen’s kernels into a 1-Dimensional function. This insight allowed the design of a two-stage estimator for $f_{\mathrm{\Omega }}\left(\omega \right)$ that circumvents both problems: infinite variance and poor scalability with dimensionality.

Figure 2. Illustration of the metric estimator behavior for dimensions 1 (one) to 5.

Figure 2. Illustration of the metric estimator behavior for dimensions 1 (one) to 5.

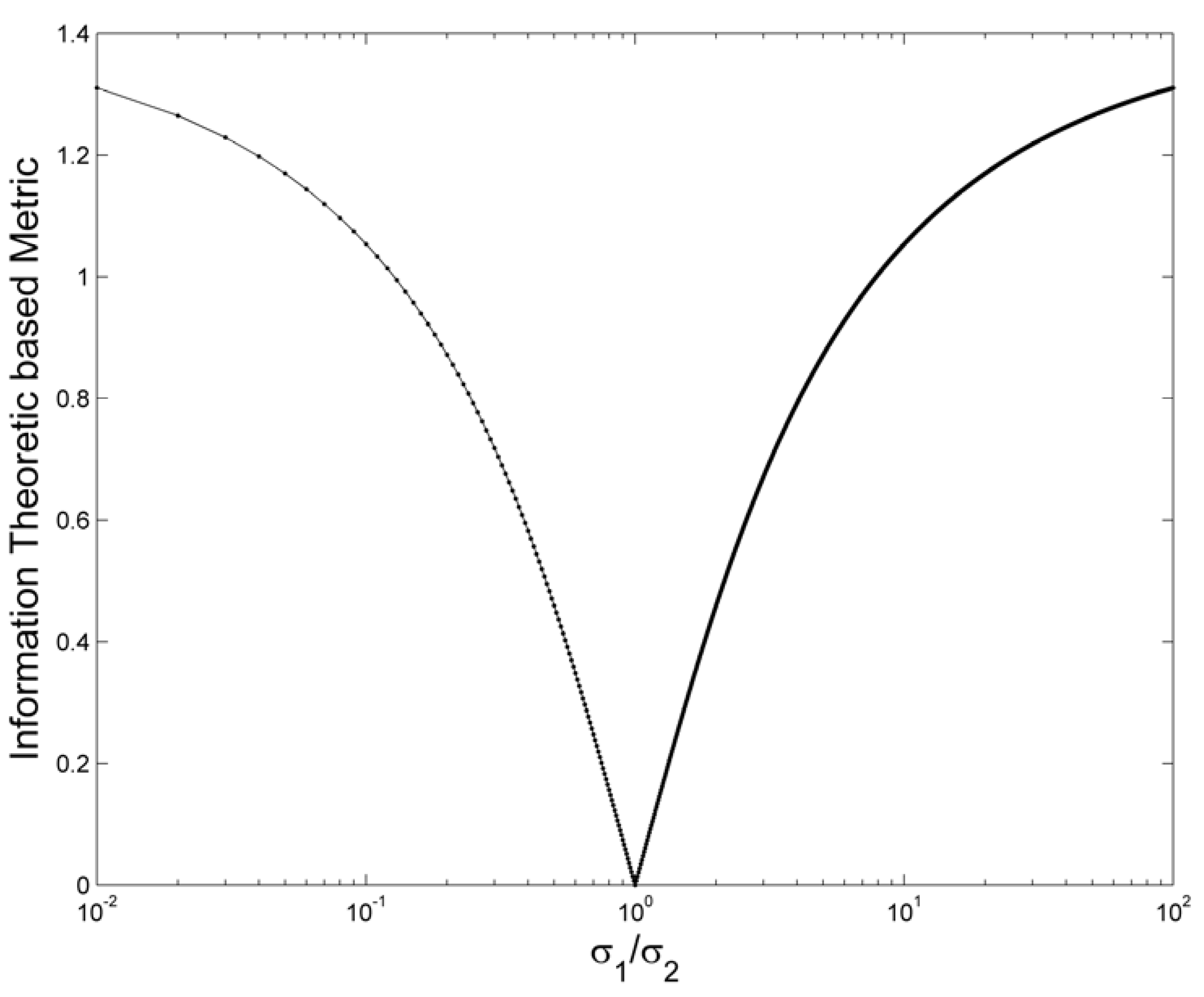
2.4. The Two Stage Resampling Estimator

We propose the generation of N₁ distance samples ${{\tilde{M}}_k}^{(n)}$ from resampling the density $f_{\mathrm{\Omega }}({\omega }_k)$, which constitutes one trial $(n)$:

$${{\tilde{M}}_k}^{(n)}={\left\{\sqrt{2-2\frac{\sqrt{C\left(f_1,f_2\right)}}{\sqrt{f_{\mathrm{\Omega }}\left({\omega }_k^{(n)}\right)}}}\right\}}_{k=\mathrm{1...}{N}_1}$$

(40)

It is possible to estimate ${\tilde{M}}^{(n)}$ as:

$${\tilde{M}}^{(n)}=\sqrt{2-\frac{2}{N_1}{\displaystyle \sum _{k=1}^{N_1}\sqrt{\frac{C\left(f_1,f_2\right)}{f_{\mathrm{\Omega }}\left({\omega }_k^{(n)}\right)}}}}$$

(41)

For each trial $(n)$, the 95% confidence limits, the upper $U^{(n)}$ and the lower $L^{(n)}$ for the respective density resampling, can be calculated:

$$\left[L^{(n)},U^{(n)}\right]={\tilde{M}}^{(n)}\pm t_{N_1-1,0.5+0.95/2}\sqrt{\frac{1}{N_1(N_1-1)}{\displaystyle \sum _{k=1}^{N_1}{\left({{\tilde{M}}_k}^{(n)}-{\tilde{M}}^{(n)}\right)}^2}}$$

(42)

It may seem that this step is enough to estimate the metric $\tilde{M}\left(f_1,f_2\right)=\sqrt{2-2\tilde{I}(f_1,f_2)}$, but the theoretically predicted undesired behavior associated to Equation (32), with large confidence intervals is present in this estimator. To demonstrate this drawback, we have simulated 100 trials of the simplest case of nonparametric Hellinger’s metric, Equation (36), with Euclidean distance $d=\Vert x_1-x_2\Vert =1$. As can be observed in Figure 3, the large confidence intervals are present, hence the motivation for the two-stage error bound estimator.

Figure 3. t-Student 95% confidence intervals for Hellinger’s metric defined by dots; the exact value is represented by a continuous line; the predicted large intervals are marked with triangles; and the miss-estimated intervals are marked with circles.

Figure 3. t-Student 95% confidence intervals for Hellinger’s metric defined by dots; the exact value is represented by a continuous line; the predicted large intervals are marked with triangles; and the miss-estimated intervals are marked with circles.

To achieve a robust error bound estimator $\left[{\tilde{L}}_R,{\tilde{U}}_R\right]$ for the expected value of $M(f_1,f_2)$ with similar results of $f_Z(z)$ in one dimension, we propose a new two-stage method. Comparing the results of the two densities resampling, we found that 31 selected trials out of 33 from ${\widehat{f}}_{\mathrm{\Omega }}({\omega }_k)$ was in good agreement with ${\tilde{f}}_Z(z)$. With 33 trails $(n)$ generated with N₁ random samples each as:

$${\left\{{\left\{\sqrt{2-2\frac{\sqrt{C\left(f_1,f_2\right)}}{\sqrt{{\widehat{f}}_{\mathrm{\Omega }}\left({\omega }_k^{(n)}\right)}}}\right\}}_{k=\mathrm{1...}{N}_1}\right\}}_{n=\mathrm{1...33}}$$

(43)

sorting the amplitude $\left|U^{(n)}-L^{(n)}\right|$ and keeping the 31 smallest intervals with the correspondent estimated affinities (${{\tilde{M}}_s}^{(n)}$), we obtain the estimator ${\tilde{M}}_s(f_1,f_2)$ for the second stage with:

$${\tilde{M}}_s(f_1,f_2)=\frac{1}{31}{\displaystyle \sum _{n=1}^{31}{{\tilde{M}}_s}^{(n)}}$$

(44)

Then, we calculated the respective t-student 95% confidence interval $\left[{\tilde{L}}_s,{\tilde{U}}_s\right]$ with the selected trials ${{\widehat{M}}_s}^{(n)}$. To overcome the miss-estimated intervals, we have defined a second estimator for the lower limit of the interval (${\tilde{L}}_2$) and a second estimator for the upper limit of the interval ( ${\tilde{U}}_2$):

$$\left[{\tilde{L}}_2,{\tilde{U}}_2\right]=\left[\frac{1}{31}{\displaystyle \sum _{n=1}^{31}{L}_s^{(n)}},\frac{1}{31}{\displaystyle \sum _{n=1}^{31}{U}_s^{(n)}}\right]$$

(45)

which is a potentially asymmetric interval, guided by the selected first-stage interval limits.

The robust estimator for the lower limit of the interval (${\tilde{L}}_R$) and the robust estimator for the upper limit of the interval (${\tilde{U}}_R$) were defined as:

$$\left[{\tilde{L}}_R,{\tilde{U}}_R\right]=\left[\min \left({\tilde{L}}_s,{\tilde{L}}_2\right),\max \left({\tilde{U}}_s,{\tilde{U}}_2\right)\right]$$

(46)

In Figure 4, we can find the intervals defined by Equation (46), and confirmed the robust interval estimator for the Hellinger’s affinity.

Figure 4. Using the new robust two-stage resampling interval estimator the exact Hellinger’s distance is more likely to be found within the interval; it should be noted that from dimension 1 to dimension 20, the exact value of the metric is always in the interval.

Figure 4. Using the new robust two-stage resampling interval estimator the exact Hellinger’s distance is more likely to be found within the interval; it should be noted that from dimension 1 to dimension 20, the exact value of the metric is always in the interval.

The detailed process of the two-stage estimator is presented in Algorithm 1. Notice that we studied up to dimension 20 with promising results. k-NN is a good alternative [31,32,33,34,35,36], but may present several difficulties, like the k determination [37], the distance measure choice [38] and the curse of dimensionality [39].

Algorithm 1—Two-stage resampling estimator

(1) COMMENT [To find the bandwidth of a cluster. Use the apriori knowledge from the instrumental data to estimate the bandwidth. If the precision of the instrumental data is not available, then use one of the preferred method to estimate bandwidth [26]; here it is used the Silverman rule and a cross validation search for maximum likelihood density [25]. (2) COMMENT [To estimate one trial. Determine the number of random samples to generate. Bootstrap method from Parzen’s kernels with random generation of samples. Obtain the metric estimate given by Equation (41). (3) COMMENT [To estimate the robust bonds, in the second step. Repeat the estimate. Calculate the 95% t-student interval from the estimates using Equation (42). Select the best intervals amplitudes given by Equation (44). Calculate the mean of the lower and the upper interval using Equation (45). Retain the maximum of the upper bound and the minimum of the lower bound given by Equation (46).

The implemented algorithm is available upon request.

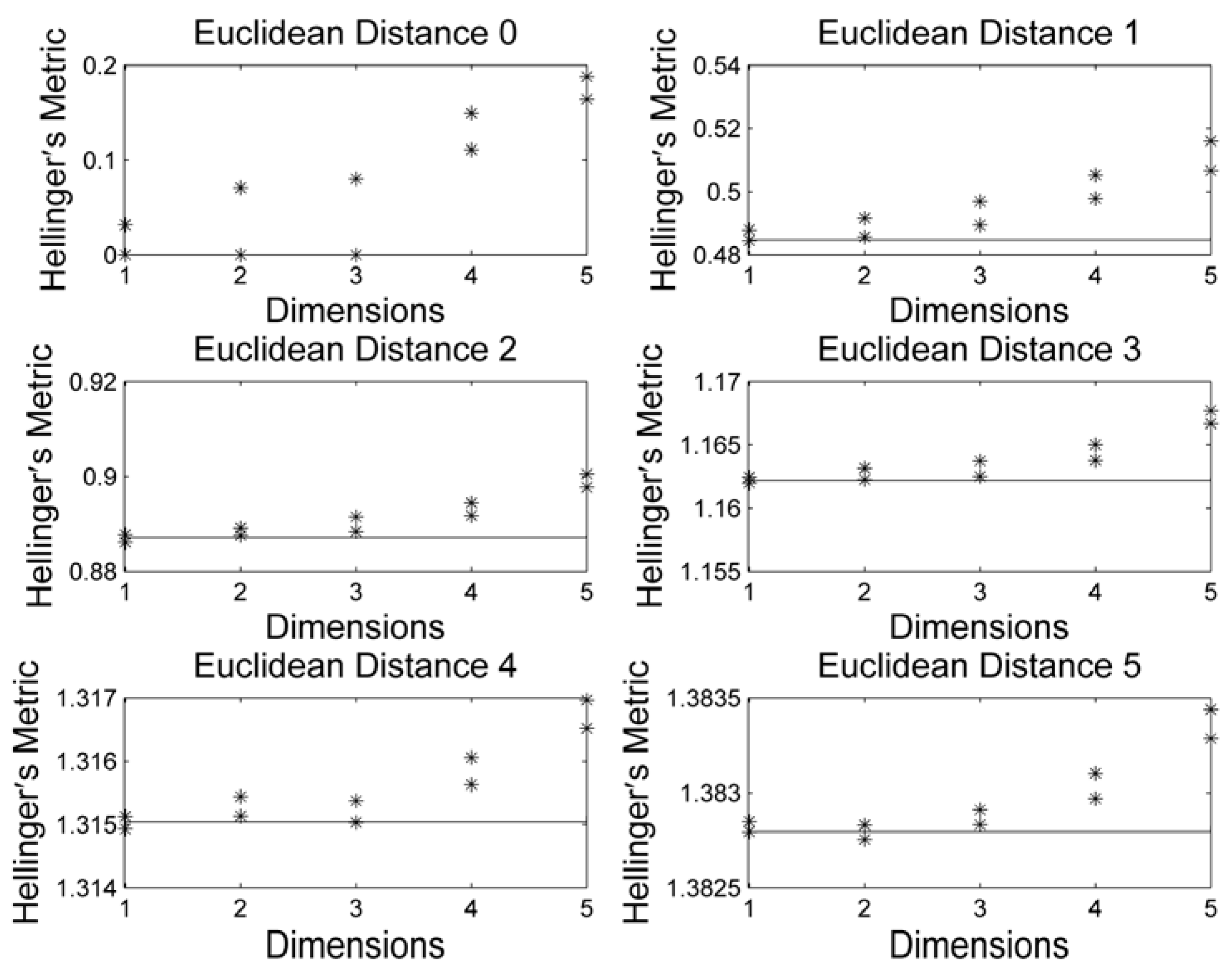
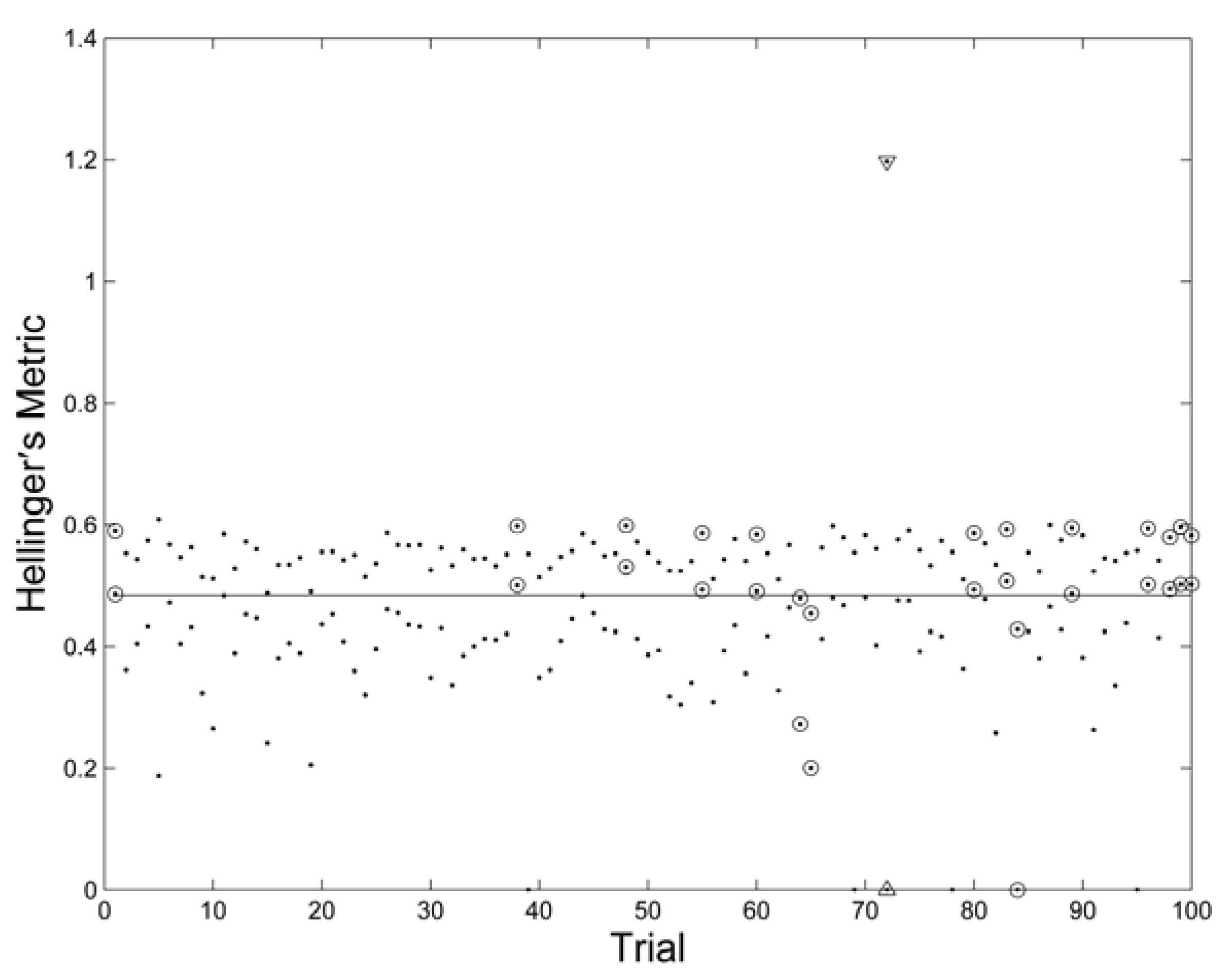
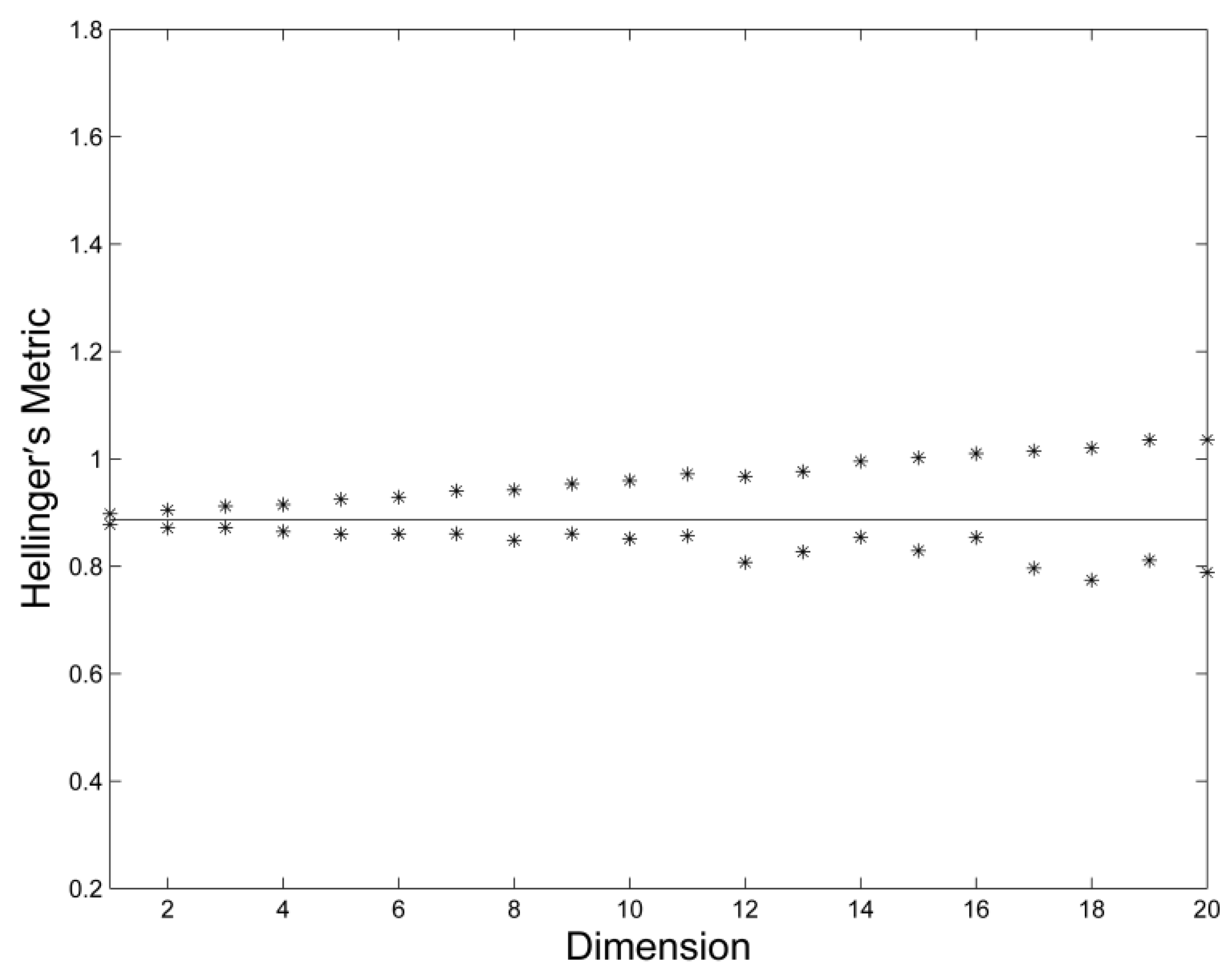
3. Results and Discussion

To study the proposed resampling estimator behavior, we addressed several dimensions $\left(\aleph \right)$, different Parzen’s coefficients $\left(\sigma ={\sigma }_1={\sigma }_2\right)$ as well as distinct Euclidean distances $\left(d=\Vert x_1-x_2\Vert \right)$.

Firstly, we studied the estimator from dimension 1 (one) to dimension 20 and obtained the results shown in Figure 5, which let us verify that the exact value was always within the estimated interval.

Figure 5. Behavior of the new robust two-stage resampling interval estimator regarding dimensions from 1 to 20. (The exact value of the nonparametric Hellinger’s metric is represented by a continuous line and is always contained in the estimated interval.)

Figure 5. Behavior of the new robust two-stage resampling interval estimator regarding dimensions from 1 to 20. (The exact value of the nonparametric Hellinger’s metric is represented by a continuous line and is always contained in the estimated interval.)

If the precision needed is not enough to generate disjoint intervals in competitive scenarios composed by multiple hypotheses, then the two-stage resampling can be repeated using a higher N₁, see Figure 6.

One can see in Figure 6 that the interval decreases with the increase of random samples, and that the exact value of nonparametric Hellinger’s metric, which is represented by a continuous line, is always contained in the estimated interval.

To verify the behavior of the resampling Estimator with the Parzen’s window ${\sigma }^2$ variation, we studied the results for 0.1 to 2 with 0.1 increases, Figure 7. In all the cases, the exact value is within the estimated error bound. Hence, the error bound estimator proposed here leads to robust intervals estimation.

Figure 6. Illustration of an asymptotic study of the novel robust two-stage resampling interval estimator between the upper and lower interval limits for different number of random samples (a detailed view regarding the Euclidean distances between 9 and 10 was added to the 1,000 samples graphic so the behavior of the estimator can be easily confirmed.)

Figure 6. Illustration of an asymptotic study of the novel robust two-stage resampling interval estimator between the upper and lower interval limits for different number of random samples (a detailed view regarding the Euclidean distances between 9 and 10 was added to the 1,000 samples graphic so the behavior of the estimator can be easily confirmed.)

Figure 7. Illustration of the behavior of the new robust two-stage resampling interval estimator with the Parzen’s window variation from 0.1 to 2; the graphics regard Euclidean distances from 0 (zero) to 5; the upper and lower interval limits always contain the exact value that is represented by a continuous line.

Figure 7. Illustration of the behavior of the new robust two-stage resampling interval estimator with the Parzen’s window variation from 0.1 to 2; the graphics regard Euclidean distances from 0 (zero) to 5; the upper and lower interval limits always contain the exact value that is represented by a continuous line.

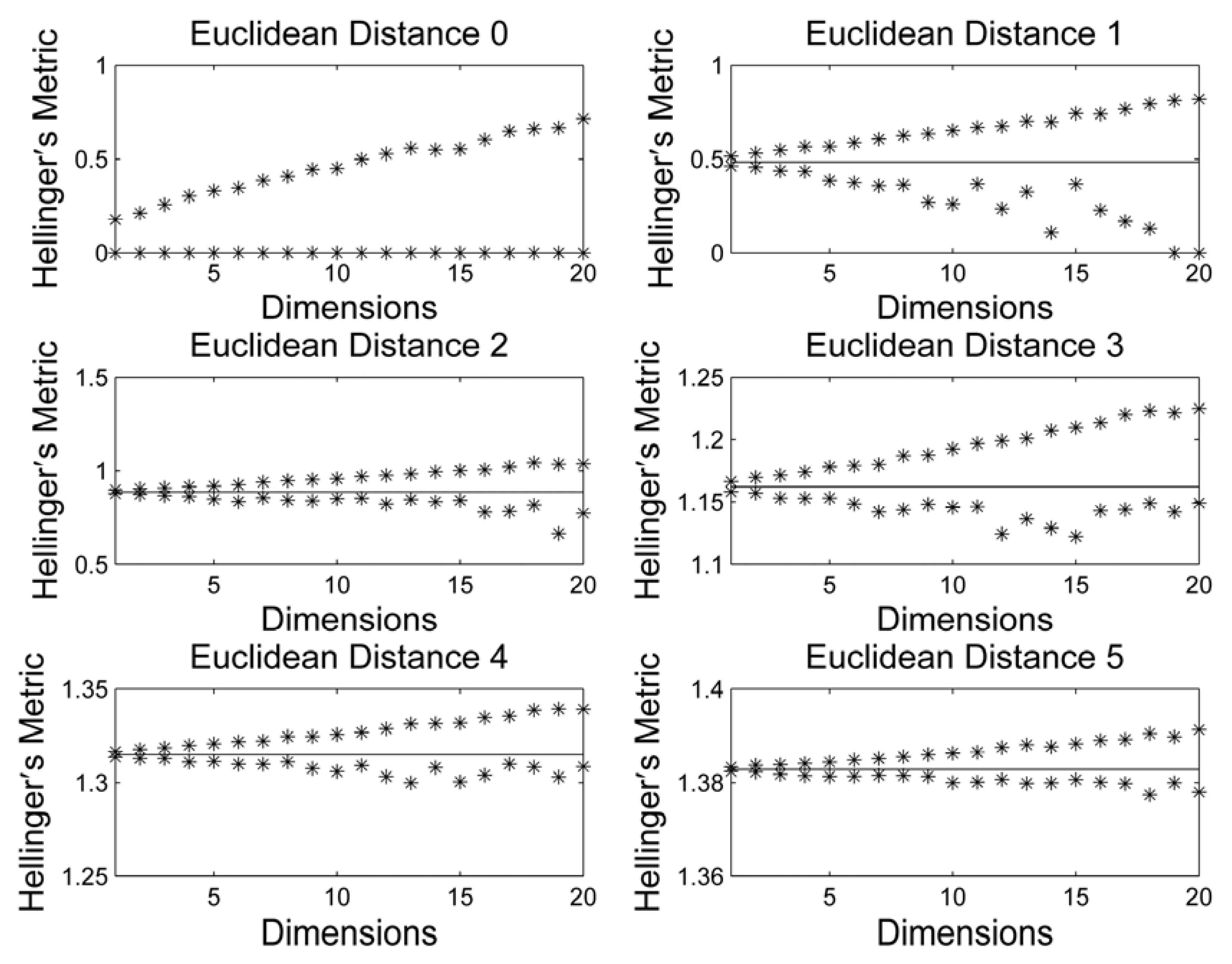
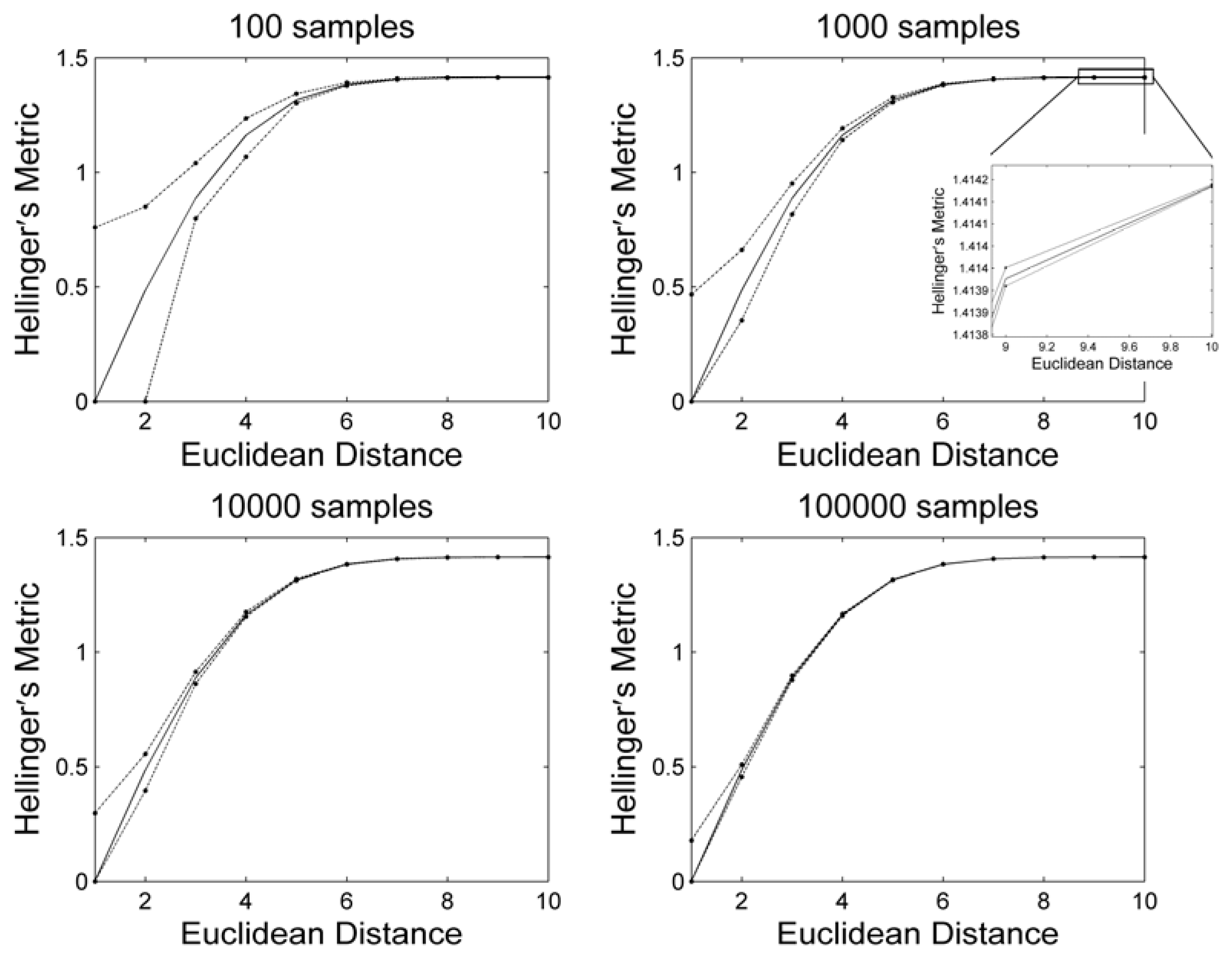
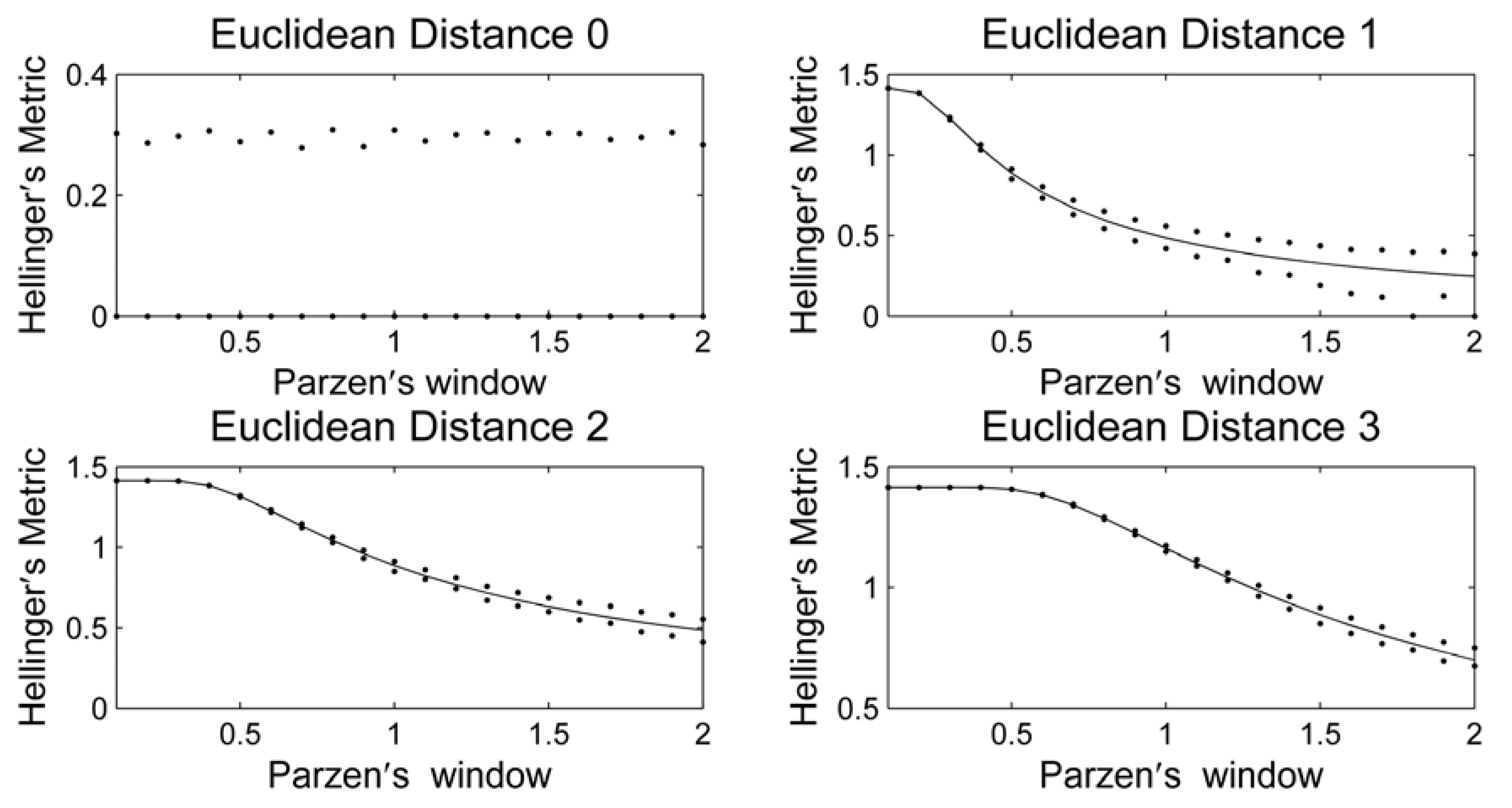
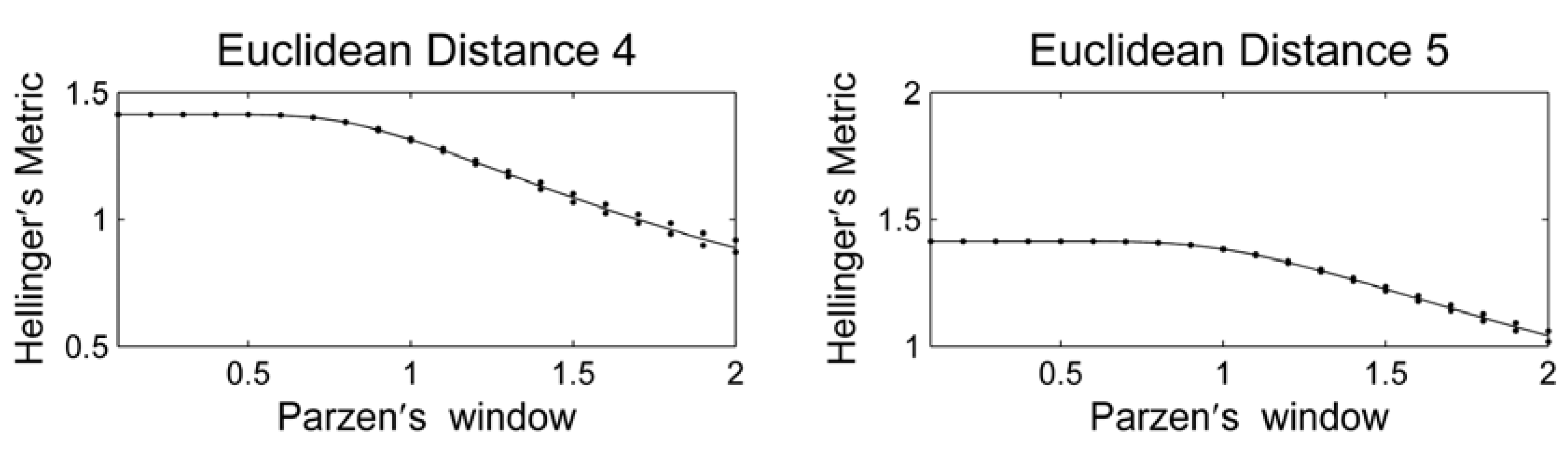
4. Conclusions

Hellinger’s metric was obtained from the generalized differential entropies and divergences. A nonparametric metric estimator based on Parzen’s window was introduced. We proposed a change of measure to allow a resampling method. With the change of measure proposed, it was possible to design a new two-stage resampling error bound estimator. The resampling error bound estimator also has the advantage of resampling just one density (the sum of normalized product densities) given by a nonparametric Parzen’s density with diagonal covariance, with asymptotic behavior. The new algorithm presented a robust behavior and very promising results. The asymptotic behavior allows to use this metric, in a competitive scenario with three or more densities, like clustering and image retrieval, to obtain disjoint intervals, simply by increasing the number of resampling samples. As to possible future work, two possible paths seem interesting: to evaluate Hellinger’s metric behavior on medical image processing and analysis as in [40,41], and to assess k-NN entropy estimation capability with the metric and heterocedastic data addressed here.