Kernel Spectral Clustering for Big Data Networks
Abstract
:1. Introduction
- We propose a novel memory-and computationally efficient model selection technique to tune the parameter of the model using angular similarity in the eigenspace between the projected vectors of the nodes in the validation set.
- We show that kernel spectral clustering is applicable for community detection in big data networks.
2. Kernel Spectral Clustering
2.1. Notations
- (1)
- A graph is mathematically represented as where V represents the set of nodes and represents the set of edges in the network. Physically, the nodes represent the entities in the network and the edges represent the relationship between these entities.
- (2)
- The cardinality of the set V is denoted as N.
- (3)
- The cardinality of the set E is denoted as e.
- (4)
- The matrix A is a matrix and represents the affinity or similarity matrix.
- (5)
- For unweighted graphs, A is called the adjacency matrix and if , otherwise .
- (6)
- The subgraph generated by the subset of nodes S is represented as . Mathematically, where and represents the set of edges in the subgraph.
- (7)
- The degree distribution function is given by . For the graph G it can written as while for the subgraph S it can be presented as . Each vertex has a degree represented as .
- (8)
- The degree matrix is represented as D, a diagonal matrix with diagonal entries .
- (9)
- The adjacency list corresponding to each vertex is given by .
- (10)
- The neighboring nodes of a given node are represented by .
- (11)
- The median degree of the graph is represented as M.
2.2. General Background
2.3. Primal-Dual Formulation
2.4. Encoding/Decoding Scheme
3. Model Selection by Means of Angular Similarity
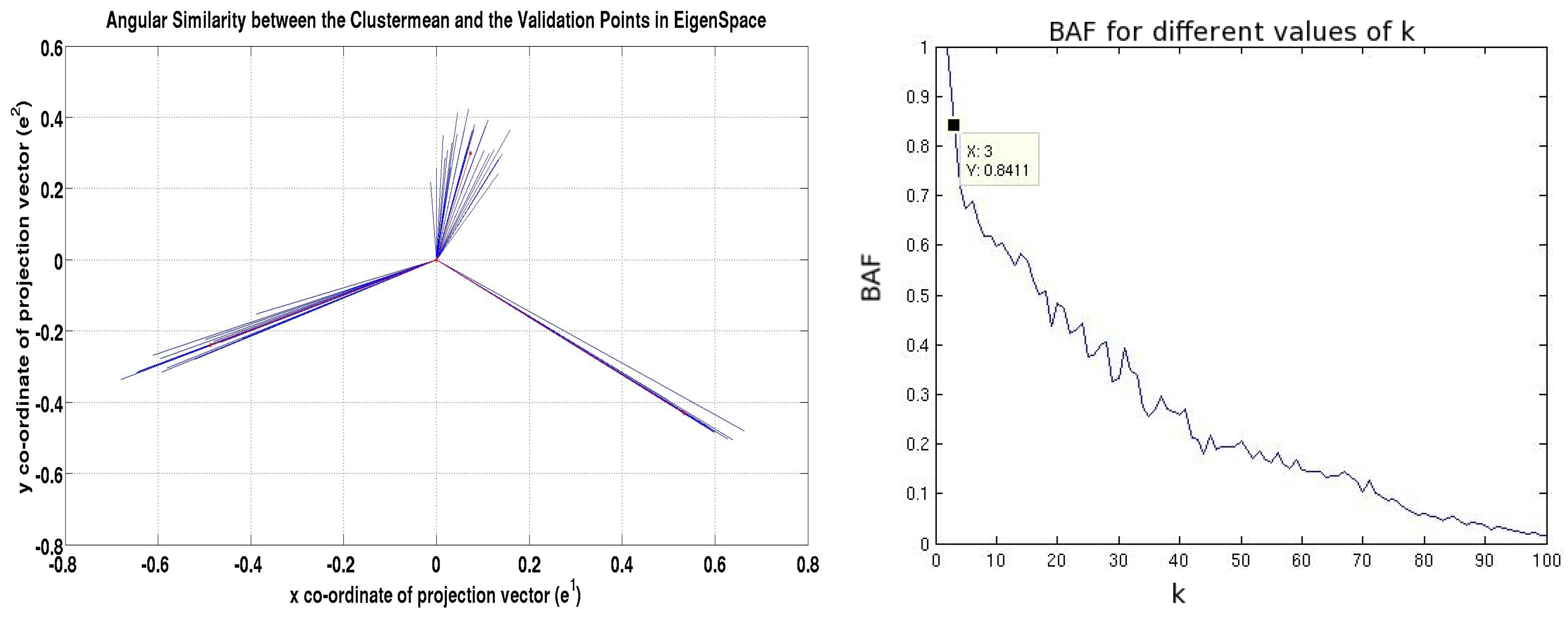
4. Selecting a Representative Subgraph

4.1. Subset Selection from Synthetic Network



4.2. Comparison with other Techniques on Synthetic Networks
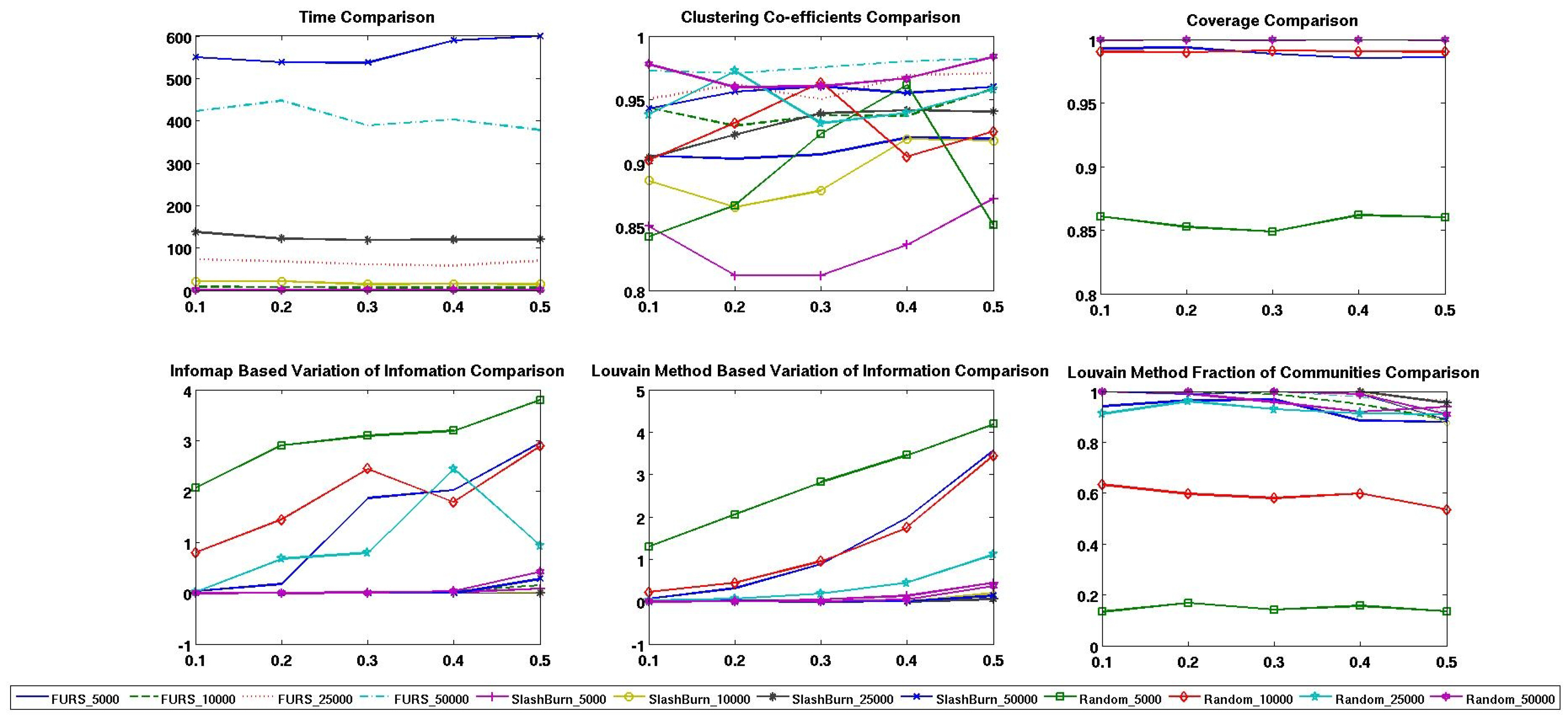
5. Experiments and Analysis
5.1. Dataset Description
- Synthetic Network: The synthetic network is generated from the software provided in [6] with a mixing parameter of . The number of nodes in the network is , the number of edges in the network is and the number of communities in the network is 6.
- YouTube Network: In YouTube social network, users form friendship with each other and the users can create groups that others can join. This network has more than 1 million nodes and around million edges. Thus the network is highly sparse.
- roadCA Network: A road network of California. Intersections and endpoints are represented by nodes and the roads connecting these intersections are represented as edges. The number of nodes in the network is around 2 million and the number of edges in the network is more than million.
- Livejournal Network: It is a free online social network where users are bloggers and they declare friendship among themselves. The number of nodes in the network is around 4 million and the network has around 35 million edges.
5.2. FURS on these Datasets
| Dataset | Nodes | Edges | Time | Coverage | Clustering Coefficient | Degree Distribution |
|---|---|---|---|---|---|---|
| Synthetic | 500,000 | 23,563,412 | 103.49 | 0.44 | 0.906 | 0.786 |
| YouTube | 1,134,890 | 2,987,624 | 20.546 | 0.28 | 0.975 | 0.959 |
| roadCA | 1,965,206 | 5,533,214 | 30.816 | 0.135 | 0.89 | 0.40 |
| Livejournal | 3,997,962 | 34,681,189 | 181.21 | 0.173 | 0.92 | 0.953 |
5.3. Results and Analysis
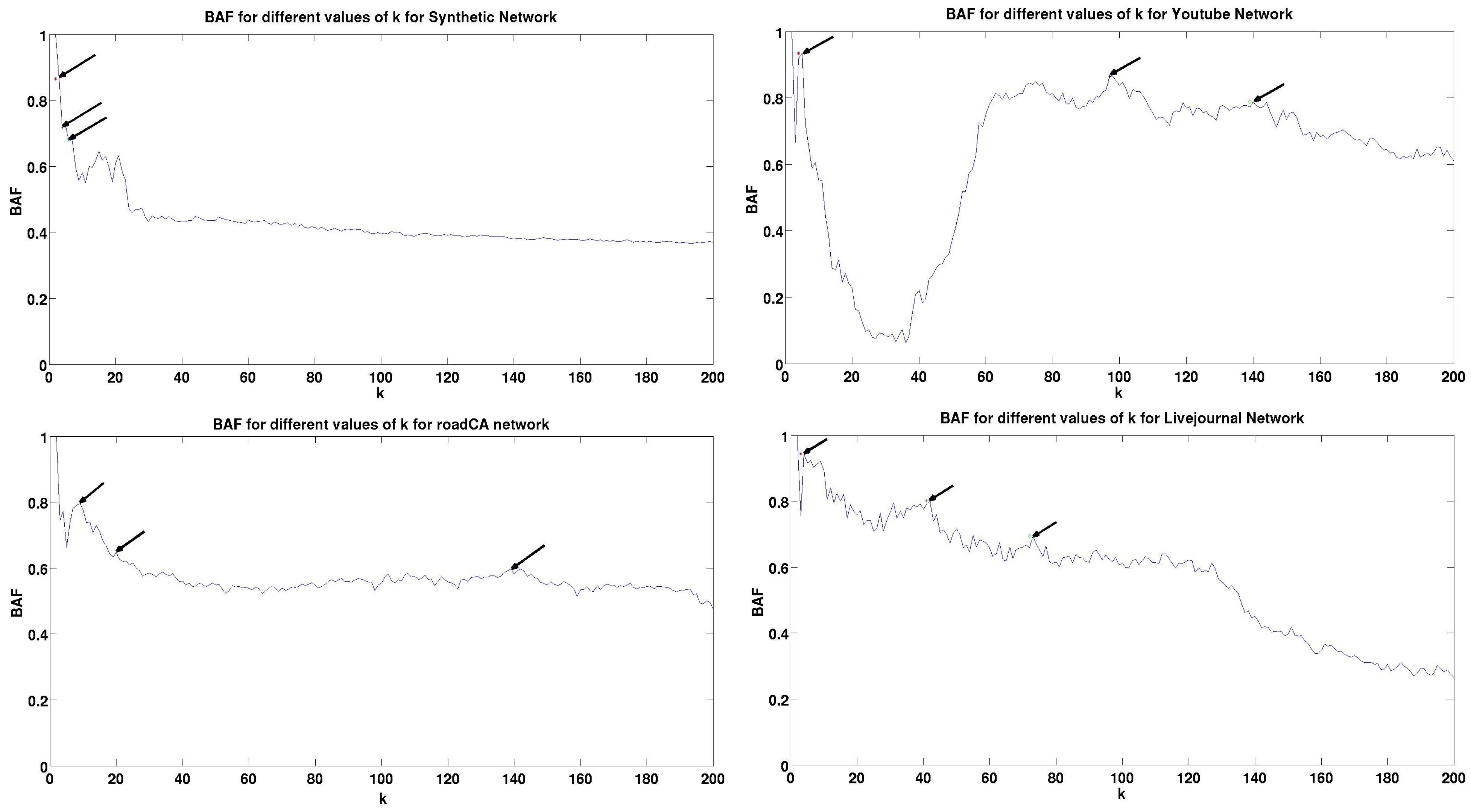
| Dataset | Peak | BAF | Peak | BAF | Peak | BAF | Train Time (Seconds) | Validation Time (Seconds) | Test Time (Seconds) |
|---|---|---|---|---|---|---|---|---|---|
| Synthetic | 3 | 0.8605 | 4 | 0.719 | 6 | 0.6817 | 103.45 | 111.42 | 10234.5 |
| YouTube | 5 | 0.9348 | 97 | 0.8654 | 139 | 0.7877 | 88.64 | 97.86 | 20055.45 |
| roadCA | 9 | 0.798 | 20 | 0.6482 | 138 | 0.5917 | 97.412 | 105.13 | 38960 |
| Livejournal | 4 | 0.94355 | 41 | 0.8014 | 73 | 0.6951 | 121.43 | 134.56 | 97221.4 |
| Dataset | BAF-KSC | BLF-KSC [14] | Louvain [9] | Infomap [7] | CNM [4] | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Clusters | Q | Con | Clusters | Q | Con | Clusters | Q | Con | Clusters | Q | Con | Clusters | Q | Con | |
| Openflights | 5 | 0.533 | 0.002 | 5 | 0.523 | 0.002 | 109 | 0.61 | 0.02 | 18 | 0.58 | 0.005 | 84 | 0.60 | 0.016 |
| PGPnet | 8 | 0.58 | 0.002 | 9 | 0.53 | 0.002 | 105 | 0.88 | 0.045 | 84 | 0.87 | 0.03 | 193 | 0.85 | 0.041 |
| Metabolic | 10 | 0.22 | 0.028 | 5 | 0.215 | 0.012 | 10 | 0.43 | 0.03 | 41 | 0.41 | 0.05 | 11 | 0.42 | 0.021 |
| HepTh | 6 | 0.45 | 0.0004 | 5 | 0.432 | 0.0004 | 172 | 0.65 | 0.004 | 171 | 0.3 | 0.004 | 6 | 0.423 | 0.0004 |
| HepPh | 5 | 0.56 | 0.0004 | 5 | 0.41 | 0.001 | 82 | 0.72 | 0.007 | 69 | 0.62 | 0.06 | 6 | 0.48 | 0.0007 |
| Enron | 10 | 0.4 | 0.002 | 7 | 0.21 | 0.001 | 1272 | 0.62 | 0.05 | 1099 | 0.37 | 0.27 | 6 | 0.25 | 0.0045 |
| Epinion | 10 | 0.22 | 0.0003 | 10 | 0.22 | 0.0 | 33 | 0.006 | 0.0003 | 17 | 0.18 | 0.0002 | 10 | 0.14 | 0.0 |
| Condmat | 6 | 0.28 | 0.0002 | 13 | 0.43 | 0.0003 | 1030 | 0.79 | 0.03 | 1086 | 0.79 | 0.025 | 8 | 0.38 | 0.0003 |
6. Conclusions
Acknowledgements
References
- Schaeffer, S. Algorithms for Nonuniform Networks. PhD thesis, Helsinki University of Technology, Helsinki, Finland, 2006. [Google Scholar]
- Danaon, L.; Diáz-Guilera, A.; Duch, J.; Arenas, A. Comparing community structure identification. J. Stat. Mech. Theory Exp. 2005, 9, P09008. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2009, 486, 75–174. [Google Scholar] [CrossRef]
- Clauset, A.; Newman, M.; Moore, C. Finding community structure in very large scale networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Lancichinetti, A.; Fortunato, S. Community detection algorithms: A comparitive analysis. Phys. Rev. E 2009, 80, 056117. [Google Scholar] [CrossRef]
- Rosvall, M.; Bergstrom, C. Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. USA 2008, 105, 1118–1123. [Google Scholar] [CrossRef] [PubMed]
- Langone, R.; Alzate, C.; Suykens, J.A.K. Kernel spectral clustering for community detection in complex networks. In Proceeding of the IEEE International Joint Conference on Neural Networks (IJCNN), Brisbane, Austrilia, 10–15 June 2012; pp. 1–8.
- Blondel, V.; Guillaume, J.; Lambiotte, R.; Lefebvre, L. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 10, P10008. [Google Scholar] [CrossRef]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On Spectral Clustering: Analysis and an Algorithm. In Proceedings of the Advances in Neural Information Processing Systems; Dietterich, T.G., Becker, S., Ghahramani, Z., Eds.; MIT Press: Cambridge, MA, USA, 2002; pp. 849–856. [Google Scholar]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Zelnik-Manor, L.; Perona, P. Self-tuning Spectral Clustering. In Advances in Neural Information Processing Systems; Saul, L.K., Weiss, Y., Bottou, L., Eds.; MIT Press: Cambridge, MA, USA, 2005; pp. 1601–1608. [Google Scholar]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Intell. 2000, 22, 888–905. [Google Scholar]
- Alzate, C.; Suykens, J.A.K. Multiway spectral clustering with out-of-sample extensions through weighted kernel PCA. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 335–347. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed]
- Maiya, A.; Berger-Wolf, T. Sampling Community Structure. In WWW ’10, Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; pp. 701–710.
- Mall, R.; Langone, R.; Suykens, J.A.K. FURS: Fast and Unique Representative Subset Selection for Large Scale Community Structure; Internal Report 13–22; ESAT-SISTA, K.U.Leuven: Leuven, Belgium, 2013. [Google Scholar]
- Kang, U.; Faloutsos, C. Beyond ‘Caveman Communities’: Hubs and Spokes for Graph Compression and Mining. In Proceedings of 2011 IEEE 11th International Coference on Data Mining (ICDM), Vancouver, Canada, 11–14 December 2011; pp. 300–309.
- Metropolis, N.; Rosenbluth, A.; Rosenbluth, M.; Teller, A.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Leskovec, J.; Faloutsos, C. Sampling from large graphs. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, USA, 20–23 August 2006; pp. 631–636.
- Langone, R.; Alzate, C.; Suykens, J.A.K. Kernel spectral clustering with memory effect. Phys. Stat. Mech. Appl. 2013, 392, 2588–2606. [Google Scholar] [CrossRef]
- Chung, F.R.K. Spectral graph theory (CBMS regional conference series in mathematics, No. 92). Am. Math. Soc. 1997. [Google Scholar]
- Suykens, J.A.K.; van Gestel, T.; de Brabanter, J.; de Moor, B.; Vandewalle, J. Least Squares Support Vector Machines; World Scientific: Singapore, Singapore, 2002. [Google Scholar]
- Muflikhah, L. Document clustering using concept space and cosine similarity measurement. In Proceedings of International Conference on Computer Technology and Development (ICCTD), Kota Kinabalu, Malaysia, 13–15 November 2009; pp. 58–62.
- Baylis, J. Error Correcting Codes: A Mathematical Introduction; CRC Press: Boca Raton, FL, USA, 1988. [Google Scholar]
- Stanford Large Network Dataset Collection Home Page. Available online: http://snap.stanford.edu/data/ (accessed on 3 May 2013).
Appendix A

© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mall, R.; Langone, R.; Suykens, J.A.K. Kernel Spectral Clustering for Big Data Networks. Entropy 2013, 15, 1567-1586. https://doi.org/10.3390/e15051567
Mall R, Langone R, Suykens JAK. Kernel Spectral Clustering for Big Data Networks. Entropy. 2013; 15(5):1567-1586. https://doi.org/10.3390/e15051567
Chicago/Turabian StyleMall, Raghvendra, Rocco Langone, and Johan A.K. Suykens. 2013. "Kernel Spectral Clustering for Big Data Networks" Entropy 15, no. 5: 1567-1586. https://doi.org/10.3390/e15051567
APA StyleMall, R., Langone, R., & Suykens, J. A. K. (2013). Kernel Spectral Clustering for Big Data Networks. Entropy, 15(5), 1567-1586. https://doi.org/10.3390/e15051567





