Molecular Dynamics Simulations on Evaporation of Droplets with Dissolved Salts
Abstract
:1. Introduction
2. Molecular Dynamics Simulations
2.1. Interatomic Potential and Initial Configuration
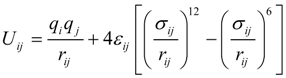
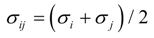
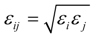
| Particle | σ (Å) | ε (KJ mol−1) | q (e) |
|---|---|---|---|
| O | 3.169 | 0.6502 | −0.8476 |
| H | 0.000 | 0.0000 | +0.4238 |
| Na+ | 2.583 | 0.4184 | +1.0000 |
| Li+ | 1.505 | 0.6904 | +1.0000 |
| K+ | 3.331 | 0.4184 | +1.0000 |
| Cl− | 4.400 | 0.4184 | −1.0000 |
| N | 3.710 | 0.6990 | +0.0000 |
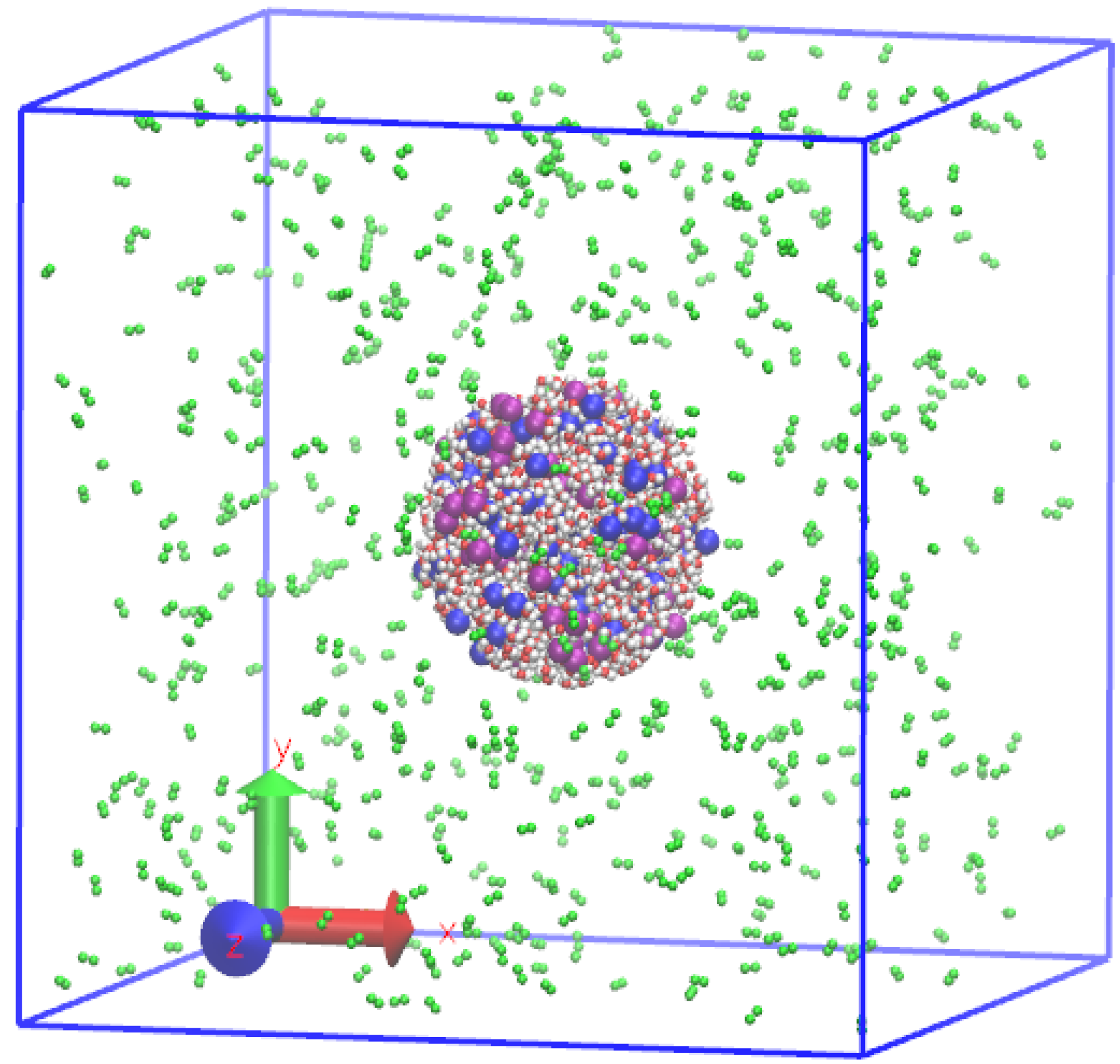
2.2. Preparation of Initial Equilibrium State
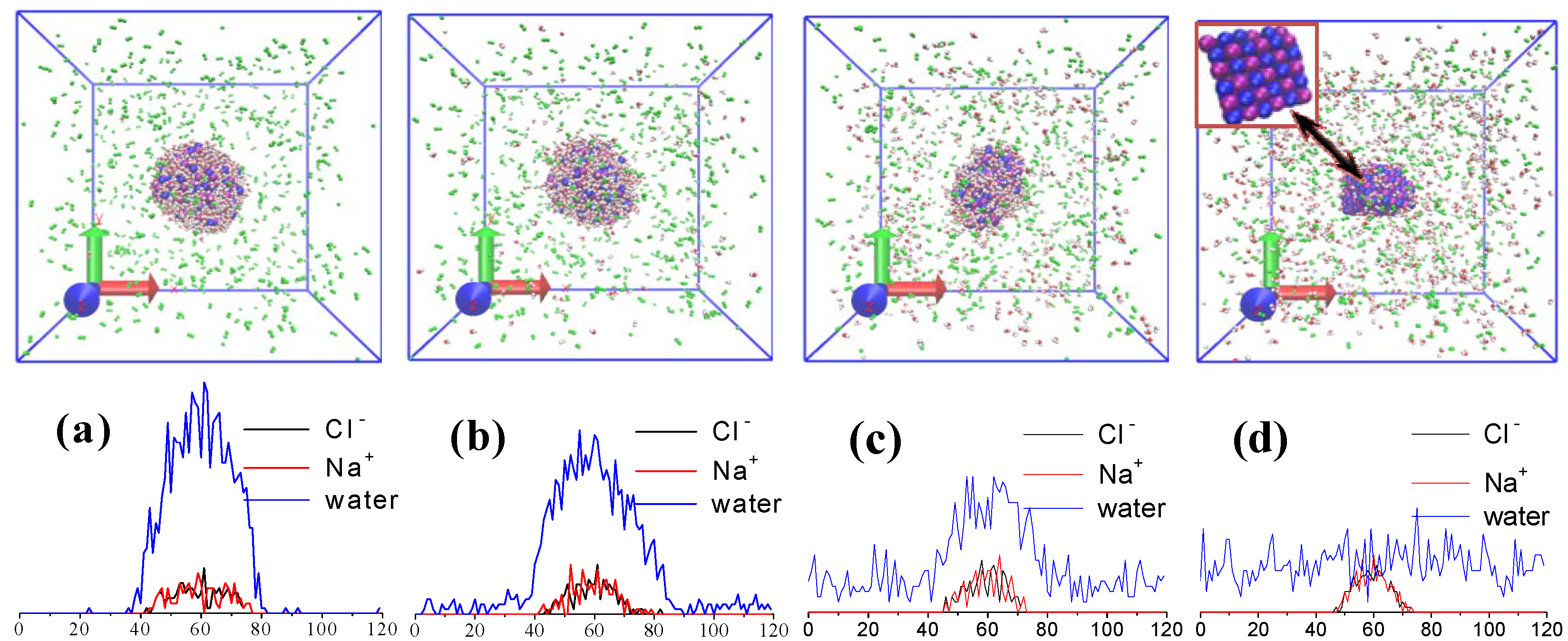
2.3. Droplet Evaporation
3. Results and Discussion
3.1. Effect of Salt Concentration


| Case | Hydration number of Li+ | Hydration number of Cl− |
|---|---|---|
| 40 LiCl | 3.76 | 9.02 |
| 80 LiCl | 3.34 | 8.65 |
| 120 LiCl | 3.06 | 8.16 |
| Case | 0 LiCl | 40 LiCl | 80 LiCl | 120 LiCl |
|---|---|---|---|---|
| Hydration number | 4.97 | 4.79 | 4.67 | 4.42 |

3.2. Effect of Salt Category
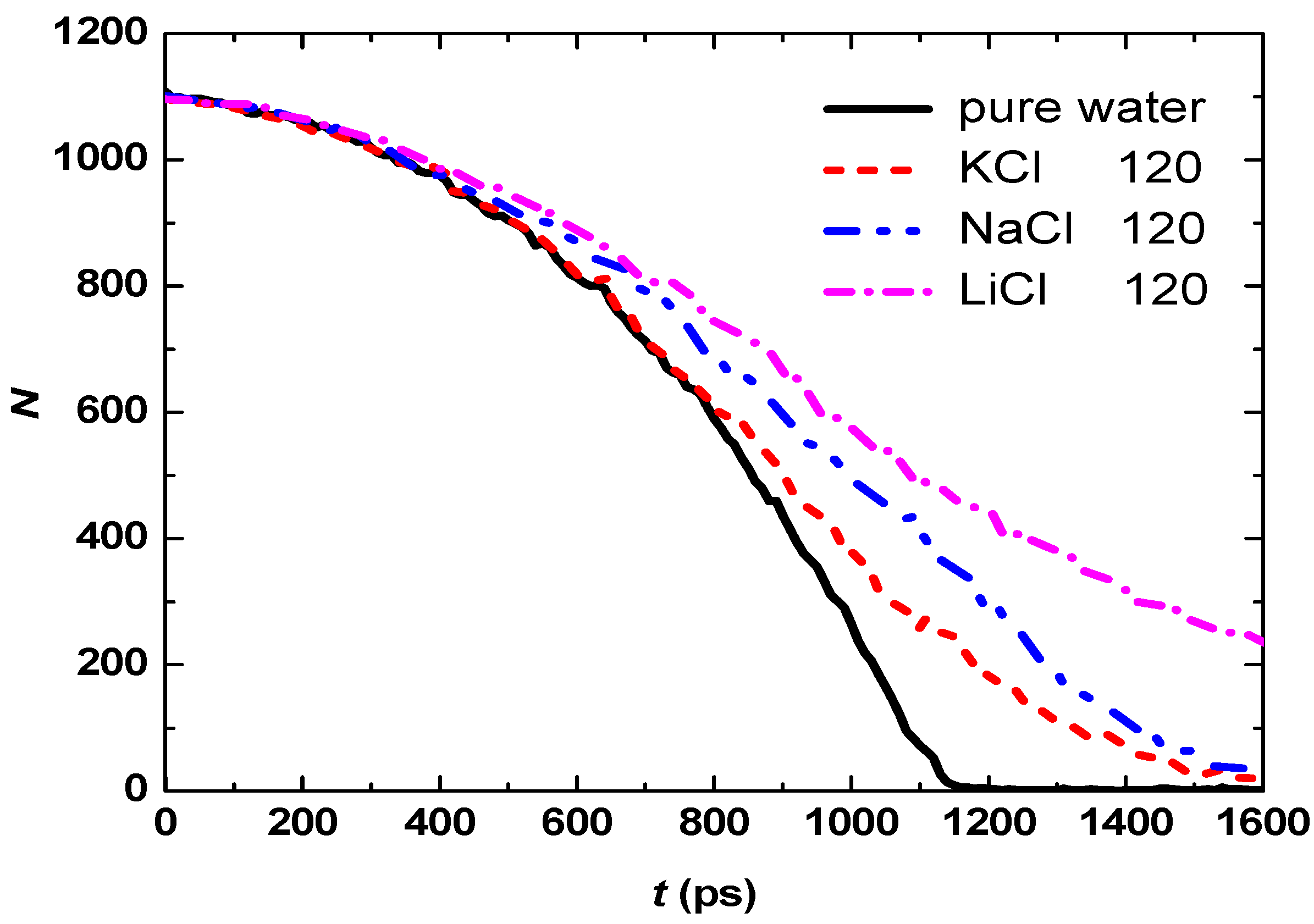

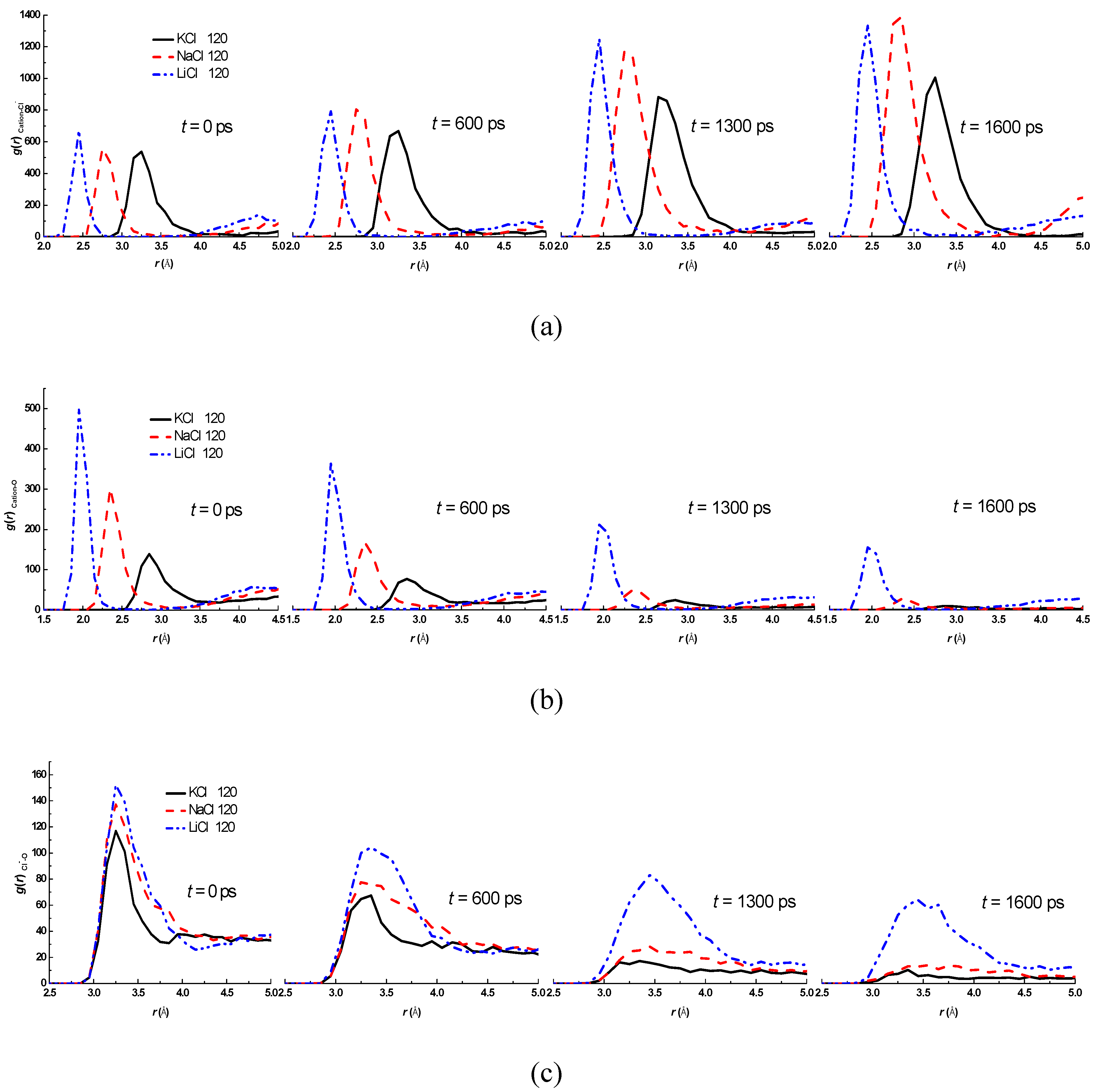
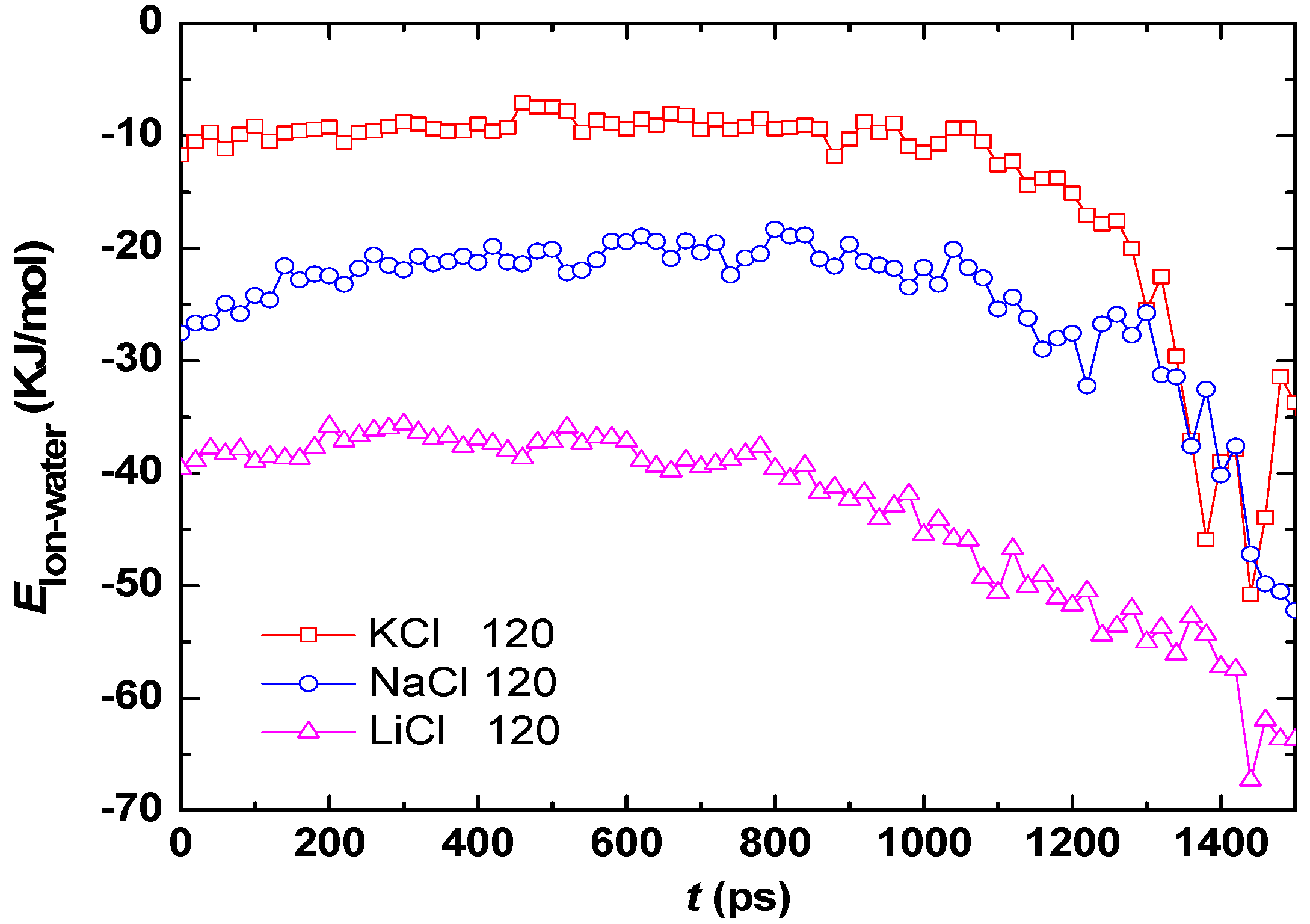

4. Conclusions
Acknowledgment
References
- Semenov, S.; Starov, V.M.; Velarde, M.G.; Rubio, R.G. Droplets evaporation: Problems and solutions. Eur. Phys. J.-Spec. Top. 2011, 197, 265–278. [Google Scholar] [CrossRef]
- Starov, V.M.; Churaev, N.V. Crystal groth at the end of a capillary on solution evaporation. J. Eng. Phys. 1988, 54, 443–446. [Google Scholar] [CrossRef]
- Sone, Y.; Sugimoto, H. Kinetic theory analysis of steady evaporating flows from a spherical condensed phase into a vacuum. Phys. Fluids. 1993, 5, 1491–1511. [Google Scholar] [CrossRef]
- Sumardiono, S.; Fischer, J. Molecular simulations of droplet evaporation by heat transfer. Microfluid. Nanofluid. 2007, 3, 127–140. [Google Scholar] [CrossRef]
- Landry, E.S.; Mikkilineni, S.; Paharia, M.; McGaughey, A.J.H. Droplet evaporation: A molecular dynamics investigation. J. Appl. Phys. 2007, 102, 124301. [Google Scholar] [CrossRef]
- Long, L.N.; Micci, M.M.; Wong, B.C. Molecular dynamics investigation of droplet evaporation. Comput. Phys. Commun. 1996, 96, 167–172. [Google Scholar] [CrossRef]
- Mason, P.E. Molecular dynamics study on the microscopic details of the evaporation of water. J. Phys. Chem. A 2011, 115, 6054–6058. [Google Scholar] [CrossRef] [PubMed]
- Consolini, L.; Aggarwal, S.K.; Murad, S. A molecular dynamics simulation of droplet evaporation. Int. J. Heat Mass Tran. 2003, 46, 3179–3188. [Google Scholar] [CrossRef]
- Walther, J.H.; Koumoutsakos, P. Molecular dynamics simulation of nanodroplet evaporation. J. Heat Tran. 2001, 123, 741–748. [Google Scholar] [CrossRef]
- Kaltz, T.L.; Long, L.N.; Micci, M.M. Supercritical vaporization of liquid oxygen droplets using molecular dynamics. Combust. Sci. Technol. 1998, 136, 279–301. [Google Scholar] [CrossRef]
- Bhansali, A.P.; Bayazitoglu, Y.; Maruyama, S.; Little, J.K. Molecular dynamics simulation of an evaporating sodium droplet. Int. J. Therm. Sci. 1999, 38, 66–74. [Google Scholar] [CrossRef]
- Wang, Z.J.; Chen, M.; Guo, Z.Y.; Yang, C. Molecular dynamics study on the liquid vapor interfacial profiles. Fluid Phase Equilibr. 2001, 183, 321–329. [Google Scholar] [CrossRef]
- Carey, V.P.; Wemhoff, A.P. Disjoining pressure effects in ultra-thin liquid films in micropassages-comparison of thermodynamic theory with predictions of molecular dynamics simulations. J. Heat Transfer 2006, 128, 1276–1284. [Google Scholar] [CrossRef]
- Yu, J.P.; Wang, H. A molecular dynamics investigation on evaporation of thin liquid films. Int. J. Heat Mass Transfer 2012, 55, 1218–1225. [Google Scholar] [CrossRef]
- Faeth, G.M. Current status of droplet and liquid combustion. Prog. Energy Combust. Sci. 1977, 3, 191–224. [Google Scholar] [CrossRef]
- Semenov, S.; Starov, V.M.; Rubio, R.G.; Agogo, H.; Velarde, M.G. Evaporation of sessile water droplets: Universal behaviour in presence of contact angle hysteresis. Colloid. Surface. A 2011, 391, 135–144. [Google Scholar] [CrossRef]
- Semenov, S.; Starov, V.M.; Rubio, R.G.; Velarde, M.G. Computer simulations of evaporation of pinned sessile droplets: influence of kinetic effects. Langmuir 2012, 28, 15203–15211. [Google Scholar] [CrossRef] [PubMed]
- Mucha, M.; Jungwirth, P. Salt crystallization from an evaporating aqueous solution by molecular dynamics simulations. J. Phys. Chem. B 2003, 107, 8271–8274. [Google Scholar] [CrossRef]
- Daub, C.D.; Cann, N.M. How are completely desolvated ions produced in electrospray ionization: Insights from molecular dynamics simulations. Anal. Chem. 2011, 83, 8372–8376. [Google Scholar] [CrossRef] [PubMed]
- Theron, S.A.; Zussman, E.; Yarin, A.L. Experimental investigation of the governing parameters in the electrospinning of polymer solution. Polymer 2004, 45, 2017–2030. [Google Scholar] [CrossRef]
- Kӧhler, H. The nucleus in and the crowth of hygroscopic droplets. Transactions of the Faraday Society. 1936, 32, 1152–1161. [Google Scholar] [CrossRef]
- Jungwirth, P.; Tobias, D.J. Molecular stucture of salt solution: A new view of the interface with implications for heterogeneous atmospheric chemistry. J. Phys. Chem. B 2001, 105, 10468–10472. [Google Scholar] [CrossRef]
- Jungwirth, P.; Tobias, D.J. Ions at the air/water interface. J. Phys. Chem. B 2002, 106, 6361–6373. [Google Scholar] [CrossRef]
- Li, X.; Hede, T.; Tu, Y.Q.; Leck, C.; Ågren, H. Surface-active cis-pinonic acid in atmopheric droplet: A molecular dynamics study. J. Phys. Chem. Lett. 2010, 1, 769–773. [Google Scholar] [CrossRef]
- Sun, L.; Li, X.; Hede, T.; Tu, Y.Q.; Leck, C.; Ågren, H. Molecular dynamics simulations of the surface tension and structure of salt solution and clusters. J. Phys. Chem. B 2012, 116, 3198–3204. [Google Scholar] [CrossRef] [PubMed]
- Caleman, C.; Spoel, D.V.D. Evaporation from water clusters containing singly charged ions. Phys. Chem. Chem. Phys. 2007, 9, 5105–5111. [Google Scholar] [CrossRef] [PubMed]
- Daub, C.D.; Cann, N.M. Molecular dynamics simulations to examine structure, energetics, and evaporation/condensation dynamics in small charged clusters of water or methanol containing a single monatomic ion. J. Phys. Chem. A 2012, 116, 10488–10495. [Google Scholar] [CrossRef] [PubMed]
- Znamenskiy, V.; Marginean, I.; Vertes, A. Solvated ion evaporation from charged water nanodroplets. J. Phys. Chem. A 2003, 107, 7406–7412. [Google Scholar] [CrossRef]
- Bouazizi, S.; Nasr, S. Local order in aqueous lithium chloride solutions as studied by X-ray scattering and molecular dynamics simulations. J. Mol. Struct. 2007, 837, 206–213. [Google Scholar] [CrossRef]
- Chowdhuri, S.; Chandra, A. Molecular dynamics simulations of aqueous NaCl and KCl solutions: Effects of ion concentration on the single-particle, pair, and collective dynamical properties of ions and water molecules. J. Phys. Chem. 2001, 115, 3732–3741. [Google Scholar] [CrossRef]
- Beckers, J.V.L.; Lowe, C.P.; Leeuw, S.W.D. An iterative PPPM method for simulating coulombic systems on distributed memory parallel computers. Mol. Simulat. 1998, 3, 369–383. [Google Scholar] [CrossRef]
- Shigeo, M.A.; Sohei, M.; Akihiro, O. Surface phenomena of molecular clusters by molecular dynamics method. Therm. Sci. Eng. 1994, 2, 77–84. [Google Scholar]
- Zhang, Y.J.; Cremer, P.S. Interactions between macromolecules and ions: the Hofmeister series. Curr. Opin. Chem. Biol. 2006, 10, 658–663. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, B.-B.; Wang, X.-D.; Chen, M.; Xu, J.-L. Molecular Dynamics Simulations on Evaporation of Droplets with Dissolved Salts. Entropy 2013, 15, 1232-1246. https://doi.org/10.3390/e15041232
Wang B-B, Wang X-D, Chen M, Xu J-L. Molecular Dynamics Simulations on Evaporation of Droplets with Dissolved Salts. Entropy. 2013; 15(4):1232-1246. https://doi.org/10.3390/e15041232
Chicago/Turabian StyleWang, Bing-Bing, Xiao-Dong Wang, Min Chen, and Jin-Liang Xu. 2013. "Molecular Dynamics Simulations on Evaporation of Droplets with Dissolved Salts" Entropy 15, no. 4: 1232-1246. https://doi.org/10.3390/e15041232
APA StyleWang, B.-B., Wang, X.-D., Chen, M., & Xu, J.-L. (2013). Molecular Dynamics Simulations on Evaporation of Droplets with Dissolved Salts. Entropy, 15(4), 1232-1246. https://doi.org/10.3390/e15041232





