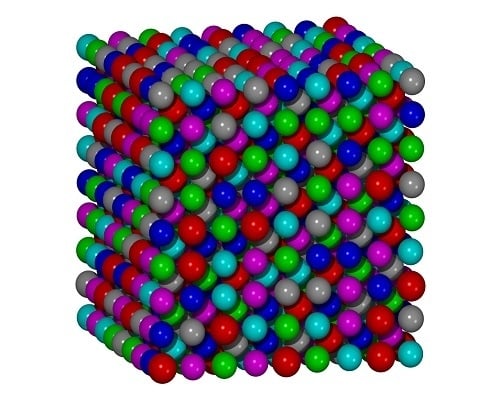
Atomic Structure Modeling of Multi-Principal-Element Alloys by the Principle of Maximum Entropy
Abstract
:1. Introduction
2. Method and Algorithm in Model Building
3. Results and Analyses
3.1. Binary Alloys
| Phase | rmin | rmax | r | Density (%) | |
|---|---|---|---|---|---|
| Fe0.915Cr0.085 | 2.2361 | 2.2361 | 2.2361 | 0.0000 | 52.6 |
| Fe0.889Cr0.111 | 2.0684 | 2.0000 | 2.1795 | 0.1795 | 54.3 |
| Fe0.794Cr0.206 | 1.4705 | 1.4142 | 1.6583 | 0.2441 | 52.0 |
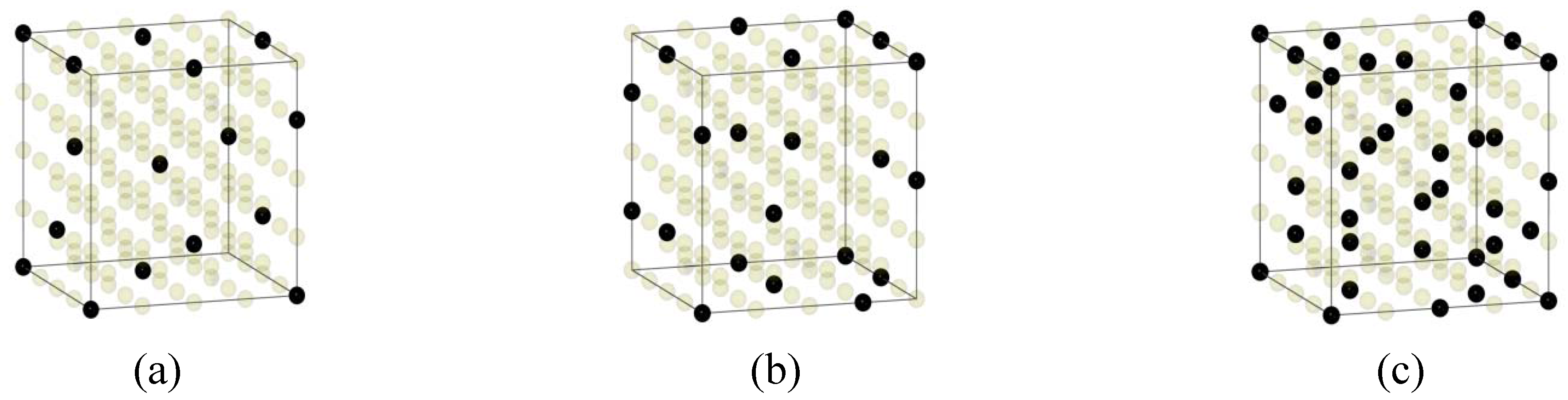
3.2. BCC Multi-Principal-Element Alloys

| Phase | Cell type | Distance distribution in nearest neighbor sites (%) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Quaternary phase | BCC | 8.5 | 83.0 | 6.9 | 1.6 | 0.0 | 0.0 |
| FCC | 74.3 | 23.8 | 1.9 | 0.0 | 0.0 | 0.0 | |
| Quinary phase | BCC | 0.0 | 65.5 | 30.6 | 3.4 | 0.5 | 0.0 |
| FCC | 47.3 | 45.0 | 7.5 | 0.2 | 0.0 | 0.0 | |
| Senary phase | BCC | 0.0 | 41.4 | 52.4 | 6.0 | 0.2 | 0.0 |
| FCC | 17.2 | 64.9 | 17.7 | 0.2 | 0.0 | 0.0 | |
| Septenary phase | BCC | 0.0 | 19.2 | 65.3 | 15.0 | 0.3 | 0.2 |
| FCC | 3.9 | 50.4 | 44.4 | 1.1 | 0.2 | 0.0 | |
| Octonary phase | BCC | 0.0 | 2.5 | 70.9 | 24.3 | 2.1 | 0.2 |
| FCC | 0.2 | 27.1 | 69.8 | 2.7 | 0.2 | 0.0 | |
3.3. FCC Multi-Principal-Element Alloys
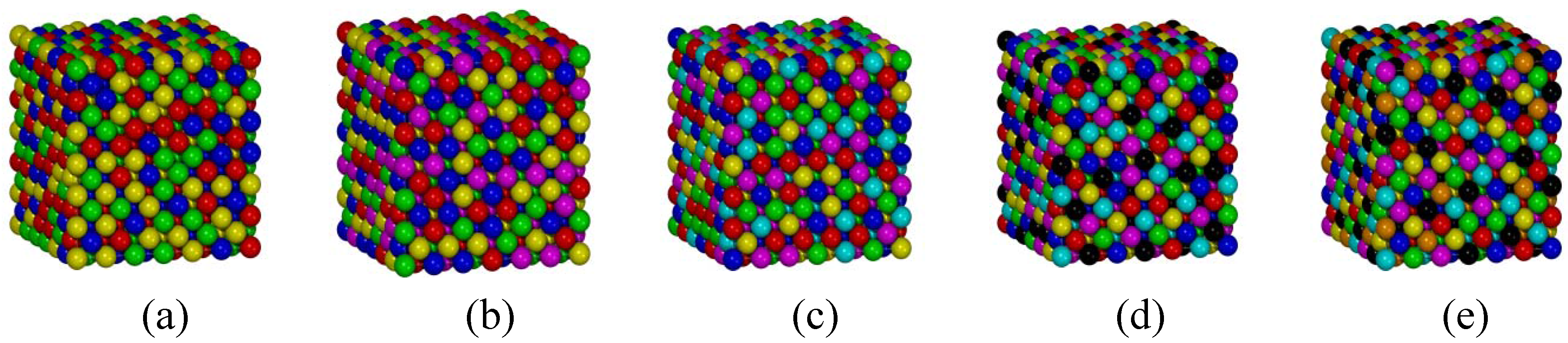
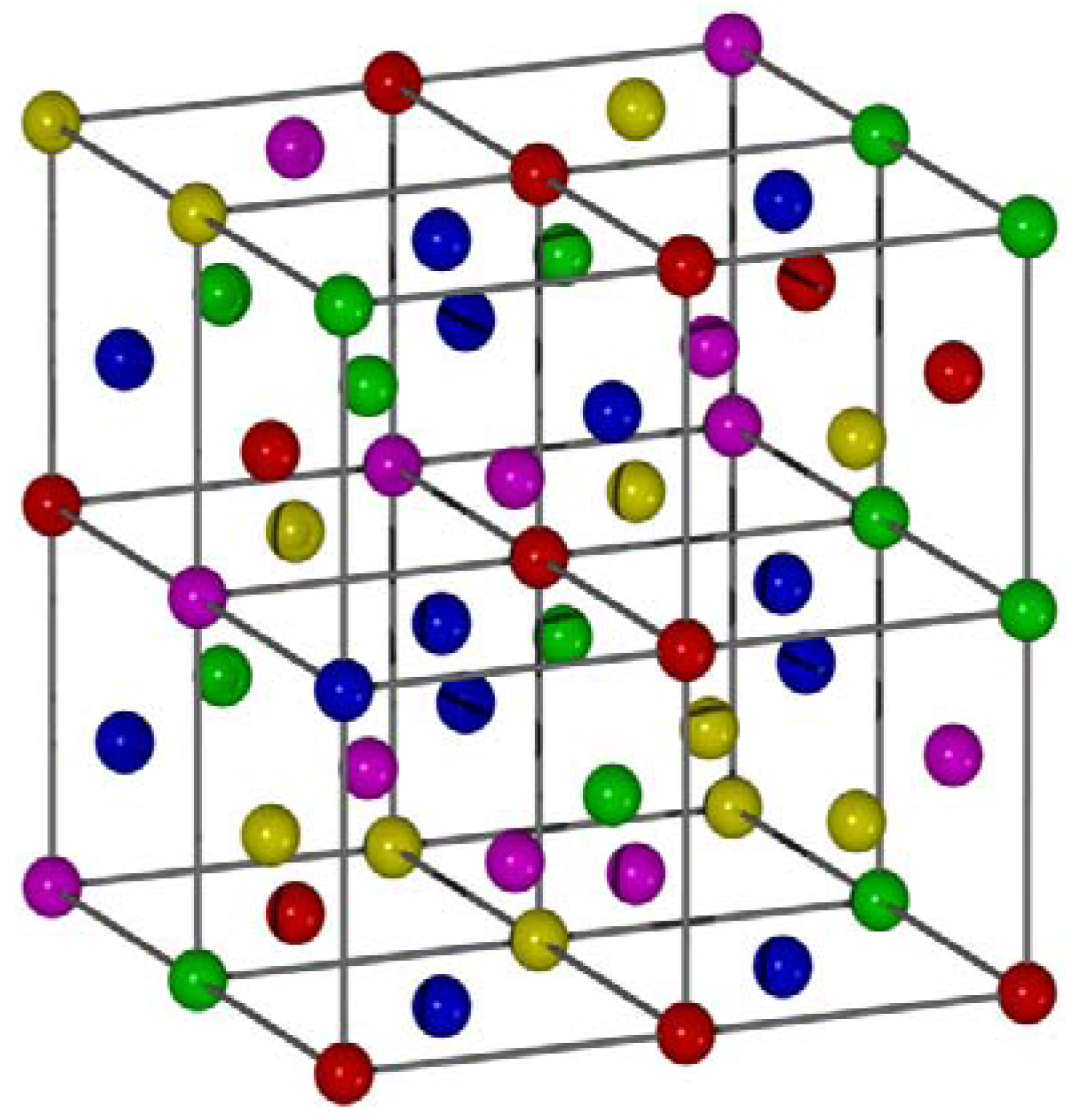
3.4. Applications to the Real Multi-Principal-Element Alloys
| Phase | a (Å) | aexpt (Å) | Error | g |
|---|---|---|---|---|
| FCC FeCoCrNi | 3.84 | 3.56 [27] | 7.9% | 0.0085 |
| FCC CoCrFeMnNi | 3.84 | 3.59 [5] | 7.0% | 0.0070 |
| BCC AlCoCrFeNi | 3.08 | 2.87 [29] | 7.3% | 0.0210 |
| BCC AlCoCrCuFeNi | 3.10 | 2.87 [30] | 8.0% | 0.0150 |


4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Yeh, J.-W.; Chen, S.-K.; Lin, S.-J.; Gan, J.-Y.; Chin, T.-S.; Shun, T.-T.; Tsau, C.-H.; Chang, S.-Y. Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Huang, P.-K.; Yeh, J.-W.; Shun, T.-T.; Chen, S.-K. Multi-principal-element alloys with improved oxidation and wear resistance for thermal spray coating. Adv. Eng. Mater. 2004, 6, 74–78. [Google Scholar] [CrossRef]
- Clausius, R. Die Energie der Welt ist konstant. Die Entropie der Welt strebt einem Maximum zu. Annalen der Physik und Chemie 1865, 125, 353–400. (in German). [Google Scholar] [CrossRef]
- Boltzmann, L. Lectures on Gas Theory; University of California Press: Berkeley, CA, USA, 1898. [Google Scholar]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375, 213–218. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, X.; Liaw, P.K. Alloy design and properties optimization of high-entropy alloys. JOM 2012, 64, 830–838. [Google Scholar] [CrossRef]
- Chen, Y.L.; Hu, Y.H.; Tsai, C.W.; Hsieh, C.A.; Kao, S.W.; Yeh, J.W.; Chin, T.S.; Chen, S.K. Alloying behavior of binary to octonary alloys based on Cu-Ni-Al-Co-Cr-Fe-Ti-Mo during mechanical alloying. J. Alloys Compd. 2009, 477, 696–705. [Google Scholar] [CrossRef]
- Senkov, O.N.; Wilks, G.B.; Miracle, D.B.; Chuang, C.P.; Liaw, P.K. Refractory high-entropy alloys. Intermetallics 2010, 18, 1758–1765. [Google Scholar] [CrossRef]
- Lucas, M.S.; Wiks, G.B.; Mauger, L.; Munoz, J.A.; Senkov, O.N.; Michel, E.; Jorwath, J.; Semiatin, S.L.; Stone, M.B.; Abernathy, D.L.; Karapetrova, E. Absence of long-range chemical ordering in equimolar FeCoCrNi. Appl. Phys. Lett. 2012, 100, 251907. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Sys. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Janes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Carlsson, A.E.; Fedders, P.A. Maximum-entropy method for electronic properties of alloys. Phys. Rev. B 1986, 34, 3567–3571. [Google Scholar] [CrossRef]
- Dobrzynski, L. Maximum-entropy reconstruction of the internal magnetization density distributions in Fe3(AlxSi1-x) alloys. J. Phys. Condens. Matter. 1995, 7, 1373–1389. [Google Scholar] [CrossRef]
- Karlin, H.V.; Gorban, A.N. Maximum entropy principle for lattice kinetic equations. Phys. Rev. Lett. 1998, 81, 6–9. [Google Scholar] [CrossRef]
- Sobczyk, K. Reconstruction of random material microstructures: patterns of maximum entropy. Prob. Eng. Mech. 2003, 18, 279–287. [Google Scholar] [CrossRef]
- Sankaran, S.; Zabaras, N. A maximum entropy approach for property prediction of random microstructures. Acta Mater. 2006, 54, 2265–2276. [Google Scholar] [CrossRef]
- Yonampto, Y. Application of maximum entropy method to semiconductor engineering. Entropy 2013, 15, 1663–1689. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Magnetocaloric effect and magnetic refrigeration. J. Magn. Magn. Mater. 1999, 200, 44–56. [Google Scholar] [CrossRef]
- Clusius, K. Origin of zero-point entropy. Nature 1932, 130, 775–776. [Google Scholar] [CrossRef]
- Verlinde, E. On the origin of gravity and the laws of Newton. J. High Ener. Phys. 2011, 4, 29–27. [Google Scholar] [CrossRef]
- Wissner-Gross, A.D.; Freer, C.E. Causal entropic forces. Phys. Rev. Lett. 2013, 110, 168702–5. [Google Scholar] [CrossRef] [PubMed]
- Python Programming Language. Available online: http://www.python.org/ (accessed on 19 September 2013).
- Numpy. Available online: http://www.numpy.org/ (accessed on 19 September 2013).
- Martin, G. Martin Gardner’s New Mathematical Diversions from Scientific American; University of Chicago Press: Chicago, IL, USA, 1983. [Google Scholar]
- Song, C.; Wang, P.; Makse, H.A. A phase diagram for jammed matter. Nature 2008, 453, 629–632. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.Q. Paracrystalline property of high-entropy alloys. AIP Adv. 2013, 3, 102105. [Google Scholar] [CrossRef]
- Lucas, M.S.; Mauger, L.; Munoz, J.A.; Xiao, Y.M.; Sheets, A.O.; Semiatin, S.L.; Horwath, J.; Turgut, Z. Magnetic and vibrational properties of high-entropy alloys. J. Appl. Phys. 2011, 109, 07E307. [Google Scholar] [CrossRef]
- Otto, F.; Dlouhy, A.; Somsen, Ch.; Bei, H.; Eggeler, G.; George, E.P. The influences of temperature and microstructure on the tensile properties of a CoCrFeMnNi high-entropy alloy. Acta Mater. 2013, 61, 5743–5755. [Google Scholar] [CrossRef]
- Kao, Y.F.; Chen, T.J.; Chen, S.K.; Yeh, J.W. Microstructure and mechanical property of as-cast, -homogenized, and -deformed AlxCoCrFeNi (0 ≤ x ≤ 2) high-entropy alloys. J. Alloys Compd. 2009, 488, 57–64. [Google Scholar] [CrossRef]
- Singh, S.; Wanderka, N.; Murty, B.S.; Glatzel, U.; Banhart, J. Decomposition in multi-component AlCoCrCuFeNi high-entropy alloy. Acta Mater. 2011, 59, 182–190. [Google Scholar] [CrossRef]
- Chen, N.X.; Shen, J.; Su, X.P. Theoretical study on the phase stability, site preference, and lattice parameters for Gd(Fe,T)12. J. Phys. Condens. Matter. 2001, 13, 2727–2736. [Google Scholar]
- Hindeleh, A.M.; Hosemann, R. Paracrystals representing the physical state of matter. J. Phys. C Solid State Phys. 1988, 21, 4155–4170. [Google Scholar] [CrossRef]
- Greenwood, N.N.; Earnshaw, A. Chemistry of the Elements; Butterworth-Heinemann: Oxford, UK, 1997. [Google Scholar]
- Wang, T. Coulomb force as an entropic force. Phys. Rev. D 2010, 81, 104045. [Google Scholar] [CrossRef]
- Hendi, S.H.; Sheykhi, A. Entropic corrections to Coulomb’s law. Int. J. Theor. Phys. 2012, 51, 1125–1136. [Google Scholar] [CrossRef]
- Sanchez, J.M.; Ducastelle, F.; Gratias, D. Generalized cluster description of multicomponent systems. Physica A 1984, 128, 334–350. [Google Scholar] [CrossRef]
- Jaros, M. Electronic properties of semiconductor alloy systems. Rep. Prog. Phys. 1985, 48, 1091–1154. [Google Scholar] [CrossRef]
- Zunger, A.; Wei, S.H.; Ferreira, L.G.; Bernard, J.E. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353–356. [Google Scholar] [CrossRef] [PubMed]
- POV-Ray Code. Available online: http://www.povray.org (accessed on 19 September 2013).
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, S. Atomic Structure Modeling of Multi-Principal-Element Alloys by the Principle of Maximum Entropy. Entropy 2013, 15, 5536-5548. https://doi.org/10.3390/e15125536
Wang S. Atomic Structure Modeling of Multi-Principal-Element Alloys by the Principle of Maximum Entropy. Entropy. 2013; 15(12):5536-5548. https://doi.org/10.3390/e15125536
Chicago/Turabian StyleWang, Shaoqing. 2013. "Atomic Structure Modeling of Multi-Principal-Element Alloys by the Principle of Maximum Entropy" Entropy 15, no. 12: 5536-5548. https://doi.org/10.3390/e15125536
APA StyleWang, S. (2013). Atomic Structure Modeling of Multi-Principal-Element Alloys by the Principle of Maximum Entropy. Entropy, 15(12), 5536-5548. https://doi.org/10.3390/e15125536