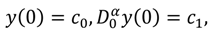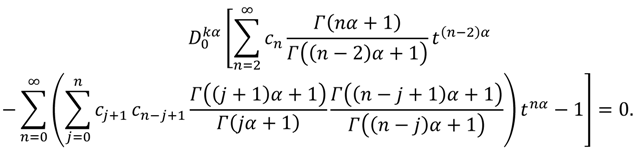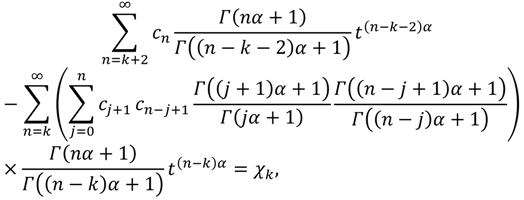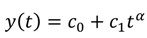1. Introduction
Fractional calculus theory is a mathematical analysis tool applied to the study of integrals and derivatives of arbitrary order, which unifies and generalizes the notions of integer-order differentiation and
n-fold integration [
1,
2,
3,
4]. Commonly these fractional integrals and derivatives were not known to many scientists and up until recent years, they have been only used in a purely mathematical context, but during these last few decades these integrals and derivatives have been applied in many science contexts due to their frequent appearance in various applications in the fields of fluid mechanics, viscoelasticity, biology, physics, image processing, entropy theory, and engineering [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14].
It is well known that the fractional order differential and integral operators are non-local operators. This is one reason why fractional calculus theory provides an excellent instrument for description of memory and hereditary properties of various physical processes. For example, half-order derivatives and integrals proved to be more useful for the formulation of certain electrochemical problems than the classical models [
1,
2,
3,
4]. Applying fractional calculus theory to entropy theory has also become a significant tool and a hotspot research domain [
15,
16,
17,
18,
19,
20,
21,
22,
23,
24] since the fractional entropy could be used in the formulation of algorithms for image segmentation where traditional Shannon entropy has presented limitations [
18] and in the analysis of anomalous diffusion processes and fractional diffusion equations [
19,
20,
21,
22,
23,
24]. Therefore, the application of fractional calculus theory has become a focus of international academic research. Excellent accounts of the study of fractional calculus theory and its applications can be found in [
25,
26].
Power series have become a fundamental tool in the study of elementary functions and also other not so elementary ones as can be checked in any book of analysis. They have been widely used in computational science for easily obtaining an approximation of functions [
27]. In physics, chemistry, and many other sciences this power expansion has allowed scientist to make an approximate study of many systems, neglecting higher order terms around the equilibrium point. This is a fundamental tool to linearize a problem, which guarantees easy analysis [
28,
29,
30,
31,
32,
33,
34,
35].
The study of fractional derivatives presents great difficulty due to their complex integro-differential definition, which makes a simple manipulation with standard integer operators a complex operation that should be done carefully. The solution of fractional differential equations (FDEs), in most methods, appears as a series solution of fractional power series (FPS) [
36,
37,
38,
39,
40,
41,
42]. Consequently, many authors suggest a general form of power series, specifically Taylor's series, including fractional ones. To mention a few, Riemann [
43] has been written a formal version of the generalized Taylor series formula as:
where
is the Riemann-Liouville fractional integral of order
m +
r. Watanabe in [
44] has been obtained the following relation:
where
and
is the Riemann-Liouville fractional derivative of order
α +
n. Trujillo
et al. [
45] have been introduced the generalized Taylor's formula as:
where
. Recently, Odibat and Shawagfeh [
46] have been represented a new generalized Taylor's formula which as follows:
where
and
is the Caputo fractional derivative of order
mα. For
α = 1, the generalized Taylor's formula reduces to the classical Taylor's formula. Throughout this paper ℕ the set of natural numbers, ℝ the set of real numbers, and
Γ is the Gamma function.
In this work, we dealt with FPS in general which is a generalization to the classical power series (CPS). Important theorems that related to the CPS have been generalized to the FPS. Some of these theorems are constructed by using Caputo fractional derivatives. These theorems have been used to approximate the fractional derivatives and integrals of functions. FPS solutions have been constructed for linear and nonlinear FDEs and a new technique is used to find out the coefficients of the FPS. Under certain conditions, we proved that the Caputo fractional derivative can be expressed in terms of the ordinary derivative. Also, the generalized Taylor's formula in Equation (4) has been derived using new approach for 0 ≤ m − 1 < α ≤ m , m ∈ ℕ.
The organization of this paper is as follows: in the next section, we present some necessary definitions and preliminary results that will be used in our work. In
Section 3, theorems that represent the objective of the paper are mentioned and proved. In
Section 4, some applications, including approximation of fractional derivatives and integrals of functions are given. In
Section 5, series solutions of linear and nonlinear FDEs are produced using the FPS technique. The conclusions are given in the final part,
Section 6.
2. Notations on Fractional Calculus Theory
In this section, we present some necessary definitions and essential results from fractional calculus theory. There are various definitions of fractional integration and differentiation, such as Grunwald-Letnikov's definition and Riemann-Liouville's definition [
1,
2,
3,
4]. The Riemann-Liouville derivative has certain disadvantages when trying to model real-world phenomena with FDEs. Therefore, we shall introduce a modified fractional differential operator
proposed by Caputo in his work on the theory of viscoelasticity [
8].
Definition 2.1: A real function f(x), x > 0 is said to be in the space Cμ, μ ∈ ℝ if there exists a real number ρ > μ such that f(x) = xρf1(x), where f1(x) ∈ C[0, ∞), and it is said to be in the space if f(n) (x) ∈ Cμ, n ∈ ℕ.
Definition 2.2: The Riemann-Liouville fractional integral operator of order
α ≥ 0 of a function
f(
x) ∈
Cμ,
μ ≥ −1 is defined as:
Properties of the operator
can be found in [
1,
2,
3,
4], we mention here only the following: for
f ∈
Cμ,
μ ≥ −1,
α,
β ≥ 0,
C ∈ ℝ, and
γ ≥ −1, we have
,
, and
.
Definition 2.3: The Riemann-Liouville fractional derivative of order α > 0 of
is defined as:
In the next definition we shall introduce a modified fractional differential operator .
Definition 2.4: The Caputo fractional derivative of order α > 0 of
is defined as:
For some certain properties of the operator , it is obvious that when , and , we have and .
Lemma 2.1: If , , , and , then and , where .
3. Fractional Power Series Representation
In this section, we will generalize some important definitions and theorems related with the CPS into the fractional case in the sense of the Caputo definition. New results related to the convergent of the series are also presented. After that, some results which focus on the radii of convergence for the FPS are utilized.
The following definition is needed throughout this work, especially, in the following two sections regarding the approximating of the fractional derivatives, fractional integrals, and solution of FDEs.
Definition 3.1: A power series representation of the form
where 0 ≤
m − 1 <
α ≤
m and
t ≥
t0 is called a FPS about
t0, where
t is a variable and
Cn’s are constants called the coefficients of the series.
As a special case, when t0 = 0 the expansion is called a fractional Maclaurin series. Notice that in writing out the term corresponding to n = 0 in Equation (8) we have adopted the convention that (t − t0)0 = 1 even when t = t0. Also, when t = t0 each of the terms of Equation (8) vanishes for n ≥ 1 and so. On the other hand, the FPS (8) always converges when t = t0. For the sake of simplicity of our notation, we shall treat only the case where t0 = 0 in the first four theorems. This is not a loss of the generality, since the translation t’ = t − t0 reduces the FPS about t0 to the FPS about 0.
Theorem 3.1: We have the following two cases for the FPS
:
- (1)
If the FPS converges when , then it converges whenever ,
- (2)
If the FPS diverges when , then it diverges whenever .
Proof: For the first part, suppose that converges. Then, we have . According to the definition of limit of sequences with , there is a positive integer such that whenever . Thus, for , we have . Again, if , then , so is a convergent geometric series. Therefore, by the comparison test, the series is convergent. Thus the series is absolutely convergent and therefore convergent. To prove the remaining part, suppose that diverges. Now, if is any number such that , then cannot converge because, by Case 1, the convergence of would imply the convergence of . Therefore, diverges whenever . This completes the proof.
Theorem 3.2: For the FPS
, there are only three possibilities:
- (1)
The series converges only when ,
- (2)
The series converges for each ,
- (3)
There is a positive real number such that the series converges whenever and diverges whenever .
Proof: Suppose that neither Case 1 nor Case 2 is true. Then, there are nonzero numbers and such that converges for and diverges for Therefore, the set converges } is not empty. By the preceding theorem, the series diverges if , so for each . This says that is an upper bound for . Thus, by the completeness axiom, has a least upper bound . If , then , so diverges. If , then is not an upper bound for and so there exists such that . Since and converges, so by the preceding theorem converges, so the proof of the theorem is complete.
Remark 3.1: The number in Case 3 of Theorem 3.2 is called the radius of convergence of the FPS. By convention, the radius of convergence is in Case 1 and in Case 2.
Theorem 3.3: The CPS has radius of convergence if and only if the FPS has radius of convergence.
Proof: If we make the change of variable t = xα, x ≥ 0 then the CPS becomes . This series converges for 0 ≤ xα < R, that is for 0 ≤ x < R1/α, and so the FPS has radius of convergence R1/α. Conversely, if we make the change of variable t = x1/α, x ≥ 0 then the FPS becomes . In fact, this series converges for 0 ≤ x1/α < R1/α that is for 0 ≤ x < R. Since the two series and −∞ < x < ∞ have the same radius of convergence , the radius of convergence for the CPS −∞ < x < ∞ is R, so the proof of the theorem is complete.
Theorem 3.4: Suppose that the FPS
has radius of convergence
. If
is a function defined by
on 0 ≤
t <
R, then for 0 ≤
m − 1 <
α <
m and 0 ≤
t <
R, we have:
Proof: Define
for 0 ≤
x <
Rα, where
Rα is the radius of convergence. Then:
where 0 ≤
τ <
x <
Rα. On the other hand, if we make the change of variable
x =
tα,
t ≥ 0 into Equation (11) and use the properties of the operator
, we obtain:
For the remaining part, considering the definition of
g(
x) above one can conclude that:
where 0 ≤
τ <
x <
Rα. Similarly, if we make the change of variable
x =
tα,
t ≥ 0 into Equation (13), we can conclude that:
So the proof of the theorem is complete.
Theorem 3.5: Suppose that
f has a FPS representation at
t0 of the form:
If f(t) ∈ C [t0, t0 + R) and for n = 0,1,2,…, then the coefficients cn in Equation (15) will take the form , where (n-times).
Proof: Assume that
f is an arbitrary function that can be represented by a FPS expansion. First of all, notice that if we put
t =
t0 into Equation (15), then each term after the first vanishes and thus we get
c0 =
f(
t0). On the other aspect as well, by using Equation (9), we have:
where
t0 ≤
t <
t0 +
R. The substitution of
t =
t0 into Equation (16) leads to
. Again, by applying Equation (9) on the series representation in Equation (16), one can obtain that:
where
t0 ≤
t <
t0 +
R. Here, if we put
t =
t0 into Equation (17), then the obtained result will be
. By now we can see the pattern and discover the general formula for
cn. However, if we continue to operate
(∙)
n-times and substitute
t =
t0, we can get
. This completes the proof.
We mention here that the substituting of
back into the series representation of Equation (15) will leads to the following expansion for
f about
t0:
which is the same of the Generalized Taylor's series that obtained in [
46] for 0 <
α ≤ 1.
Theorem 3.6: Suppose that
f has a Generalized Taylor's series representation at
t0 of the form:
If
for
then
where
,
.
Proof: If we make the change of variable
,
into Equation (19), then we obtain:
But since, the CPS representation of
g(
x) about
t0 takes the form:
Then the two power series expansion in Equations (20) and (21) converge to the same function
g(
x). Therefore, the corresponding coefficients must be equal and thus
. This completes the proof.
As with any convergent series, this means that f(t) is the limit of the sequence of partial sums. In the case of the Generalized Taylor's series, the partial sums are . In general, f(t) is the sum of its Generalized Taylor's series if . On the other aspect as well, if we let Rn(t) = f(t) − Tn(t), then Rn(t) is the remainder of the Generalized Taylor's series.
Theorem 3.7: Suppose that
f(
t) ∈
C[
t0,
t0 +
R) and
for
j = 0,1,2,…,
n+ 1, where 0 < α ≤ 1. Then
f could be represented by:
Proof: From the certain properties of the operator
and Lemma 2.1, one can find that:
If we keep repeating of this process, then after
n-times of computations, we can find that
, so the proof of the theorem is complete.
Theorem 3.8: If
on
t0 ≤
t ≤
d, where 0 <
α ≤ 1, then the reminder
Rn(
t) of the Generalized Taylor's series will satisfies the inequality:
Proof: First of all, assume that
exist for
and that:
From the definition of the reminder
one can obtain
and
It follows from Equation (25) that
. Hence,
. On the other hand, we have:
But since from Theorem 3.7, we get
. Thus, by performing the operations in Equation (26), we can find the inequality
which is equivalent to
, so the proof of the theorem is complete.
Theorem 3.9: Suppose that
has a FPS representation at
of the form
where
R is the radius of convergence. Then
f is analytic in (
t0,
t0 +
R)
Proof: Let and h(t) = (t − t0)α, t0 ≤ t < t0 + R, 0 ≤ m − 1 < α ≤ m. Then g(t) and h(t) are analytic functions and thus the composition (g ∘ h)(t) = f(t) is analytic in (t0, t0 + R). This completes the proof.
4. Application I: Approximation Fractional Derivatives and Integrals of Functions
In order to illustrate the performance of the presented results in approximating the fractional derivatives and integrals of functions at a given point we consider two examples. On the other hand, we use Theorems 3.4, 3.6, and the generalized Taylor's series (18) in the approximation step. However, results obtained are found to be in good agreement with each other. In the computation process all the symbolic and numerical computations were performed using the Mathematica 7 software packages.
Application 4.1: Consider the following non-elementary function:
The fractional Maclaurin series representation of
f(
t) about
t = 0 is
. According to Theorem 3.6, we can conclude that
, where
and
g(n)(0) =
n!. In other words, the fractional Maclaurin series of
can be written as
. In fact, this is a convergent geometric series with ratio
. Thus, the series is convergent for each
and then for each
. Therefore
is the sum of its fractional Maclaurin series representation. Note that, this result can be used to approximate the functions
and
on
However, according to Equation (9), the function
can be approximated by the
-partial sum of its expansion as follows:
Our next goal is to approximate the function
in numerical values. To do so,
Table 1 shows approximate values of
for different values of
t and
α on
in step of 0.1 when
. It is to be noted that in order to improve the results, we can compute more approximation terms for different values of
and
.
Similarly, we can use Equation (10) to approximate the function
in numerical values by the
-partial sum of its expansion as:
Table 2 shows approximate values of
for different values of
t and
α on 0 ≤
t < 1 in step of 0.1 when
k = 10. As in the previous table and results, it should to be noted that computing more terms of the series representation will increase the accuracy of the approximations and thus a good approximation can be obtained.
Table 1.
The approximate values of when k = 10 for Application 4.1.
Table 1.
The approximate values of when k = 10 for Application 4.1.
| t | | α = 0.5 | | α = 0.75 | | α = 1.5 | | α = 2 |
|---|
| 0 | | 0.886227 | | 0.919063 | | 1.329340 | | 2 |
| 0.1 | | 1.448770 | | 1.253617 | | 1.481250 | | 2.123057 |
| 0.2 | | 1.918073 | | 1.619507 | | 1.814089 | | 2.531829 |
| 0.3 | | 2.499525 | | 2.113559 | | 2.385670 | | 3.370618 |
| 0.4 | | 3.261329 | | 2.825448 | | 3.371164 | | 4.994055 |
| 0.5 | | 4.277607 | | 3.899429 | | 5.179401 | | 8.295670 |
| 0.6 | | 5.635511 | | 5.569142 | | 8.843582 | | 15.839711 |
| 0.7 | | 9.803122 | | 8.201646 | | 17.203979 | | 36.370913 |
| 0.8 | | 9.803122 | | 12.353432 | | 38.389328 | | 104.441813 |
| 0.9 | | 12.869091 | | 18.839971 | | 95.486744 | | 365.976156 |
Table 2.
The approximate values of when k = 10 for Application 4.1.
Table 2.
The approximate values of when k = 10 for Application 4.1.
| t | | α = 0.5 | | α = 0.75 | | α = 1.5 | | α = 2 |
|---|
| 0 | | 0 | | 0 | | 0 | | 0 |
| 0.1 | | 0.121746 | | 0.025296 | | 0.025296 | | 0.000008 |
| 0.2 | | 0.289460 | | 0.080361 | | 0.001859 | | 0.000136 |
| 0.3 | | 0.509120 | | 0.165975 | | 0.006551 | | 0.000700 |
| 0.4 | | 0.795368 | | 0.289398 | | 0.016399 | | 0.002283 |
| 0.5 | | 1.169853 | | 0.463570 | | 0.034285 | | 0.005812 |
| 0.6 | | 1.662260 | | 0.709964 | | 0.064487 | | 0.012745 |
| 0.7 | | 2.311743 | | 1.063626 | | 0.114028 | | 0.025437 |
| 0.8 | | 3.168540 | | 1.580987 | | 0.195965 | | 0.048045 |
| 0.9 | | 4.295695 | | 2.351284 | | 0.338186 | | 0.089143 |
Application 4.2: Consider the following Mittag-Leffler function:
The Mittag-Leffler function [
47] plays a very important role in the solution of linear FDEs [
3,
8]. In fact, the solutions of such FDEs are obtained in terms of
Eα(
tα). Note that
(
Eα(
tα)) ∈
C(0, ∞) for
n ∈ ℕ and
α > 0. In [
46] the authors have approximated the function
Eα(
tα) for different values of
t when 0 <
α ≤ 1 by 10-th partial sum of its expansion. However, using Equations (9) and (10) both functions
(
Eα(
tα)) and
(
Eα(
tα)) can be approximated, respectively, by the following
k-partial sums:
Again, to show the validity of our FPS representation in approximating the Mittag-Leffler function,
Table 3 and
Table 4 will tabulate the approximate results of
(
Eα(
tα)) and
J(
Eα(
tα)) for different values of
t and α on 0 ≤
t ≤ 4 in step of 0.4 when
k = 10.
Table 3.
The approximate values of (Eα(tα)) when k = 10 for Application 4.2.
Table 3.
The approximate values of (Eα(tα)) when k = 10 for Application 4.2.
| t | | α = 0.5 | | α = 0.75 | | α = 1.5 | | α = 2 |
|---|
| 0 | | 1 | | 1 | | 1 | | 1 |
| 0.4 | | 2.430013 | | 1.800456 | | 1.201288 | | 1.081072 |
| 0.8 | | 3.991267 | | 2.816662 | | 1.630979 | | 1.337435 |
| 1.2 | | 6.220864 | | 4.298057 | | 2.324700 | | 1.810656 |
| 1.6 | | 9.451036 | | 6.489464 | | 3.389416 | | 2.577464 |
| 2.0 | | 14.097234 | | 9.743204 | | 4.996647 | | 3.762196 |
| 2.4 | | 20.683136 | | 14.543009 | | 7.407121 | | 5.556947 |
| 2.8 | | 29.857007 | | 21.721976 | | 11.012177 | | 8.252728 |
| 3.2 | | 42.406132 | | 32.250660 | | 16.396938 | | 12.286646 |
| 3.6 | | 59.270535 | | 47.649543 | | 24.435073 | | 18.312779 |
| 4.0 | | 81.556340 | | 69.980001 | | 36.430382 | | 27.308232 |
Table 4.
The approximate values of (Eα(tα))when k = 10 for Application 4.2.
Table 4.
The approximate values of (Eα(tα))when k = 10 for Application 4.2.
| t | | α = 0.5 | | α = 0.75 | | α = 1.5 | | α = 2 |
|---|
| 0 | | 0 | | 0 | | 0 | | 0 |
| 0.4 | | 1.430036 | | 0.800456 | | 0.201288 | | 0.081072 |
| 0.8 | | 2.992286 | | 1.816664 | | 0.630979 | | 0.337435 |
| 1.2 | | 5.230333 | | 3.298122 | | 1.324701 | | 0.810656 |
| 1.6 | | 8.497108 | | 5.490163 | | 2.389416 | | 1.577464 |
| 2.0 | | 13.254431 | | 8.747610 | | 3.996647 | | 2.762196 |
| 2.4 | | 20.111627 | | 13.592834 | | 6.407121 | | 4.556947 |
| 2.8 | | 29.857352 | | 20.792695 | | 10.012177 | | 7.252728 |
| 3.2 | | 43.491129 | | 31.463460 | | 15.396941 | | 11.286646 |
| 3.6 | | 62.255682 | | 47.211856 | | 23.435091 | | 17.312779 |
| 4.0 | | 87.670285 | | 70.321152 | | 35.430382 | | 26.308232 |
5. Application II: Series Solutions of Fractional Differential Equations
In this section, we use the FPS technique to solve the FDEs subject to given initial conditions. This method is not new, but it is a powerful application on the theorems in this work. Moreover, a new technique is applied on the nonlinear FDEs to find out the recurrence relation which gives the value of coefficients of the FPS solution as we will see in Applications (5.3) and (5.4).
Application 5.1: Consider the following linear fractional equation [
48]:
subject to the initial conditions:
where ω,
y0, and ρ
0 are real finite constants.
The FPS technique consists in expressing the solution of Equations (33) and (34) as a FPS expansion about the initial point
t = 0. To achieve our goal, we suppose that this solution takes the form of Equation (8) which is:
From formula (9), we can obtain
![]()
. On the other hand, it easy to see that:
In order to approximate the solution of Equations (33) and (34) substitute the expansion formulas of Equations (35) and (36) into Equation (33), yields that:
The equating of the coefficients of
tnα to zero in both sides of Equation (37) leads to the following:
![]()
. Considering the initial conditions (34) one can obtain
c0 =
y0 and
![]()
. In fact, based on these results the remaining coefficients of
tnα can be divided into two categories. The even index terms and the odd index terms, where the even index terms take the form
![]()
and so on, and the odd index term which are
![]()
, and so on. Therefore, we can obtain the following series expansion solution:
On the other aspect as well, the exact solution of Equations (33) and (34) in term of the Mittag-Leffler function has the general form which are coinciding with the exact solution:
Application 5.2: Consider the following composite linear fractional equation [
39]:
subject to the initial conditions:
Using FPS technique and considering formula (8), the solution
y(
t) of Equations (40) and (41) can be written as:
In order to complete the formulation of the FPS technique, we must compute the functions
![]()
. However, the forms of these functions are giving, respectively, as follows:
But since {
t|
t ≥ 0} is the domain of solution, then the values of the coefficients
c1 and
c3 must be zeros. On the other aspect as well, the substituting of the initial conditions (41) into Equation (42) and into
y(
t) in Equation (43) gives
c0 = 0 and
c2 = 0. Therefore, the discretized form of the functions
y(
t),
y(
t), and
y(
t) is obtained. The resulting new form will be as follows:
Now, substituting Equation (44) back into Equation (40), equating the coefficients of
tn/2 to zero in the resulting equation, and finally identifying the coefficients, we then will obtain recursively the following results:
![]()
, and
![]()
. So, the 15th-truncated series approximation of
y(
t) is:
The FPS technique has an advantage that it is possible to pick any point in the interval of integration and as well the approximate solution and all its derivatives will be applicable. In other words a continuous approximate solution will be obtained. Anyway,
Tables 5 shows the 15th-approximate values of
y(
t),
y(
t),
y(
t) and and the residual error function for different values of
t on 0 ≤
t ≤ 1 in step of 0.2, where the residual error function is defined as
![]()
.
Table 5.
The 15th-approximate values of y(t), y(t), and y(t) and Res(t) for Application 5.2.
Table 5.
The 15th-approximate values of y(t), y(t), and y(t) and Res(t) for Application 5.2.
| t | | y(t) | | y(t) | | y(t) | | Res(t) |
|---|
| 0.0 | | 0 | | 0 | | 0 | | 0 |
| 0.2 | | 0.157037 | | 0.525296 | | 7.317668 | | 6.211481 × 10−7 |
| 0.4 | | 0.604695 | | 1.413213 | | 5.982030 | | 6.167617 × 10−5 |
| 0.6 | | 1.290452 | | 2.420120 | | 4.288506 | | 9.217035 × 10−4 |
| 0.8 | | 2.1472288 | | 3.409426 | | 2.437018 | | 6.327666 × 10−3 |
| 1.0 | | 3.101501 | | 4.282177 | | 0.587987 | | 2.833472 × 10−2 |
From the table above, it can be seen that the FPS technique provides us with the accurate approximate solution for Equations (40) and (41). Also, we can note that the approximate solution more accurate at the beginning values of the independent interval.
Application 5.3: Consider the following nonlinear fractional equation [
40]:
subject to the initial conditions:
where
m is a positive integer number.
Similar to the previous discussions, the FPS solution takes the form
![]()
. On the other hand, according to the initial conditions (47), the coefficient
c0 must be equal to zero. Therefore:
It is known that in the nonlinear FDEs case the finding of recurrence relation that corresponding to the FPS representation and then discovering the values of the coefficients is not easy in general. Therefore, a new technique will be used in this application in order to find out the value of the coefficients of the FPS solution. To achieve our goal, we define the so-called
αkth-order differential equation as follows:
It is obvious that when
k = 0, Equation (49) is the same as Equation (46). So, the FPS representation in Equation (48) is a solution for the
αkth-order differential Equation (49); that is:
According to Equation (9) a new discretized version of Equation (50) will be obtained and is given as:
where
Xk = 1 if
k = 0 and
Xk = 0 if
k ≥ 1. From Theorems 3.2 and 3.4, the
αkth-derivative of the FPS representation, Equation (48), is convergent at least at
t = 0, for
k = 0,1,2,…. Therefore, the substituting
t = 0 into Equation (51) gives the following recurrence relation which determine the values of the coefficients
cn of
tnα:
c0 = 0,
, and
![]()
for
k = ,1,2,…. If we collect and substitute these value of the coefficients back into Equation (48), then the exact solution of Equations (46) and (47) has the general form which is coinciding with the general expansion:
In fact, these coefficients are the same as coefficients of the series solution that obtained by the Adomian decomposition method [
40]. Moreover, if
α = 1, then the series solution for Equations (46) and (47) will be:
which agrees well with the exact solution of Equations (46) and (47) in the ordinary sense.
Table 6 shows the 15th-approximate values of
y(
t) and the residual error function for different values of
t and
α on 0 ≤
t ≤ 1 in step of 0.2, where the residual error function is defined as
![]()
. However, the computational results below provide a numerical estimate for the convergence of the FPS technique. It is also clear that the accuracy obtained using the present technique is advanced by using only a few approximation terms. In addition, we can conclude that higher accuracy can be achieved by evaluating more components of the solution. In fact, the results reported in this table confirm the effectiveness and good accuracy of the technique.
Application 5.4: Consider the following composite nonlinear fractional equation [
40]:
subject to the initial conditions:
where
c0 and
c1 are real finite constants.
Table 6.
The 15th-approximate values of y(t) and Res(t) for Application 5.3.
Table 6.
The 15th-approximate values of y(t) and Res(t) for Application 5.3.
| t | | y(t;α = 1.5) | | Res(t;α = 1.5) | | y(t;α = 2.5) | | Res(t;α = 2.5) |
|---|
| 0.0 | | 0 | | 0 | | 0 | | 0 |
| 0.2 | | 0.067330 | | 2.034437 × 10−17 | | 0.005383 | | 3.103055 × 10−16 |
| 0.4 | | 0.191362 | | 4.370361 × 10−17 | | 0.030450 | | 1.252591 × 10−15 |
| 0.6 | | 0.356238 | | 2.850815 × 10−13 | | 0.083925 | | 7.275543 × 10−16 |
| 0.8 | | 0.563007 | | 2.897717 × 10−10 | | 0.172391 | | 1.022700 × 10−15 |
| 1.0 | | 0.822511 | | 6.341391 × 10−8 | | 0.301676 | | 1.998026 × 10−16 |
Again, using FPS expansion, we assume that the solution
y(
t). of Equations (54) and (55) can be expanded in the form of
. Thus, the so-called
th-order differential equation of Equations (54) and (55) is:
According to Equation (9) and the Cauchy product for infinite series, the discretized form of Equation (56) is obtained as follows:
In fact, Equation (57) can be easily reduces depending on Equation (9) once more into the equivalent form as:
where
if
and
if
. However, the substituting of
into Equation (58) gives the following recurrence relation which determines the values of the coefficients
of
:
c0 and
c1 are arbitrary,
and
for
. Therefore, by easy calculations we can obtain that the general solution of Equations (54) and (55) agree well with the following expansion:
For easy calculations and new generalization, one can assigns some specific values for the two constant c0 and c1 in the set of real or complex numbers.
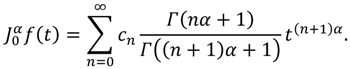
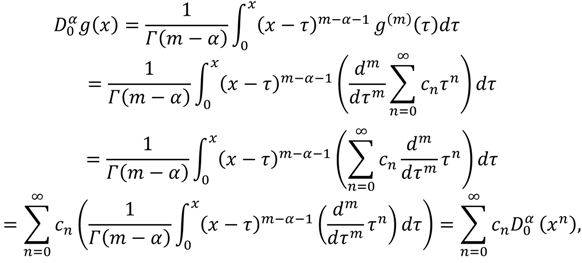
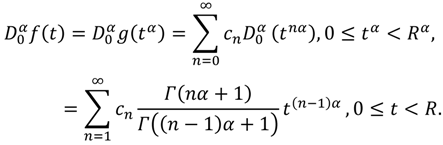
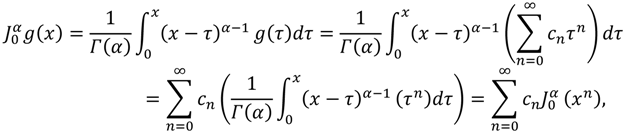
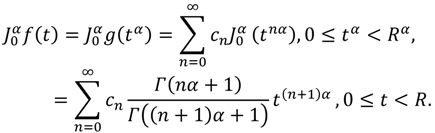
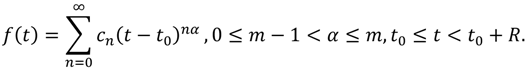
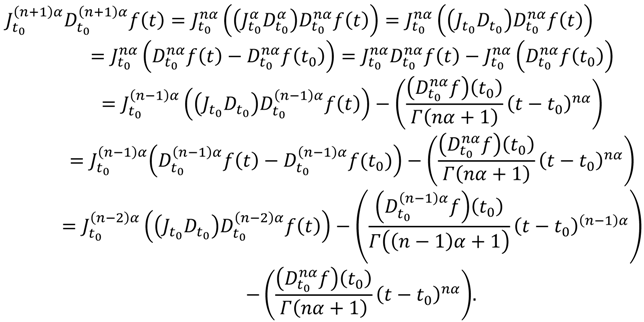
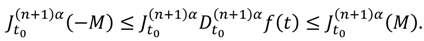
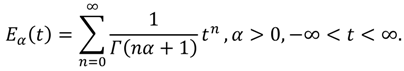
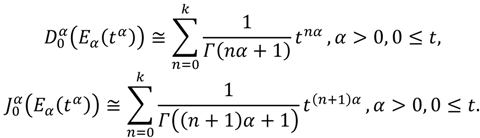
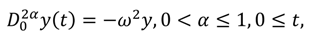
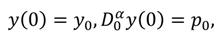
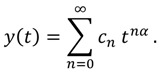
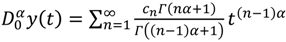 . On the other hand, it easy to see that:
. On the other hand, it easy to see that:
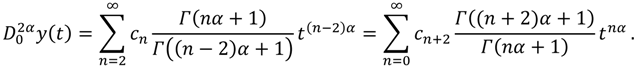
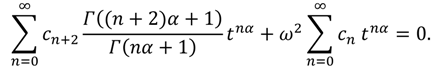
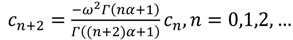 . Considering the initial conditions (34) one can obtain c0 = y0 and
. Considering the initial conditions (34) one can obtain c0 = y0 and 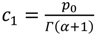 . In fact, based on these results the remaining coefficients of tnα can be divided into two categories. The even index terms and the odd index terms, where the even index terms take the form
. In fact, based on these results the remaining coefficients of tnα can be divided into two categories. The even index terms and the odd index terms, where the even index terms take the form 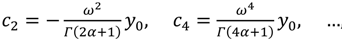 and so on, and the odd index term which are
and so on, and the odd index term which are 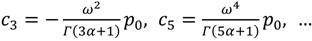 , and so on. Therefore, we can obtain the following series expansion solution:
, and so on. Therefore, we can obtain the following series expansion solution:
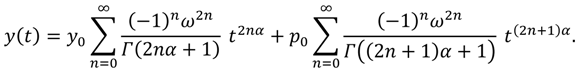
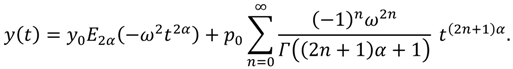
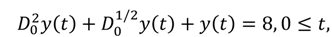
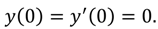
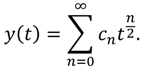
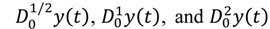 . However, the forms of these functions are giving, respectively, as follows:
. However, the forms of these functions are giving, respectively, as follows:
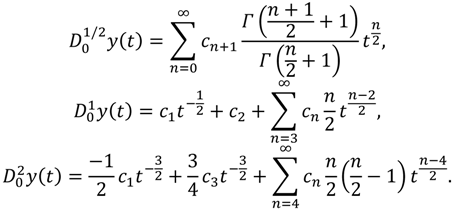
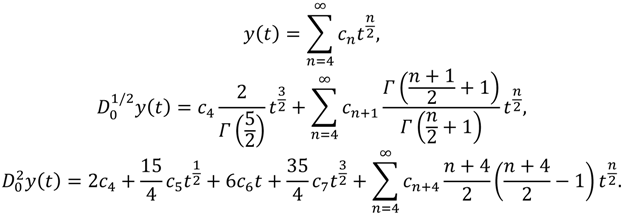
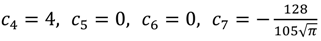 , and
, and  . So, the 15th-truncated series approximation of y(t) is:
. So, the 15th-truncated series approximation of y(t) is:
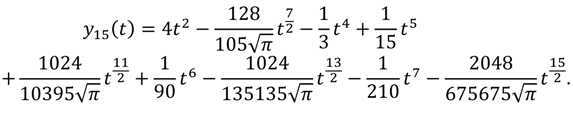
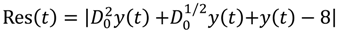 .
.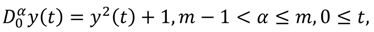
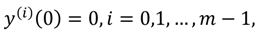
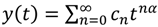 . On the other hand, according to the initial conditions (47), the coefficient c0 must be equal to zero. Therefore:
. On the other hand, according to the initial conditions (47), the coefficient c0 must be equal to zero. Therefore:
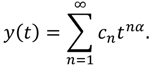
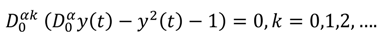
 for k = ,1,2,…. If we collect and substitute these value of the coefficients back into Equation (48), then the exact solution of Equations (46) and (47) has the general form which is coinciding with the general expansion:
for k = ,1,2,…. If we collect and substitute these value of the coefficients back into Equation (48), then the exact solution of Equations (46) and (47) has the general form which is coinciding with the general expansion:
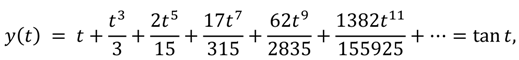
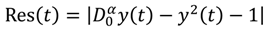 . However, the computational results below provide a numerical estimate for the convergence of the FPS technique. It is also clear that the accuracy obtained using the present technique is advanced by using only a few approximation terms. In addition, we can conclude that higher accuracy can be achieved by evaluating more components of the solution. In fact, the results reported in this table confirm the effectiveness and good accuracy of the technique.
. However, the computational results below provide a numerical estimate for the convergence of the FPS technique. It is also clear that the accuracy obtained using the present technique is advanced by using only a few approximation terms. In addition, we can conclude that higher accuracy can be achieved by evaluating more components of the solution. In fact, the results reported in this table confirm the effectiveness and good accuracy of the technique.