Statistical Mechanics and Information-Theoretic Perspectives on Complexity in the Earth System
Abstract
:1. Introduction
2. Methods
2.1. Entropy Measures from Symbolic Sequences
2.1.1. Symbolic Dynamics
2.1.2. Block Entropies
2.1.3. Non-Extensive Tsallis Entropy
2.1.4. Order-Pattern Based Approaches
2.2. Entropy Measures from Continuous Data
2.2.1. Approximate Entropy
2.2.2. Sample Entropy
2.2.3. Fuzzy Entropy
2.3. Measures of Statistical Interdependence and Causality
2.3.1. Mutual Information
2.3.2. Conditional Mutual Information and Transfer Entropy
2.3.3. Graphical Models
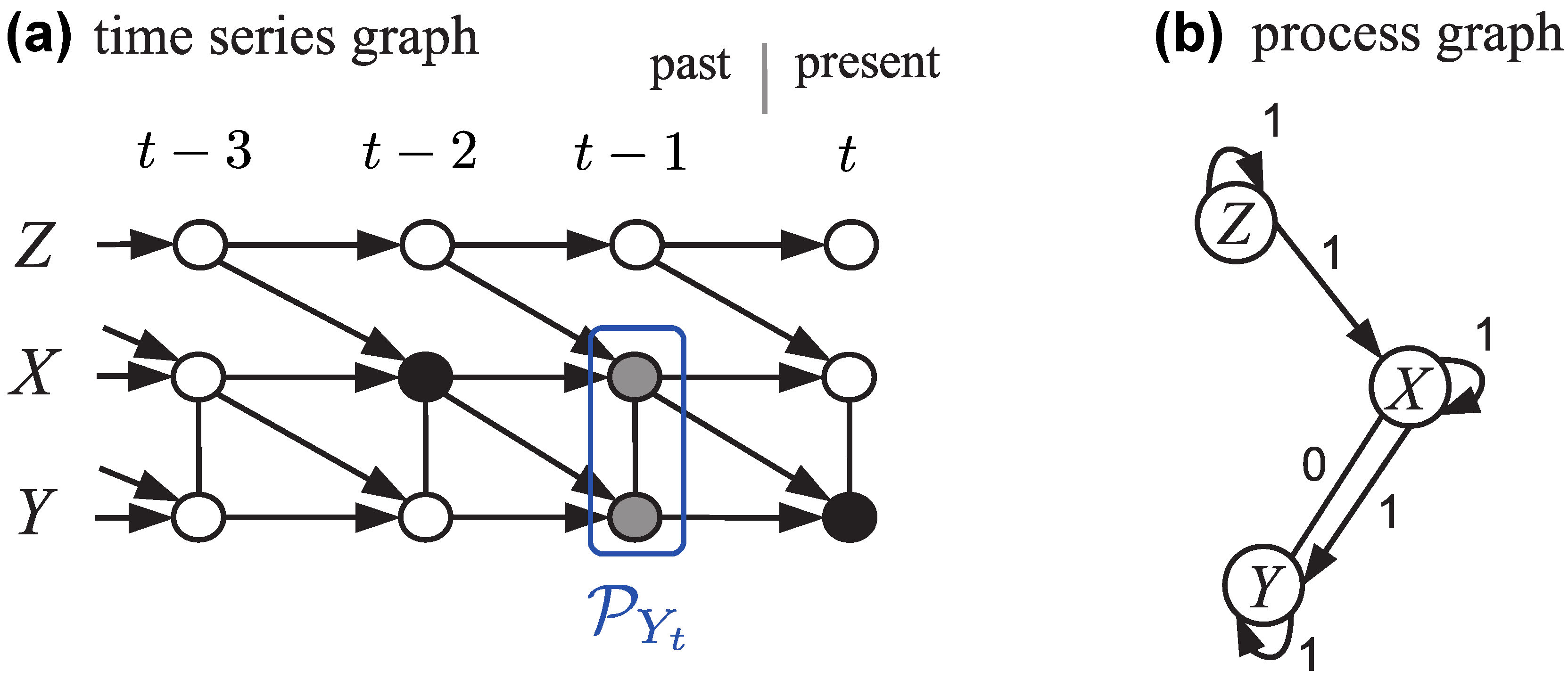
2.4. Linkages with Phase Space Methods
2.4.1. Reinterpreting Entropies As Phase Space Characteristics
2.4.2. Other Entropy Measures from Phase Space Methods
2.4.3. Causality from Phase Space Methods
3. Applications
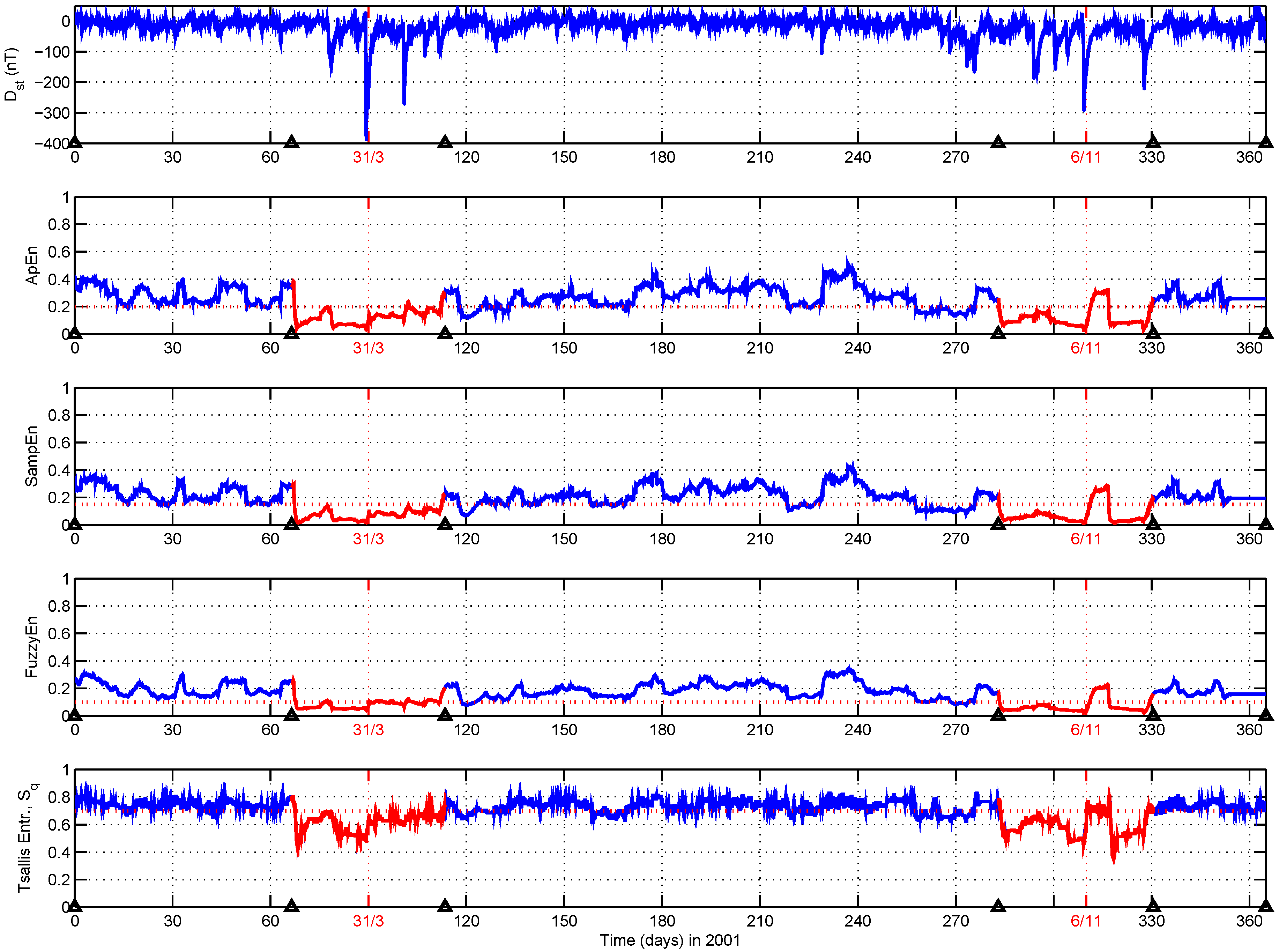
3.1. Space Weather and Magnetosphere
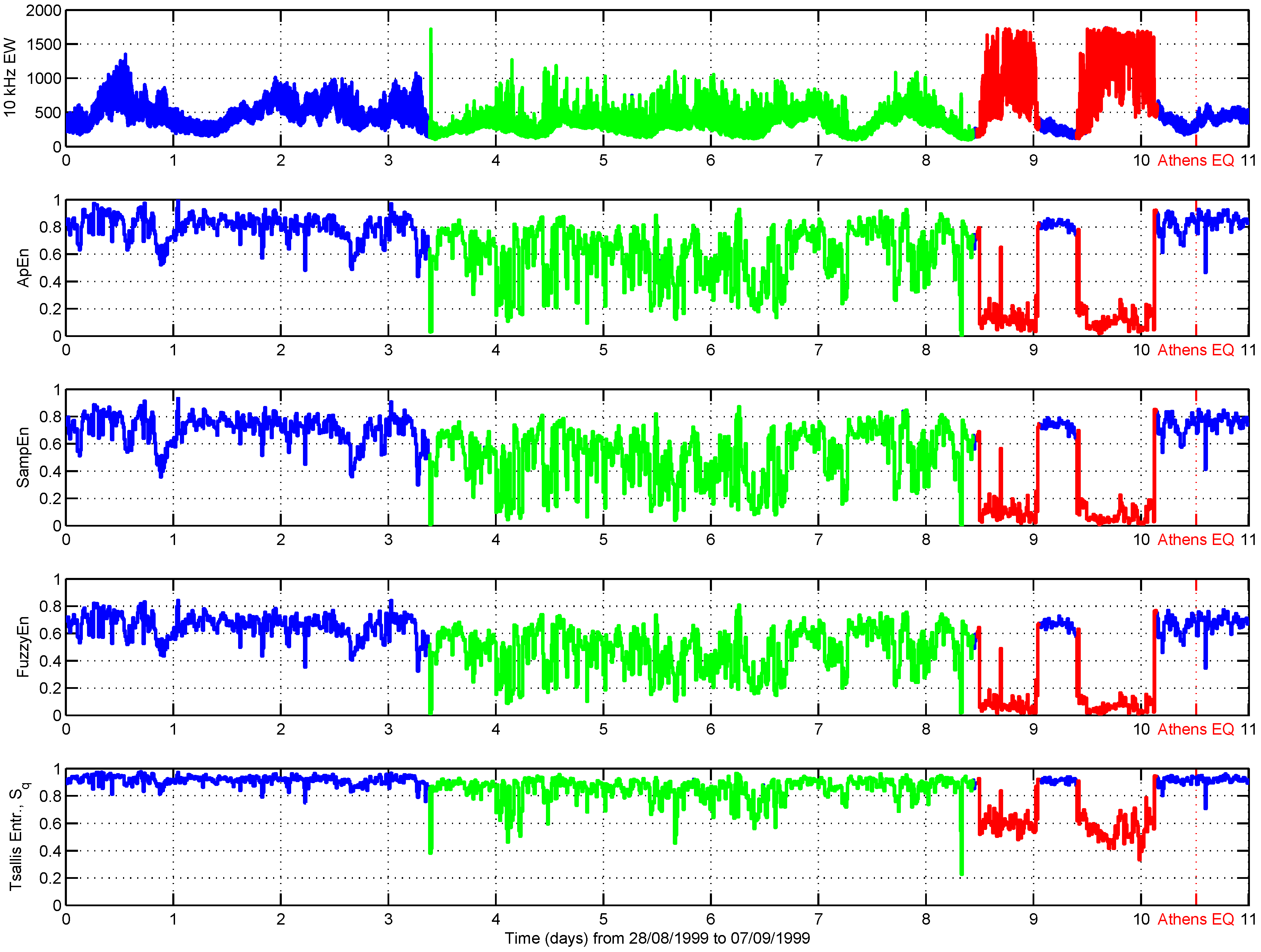
3.2. Preseismic Electromagnetic Emissions
3.3. Climate and Related Fields
3.3.1. Complexity of Present-Day Climate Variability
3.3.2. Dynamical Transitions in Paleoclimate Variability
3.3.3. Hydro-Meteorology and Land-Atmosphere Exchanges
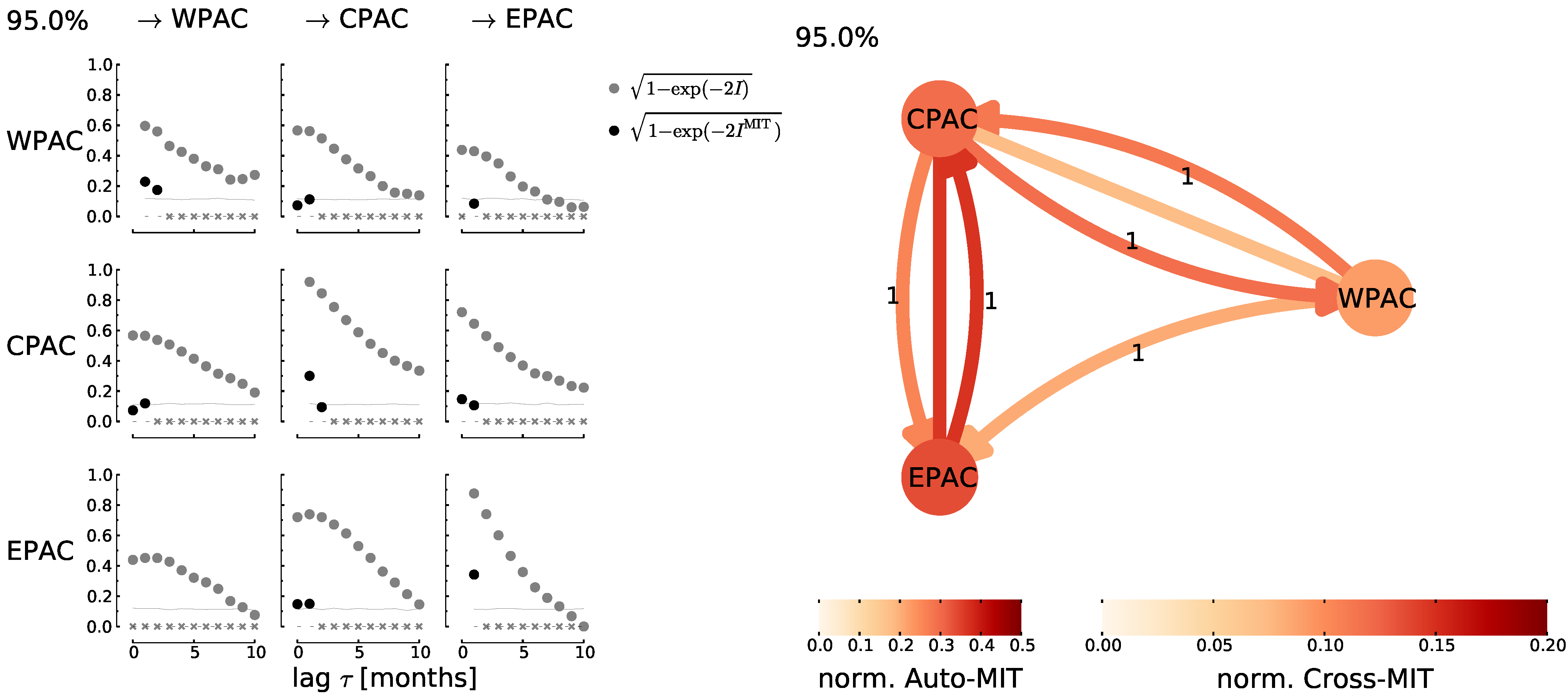
3.3.4. Interdependencies and Causality between Atmospheric Variability Patterns
4. Discussion
5. Conclusion
- the measurement of complexity of stationary records (e.g., for identifying spatial patterns of complexity in climate data);
- the identification of dynamical transitions and their preparatory phases from non-stationary time series (i.e., critical phenomena associated with approaching “singular” extreme events, like earthquakes, magnetic storms or climatic regime shifts known from paleoclimatology, but expected to be possible in the future climate, associated with the presence of climatic tipping points [235,236]);
- the characterization of complexity and information transfer between variables, subsystems or different spatial and/or temporal scales (e.g., couplings between solar wind and the magnetosphere or the atmosphere and vegetation);
- the identification of directed interdependencies between variables related to causal relationships between certain geoscientific processes, which are necessary for an improved process-based understanding of the coupling between different variables or even systems, a necessary prerequisite for the development of appropriate numerical simulation models.
- Symbolic dynamics approaches (e.g., block entropies, permutation entropy, Tsallis’ non-extensive entropy) typically require a considerable amount of data for their accurate estimation, which is mainly due to the systematic loss of information detail in the discretization process. Consequently, we suggest that such approaches are particularly well suited for studying long time series of approximately stationary processes (e.g., climate or hydrological time series) and high-resolution data from non-stationary and/or non-equilibrium systems (e.g., electromagnetic recordings associated with seismic activity).
- Tsallis’ non-extensive entropy is specifically tailored for describing non-equilibrium phenomena associated with changes in the dynamical complexity of recorded fluctuations, as arising in the context of critical phenomena, certain extreme events or dynamical regime shifts.
- Distance-based entropies (, and ) provide a higher degree of robustness to short and possibly noisy data than other entropy characteristics based on any kind of symbolic discretization. This suggests their specific usefulness for studying changes of dynamical complexity across dynamical transitions in a sliding windows framework.
- Directional bivariate measures and graphical models allow for a statistical evaluation of causality between variables. In this spirit, this class of approaches provides a versatile and widely applicable toolbox, where the graphical model idea gives rise to a multitude of bivariate characteristics (including conditional mutual information and transfer entropy as special cases), but may exhibit a considerable degree of algorithmic complexity in practical estimation.
Acknowledgments
Conflicts of Interest
References
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics, Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Turcotte, D.L. Modeling Geocomplexity: “A New Kind of Science”. In Earth & Mind: How Geoscientists Think and Learn about the Earth. GSA Special Papers volume 413, 2006; Manduca, C., Mogk, D., Eds.; Geological Society of America: Boulder, CO, USA, 2007; pp. 39–50. [Google Scholar]
- Donner, R.V.; Barbosa, S.M.; Kurths, J.; Marwan, N. Understanding the earth as a complex system—Recent advances in data analysis and modelling in earth sciences. Eur. Phys. J. Spec. Top. 2009, 174, 1–9. [Google Scholar] [CrossRef]
- Donner, R.V.; Barbosa, S.M. (Eds.) Nonlinear Time Series Analysis in the Geosciences —Applications in Climatology, Geodynamics, and Solar-Terrestrial Physics; Springer: Berlin, Germany, 2008.
- Kurths, J.; Voss, A.; Saparin, P.; Witt, A.; Kleiner, H.; Wessel, N. Quantitative analysis of heart rate variability. Chaos 1995, 5, 88–94. [Google Scholar] [CrossRef] [PubMed]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Sprott, J.C. Chaos and Time Series Analysis; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Hao, B.-L. Elementary Symbolic Dynamics and Chaos in Dissipative Systems; World Scientific: Singapore, Singapore, 1989. [Google Scholar]
- Karamanos, K.; Nicolis, G. Symbolic dynamics and entropy analysis of Feigenbaum limit sets. Chaos Solitons Fractals 1999, 10, 1135–1150. [Google Scholar] [CrossRef]
- Daw, C.S.; Finney, C.E.A.; Tracy, E.R. A review of symbolic analysis of experimental data. Rev. Scient. Instrum. 2003, 74, 915–930. [Google Scholar] [CrossRef]
- Donner, R.; Hinrichs, U.; Scholz-Reiter, B. Symbolic recurrence plots: A new quantitative framework for performance analysis of manufacturing networks. Eur. Phys. J. Spec. Top. 2008, 164, 85–104. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Saparin, P.; Witt, A.; Kurths, J.; Anishchenko, V. The renormalized entropy—An appropriate complexity measure? Chaos, Solitons Fractals 1994, 4, 1907–1916. [Google Scholar] [CrossRef]
- Rényi, A. On Measures of Entropy and Information. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20–30 June 1960; University of California Press: Berkeley, CA, USA, 1961; volume I, pp. 547–561. [Google Scholar]
- Hartley, R.V.L. Transmission of Information. Bell Syst. Tech. J. 1928, 7, 535–563. [Google Scholar] [CrossRef]
- Graben, P.; Kurths, J. Detecting subthreshold events in noisy data by symbolic dynamics. Phys. Rev. Lett. 2003, 90. [Google Scholar] [CrossRef] [PubMed]
- Eftaxias, K.; Athanasopoulou, L.; Balasis, G.; Kalimeri, M.; Nikolopoulos, S.; Contoyiannis, Y.; Kopanas, J.; Antonopoulos, G.; Nomicos, C. Unfolding the procedure of characterizing recorded ultra low frequency, kHz and MHz electromagnetic anomalies prior to the L’Aquila earthquake as pre-seismic ones. Part I. Nat. Hazards Earth Syst. Sci. 2009, 9, 1953–1971. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Minadakis, G.; Eftaxias, K. Analysis of electromagnetic pre-seismic emissions using Fisher Information and Tsallis entropy. Physica A 2012, 391, 300–306. [Google Scholar] [CrossRef]
- Nicolis, G.; Gaspard, P. Toward a probabilistic approach to complex systems. Chaos, Solitons Fractals 1994, 4, 41–57. [Google Scholar] [CrossRef]
- Ebeling, W.; Nicolis, G. Word frequency and entropy of symbolic sequences: A dynamical perspective. Chaos, Solitons Fractals 1992, 2, 635–650. [Google Scholar] [CrossRef]
- Khinchin, A.I. Mathematical Foundations of Information Theory; Dover: New York, NY, USA, 1957. [Google Scholar]
- McMillan, B. The basic theorems of information theory. Ann. Math. Stat. 1953, 24, 196–219. [Google Scholar] [CrossRef]
- Grassberger, P. Toward a quantitative theory of self-generated complexity. Int. J. Theor. Phys. 1986, 25, 907–938. [Google Scholar] [CrossRef]
- Wackerbauer, R.; Witt, A.; Atmanspacher, H.; Kurths, J.; Scheingraber, H. A comparative classification of complexity measures. Chaos Solitons Fractals 1994, 4, 133–173. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Generalized entropy-based criterion for consistent testing. Phys. Rev. E. 1998, 58, 1442–1445. [Google Scholar] [CrossRef]
- Zunino, L.; Perez, D.; Kowalski, A.; Martin, M.; Garavaglia, M.; Plastino, A.; Rosso, O. Fractional Brownian motion, fractional Gaussian noise and Tsallis permutation entropy. Physica A 2008, 387, 6057–6068. [Google Scholar]
- Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Kalimeri, M.; Anastasiadis, A.; Eftaxias, K. Dynamical complexity in Dst time series using nonextensive Tsallis entropy. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Kalimeri, M.; Anastasiadis, A.; Eftaxias, K. Investigating dynamical complexity in the magnetosphere using various entropy measures. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Bandt, C. Ordinal time series analysis. Ecol. Model. 2005, 182, 229–238. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2005, 88. [Google Scholar] [CrossRef] [PubMed]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy—A tutoral review. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Amigó, J.; Keller, K. Permutation entropy: One concept, two approaches. Eur. Phys. J. Spec. Top. 2013, 222, 263–273. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Generalized statistical complexity measures: Geometrical and analytical properties. Physica A 2006, 369, 439–462. [Google Scholar] [CrossRef]
- Rosso, O.A.; Larrondo, H.A.; Martin, M.T.; Plastino, A.; Fuentes, M.A. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99. [Google Scholar] [CrossRef] [PubMed]
- Lange, H.; Rosso, O.A.; Hauhs, M. Ordinal pattern and statistical complexity analysis of daily stream flow time series. Eur. Phys. J. Spec. Top. 2013, 222, 535–552. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M.; Goldberger, A.L. Physiological time-series analysis: What does regularity quantify? Am. J. Physiol. 1994, 266, H1643–H1656. [Google Scholar] [PubMed]
- Pincus, S.M.; Singer, B.H. Randomness and degrees of irregularity. Proc. Natl. Acad. Sci. USA 1996, 93, 2083–2088. [Google Scholar] [CrossRef] [PubMed]
- Grassberger, P.; Procaccia, I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591–2593. [Google Scholar] [CrossRef]
- Pincus, S.M.; Keefe, D. Quantification of hormone pulsatility via an approximate entropy algorithm. Am. J. Physiol. Endocrinol. Metab. 1992, 262, E741–E754. [Google Scholar]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–2049. [Google Scholar] [PubMed]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehab. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhuang, J.; Yu, W.; Wang, Z. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [PubMed]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [PubMed]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69. [Google Scholar] [CrossRef] [PubMed]
- Cellucci, C.J.; Albano, A.M.; Rapp, P.E. Statistical validation of mutual information calculations: Comparison of alternative numerical algorithms. Phys. Rev. E 2005, 71. [Google Scholar] [CrossRef] [PubMed]
- Kozachenko, L.F.; Leonenko, N.N. Sample estimate of the entropy of a random vector. Probl. Peredachi Inf. 1987, 23, 95–101. [Google Scholar]
- Pompe, B. On some entropy methods in data analysis. Chaos Solitons Fractals 1994, 4, 83–96. [Google Scholar] [CrossRef]
- Prichard, D.; Theiler, J. Generalized redundancies for time series analysis. Physica D 1995, 84, 476–493. [Google Scholar] [CrossRef]
- Paluš, M. Testing for nonlinearity using redundancies: Quantitative and qualitative aspects. Physica D 1995, 80, 186–205. [Google Scholar] [CrossRef]
- Paluš, M. Detecting nonlinearity in multivariate time series. Phys. Lett. A 1996, 213, 138–147. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Granger, C. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Chen, Y.; Rangarajan, G.; Feng, J.; Ding, M. Analyzing multiple nonlinear time series with extended Granger causality. Phys. Lett. A 2004, 324, 26–35. [Google Scholar] [CrossRef]
- Ancona, N.; Marinazzo, D.; Stramaglia, S. Radial basis function approach to nonlinear Granger causality of time series. Phys. Rev. E 2004, 70. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Barrett, A.; Seth, A. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef] [PubMed]
- Runge, J.; Heitzig, J.; Petoukhov, V.; Kurths, J. Escaping the curse of dimensionality in estimating multivariate transfer entropy. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef] [PubMed]
- Hlinka, J.; Hartman, D.; Vejmelka, M.; Runge, J.; Marwan, N.; Kurths, J.; Paluš, M. Reliability of inference of directed climate networks using conditional mutual information. Entropy 2013, 15, 2023–2045. [Google Scholar] [CrossRef]
- Lauritzen, S.L. Graphical Models; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Dahlhaus, R. Graphical interaction models for multivariate time series. Metrika 2000, 51, 157–172. [Google Scholar] [CrossRef]
- Eichler, M. Graphical modelling of multivariate time series. Probab. Theor. Rel. Fields 2012, 153, 233–268. [Google Scholar] [CrossRef]
- Runge, J.; Heitzig, J.; Marwan, N.; Kurths, J. Quantifying causal coupling strength: A lag-specific measure for multivariate time series related to transfer entropy. Phys. Rev. E 2012, 86. [Google Scholar] [CrossRef] [PubMed]
- Pompe, B.; Runge, J. Momentary information transfer as a coupling measure of time series. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef] [PubMed]
- Frenzel, S.; Pompe, B. Partial mutual information for coupling analysis of multivariate time series. Phys. Rev. Lett. 2007, 99. [Google Scholar] [CrossRef] [PubMed]
- Grassberger, P.; Procaccia, I. Measuring the strangeness of strange attractors. Physica D 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Characterization of strange attractors. Phys. Rev. Lett. 1983, 50, 346–349. [Google Scholar] [CrossRef]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Thiel, M.; Romano, M.C.; Read, P.L.; Kurths, J. Estimation of dynamical invariants without embedding by recurrence plots. Chaos 2004, 14, 234–243. [Google Scholar] [CrossRef] [PubMed]
- Letellier, C. Estimating the Shannon entropy: Recurrence plots versus symbolic dynamics. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef] [PubMed]
- Faure, P.; Lesne, A. Recurrence plots for symbolic sequences. Int. J. Bifurcation Chaos 2011, 20, 1731–1749. [Google Scholar] [CrossRef]
- Beim Graben, P.; Hutt, A. Detecting recurrence domains of dynamical systems by symbolic dynamics. Phys. Rev. Lett. 2013, 110. [Google Scholar] [CrossRef] [PubMed]
- Groth, A. Visualization of coupling in time series by order recurrence plots. Phys. Rev. E. 2005, 72. [Google Scholar] [CrossRef] [PubMed]
- Schinkel, S.; Marwan, N.; Kurths, J. Order patterns recurrence plots in the analysis of ERP data. Cogn. Neurodyn. 2007, 1, 317–325. [Google Scholar] [CrossRef] [PubMed]
- Arnhold, J.; Grassberger, P.; Lehnertz, K.; Elger, C.E. A robust method for detecting interdependencies: Application to intracranially recorded EEG. Physica D 1999, 134, 419–430. [Google Scholar] [CrossRef]
- Quian Quiroga, R.; Kraskov, A.; Kreuz, T.; Grassberger, P. Performance of different synchronization measures in real data: A case study on electroencephalographic signals. Phys. Rev. E 2002, 65. [Google Scholar] [CrossRef] [PubMed]
- Andrzejak, R.G.; Kraskov, A.; Stögbauer, H.; Mormann, F.; Kreuz, T. Bivariate surrogate techniques: Necessity, strengths, and caveats. Phys. Rev. E 2003, 68. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, D.A.; Andrzejak, R.G. Detection of weak directional coupling: Phase-dynamics approach versus state-space approach. Phys. Rev. E 2005, 71. [Google Scholar] [CrossRef] [PubMed]
- Andrzejak, R.G.; Ledberg, A.; Deco, G. Detecting event-related time-dependent directional couplings. New J. Phys. 2006, 8. [Google Scholar] [CrossRef]
- Chicharro, D.; Andrzejak, R.G. Reliable detection of directional couplings using rank statistics. Phys. Rev. E 2009, 80. [Google Scholar] [CrossRef] [PubMed]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.-H.; Deyle, E.; Fogarty, M.; Munch, S. Detecting causality in complex ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef] [PubMed]
- Romano, M.C.; Thiel, M.; Kurths, J.; Grebogi, C. Estimation of the direction of the coupling by conditional probabilities of recurrence. Phys. Rev. E 2007, 76. [Google Scholar] [CrossRef] [PubMed]
- Zou, Y.; Romano, M.C.; Thiel, M.; Marwan, N.; Kurths, J. Inferring indirect coupling by means of recurrences. Int. J. Bifurcation Chaos 2011, 21, 1009–1111. [Google Scholar] [CrossRef]
- Feldhoff, J.H.; Donner, R.V.; Donges, J.F.; Marwan, N.; Kurths, J. Geometric detection of coupling directions by means of inter-system recurrence networks. Phys. Lett. A 2012, 376, 3504–3513. [Google Scholar] [CrossRef]
- Klimas, A.J.; Vassiliadis, D.; Baker, D.N.; Roberts, D.A. The organized nonlinear dynamics of the magnetosphere. J. Geophys. Res. 1996, 101, 13089–13113. [Google Scholar] [CrossRef]
- Tsurutani, B.; Sugiura, M.; Iyemori, T.; Goldstein, B.; Gonzalez, W.; Akasofu, A.; Smith, E. The nonlinear response of AE to the IMF BS driver: A spectral break at 5 hours. Geophys. Res. Lett. 1990, 17, 279–282. [Google Scholar] [CrossRef]
- Baker, D.N.; Klimas, A.J.; McPherron, R.L.; Buchner, J. The evolution from weak to strong geomagnetic activity: An interpretation in terms of deterministic chaos. Geophys. Res. Lett. 1990, 17, 41–44. [Google Scholar] [CrossRef]
- Vassiliadis, D.V.; Sharma, A.S.; Eastman, T.E.; Papadopoulos, K. Low-dimensional chaos in magnetospheric activity from AE time series. Geophys. Res. Lett. 1990, 17, 1841–1844. [Google Scholar] [CrossRef]
- Sharma, A.S.; Vassiliadis, D.; Papadopoulos, K. Reconstruction of low-dimensional magnetospheric dynamics by singular spectrum analysis. Geophys. Res. Lett. 1993, 20, 335–338. [Google Scholar] [CrossRef]
- Pavlos, G.P.; Athanasiu, M.A.; Rigas, A.G.; Sarafopoulos, D.V.; Sarris, E.T. Geometrical characteristics of magnetospheric energetic ion time series: Evidence for low dimensional chaos. Ann. Geophys. 2003, 21, 1975–1993. [Google Scholar] [CrossRef]
- Vörös, Z.; Baumjohann, W.; Nakamura, R.; Runov, A.; Zhang, T.L.; Volwerk, M.; Eichelberger, H.U.; Balogh, A.; Horbury, T.S.; Glassmeier, K.-H.; et al. Multi-scale magnetic field intermittence in the plasma sheet. Ann. Geophys. 2003, 21, 1955–1964. [Google Scholar] [CrossRef]
- Chang, T. Low-dimensional behavior and symmetry breaking of stochastic systems near criticality-can these effects be observed in space and in the laboratory? IEEE Trans. Plasma Sci. 1992, 20, 691–694. [Google Scholar] [CrossRef]
- Chang, T. Intermittent turbulence in the magnetotail. EOS Trans. Suppl. 1998, 79, S328. [Google Scholar]
- Chang, T. Self-organized criticality, multi-fractal spectra, sporadic localized reconnections and intermittent turbulence in the magnetotail. Phys. Plasmas 1999, 6, 4137–4145. [Google Scholar] [CrossRef]
- Chang, T.; Wu, C.C.; Angelopoulos, V. Preferential acceleration of coherent magnetic structures and bursty bulk flows in Earth’s magnetotail. Phys. Scr. 2002, T98, 48–51. [Google Scholar] [CrossRef]
- Consolini, G. Sandpile Cellular Automata and Magnetospheric Dynamics. In Cosmic Physics in the Year 2000; Aiello, S., Ed.; SIF: Bologna, Italy, 1997; pp. 123–126. [Google Scholar]
- Consolini, G.; Chang, T. Complexity, magnetic field topology, criticality, and metastability in magnetotail dynamics. J. Atmos. Sol. Terr. Phys. 2002, 64, 541–549. [Google Scholar] [CrossRef]
- Lui, A.T.Y.; Chapman, S.C.; Liou, K.; Newell, P.T.; Meng, C.I.; Brittnacher, M.; Parks, G.K. Is the dynamic magnetosphere an avalanching system? Geophys. Res. Lett. 2000, 27, 911–914. [Google Scholar] [CrossRef]
- Uritsky, V.M.; Klimas, A.J.; Vassiliadis, D.; Chua, D.; Parks, G.D. Scalefree statistics of spatiotemporal auroral emissions as depicted by POLAR UVI images: The dynamic magnetosphere is an avalanching system. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Angelopoulos, V.; Mukai, T.; Kokubun, S. Evidence for intermittency in Earth’s plasma sheet and implications for self-organized criticality. Phys. Plasmas 1999, 6, 4161–4168. [Google Scholar] [CrossRef]
- Borovsky, J.E.; Funsten, H.O. MHD turbulence in the Earth’s plasma sheet: Dynamics, dissipation, and driving. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Weygand, J.M.; Kivelson, M.G.; Khurana, K.K.; Schwarzl, H.K.; Thompson, S.M.; McPherron, R.L.; Balogh, A.; Kistler, L.M.; Goldstein, M.L.; Borovsky, J.; et al. Plasma sheet turbulence observed by Cluster II. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Consolini, G.; Lui, A.T.Y. Sign-singularity analysis of current disruption. Geophys. Res. Lett. 1999, 26, 1673–1676. [Google Scholar] [CrossRef]
- Consolini, G.; Lui, A.T.Y. Symmetry Breaking and Nonlinear Wave-Wave Interaction in Current Disruption: Possible Evidence for a Phase Transition. In Magnetospheric Current Systems—Geophysical Monograph; Ohtani, S., Fujii, R., Hesse, M., Lysak, R.L., Eds.; 2000; Volume 118, pp. 395–401. [Google Scholar]
- Sitnov, M.I.; Sharma, A.S.; Papadopoulos, K.; Vassiliadis, D.; Valdivia, J.A.; Klimas, A.J.; Baker, D.N. Phase transition-like behavior of the magnetosphere during substorms. J. Geophys. Res. 2000, 105, 12955–12974. [Google Scholar] [CrossRef]
- Sitnov, M.I.; Sharma, A.S.; Papadopoulos, K.; Vassiliadis, D. Modeling substorm dynamics of the magnetosphere: From self-organization and self-organized criticality to non-equilibrium phase transitions. Phys. Rev. E 2001, 65. [Google Scholar] [CrossRef] [PubMed]
- Consolini, G.; Chang, T. Magnetic field topology and criticality in geotail dynamics: Relevance to substorm phenomena. Space Sci. Rev. 2001, 95, 309–321. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Kapiris, P.; Mandea, M.; Vassiliadis, D.; Eftaxias, K. From pre-storm activity to magnetic storms: A transition described in terms of fractal dynamics. Ann. Geophys. 2006, 24, 3557–3567. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Tozzi, R. On the multi-scale nature of large geomagnetic storms: An empirical mode decomposition analysis. Nonlinear Processes Geophys. 2012, 19, 667–673. [Google Scholar] [CrossRef]
- Wanliss, J.A.; Anh, V.V.; Yu, Z.-G.; Watson, S. Multifractal modeling of magnetic storms via symbolic dynamics analysis. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Uritsky, V.M.; Pudovkin, M.I. Low frequency 1/f-like fluctuations of the AE-index as a possible manifestation of self-organized criticality in the magnetosphere. Ann. Geophys. 1998, 16, 1580–1588. [Google Scholar] [CrossRef]
- Freeman, M.P.; Watkins, N.W.; Riley, D. J. Power law distributions of burst duration and interburst interval in the solar wind: Turbulence or dissipative self-organized criticality? Phys. Rev. E 2000, 62, 8794–8797. [Google Scholar] [CrossRef]
- Chapman, S. C.; Watkins, N. W.; Dendy, R. O.; Helander, P.; Rowlands, G. A simple avalanche model as an analogue for the magnetospheric activity. Geophys. Res. Lett. 1998, 25, 2397–2400. [Google Scholar] [CrossRef]
- Chapman, S.; Watkins, N. Avalanching and self organised criticality. A paradigm for geomagnetic activity? Space Sci. Rev. 2001, 95, 293–307. [Google Scholar] [CrossRef]
- Consolini, G. Self-organized criticality: A new paradigm for the magnetotail dynamics. Fractals 2002, 10, 275–283. [Google Scholar] [CrossRef]
- Leubner, M.P.; Vörös, Z. A nonextensive entropy approach to solar wind intermittency. Astrophys. J. 2005a, 618, 547–555. [Google Scholar] [CrossRef]
- Daglis, I.A.; Baker, D.N.; Galperin, Y.; Kappenman, J.G.; Lanzerotti, L.J. Technological impacts of space storms: Outstanding issues. EOS Trans. AGU 2001, 82, 585–592. [Google Scholar] [CrossRef]
- Daglis, I.A.; Kozyra, J.; Kamide, Y.; Vassiliadis, D.; Sharma, A.; Liemohn, M.; Gonzalez, W.; Tsurutani, B.; Lu, G. Intense space storms: Critical issues and open disputes. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Daglis, I.A.; Balasis, G.; Ganushkina, N.; Metallinou, F.-A.; Palmroth, M.; Pirjola, R.; Tsagouri, I.A. Investigating dynamic coupling in geospace through the combined use of modeling, simulations and data analysis. Acta Geophys. 2009, 57, 141–157. [Google Scholar] [CrossRef]
- Baker, D.N.; Daglis, I.A. Radiation Belts and Ring Current. In Space Weather: Physics and Effects; Bothmer, V., Daglis, I.A., Eds.; Springer: Berlin, Germany, 2007; pp. 173–202. [Google Scholar]
- Geomagnetic Equatorial Dst index Home Page. Available online: http://wdc.kugi.kyoto-u.ac.jp/dst-dir/index.html (accessed on 1 August 2013).
- Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Anastasiadis, A.; Sandberg, I.; Eftaxias, K. Quantifying dynamical complexity of magnetic storms and solar flares via nonextensive tsallis entropy. Entropy 2011, 13, 1865–1881. [Google Scholar] [CrossRef]
- Uyeda, S.; Kamogawa, M.; Nagao, T. Earthquakes, Electromagnetic Signals of. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer–Verlag: New York, NY, USA, 2009; pp. 2621–2635. [Google Scholar]
- Uyeda, S.; Nagao, T.; Kamogawa, M. Short-term earthquake prediction: Current status of seismo-electromagnetics. Tectonophysics 2009, 470, 205–213. [Google Scholar] [CrossRef]
- Kalashnikov, A.D. Potentialities of magnetometric methods for the problem of earthquake forerunners. Tr. Geofiz. Inst. Akad. Nauk. SSSR. 1954, 25, 180–182. [Google Scholar]
- Varotsos, P.; Kulhanek, O. (Eds.) Measurements and theoretical models of the Earth’s electric field variations related to earthquakes. Tectonophysics 1993, 224, 1–88. [CrossRef]
- Varotsos, P.A. The Physics of Seismic Electric Signals; TerraPub: Tokyo, Japan, 2005. [Google Scholar]
- Park, S.; Johnston, M.; Madden, T.; Morgan, F.; Morrison, H. Electromagnetic precursors to earthquakes in the ULF band: A review of observations and mechanisms. Rev. Geophys. 1993, 31, 117–132. [Google Scholar] [CrossRef]
- Hayakawa, M.; Ito, T.; Smirnova, N. Fractal analysis of ULF geomagnetic data associated with the Guam eartquake on 8 August 1993. Geophys. Res. Lett. 1999, 26, 2797–2800. [Google Scholar] [CrossRef]
- Hayakawa, M.; Itoh, T.; Hattori, K.; Yumoto, K. ULF electromagnetic precursors for an earthquake at Biak, Indonesia in 17 February 1996. Geophys. Res. Lett. 2000, 27, 1531–1534. [Google Scholar] [CrossRef]
- Hattori, K. ULF geomagnetic changes associated with large earthquakes. Terr. Atmos. Ocean Sci. 2004, 15, 329–360. [Google Scholar]
- Eftaxias, K.; Kapiris, P.; Polygiannakis, J.; Peratzakis, A.; Kopanas, J.; Antonopoulos, G.; Rigas, D. Experience of short term earthquake precursors with VLF-VHF electromagnetic emissions. Nat. Hazards Earth Syst. Sci. 2003, 3, 217–228. [Google Scholar] [CrossRef]
- Gokhberg, M.B.; Morgounov, V.A.; Yoshino, T.; Tomizawa, I. Experimental measurement of electromagnetic emissions possibly related to earthquakes in Japan. J. Geophys. Res. 1982, 87, 7824–7828. [Google Scholar] [CrossRef]
- Asada, T.; Baba, H.; Kawazoe, K.; Sugiura, M. An attempt to delineate very low frequency electromagnetic signals associated with earthquakes. Earth Planets Space 2001, 53, 55–62. [Google Scholar] [CrossRef]
- Contoyiannis, Y.F.; Potirakis, S.M.; Eftaxias, K. The Earth as a living planet: human-type diseases in the earthquake preparation process. Nat. Hazards Earth Syst. Sci. 2013, 13, 125–139. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Kalimeri, M.; Eftaxias, K. Nonextensivity and universality in the earthquake preparation process. Phys. Rev. E 2008, 77. [Google Scholar] [CrossRef] [PubMed]
- Potirakis, S.M.; Minadakis, G.; Eftaxias, K. Relation between seismicity and pre-earthquake electromagnetic emissions in terms of energy, information and entropy content. Nat. Hazards Earth Syst. Sci. 2012, 12, 1179–1183. [Google Scholar] [CrossRef]
- Seismo Electromagnetics: Lithosphere-Atmosphere-Ionosphere Coupling; Hayakawa, M.; Molchanov, O. (Eds.) TerraPub: Tokyo, Japan, 2002.
- Pulinets, S.; Boyarchuk, K. Ionospheric Precursors of Earthquakes; Springer: Berlin, Germany, 2005. [Google Scholar]
- Kamagowa, M. Preseismic lithosphere-atmosphere-ionosphere coupling. EOS Trans. AGU 2006, 87, 417–424. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, X.; Wang, L.; Chen, H.; Wu, Y.; Yuan, S.; Shen, J.; Zhao, S.; Qian, J.; Ding, J. The earthquake-related disturbances in ionosphere and project of the first China seismo-electromagnetic satellite. Earthq. Sci. 2011, 24, 639–650. [Google Scholar] [CrossRef]
- Parrot, M.; Achache, J.; Berthelier, J.J.; Blanc, E.; Deschamps, A.; Lefeuvre, F.; Menvielle, M.; Plantet, J.L.; Tarits, P.; Villain, J.P. High-frequency seismo-electromagnetic effects. Phys. Earth Planet. Inter. 1993, 77, 65–83. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Hayakawa, M. Seismo-Electromagnetics and Related Phenomena: History and Latest Results; TerraPub: Tokyo, Japan, 2008. [Google Scholar]
- Hayakawa, M.; Hobara, Y. Current status of seismo-electromagnetics for short-term earthquake prediction. Geomat. Nat. Hazards Risk 2010, 1, 115–155. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: New York, NY, USA, 1983. [Google Scholar]
- Sornette, D. Critical Phenomena in Natural Sciences: Chaos, Fractals, Selforganization and Disorder: Concepts and Tools; Springer: Berlin, Germany, 2000. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Skordas, E.; Uyeda, S.; Kamogawa, M. Natural time analysis of critical phenomena. Proc. Natl. Acad. Sci. USA 2011, 108, 11361–11364. [Google Scholar] [CrossRef] [PubMed]
- Bak, P. How Nature Works; Springer: New York, NY, USA, 1996. [Google Scholar]
- Rundle, J.B.; Holliday, J.R.; Turcotte, D. L.; Klein, W. Self-Organized Earthquakes. In American Geophysical Union Fall Meeting Abstracts; AGU: San Francisco, CA, USA, 2011; volume 1, p. 01. [Google Scholar]
- Yoder, M.R.; Turcotte, D.L.; Rundle, J.B. Earthquakes: Complexity and Extreme Events. In Extreme Events and Natural Hazards: The Complexity Perspective, Geophysical Monograph; Sharma, A.S., Bunde, A., Dimri, V.P., Baker, D.N., Eds.; American Geophysical Union: Washington, D.C., WA, USA, 2012; Volume 196, pp. 17–26. [Google Scholar]
- Main, I.G.; Naylor, M. Entropy production and self-organized (sub)criticality in earthquake dynamics. Phil. Trans. R. Soc. A 2010, 368, 131–144. [Google Scholar] [CrossRef] [PubMed]
- Potirakis, S.M.; Minadakis, G.; Nomicos, C.; Eftaxias, K. A multidisciplinary analysis for traces of the last state of earthquake generation in preseismic electromagnetic emissions. Nat. Hazards Earth Syst. Sci. 2011, 11, 2859–2879. [Google Scholar] [CrossRef]
- Eftaxias, K. Are There Pre-Seismic Electromagnetic Precursors? A Multidisciplinary Approach. In Earthquake Research and Analysis—Statistical Studies, Observations and Planning; D’Amico, S., Ed.; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Potirakis, S.M.; Karadimitrakis, A.; Eftaxias, K. Natural time analysis of critical phenomena: The case of pre-fracture electromagnetic emissions. Chaos 2013, 23. [Google Scholar] [CrossRef] [PubMed]
- Potirakis, S.M.; Minadakis, G.; Eftaxias, K. Sudden drop of fractal dimension of electromagnetic emissions recorded prior to significant earthquake. Nat. Hazards 2012, 64, 641–650. [Google Scholar] [CrossRef]
- Minadakis, G.; Potirakis, S.M.; Nomicos, C.; Eftaxias, K. Linking electromagnetic precursors with earthquake dynamics: An approach based on nonextensive fragment and self-affine asperity models. Physica A 2012, 391, 2232–2244. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Nagao, T.; Kamogawa, M.; Tanaka, H.; Uyeda, S. Minimum of the order parameter fluctuations of seismicity before major earthquakes in Japan. Proc. Natl. Acad. Sci. USA 2013, 110, 13734–13738. [Google Scholar] [CrossRef] [PubMed]
- Ida, Y.; Yang, D.; Li, Q.; Sun, H.; Hayakawa, M. Fractal analysis of ULF electromagnetic emissions in possible association with earthquakes in China. Nonlinear Processes Geophys. 2012, 19, 577–583. [Google Scholar] [CrossRef]
- Abe, S.; Herrmann, H.; Quarati, P.; Rapisarda, A.; Tsallis, C. Complexity, Metastability, and Nonextensivity. In Proceedings of the AIP Conference, Zaragoza, Spain, 18–20 April 2007; American Institute of Physics: College Park, MD, USA, 2007; Volume 95. [Google Scholar]
- Rundle, J.; Turcotte, D.; Shcherbakov, R.; Klein, W.; Sammis, C. Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef]
- Eftaxias, K.; Kapiris, P.; Polygiannakis, J.; Bogris, N.; Kopanas, J.; Antonopoulos, G.; Peratzakis, A.; Hadjicontis, V. Signatures of pending earthquake from electromagnetic anomalies. Geophys. Res. Lett. 2001, 28, 3321–3324. [Google Scholar] [CrossRef]
- Kapiris, P.; Balasis, G.; Kopanas, J.; Antonopoulos, G.; Peratzakis, A.; Eftaxias, K. Scaling similarities of multiple fracturing of solid materials. Nonlinear Processes Geophys. 2004, 11, 137–151. [Google Scholar] [CrossRef]
- Contoyiannis, Y.; Kapiris, P.; Eftaxias, K. Monitoring of a preseismic phase from its electromagnetic precursors. Phys. Rev. E 2005, 71. [Google Scholar] [CrossRef] [PubMed]
- Karamanos, K.; Dakopoulos, D.; Aloupis, K.; Peratzakis, A.; Athanasopoulou, L.; Nikolopoulos, S.; Kapiris, P.; Eftaxias, K. Pre-seismic electromagnetic signals in terms of complexity. Phys. Rev. E 2006, 74. [Google Scholar] [CrossRef] [PubMed]
- Eftaxias, K.; Sgrigna, V.; Chelidze, T. Mechanical and electromagnetic phenomena accompanying preseismic deformation: From laboratory to geophysical scale. Tectonophysics 2007, 431, 1–301. [Google Scholar] [CrossRef]
- Paluš, M.; Novotná, D. Testing for nonlinearity in weather records. Phys. Lett. A 1994, 193, 67–74. [Google Scholar] [CrossRef]
- Von Bloh, W.; Romano, M.C.; Thiel, M. Long-term predictability of mean daily temperature data. Nonlinear Processes Geophys. 2005, 12, 471–479. [Google Scholar] [CrossRef]
- Paluš, M.; Hartman, D.; Hlinka, J.; Vejmelka, M. Discerning connectivity from dynamics in climate networks. Nonlinear Processes Geophys. 2011, 18, 751–763. [Google Scholar] [CrossRef]
- Bunde, A.; Havlin, S. Power-law persistence in the atmosphere and the oceans. Physica A 2002, 314, 15–24. [Google Scholar] [CrossRef]
- Vjushin, D.; Govindan, R.B.; Brenner, S.; Bunde, A.; Havlin, S.; Schellnhuber, H.-J. Lack of scaling in global climate models. J. Phys. Condens. Matter 2002, 14, 2275–2282. [Google Scholar] [CrossRef]
- Govindan, R.B.; Vjushin, D.; Bunde, A.; Brenner, S.; Havlin, S.; Schellnhuber, H.-J. Global climate models violate scaling of the observed atmospheric variability. Phys. Rev. Lett. 2002, 89. [Google Scholar] [CrossRef] [PubMed]
- Fraedrich, K.; Blender, R. Scaling of atmosphere and ocean temperature correlations in observations and climate models. Phys. Rev. Lett. 2003, 90. [Google Scholar] [CrossRef] [PubMed]
- Ausloos, M.; Petroni, F. Tsallis non-extensive statistical mechanics of El Niño southern oscillation index. Physica A 2007, 373, 721–736. [Google Scholar] [CrossRef]
- Tsallis, C. Dynamical scenario for nonextensive statistical mechanics. Physica A 2004, 340, 1–10. [Google Scholar] [CrossRef]
- Petroni, F.; Ausloos, M. High frequency (daily) data analysis of the Southern Oscillation Index: Tsallis nonextensive statistical mechanics approach. Eur. Phys. J. Spec. Top. 2011, 143, 201–208. [Google Scholar] [CrossRef]
- Ferri, G.L.; Reynoso Savio, M.F.; Plastino, A. Tsallis’ q-triplet and the ozone layer. Physica A 2010, 389, 1829–1833. [Google Scholar] [CrossRef]
- Pavlos, G.P.; Xenakis, M.N.; Karakatsanis, L.P.; Iliopoulos, A.C.; Pavlos, A.E.G.; Sarafopoulos, D.V. University of Tsallis non-extensive statistics and fractal dynamics for complex systems. Chaotic Model. Simul. 2012, 2, 395–447. [Google Scholar]
- Zemp, D. The Complexity of the Fraction of Absorbed Photosynthetically Active Radiation on a Global Scale. Diploma Thesis, Norwegian Forest and Landscape Institute, Ås and French National College of Agricultural Sciences and Engineering, Toulouse, France, 2012. [Google Scholar]
- Carpi, L.C.; Rosso, O.A.; Saco, P.M.; Gómez Ravetti, M. Analyzing complex networks evolution through Information Theory quantifiers. Phys. Lett. A 2011, 375, 801–804. [Google Scholar] [CrossRef]
- Saco, P.M.; Carpi, L.C.; Figliola, A.; Serrano, E.; Rosso, O.A. Entropy analysis of the dynamics of El Niño/Southern Oscillation during the Holocene. Physica A 2010, 389, 5022–5027. [Google Scholar] [CrossRef]
- Mayewski, P.A.; Rohling, E.E.; Stager, J.C.; Karlén, W.; Maasch, K.A.; Meeker, L.D.; Meyerson, E.A.; Gasse, F.; van Kreveld, S.; Holmgren, K.; et al. Holocene climate variability. Quatern. Res. 2004, 63, 243–255. [Google Scholar] [CrossRef]
- Ferri, G.L.; Figliola, A.; Rosso, O.A. Tsallis’ statistics in the variability of El Niño/Southern Oscillation during the Holocene epoch. Physica A 2012, 391, 2154–2162. [Google Scholar] [CrossRef]
- Gonzalez, J.J.; de Faria, E.L.; Albuquerque, M.P.; Albuquerque, M.P. Nonadditive Tsallis entropy applied to the Earth’s climate. Physica A 2011, 390, 587–594. [Google Scholar] [CrossRef]
- Marwan, N.; Trauth, M.H.; Vuille, M.; Kurths, J. Comparing modern and Pleistocene ENSO-like influences in NW Argentina using nonlinear time series analysis methods. Clim. Dyn. 2003, 21, 317–326. [Google Scholar] [CrossRef]
- Trauth, M.H.; Bookhagen, B.; Marwan, N.; Strecker, M.R. Multiple landslide clusters record Quaternary climate changes in the northwestern Argentine Andes. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2003, 194, 109–121. [Google Scholar] [CrossRef]
- Donges, J.F.; Donner, R.V.; Rehfeld, K.; Marwan, N.; Trauth, M.H.; Kurths, J. Identification of dynamical transitions in marine palaeoclimate records by recurrence network analysis. Nonlinear Processes Geophys. 2011, 18, 545–562. [Google Scholar] [CrossRef]
- Donges, J.F.; Donner, R.V.; Trauth, M.H.; Marwan, N.; Schellnhuber, H.-J.; Kurths, J. Nonlinear detection of paleoclimate-variability transitions possibly related to human evolution. Proc. Natl. Acad. Sci. USA 2011, 20422–20427. [Google Scholar] [CrossRef] [PubMed]
- Malik, N.; Zou, Y.; Marwan, N.; Kurths, J. Dynamical regimes and transitions in Plio-Pleistocene Asian monsoon. Europhys. Lett. 2012, 97. [Google Scholar] [CrossRef]
- Witt, A.; Schumann, A.Y. Holocene climate variability on millennial scales recorded in Greenland ice cores. Nonlinear Processes Geophys. 2005, 12, 345–352. [Google Scholar] [CrossRef]
- Telford, R.J.; Heegaard, E.; Birks, H.J.B. All age-depth models are wrong: But how badly? Quat. Sci. Rev. 2004, 23, 1–5. [Google Scholar] [CrossRef]
- Rehfeld, K.; Marwan, N.; Heitzig, J.; Kurths, J. Comparison of correlation analysis techniques for irregularly sampled time series. Nonlinear Processes Geophys. 2011, 18, 389–404. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Young, C.B. Land surface response to precipitation events using MODIS and NEXRAD data. Int. J. Remote Sens. 2008, 29, 1965–1982. [Google Scholar] [CrossRef]
- Brunsell, N.; Ham, J.; Owensby, C. Assessing the multi-resolution information content of remotely sensed variables and elevation for evapotranspiration in a tall-grass prairie environment. Remote Sens. Environ. 2008, 112, 2977–2987. [Google Scholar] [CrossRef]
- Stoy, P.C.; Williams, M.; Spadavecchia, L.; Bell, R.A.; Prieto-Blanco, A.; Evans, J.G.; Wijk, M.T. Using information theory to determine optimum pixel size and shape for ecological studies: Aggregating land surface characteristics in Arctic ecosystems. Ecosystems 2009, 12, 574–589. [Google Scholar] [CrossRef]
- Brunsell, N.A. A multiscale information theory approach to assess spatial-temporal variability of daily precipitation. J. Hydrol. 2010, 385, 165–172. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Anderson, M.C. Characterizing the multi-scale spatial structure of remotely sensed evapotranspiration with information theory. Biogeosciences 2011, 8, 2269–2280. [Google Scholar] [CrossRef]
- Cochran, F.V.; Brunsell, N.A.; Mechem, D.B. Comparing surface and mid-tropospheric CO2 concentraltions from Central U.S. grasslands. Entropy 2013, 15, 606–623. [Google Scholar] [CrossRef]
- Ruddell, B.L.; Kumar, P. Ecohydrological process networks: I. Identification. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Ruddell, B.L.; Kumar, P. Ecohydrological process networks: II. Analysis and characterization. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Kumar, P.; Ruddell, B.L. Information driven ecohydrological self-organization. Entropy 2010, 12, 2085–2096. [Google Scholar] [CrossRef]
- Rybski, D. Untersuchung von Korrelationen, Trends und synchronem Verhalten in Klimazeitreihen. Ph.D. Thesis, Justus Liebig University of Gießen, Gießen, Germany, 2006. [Google Scholar]
- Yamasaki, K.; Gozolchiani, A.; Havlin, S. Climate networks based on phase synchronization analysis track El Niño. Prog. Theor. Phys. Suppl. 2009, 179, 178–188. [Google Scholar] [CrossRef]
- Malik, N.; Marwan, N.; Kurths, J. Spatial structures and directionalities in monsoonal precipitation over south Asia. Nonlinear Processes Geophys. 2010, 17, 371–381. [Google Scholar] [CrossRef]
- Malik, N.; Bookhagen, B.; Marwan, N.; Kurths, J. Analysis of spatial and temporal extreme monsoonal rainfall over South Asia using complex networks. Clim. Dyn. 2012, 39, 971–987. [Google Scholar] [CrossRef]
- Rybski, D.; Havlin, S.; Bunde, A. Phase synchronization in temperature and precipitation records. Physica A 2003, 320, 601–610. [Google Scholar] [CrossRef]
- Maraun, D.; Kurths, J. Epochs of phase coherence between El Niño/Southern Oscillation and Indian monsoon. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Donges, J.F.; Zou, Y.; Marwan, N.; Kurths, J. Complex networks in climate dynamics. Comparing linear and nonlinear network construction methods. Eur. Phys. J. Spec. Top. 2009, 174, 157–179. [Google Scholar] [CrossRef]
- Donges, J.F.; Zou, Y.; Marwan, N.; Kurths, J. The backbone of the climate network. Europhys. Lett. 2009, 87. [Google Scholar] [CrossRef]
- Barreiro, M.; Marti, A.C.; Masoller, C. Inferring long memory processes in the climate network via ordinal pattern analysis. Chaos 2011, 21. [Google Scholar] [CrossRef] [PubMed]
- Deza, J.I.; Barreiro, M.; Masoller, C. Inferring interdependencies in climate networks constructed at inter-annual, intra-season and longer time scales. Eur. Phys. J. Spec. Top. 2013, 222, 511–523. [Google Scholar] [CrossRef]
- Hlinka, J.; Hartman, D.; Vejmelka, M.; Novotná, D.; Paluš, M. Non-linear dependence and teleconnections in climate data: Sources, relevance, nonstationarity. Clim. Dyn. 2013. [Google Scholar] [CrossRef]
- Runge, J.; Petoukhov, V.; Kurths, J. Quantifying the strength and delay of climatic interactions: The ambiguities of cross correlation and a novel measure based on graphical models. J. Clim. 2013. [Google Scholar] [CrossRef]
- Bjerknes, J. Atmospheric teleconnections from the equatorial pacific. Mon. Weather Rev. 1969, 97, 163–172. [Google Scholar] [CrossRef]
- Walker, G.T. Correlation in seasonal variations of weather, VIII: A preliminary study of world weather. Mem. Ind. Meteorol. Dep. 1923, 24, 75–131. [Google Scholar]
- Walker, G.T. Correlation in seasonal variations of weather, IX: A further study of world weather. Mem. Ind. Meteorol. Dep. 1924, 24, 275–332. [Google Scholar]
- Wang, C. Atmospheric circulation cells associated with the El-Niño-Southern Oscillation. J. Clim. 2002, 15, 399–419. [Google Scholar] [CrossRef]
- Held, H.; Kleinen, T. Detection of climate system bifurcations by degenerate fingerprinting. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Livina, V.N.; Lenton, T.M. A modified method for detecting incipient bifurcations in a dynamical system. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Dakos, V.; Scheffer, M.; van Nes, E.H.; Brovkin, V.; Petoukhov, V.; Held, H. Slowing down as an early warning signal for abrupt climate change. Proc. Natl. Acad. Sci. USA 2008, 105, 14308–14312. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-warning signals for critical transitions. Nature 2009, 461, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Kühn, C. A mathematical framework for critical transitions: bifurcations, fast-slow systems and stochastic dynamics. Physica D 2011, 240, 1020–1035. [Google Scholar] [CrossRef]
- Stanley, H.E. Scaling, universality, and renormalization: Three pillars of modern critical phenomena. Rev. Mod. Phys. 1999, 71, S358–S366. [Google Scholar] [CrossRef]
- Stanley, H.E.; Amaral, L.; Gopikrishnan, P.; Ivanov, P.; Keitt, T.; Plerou, V. Scale invariance and universality: Organizing principles in complex systems. Physica A 2000, 281, 60–68. [Google Scholar] [CrossRef]
- Sornette, D.; Helmstetter, A. Occurrence of finite-time singularities in epidemic models of rupture, earthquakes, and starquakes. Phys. Rev. Lett. 2002, 89. [Google Scholar] [CrossRef] [PubMed]
- Sornette, D. Predictability of catastrophic events: Material rupture, earthquakes, turbulence, financial crashes and human birth. Proc. Natl. Acad. Sci. USA 2002, 99, 2522–2529. [Google Scholar] [CrossRef] [PubMed]
- Kossobokov, V.; Keillis-Borok, V.; Cheng, B. Similarities of multiple fracturing on a neutron star and on Earth. Phys. Rev. E 2000, 61, 3529–3533. [Google Scholar] [CrossRef]
- De Arcangelis, L.; Godano, C.; Lippiello, E.; Nicodemi, M. Universality in solar flare and earthquake occurrence. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef] [PubMed]
- Balasis, G.; Daglis, I.A.; Anastasiadis, A.; Papadimitriou, C.; Mandea, M.; Eftaxias, K. Universality in solar flare, magnetic storm and earthquake dynamics using Tsallis statistical mechanics. Physica A 2011, 390, 341–346. [Google Scholar] [CrossRef]
- Balasis, G.; Papadimitriou, C.; Daglis, I.A.; Anastasiadis, A.; Sandberg, I.; Eftaxias, K. Similarities between extreme events in the solar-terrestrial system by means of nonextensivity. Nonlinear Processes Geophys. 2011, 18, 563–572. [Google Scholar] [CrossRef]
- Balasis, G.; Papadimitriou, C.; Daglis, I.A.; Anastasiadis, A.; Athanasopoulou, L.; Eftaxias, K. Signatures of discrete scale invariance in Dst time series. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Zscheischler, J.; Mahecha, M.D.; Harmeling, S.; Reichstein, M. Detecting and attribution of large spatiotemporal extreme events in Earth observation data. Ecol. Inform. 2013, 15, 66–73. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Materassi, M.; Tozzi, R. An information theory approach to the storm-substorm relationship. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Jimenez, A. A complex network model for seismicity based on mutual information. Physica A 2013, 10, 2498–2506. [Google Scholar] [CrossRef]
- Lenton, T.M.; Held, H.; Kriegler, E.; Hall, J.W.; Lucht, W.; Rahmstorf, S.; Schellnhuber, H.J. Tipping elements in the Earth’s climate system. Proc. Natl. Acad. Sci. USA 2008, 105, 1786–1793. [Google Scholar] [CrossRef] [PubMed]
- Lenton, T.M. Early warning of climate tipping points. Nat. Clim. Chang. 2011, 1, 201–209. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Balasis, G.; Donner, R.V.; Potirakis, S.M.; Runge, J.; Papadimitriou, C.; Daglis, I.A.; Eftaxias, K.; Kurths, J. Statistical Mechanics and Information-Theoretic Perspectives on Complexity in the Earth System. Entropy 2013, 15, 4844-4888. https://doi.org/10.3390/e15114844
Balasis G, Donner RV, Potirakis SM, Runge J, Papadimitriou C, Daglis IA, Eftaxias K, Kurths J. Statistical Mechanics and Information-Theoretic Perspectives on Complexity in the Earth System. Entropy. 2013; 15(11):4844-4888. https://doi.org/10.3390/e15114844
Chicago/Turabian StyleBalasis, Georgios, Reik V. Donner, Stelios M. Potirakis, Jakob Runge, Constantinos Papadimitriou, Ioannis A. Daglis, Konstantinos Eftaxias, and Jürgen Kurths. 2013. "Statistical Mechanics and Information-Theoretic Perspectives on Complexity in the Earth System" Entropy 15, no. 11: 4844-4888. https://doi.org/10.3390/e15114844
APA StyleBalasis, G., Donner, R. V., Potirakis, S. M., Runge, J., Papadimitriou, C., Daglis, I. A., Eftaxias, K., & Kurths, J. (2013). Statistical Mechanics and Information-Theoretic Perspectives on Complexity in the Earth System. Entropy, 15(11), 4844-4888. https://doi.org/10.3390/e15114844






