Estimating Functions of Distributions Defined over Spaces of Unknown Size
Abstract
:1. Background
2. Contribution of This Paper
3. Preliminaries
4. Irrelevance of Unseen Variables
4.1. The Problem of Unseen Variables
4.2. Dirichlet-Independent (DI) Hyperpriors
5. Calculational Benefits
6. Uncertainty in the Concentration Parameter and Event Space Size
6.1. Uncertainty in c
6.2. Likelihood of the Event Space Size
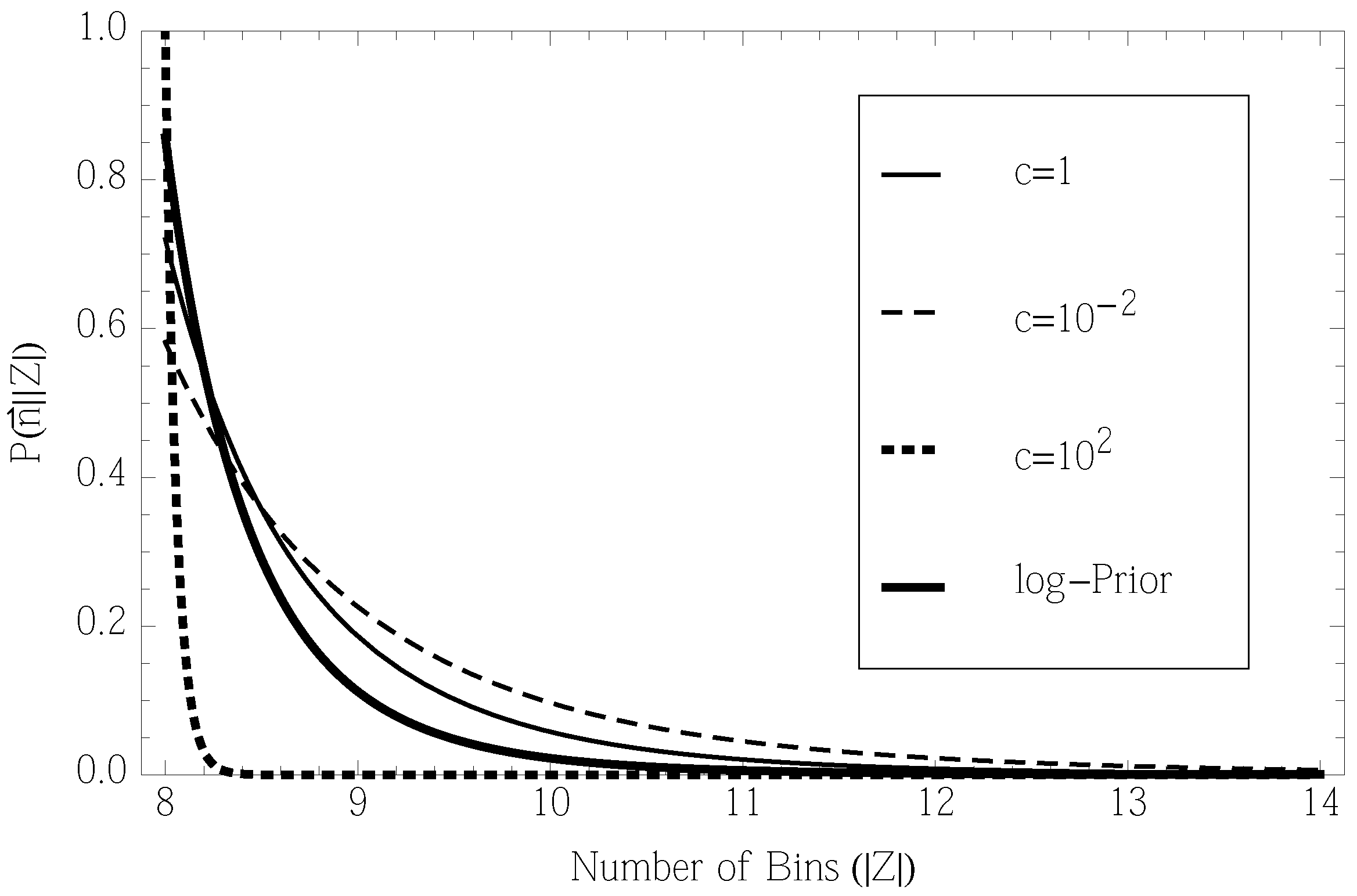

6.3. Uncertainty in the Event Space Size
6.4. Specifying a Single Event Space Size
7. Posterior Expected Entropy When is a Random Variable
7.1. Fixed c
7.2. Uncertain c
7.3. Experimental Tests
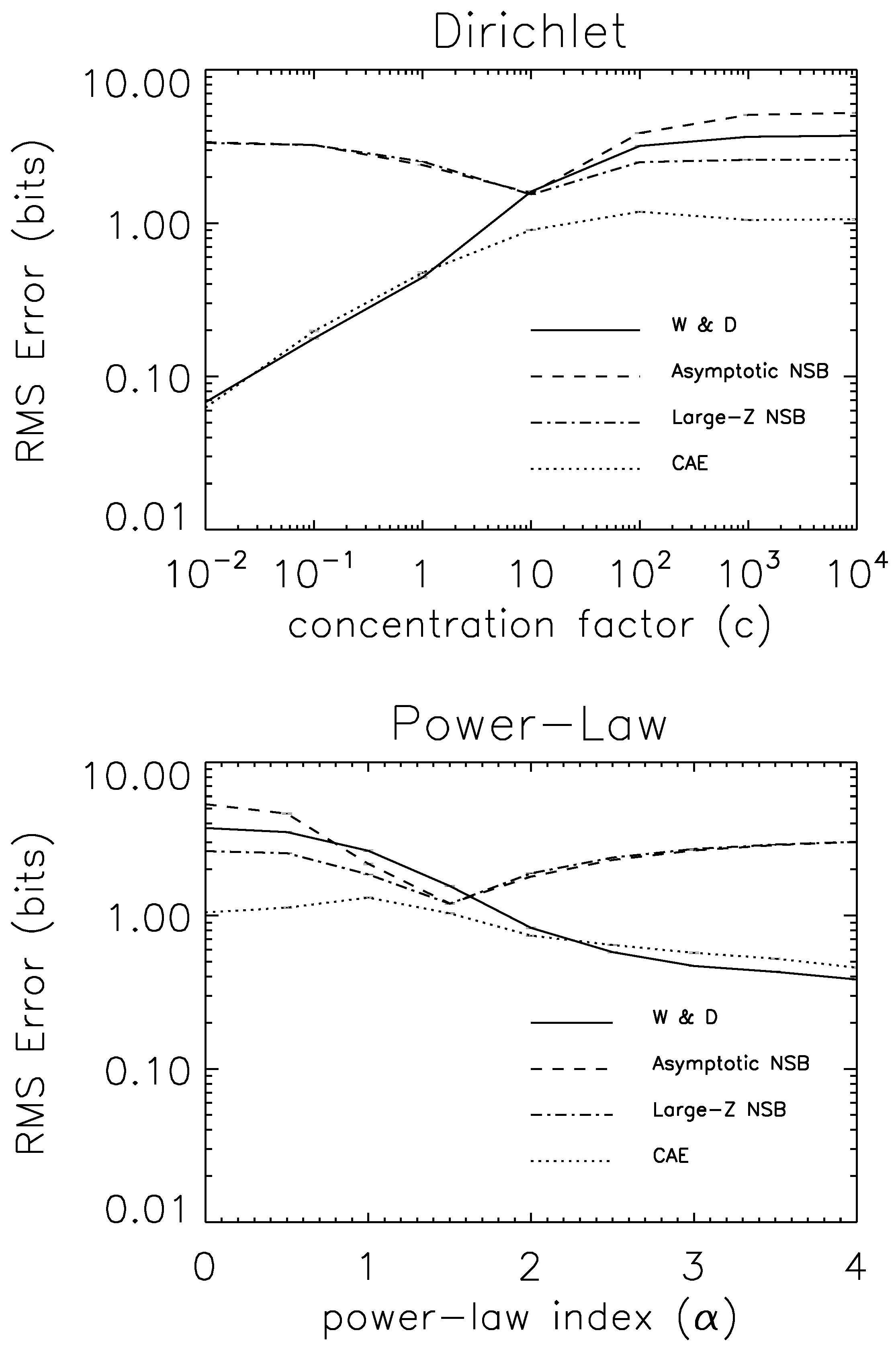
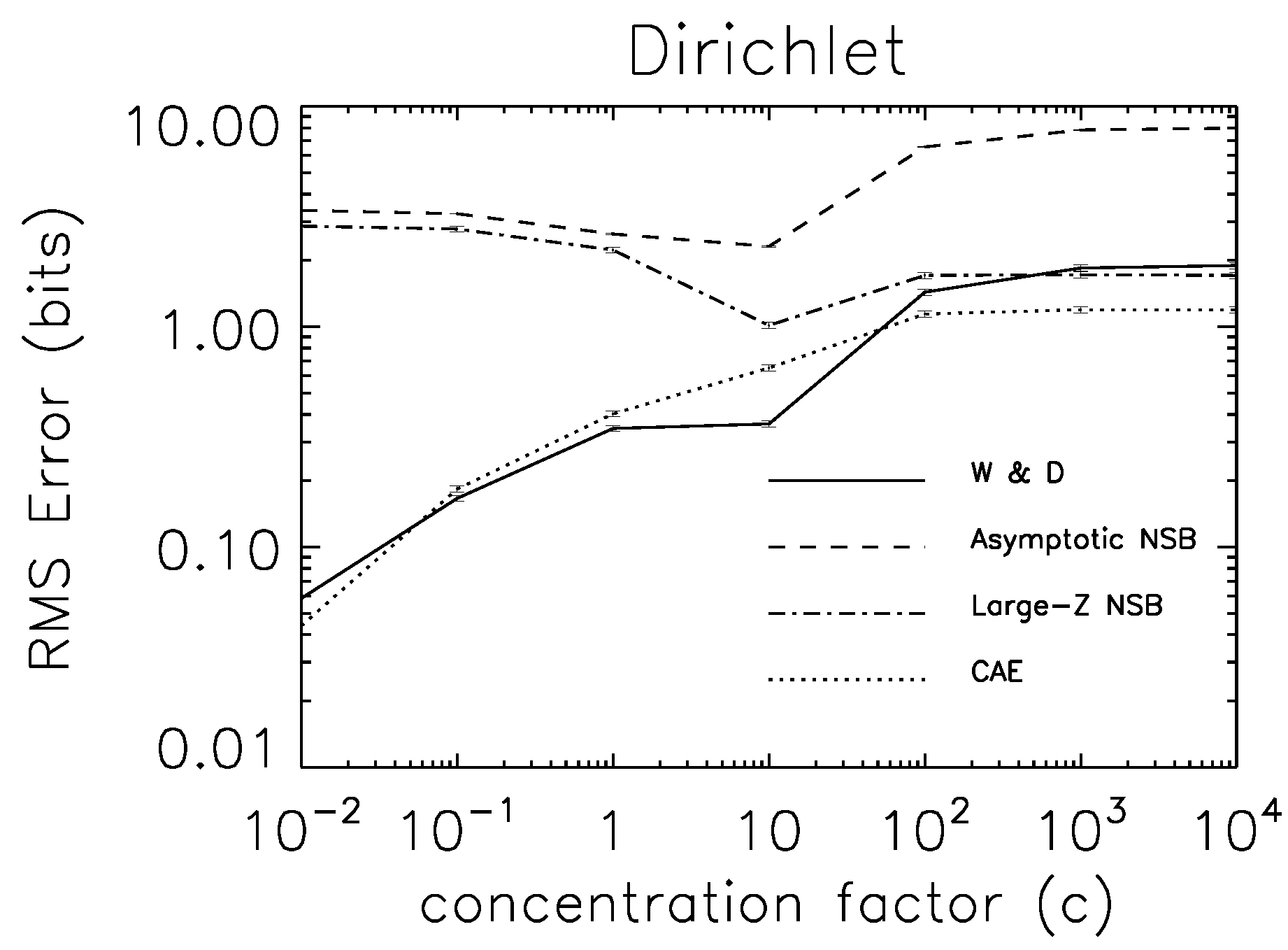
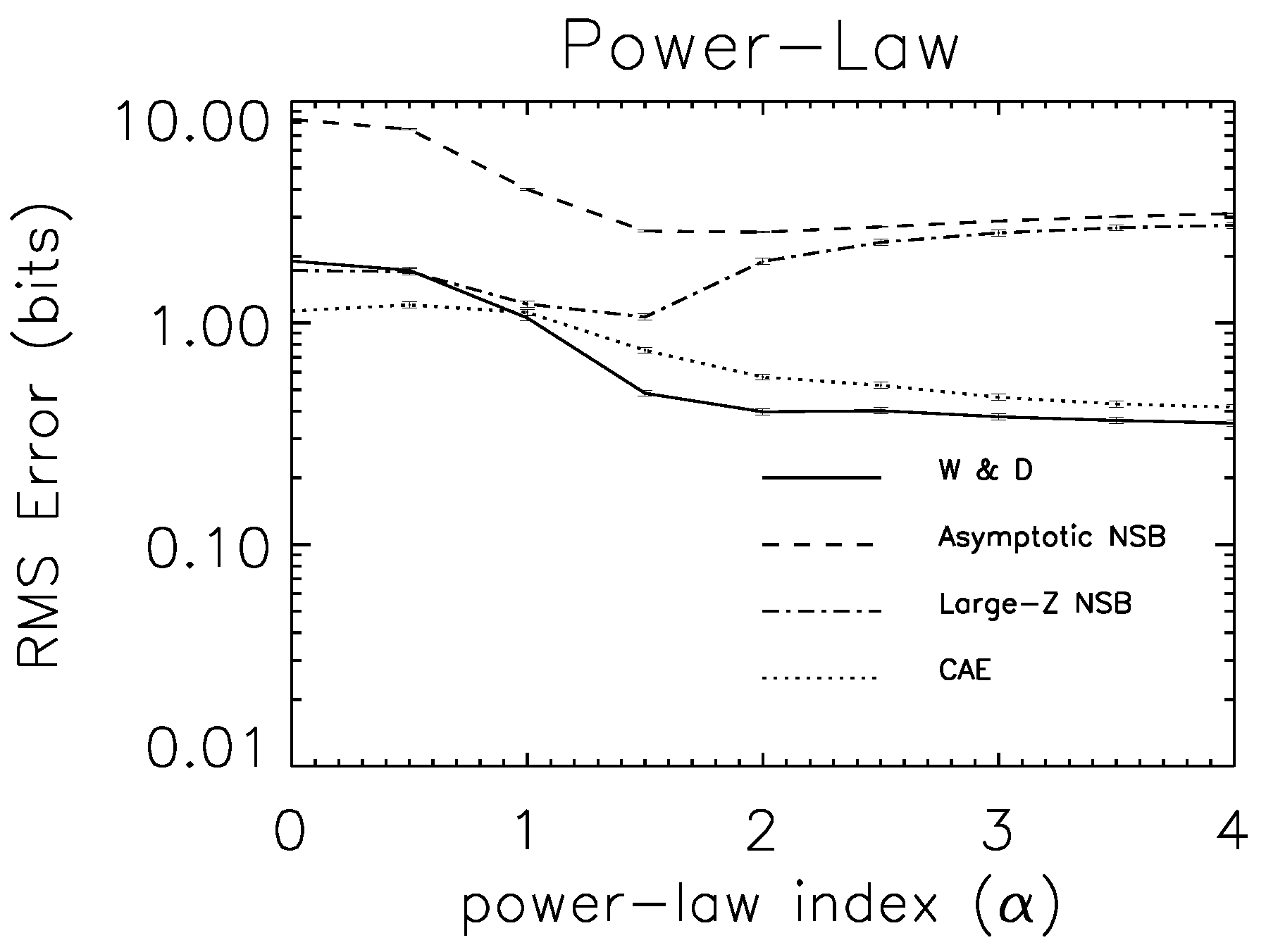
8. Generative Models of Z
8.1. Mapping Physical Samples to Bin Labels
- is sampled to get m, the number of fish species in the lake. At this point, nothing is specified about the physical characteristics of each of those m species.
- Next, a Dirichlet distribution is sampled that extends over distributions ρ that themselves are defined over m bins.
- Next, a vector, , is randomly assigned to each of , e.g., where each of the m vectors is drawn from a Gaussian centered at zero (the precise distribution does not matter). is the set of K real-valued physical characteristics that we will use to define an idealized canonical specimen of fish species, j. By identifying the subscript, j, on each as the associated bin integer, we can view ρ as defined over m separate K-dimensional vectors of fish species characteristics.
- ρ is IID sampled to get a dataset of counts for each species, one through m. Physically, this means that the biologist draws a fish from bin j with probability , i.e., they draw a fish with characteristics with probability .
8.2. Subset Selection Effects
- ;
9. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A—Relevant Results and Errata from WW
- The Dirichlet prior equation in the continued paragraph on page 6843 should have the summation symbol replaced with the product symbol.
- Theorem 8 on page 6846—error as described above, corrected in Equation (30). The analogous equation, (WW1, page 6852), does not contain the analogous error.
- Definitions necessary for various subsets, on page 6851, have errors. In particular, should be , and should be .
- There is an error in the definition of (page 6852.) In particular, the ν symbols in the denominators of the term:should be replaced by , and the symbols in the termsshould be replaced by:
Appendix B—Miscellaneous Proofs
References
- Cover, T.; Thomas, J. Elements of Information Theory; Wiley-Interscience: New York, NY, USA, 1991. [Google Scholar]
- Mackay, D. Information Theory, Inference, and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef]
- Grassberger, P. Entropy estimates from insufficient samplings. 2003; arXiv:physics/ 0307138. [Google Scholar]
- Korber, B.; Farber, R.M.; Wolpert, D.H.; Lapedes, A.S. Covariation of mutations in the V3 loop of human immunodeficiency virus type 1 envelope protein: An information theoretic analysis. Proc. Natl. Acad. Sci. USA 1993, 90, 7176–7180. [Google Scholar] [CrossRef] [PubMed]
- Wolpert, D.; Wolf, D. Estimating functions of probability distributions from a finite set of samples. Phys. Rev. E 1995, 52, 6841–6854. [Google Scholar] [CrossRef]
- Wolf, D.R.; Wolf, D.R.; Wolpert, D.H. Estimating functions of probability distributions from a finite set of samples, Part II: Bayes Estimators for Mutual Information, Chi-Squared, Covariance, and other Statistics. Bayes Estimators for Mutual Information, 1994; arXiv:comp-gas/9403002. [Google Scholar]
- Wolpert, D.; Wolf, D. Erratum: Estimating functions of probability distributions from a finite set of samples. Phys. Rev. E 1996, 54, 6973. [Google Scholar] [CrossRef]
- Hutter, M. Distribution of mutual information. Adv. Neural Inform. Process. Syst. 2002, 1, 399–406. [Google Scholar]
- Hurley, M.; Kao, E. Numerical Estimation of Information Numerical Estimation of Information Theoretic Measures for Large datasets. MIT Lincoln Laboratory Technical Report 1169; Massachusetts Institute of Technology: Lexington, MA, USA, 2013; Available online: http://www.dtic.mil/dtic/tr/fulltext/u2/a580524.pdf (accessed on 28 October 2013).
- Archer, E.; Park, I.; Pillow, J. Bayesian estimation of discrete entropy with mixtures of stick-breaking priors. In Advances in Neural Information Processing Systems 25, Proceedings of the 26th Annual Conference on Neural Information Processing Systems 2012, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 2024–2032.
- Nemenman, I.; Shafee, F.; Bialek, W. Entropy and inference, revisited. In Advances in Neural Information Processing System; Dietterich, T., Ed.; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Nemenman, I.; Bialek, W.; van Steveninck, R.D.R. Entropy and information in neural spike trains: Progress on the sampling problem. Phys. Rev. E 2004, 69, e056111. [Google Scholar] [CrossRef] [PubMed]
- Nemenman, I.; Lewen, G.D.; Bialek, W.; van Steveninck, R.R.D.R. Neural coding of natural stimuli: information at sub-millisecond resolution. PLoS Comput. Biol. 2008, 4, e1000025. [Google Scholar] [CrossRef] [PubMed]
- Archer, E.; Park, I.M.; Pillow, J.W. Bayesian and quasi-Bayesian estimators for mutual information from discrete data. Entropy 2013, 15, 1738–1755. [Google Scholar] [CrossRef]
- Vu, V.; Yu, B.; Kass, R. Coverage-adjusted entropy estimation. Stat. Med. 2007, 26, 4039–4060. [Google Scholar] [CrossRef] [PubMed]
- Jaynes, E.T.; Bretthorst, G.L. Probability Theory : The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- James, R.G.; Ellison, C.J.; Crutchfield, J.P. Anatomy of a bit: Information in a time series observation. 2011; arXiv:1105.2988. [Google Scholar]
- Nemenman, I. Coincidences and estimation of entropies of random variables with large cardinalities. Entropy 2011, 13, 2013–2023. [Google Scholar] [CrossRef]
- Wolpert, D.H. Reconciling Bayesian and non-Bayesian Analysis. In Maximum Entropy and Bayesian Methods; Kluwer Academic Publishers: Dordrecht, Netherlands, 1996; pp. 79–86. [Google Scholar]
- Wolpert, D.H. The Relationship between PAC, the Statistical Physics Framework, the Bayesian Framework, and the VC Framework. In The Mathematics of Generalization; Addison-Wesley: Indianapolis, IN, USA, 1995; pp. 117–215. [Google Scholar]
- Note that no particular property is required of the relation among multiple unseen random variables that may (or may not) exist.
- Bunge, J.; Fitzpatrick, M. Estimating the number of species: A review. J. Am. Stat. Assoc. 1993, 88, 364–373. [Google Scholar]
- The proof of this proposition uses moment-generating functions with Fourier decompositions of the prior, π. To ensure we do not divide by zero, we have to introduce the constant 1 + ϵ into that proof, and to ensure the convergence of our resultant Taylor decompositions, we have to assume infinite differentiability. This is the reason for the peculiar technical condition.
- Berger, J.M. Statistical Decision theory and Bayesian Analysis; Springer-Verlag: Heidelberg, Germany, 1985. [Google Scholar]
- The proof of this proposition uses moment-generating functions with Fourier decompositions of the prior, π. To ensure we do not divide by zero, we have to introduce the constant 1 + ϵ into that proof, and to ensure the convergence of our resultant Taylor decompositions, we have to assume infinite differentiability. This is the reason for the peculiar technical condition.
- Intuitively, for that P(c), the likelihood says that a dataset, {125, 125,…}, would imply a relatively high value of c and, therefore, a high probability that ρ is close to uniform over all bins. Given this, it also implies a low value of |Z|, since if there were any more bins than the eight that have counts, we almost definitely would have seen them seen them for almost-uniform ρ. Conversely, for the dataset, {691, …, 6}, the implication is that c must be low where some rare bins trail out, and as a result, there might be a few more bins who had zero counts.
- Of course, since the formulas in WW implicitly assume c = m, care must be taken to insert appropriate pseudo-counts into those formulas if we want to use a value, c, that differs from m.
- Wolpert, D.; Wolf, D. Estimating functions of probability distributions from a finite set of samples, Part 1: Bayes Estimators and the Shannon Entropy. 1994; arXiv:comp-gas/9403001. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wolpert, D.H.; DeDeo, S. Estimating Functions of Distributions Defined over Spaces of Unknown Size. Entropy 2013, 15, 4668-4699. https://doi.org/10.3390/e15114668
Wolpert DH, DeDeo S. Estimating Functions of Distributions Defined over Spaces of Unknown Size. Entropy. 2013; 15(11):4668-4699. https://doi.org/10.3390/e15114668
Chicago/Turabian StyleWolpert, David H., and Simon DeDeo. 2013. "Estimating Functions of Distributions Defined over Spaces of Unknown Size" Entropy 15, no. 11: 4668-4699. https://doi.org/10.3390/e15114668
APA StyleWolpert, D. H., & DeDeo, S. (2013). Estimating Functions of Distributions Defined over Spaces of Unknown Size. Entropy, 15(11), 4668-4699. https://doi.org/10.3390/e15114668




