From Observable Behaviors to Structures of Interaction in Binary Games of Strategic Complements

Abstract

Consider a setting in which agents can take one of two ordered actions and in which the incentive to take the high action increases in the number of other agents taking it. Furthermore, assume that we do not know anything else about the game being played. What can we say about the details of the interaction between actions and incentives when we observe a set or a subset of all possible equilibria? In this paper, we study this question by exploring three nested classes of games: (a) binary games of strategic complements; (b) games in (a) that admit a network representation; and (c) games in (b) in which the network is complete. Our main results are the following: It has long been established in the literature that the set of pure strategy Nash equilibria of any binary game of strategic complements among a set, N, of agents can be seen as a lattice on the set of all subsets of N under the partial order defined by the set inclusion relation (⊆). If the game happens to be strict in the sense that agents are never indifferent among outcomes (games in (a)), then the resulting lattice of equilibria satisfies a straightforward sparseness condition. (1) We show that, in fact, for each such lattice, $\mathcal{L}$, there is a game in (a), such that its set of equilibria is $\mathcal{L}$ (we say that such a game expresses $\mathcal{L}$); (2) We show that there exists a game in (b), whose set of equilibria contains a given collection, $\mathcal{C}$, of subsets of N, if and only $\mathcal{C}$ satisfies the sparseness condition, and the smallest game in (a) expressing $\mathcal{C}$ is trade robust; (3) We show that there exists a game on the complete graph (games in (c)), whose set of equilibria coincides with some collection, $\mathcal{C}$, if and only if $\mathcal{C}$ is a chain satisfying the sparseness condition.

1. Introduction

Games of strategic complements represent situations in which actions admit a natural ordering, and in which the incentives of any one agent to take a higher action (given that ordering) are increasing in the actions taken by other agents. These games have been widely studied by the literature due to their broad applicability and their tractability (see Vives (1990) [1], and Vives (2005) [2]). They are well suited for representing and analyzing at a stylized level a wide range of social phenomena including the adoption of new technologies and innovations (Jackson and Yariv (2007) [3]), the diffusion of socially beneficial conventions (Young (2009) [4]), the willingness of firms to comply with the law (Decker and Pope (2005) [5]), the decision of whether to take an action in the presence of peer pressure (Calvó-Armengol and Jackson (2010) [6]) and how much of an action to exert (Ballester et al. (2006) [7]). The set of equilibria of these games have several very nice properties stemming from the fact that they are complete lattices (See Zhou (1994) [8] for a proof of the fact that the set of equilibria of any supermodular game (of which games of strategic complements are a special case) is a complete lattice, and Topkis (1998) [9] for an extensive survey of supermodularity, including games of strategic complements), and these properties often imply that they can be profitably analyzed using monotone comparative statics techniques (see Milgrom and Shannon (1994) [10], Athey (2002) [11]). Besides being analytically tractable, these games are also computationally tractable: there are general constructive algorithms for finding equilibria in any given game of strategic complements, and, in fact, the full set of pure strategy Nash equilibria of these games can be relatively easily computed (Echenique (2007) [12]).

Most of the literature studying games of strategic complements has focused on taking a given game as a starting point and, then, deriving and analyzing its set of equilibria. Conversely, under the hypothesis that agents’ behaviors in a given setting positively reinforce each other, one can start from an observed set of behaviors (equilibria) and attempt to say something about the class of games that may have given rise to them. Besides being tractable, this problem is meaningful in the case of binary games of strategic complements, because in this simple subclass of games, the answer to this question can be interpreted in terms of what sets of agents influence which other agents. While this approach can be taken with respect to any class of games, the payoff interactions among agents in an arbitrary game may be very non-monotonic: The effect of $j^{\prime }s$ action on $i^{\prime }s$ incentives can have different signs, depending on the action taken by a third agent, k. In contrast, in the case of games of strategic complements, the interaction between the incentives of a given agent to take an action, and the actions taken by other agents, is stable throughout the entire action space. Concretely, any observed set of behaviors implies some restrictions on the best response correspondence of the game that may have given rise to them as equilibria, and in the case of games of strategic complements, any such best response correspondence can be seen as stemming from a simple model of peer influence. (Consider a game with just two actions. Due to the strategic complementarity, it must be the case that if an agent, i, finds it optimal to take the higher action when the subset of other agents taking that action is S, then he must find it optimal to take the action whenever all agents in any superset of S, $S^{\prime }\supseteq S$ are taking it. This means that we can think of i as being influenced into acting precisely by all the minimal sets that trigger him to take the higher action and all their supersets. This will become clear at the beginning of Section 2.)

In this paper, we explore this problem in the context of two action (binary) games of strategic complements. Restricting attention to two action games greatly simplifies the analysis and, importantly, many of the applications already cited (for instance, the adoption of new technologies and the diffusion of conventions). often involve just two actions. The following example will be useful to explain our results.

A third grade teacher has twenty-five nine-year-olds in his charge for half of the day of a whole academic year, each half day divided into two different periods. The teacher observes that he can classify the mood of each child, i, at a given time as either tranquil ($a_i=0$) or active ($a_i=1$). He is interested in understanding the patterns of tranquility/activity that he observes in his pupils and begins by noting the following:

• Children seem to be quite volatile. Once they settle down after the short break between periods, they can display a very different pattern of behavior from the one in the previous period.
• Children are excited by their peers and, in turn, excite their peers. While important external factors, such as time of day, sugar intake and the subject being studied, are fundamental determinants of the broad activity level, all the patterns that he observes seem to display a high level of internal consistency. The mood of any one child seems to be positively highly correlated with that of some of his peers. When focusing on any given student, it seems that the probability that he is in the active state is increasing in the activity level of at least some of his peers.
• Over the whole year, he observes a wide range of patterns of activity levels.

Under the assumption that all the observed patterns are simply different equilibria of a single game, the teacher would like to infer as much as possible about how that game looks. Some of the questions that the teacher could answer by understanding the game are: Does child i tend to be active because he is very socially sensitive or because he is triggered by a specific group in the class that always tends to be active? Are there any key individuals or groups that by and large determine the mood of the whole class? Would curbing the influence that group S has over child j alter in a significant way the overall behavior patterns of the whole class? Assuming that the children’s influence over each other is only positively reinforcing and restricting attention to static models, the teacher could take one of the following three different starting points (from the most general, to the most restrictive): (1) an arbitrary binary game of strategic complements; (2) a graphical game of thresholds; and (3) a mean peer effects model.

(1)

Arbitrary binary game of strategic complements: Any game with the property that the incentive of each child, i, to move from the low activity level $a_i=0$ to the high activity level $a_i=1$ is weakly increasing in the vector ${\mathbf{a}}_{-i}=(a_1,a_2,...,a_{i-1},a_{i+1},...,a_n)$ of activity levels of the other children.

(2)

Graphical game of thresholds: A game like those in (1), but with the property of being semi-anonymous. The weighted graphical games of strategic complements that we consider in this context are a special case of the general graphical games introduced by Kearns et al. (2001) [13]. The defining property of a graphical game on a set, N, of agents that live in a graph, G, is that the payoff to any given agent is only affected by his own action and the actions of his direct neighbors. These models are, in turn, a special case of games in Multi-Agent Influence Diagrams (MAIDS) introduced by Koller and Milch (2003) [14] (for an introduction to graphical games in economics, see Chapter 9 in Jackson (2008) [15]). That is, the effect of the actions of a subset, S, of children over child i can only depend on the weighted sum of the actions taken by the children in S, where the weight given to child $j\in S$ represents the strength of the relationship between i and j. Therefore, if there is any other group, $S^{\prime }\ne S$, with the same weighted sum of actions (as viewed by i), its effect over i must be the same as that of S. Despite this restriction, children can differ greatly from each other, both in terms of the groups that can influence them and in their social sensitivity.

(3)

Mean peer effects model: A game like those in (2), but in which the relationships of every pair of children carry the same weight; that is, each child is influenced by the whole class, and the only possible differences between children are in their sensitivity. (See Manski (1993) [16] and Lee (2004) [17] for examples of models relying on the standard “average interactions" assumption, whereby agents are partitioned into groups, within which every agent interacts with every other agent.)

In general, models in these three classes have multiple pure strategy Nash equilibria and, thus, predict sets of behavior as opposed to single patterns of behavior. In some cases, mixed strategy Nash equilibrium may also be of interest; however, the strategic complements literature has mainly focused on pure strategy equilibria. (This has mostly been the case due to the fact that pure strategy Nash equilibria always exist in these games and are tractable. However Echenique and Edlin (2004) [18] provides a deeper justification: Under many learning dynamics, mixed strategy equilibria are unstable and, thus, not good predictions of behavior.) Furthermore, any given single pattern of behavior (a vector describing the behavior of each child) can be the equilibrium of an appropriate model of kinds (1), (2) or (3). It follows that the only way in which we may get some clues as to whether a model in one of these families captures the interaction among the children well is by relying on non-singleton sets of behavior.

The main question that articulates this paper is: What is the difference between the sets of behaviors that are the set (or a subset) of equilibria of a game in (1), (2) and (3)? (Note that by definition, any set of behaviors that is expressed by one of the more restrictive classes is automatically being expressed by one of the more general ones.)

The paper contributes to answering this question in three ways:

• It characterizes the class of sets of pure strategy Nash equilibria that can be expressed (throughout, we say that a set of equilibria is expressed by a given family of games, if it is the set of equilibria of some game in that family) by the class of all strict binary games of strategic complements among a set N of agents (henceforth, increasing games of influence). Note that we can identify any profile of actions $\mathbf{a}=(a_1,a_2,...,a_i,...,a_n)\in {\{0,1\}}^n$ with the set of agents taking the high action. $\{j:a_j=1\}$, and thus, we can think of any set of equilibria as a subset of $2^N$ (the set of all subsets of N). It has long been established in the literature that the set of pure strategy Nash equilibria of any binary game of strategic complements among a set N of agents can be seen as a lattice (a lattice is a partially-ordered set with the property that every pair of elements has a minimum upper bound (a join ∧) and a maximum lower bound (a meet ∨)) on $2^N$ under the partial order defined by the set inclusion relation (⊆). (See Zhou (1994) [8] which shows that the set of equilibria of any supermodular game is a complete lattice, under the ordering with which the action space is endowed. The fact that set inclusion is the relevant relation in the case of binary games just stems from the correspondence between any profile of actions and the set of agents that take the higher action. Set inclusion corresponds to the product order, inherited from the ordering of the two possible actions. See Topkis (1988) [9] for an in-depth treatment of strategic complementarities.) If the game happens to be strict in the sense that agents are never indifferent among outcomes, then the resulting lattice of equilibria satisfies a straightforward sparseness condition. In Proposition 1, we show that, in fact, this class of games expresses all such lattices. In particular, we prove that any lattice, $\mathcal{L}$, under set inclusion on $2^N$ satisfying this sparseness condition is the set of pure strategy Nash equilibria of some binary game of strategic complements with no indifference.
  It may be the case that we are interested in knowing whether there is a game in (1), such that its set of equilibria contains a given set of behaviors, $\mathcal{C}$ (throughout, we refer to this case as weak expressibility). This question is interesting if, for instance, we do not have too many observations and believe that the system at hand is capable of producing other yet unobserved patterns. In Corollary 1 of Proposition 1, we note that the answer is affirmative, as long as $\mathcal{C}$ satisfies the sparseness condition. The fact that all sets of equilibria are lattices and every lattice satisfying the sparseness condition is the set of equilibria of some game in the class, then, implies that we can systematically enumerate all the models that could have produced $\mathcal{C}$ and identify the additional patterns of behaviors that would falsify each of them. Corollary 1 also notes that given any set $\mathcal{C}$ that is weakly expressible by some game in (1), there exists a minimum game, $mi{n}_{win}\mathcal{C}$, that weakly expresses it (the partial order in which this is the case is described in Section 2). This simple fact turns out to be very useful for our analysis of sets of behaviors expressible by games in $\left(2\right)$.
• We study weighted graphical games of thresholds (2) as a special subclass of (1) and relate the problem of determining when a given lattice can be expressed by a game in this class to the classical cooperative game theory problem of determining when a simple game can be represented as a weighted majority game (A simple game on N is a collection of winning coalitions, $\mathcal{W}\subset 2^N$, with the property that $N\in \mathcal{W}$ and $\varnothing \notin \mathcal{W}$. See Elgot (1961) [19] and Taylor and Zwicker (1992) [20]). Taylor and Zwicker (1992) [20] provide a characterization of weighted simple games using a concept called trade robustness. Proposition 2 shows that a set, $\mathcal{C}$, is weakly expressible by a weighted graphical game, if and only if it satisfies the sparseness condition and $mi{n}_{win}\mathcal{C}$ is trade robust. It follows as an immediate consequence that if $\mathcal{C}$ itself does not satisfy trade robustness, it cannot possibly stem from a weighted graphical game of thresholds.
• Claims 1 and 2 show that a collection of subsets of N is the set of equilibria of a game of thresholds in the complete graph (games in $\left(3\right)$), if and only if it is a chain in which any two sets differ by at least two elements. This statement also applies to weak expressibility, as any superset of a set that is not a chain cannot possibly be a chain.

Our paper is related to the non-cooperative game theory literature, which models situations in which agents’ decisions or opinions are swayed in the direction of the agents that they have contact with. (See Granovetter (1978) [21] for an early threshold model, Koller and Milch (2003) [14] for the most general framework available explicitly tracking the dependencies between agents’ decisions and Jackson and Yariv (2007) [3], López-Pintado (2008) [22] or Golub and Jackson (2010) [23] for some recent contributions.) More narrowly, this paper contributes to the growing literature on graphical games of strategic complements (see Kearns et al. (2001) [13] and Galeotti et al. (2010) [24]) by analyzing graphical games of strategic complements as a subset of the class of complete information, simultaneous move-two action games of strategic complements and characterizing the sets of behaviors that can be seen as equilibria of games in the broader class, but not in the more restricted one. In contrast to our work, most of the literature on graphical games (under complete or incomplete information) has been concerned with making predictions based on pre-defined games and understanding how those predictions respond to changes in some of the exogenous parameters, notably, the graph describing the relationships between the agents.

There is extensive work on models of influence in cooperative game theory. As described above, our work focuses on the patterns of influence that are inferable by equilibrium behavior and is thus firmly anchored in the non-cooperative (strategic) game theoretic tradition. The different points of departure imply that the overlap between our work and the insights provided by the large cooperative literature on influence is limited. There are two strands of work in cooperative game theory that have recently addressed influence. The first one is called the model of influence and is based on a framework first introduced by Hoede and Bakker (1982) [25] in order to measure the decisional power of agents in a social network and, subsequently, extended by Grabisch and Rusinowska (2010b) [26] to study influence. (This framework has been studied in-depth by Rusinowska and De Swart (2007) [27], Grabisch and Rusinowska (2009) [28], (2010a) [29], (2010b) [26], (2011) [30] and Rusinowska (2008) [31]. For a survey of the work, see Grabisch and Rusinowska (2010c) [32].) The second one is based on the concept of command game, introduced by Hu and Shapley (2003a) [33] and (2003b) [34].

The model of influence has three main components: (1) initial inclinations—each agent in a set N has an initial inclination (accept or reject) towards a binary decision; (2) an influence function, which maps each possible inclination vector to a vector of final decisions and reflects the idea that due to other agents’ influence, any given agent’s final decision may differ from his initial inclination; (3) a follower function, which is derived from the influence function and maps each coalition of agents (a subset of N) to the set of agents whose final decision corresponds to the initial inclination of the coalition, whatever the initial inclination vector, as long as all members of the coalition have the same initial inclination. A natural question that emerges in the context of the model of influence and which is analogous to the main question addressed by our paper is (to recall, our main question is, What is the difference between the sets of behaviors that are the set (or a subset) of equilibria of a game in (1), (2) and (3)?): When is an arbitrary function from $2^N$ to $2^N$ the follower function generated by some influence function? The relation is just by analogy, since ours is an approach to influence as reflected in equilibrium behavior, whereas the model of influence addresses influence as reflected on the differences between initial inclinations and final decisions. In that framework, the final decision of an agent is influenced by other agents’ initial inclinations, but not by their final decision. In particular, a follower of a coalition may be influenced to make a decision that is different from his initial inclination by some coalition, yet the final decisions of the members of the coalition itself may end up being different (among themselves and with respect to that of the agent); thus, the key pieces of data are the vectors of initial inclinations and the vectors of final decisions. The point is that, theoretically, there are certain observations of coalitions’ initial inclinations and followers’ behaviors capable of ruling out the possibility that the final decisions are the result of an influence process of the form captured by their model. Grabisch and Rusinowska (2011) [30] tells us precisely what those observations are. The paper provides necessary and sufficient conditions for any given function mapping subsets of N to subsets of N to be the follower function of some influence function.

The Hu and Shapley (2003a) [33] (2003b) [34] command games framework is closely related to the Grabisch and Rusinowska model of influence (Grabisch and Rusinowska (2011) [30] studies the relation between them). Given a set, N, of agents and two possible actions, the central element in the command games literature is a simple game for each agent i describing the coalitions that lead the agent to take the high action i. There are two kinds of such coalitions: boss coalitions, which never include agent i and can force agent i to take an action, and approving coalitions, which include agent i. The starting point of our model is equivalent to a collection of command games in which all coalitions are boss coalitions. Hu and Shapley (2003b) [34] addresses the problem of deriving an equilibrium measure of authority from the command game description of the way in which agents can influence each other. It is an equilibrium measure of authority in the sense that it takes into account the fact that, in general, there are pairs of agents, i and j, such that j is in some of the winning coalitions of $i^{\prime }s$ command game and i is in some of the winning coalitions of $j^{\prime }s$ command game. Related to this, Grabisch and Rusinowska (2009) [28] develops a measure of influence (as different from authority) in command games. The problems of constructing measures of influence or authority in cooperative game theory take into account the possible circularity of influence. Additionally, in that sense, they are related to the problems that we face in our paper. Since their approach builds up directly on the description of influence (either the model of influence or the command game) and not on first predicting possible behaviors based on a notion of equilibrium, their theorems are not directly applicable to our work. The richness of these two cooperative frameworks and the simple technical bridge with the non-cooperative literature noted in this paper, allowing us to derive our results regarding weighted graphical games, suggests that there may be very useful further connections between the cooperative and non-cooperative approaches to the question of influence.

The paper is divided into two sections, besides this introduction. Section 2 presents the main definitions that are used throughout, and Section 3 presents and discusses the results.

2. Peer Influence Structures and Games of Social Influence

A peer influence structure on a set of agents $N=\{1,2,3,...,n\}$ is a an n-tuple of functions, ${\mathcal{I}}_i:2^N\to \{0,1\}$, one for each $i\in N$, satisfying the property that $\forall i\in N$, ${\mathcal{I}}_i\left(x\right)={\mathcal{I}}_i(x\cup \left\{i\right\})$. For a given set, $x\in 2^N$, ${\mathcal{I}}_i\left(x\right)=1$ is interpreted as meaning that when all agents, $j\in x$, set $a_j=1$, then i strictly prefers to set $a_i=1$. Similarly, ${\mathcal{I}}_i\left(x\right)=0$ is interpreted as meaning that when all agents, $j\in x$, set $a_j=1$, then i strictly prefers to set $a_i=0$. The idea behind the only requirement in the definition of influence structure is to preclude self-reference in action: that is, an agent is influenced by what other agents do, but not by what he himself does. Note that the best response function (since agents are never indifferent, we speak of the best response function, rather than correspondence) of any binary game of strategic complements with two actions and no indifference is a peer influence structure. The point of the definition is that given any agent, i, we are interested in the identities of those agents whose actions affect his incentives (influence him), and that is our starting point. For the purpose of making comparisons between influence structures, we rely on the partial order, ⪯, on the collection of all influence structures on N defined by letting ${\mathcal{I}}^{\prime }⪯\mathcal{I}$ if ${\mathcal{I}}_i^{\prime }\left(x\right)\le {\mathcal{I}}_i\left(x\right)$ $\forall x,i$. Note that, if $\mathcal{I}$ and ${\mathcal{I}}^{\prime }$ are influence structures, then so is $\mathcal{I}\vee {\mathcal{I}}^{\prime }$ defined by ${(\mathcal{I}\vee {\mathcal{I}}^{\prime })}_i\left(x\right)=max\{{\mathcal{I}}_i\left(x\right),{\mathcal{I}}_i^{\prime }\left(x\right)\}$ and $\mathcal{I}\wedge {\mathcal{I}}^{\prime }$ defined by ${(\mathcal{I}\wedge {\mathcal{I}}^{\prime })}_i\left(x\right)=min\{{\mathcal{I}}_i\left(x\right),{\mathcal{I}}_i^{\prime }\left(x\right)\}$. In this way, the collection of influence structures in itself forms a lattice.

Throughout this paper, we will only be concerned with increasing influence structures. An influence structure is increasing if $\forall i\in N$ and $x\subseteq x^{\prime }$, we have that ${\mathcal{I}}_i\left(x\right)=1\Rightarrow {\mathcal{I}}_i\left(x^{\prime }\right)=1$.

A game of social influence induced by a peer influence structure, $\mathcal{I}$, is a simultaneous move game, ${\Gamma }_{\mathcal{I}}$, in which each agent has strategies, 0 and 1, and whose best response function $BR:{\{0,1\}}^n\to {\{0,1\}}^n$ is given by $\mathcal{I}$, that is, $BR\left(\mathbf{a}\right)=╳{\mathcal{I}}_{i=1}^n$. This paper is only concerned with strategic behavior depending on pure strategies and makes no observations related to welfare. (See the introduction for an explanation of why pure strategy Nash equilibria are interesting in the case of games of strategic complements.) From this perspective, the best response function fully defines the game.

A pure strategy Nash equilibrium of a game of influence is a strategy profile, ${\sigma }_1\times {\sigma }_2\times ,...,\times {\sigma }_n$, where ${\sigma }_i\in \{0,1\}$ has the property that $\forall i\in \{j\in N:{\sigma }_j=1\}$, ${\mathcal{I}}_i\left(\{j\in N:{\sigma }_j=1\}\right)=1$ and $\forall i\notin \{j\in N:{\sigma }_j=1\}$, ${\mathcal{I}}_i\left(\{j\in N:{\sigma }_j=1\}\right)=0$. Note that any strategy profile in a game of social influence can be described succinctly by the set, $\{i\in N:{\sigma }_i=1\}$. In this way, and for convenience, throughout the paper, we will be thinking of strategy profiles and, in particular, of Nash equilibria as subsets of N. We will denote the set of Nash equilibria of game ${\Gamma }_{\mathcal{I}}$ as $NE\left({\Gamma }_{\mathcal{I}}\right)$. We say that an influence structure, $\mathcal{I}$, expresses a collection of subsets of N, $\mathcal{C}\subseteq 2^N$, if $\mathcal{C}=NE\left({\Gamma }_{\mathcal{I}}\right)$, and that it weakly expresses $\mathcal{C}$ if $\mathcal{C}\subseteq NE\left({\Gamma }_{\mathcal{I}}\right)$. Similarly, we say that a collection, $\mathcal{C}\subseteq 2^N$, is (weakly) expressible by a given family of influence structures, $\left\{\mathcal{I}\right\}$, if there exists some structure, ${\mathcal{I}}^{*}$, in the family, so that $NE\left({\Gamma }_{{\mathcal{I}}^{*}}\right)(\subseteq )=\mathcal{C}$. When talking about a collection of sets, $\mathcal{C}$, we think of it as endowed with the partial order induced by the weak set containment relation (⊆).

3. Results

We begin with a straightforward observation.

A nonempty collection of subsets of N, $\mathcal{C}\subseteq 2N$, is expressible by some influence structure, if and only if $x\in \mathcal{C}$ and $i\in x⟹x\setminus \left\{i\right\}\notin \mathcal{C}$. (1)

This condition immediately follows from the definition of social influence structure. If $\mathcal{I}$ is an influence structure that expresses $\mathcal{C}$, it must be the case that $\forall x\in \mathcal{C}$, ${\mathcal{I}}_i\left(x\right)=1$ for all $i\in x$ and ${\mathcal{I}}_i\left(x\right)=0$ for all $i\notin x$. If for some $x\in \mathcal{C}$, it is the case that $x\setminus \left\{i\right\}\in \mathcal{C}$ for some $i\in x$, we would have ${\mathcal{I}}_i\left(x\right)=1$ and ${\mathcal{I}}_i(x\setminus \left\{i\right\})=0$, which violates the definition of social influence structure. Given any collection, $\mathcal{C}$, satisfying the condition in (1), we can define $\mathcal{I}$, which expresses it as follows: begin by letting ${\mathcal{I}}_i\left(x\right)=0$ $\forall x$ and $\forall i$, and then, for each $x\in \mathcal{C}$ and i in x, set ${\mathcal{I}}_i\left(x\right)=1$. If $\varnothing \in \mathcal{C}$, we are done; otherwise, for each minimal element, x of, $\mathcal{C}$, set ${\mathcal{I}}_i\left(x^{\prime }\right)=1$ $\forall i\in x$ and $x^{\prime }\subseteq x$. Given that $\mathcal{C}$ satisfies the condition in (1), this collection of functions will be a well-defined influence structure. It is clear that there are many influence structures which express a given collection of subsets, $\mathcal{C}\subseteq 2^N$.

3.1. Increasing Influence Structures

One very useful result that applies to our setting from the general theory of games of strategic complements is the following (see Zhou (1994) [8] and the introduction):

If $\mathcal{I}$ is an increasing influence structure, then $NE\left({\Gamma }_{\mathcal{I}}\right)$ forms a lattice (with respect to the set containment (⊆) partial order). (2)

(Note: completeness is automatic, because our lattices are always finite)

We present a proof of this statement, as it showcases an argument that frequently arises when working within this classes of games of influence.

If $NE\left({\Gamma }_{\mathcal{I}}\right)$ is empty or a singleton, then it is immediately true that it is a lattice. Therefore, suppose that there exist $x\ne x^{\prime }$, such that $x,x^{\prime }\in NE\left({\Gamma }_{\mathcal{I}}\right)$. Note that $\{y\in NE\left({\Gamma }_{\mathcal{I}}\right):y\supseteq x\cup x^{\prime }\}$ is nonempty. If ${\mathcal{I}}_j\left(N\right)$ for all j, then $N\in \{y\in NE\left({\Gamma }_{\mathcal{I}}\right):y\supseteq x\cup x^{\prime }\}$. If this is not the case, then we can remove the elements $j\in N$, such that ${\mathcal{I}}_j\left(N\right)=0$. We can proceed iteratively, until we stop at a set, $x^{\prime \prime }\subset N$, such that ${\mathcal{I}}_j\left(x^{\prime \prime }\right)=1$ for all $j\in x^{\prime \prime }$. By construction and the fact that $\mathcal{I}$ is increasing, it is true that ${\mathcal{I}}_j\left(x^{\prime \prime }\right)=0$ for all $j\notin x^{\prime \prime }$ and, thus, $x^{\prime \prime }\in NE\left({\Gamma }_{\mathcal{I}}\right)$. Furthermore it must be the case that $x^{\prime \prime }\supseteq x\cup x^{\prime }$. This will surely be the case, since at no point in the process do we remove any elements in $x\cup x^{\prime }$. The reason is that ${\mathcal{I}}_i\left(N\right)=1$ for all $j\in x\cup x^{\prime }$ given that x and $x^{\prime }$ are equilibria and $\mathcal{I}$ is increasing, so inductively, at each stage of the process, we have that $x\cup x^{\prime }$ is contained in the set under consideration. It follows that $x^{\prime \prime }\in \{y\in NE\left({\Gamma }_{\mathcal{I}}\right):y\supseteq x\cup x^{\prime }\}$.

To see that $x^{\prime }\vee x=min\{y\in NE\left({\Gamma }_{\mathcal{I}}\right):y\supseteq x\cup x^{\prime }\}$ exists, suppose it does not. Then, it must be the case that the set $\{y\in NE\left({\Gamma }_{\mathcal{I}}\right):y\supseteq x\cup x^{\prime }\}$ has at least two minimal elements, z and $z^{\prime }$. Then, some set, w, $x\cup x^{\prime }\subseteq w\subseteq z\cap z^{\prime }$, must be an equilibrium: if $i\notin z\cap z^{\prime }$, then either $i\notin z$ or $i\notin z^{\prime }$. Without loss of generality, suppose that $i\notin z$. Then, as z is an equilibrium, it must be the case that ${\mathcal{I}}_i\left(z\right)=0$ and, because $z^{\prime }\cap z\subseteq z$ and $\mathcal{I}$ is increasing, we must also have ${\mathcal{I}}_i(z\cap z^{\prime })=0$. On the other hand, if $i\in x\cup x^{\prime }$, then ${\mathcal{I}}_i(x\cup x^{\prime })=1$, because i belongs to either x or $x^{\prime }$, $\mathcal{I}$ is increasing and both x and $x^{\prime }$ are equilibria. Therefore, starting at $z\cap z^{\prime }$, we can iteratively remove the elements that prefer not to be active from the set. Due to the fact that $\mathcal{I}$ is increasing, it will be the case that elements not belonging to the set prefer not to be active at each iteration. Additionally, at some point, before reaching $x\cup x^{\prime }$ or at $x\cup x^{\prime }$, it will also be the case that all elements in the set will prefer to be in the set. This set is the equilibrium, w, that we were looking for, and as $w\subset z$ and $w\subset z^{\prime }$, its existence contradicts the minimality of z and $z^{\prime }$. We conclude that the set, $\{y:y\supseteq x\text{and}y\supseteq x^{\prime }\}$, only has one minimal element; the minimum we were looking for. With an analogous argument, we can show the existence of the meet $x\wedge x^{\prime }=max\{y:y\subseteq x\cap x^{\prime }\}$.

Given a lattice, $\mathcal{L}$, how can we know whether it is expressible by an increasing influence structure? The sparseness condition (SC) in the following proposition is clearly necessary, as it just demands that the minimal restrictions imposed on the influence structure by the sets in $\mathcal{L}$ are consistent with it being increasing. The work goes into showing that it is also sufficient.

PROPOSITION 1 

There exists an increasing influence structure expressing a lattice, $\mathcal{L}\subseteq 2^N$, if and only if :

Sparseness Condition$\left(SC\right)$: $i\in y\in \mathcal{L}\Rightarrow$ $\forall x\in \mathcal{L}$, such that $y\setminus \left\{i\right\}\subseteq x$, we have $i\in x$.

Proof of Proposition 1: 

Necessity: Suppose condition (1) does not hold. That is, assume that there exist $x,y\in \mathcal{L}$ and $i\in N$, such that $i\notin x$, $i\in y$ and $y\setminus \left\{i\right\}\subseteq x$. However, then any peer influence structure inducing the game satisfies ${\mathcal{I}}_i(y\setminus \left\{i\right\})={\mathcal{I}}_i\left(y\right)=1$ and ${\mathcal{I}}_i\left(x\right)=0$, so $\mathcal{I}$ is not increasing.

Sufficiency: We begin by setting ${\mathcal{I}}_i\left(x\right)=0$ for all i and $x\in 2^N$ and, then, modify it in two steps. We first modify it to guarantee that it induces as all elements of $\mathcal{L}$ reach equilibria, and then, we tweak it in order to remove all unwanted elements, $x\in NE\left({\Gamma }_{\mathcal{I}}\right)\cap {\mathcal{L}}^c$.

(S1) Induce all required equilibria:

For each $x\in \mathcal{L}$ and $i\in x$, let ${\mathcal{I}}_i\left(x^{\prime }\right)=1$ for $x^{\prime }\supseteq x\setminus \left\{i\right\}$.

Note that, in step (S1), we construct an increasing peer influence structure, and by virtue of $\left(SC\right)$, each $x\in \mathcal{L}$ is an equilibrium of the game that it induces. By construction, if $i\in x\in \mathcal{L}$, then ${\mathcal{I}}_i\left(x\right)=1$. Moreover, if $i\notin x\in \mathcal{L}$, then ${\mathcal{I}}_i\left(x\right)=0$. To see this, note that to have ${\mathcal{I}}_i\left(x\right)=1$, it needs to be the case that $y\setminus \left\{i\right\}\subset x$ for some $y\in \mathcal{L}$, such that $i\in y$, but by $\left(SC\right)$, this would imply $i\in x$, which by assumption is false.

The issue is that ${\Gamma }_{\mathcal{I}}$, where $\mathcal{I}$ is as defined in (S1), may have other equilibria. To see this in a simple example, consider the influence structure that results from the application of (S1) to the lattice satisfying $\left(SC\right)$ depicted on the left in Figure 1 and note that it actually expresses the lattice shown on the right. (As it generally seems to be the case when attempting to construct games that express a given set of equilibria, it is easy to guarantee that the members of the set are all equilibria of the game, but harder to guarantee that those are the only equilibria.)

We now remove all the unwanted equilibria, and this can be done thanks to the fact that the set in question is a lattice. Therefore, let ${\mathcal{I}}^0$ denote the influence structure constructed in (S1) and ${\Gamma }_{{\mathcal{I}}^0}$, the game that it induces.

(S2) Remove all unwanted equilibria: We remove the unwanted equilibria iteratively and prove that the procedure does not damage any of the desired equilibria by induction.

The base case:

If $NE\left({\Gamma }_{{\mathcal{I}}^0}\right)=\mathcal{L}$, we are done. Therefore, suppose there exists $y\in NE\left({\Gamma }_{{\mathcal{I}}^0}\right)\cap {\mathcal{L}}^c$. Note that $y\in NE\left({\Gamma }_{{\mathcal{I}}^0}\right)$ implies ${\mathcal{I}}_j^0\left(y\right)=1$ for each $j\in y$. By construction, in (S1), ${\mathcal{I}}_j^0\left(y\right)=1$ can only hold if there is $x\in \mathcal{L}$, such that $x\subseteq y$ and $j\in x$. Therefore, it follows that:

${\displaystyle \forall j\in y,\exists x_j\in \mathcal{L}}$ where $x_j\subset y$, and $j\in x$. (*)

where the strict containment (⊂) follows from the fact that $y\notin \mathcal{L}$.

Figure 1. The figure on the right is the lattice expressed by the game induced by the influence structure constructed by applying (S1) to the lattice on the left.

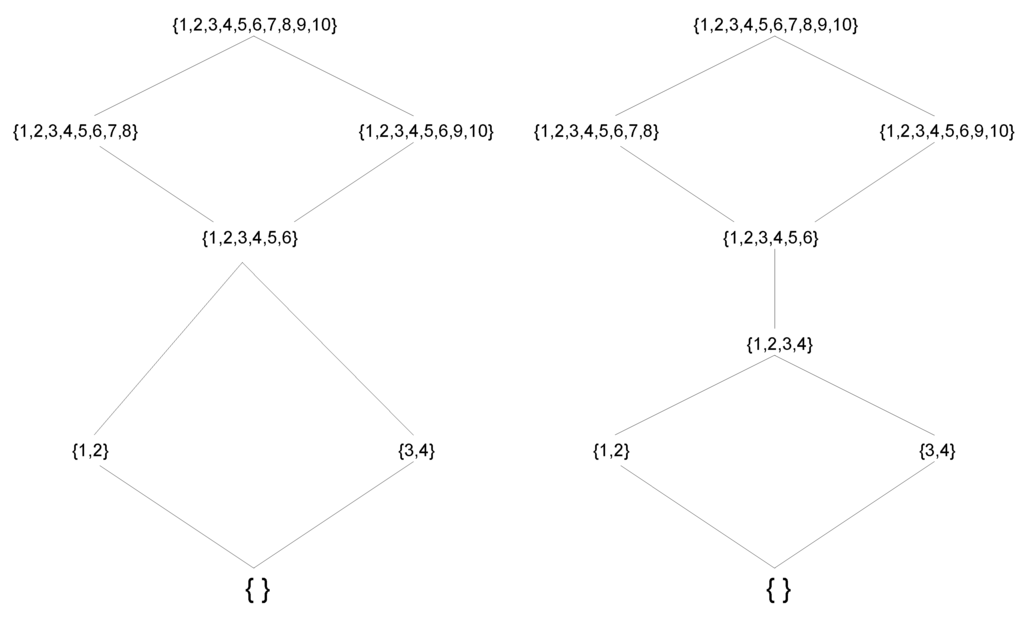
Figure 1. The figure on the right is the lattice expressed by the game induced by the influence structure constructed by applying (S1) to the lattice on the left.

The key in what follows is that (*) implies that the unique successor of y in $\mathcal{L}$ is ${\displaystyle \underset{j\in y}{\bigvee }}{x}_j$, where the $x_j$’s are the elements of $\mathcal{L}$ described in (*). To see that this is the case, first note that ${\displaystyle \underset{j\in y}{\bigvee }}{x}_j$ (the smallest upper bound of ${\left\{x_j\right\}}_{j\in y}$ in $\mathcal{L}$) is well defined by virtue of the fact that $\mathcal{L}$ is a lattice. The fact that ${\displaystyle \underset{j\in y}{\bigvee }}{x}_j$ is a successor of y in $\mathcal{L}$ follows from the fact that if there existed $w\in \mathcal{L}$, $y\subset w\subset {\displaystyle \underset{j\in y}{\bigvee }}{x}_j$, then we would have $x_j\subset y\subset w\subset {\displaystyle \underset{j\in y}{\bigvee }}{x}_j$ for all $j\in y$, contradicting the fact that ${\displaystyle \underset{j\in y}{\bigvee }}{x}_j$ is the smallest upper bound of ${\left\{x_j\right\}}_{j\in y}$ in $\mathcal{L}$. ${\displaystyle \underset{j\in y}{\bigvee }}{x}_j$ is the unique successor, because any other $z\in \mathcal{L}$, such that $z\supseteq y$, is an upper bound for ${\left\{x_j\right\}}_{j\in y}$ and, therefore, ${\displaystyle \underset{j\in y}{\bigvee }}{x}_j\subset z$.

Let:

$${\mathcal{I}}_i^1\left(z\right)=\left\{\begin{array}{cc}1\hfill & :z\supseteq y\text{and}i\in ({\displaystyle \underset{j\in x}{\bigvee }}{x}_i)\setminus y\hfill \\ {\mathcal{I}}_i^0\left(z\right)\hfill & :otherwise\hfill \end{array}\right.$$

We will now show that $\mathcal{L}\subseteq NE\left({\Gamma }_{{\mathcal{I}}^1}\right)$. The definition of ${\mathcal{I}}^1$ only makes adjustments to ${\mathcal{I}}^0$ on sets, $z\supseteq y$. Therefore, if $z\in \mathcal{L}$ and $z⊉y$, then $z\in NE\left({\Gamma }_{{\mathcal{I}}^1}\right)$ (as $z\in NE\left({\Gamma }_{{\mathcal{I}}^0}\right)$). Therefore, consider some $z\in \mathcal{L}$, such that $z\supset y$. Any such z must contain ${\displaystyle \underset{j\in y}{\bigvee }}{x}_j$, as any set containing $y={\displaystyle \bigcup _{j\in y}}{x}_j$, and the only possible difference between ${\mathcal{I}}^1$ and ${\mathcal{I}}^0$ can be on components (${\mathcal{I}}_i^1$ vs. ${\mathcal{I}}_i^0$) involving elements i in ${\displaystyle \underset{j\in y}{\bigvee }}{x}_j$. However, ${\displaystyle \underset{j\in y}{\bigvee }}{x}_j\subseteq z\in NE\left({\Gamma }_{{\mathcal{I}}^0}\right)$ implies ${\mathcal{I}}_i^0\left(z\right)=1$ for any such element, i. Therefore, actually no change was really made to the function in z.

We now show that $NE\left({\Gamma }_{{\mathcal{I}}^1}\right)\cap {\mathcal{L}}^c\subset NE\left({\Gamma }_{{\mathcal{I}}^0}\right)\cap {\mathcal{L}}^c$. By construction of ${\mathcal{I}}^1$, $y\notin NE\left({\Gamma }_{{\mathcal{I}}^1}\right)$, and we will show that no other element $y^{\prime }\in {\mathcal{L}}^c$ that was not in $NE\left({\Gamma }_{{\mathcal{I}}^0}\right)$ can now be part of $NE\left({\Gamma }_{{\mathcal{I}}^1}\right)$. As above, we only need to be concerned with sets $y^{\prime }\supset y$. If $y^{\prime }\supseteq {\displaystyle \underset{j\in y}{\bigvee }}{y}_j$, then, as seen above, ${\mathcal{I}}^1$ and ${\mathcal{I}}^0$ are identical, so the only possible occurrence of a new equilibrium in $\Gamma \left({\mathcal{I}}^1\right)$ must involve sets $y^{\prime }$, such that $y\subset y^{\prime },y^{\prime }\not\subset {\displaystyle \underset{i\in y}{\bigvee }}{x}_i$. Note, however, that any such set must lack some element $j^{*}\in ({\displaystyle \underset{j\in y}{\bigvee }}{x}_j)\setminus y$, and for such an element, ${\mathcal{I}}_{j^{*}}^1\left(y\right)=1$, and therefore, $y^{\prime }$ cannot be an equilibrium of ${\Gamma }_{{\mathcal{I}}^1}$.

The inductive step:

Assume that for $k>1$, we have $\{{\mathcal{I}}^0,{\mathcal{I}}^1,...,{\mathcal{I}}^k\}$, such that for each m, $1\le m\le k$, $NE\left({\Gamma }_{{\mathcal{I}}^m}\right)\supseteq \mathcal{L}$ and $NE\left({\Gamma }_{{\mathcal{I}}^m}\right)\cap {\mathcal{L}}^c\subset NE\left({\Gamma }_{{\mathcal{I}}^{m-1}}\right)\cap {\mathcal{L}}^c$. If $NE\left({\Gamma }_{{\mathcal{I}}^k}\right)\cap {\mathcal{L}}^c=\varnothing$, then we are done. Otherwise, suppose that there exists $y\in NE\left({\Gamma }_{{\mathcal{I}}^k}\right)\cap {\mathcal{L}}^c$. By assumption $NE\left({\Gamma }_{{\mathcal{I}}^k}\right)\cap {\mathcal{L}}^c\subset NE\left({\Gamma }_{{\mathcal{I}}^m}\right)\cap {\mathcal{L}}^c$ for all $m<k$, and therefore, $y\in NE\left({\Gamma }_{{\mathcal{I}}^0}\right)\cap {\mathcal{L}}^c$. However, this means that $(*)$ above holds, and we can therefore construct ${\mathcal{I}}^{k+1}$ from ${\mathcal{I}}^k$ just as we constructed ${\mathcal{I}}^1$ from ${\mathcal{I}}^0$. The augmented sequence $\{{\mathcal{I}}^0,{\mathcal{I}}^1,...,{\mathcal{I}}^{k+1}\}$ has the property that for each m, $1\le m\le k+1$, we have $NE\left({\Gamma }_{{\mathcal{I}}^m}\right)\supseteq \mathcal{L}$ and $NE\left({\Gamma }_{{\mathcal{I}}^m}\right)\cap {\mathcal{L}}^c\subset NE\left({\Gamma }_{{\mathcal{I}}^{m-1}}\right)\cap {\mathcal{L}}^c$.

Note that the construction of ${\mathcal{I}}^0$, satisfying $NE\left({\Gamma }_{{\mathcal{I}}^0}\right)\supseteq \mathcal{L}$ in the proof of Proposition 1 only relies on the fact that $\mathcal{L}$ satisfies (SC) and, in particular, does not depend on $\mathcal{L}$’s lattice structure. Therefore, the following corollary immediately follows.

COROLLARY 1 

A set, $\mathcal{C}\subseteq 2^N$, is weakly expressible by an increasing influence structure, $\mathcal{I}$, if and only if it satisfies (SC). Furthermore, ${\mathcal{I}}^0$, as constructed in $\left(S1\right)$ based on $\mathcal{C}$ and which we denote $mi{n}_{win}\left(\mathcal{C}\right)$, is the smallest increasing influence structure weakly expressing $\mathcal{C}$ (according to the order defined in Section 2).

Corollary 1 shows that, as long as $\left(SC\right)$ is satisfied by a given set $\mathcal{C}$ of patterns of behavior, there is some increasing influence structure inducing a game whose set of equilibria contains $\mathcal{C}$. The fact that $mi{n}_{win}\left(\mathcal{C}\right)$ is the smallest such influence structure follows from the fact that in (S1) in the proof of Proposition 1, we begin with ${\mathcal{I}}^0\left(x\right)=0$ for all i and x and, then, only make the adjustments ${\mathcal{I}}^0\left(x\right)=0\to {\mathcal{I}}^0\left(x\right)=1$ that are strictly necessary to guarantee $\mathcal{C}\subseteq NE\left({\mathcal{I}}^0\right)$. It is worth pointing out that even in cases in which we are just concerned with whether some binary game of strategic complements weakly expresses a set of behavior patterns, Proposition 1 is very useful. In particular, it tells us that if some $\mathcal{C}$ satisfying (SC) has indeed been generated by an increasing influence structure, then the complete set of equilibria of the game must be in the set $\{\mathcal{L}\supseteq \mathcal{C}:\mathcal{L}$ is a lattice satisfying (SC)}. We can thus know which other yet unobserved behaviors we can expect and which behaviors to look out for in order to further narrow down our understanding, by falsifying some of the models in $\{\mathcal{L}\supseteq \mathcal{C}:\mathcal{L}$ is a lattice satisfying (SC)}.

3.2. Increasing Influence Structures That Admit a Network Representation

An influence structure, $\mathcal{I}$, admits a network representation when for each agent i, there exist weights ${\left\{w_{ij}\right\}}_{j=1}^n$, $w_{ij}\ge 0$, $w_{ii}=0$ and a threshold $t_i\ge 0$, such that ${\mathcal{I}}_i\left(x\right)=1$, if and only if, ${\displaystyle \sum _{j\in x}}{w}_{ij}\ge t_i$. Without loss of generality, we will restrict attention to cases in which $0<t_i<{\displaystyle \sum _{j\in N}}{w}_{ij}$. Throughout this section, we will also restrict attention to collections of subsets of N, $\mathcal{C}$ (and lattices $\mathcal{L}$), such that $\varnothing ,N\in \mathcal{C}$ ($\varnothing ,N\in \mathcal{L}$). (If this condition is violated for some i, this means that either (1) i sets $a_i=0$ regardless of what other agents do; or (2) i sets $a_i=1$ regardless of what other agents do. In both cases, we can remove some agents from the game and adjust the thresholds of the remaining ones, obtaining a game on a set, $N^{\prime }\subset N$, of agents with an equivalent set of equilibria. If (1) holds, then we can remove i without doing any adjustments. If $\left(2\right)$ holds, then we remove i and let $t_j^{\prime }=t_j-w_{ij}$ for all the remaining agents, and if $t_j^{\prime }\le 0$, then we remove j and continue iterating, until we only have agents with strictly positive thresholds. The argument for restricting attention to $\mathcal{C}$ and lattices $\mathcal{L}$, such that $\varnothing ,N\in \mathcal{C}$ or $\varnothing ,N\in \mathcal{L}$, is analogous.) We can group all the individual weights in a matrix, W, and let $\mathbf{t}={(t_1,t_2,...,t_i,...,t_n)}^{\prime }$ denote the vector of thresholds. As W and $\mathbf{t}$ fully capture an influence structure, we will directly denote it by $(W,\mathbf{t})$, instead of using $\mathcal{I}$. The games induced by increasing structures that admit a network representation are well known in the literature as graphical games of strategic complements or games of thresholds. Throughout this section, we refer to the game induced by $(W,\mathbf{t})$ as a game of thresholds and denote it by ${\Gamma }_{(W,\mathbf{t})}$. Given a lattice, $\mathcal{L}$, we say that it is (weakly) expressible by a game of thresholds if there exist some weights, W, and a vector of thresholds, $\mathbf{t}$, such that $NE\left({\Gamma }_{(W,\mathbf{t})}\right)(\subseteq )=\mathcal{L}$.

As seen in Example 1, there are some increasing influence structures that do not admit network representations.

EXAMPLE 1 

An influence structure that does not admit a network representation.

Let $\mathcal{I}$ be an increasing influence structure on $\{1,2,3,4,5\}$, such that ${\mathcal{I}}_1\left(x\right)=1$, if and only if $x\supseteq \{2,3\}$ or $x\supseteq \{4,5\}$. This influence structure does not admit a network representation: The reason is that ${\mathcal{I}}_1\left(\{2,3\}\right)=1$ implies that either $w_{12}\ge \frac{t_1}{2}$ or $w_{13}\ge \frac{t_1}{2}$. Similarly, it must be the case that either $w_{14}\ge \frac{1}{2}$ or $w_{15}\ge \frac{1}{2}$. However, this, in turn, implies that at least one of ${\mathcal{I}}_1\left(\{2,4\}\right)$, ${\mathcal{I}}_1\left(\{2,5\}\right)$, ${\mathcal{I}}_1\left(\{3,4\}\right)$ or ${\mathcal{I}}_1\left(\{3,5\}\right)$ must also be one. ⋄

Example 1 shows that if we want agent 1 to be triggered by groups of agents $\{2,3\}$ and $\{4,5\}$, while depicting his incentives using weights and a threshold, then it must be the case that he is also triggered by at least one other group of agents that is not a superset of either of these. In general, this is the only kind of limitation that we encounter when constructing network representations of influence structures: it is straightforward to assign the weights and pick the threshold in order to have an agent prefer to be active when every element in a specified collection of subsets of N is active. What can be difficult and sometimes impossible is choosing them in order to ensure that these are the only triggers.

We now turn to the question of which sub-collection of lattices expressible by increasing influence structures are also expressible by games of thresholds. There are two different kinds of problems that we may face in trying to express a given lattice. The first one is that due to the approximation limitations seen in Example 1, we may gain some equilibria, which we cannot destroy without compromising the equilibria that we do want to include. The other possibility is that none of the approximations expresses supersets of the lattice in question. Example 2 shows that the collection of lattices expressible by games of thresholds is a strict subset of the collection of lattices expressible by increasing influence structures.

EXAMPLE 2 

A set of equilibria of an increasing influence structure that cannot be expressed by a game of thresholds.

Let ${\mathcal{I}}_1$ be an increasing influence structure on $\{1,2,3,4,5,6,7,8,9\}$, such that $B_1=\{\{2,3,4,5\},\{6,7,8,9\}\}$, $B_2=\{\{3,4,5\},\{3,6,7\}\}$, $B_3=\{\{2,4,5\},\{2,6,7\}\}$, $B_4=\{\{2,3,5\},\{5,8,9\}\}$, $B_5=\{\{2,3,4\},\{4,8,9\}\}$, $B_6=\{\{2,3,7\},\{7,8,9\}\}$, $B_7=\{\{2,3,6\},\{6,8,9\}\}$, $B_8=\{\{6,7,9\},\{4,5,9\}\}$, $B_9=\{\{6,7,8\},\{4,5,8\}\}$. The set of equilibria of the associated game of influence is shown in Figure 2. This lattice is not expressible by any game of thresholds. The reason is that $\{1,6,7,8,9\}$ and $\{1,2,3,4,5\}$ are equilibria, and therefore, ${\displaystyle \sum _{j=2}^9}{w}_{1j}\ge 2t_1$. This means that either $w_4+w_5+w_8+w_9\ge t_1$ or $w_2+w_3+w_6+w_7\ge t_1$, so it cannot be the case that $\{4,5,8,9\}$ and $\{2,3,6,7\}$ are both equilibria. Agent 1 would strictly prefer to join at least one of them. ⋄

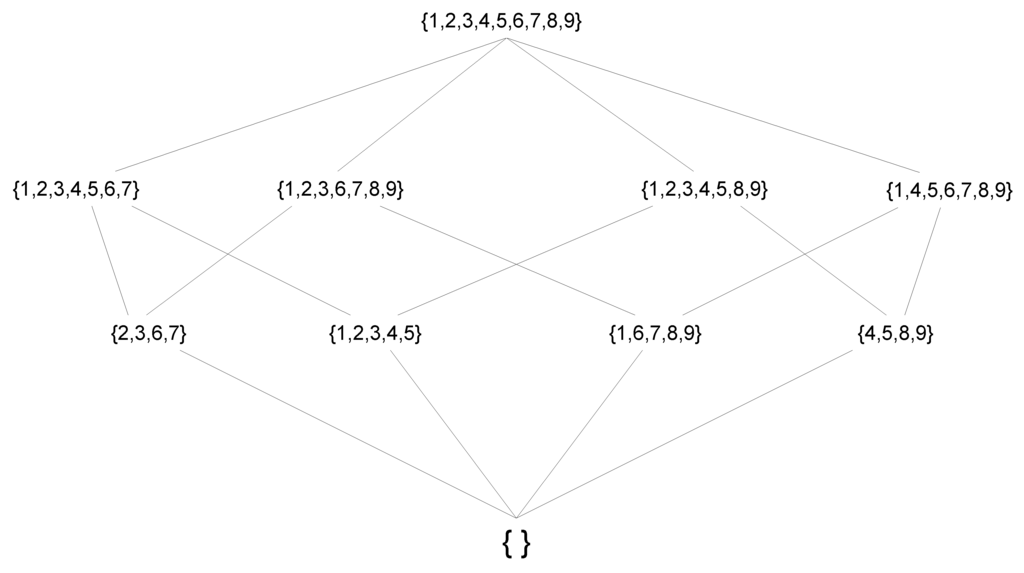
Figure 2. The set of equilibria of ${\Gamma }_{{\mathcal{I}}_1}$.

Figure 2. The set of equilibria of ${\Gamma }_{{\mathcal{I}}_1}$.

3.2.1. Relation to Monotonic Simple Games

We begin this section with a few definitions from the literature on simple and weighted games that we use in the subsequent analysis.

A simple game on N is a collection of coalitions, $\mathcal{W}\subset 2^N$ with the property that $N\in \mathcal{W}$ and $\varnothing \notin \mathcal{W}$. A simple game is monotonic if $S\in \mathcal{W}\Rightarrow S^{\prime }\in \mathcal{W}$ for each pair $S,S^{\prime }\in 2^N$, such that $S\subseteq S^{\prime }$. (More generally, simple games are usually defined over arbitrary algebras of subsets of N.) The subsets of N that belong to $\mathcal{W}$ are called winning coalitions, and the subsets belonging to ${\mathcal{W}}^c$ are called losing coalitions.

Note that any given increasing influence function, ${\mathcal{I}}_i$, for $i\in N$, with the property that ${\mathcal{I}}_i\left(\varnothing \right)=0$ and ${\mathcal{I}}_i\left(N\right)=1$ corresponds to the monotonic simple game, ${\mathcal{W}}_i$, on $N\setminus \left\{i\right\}$ in which $x\in {\mathcal{W}}_i$, if and only if ${\mathcal{I}}_i\left(x\right)=1$. In these terms, an increasing influence structure is just a collection of monotonic simple games.

A simple game, $\mathcal{W}$, on N is said to be weighted if there exists a collection of weights ${\left\{w_j\right\}}_{j\in N}$, $w_j\ge 0$ for all j and a threshold q, such that for all coalitions $S\subseteq N$, $S\in \mathcal{W}$, if and only if $\sum _{j\in S}{w}_j\ge q$. (Note that all weighted simple games are monotonic by definition.) Taylor and Zwicker provide a characterization of the set of simple games that are weighted.

We say that a sequence of elements, $A_1,A_2,...,A_m$ (not necessarily different), of $2^N$ can be trade-transformed into a sequence of elements, $B_1,B_2,...,B_m$ (not necessarily different), if $|\{j:i\in A_j\}|=|\{j:i\in B_j\}|$ for all $i\in N$.

DEFINITION 1 (Trade robustness) 

A simple game is k-trade robust, if it is not possible to trade-transform k winning coalitions (not necessarily different) into k losing coalitions. The game is trade robust if it is k-trade robust for all values of k.

With the above definition in mind, we can enunciate one of Taylor and Zwicker’s main theorems.

THEOREM 1 (Taylor and Zwicker 1992)) 

A simple game is weighted, if and only if it is trade robust.

Any set of behaviors automatically implies some minimal restrictions on the collection of winning coalitions and losing coalitions of the simple game representing each agent’s influence structure. For example, the lattice shown in Figure 2 requires $\varnothing \notin {\mathcal{W}}_1$, $\{2,3,6,7\}\notin {\mathcal{W}}_1$, $\{4,5,8,9\}\notin {\mathcal{W}}_1$, $\{2,3,4,5\}\in {\mathcal{W}}_1$, $\{6,7,8,9\}\in {\mathcal{W}}_1$, $\{2,3,4,5,6,7\}\in {\mathcal{W}}_1$, $\{2,3,6,7,8,9\}\in {\mathcal{W}}_1$, $\{2,3,4,5,8,9\}\in {\mathcal{W}}_1$, $\{4,5,6,7,8,9\}\in {\mathcal{W}}_1$ and $\{2,3,4,5,6,7,8,9\}\in {\mathcal{W}}_1$.

Given a collection, $\mathcal{C}\in 2^N$, satisfying $\left(SC\right)$ and some $i\in n$, let $mi{n}_{wi{n}_i}\left(\mathcal{C}\right)$ denote the collection of winning coalitions in $N\setminus \left\{i\right\}$ describing i’s influence structure in the game $mi{n}_{win}\left(\mathcal{C}\right)$ defined in Corollary 1 of Proposition 1. $mi{n}_{wi{n}_i}\left(\mathcal{C}\right)$ therefore satisfies that $y\in mi{n}_{wi{n}_i}\left(\mathcal{C}\right)$, if and only if $\exists x\in \mathcal{C}$, $i\in x$ and $y\supseteq x\setminus \left\{i\right\}$. It also follows from Corollary 1 that $mi{n}_{wi{n}_i}\left(\mathcal{C}\right)$ is a monotonic simple game. (Note that $mi{n}_{wi{n}_i}\left(\mathcal{C}\right)\ne \varnothing$ and $mi{n}_{wi{n}_i}\left(\mathcal{C}\right)\ne 2^N$, given that we only consider collections $\mathcal{C}$, such that $N\in \mathcal{C}$ and $\varnothing \in \mathcal{C}$. Coupled with $\left(SC\right)$, $\varnothing \in \mathcal{C}$ implies $\left\{i\right\}\notin \mathcal{C}$ and, therefore, $\varnothing \notin mi{n}_{wi{n}_i}\left(\mathcal{C}\right)$.) The following proposition, based on Taylor and Zwicker’s characterization, tells us exactly when it is the case that a collection, $\mathcal{C}\in 2^N$, is weakly expressible by a game of thresholds.

PROPOSITION 2 

There exists a game of thresholds weakly expressing a collection, $\mathcal{C}\subseteq 2^N$, if and only if $\mathcal{C}$ satisfies $\left(SC\right)$ and $mi{n}_{wi{n}_i}\left(\mathcal{C}\right)$ is trade robust for each $i\in N$.

Proof of Proposition 2: 

Sufficiency follows immediately by applying Theorem 1 (Taylor and Zwicker) to the influence structure, $mi{n}_{wi{n}_i}\left(\mathcal{C}\right)$.

Necessity: If $\mathcal{C}$ is weakly expressible by a game of thresholds, then by Corollary 1, we know that it satisfies (SC). By definition, there exists $(W,\mathbf{t})$, such that $\mathcal{C}\subseteq NE\left({\Gamma }_{(W,\mathbf{t})}\right)$. Define $(W^{\prime },{\mathbf{t}}^{\prime })$ by letting ${\mathbf{t}}^{\prime }=\mathbf{t}$ and for each $i,j\in N$, $w_{ij}^{\prime }=w_{ij}$ if $i,j\in x$ for some $x\in \mathcal{C}$ and $w_{ij}=0$ otherwise. Then, $\mathcal{C}\subseteq NE\left({\Gamma }_{(W^{\prime },{\mathbf{t}}^{\prime })}\right)$. To see this, let $x\in \mathcal{C}$, and suppose that $i\notin x$; then, by definition of $W^{\prime }$, ${\sum }_{j\in x}{w}_{ij}^{\prime }<={\sum }_{j\in x}{w}_{ij}<t_i=t_i^{\prime }$. If $i\in x$, then ${\sum }_{j\in x}{w}_{ij}^{\prime }={\sum }_{j\in x}{w}_{ij}>=t_i=t_i^{\prime }$. So $(W^{\prime },{\mathbf{t}}^{\prime }))$ weakly expresses $\mathcal{C}$. Furthermore, for each i, $mi{n}_{wi{n}_i}\left(\mathcal{C}\right)$ is the simple game generated by ${\{w_{ij}^{\prime }\}}_{j\in N\setminus \left\{i\right\}}$ and $t_i^{\prime }$. Since it is a weighted game it follows from Theorem 1 (Taylor and Zwicker) that it must be trade robust. ▐

It follows from Proposition 2 that a necessary condition for a collection of sets $\mathcal{C}$ satisfying (SC) to be weakly expressible by a game of thresholds, is that $\mathcal{C}$ is trade robust.

EXAMPLE 3 

Going back to example 2, note that $\mathcal{L}$ is not trade robust, since we can trade-transform the winning coalitions for agent 1, $\{6,7,8,9\})$ and $\{2,3,4,5\}$ into the losing coalitions, $\{2,3,6,7\}$, $\{4,5,8,9\}$. As shown above, $\mathcal{L}$ is not weakly expressible by a game of thresholds. Note, however, that facing the question of whether $\mathcal{C}=\{\varnothing ,\{2,3\},\{4,5\},\{1,2,3,4,5\},\{1,6,7,8,9\}$, $\{1,2,3,4,5,6,7,8,9\}\}$ is weakly expressible by a game of thresholds, examining the trade robustness of $\mathcal{C}$ is not enough, and we need to look at the trade robustness of the simple games, ${\left\{mi{n}_{wi{n}_i}\left(\mathcal{C}\right)\right\}}_{i\in N}$. ⋄

3.3. Games of Thresholds on the Complete Graph

We end by examining the problem of expressing $\mathcal{L}$ using games of thresholds on the complete graph, that is, the graph in which the weights $w_{ij}=w$ are the same for all pairs of agents, $i\ne j$. This special case is of interest, because it is equivalent to many models of peer effects in the applied literature (as discussed in the introduction), in which each agent chooses his activity level in response to some measure of mean activity level in the environment. In these models, the agents may have different sensitivities to the environment (in our language, different thresholds), but the environment is the same for everyone, which is analogous to all the weights being equal.

CLAIM 1 

If x and y are equilibria of a game of thresholds in the complete graph, then either $x\subseteq y$ or $y\subseteq x$. That is, the set of equilibria must be a chain, and the chain satisfies $\left(SC\right)$.

Proof of Claim 1: 

Suppose that we have two equilibria, x and y. Without loss of generality, assume that $\left|x\right|\le \left|y\right|$, and let $i\in x$. Then, $t_i\le {\displaystyle \sum _{j\in x}}{w}_{ij}=w\left|x\right|\le w\left|y\right|={\displaystyle \sum _{j\in y}}{w}_{ij}$. Therefore, it must be the case that $i\in y$. The fact that the chain satisfies $\left(SC\right)$ follows from Proposition 1.▐

The sparseness condition (SC) and the strictness condition $\left(1\right)$ of Section 2 are equivalent in the case of chains and take the simpler form: $x\setminus \left\{i\right\}\notin \mathcal{L}$ $\forall i\in x$, whenever $x\in \mathcal{L}$. The converse of the claim above is also true: any chain that satisfies (SC) is expressible by a game of thresholds on the complete graph.

CLAIM 2 

If $\mathcal{L}$ is a chain with the property that $x\setminus \left\{i\right\}\notin \mathcal{L}$ $\forall i\in x$ whenever $x\in \mathcal{L}$, then it is expressible by a game of thresholds on the complete graph.

Proof of Claim 2: 

Let $C=\{x_1,x_2,...,x_m\}$ be a chain satisfying the condition of the claim, and without loss of generality, suppose $k^{\prime }>k$ implies $x_k\subseteq x_{k^{\prime }}$. Then, it must be true that $|x_{k+1}\setminus x_k|>1$. Therefore, let, $t_i=\frac{|x_1|-1}{n}$, $\forall i\in x_1$, and in general, $t_i=\frac{|x_k|-1}{n}$, $\forall i\in x_k\setminus x_{k-1}$, for each $k\le m$. Finally, let $t_i=1$, $\forall i\notin x_m$. Let $w_{ij}=\frac{1}{n}$ $\forall i\ne j$. By construction, the set of equilibria of this game of thresholds is precisely $C=\{x_1,x_2,...,x_m\}$.▐

The simple structure of the lattices that are expressible by games of thresholds on the complete network (see Figure 3) means that we are able to count the number of different (up to re-labeling of the agents) possible sets of equilibria of these games. In enunciating this counting result, we restrict attention to sets of equilibria that include ∅ and N.

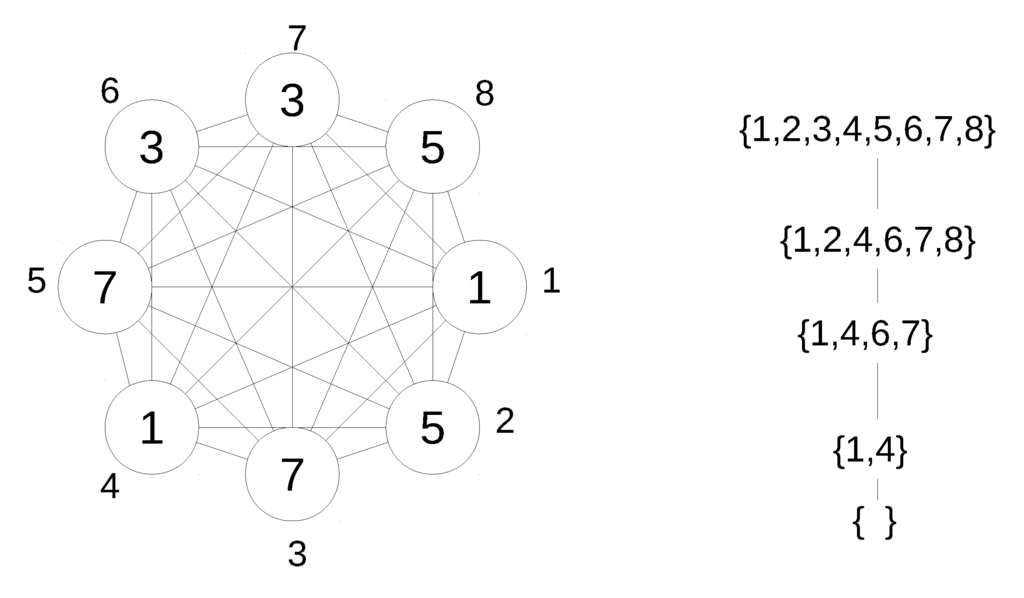
Figure 3. An example of a game of thresholds on the complete graphs. The numbers outside the circles are the names of the nodes, and the respective thresholds are shown inside the circles.

Figure 3. An example of a game of thresholds on the complete graphs. The numbers outside the circles are the names of the nodes, and the respective thresholds are shown inside the circles.

COROLLARY 2 

There are $F_{n-1}$ different chains, which can be expressed as equilibria of games of thresholds on the complete network on the set $N=\{1,2,...,n\}$ that include the set N; where $F_{n-1}$ denotes the $n-1th$ Fibonacci number.

Proof of Corollary 2: 

Since we are counting the number of different chains up to re-labeling of the agents, two chains, $C_1$ and $C_2$, are different, if and only if one of them contains a set different in size from all the sets contained in the other chain. Therefore, in what follows, when referring to a given set, we only speak of its size. We can partition the set of expressible chains on $\left|N\right|$ agents into two groups: (1) those that contain an element of size $\left|N\right|-2$; and (2) those that do not contain an element of size $\left|N\right|-2$. Each of the chains in (1) corresponds to a unique chain expressible with $\left|N\right|-2$ elements. On the other hand, each of the chains in (2) corresponds to a unique chain expressible with $\left|N\right|-1$ elements. Therefore, if we denote the number of expressible chains on $\left|N\right|$ agents by $c_N$, we have that $c_N=c_{N-1}+c_{N-2}$. Moreover, $c_1=0=F_0$, $c_2=1=F_1$.▐

We can compute a conservative lower bound on the collection of structurally different lattices that can be expressed by games of thresholds without restrictions on the weights, by counting the number of different lattices corresponding to different partitions of the set of N agents into completely connected components, each of a size of at least two. (There are no chains on less than two elements satisfying (SC) and the requirement that $N\in \mathcal{C}$ and $\varnothing \in \mathcal{C}$.) If we let $p(n,k)$ denote the number of partitions of n into k parts, each of them of a size of at least two, then there are ${\displaystyle \sum _{k_1+k_2+...+k_m=n,k_j\ge 2}}\prod _{}{F}_{|k_j|-1}$ structurally different lattices. Therefore, for example, when $n=15$, there are only 377 different lattices expressible by games of thresholds on the complete graph, whereas our lower bound for the number of lattices expressible by some game of thresholds is 4,297, slightly over 10 times. When n = 60, there are over 1,000 times as many structurally different lattices expressible by some game of thresholds as there are lattices expressible by some game of thresholds on the complete graph. The lower bound is conservative, since we are only considering what can be expressed ¡by graphs that are the union of complete subgraphs. Claims 1 and 2 show that games of thresholds owe their expressive power to the interplay between thresholds and network structure. No matter how much freedom we have to play with the thresholds, we lose the ability to express anything other than chains, if we restrict all relationships to have the same weight.

A common network representation across applications restricts relations to either have a given positive weight or to have no weight at all (games of thresholds on unweighted, undirected graphs (see Galeotti et al. (2010) [24]). As seen in Example 4, this restriction also limits the expressive power of the games of thresholds.

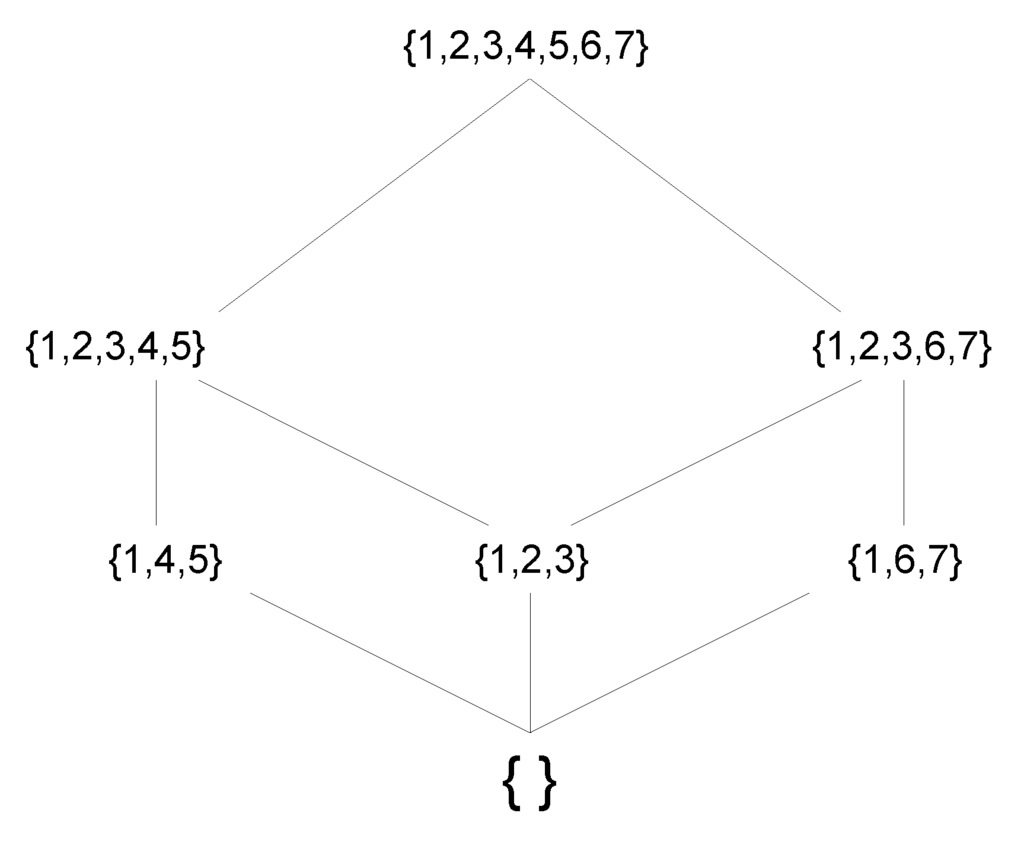
Figure 4. A lattice, $\mathcal{L}$, that can only be expressed by games of thresholds on graphs with weighted links.

Figure 4. A lattice, $\mathcal{L}$, that can only be expressed by games of thresholds on graphs with weighted links.

EXAMPLE 4 

The expressive power added by weights.

The lattice, $\mathcal{L}$, shown in Figure 4 cannot be expressed by a game of thresholds on a network in which all links have the same weight. To see this, suppose that there existed a game $(W,\mathbf{t})$, in which $w_{ij}=0$ or $w_{ij}=w$ and such that $NE\left({\Gamma }_{W,\mathbf{t}}\right)=\mathcal{L}$. We begin by noting that the agents in $\{1,2,3\}$ need to be connected, as otherwise, one of them would need to have threshold of zero, but this cannot be the case, since $\varnothing \in \mathcal{L}$. Whoever among 2 and 3 is linked to 1 must have a threshold of at most $2w$ and, therefore, cannot be linked to $4,5,6,7$, since, otherwise, at least one of $\{1,4,5\}$ or $\{1,6,7\}$ would not be an equilibrium. If j among 2 and 3 is not directly linked to 1, then j must have a threshold of at most w, and just as before, it cannot be linked to $4,5,6$ or 7, since, as above, at least one of $\{1,4,5\}$ or $\{1,6,7\}$ would not be an equilibrium. We can therefore conclude that neither 2 nor 3 can be linked to $4,5,6$ or 7. Therefore $\{1,4,5,6,7\}$ has to be an equilibrium, as well. This contradicts the existence of an unweighted network, W, and a vector of weights, $\mathbf{t}$, satisfying $NE\left({\Gamma }_{W,\mathbf{t}}\right)=\mathcal{L}$. ⋄