Time Eigenstates for Potential Functions without Extremal Points
Abstract
:1. Introduction
2. Time Eigenstates for Classical Systems
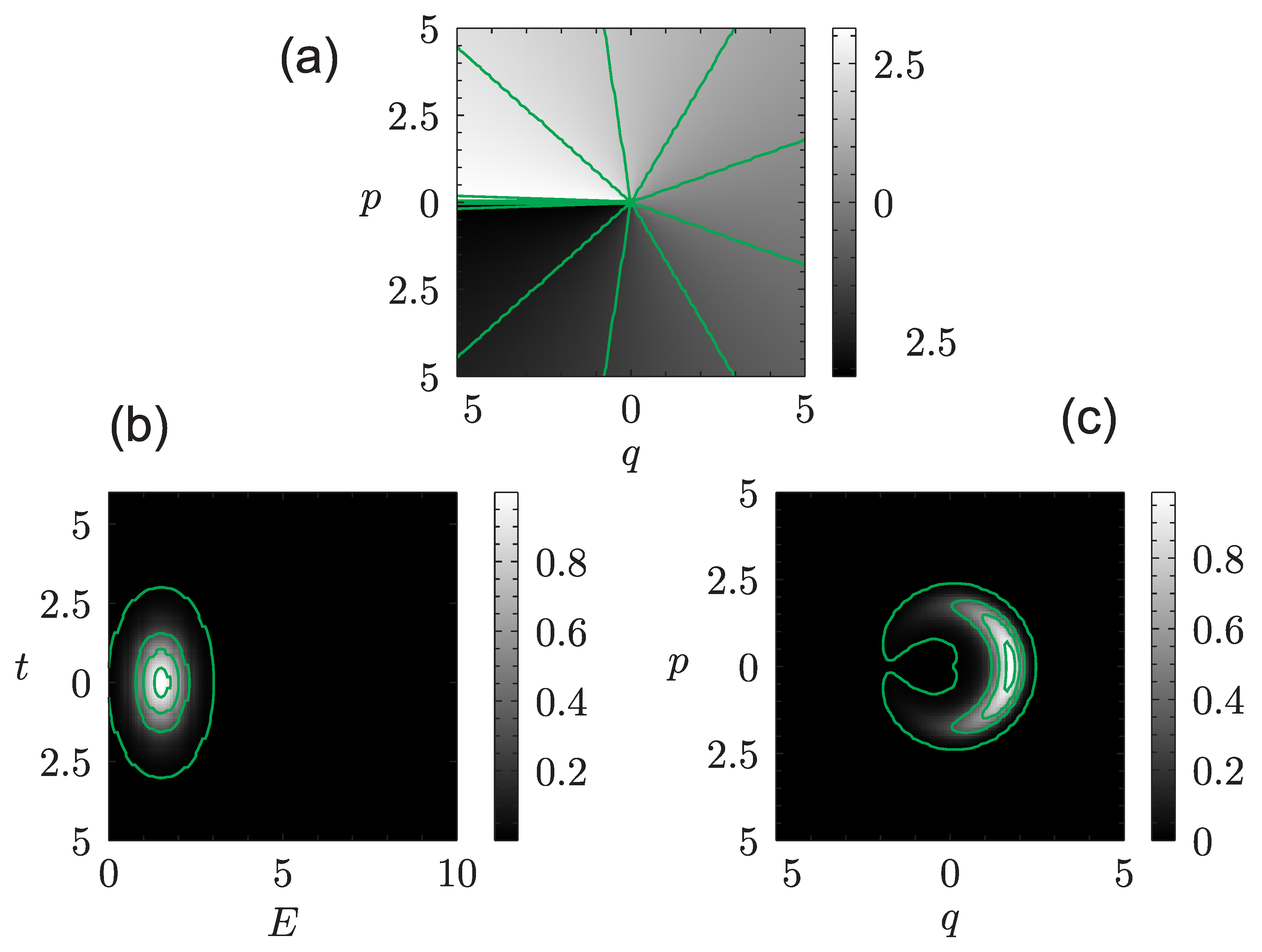
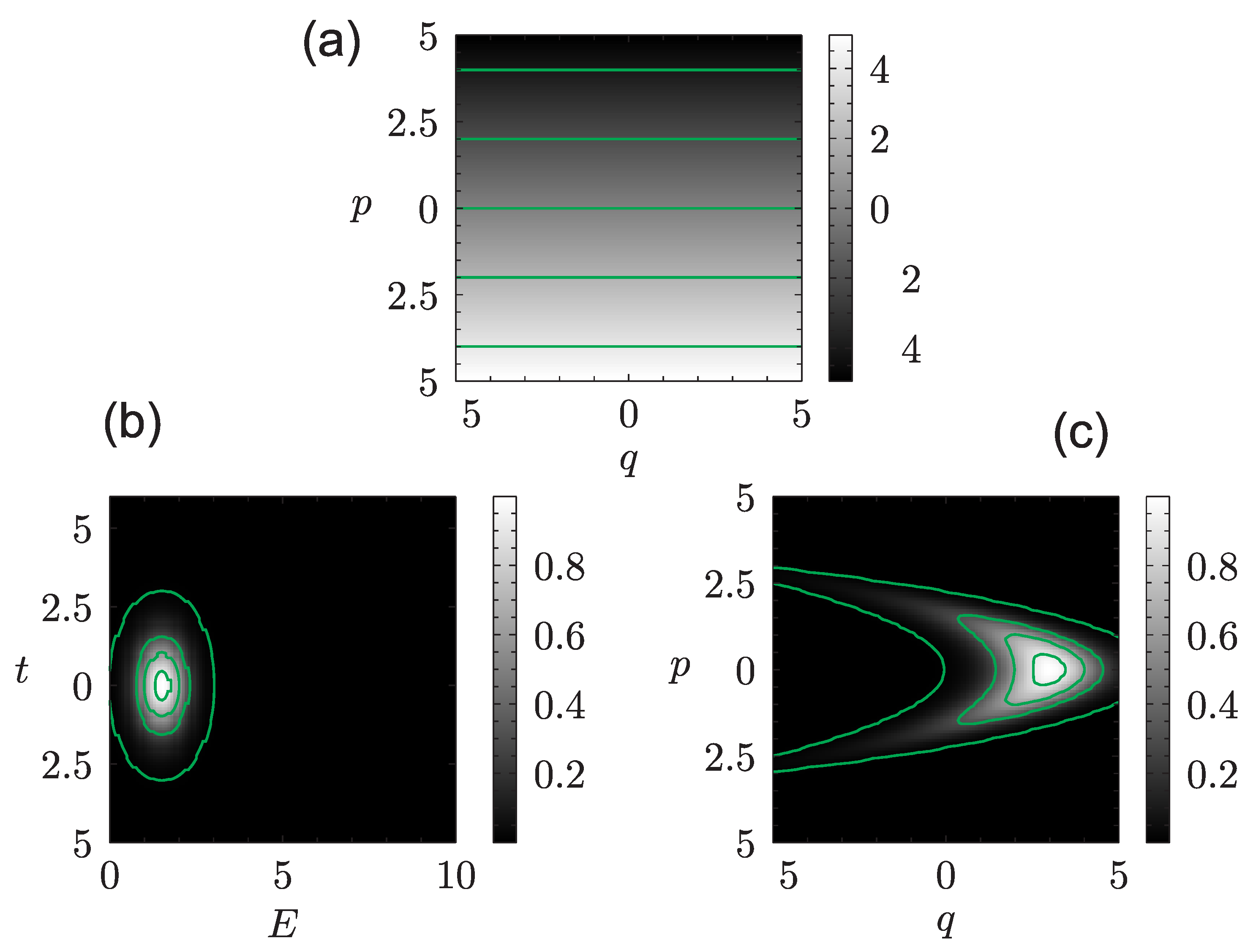
3. Quantum Systems: Continuous Spectrum
3.1. Derivation of Time Eigenstates
3.2. Equalities Involving Powers of Time
3.3. Change of Representation
3.4. Orthogonality between Time Eigenstates
4. Quantum Systems: Discrete Spectrum
4.1. Derivation of Time Eigenstates
4.2. Change of Representation
4.3. Orthogonality between Time Eigenstates
5. Matrix Elements of Operators

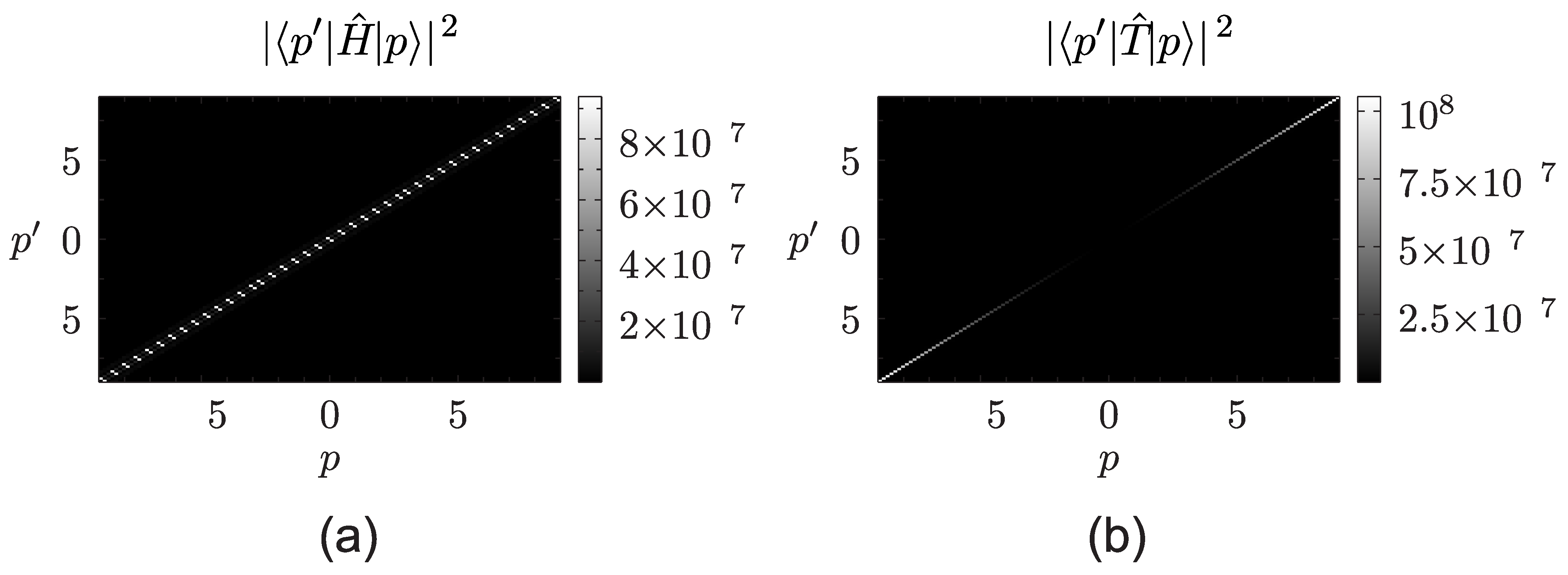
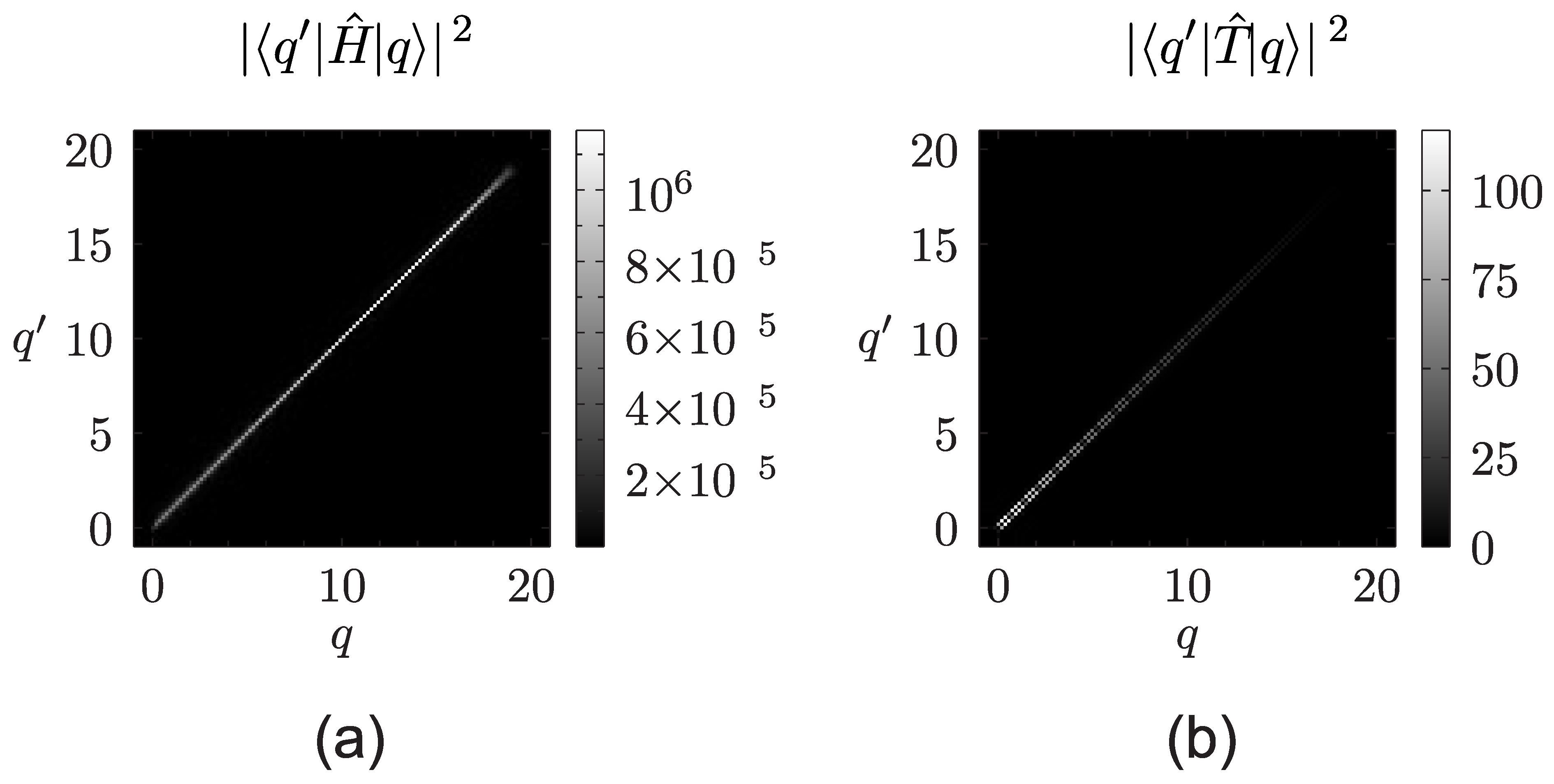
6. Remarks
Conflicts of Interest
References
- Holevo, A.S. Probabilistic and Statistical Aspects of Quantum Theory; North-Holland: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Grot, N.; Rovelli, C.; Tate, R.S. Time of arrival in quantum mechanics. Phys. Rev. A 1996, 54, 4676–4690. [Google Scholar] [CrossRef] [PubMed]
- Rovelli, C. Quantum mechanics without time: A model. Phys. Rev. D 1990, 42, 2638–2646. [Google Scholar] [CrossRef]
- Rovelli, C. Time in quantum gravity: An hypothesis. Phys. Rev. D 1991, 43, 442–456. [Google Scholar] [CrossRef]
- Kijowski, J. On the time operator in quantum mechanics and the Heisenberg uncertainty relation for energy and time. Rep. Math. Phys. 1974, 6, 361–386. [Google Scholar] [CrossRef]
- Hegerfeldt, G.C.; Muga, J.G.; Muñoz, J. Manufacturing time operators: Covariance, selection criteria, and examples. Phys. Rev. A 2010, 82, 012113. [Google Scholar] [CrossRef]
- Jaffé, C.; Brumer, P. Classical liouville mechanics and intramolecular relaxation dynamics. J. Phys. Chem. 1984, 88, 4829–4839. [Google Scholar] [CrossRef]
- Muga, J.G.; Sala-Mayato, R.; Egusquiza, I.L. (Eds.) Time in Quantum Mechanics; Springer: Berlin, Germany, 2008; Lecture Notes in Physics; Volume 734.
- Muga, J.G.; Leavens, C.R. Arrival time in quantum mechanics. Phys. Rep. 2000, 338, 353–438. [Google Scholar] [CrossRef]
- Galapon, E.A. Paulis theorem and quantum canonical pairs: The consistency of a bounded, self-adjoint time operator canonically conjugate to a Hamiltonian with non-empty point spectrum. Proc. R. Soc. Lond. A 2002, 458, 451–472. [Google Scholar] [CrossRef]
- Sombillo, D.L.B.; Galapon, E.A. Quantum time of arrival Goursat problem. J. Math. Phys. 2012, 53, 043702. [Google Scholar] [CrossRef]
- Pauli, W. Handbuch der Physik, 1st ed.; Geiger, H., Scheel, K., Eds.; Springer: Berlin, Germany, 1926; Volume 23. [Google Scholar]
- De la Madrid, R.; Isidro, J.M. The HFT selfadjoint variant of time operators. Adv. Stud. Theor. Phys. 2008, 2, 281–289. [Google Scholar]
- Razavy, M. Time of arrival operator. Can. J. Phys. 1971, 49, 3075–3081. [Google Scholar] [CrossRef]
- Razavy, M. Quantum-mechanical time operator. Am. J. Phys. 1967, 35, 955–960. [Google Scholar] [CrossRef]
- Isidro, J.M. Bypassing Paulis theorem. Phys. Lett. A 2005, 334, 370–375. [Google Scholar] [CrossRef]
- Muga, J.G. The time of arrival concept in quantum mechanics. Superlattices Microstruct. 1998, 23, 833–842. [Google Scholar] [CrossRef]
- Torres-Vega, G. Marginal picture of quantum dynamics related to intrinsic arrival times. Phys. Rev. A. 2007, 76, 032105. [Google Scholar] [CrossRef]
- Torres-Vega, G. Energy-time representation for quantum systems. Phys. Rev. A. 2007, 75, 032112. [Google Scholar] [CrossRef]
- Torres-Vega, G. Quantum-like picture for intrinsic, classical, arrival distributions. J. Phys. A 2009, 42, 465307. [Google Scholar] [CrossRef]
- Torres-Vega, G. Dynamics as the preservation of a constant commutator. Phys. Lett. A 2007, 369, 384–392. [Google Scholar] [CrossRef]
- Torres-Vega, G. Correspondence, Time, Energy, Uncertainty, Tunnelling, and Collapse of Probability Densities. In Theoretical Concepts of Quantum Mechanics; Pahlavani, M.R., Ed.; InTech: Rijeka, Croatia, 2012; Chapter 4. [Google Scholar]
- Torres-Vega, G. Classical and Quantum Conjugate Dynamics—The Interplay Between Conjugate Variables. In Advances in Quantum Mechanics; Bracken, P., Ed.; InTech: Rijeka, Croatia, 2013; Chapter 1. [Google Scholar]
- Jaffé, C.; Brumer, P. Classical-quantum correspondence in the distribution dynamics of integrable systems. J. Chem. Phys. 1985, 82, 2330–2340. [Google Scholar] [CrossRef]
- Bokes, P. Time operators in stroboscopic wave-packet basis and the time scales in tunneling. Phys. Rev. A 2011, 83, 032104. [Google Scholar] [CrossRef]
- Bokes, P.; Corsetti, F.; Godby, R.W. Stroboscopic wave-packet description of nonequilibrium many-electron problems. Phys. Rev. Lett. 2008, 101, 046402. [Google Scholar] [CrossRef] [PubMed]
- Bokes, P.; Corsetti, F.; Godby, R.W. Stroboscopic wavepacket description of non-equilibrium many-electron problems: Demonstration of the convergence of the wavepacket basis. 2008; arXiv:0803.2448. [Google Scholar]
- Baute, A.D.; Sala Mayato, R.; Palao, J.P.; Muga, J.G.; Egusquiza, I.L. Time of arrival distribution for arbitrary potentials and Wigner’s time-energy uncertainty relation. Phys. Rev. A 2000, 61, 022118. [Google Scholar] [CrossRef]
- Giannitrapani, R. Positive-operator-valued time observable in quantum mechanics. Int. J. Theor. Phys. 1997, 36, 1575–1584. [Google Scholar] [CrossRef]
- Kobe, D.H. Canonical transformation to energy and “tempus” in classical mechanics. Am. J. Phys. 1993, 61, 1031–1037. [Google Scholar] [CrossRef]
- Kobe, D.H.; Aguilera-Navarro, V.C. Derivation of the energy-time uncertainty relation. Phys. Rev. A 1994, 50, 933–938. [Google Scholar] [CrossRef] [PubMed]
- Rosenbaum, D.M. Super Hilbert space and the quantum-mechanical time operators. J. Math. Phys. 1969, 10, 1127–1144. [Google Scholar] [CrossRef]
- Johns, O.D. Canonical transformation with time as a coordinate. Am. J. Phys. 1989, 57, 204–215. [Google Scholar] [CrossRef]
- Leavens, C.R. Time of arrival in quantum and Bohmian mechnaics. Phys. Rev. A 1998, 58, 840–847. [Google Scholar] [CrossRef]
- Lippmann, B.A. Operator for time delay induced by scattering. Phys. Rev. 1966, 151, 1023–1024. [Google Scholar] [CrossRef]
- Werner, R.F. Wigner quantisation of arrival time and oscillator phase. J. Phys. A 1988, 21, 4565–4575. [Google Scholar] [CrossRef]
- Marshall, T.W.; Watson, E.J. A drop of ink falls from my pen...It comes to earth, I know not when. J. Phys. A 1985, 18, 3531–3559. [Google Scholar] [CrossRef]
- Wigner, E.P. Lower limit for the energy derivative of the scattering phase shift. Phys. Rev. 1955, 98, 145–147. [Google Scholar] [CrossRef]
- Allcock, G.R. The time of arrival in quantum mechanics I. Formal considerations. Ann. Phys. 1969, 53, 253–285. [Google Scholar] [CrossRef]
- Allcock, G.R. The time of arrival in quantum mechanics II. The individual measurement. Ann. Phys. 1969, 53, 286–310. [Google Scholar] [CrossRef]
- Allcock, G.R. The time of arrival in quantum mechanics III. The measurement ensemble. Ann. Phys. 1969, 53, 311–348. [Google Scholar] [CrossRef]
- Delgado, V. Probability distribution of arrival times in quantum mechanics. Phys. Rev. A 1998, 57, 762–770. [Google Scholar] [CrossRef]
- Delgado, V.; Muga, J.G. Arrival time in quantum mechanics. Phys. Rev. A 1997, 56, 3425–3435. [Google Scholar] [CrossRef]
- Halliwell, J.J. Arrival time in quantum theory from an irreversible detector model. Prog. Theor. Phys. 1999, 102, 707–717. [Google Scholar] [CrossRef]
- Muga, J.G.; Baute, A.D.; Damborenea, J.A.; Egusquiza, I.L. Model for the arrival-time distribution in fluorescence time-of-flight experiments. 2000; arXiv:quant-ph/0009111. [Google Scholar]
- Galapon, E.A.; Caballar, R.F.; Bahague, R.T., Jr. Confined quantum time of arrivals. Phys. Rev. Lett. 2004, 93, 180406. [Google Scholar] [CrossRef] [PubMed]
- Eric, A.; Galapon, F.; Delgado, J.; Gonzalo, M.; Iñigo, E. Transition from discrete to continuous time-of-arrival distribution for a quantum particle. Phys. Rev. A 2005, 72, 042107. [Google Scholar]
- Galapon, E.A.; Caballar, R.F.; Bahague, R.T., Jr. Confined quantum time of arrival for the vanishing potential. Phys. Rev. A 2005, 72, 062107. [Google Scholar] [CrossRef]
- Galapon, E.A. What could have we been missing while Pauli’s theorem was in force? 2003; arXiv:quant-ph/0303106. [Google Scholar]
- Muga, J.G.; Leavens, C.R.; Palao, J.P. Space-time properties of free-motion time-of-arrival eigenfunctions. Phys. Rev. A 1998, 58, 4336–4344. [Google Scholar] [CrossRef]
- Delgado, V.; Muga, J.G. Arrival time in quantum mechanics. Phys. Rev. A 1997, 56, 3425–3435. [Google Scholar] [CrossRef]
- Skulimowski, M. Construction of time covariant POV measures. Phys. Lett. A 2002, 297, 129–136. [Google Scholar] [CrossRef]
- Damborenea, J.A.; Egusquiza, I.L.; Hegerfeldt, G.C.; Muga, J.G. Measurement-based approach to quantum arrival times. Phys. Rev. A 2002, 66, 052104. [Google Scholar] [CrossRef]
- Baute, A.D.; Egusquiza, I.L.; Muga, J.G. Time of arrival distributions for interaction potentials. Phys. Rev. A 2001, 64, 012501. [Google Scholar] [CrossRef]
- Brunetti, R.; Fredenhagen, K. Time of occurrence observable in quantum mechanics. Phys. Rev. A 2002, 66, 044101. [Google Scholar] [CrossRef]
- Hegerfeldt, G.C.; Seidel, D. Operator-normalized quantum arrival times in the presence of interaction. Phys. Rev. A 2004, 70, 012110. [Google Scholar] [CrossRef]
- Kochański, P.; Wódkiewicz, K. Operational time of arrival in quantum phase space. Phys. Rev. A 1999, 60, 2689–2699. [Google Scholar] [CrossRef]
- Baute, A.D.; Egusquiza, I.L.; Muga, J.G.; Sala-Mayato, R. Time of arrival distributions from position-momentum and energy-time joint measurements. Phys. Rev. A 2000, 61, 052111. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bohm, D. Time in quantum theory and the uncertainty relation for time and energy. Phys. Rev. 1961, 122, 1649–1658. [Google Scholar] [CrossRef]
- Bracken, A.J.; Melloy, G.F. Probability backflow and a new dimensionless quantum number. J. Phys. A Math. Gen. 1994, 27, 2197–2211. [Google Scholar] [CrossRef]
- Martens, H.; de Muynck, W.M. The inaccuracy principle. Found. Phys. 1990, 20, 357–380. [Google Scholar] [CrossRef]
- Smith, F.T. Lifetime matrix in collision theory. Phys. Rev. 1960, 118, 349–356. [Google Scholar] [CrossRef]
- Landauer, R. Barrier interaction time in tunneling. Rev. Mod. Phys. 1994, 66, 217–228. [Google Scholar] [CrossRef]
- Leavens, C.R. On the “standard” quantum mechanical approach to times of arrival. Phys. Lett. A 2002, 303, 154–165. [Google Scholar] [CrossRef]
- Peres, A. Measurement of time by quantum clocks. Am. J. Phys. 1980, 48, 552–557. [Google Scholar] [CrossRef]
- León, J. Time-of-arrival formalism for the relativistic particle. J. Phys. A 1997, 30, 4791–4801. [Google Scholar] [CrossRef]
- León, J.; Julve, J.; Pitanga, P.; de Urríes, F.J. Time of arrival in the presence of interactions. Phys. Rev. A 2000, 61, 062101. [Google Scholar] [CrossRef]
- Galindo, A. Phase and number. Lett. Math. Phys. 1984, 8, 495–500. [Google Scholar] [CrossRef]
- Kuusk, P.; Kõiv, M. Measurement of time in nonrelativistic quantum and classical mechanics. 2001; arXiv:quant-ph/0102003. [Google Scholar]
- Mikuta-Martinis, V.; Martinis, M. Existence of time operator for a singular harmonic oscillator. Concepts Phys. 2005, 2, 69–80. [Google Scholar]
- Helstrom, C.W. Estimation of a displacement parameter of a quantum system. Int. J. Theor. Phys. 1974, 11, 357–378. [Google Scholar] [CrossRef]
- Garrison, J.C.; Wong, J. Canonically conjugate pairs, uncertainty relations, and phase operators. J. Math. Phys. 1970, 11, 2242–2249. [Google Scholar] [CrossRef]
- Torres-Vega, G.; Jiménez-García, M.N. A method for choosing an initial time eigenstate in classical and quantum systems. Entropy 2013, 15, 2415–2430. [Google Scholar] [CrossRef]
- Galapon, E.A. Self-adjoint time operator is the rule for discrete semi-bounded Hamiltonians. Proc. R. Soc. Lond. A 2002, 458, 2671–2689. [Google Scholar] [CrossRef]
- Arai, A. Necessary and sufficient conditions for a Hamiltonian with discrete eigenvalues to have time operators. Lett. Math. Phys. 2009, 87, 67–80. [Google Scholar] [CrossRef]
- Arai, A.; Matsuzawa, Y. Time operators of a Hamiltonian with purely discrete spectrum. Rev. Math. Phys. 2008, 20, 951–978. [Google Scholar] [CrossRef]
© 2013 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Torres-Vega, G. Time Eigenstates for Potential Functions without Extremal Points. Entropy 2013, 15, 4105-4121. https://doi.org/10.3390/e15104105
Torres-Vega G. Time Eigenstates for Potential Functions without Extremal Points. Entropy. 2013; 15(10):4105-4121. https://doi.org/10.3390/e15104105
Chicago/Turabian StyleTorres-Vega, Gabino. 2013. "Time Eigenstates for Potential Functions without Extremal Points" Entropy 15, no. 10: 4105-4121. https://doi.org/10.3390/e15104105
APA StyleTorres-Vega, G. (2013). Time Eigenstates for Potential Functions without Extremal Points. Entropy, 15(10), 4105-4121. https://doi.org/10.3390/e15104105





