Abstract
This study deals with the combined effects of convective heating and suction/injection on the entropy generation rate in a steady flow of an incompressible viscous fluid through a channel with permeable walls. The model equations for momentum and energy balance are solved numerically using shooting quadrature. Both the velocity and temperature profiles are obtained and utilized to compute the entropy generation number. The effects of the key parameters on the fluid velocity, temperature, entropy generation rate and Bejan number are depicted graphically and analyzed in detail.
1. Introduction
Considerable attention had been given to convective heating conditions in recent years due to their numerous practical applications in engineering devices. For example in heat exchangers, the conduction in a solid tube wall is mostly influenced by the convection in the fluid flowing over it. Different driving mechanisms for the natural convection flow set-up by Newtonian heating from a flat surface were investigated by Merkin [1]. Aziz [2] reported a similarity solution for boundary layer flow over a convectively heated flat plate. Lesnic et al. [3] studied the effects of Newtonian heating on boundary layer over a vertical and horizontal surface embedded in a porous medium. Mebine and Adigio [4] analyzed the unsteady free convection flow with thermal radiation past a vertical porous plate with Newtonian heating. Makinde [5] investigated the combined effects of Navier slip and Newtonian heating on an unsteady hydromagnetic boundary layer flow over a flat surface and concluded that the thermal boundary layer thickness is enhanced by increasing the intensity of Newtonian heating and flow unsteadiness.
Efficient energy utilization during the convection in any fluid flow is one of the fundamental problems of the engineering processes to improve the system. Entropy generation is a measure of the account of irreversibility associated with the real processes. Considerable research studies were carried out to examine entropy generation in permeable walls for various applications after the pioneering work of Bejan [6]. Mahmud and Fraser [7] presented a numerical solution for the flow, thermal and entropy generation characteristic inside a porous channel with viscous dissipation. Makinde and Osalusi [8] analyzed the entropy generation rate in a liquid film falling along an inclined porous heated plate and concluded that the entropy generation rate is enhanced by viscous dissipation and generally reduced by increasing wall suction. Eegunjobi and Makinde [9] studied the combined effect of buoyancy force and Navier slip on entropy generation in a vertical porous channel. Several other investigators e.g. Chauhan and Kumar [10], Eegunjobi and Makinde [11], Tasnim et al. [12], etc., have investigated entropy generation rate in a thermal system under different physical situations.
In this study, our objective was to investigate the combined effects of convective heating and wall suction/injection on entropy generation rate in fluid flows through a channel with permeable walls. The model equations are obtained and solved numerically using shooting quadrature method. Graphical results are presented to analyse the effects of various thermophysical parameters on the velocity and temperature profiles, as well as the entropy generation rate and Bejan number.
2. Mathematical Model
We consider the steady flow of an incompressible viscous fluid through a channel with permeable walls (see Figure 1). It is assumed that the fluid is injected uniformly into the channel at the lower wall and fluid suction occurs at the upper wall. The channel lower wall is heated by convection from a hot fluid with temperature Tf which provides a heat transfer coefficient
while the upper wall losses heat to the ambient with heat transfer coefficient
.
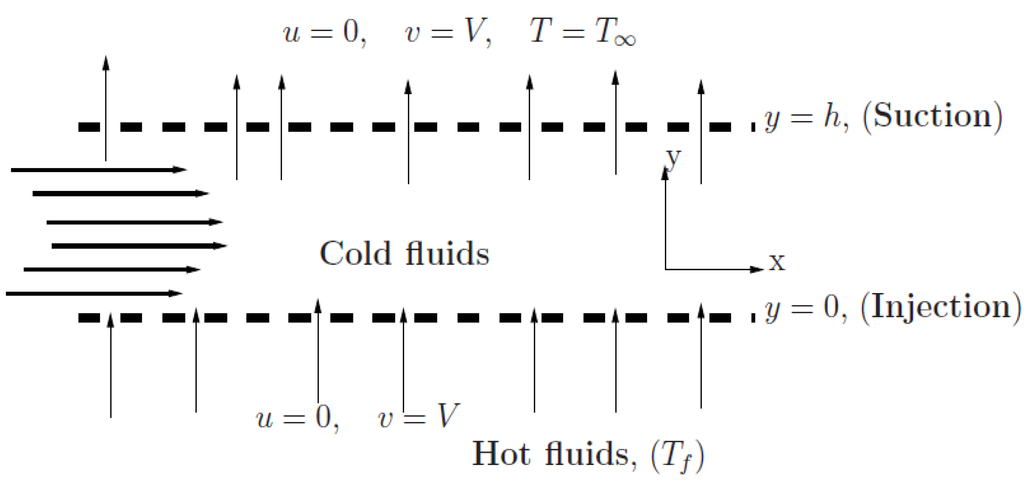
Figure 1.
Schematic diagram of the problem.
Under these assumptions, the governing equations for the momentum and energy balance in one dimension can be written as follows [8,9,11]:
and
The boundary conditions are:
where h is the channel width, u is the velocity of the fluid, P is the fluid pressure, V is the uniform suction/injection velocity at the channel walls,
is the fluid viscosity,
is the thermal diffusivity, k is the thermal conductivity coefficient,
is the specific heat at constant pressure, T is the temperature and T∞ is the ambient temperature. We introduce the following non-dimensional quantities:
Substituting Equation (4) into Equations (1), (2), (3), we obtain:
with the boundary conditions:
where G is the pressure gradient parameter,
(Reynolds number),
(Prandtl number)
(Eckert number),
(lower wall Biot number),
(upper wall Biot number). Equation (5) subject to the corresponding boundary conditions in Equation (7) can be solved exactly and we obtain:
Moreover, the coupled nonlinear boundary value problems represented by Equations (5) and(6) together with their boundary conditions in Equation (7) have been solved numerically using the shooting iteration technique together with Runge-kutta fourth-order integration scheme, Nachtsheim and Swigert [13].
3. Entropy Analysis
According to Mahmud and Fraser [7] the local volumetric rate of entropy generation for a viscous incompressible fluid defined by:
It is quite evident from Equation (9) that two sources are responsible for entropy generation in the considered problem. The first and the second terms on the right side of Equation (9) represent the irreversibility due to heat transfer and fluid friction respectively. Equation (9) is transformed into dimensionless form using Equation (4) and we obtain:
where
is the temperature difference parameter and Br = EcPr is the Brinkman number.
Let:
We then define the Bejan number as:
where
is the irreversibility ratio. Clearly, Bejan number ranges from 0 to 1 and Be = 0 is the limit where the irreversibility is dominated by fluid friction effects and Be = 1 is the limit where the irreversibility due to heat transfer dominates the flow system by virtue of finite temperature differences.
4. Results and Discussion
Numerical solutions of this problem is performed and the results are illustrated graphically in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 to show the interesting features of significant physical parameters on velocity, temperature, skin friction, entropy generation rate and Bejan number distributions. To ascertain the accuracy of the numerical results, the exact solution for the velocity profile in Equation (8) is compared with the numerical solution as are shown in Table 1 below. We notice that the comparison shows a good agreement. Therefore, we are confident that the present results are very accurate.

Table 1.
Computation showing comparison between the exact and numerical solution of velocity profile for G = 1, Re = 1.
| η | Exact Solutionw(η) | Numerical Solution w(η) |
|---|---|---|
| 0 | 0 | 0 |
| 0.1 | 0.03879297 | 0.03879297 |
| 0.2 | 0.07114875 | 0.07114875 |
| 0.3 | 0.09639032 | 0.09639032 |
| 0.4 | 0.11376948 | 0.09639032 |
| 0.5 | 0.12245933 | 0.11376948 |
| 0.6 | 0.12154600 | 0.12154600 |
| 0.7 | 0.11001953 | 0.11001953 |
| 0.8 | 0.08676372 | 0.08676372 |
| 0.9 | 0.05054498 | 0.05054498 |
| 1.0 | 0 | 0 |
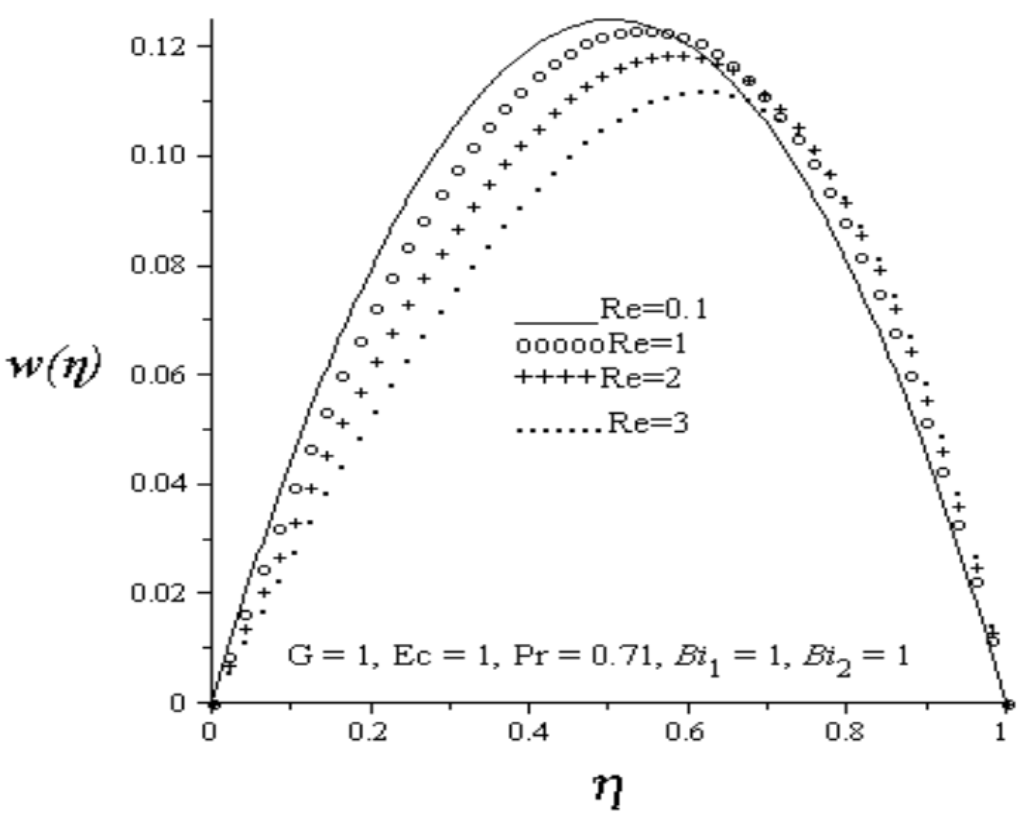
Figure 2.
Effect of increasing Re on velocity profiles.
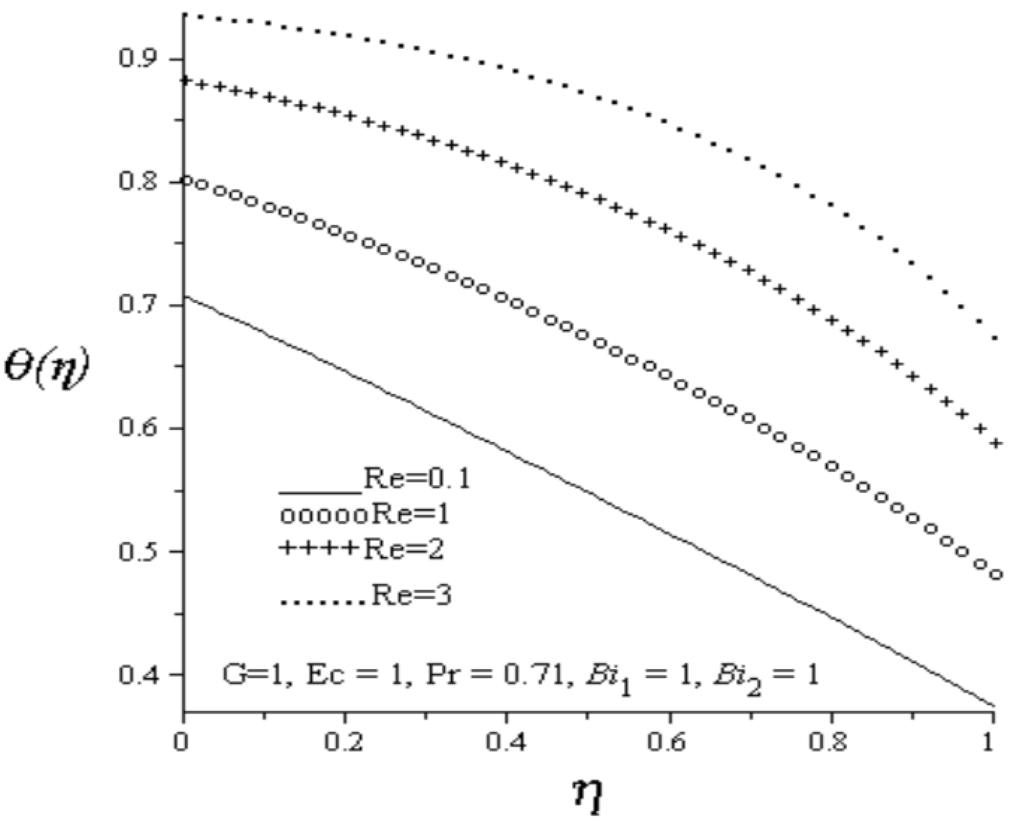
Figure 3.
Effect of increasing Re on temperature profiles.
4.1. Effects of Parameter Variations on Velocity and Temperature Profiles
Figure 2 depicts the effect of an increase in Reynolds number (Re) on the axial velocity profile. As Re increases, the injection of hot fluids from the lower permeable wall into the cold fluid flowing inside the channel increases as well as the fluid suction at the upper permeable wall increases. It is observed that fluid axial velocity profile decreases and skewed towards the upper wall due to increasing fluid suction at the upper wall. Figure 3 depicts the effect of an increase in Reynolds number on temperature profile. Generally, the fluid temperature increases with increasing values of Re. Meanwhile, the fluid temperature at the lower wall is higher than the fluid temperature at the upper wall due to combined effects of convective heating and hot fluid injection at the lower wall. Figure 4 and Figure 5 depict the effect of increasing lower and upper walls Biot numbers on temperature profile. As lower wall Biot number () increases, the convective heat transfer from the hot fluid at the lower wall into the channel fluid increases, consequently, the fluid temperature in the channel increases. An increase in the upper wall Biot number () causes a convective cooling on the channel fluid, consequently, the fluid temperature inside the channel decreases. Figure 6 illustrates the effects of increasing Eckert number (Ec) on the fluid temperature. It is observed that fluid temperature increases due to viscous heating as Ec increases. From Figure 7, it is observed that increase in Pr increases fluid temperature in the channel.
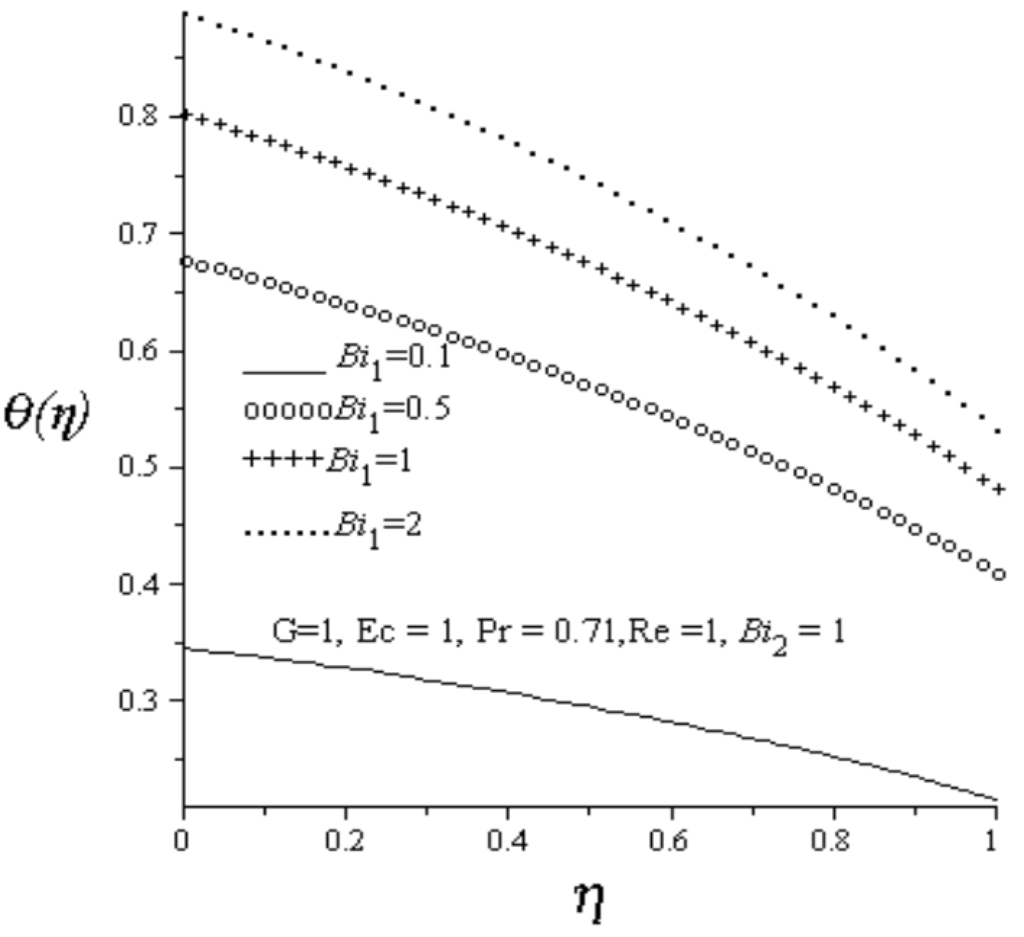
Figure 4.
Effect of increasing Bi1 on temperature profiles.
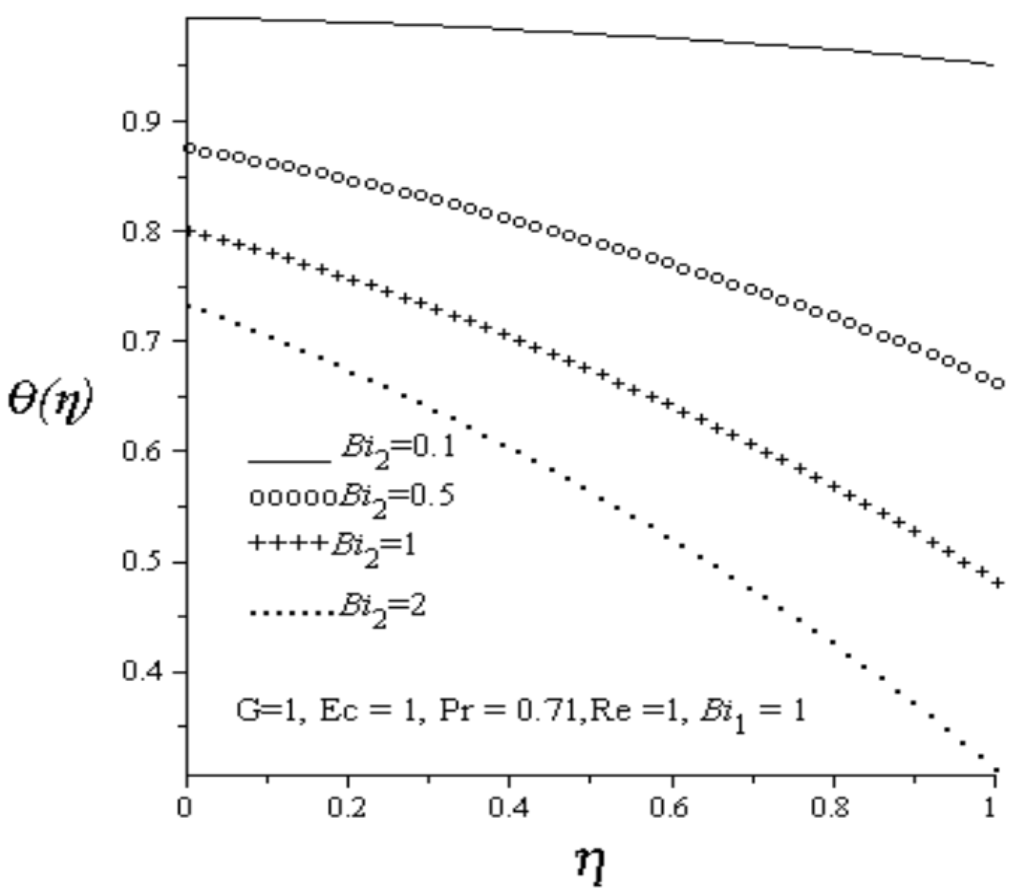
Figure 5.
Effect of increasing Bi2 on temperature profiles.
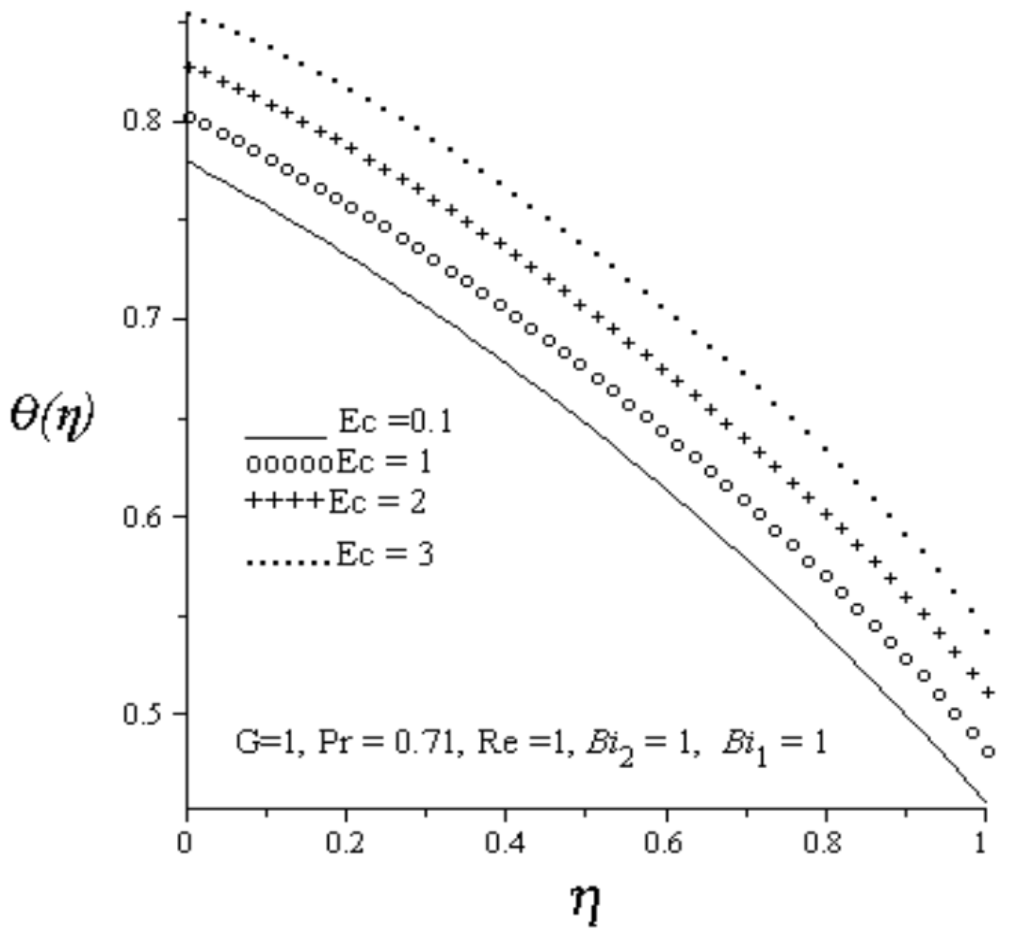
Figure 6.
Effect of increasing Ec on temperature profiles.
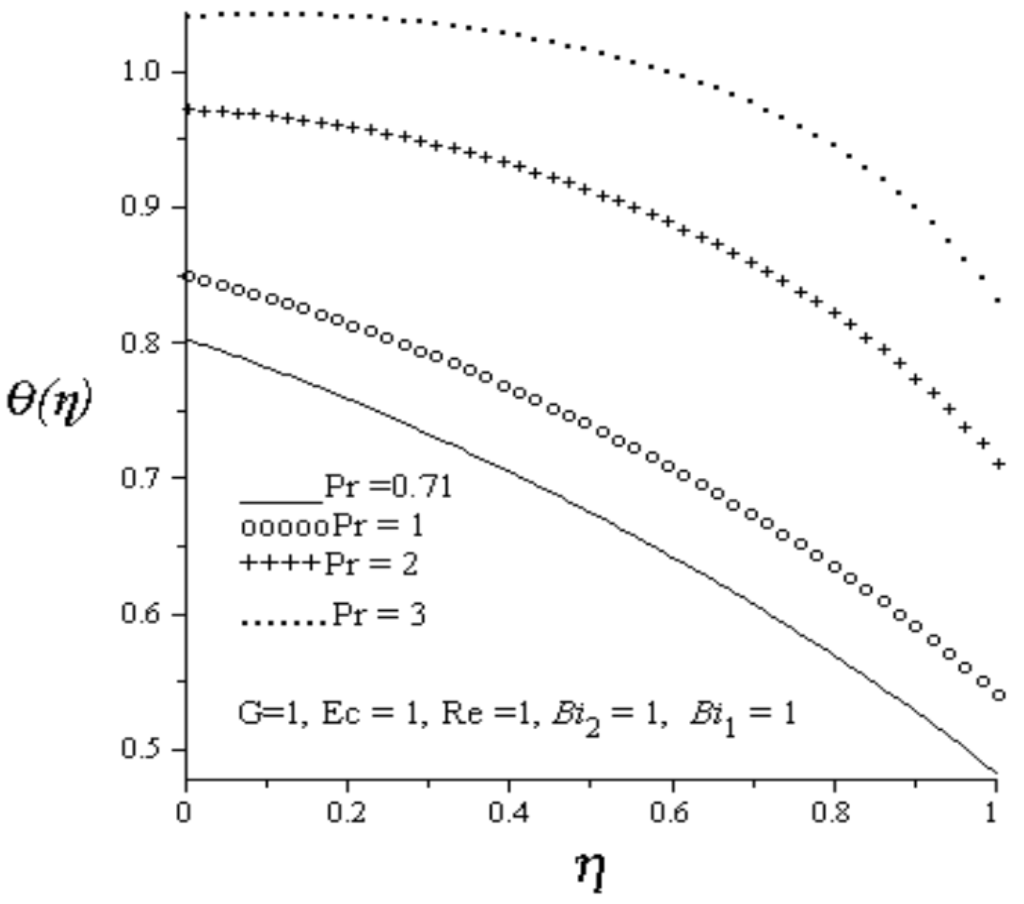
Figure 7.
Effect of increasing Pr on temperature profiles.
4.2. Effects of Parameter Variations on Entropy Generation Rate
The effects of various thermophysical parameters on entropy generation rate are considered in this section. Figure 8 depicts the effects of increasing Reynolds number on entropy generation rate. As Re increases, it is observed that the entropy generation rate decreases in the lower wall region due to fluid injection and increases at the upper wall due to suction. Figure 9 and Figure 10 illustrate the effects of increasing the lower and upper wall Biot numbers on entropy generation rate. Generally, it is observed that the entropy production increases as both
and
increase. It is noteworthy that the entropy generation rate is lowest within the channel centerline region and highest at the upper wall. The effect of increasing values of group parameter ( ) on entropy generation rate is displayed in Figure 11. As
increases due to viscous dissipation, the entropy production within the lower and upper walls region increases but more severe at the upper wall. It is interesting to note that the entropy production is not affect by the group parameter within the centerline region of the channel.
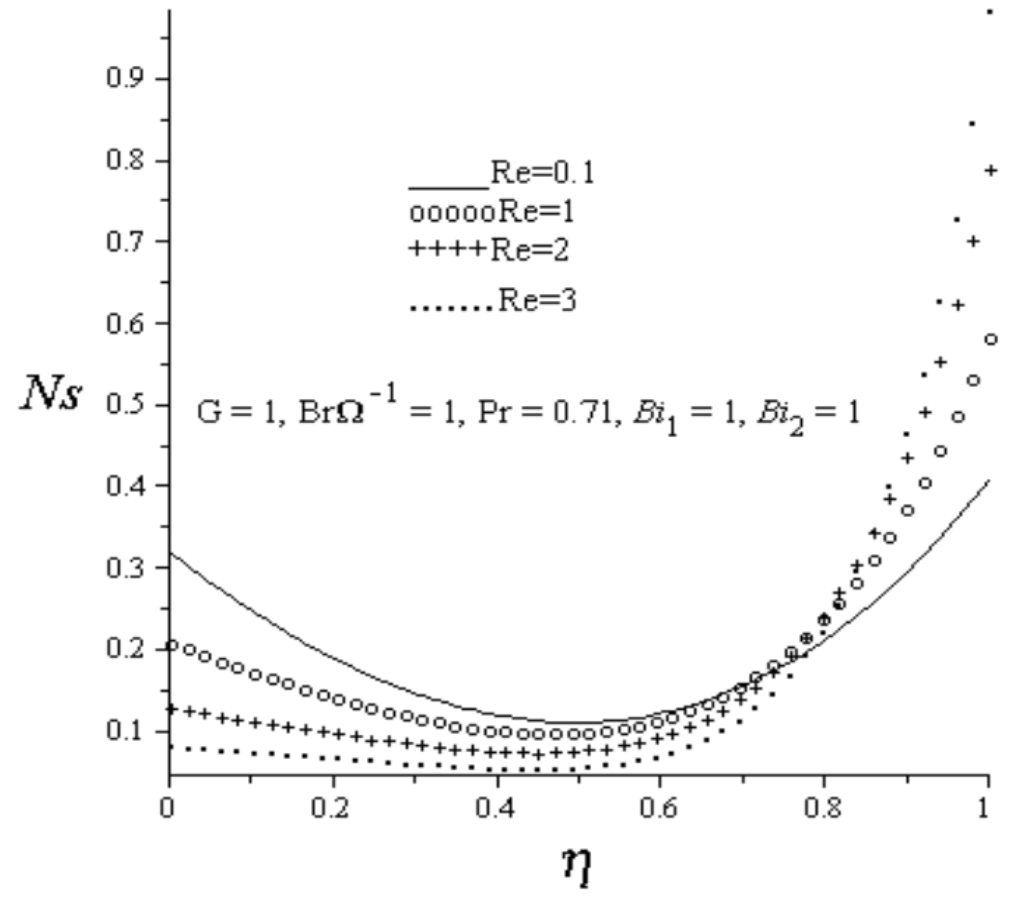
Figure 8.
Effect of increasing Re on entropy generation rate.
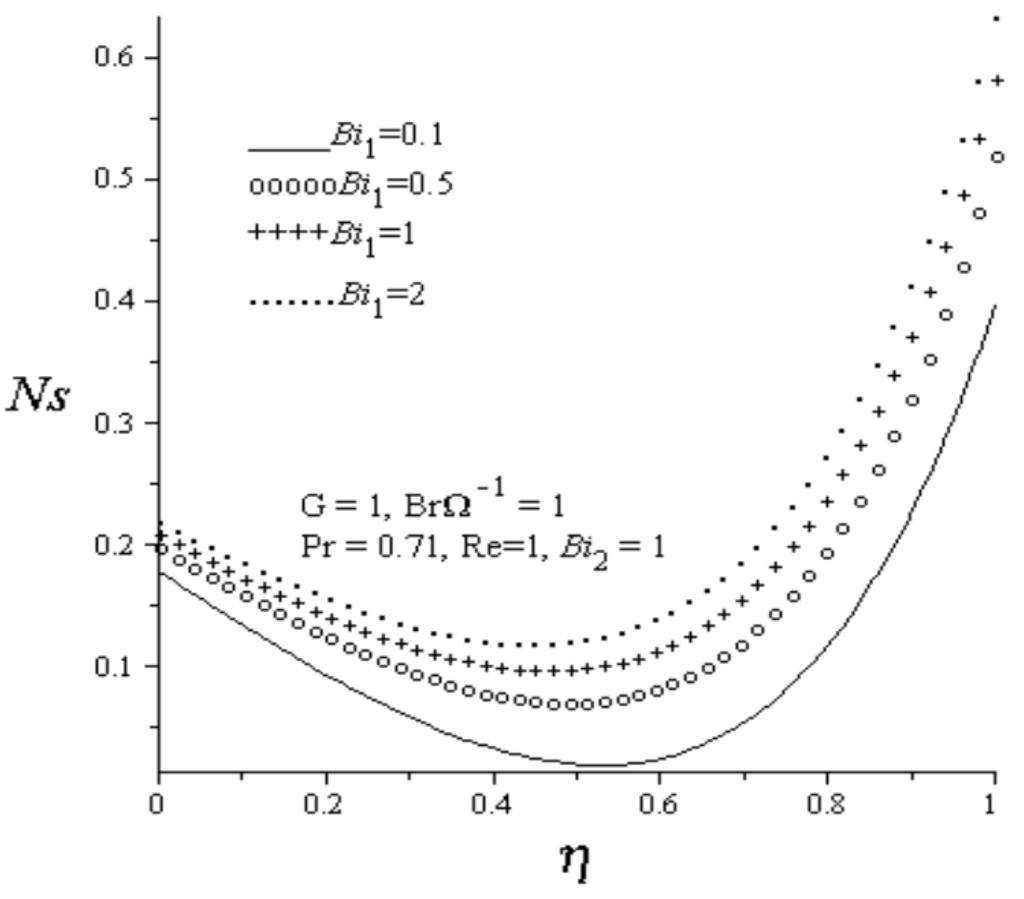
Figure 9.
Effect of increasing Bi1 on entropy generation rate.
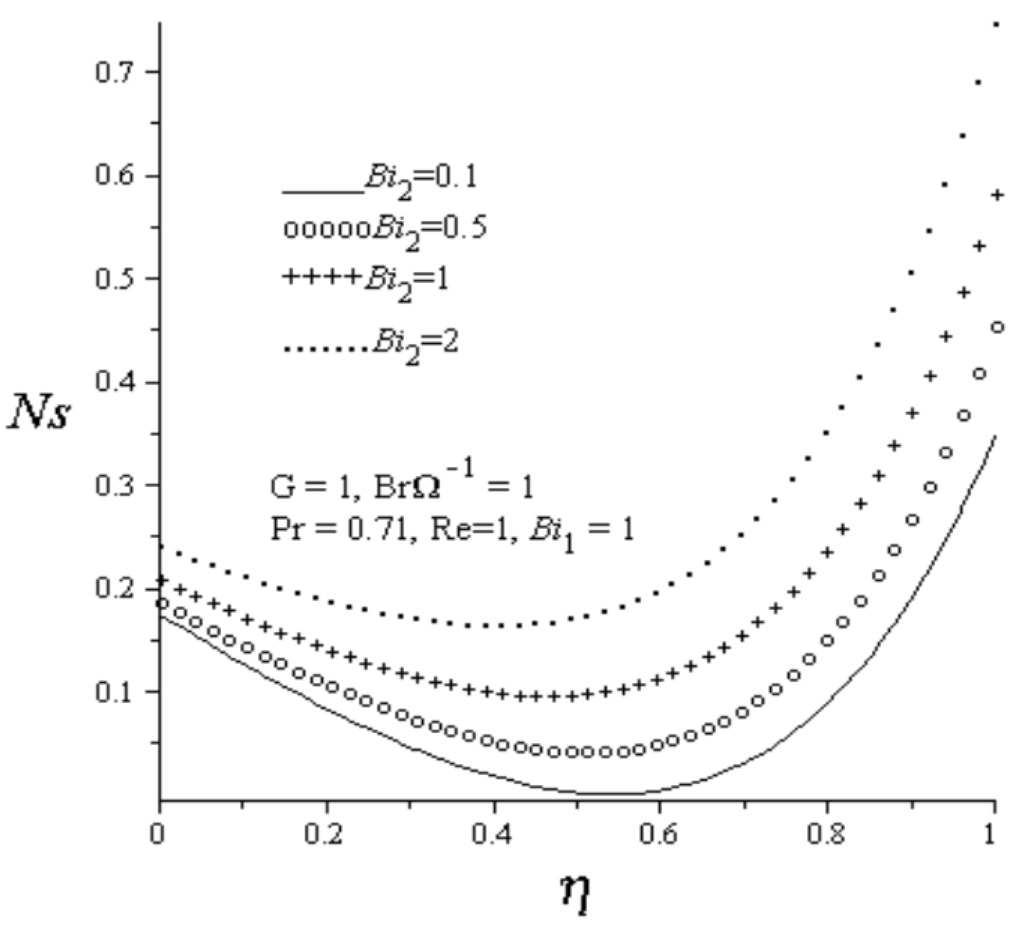
Figure 10.
Effect of increasing Bi2 on entropy generation rate.
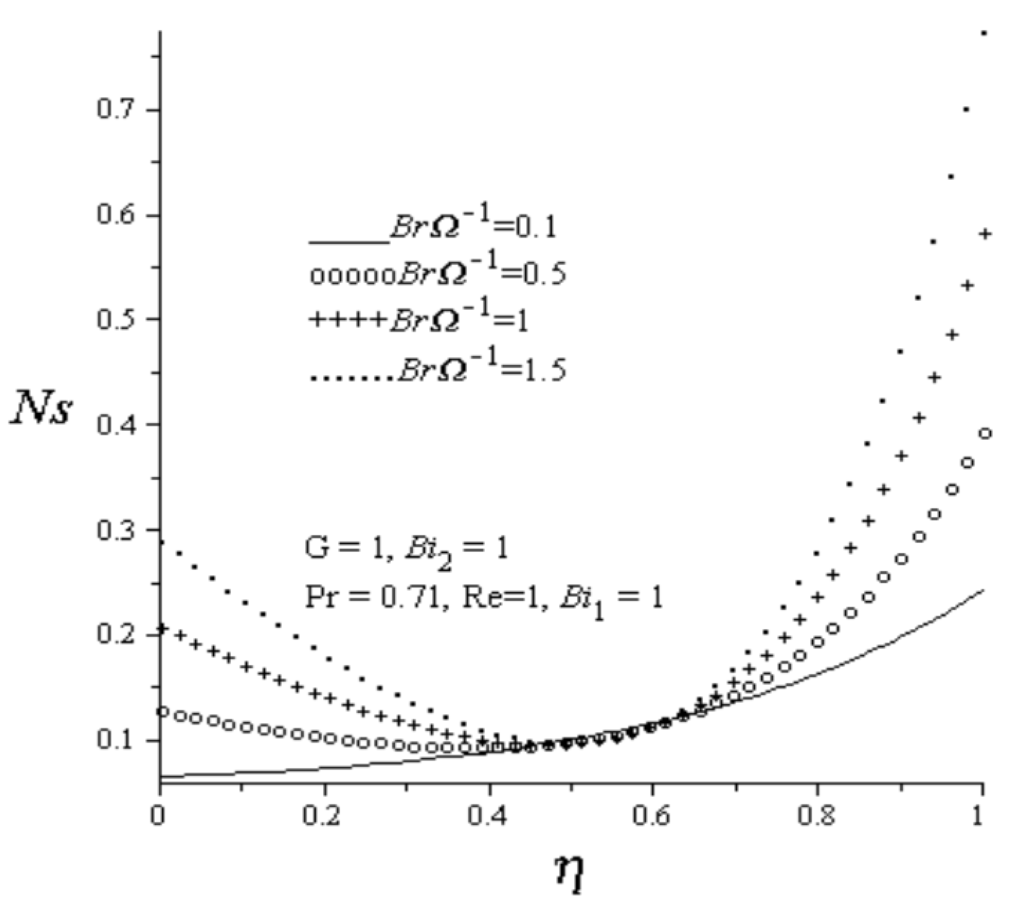
Figure 11.
Effect of increasing BrΩ−1 on entropy generation rate.
4.3. Effects of Parameter Variations on Bejan Number
The effect of different parameter values on Bejan number are analyzed in Figure 12, Figure 13, Figure 14 and Figure 15. Generally, the Bejan number is highest within the channel centerline with heat transfer irreversibility dominating the flow in this region. As the Reynolds number increases, the Bejan number decreases at the lower wall region with dominant effect of fluid friction irreversibility and increases at the upper wall region with increasing effect of heat transfer irreversibility as demonstrated in Figure 12. Figure 13 and Figure 14 show the effects of increasing convective heat transfer at both walls. As
and increase, the convective heating at the lower wall and the convective cooling at the upper wall increases, leading to an increase in the Bejan number, consequently, the dominant effects of heat transfer irreversibility increases. Figure 15 depicts the effect of group parameters () on Bejan number. As the group parameter () increases due to viscous dissipation effect, the Bejan number at both walls decreases, consequently, the dominant effects of fluid friction irreversibility within the lower and upper wall region increases.
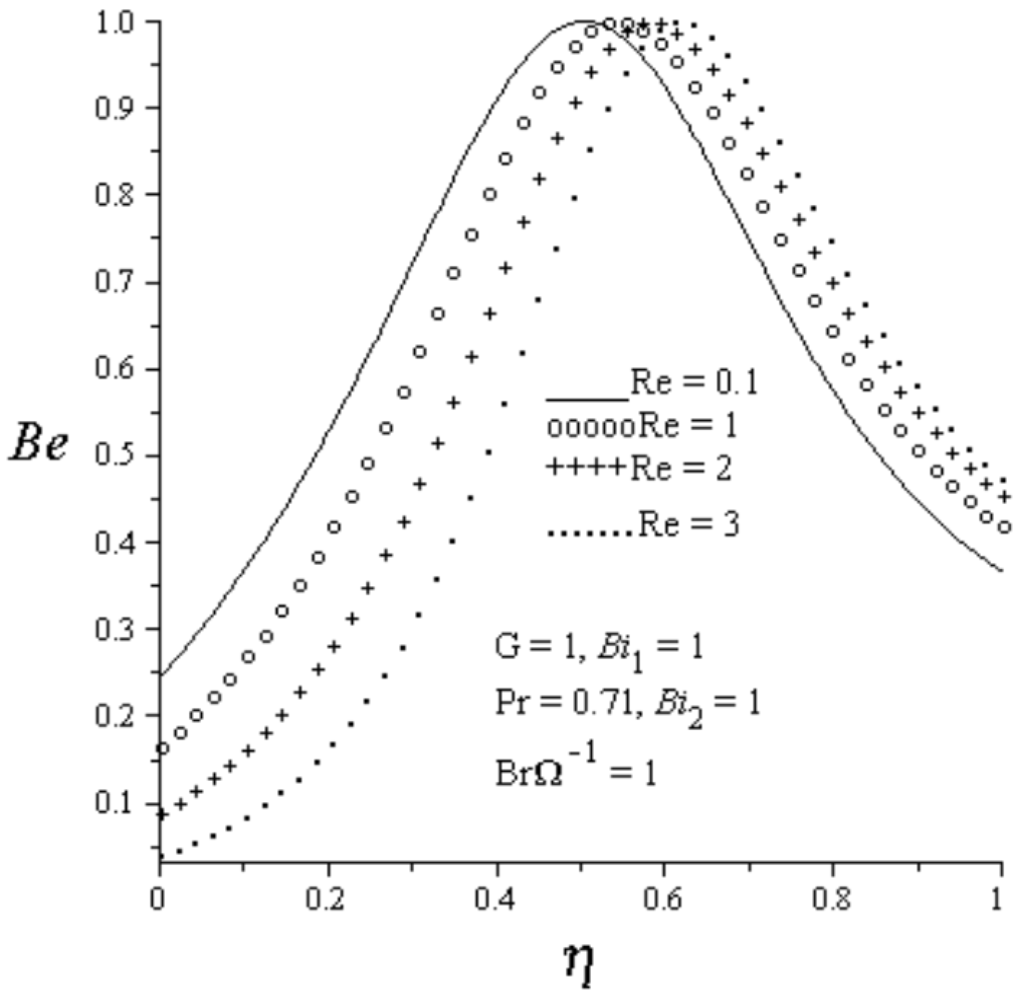
Figure 12.
Effect of increasing Re on Bejan number.
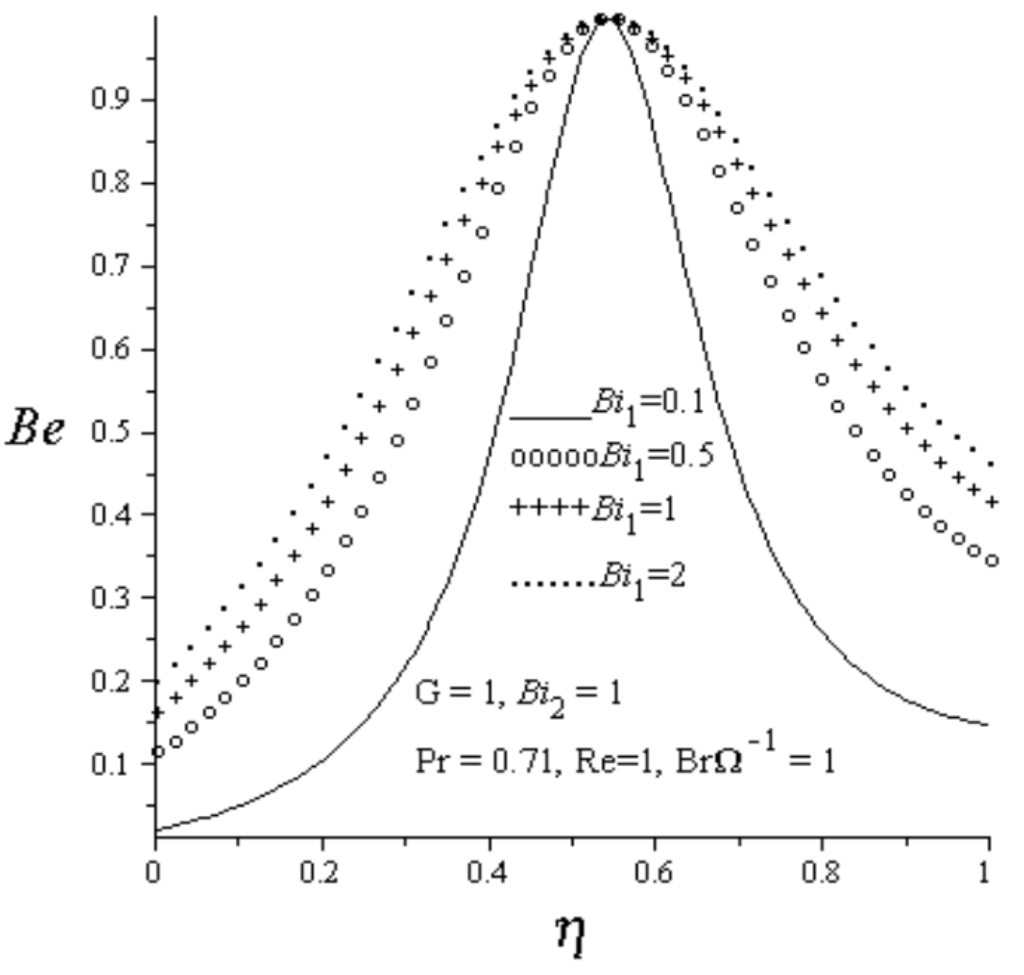
Figure 13.
Effect of increasing Bi1 on Bejan number.
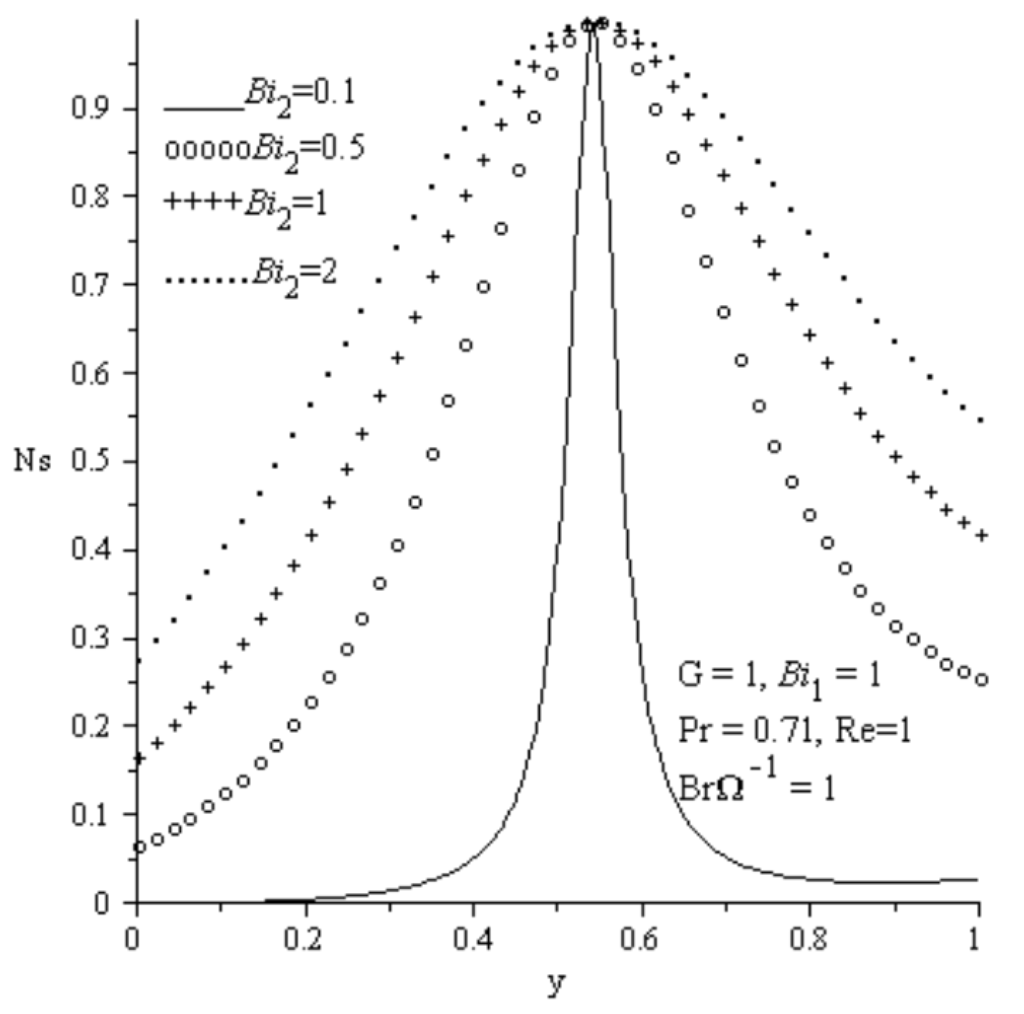
Figure 14.
Effect of increasing Bi2 on Bejan number.
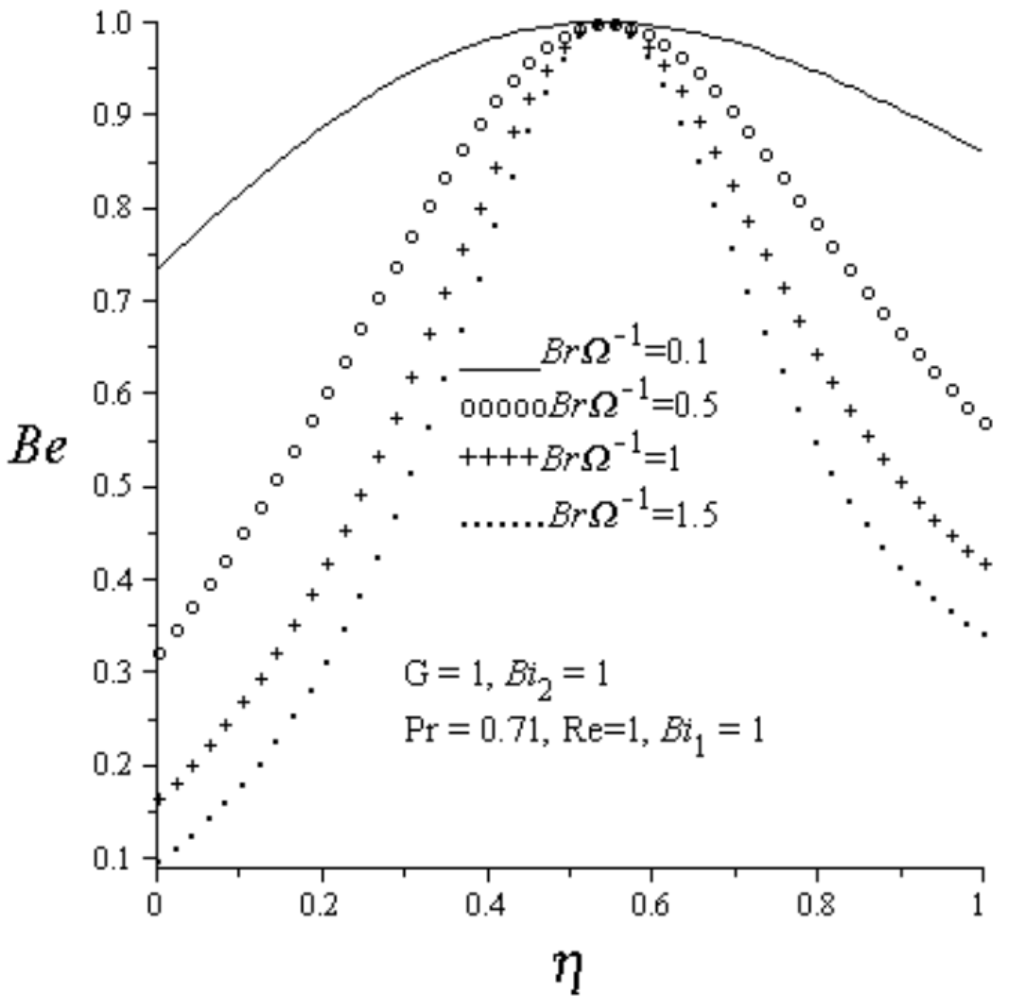
Figure 15.
Effect of increasing BrΩ−1 on Bejan number.
5. Conclusions
In this paper the combined effect of convective heat transfer and suction/injection on entropy generation rate in a steady flow of fluid through a channel with permeable walls has been considered. The model problems are tackled numerically using shooting method together with Runge-kutta fourth-order integration scheme. Our results revealed the following:
- (1)
- The fluid temperature increases with increasing Re, Ec, Bi1, Pr and decreases with increasing values of Bi2.
- (2)
- Entropy generation rate increases with increasing values of Bi1, Bi2, . As Re increases, entropy production decreases at lower wall and increases at the upper wall.
- (3)
- Increase in Bi1, Bi2 enhance dominant effects of heat transfer irreversibility while increase in enhance dominant effects of fluid friction irreversibility.
- (4)
- Increase in Re decrease Bejan number at the lower wall region and increase Bejan number at the upper wall region.
- (5)
- Heat transfer irreversibility dominates the centerline region of the channel.
Nomenclature
Specific heat at a constant pressure | |
Entropy generation due to viscous dissipation | |
Fluid velocity | |
Thermal conductivity | |
Uniform suction/injection velocity | |
Fluid pressure | |
Entropy generation due to heat transfer | |
Temperature | |
Local volumetric rate of entropy generation | |
Bejan number | |
Hot fluid temperature | |
Ambient temperature | |
Temperature at suction wall | |
Temperature at injection wall | |
Channel width. | |
Pressure gradient | |
Reynolds number | |
Prandtl number | |
Brinkman number | |
Eckert number | |
Lower wall Biot number | |
Upper wall Biot number | |
Cartesian coordinates | |
Dimensionless velocity | |
Dimensionless axial coordinate |
Greek symbols
Thermal diffusivity | |
Fluid viscosity | |
Dimensionless temperature | |
Irreversibility ratio | |
Lower heat transfer coefficient | |
Upper heat transfer coefficient | |
Temperature difference | |
Fluid density | |
Dimensionless transverse coordinate |
References
- Merkin, J.H. Natural convection boundary-layer flow on a vertical surface with Newtonian heating. Int. J. Heat Fluid Flow 1992, 15, 392–398. [Google Scholar] [CrossRef]
- Aziz, A. A similarity solution for laminar thermal boundary over a flat plate with a convective boundary condition. Commun. Nonlinear Sci. Numer. Simulat. 2009, 14, 1064–1068. [Google Scholar] [CrossRef]
- Lesnic, D.; Ingham, B.; Pop, I.; Storr, C. Free convection boundary-layer flow above a nearly horizontal surface in a porous medium with Newtonian heating. J. Heat Mass Transfer 2004, 40, 665–672. [Google Scholar] [CrossRef]
- Mebine, P.; Adigio, E.M. Unsteady free convection flow with thermal radiation past a vertical porous plate with Newtonian heating. Turk. J. Phys. 2009, 33, 109–119. [Google Scholar]
- Makinde, O.D. Computational modelling of MHD unsteady flow and heat transfer toward a flat plate with Navier slip and Newtonian heating. Braz. J. Chem. Eng. 2012, 29, 159–166. [Google Scholar] [CrossRef]
- Bejan, A. Second-Law analysis in heat transfer and thermal design. Adv. Heat Transfer 1982, 15, 1–58. [Google Scholar]
- Mahmud, S.; Fraser, R.A. Flow, thermal and entropy generation characteristic inside a porous channel with viscous dissipation. Int. J. Therm. Sci. 2005, 44, 21–32. [Google Scholar] [CrossRef]
- Makinde, O.D.; Osalusi, E. Entropy generation in a liquid film falling along an inclined porous heated plate. Mech. Res. Commun. 2006, 33, 692–698. [Google Scholar] [CrossRef]
- Eegunjobi, A.S.; Makinde, O.D. Combined effect of buoyancy force and Navier slip on entropy generation in a vertical porous channel. Entropy 2012, 14, 1028–1044. [Google Scholar] [CrossRef]
- Chauhan, D.S.; Kumar, V. Heat transfer and entropy generation during compressible fluid flow in a channel partially filled with porous medium. Int. J. Energ. Tech. 2011, 3, 1–10. [Google Scholar]
- Eegunjobi, A.S.; Makinde, O.D. Effects of Navier slip on entropy generation in a porous channel with suction/injection. J. Therm. Sci. Technol. 2012, 7, 522–535. [Google Scholar] [CrossRef]
- Tasnim, S.M.; Mahmud, S.; Mamum, M.A.H. Entropy generation in a porous channel with hydromagetic effect. Int. J. Exergy 2002, 3, 300–308. [Google Scholar] [CrossRef]
- Nachtsheim, P.R.; Swigert, P. Satisfaction of the Asymptotic Boundary Conditions in Numerical Solution of the System of Nonlinear Equations of Boundary Layer Type; National Aeronautics and Space Administration: Washington, DC, USA, 1965; NASA TND-3004. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).