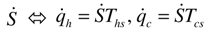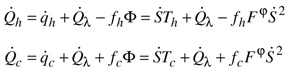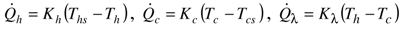Association of Finite-Dimension Thermodynamics and a Bond-Graph Approach for Modeling an Irreversible Heat Engine
Abstract
:1. Introduction

2. Modeling of Exo-Reversible Heat Engine at Steady State
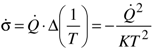 . Since the thermal power transferred is finite and the thermal conductance K is infinite, the rate of entropy generation is zero.
. Since the thermal power transferred is finite and the thermal conductance K is infinite, the rate of entropy generation is zero.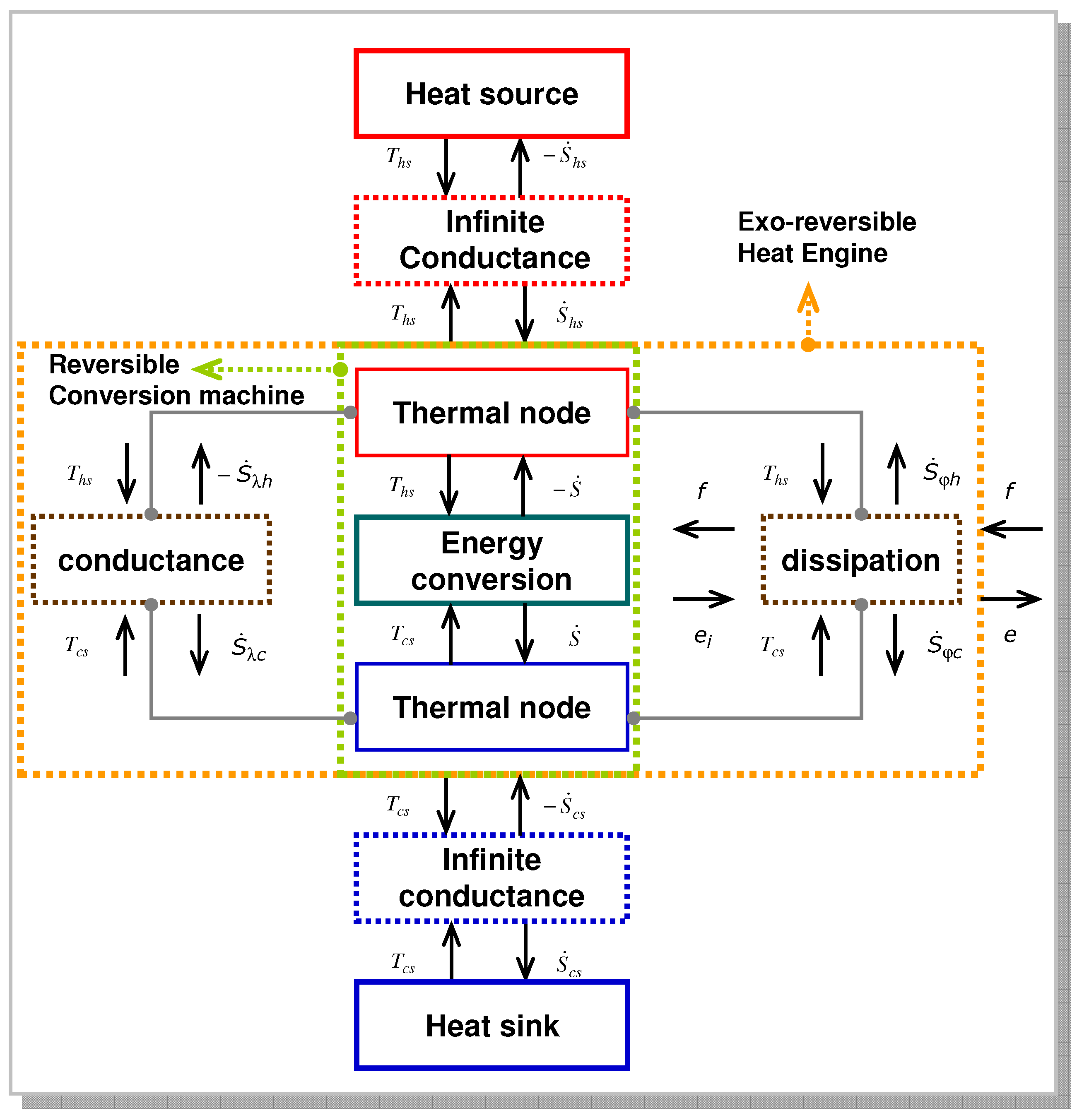
- The temperatures of heat source and heat sink are constant (Ths and Tcs).
- The energy conversion is a reversible process (conservation of entropy flow rate
).
- The law of heat transfer is linear (constant conductance Kλ).
- The internal dissipation Φ depends only on the control variable Ṡ: Φ = Φ(Ṡ). This assumption can be justified when the entropy flow rate Ṡ involved in reversible energy conversion completely defines the operating point of the machine. Moreover, in the case of a thermoelectric generator where the internal dissipation is related to the Joule effect, we have:
where R is the electric resistance of the thermoelectric generator and α the Seebeck coefficient.
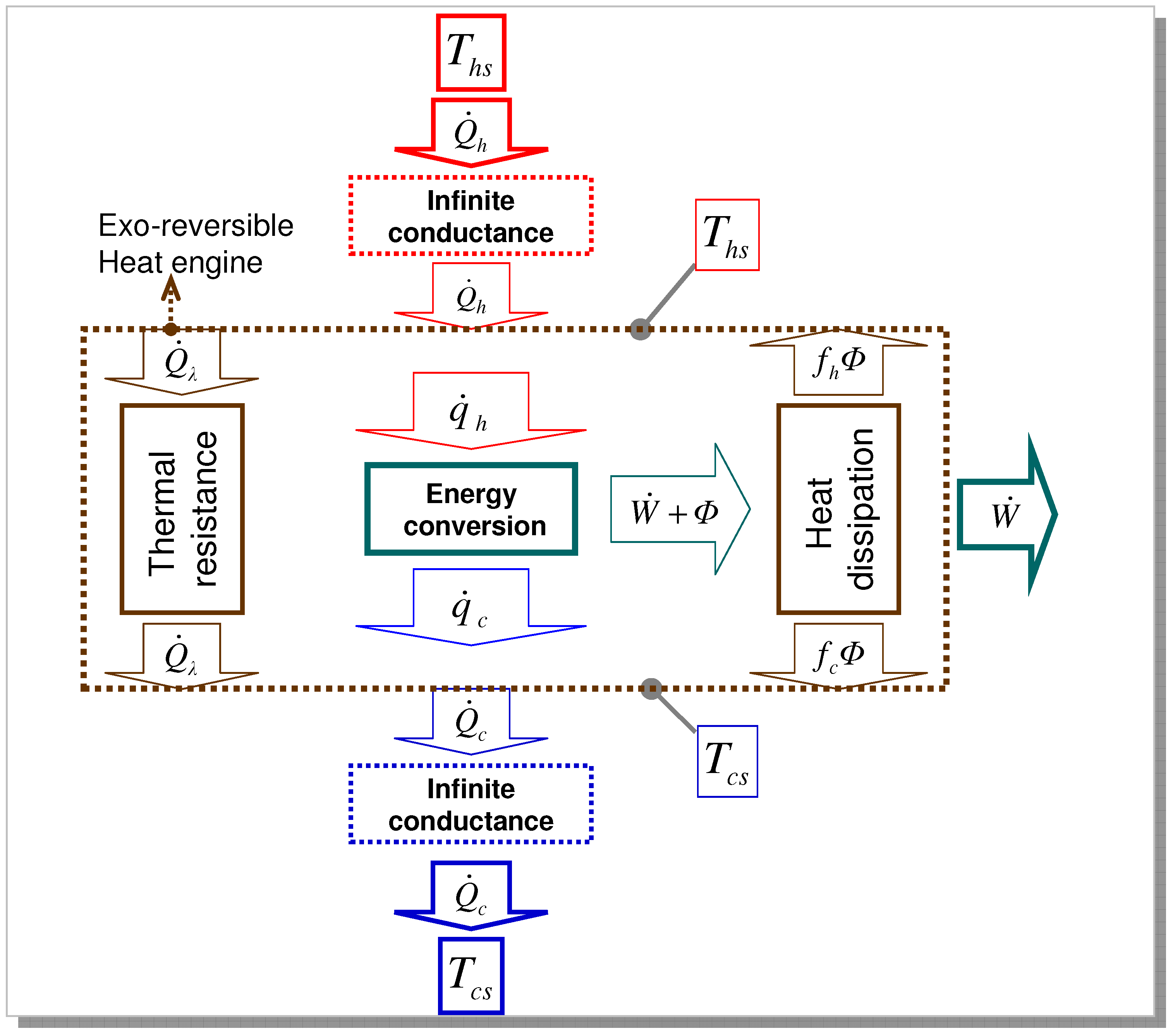
2.1. Energy Balance at Steady State








2.2. Determination of the Maximum Mechanical Power and the Associated Efficiency
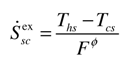
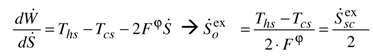
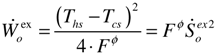
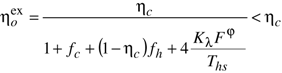
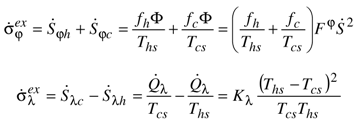

 which in the case of a thermoelectric conversion, represents a quarter of the figure of merit ZT at temperature (fhTcs + fcThs).
which in the case of a thermoelectric conversion, represents a quarter of the figure of merit ZT at temperature (fhTcs + fcThs).3. Modeling of an Irreversible Heat Engine at Steady State
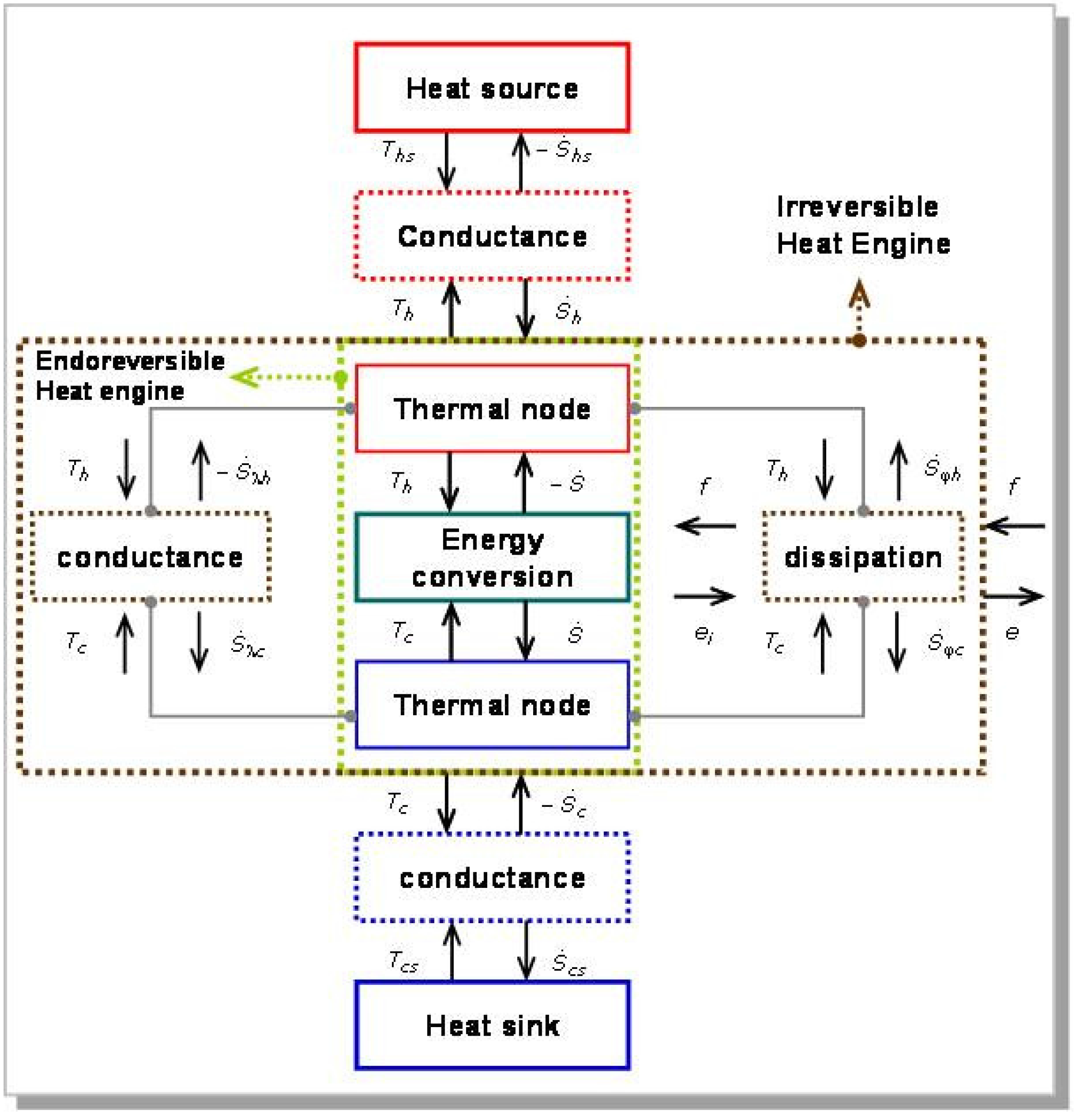
3.1. Power Balance at Steady State


3.2. Analytical Expressions of the Operating Point

3.3. Analysis of Effects of Internal Dissipation
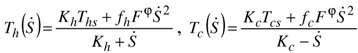
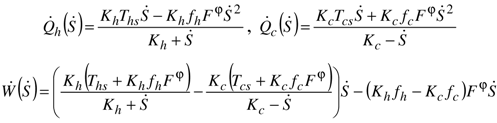
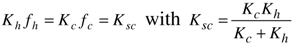


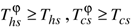 and
and 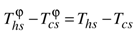 ).
).

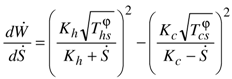

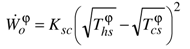
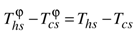 ), the “thermal potential”
), the “thermal potential”  involved in the expression of the maximum power (26) is lower than that of the endoreversible heat engine
involved in the expression of the maximum power (26) is lower than that of the endoreversible heat engine 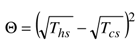 . In fact, by making a first-order Taylor expansion of Θϕ with respect to the term ϕTsc, we obtain the following expression:
. In fact, by making a first-order Taylor expansion of Θϕ with respect to the term ϕTsc, we obtain the following expression:

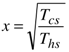 in the range [0, 1], we can easily demonstrate the inequality
in the range [0, 1], we can easily demonstrate the inequality 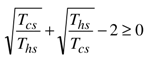 .
.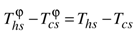 which shows that the slope at the origin of mechanical power is not affected by the internal dissipation. Similarly, one can demonstrate that the slope at the origin of the thermal power
which shows that the slope at the origin of mechanical power is not affected by the internal dissipation. Similarly, one can demonstrate that the slope at the origin of the thermal power 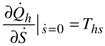 [Equation (19)] is not affected by the dissipation either. This explains why the energy conversion efficiency of the machine at Ṡ = 0 is equal to the Carnot efficiency
[Equation (19)] is not affected by the dissipation either. This explains why the energy conversion efficiency of the machine at Ṡ = 0 is equal to the Carnot efficiency 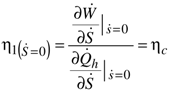 (cf. Figure 8).
(cf. Figure 8). 

3.4. Analysis of Effects of Internal Heat Leakage



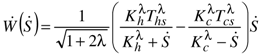

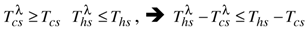
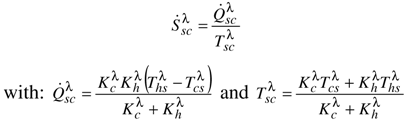

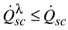 ). This confirms the interest of selecting the entropy flow rate Ṡ involved in reversible energy conversion as the control variable of the heat engine.
). This confirms the interest of selecting the entropy flow rate Ṡ involved in reversible energy conversion as the control variable of the heat engine.
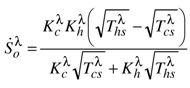

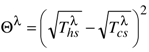 . Finally, we have two contradictory effects: a dominant effect related to the temperatures Θλ which degrades the mechanical power and a second effect of the overall thermal conductance which reduces the degradation « ≥ Ksc ». In fact, from Equation (38) we prove that the slope at the origin point of the curve of mechanical power
. Finally, we have two contradictory effects: a dominant effect related to the temperatures Θλ which degrades the mechanical power and a second effect of the overall thermal conductance which reduces the degradation « ≥ Ksc ». In fact, from Equation (38) we prove that the slope at the origin point of the curve of mechanical power  is lower than that of the endoreversible heat engine λ = 0. And as the cutoff entropy flow rate is not modified by the internal heat leakage, the curve of mechanical power is reduced by the heat leakage (cf. Figure 9), as is the maximum power ( ≤ Ẇo).
is lower than that of the endoreversible heat engine λ = 0. And as the cutoff entropy flow rate is not modified by the internal heat leakage, the curve of mechanical power is reduced by the heat leakage (cf. Figure 9), as is the maximum power ( ≤ Ẇo).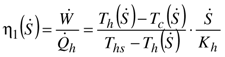
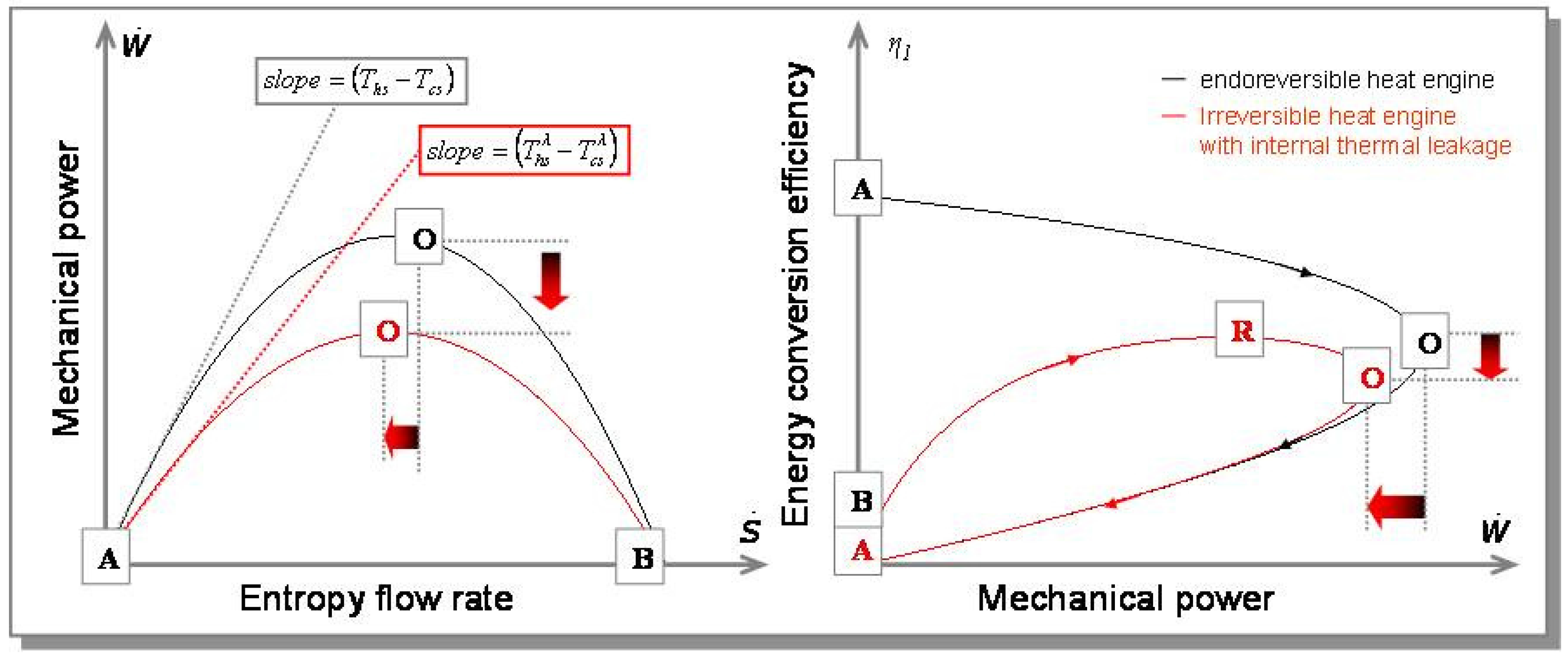
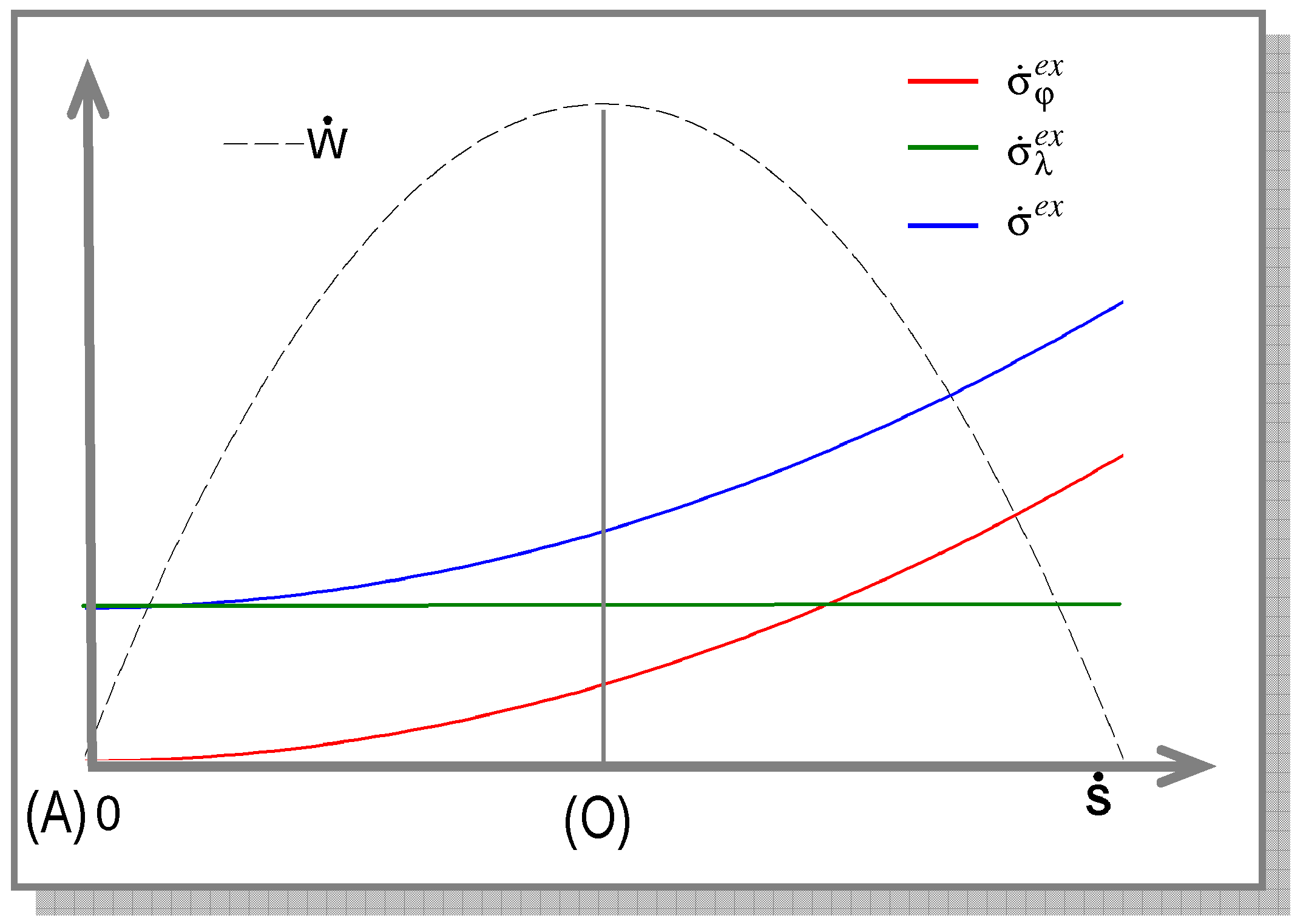
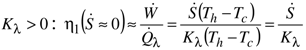 . As a result, unlike the case of an endoreversible heat engine, even the case including internal dissipation, the energy conversion efficiency at point (A) in presence of internal heat leakage is zero. The heat engine behaves at this point as three thermal resistances in series with the only effect that the thermal power is transferred from heat source to heat sink without any production of mechanical power.
. As a result, unlike the case of an endoreversible heat engine, even the case including internal dissipation, the energy conversion efficiency at point (A) in presence of internal heat leakage is zero. The heat engine behaves at this point as three thermal resistances in series with the only effect that the thermal power is transferred from heat source to heat sink without any production of mechanical power.3.5. Analysis of Combined Effects of Internal Dissipation and Heat Leakage
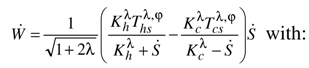

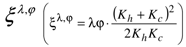 . In the case of a thermoelectric conversion, we have
. In the case of a thermoelectric conversion, we have  which is the inverse of figure of merit of thermoelectric material at temperature Tsc.
which is the inverse of figure of merit of thermoelectric material at temperature Tsc.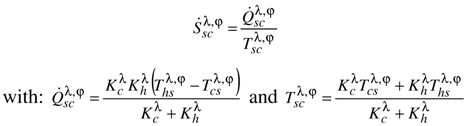

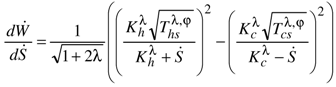

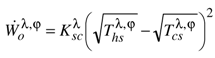
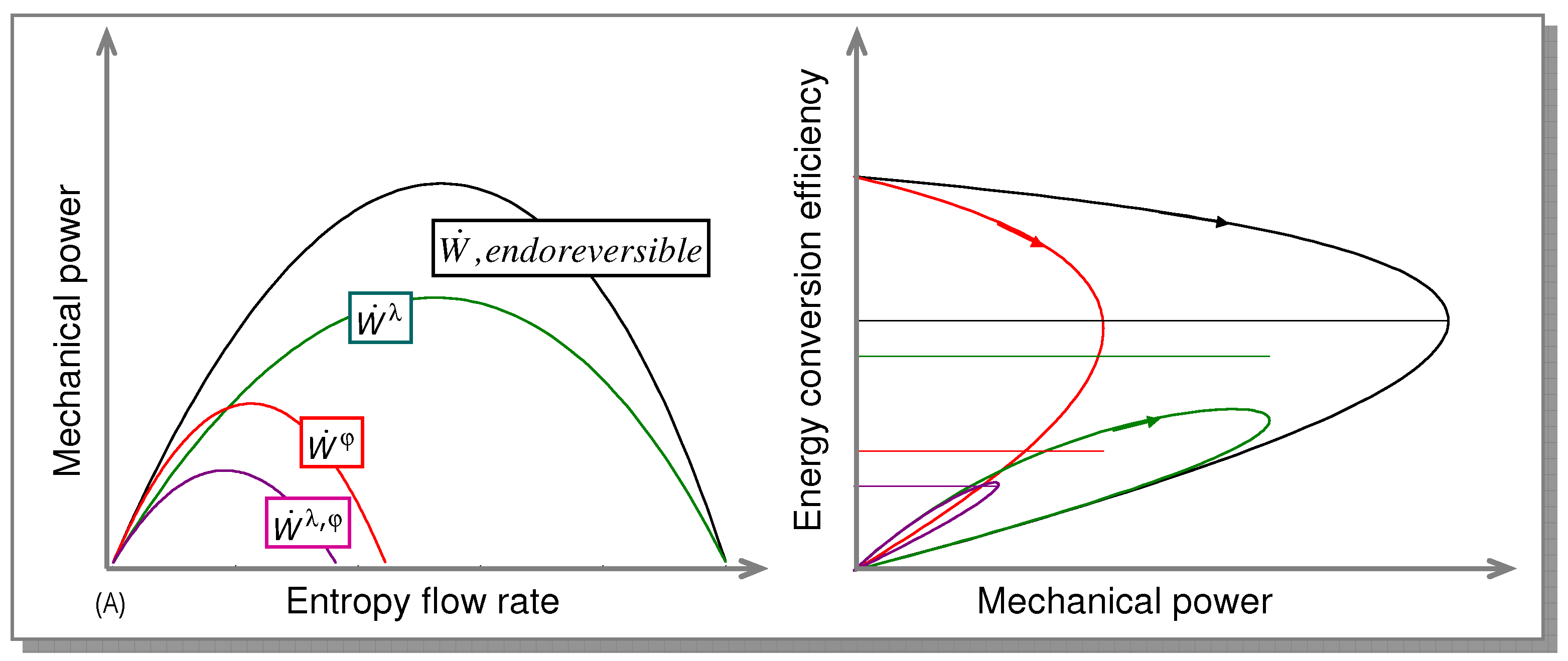
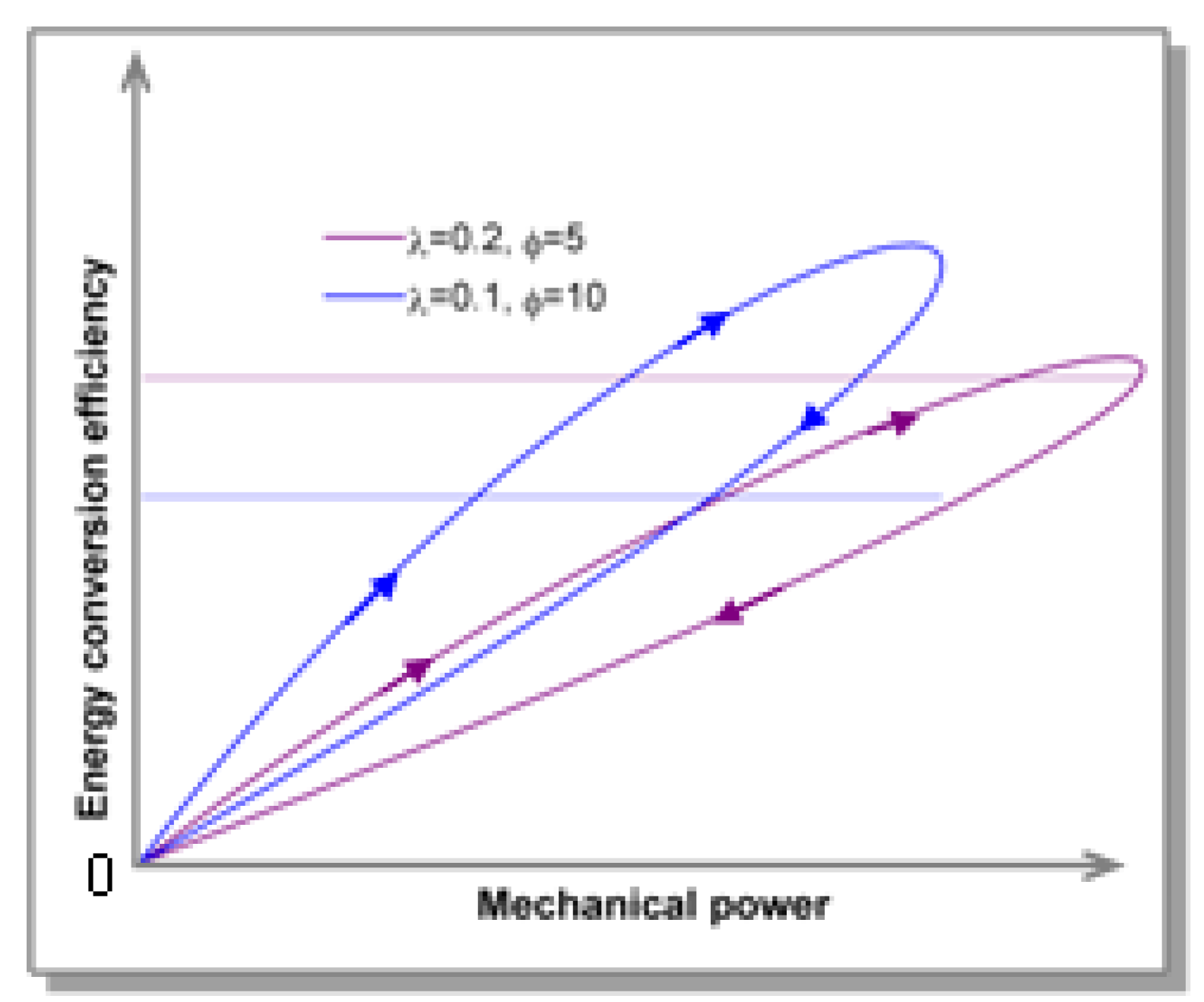
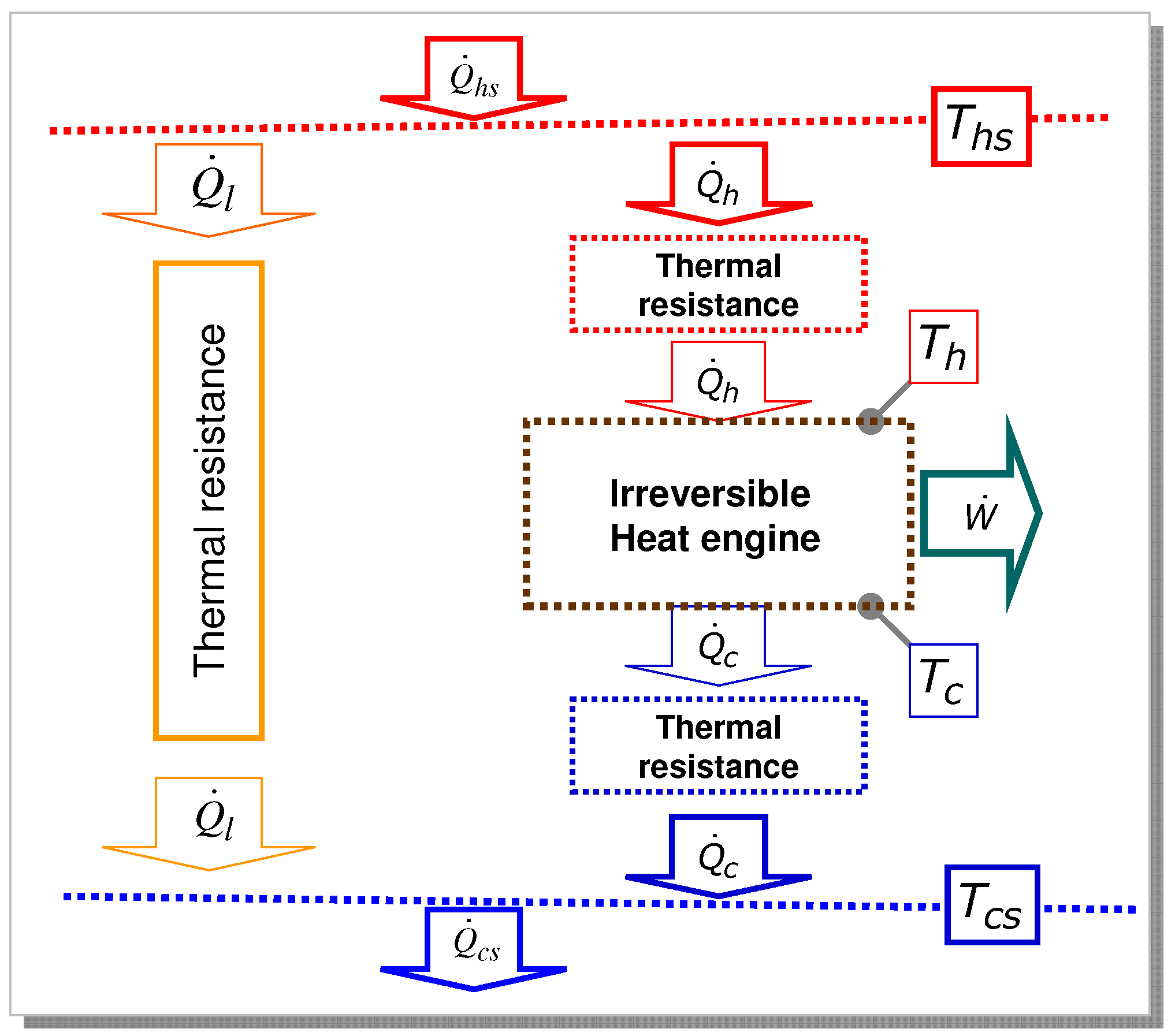
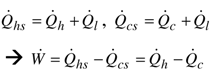
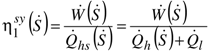 (cf. Figure 13).
(cf. Figure 13). 
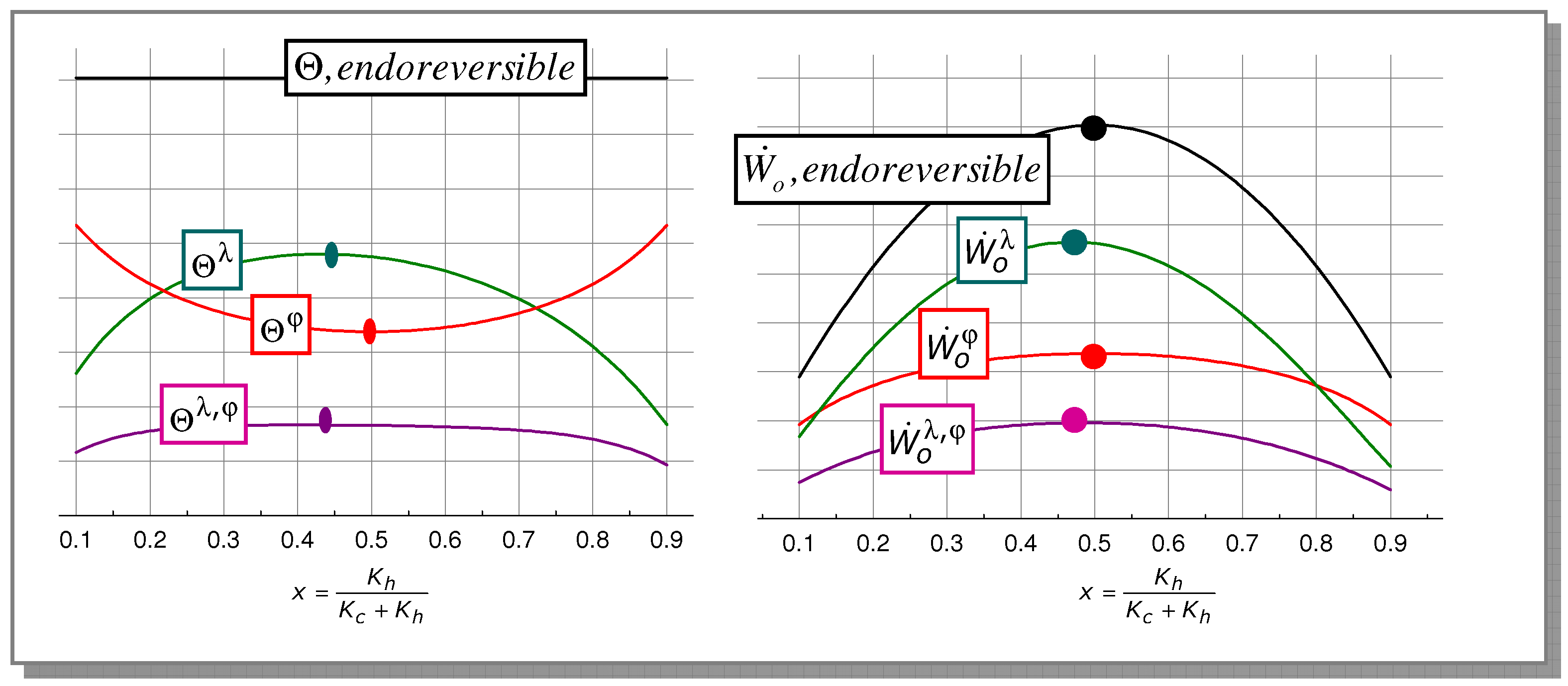
3.6. Optimal Allocation of Conductances
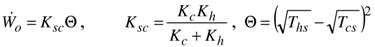
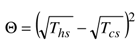 represents the effect of the temperatures of heat source and heat sink on the maximum output power. This term is considerably lower than the difference of temperatures ΔT = Ths − Tcs. For example, for Tcs = 300 K and Ths = 900 K, we have ΔT = 600 K and Θ = 161 K only!
represents the effect of the temperatures of heat source and heat sink on the maximum output power. This term is considerably lower than the difference of temperatures ΔT = Ths − Tcs. For example, for Tcs = 300 K and Ths = 900 K, we have ΔT = 600 K and Θ = 161 K only!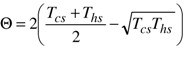
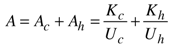
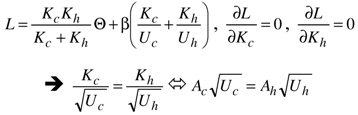
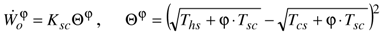
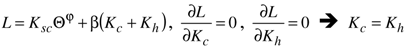

4. Conclusions and Perspectives
| Heat Engine Classification | Endoreversible Heat Engine | Irreversible Heat Engine |
|---|---|---|
| Cutoff entropy flow rate: | 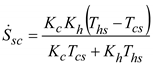 | 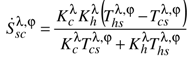 |
| Optimal entropy flow rate: | 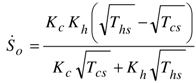 | 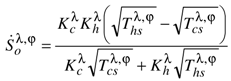 |
| Maximum output power: | 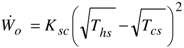 | 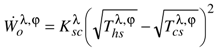 |
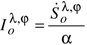 for which the output electric power is maximized [50].
for which the output electric power is maximized [50]. 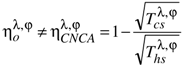 .
.Nomenclature
| Variable | Unit | Description |
| Ths | K | Temperature of heat source |
| Tcs | K | Temperature of heat sink |
| Th | K | Hot side temperature of heat engine |
| Tc | K | Cold side temperature of heat engine |
| Tsc | K | Cutoff temperature of heat engine |
| Ṡhs | W/K | Entropy flow rate transferred at heat source |
| Ṡcs | W/K | Entropy flow rate transferred at heat sink |
| Ṡ | W/K | Entropy flow rate involved in reversible energy conversion |
| Ṡsc | W/K | Cutoff entropy flow rate |
| Ṡo | W/K | Optimal entropy flow rate |
| Kλ | W/K | Internal thermal conductance of heat engine |
| Kl | W/K | Conductance of heat leakage between heat source and heat sink |
| Kh | W/K | Global thermal conductance of heat exchanger at hot side |
| Kc | W/K | Global thermal conductance of heat exchanger at cold side |
| Ksc | W/K | Equivalent thermal conductance |
| ex | W/K | Rate of total entropy generation within exo-reversible heat engine |
| W/K | Rate of entropy generation related to internal heat transfer | |
| W/K | Rate of entropy generation related to internal dissipation | |
| W | Thermal power supplied by heat source | |
| W | Thermal power received by heat link | |
| W | Thermal power exchanged between heat source and heat engine | |
| W | Thermal power exchanged between heat sink and heat engine | |
| W | Internal heat leakage | |
| W | External heat leakage between heat source and heat link | |
| W | Cutoff thermal power | |
| Φ | W | Internal dissipation within heat engine |
| W | Input thermal power of converter | |
| W | Output thermal power of converter | |
| Ẇ | W | Output mechanical power of heat engine |
| Ẇo | W | Maximum mechanical power of heat engine |
| η1 | -- | Energy conversion efficiency |
| ηo | -- | Energy conversion efficiency at optimal operating point of heat engine |
| ηC | -- | Carnot efficiency |
| ηCNCA | -- | Chambadal-Novikov-Curzon-Ahlborn efficiency |
| ZT | -- | Figure of merit of thermoelectric material at temperature T |
| ϕ | -- | dimensionless number of internal dissipation within heat engine |
| λ | -- | dimensionless number of internal heat loss within heat engine |
| fh | -- | Distribution parameter of internal dissipation at hot side |
| fc | -- | Distribution parameter of internal dissipation at cold side |
| Fϕ | K2/W | Internal “resistance” of heat engine |
| K2/W | External “resistance” of heat engine | |
| R | Ω | Internal electric resistance of thermoelectric generator |
| A | m2 | Heat exchange surface |
| U | W/K/m2 | Heat exchange coefficient |
| I | A | Electric current of thermoelectric generator |
| α | V/K | Coefficient of Seebeck |
| U0 | V | Open circuit voltage of thermoelectric generator03B1 |
References
- Dong, Y.; El-Bakkali, A.; Descombes, G.; Feidt, M.; Périlhon, C. Association of finite-time thermodynamics and a bond-graph approach for modeling an endoreversible heat engine. Entropy 2012, 14, 642–653. [Google Scholar] [CrossRef]
- Chen, L.; Wu, C.; Sun, F. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J. Non-Equilib. Thermodyn. 1999, 24, 327–359. [Google Scholar] [CrossRef]
- Chen, L.; Wu, C.; Sun, F.; Chen, W. Optimal performance of an endoreversible Carnot heat pump. Energy Convers. Manag. 1997, 38, 1439–1443. [Google Scholar] [CrossRef]
- Chen, L.; Wu, C.; Sun, F.; Chen, W. General performance characteristics of finite speed Carnot refrigerator. Appl. Therm. Eng. 1996, 16, 299–303. [Google Scholar]
- Wu, C.; Kiang, R.L. Finite-time thermodynamic analysis of a Carnot engine with internal irreversibility. Energy 1992, 17, 1173–1178. [Google Scholar] [CrossRef]
- Feidt, M. Optimal thermodynamics—New upperbounds. Entropy 2009, 11, 529–547. [Google Scholar] [CrossRef]
- Feidt, M.; Costea, M.; Petre, C.; Petrescu, S. Optimization of the direct Carnot cycle. Appl. Therm. Eng. 2007, 27, 829–839. [Google Scholar] [CrossRef]
- Feidt, M. Reconsideration of criteria and modeling in order to optimize the efficiency of irreversible thermomechanical heat engines. Entropy 2010, 12, 2470–2484. [Google Scholar] [CrossRef]
- De Vos, A. Endoreversible thermoeconomics. Energy Convers. Manag. 1995, 36, 1–5. [Google Scholar] [CrossRef]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465. [Google Scholar] [CrossRef]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power conditions. Am. J. Phys. 1975, 53, 570–573. [Google Scholar]
- Tyagi, S.K.; Chen, J.; Kaushik, S.C. Thermoeconomic optimization and parametric study of an irreversible Stirling heat pump cycle. Int. J. Thermal Sci. 2004, 43, 105–112. [Google Scholar] [CrossRef]
- Borel, L.; Favrat, D. de l’énergie à l’exergie. In Thermodynamique et énergétique; (in French). Presses polytechniques et universitaires romandes: Lausanne, France, 2005; Volume 1, p. 814. [Google Scholar]
- Bejan, A. Advanced Engineering Thermodynamics; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Chen, L.; Zhou, J.; Sun, F.; Wu, C. Ecological optimization for generalized irreversible Carnot engines. Appl. Energy 2004, 77, 327–338. [Google Scholar] [CrossRef]
- Chambadal, P. Les Centrales Nucléaires; (in French). Armand Colin: Paris, France, 1957. [Google Scholar]
- Novikov, I.I. The efficiency of atomic power station. J. Nucl. Energ. 1958, 7, 125–128. [Google Scholar]
- Feidt, M. Thermodynamique et Optimisation Energétique des Systèmes et Procédés; (in French). Lavoisier: Paris, France, 1987; ISBN 2852063727. [Google Scholar]
- Jou, D.; Casas-Vasquez, J.; Lebon, G. Extended Irreversible Thermodynamics, 3rd ed.; Springer Verlag: Berlin, Germany, 2001. [Google Scholar]
- Andresen, B. Finite Time Thermodynamics; Physics Laboratory, University of Copenhagen: Copenhagen, Denmark, 1983. [Google Scholar]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite size, and finite time processes. J. Appl. Phys. 1997, 79, 1191–1218. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal Design and Optimization; J. Wiley and Sons Inc.: New York, NY, USA, 1996. [Google Scholar]
- Goth, Y.; Feidt, M. Recherche sur les conditions optimales de fonctionnement des pompes à chaleur ou machines à froid associées à un cycle de Carnot endoreversible (in French). C. R. Acad. Sci. 1986, 303, 113–122. [Google Scholar]
- Van den Broeck, C. Thermodynamic efficiency at maximum power. Phys. Rev. Lett. 2005, 95, 190602. [Google Scholar] [CrossRef] [PubMed]
- Jimenez de Cisneros, B.; Calvo Hernandez, A. Collective working regimes for coupled heat engines. Phys. Rev. Lett. 2007, 98, 130602. [Google Scholar] [CrossRef] [PubMed]
- Jimenez de Cisneros, B.; Calvo Hernandez, A. Coupled heat devices in linear irreversible thermodynamics. Phys. Rev. E 2008, 77, 041127. [Google Scholar] [CrossRef]
- Schmiedl, T.; Seifert, U. Efficiency at maximum power: An analytically solvable model for stochastic heat engines. Europhys. Lett. 2008, 81, 20003. [Google Scholar] [CrossRef]
- Apertet, Y.; Ouerdane, H.; Goupil, C.; Lecoeur, Ph. Irreversibilities and efficiency at maximum power of heat engines: The illustrative case of a thermoelectric generator. Phys. Rev. E 2012, 85, 031116. [Google Scholar] [CrossRef]
- Apertet, Y.; Ouerdane, H.; Goupil, C.; Lecoeur, Ph. Efficiency at maximum power of thermally coupled heat engines. Phys. Rev. E 2012, 85, 041144. [Google Scholar] [CrossRef]
- Andresen, B.; Salamon, P.; Berry, R.S. Thermodynamics in finite time: Extremals for imperfect heat engines. J. Chem. Phys. 1977, 66, 1571–1577. [Google Scholar] [CrossRef]
- Andresen, B.; Salamon, P.; Berry, R.S.; Nitzan, A. Thermodynamics in finite time. I. The step-Carnot cycle. Phys. Rev. A 1977, 15, 2086–2093. [Google Scholar] [CrossRef]
- Andresen, B.; Salamon, P.; Berry, R.S. Thermodynamics in finite time. II. Potentials for finite-time processes. Phys. Rev. A 1977, 15, 2094–2102. [Google Scholar]
- Andresen, B. Current trends in finite-time thermodynamics. Angew. Chem. Int. Ed. Engl. 2011, 50, 2690–2704. [Google Scholar] [CrossRef] [PubMed]
- Tu, Z.C. Recent advance on the efficiency at maximum power of heat engines. Chin. Phys. B 2012, 21, 020513. [Google Scholar] [CrossRef]
- Feidt, M. Thermodynamics of energy systems and processes: A review and perspectives. J. Appl. Fluid Mech. 2012, 5, 85–98. [Google Scholar]
- Xuan, X.C. Optimum staging of multistage exo-reversible refrigeration systems. Cryogenics 2003, 43, 117–124. [Google Scholar] [CrossRef]
- Popescu, C.; Radcenco, V.; Costea, M.; Feidt, M. Optimisation thermodynamique en temps fini du moteur de Stirling endo- et exo-irréversible. Rev. Gin. Therm. 1996, 35, 656–661. [Google Scholar] [CrossRef]
- Vijay, P.; Samantaray, A.K.; Mukherjee, A. A bond graph model-based evaluation of a control scheme to improve the dynamic performance of a solid oxide fuel cell. Mechatronics 2009, 19, 489–502. [Google Scholar] [CrossRef]
- Boulon, L. Modélisation multi physique des éléments de stockage et de conversion d’énergie pour les véhicules électriques hybrides. Approche systémique pour la gestion d’énergie (in French). Ph.D. disertation, Université de Franche-Comté, France, July 2009. [Google Scholar]
- Wu, C. Analysis of waste heat thermoelectric power generators. Appl. Therm. Eng. 1996, 16, 63–69. [Google Scholar] [CrossRef]
- Lenoir, B.; Michenaud, J.; Dauscher, A. Thermoélectricité: Des principes aux applications (in French). Technique de l’ingénieur 2010. Référence K730. [Google Scholar]
- Durmayaza, A.; Sogub, O.S.; Sahin, B.; Yavuz, H. Optimization of thermal systems based on finite-time thermodynamics and thermoeconomics. Prog. Energy Combust. Sci. 2004, 30, 175–217. [Google Scholar] [CrossRef]
- Kodal, A.; Sahin, B.; Yilmaz, T. A comparative performance analysis of irreversible Carnot heat engines under maximum power density and maximum power conditions. Energy Convers. Manag. 2000, 41, 235–248. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, Y.; Peng, Z.; Shu, G. A review of researches on thermal exhaust heat recovery with Rankine cycle. Renew. Sustain. Energy Rev. 2011, 15, 2862–2871. [Google Scholar] [CrossRef]
- Tchanche, B.F.; Lambrinos, Gr.; Frangoudakis, A.; Papadakis, G. Low-grade heat conversion into power using organic Rankine cycles—A review of various applications. Renew. Sustain. Energy Rev. 2011, 15, 3963–3979. [Google Scholar] [CrossRef]
- Goupil, C.; Seifert, W.; Zabrocki, K.; Müller, E.; Snyder, G.J. Thermodynamics of thermoelectric phenomena and applications. Entropy 2011, 13, 1481–1517. [Google Scholar] [CrossRef]
- Apertet, Y.; Ouerdane, H.; Glavatskaya, O.; Goupil, C.; Lecoeur, Ph. Optimal working conditions for thermoelectric generators with realistic thermal coupling. Europhys. Lett. 2012, 97, 28001. [Google Scholar] [CrossRef]
- Arias-Hernandez, L.A.; Barranco-Jiménez, M.A.; Angulo-Brown, F. Comparative analysis of two ecological type modes of performance for a simple energy converter. J. Energy Inst. 2009, 82, 223–227. [Google Scholar] [CrossRef]
- Arias-Hernandez, L.A.; Angulo-Brown, F.; Paez-Hernandez, R.T. First-order irreversible thermodynamic approach to a simple energy converter. Phys. Rev. E 2008, 77, 011123. [Google Scholar] [CrossRef]
- Dong, Y.; El-Bakkali, A.; Descombes, G.; Feidt, M.; Périlhon, C. Assessment of the fuel saving enabled by the heat recovery of exhaust gases using a thermoelectric generator. In Proceedings of the Conference CAR2011 International Congress Automotive and Environment, Pitesti, Romania, 2–4 November 2011.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dong, Y.; El-Bakkali, A.; Feidt, M.; Descombes, G.; Périlhon, C. Association of Finite-Dimension Thermodynamics and a Bond-Graph Approach for Modeling an Irreversible Heat Engine. Entropy 2012, 14, 1234-1258. https://doi.org/10.3390/e14071234
Dong Y, El-Bakkali A, Feidt M, Descombes G, Périlhon C. Association of Finite-Dimension Thermodynamics and a Bond-Graph Approach for Modeling an Irreversible Heat Engine. Entropy. 2012; 14(7):1234-1258. https://doi.org/10.3390/e14071234
Chicago/Turabian StyleDong, Yuxiang, Amin El-Bakkali, Michel Feidt, Georges Descombes, and Christelle Périlhon. 2012. "Association of Finite-Dimension Thermodynamics and a Bond-Graph Approach for Modeling an Irreversible Heat Engine" Entropy 14, no. 7: 1234-1258. https://doi.org/10.3390/e14071234
APA StyleDong, Y., El-Bakkali, A., Feidt, M., Descombes, G., & Périlhon, C. (2012). Association of Finite-Dimension Thermodynamics and a Bond-Graph Approach for Modeling an Irreversible Heat Engine. Entropy, 14(7), 1234-1258. https://doi.org/10.3390/e14071234