Abstract
We propose a quantum protocol to authenticate classical messages that can be used to replace Wegman–Carter’s classical authentication scheme in quantum key distribution (QKD) protocols. We show that the proposed scheme achieves greater conditional entropy of the seed for the intruder given her (quantum) observation than the classical case. The proposed scheme is suitable for situations where the shared symmetric key used in authentication becomes dangerously short (due to noise or eavesdropping), and there is a threat that it might be completely consumed without being replaced. Our protocol is an improvement over a classical scheme by Brassard and takes advantage of quantum channel properties. It is motivated by information-theoretical results. We stress that the proposed authentication protocol can also be used as an independent authentication protocol that is not a part of a QKD. However by adopting it, QKD becomes a fully quantum protocol. We prove that quantum resources can improve both the secrecy of the key generated by the PRG and the secrecy of the tag obtained with a hidden hash function. We conclude that the proposed quantum encoding offers more security than the classical scheme and, by applying a classical result, we show that it can be used under noisy quantum channels.
1. Introduction
The authentication of public messages is a fundamental problem nowadays for bipartite and network communications. The scenario is the following: Alice sends a (classical) message to Bob through a public channel, together with an authentication tag through a private or public channel. The tag will allow Bob to verify if the message he received via the public channel has been tampered with or if it is indeed the authentic message, originally sent by Alice. A third character, Eve, wants to sabotage this scheme by intercepting Alice’s message and sending her own message to Bob, together with a false tag which will convince Bob he is receiving the authentic message. For instance, one could imagine that Alice is sending Bob her bank account number, to which Bob will transfer some money, and Eve wants to interfere in the communication in such a way that Bob will receive her bank account number believing it is Alice’s one, thus giving his money to Eve. Authentication tags allow to separate the secrecy problem in message transmission from the authentication problem and they are useful even if a secure communication channel is available [1].
In quantum key distribution (QKD) protocols [2] it is fundamental to authenticate classical messages since the communicating agents need an authenticated channel to publish in which basis they prepared/measured their qubits. For such authentication to happen it is assumed that each pair of agents shares an initial small (classical) key that is given at the startup of the quantum network and allows the QKD protocol to bootstrap. The authentication scheme commonly used in QKD is the Wegman–Carter protocol [1], which requires the authentication key to be used only once, and therefore the key needs to be renewed after being used. Assuming ideal conditions, QKD allows the shared key between two agents to be renovated with perfect security and so the agents can communicate with a high level of security for long time. If for some reason this key is lost, the two agents sharing this key cannot communicate securely anymore. We stress that in a realistic scenario, where the quantum communication channels might lose or modify qubits, it may happen that the shared key between the parties is consumed without being renovated by a new QKD round. There are several ways to address this problem. For instance, the parties might meet physically, rely on asymmetric cryptography or communicate via a trusted service in order to share the authentication key. This situation needs careful analysis, as in many cases it is impossible for parties to meet physically or to have trusted services. Moreover, relying on asymmetric cryptography might be a limitation in the future, as it could be broken with quantum computers.
In this paper we address this problem by proposing a scheme for which the conditional entropy of the intruder knowledge over a random string given her observation is greater than the classical case. To this end, we propose an authentication protocol that does not consume the shared key, at the price of having lower security than the one provided by Wegman–Carter scheme. Two approaches are considered. Firstly, a pseudorandom generator is considered to approximate a fair random generator. Note, that even empowered with a quantum computer, and given current knowledge, it is not possible to attack in polynomial-time the proposed protocol. For this reason, it should be considered as an alternative to asymmetric cryptography in a situation where the authentication key is about to be lost, and the communication between two agents is threatened. A second approach is to consider almost-random string that consists of a random sequence where ℓ out of k bits, with , are determined by knowing the seed (or key) and the remaining bits are pure random numbers. The idea is to consider ℓ large enough so that if Eve wants to interfere with the protocol she will be detected with high probability. On the other hand, it should be small enough in order to have small keys. Moreover, by using the proposed protocols, QKD becomes a fully quantum protocol. The proposed protocol will work with noisy channels, assuming that a few blocks of qubits of size k are able to be sent without (or with negligible) noise, even if the majority of these blocks are lost. Our protocol takes advantage of a quantum channel to increase the entropy of the random string, from the intruder’s point of view, in the computationally secure scheme by Brassard [3] for classical authentication. This scheme is presently used in classical authentication schemes [4,5,6]. Note that Brassard’s scheme is itself a modification of the Wegman–Carter protocol, and therefore it is a natural candidate for application in QKD. Brassard showed that a relatively short seed of a pseudorandom generator (PRG) can be used as a secret key shared between Alice and Bob that will allow the exchange of at least computationally-secure authentication tags. We extend Brassard’s protocol to include quantum-encoded authentication tags, and, as expected, we show that our approach attains higher security than Brassard’s scheme by using the fact that quantum encoding scheme has higher entropy from the intruder’s point of view.
It is essential to consider PRGs or almost-random generators (ARGs) and not random generators based on thermal noise (or other methods), as the strings generated by the latter cannot be predicted by two physically separated parties, even if they share some kind of key. The security of modern PRG’s is based on the alleged hardness of some problems of number theory, e.g., the factorization of a large Blum integer, such as the Blum–Blum–Shub PRG [7]. However, most of the research concerning attacking PRGs has been focused in distinguishing with some advantage the pseudorandom generated string from a uniformly generated one [7] and not to recover the PRG seed (the latter problem is harder than the former [8]). The problem becomes much harder if this generated string is encoded in a quantum channel and the adversary can only access the generated string with a certain level of uncertainty (and might not even know the large Blum integer to factor). In this case, even in the possession of an oracle/quantum computer that is able to solve these hard problems, it is not obvious how to recover efficiently the seed of a PRG given a noisy generated string of polynomial size or to obtain any probabilistic advantage to predict the next bit. There have been several results addressing the use of PRG’s and public-key cryptosystems (PKC) together with quantum cryptography [9,10,11]. It is even well known that there exist PKC’s if and only if there exist PRG’s [12]. However, as discussed above, for this equivalence to hold, the setup of the PRG must be known by the attacker (for instance the Blum integer must be known by the attacker in the Blum–Blum–Shub PRG), where this setup is the PRG counterpart of the public key in the PKC. In our approach, we assume that this setup is not known by the attacker, which essentially is equivalent to considering that the public key of the cryptosystem is not known by the attacker. By hiding the public key in a PKC, the system becomes a simple symmetric cryptosystem. Thus, the hardness of attacking a PRG where such setup is unknown to the attacker is at the same level of attacking a symmetric cryptosystem.
For the results in this paper, we have used several concepts and theorems from information theory (Cover and Thomas [13]), whose notation is adopted in the entire paper. In the following comments about channel models, and stand for the entropy of the random variable X and the mutual information between random variables X and Y, respectively. Two different models are considered to set fundamental limits on communication secrecy. In the first model, Alice and Bob share a secret key K used by Alice to create a cipher text C as a function of the message M, and Eve is assumed to receive an identical copy of C (which means she owns a noiseless channel). Unconditional security is defined by . The second model, introduced by Wyner [14], assumes noisy channels and no a priori secret key. A secrecy capacity is defined to be the largest transmission rate such that Bob’s decoding error is arbitrarily small and Eve’s equivocation rate [15] is arbitrarily close to the transmission rate. It is noticed that the result due to Shannon for the first model is a very negative result in contrast with the results obtained for the second one, namely the wiretap channel model [14]. Concerning message authentication, only the first (noiseless) model was studied by Simmons’s work [16]. However, recently Poor et al. [17] introduced new limits for message authentication based on the second (noisy) model. We note that Brassard’s proposal concerns the first model (noiseless), whereas our generalization is dealing with the second model. This is because quantum channels are noisy from the point of view of the attacker (Eve cannot read perfectly from a noisy quantum channel).
The paper is organized as follows. In Section 2 we present preliminary results concerning Brassard’s protocol. In Section 3 we discuss how quantum encoding increases the equivocation from the adversary’s point of view, even when PRG’s are used instead of fair coin tossing. In Section 4, we show that by changing the hash function with the generated PRG we improve the security of the scheme, and we finish by discussing the robustness of the proposed authentication scheme under noisy channels.
2. Preliminary Results
In this section we set up basic notation, briefly review Brassard’s protocol and describe our proposal. We conclude the section with a negative result on the robustness of an attackable PRG when its output is hidden by a specific quantum coding.
We denote the set of messages and the set of tags, where . As hash functions are an important ingredient for all protocols described here we start by presenting their formal definition [18]:
Definition 2.1 (almost strongly universal-2 hash functions)Let and be finite sets and call functions from to hash functions. Let ε be a positive real number. A set of hash functions is almost strongly universal-2 if the following two conditions are satisfied
- (1)
- The number of hash functions in that takes an arbitrary to an arbitrary is exactly
- (2)
- The fraction of those functions that also takes in to an arbitrary (possibly equal to T) is no more than
The number ε is related to the probability of guessing the correct tag with respect to an arbitrary message Y. Notice that the smaller ε is, the larger is.
For additional details on universal-2 functions we refer the reader to [1].
Brassard’s protocol (see Figure 1) makes use of two secret keys. The first one, specifies a fixed universal-2 hash function where The second specifies the seed , for a PRG, a sequence of n bits. Observe that Brassard’s protocol is a weakening of the Wegnar–Carter protocol [1] where pure random number are replaced by PRG’s at the price of loosing perfect security but making the protocol much more practical. The main advantage of our first quantum-enhanced protocol proposed here (see Figure 2) is replacing the classical gate XOR of Brassard’s protocol with a quantum coder (QC) similar to that used in the BB84 protocol [2]. As we shall see later on, the key may be discarded. Assume that Alice and Bob agree on two orthonormal bases and for the 2-dimensional Hilbert space,
These bases will be used to prepare four quantum states. We shall refer to this preparation process as quantum coding. For each bit of the bits long tag , Alice prepares a quantum state determined by the bit from the PRG and the corresponding bit of 2-radix representation of the tag Then, if the bit Alice prepares using basis , such that
Similarly, if the bit , Alice prepares using basis , such that
After qubit generation, Alice sends the separable state to Bob through a noiseless quantum channel and the message Y through an unauthenticated classical channel. At reception, Bob performs measurements to obtain a sequence of k bits from the quantum encoded version of For the i-th received qubit, Bob measures it using the basis or depending on whether the i-th bit of X is 0 or 1, respectively, in that way a k-bit long string will be recovered.
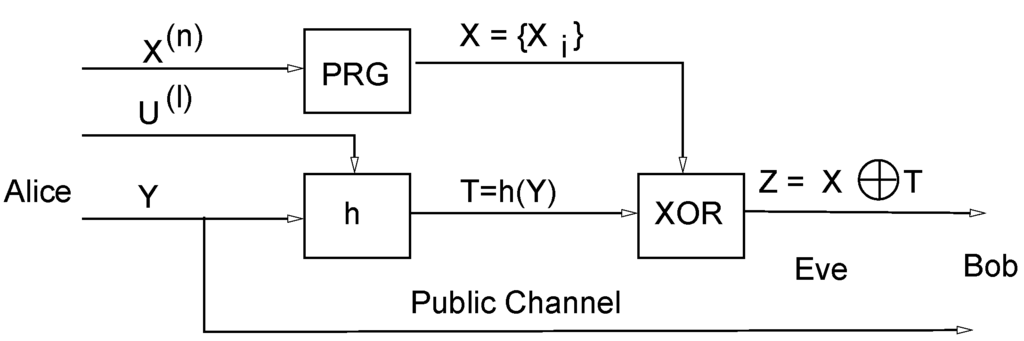
Figure 1.
Brassard’s classical authentication protocol [3].
Because the quantum channel is assumed to be perfect, Bob recognizes that the message is authentic if , where is the message received from the classical channel. Otherwise, Bob assumes that Eve tried to send him an unauthentic message. This concludes the authentication protocol for one message. Throughout this article it is always assumed that the above coding rule is public.
Even though we assume for the moment a noise-free quantum channel, we observe that if the quantum channel is noisy, the only piece of information requiring error-protecting codes is the block of bits of the tag . The sequence of bases to be prepared by Alice and Bob is known a priori, determined locally by the sequence of bits from the PRG. We leave for future work the evaluation of the effects of error-correcting codes on the bits of .
In a warning against alleged collective attacks, we notice that our analysis allows Eve to make general attacks (suggested in Figure 2 by the block labeled as POVM) without being detected. This assumption agrees with the fact that the channel is noisy and so, we do not distinguish between noise and Eve’s interference. Our results are robust to such powerful assumptions for the attacker. Note that our quantum scheme aims at minimizing the key length for one-way transmission. Another example of such approach is given in [19]. Next we focus on crucial aspects of the PRGs.
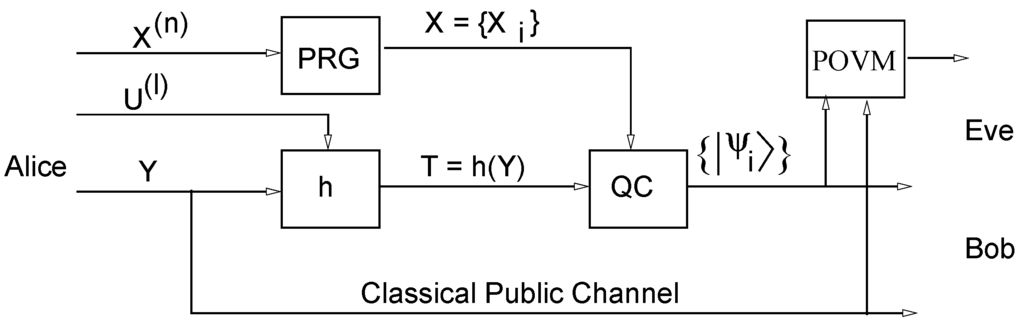
Figure 2.
First proposal of quantum-enhanced authentication scheme.
Weak Pseudorandom Generators
Clearly, it is important to understand how secure the authentication code described above is. As we shall see, the security of the authentication code is deeply related to the quality of the pseudorandom generator. The quality of a pseudorandom generator is evaluated by the hardness to discriminate its pseudorandom sequence output from a truly random sequence or by the hardness to find its seed. The first quality evaluation relates to the PRG’s robustness against distinguishing attacks, the second relates to the so-called state recovery attacks. In [8] it is shown that state recovery attacks are harder than distinguishing attacks.
As a matter of fact, if the pseudorandom generator can be attacked by a quantum computer, so does the authentication code. To set this result we refer to Figure 3, which describes a simple scheme to assist us the proof. In this scheme, we simply allow Eve to compare a sequence of classical bits with the corresponding sequence obtained from the measurement apparatus POVM.
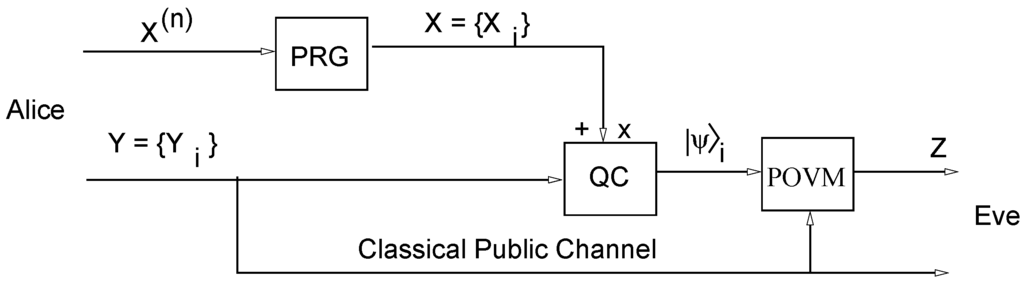
Figure 3.
Scheme for Theorem 2.3.
Recall that a pseudorandom generator is a polynomial-time family of functions where is the set and is the pseudo-generator for seeds with n-bit size, that is, returns the i-th bit generated from n bits long seed . Pseudorandom generators are expected to be indistinguishable from fair coin tossing by a polynomial-time algorithm (more details in [20]). In the following definition we write to denote a subsequence of (not necessarily contiguous) bits generated by
Definition 2.2 We say that a pseudorandom generator G is attackable in (quantum/probabilistic) polynomial time if there exists a (quantum/probabilistic) polynomial time algorithm P and polynomial p such that if P is fed with a subsequence of (not necessarily contiguous) generated bits of G we have that:
For a pseudorandom generator to be attackable, there must exist an algorithm (quantum or probabilistic) that receives a subsequence of generated bits (not necessarily contiguous) and is able to compute the seed up to a negligible uncertainty. We observe that the security/randomness of the pseudorandom generator cannot be grounded in the fact that the attack can only be performed to a contiguous subsequence of generated bits, since the attacker may have access just to a particular set of generated bits. Indeed, if the attack required say, a contiguous subsequences of bits, a simple defense would consist of discarding some generated bits. A simple example of pseudorandom generators that can be attackable in polynomial time is the pseudo-number generator based on linear congruence [8].
Theorem 2.3 If a pseudorandom generator G is attackable in (quantum/probabilistic) polynomial time then the scheme presented in Figure 3 is not secure in polynomial-time for a quantum adversary that has access to .
Proof. Since G is attackable, there exists a quantum polynomial time algorithm P and a polynomial p such that if P is fed with bits of the string X generated by G, then P computes (up to negligible uncertainty) the seed of G. So it is enough to show that Eve, upon capturing the qubits generated by (the quantum coder in page 5), is able to recover (with non-negligible probability) bits of X.
Indeed, assume that Eve has captured qubits and has measured them in a random basis (that is, either the computational or the diagonal basis). Eve can now verify if If this occurs, Eve does not know if the basis chosen to encode the bit was the basis she measured or if she got with probability the correct bit due to encoding in the wrong basis. However, if the outcome is different (that is, ), then she knows that the basis at the i-th bit is the basis she did not choose to measure, because no mismatch would be possible if the encoding was performed with the same basis. In the latter case, she knows that is either 0 or 1 depending if she measured in the diagonal or the computational basis, respectively. Moreover, this happens with probability. So the probability of Eve not to obtain elements of X y measuring qubits is given by the cumulative function of a binomial distribution with Bernoulli trial; trials and success of at most . By Hoeffding’s inequality this probability is upper-bounded by which decreases exponentially with n. In other words, Eve has an exponentially increasing probability of obtaining bits of X with qubits measurements. Since G is attackable by knowing bits of X, Eve is able to perform this attack up to negligible probability. ☐
Corollary 1 If a pseudorandom generator G is attackable, then the scheme presented in Figure 2 is not secure in polynomial-time for a quantum adversary that has access to hash function
Proof. Eve is able to calculate from Y that is public. Therefore she can apply Theorem 2.3 by observing a number N of tags such that ☐
Although Theorem 2.3 points that the quantum coding of Figure 3 is not better asymptotically than the classical coding (where we simply replace the quantum coder by a gate), it seems harder to attack the quantum scheme. We will now show that this is true for the simple case where the encoder is fed by an independent and identically distributed (i.i.d.) fair Bernoulli sequence (a pure random sequence generated by fair coin tossing). The following example illustrates that this is true even for a very simple generator.
Example 2.4 (State Recovery Attack for Linear Congruential Generator(LCG)) Let A be a positive integer and the set of integers modulo The seed of the LCG is the vector , where . The length of the seed is . A binary pseudorandom sequence with length bits is obtained from the 2-radix expansion of the sequence created by the following recursion:
It is well known (see [8]) that for all , the numbers
are multiple of A. As a consequence, the greatest common divisor of some gives the value of A. The rest of the seed, that is and , follow then from a system of linear equations. In practice five values of are enough.
Figure 4 (right) displays a simplified version of the scheme shown in Figure 3, where X stands for the pseudorandom sequence from the output of the PRG. The left side of Figure 4 displays the situation when a gate XOR is utilized. We notice that the state recovery attack is applicable without change to the XOR-based scheme. It is enough to compute before applying the algorithm. In contrast, for the quantum scheme, Eve has an irreducible uncertainty on the X values due to quantum coding. In particular, if she employs the procedure described in the proof of the Theorem 2.3 it is expected only one fourth of the X’s to be correct. The problem from Eve’s point of view is how to solve the seed from a degraded version of the algorithm input X.
3. Comparing XOR with Quantum Coding
In the last section we have considered the problem of the state recovering attack and defined the weakness of a PRG. In this section we make a rigorous comparison between the XOR and the quantum coding performances using information-theoretical measures.
To this end, consider Figure 4 where both classical and quantum encodings are displayed. The denotes the quantum encoder defined before, in (1) and (2), where X is the variable that sets the basis. The block POVM stands for the measurement apparatus defined by the positive operator-valued measure
where O is the set of outcomes. Observe that the measurement may depend on the message Y, which is public. The goal of Eve is to maximize the knowledge of X, that is, minimize the entropy .
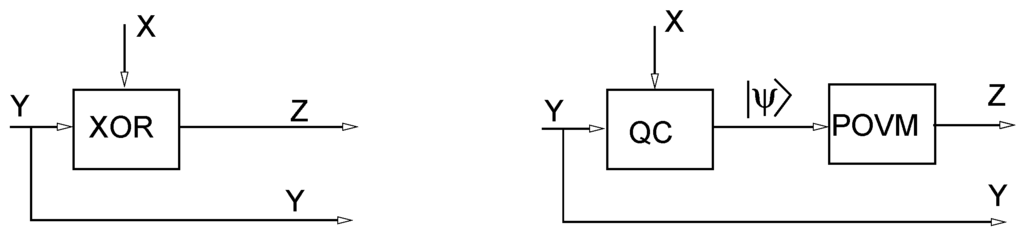
Figure 4.
XOR (left) and quantum coding (right).
We consider the classical and quantum scheme presented in Figure 4 in two ways: firstly, we will assume that X is a sequence of fair and independent Bernoulli random variables, that is, the PRG describing X is perfect; secondly, we consider a biased PRG (unfair) to describe X and introduce blocks of random variables into the analysis.
3.1. Fair Input Single-Sized Block
We start with the simple case of a single-sized block and where . In the classical XOR encoding case we have that and thus . So, Eve has no doubt about X. In the quantum encoding case, we begin by observing that one can compute easily the von Neumann entropy of . Therefore we have:
Theorem 3.1 Following the notation in Figure 4 (right), the minimum uncertainty for X given Z and Y is
where is given by (4).
Proof. The Holevo bound states that
where is the density operator that describes the encoding done by in the following way:
where , , and . Since there are only pure states in the sum of (6) we can simplify that to
However, it is easy to verify that the Holevo bound can be achieved by a simple von Neumann measurement ([21], p. 421) described by the Hermitian operator
with , and . Therefore we have indeed
yielding the maximum accessible information to Eve. Therefore, since and , the minimum uncertainty that Eve may attain about X is given by
☐
3.2. Fair Input k-Blocks
First, consider the classical setup, then , since the block is completely determined from the knowledge of and .
For the quantum setup, the subsystem that Eve owns is described by
By the Holevo bound we get that
Example 3.2 Table 1 illustrates the scenario for . Rows are indexed by the four possible values of and columns are indexed by the bases corresponding to the four values of Notice that Eve is not able to distinguish which column is being used. Then, her uncertainty is lower bounded by the von Neumann entropy of the quantum system formed by states listed in row indexed by the values of that she can access.

Table 1.
Encoding for blocks of length 2.
| Bases | ||||
|---|---|---|---|---|
| 00 | ||||
| 01 | ||||
| 10 | ||||
| 11 | ||||
In order to get a bound for in Equation (14), we need to recall the following property concerning the von Neumann entropy [22].
Property 3.3 Let ρ and σ be quantum states; then
As a consequence of Equation (13) and Property 3.3, for a sequence of fair Bernoulli trials we have
where is given by (11). So, from Equation (14), we have that
Again, the equality can be achieved by a simple von Neumann measurement, namely that defined by . We summarize the results from the prior discussion in the following theorem.
Theorem 3.4 (Generalization of Theorem 3.1) Following the notation in Figure 4 (right), the minimum uncertainty for k-blocks given and is
This is the best scenario one can imagine to defeat Eve. However, for the protocol to be practical, the should be generated by a PRG, which is the case we examine next.
3.3. Unfair Input k-Blocks
The results above were obtained assuming that was a sequence of i.i.d. fair Bernoulli random variables. In this section we study the general case, with the purpose of clarifying how the use of a real PRG affects the uncertainty about X. Our main point is to stress that even when using PRG, the uncertainty given by remains positive, contrarily to the classical XOR encoding case where (since ). As expected, we show that the uncertainty is directly proportional to the size of the seed of the PRG under reasonable assumptions.
Consider k-length blocks and where is a contiguous subsequence of and similarly to and Note that, to ease notation, we omit the index i in defining However, it is crucial to remark that the probability distribution of is, in general, dependent on i. As a matter of fact, can even degenerate to a distribution with a single component equal to 1, depending on the robustness of the PRG. We shall simplify the notation denoting by . We consider that a PRG is as robust as possible, that is, with a seed of size s the PRG generates precisely blocks of size k with . Note that this assumption is more than acceptable as k should be much larger than s. Thus, for some indexes and if . Thanks to the fact that only sequences are generated by the PRG among the possible sequences, we can rewrite, by change of basis, as
where the states
and is the i-th bit of the binary representation of j. Observe that in this case we have
since in this basis, by knowing and , there is no uncertainty in the last qubits. So if the PRG has a seed of size s, we can see the pseudorandom string of size k as one string where the first s bits are completely random and the last bits are fixed. Then, by Theorem 3.4 we have that
Therefore, we can conclude that the quantum encoding protects better the secret than the classical one, even in the presence of PRG’s. In the next section we further improve the scheme by exploiting the uncertainty derived above. As we shall see, the entropy given in (19) is the upper-bound for the equivocation caused by the noise in the channel between Alice an Bob (which includes Eve’s intervention) for the proposed scheme to work in practice.
Note that in the original scheme by Brassard (see Figure 1) the stream Y is hashed before being ed and so, if we consider the full encryption scheme, the total entropy for the eavesdropper is
for s large enough. For the quantum scheme, (see Figure 2) the stream Y is also hashed before being quantum encoded. In this case the total entropy for the eavesdropper is
for s large enough. Note that we are able to make the equivocation (conditional entropy) dependent on the size of the seed of the PRG and, in the quantum case the equivocation is greater than in the classical case.
3.4. Almost Fair Input k-Blocks
The above unfair case renders the authentication to be only computationally secure, as its security relies only on the size of the seed. In order to improve this result we have considered almost-random sequences instead of pseudorandom sequences. In an almost-random sequence of size k all the bits are random with exception of ℓ control bits. So, contrarily to a pseudorandom generator where all the k-long sequence depends on the seed, in almost-random sequences only some control bits depend on the key. Indeed, to represent ℓ bits in a k long almost-random sequence we need a key with bits.
Our aim is to estimate the minimal uncertainty of the eavesdropped in the case that X is an almost-random sequence. When Alice and Bob use the scheme in Figure 3 with an almost-random sequence X, a full message of size k is authenticated, but only ℓ control bits are used to check whether the message is authentic. Since the eavesdropper does not know in which positions the control bits are, if he randomly changes the sequence he would alter, with very high probability, at least one of these bits and therefore, he will be detected. The good thing is that the entropy of the almost-random sequence is much higher than the entropy of the pseudorandom sequence, since only ℓ bits are constrained given the key.
Actually, an almost fair random sequence is a sequence produced as an output of random-number generator in a way that if we compare its two output sequences from the same key, only ℓ out of total k bits () are going to be the same and other are going to be totally uncorrelated (which means that from knowing the key we are able to get the values of only ℓ bits as well as their positions). Thus, if Eve has no knowledge about the seed, then her uncertainty concerning given and is precisely the same as that in the case of fair random sequences. This is so because all generated bits of are random, and not pseudorandom, even for the ℓ control bits that used to authenticate, and so we have that the minimum conditional entropy is given by
Note, however, that this result comes with the price of Eve being able to change several qubits without being detected. She does not know a priori in which position control qubits are going to occur; and so, if she risks too much then she will be detected. It remains to understand what is the probability that Eve can modify the quantum channel without being detected. Indeed, if we assume that Eve needs to modify s bits in order to make the attack, then the probability of her not being detected can be computed by
where and . First we notice that by applying McLauren approximation to (23)
for a positive x close to zero, we have
Introducing the substitution , we obtain:
where is the k-th harmonic number. By using the approximation for the harmonic sum (where γ is the Euler–Mascheroni constant), we obtain the final expression
This expression states that the probability for an eavesdropper not to be detected decreases exponentially with ℓ.
4. Improving Key-Tag Secrecy
In the last section we compared Eve’s equivocation on X for the and schemes when she has access both to the message Y and its quantum encoded version, which she observes from the quantum channel. We concluded that the equivocation is kept above some lower bound depending on the size of the seed of the PRG. In this section we include a hash function h in the scheme (see Figure 5) in such a way that Eve only accesses the public message Y and the quantum encoded version of the tag . Thanks to that modification we shall demonstrate that is feasible to improve the secrecy of the key and of the tag simultaneously. Note that if the random string was truly random (and not pseudorandom) then the whole construction yields perfectly secure authentication even if the secret almost strong 2-universal function is used many times [1]. However, we are not using truly random strings, and as we shall see, by changing the hash function as the pseudorandom string is generated we improve the security of the scheme.
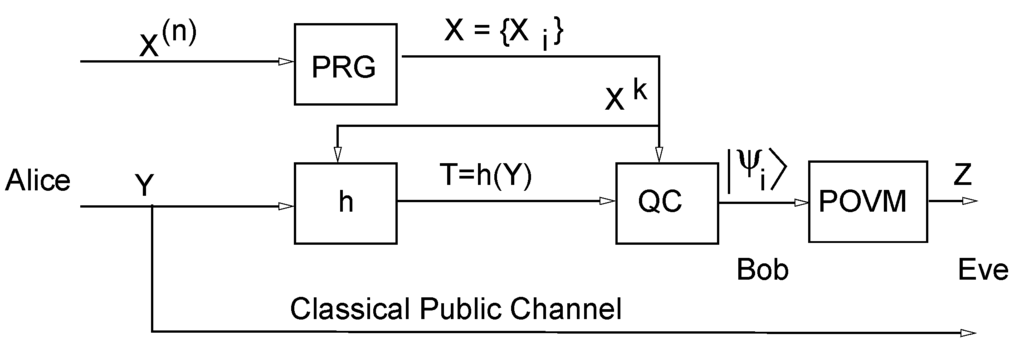
Figure 5.
Authentication scheme with a single key .
By information-theoretic secrecy, as usually, we mean or equivalently, the equivocation , where W is the secret to be protected and V is the piece of data available to the eavesdropper. Our derivations will focus on the equivocation to measure the quality of the scheme. Then, the information to be protected is and the information available, from Eve’s viewpoint, is . We investigate the uncertainty of the tag and the uncertainty of the key .
We assume that is independent of the message Y and that the hash function is selected from the almost strongly universal-2 class of hash functions, which we refer in the following just as hash functions.
4.1. Modified Classical Case
Consider a simple modified setup where a gate is taken in place of the block in the scheme displayed in Figure 5.
If is a fair Bernoulli sequence and a k-block of bits such that
it is utilized per message, then the scheme turns to be equivalent to the Wegman–Carter scheme. Indeed, in this situation h is in fact drawn uniformly from . Then we have
Equality is due to the chain rule for Shannon entropy, is due to the fact that in the classical setup it is known that . The equality (c) is harder to obtain, indeed it follows from the properties of the almost universal-2 class of hash function. Note that has a uniform distribution. Moreover has also uniform distribution, and therefore, T is independent of . Since we have that . Equality is also due to the properties of hash functions. On the other hand, if comes from a PRG, the Eve’s uncertainty on the tag can, eventually, decreases by observing the random variable . Indeed, in general, . Consequently, unconditional secrecy relative to T, cannot be assured.
4.2. Uncertainty of the Tag in the Quantum Case
We start by giving a condition to attain unconditional security of the tag in terms of the conditioned mutual information between T and the block of bits of the key. This condition will motivate our final proposal for the authentication protocol.
Theorem 4.1 If then the tag is secure in the information theoretical sense, that is, .
Proof.
From the standard chain rule for Shannon entropy we have:
Then, comparing (32) and (33) we obtain
Equality is due to a simple manipulation of (32) and (33), is definition of mutual information and follows because the hash function is determined by and so, then is immediately calculated. That is, The results follows from (36). ☐
Observe that Equation (36) clearly indicates that in order to increase Eve’s uncertainty about T, we must maximize the mutual information between the block and the tag T. This is the information-theoretical intuition that motivates the scheme presented in Figure 5. Note that in this case we make the tag T dependent of , thus increasing their mutual information. In Brassard scheme (see Figure 1) the hash function is fixed in the beginning, and therefore where is the observation that Eve can perform in Brassard’s scheme.
Now we can compare the scheme from Figure 5 with that in Figure 2. For the latter recall Equation (21) and note that the key for Alice and Bob is the seed s together with a chosen hash function, which has to be encoded in bits. However for the scheme in Figure 5 we only have one key and for this key it is straightforward to derive the following entropy bounds following the same reasoning as in Section 3
which improve those in (21) since .
4.3. Robustness of the Protocol under Noisy Quantum Channels
As we discussed in the introduction, one of the points of the protocol proposed in Figure 5 is to address the scenario where the quantum communication channels have noise. In this case, the shared key might be lost and therefore there is no way to bootstrap a new QKD round. Considering noise, we now discuss how the protocol copes with the quantum channel erasing qubits or modifying them.
When qubits are removed from the channel, Bob will lose the corresponding message authentication tag for a given message, and therefore the authentication will be lost. As usual, to avoid this problem Alice and Bob have to make synchronous emissions of qubits in such a way that Bob knows the time each qubit should arrive. This measure requires Alice and Bob to have a synchronous clock. If a qubit is lost, Bob can disregard it (assuming the message has enough redundancy) and tell this fact afterwards to Alice. Another option is to send through the public channel the list of qubits that were not received (authenticated with those that were). If qubits are added by an attacker, then Bob can also disregard them if they arrive out of schedule.
In the case qubits are modified by the channel, it is well known that if the attacker Eve has access to a degraded version of the channel between Alice and Bob, even when this channel is not perfect, it is possible to exchange perfectly secure messages between Alice and Bob [14,23]. By the results established in Section 3 and Section 4, namely Equation (37), if the mutual information between messages sent by Alice and received by Bob is higher than , then Alice and Bob can communicate securely regarding Eve, where s is the number of bits of the seed of the PRG that Eve does not known. We formalize this statement in the following result, which follows immediatly from [23] (namely Corollary 2 page 341) and Equation (37).
Corollary 2 Let be the degraded version of observed by Bob caused by noise and let s be the number of bits from the seed of the PRG that Eve does not know. Then, if then Alice and Bob can exchange tags with perfect security at rate smaller than .
Note however that this does not imply that this scheme is perfectly secure, as s decreases while messages are exchanged between Alice and Bob. So, in practice our authentication protocol can be used as follows: (i) estimate the mutual information between messages exchanged between Alice and Bob (that is the noise of the channel); (ii) estimate the information gain concerning the PRG seed that Eve can obtain by analysing blocks of exchanged tags; (iii) choose s large enough such that the mutual information between the message sent by Alice and that received by Bob is always greater than , where is the minimum number of bits of the seed of the PRG that Eve will never known, taking into account (ii) and the number of tags exchanged.
5. Summary
In this work, we have investigated how quantum resources can improve the security of classical message authentication protocols. We have started by showing that a quantum coding of secret bits offers more security than the classical XOR function. Then, we have used this quantum coding to propose a quantum-enhanced protocol to authenticate classical messages, with improved security with respect to the classical scheme introduced by Brassard in 1983. Our protocol is also more practical in the sense that it requires a shorter key than the classical scheme by using the pseudorandom bits to choose the hash function. Finally, we prove that quantum resources can improve both the secrecy of the key generated by the PRG and the secrecy of the tag obtained with a hidden hash function.
The usefulness of our proposal follows from three facts. Firstly, the shared key between Alice and Bob is not consumed while generating the pseudorandom sequence [24], which allows for tentative recovery of the system under noisy channels.
Secondly, even empowered with a quantum computer, it is not known how to attack our protocol in polynomial-time. The latter fact follows since it is very hard to attack a PRG if the generated string is encoded in a quantum channel and the adversary can only access each pseudorandom bit with 1/4 probability, that is, the attacker only knows the pseudorandom sequence with a high level of uncertainty. Moreover, if one assumes the Blum–Blum–Shub PRG and consider that the Blum integer is kept secret between Alice and Bob (which is not assumed in the classical reduction to the quadratic residuosity in [7]), then the attacker would also need to guess this integer, making the attack much harder than if the integer is known. As far as the authors know, there are no results on attacking PRG’s in this case. Moreover, by taking into account the equivalence between the existence of PRG’s and public key cryptosystems, such attack is equivalent to attacking a public-key cryptosystem without having access to the public key, which essentially consists of attacking a symmetric key encryption. Such attack is believed to be much harder than attacking a public-key cryptosystem. The same argument can be used for other PRG’s based on hardness assumptions [25]. In the setting of our protocol, where Alice and Bob start with a shared symmetric private key, there is no reason to assume that such information is known by Eve, since Alice and Bob could privately and secretly choose the Blum integer in the same way they choose the initial shared symmetric key.
Thirdly, by taking into account the noise of the quantum channel, it is possible to choose the size of the seed of the PRG to be large enough so that the equivocation of the attacker (due to the quantum encoding) is larger than that equivocation caused by the noise between Alice and Bob (and assuming the attacker has access to the channel near Alice, that is, without noise). In such a case, and while the attacker cannot discover enough bits of the PRG, the communication between Alice and Bob remains perfectly secret according to [23].
Finally, we stress that by using the proposed protocol, QKD becomes a fully quantum protocol.
Acknowledgments
F. M. Assis acknowledges partial support from Brazilian National Council for Scientific and Technological Development (CNPq) under Grants No. 302499/2003-2 and CAPES-GRICES No. 160. A. Stojanovic, P. Mateus and Y. Omar thank the support from project IT-QuantTel, as well as from Fundação para a Ciência e a Tecnologia (Portugal), namely through programs POCTI/POCI/PTDC and projects PTDC/EIA/67661/2006 QSec and PTDC/EEA-TEL/103402/2008 QuantPrivTel, partially funded by FEDER (EU).
References and Notes
- Wegman, M.N.; Carter, J.L. New hash functions and their use in authentication and set equality. J. Comput. Syst. Sci. 1981, 22, 265–279. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public-key distribution and coin tossing. In Proceedings of IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 1984; pp. 175–179.
- Brassard, G. On computationally secure authentication tags requiring short secret shared keys. In Advances in Cryptology; Springer-Verlag: New York, NY, USA, 1983; pp. 79–86. [Google Scholar]
- Krawczyk, H. LFSR-based hashing and authentication. In Advances in Cryptology; Springer-Verlag: New York, NY, USA, 1994; pp. 29–42. [Google Scholar]
- Rogaway, P. Bucket hashing and its application to fast messages authentication. In Advances in Cryptology; Springer-Verlag: New York, NY, USA, 1995; pp. 29–42. [Google Scholar]
- Shoup, V. On fast and provably secure message authentication based on universal hashing. In Advances in Cryptology; Springer-Verlag: New York, NY, USA, 1996; pp. 313–328. [Google Scholar]
- Blum, L.; Blum, M.; Shub, M. A simple unpredictable pseudo random number generator. SIAM J. Comput. 1986, 15, 364–383. [Google Scholar] [CrossRef]
- Sidorenko, A.; Shoenmakers, B. State recovery attacks on pseudorandom generators. In Western European Workshop on Research in Cryptology, Lectures Notes in Informatics (LNI); GI: Bonn, Germany, 2005; Volume 74, pp. 53–63. [Google Scholar]
- Alleaume, R.; Bouda, J.; Branciard, C.; Debuisschert, T.; Dianati, M.; Gisin, N.; Godfrey, M.; Grangier, P.; Langer, T.; Leverrier, A.; et al. SECOQC white paper on quantum key distribution and cryptography. arXiv 2007. [Google Scholar]
- Ioannou, L.M.; Mosca, M. A new spin on quantum cryptography: Avoiding trapdoors and embracing public keys. Post-Quantum Cryptography 2011, 7071, 255–274. [Google Scholar]
- Kunz-Jacques, S.; Jouguet, P. Using hash-based signatures to bootstrap quantum key distribution. arXiv 2012. [Google Scholar]
- Goldreich, O. Modern Cryptography, Probabilistic Proofs and Pseudorandomness; Springer: Berlin, Germany, 1999. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Jonh Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Maurer, U.M. Secret key agreement by public discussion from common information. IEEE Trans. Inform. Theor. 1993, 39, 733–742. [Google Scholar] [CrossRef]
- Simmons, G.J. Authentication theory/coding theory. In Proceedings of the CRYPTO 84 on Advances in Cryptology, Santa Barbara, CA, USA, 1984; Springer-Verlag: New York, NY, USA, 1975; pp. 411–431. [Google Scholar]
- Lai, L.; El Gamal, H.; Poor, H.V. Authentication over noisy channels. IEEE Trans. Inform. Theor. 2009, 55, 906–916. [Google Scholar] [CrossRef]
- Cederlörf, J.; Larsson, J. Security aspects of the authentication used in quantum cryptography. IEEE Trans. Inform. Theor. 2008, 54, 1735–1741. [Google Scholar] [CrossRef]
- Damgaard, I.; Pedersen, T.; Salvail, L. On the key-uncertainty of quantum ciphers and the computational security of one-way quantum transmission. arXiv 2004. [Google Scholar]
- Goldreich, O. Foundations of Cryptography: Volume I Basic Tools; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Paris, M.G.A.; Rehácek, J. Lectures Notes in Physics, Quantum State Estimation; Springer: Berlin, Germany, 2004. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Csiszar, I.; Korner, J. Broadcast channels with confidential messages. IEEE Trans. Inform. Theor. 1978, 24, 339–238. [Google Scholar] [CrossRef]
- Although this sequence is cyclic, the cycle is exponential in the size of the seed, and so the standard QKD key maintenance will eventually be restored before the cycle ends.
- A similar analysis can be made to the Blum-Micali PRG assuming the large prime is kept secret [26].
- Blum, M.; Micali, S. How to generate cryptographically strong sequences of pseudorandom bits. SIAM J. Comput. 1984, 13, 850–864. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).