1. Introduction
The demands for innovative solar heat collection and enhanced transport from micro-channel assemblies are outpacing advances in micro-fabrication technology [
1]. The micro-channel assembly represents a promising technology for improved heat collection and transport capabilities. In micro-channel flows, the relationship between pressure gradient, fluid transport, potential difference and electric potential are characterized thermodynamically by the Onsager reciprocal relations [
2]. Effective pumping of fluid through micro and nano-channels is affected by the pressure gradient (pumping mode) and electric potential gradient (generating mode of the driving force) of electro-kinetic operation [
3]. Past studies of these mechanisms [
4] have employed the principles of non-equilibrium thermodynamics. Consequently, increasing attention has been directed to the study of fluid flow and heat transfer in micro-channels, including the effects of slip irreversibilities [
5].
Parallel micro-channels are utilized in the design configuration of fluid flows in micro fuel cells and micro heat sinks for electronic packages. This configuration has been proposed as effective and promising for cooling micro-electronic devices [
6]. Also, increasing attention has been paid to the study of fluid flow and heat transfer characteristics in a single micro-channel [
7,
8]. Consequently, the application of these flow characteristics and heat recovery techniques can be leveraged for developing enhanced heat recovery and sustainable energy conversion systems, especially by using concentrating solar energy technologies. Reducing the exergy destruction of fluid motion through micro-channels can have beneficial impacts by reducing pressure losses and the input power needed for these flow control methods. Although these effects are not of significance in high-temperature applications like solid electrolyte fuel cells and compact heat exchangers, where effective heat recovery is possible for micro-scale treatment of environmental barrier coatings, irreversibility treatments in micro devices can provide efficient designs of other constituent energy systems like micro-channel assemblies in a solar collector. Previous studies by Ogedengbe
et al. [
5] have identified the importance of pressure ratio, channel size perturbation and entropy production in the optimal design of micro-fluidic devices. These studies focused on flow characteristics with irreversibility effects in a single micro-channel. Maxwell’s first-order boundary conditions were imposed explicitly at the wall of the micro-channel. While the interactions of kinetic and thermal energies at the near-wall were analyzed, the effect of the second component of the wall-slip, based on the axial thermal gradient, was not investigated since the problem involves single channel flow. However, with a network of micro-channel assemblies, it is anticipated that this effect will be pronounced, especially when the electro-kinetic phenomenon represents the source term that is responsible for driving the temperature distribution.
In this paper, an experimental configuration is described and numerical studies of the entropy distribution within the influence layer of the charged counter-ions are presented, where an increasing pumping effect of pressure-driven flow with possible electro-kinetic coupling in micro-channel assemblies is established. This configuration enables transport of the heat carrier from a concentrating solar reactor to thermochemical energy conversion and food waste storage/homogenizing subsystems.
2. Electro-Kinetic Phenomena
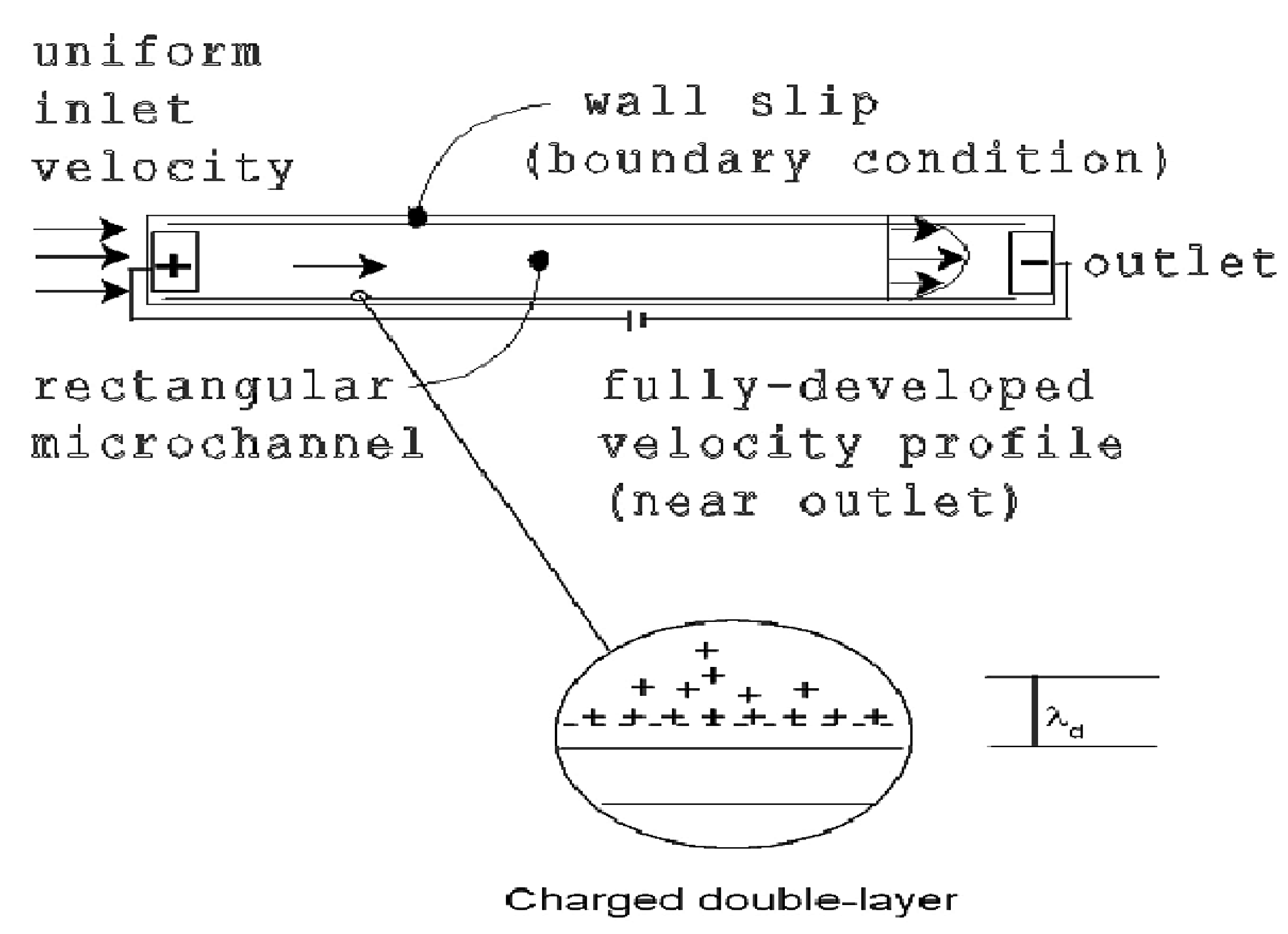
The micro-channel (
Figure 1), within the board of a system-level design, represents a plate topology that can be packaged in a variety of ways. The governing equations for incompressible transport of mass, momentum and energy are as follows [
9]:
Figure 1.
Electro-kinetically driven micro-channel flow schematic.
Figure 1.
Electro-kinetically driven micro-channel flow schematic.
The heat source depicted by the electromagnetic field in Equation (4) directly influences the increasing gradient of temperature at the near-wall of the micro-channel assemblies. The application of micro-channel heat exchangers is desirable for the development of concentrating solar power (CSP) based thermochemical cycles [
10,
11]. Wegeng
et al. [
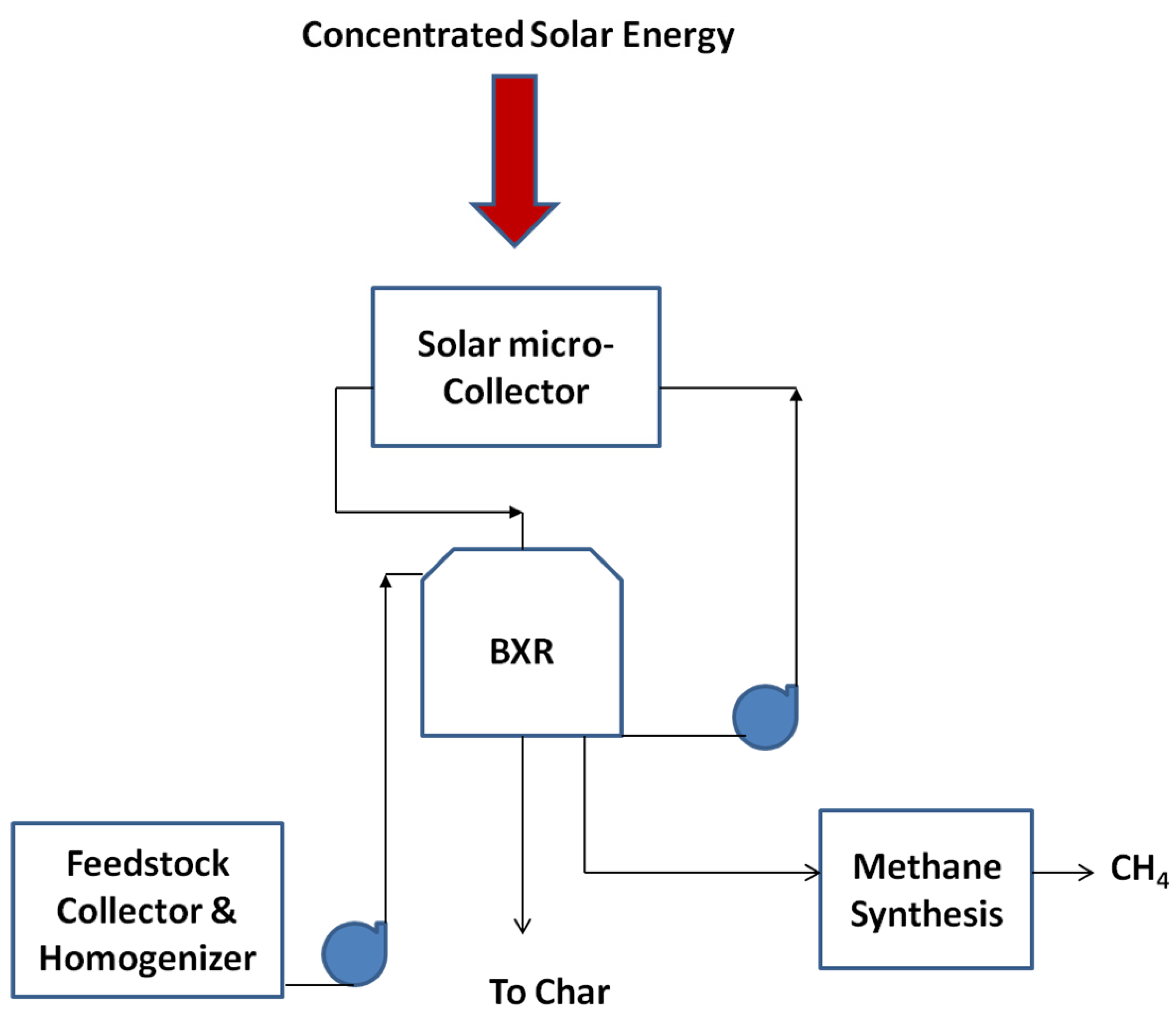
10] studied the feasibility of a CSP-based methane reformer, where solar energy is converted to chemical energy, for storage and power supply to a heat engine. Many methane reforming cycles have been identified based on methane reforming and methanol synthesis, followed by remethanation (for closed-loop cycles) or combustion (for open-loop cycles). However, open-loop cycles are preferred over closed-loop cycles because of their comparative cost advantages over fossil fuel generation cycles. Although derivatives of the open-loop cycles depend on sources of methane and the solar energy boost, the chemical feedstock represents the source of the majority of the energy conversion from methane. The foci of this paper are: (1) the configuration of a bio-digester, accounting for slip irreversibility and its effects on selected thermal and flow parameters, and (2) a review of the electro-kinetic effects, which can enhance the pumping performance of the heat carrier from assemblies of a solar micro-collector to a bio-digester (see
Figure 2). There the thermal energy for thermochemical energy conversion through combustion and gasification of methane-rich biomass is supplied by the carrier between the solar micro-collector and the biodigester.
Figure 2.
Configuration of a CSP-powered Bio-digester (BXR).
Figure 2.
Configuration of a CSP-powered Bio-digester (BXR).
2.1. Slip-Irreversibility
A major concern with slip flow conditions at the near wall in micro-channels (when the Knudsen number is between 0.001 and 0.1) is that the mechanism of exchange between kinetic and thermal energies is often treated in various ways. Since entropy production encompasses both friction and thermal irreversibilities, it provides key insights for enhancing heat exchange without incurring excessive pressure losses that contribute to higher pumping power. Maxwell’s first-order slip velocity [
12] is used for boundary conditions at the walls of the micro-channel. This boundary model incorporates two coefficients, involving both velocity and temperature gradients at the wall,
i.e.:
where
and
.
The coupled conjugate wall boundary conditions [
13]:
are imposed at the solid-fluid interface. All other wall surfaces are treated as adiabatic.
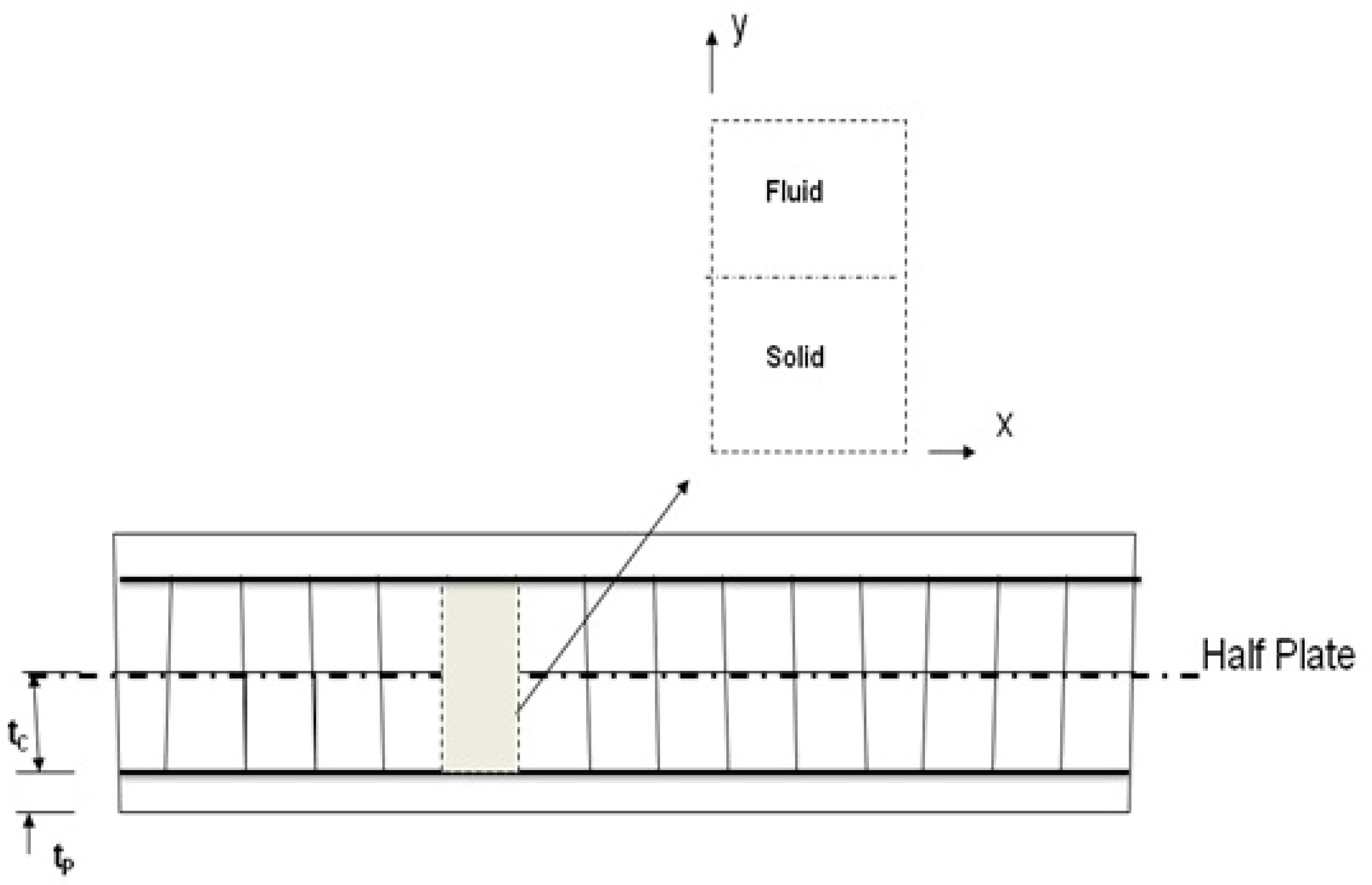
The modelling of the heat and mass equations governing the energy system, within the computational domain for the cross-section of a micro-channel, as depicted in
Figure 3, does not include the quality of the available quantities of energies. The design of energy systems without consideration of the transport of entropy is based on the First Law of Thermodynamics, while Second Law analysis allow for a quality-based design. The next section presents a review of the additional pumping from the potential integration of the electro-magnetic field across the micro-channel.
Figure 3.
Staggered solid-fluid interface of a micro-channel assembly.
Figure 3.
Staggered solid-fluid interface of a micro-channel assembly.
2.2. Electro-Kinetic Pumping
Miniaturization of parallel slots of heat-carrier passages within two half-plates, with the arrangement of the solid and fluid sections staggered as shown in
Figure 3, enables the application of non-linear electro-kinetic phenomena into the study of the micro-channel assemblies. The main challenge is the fundamental gaps in the understanding of induced-charge electro-kinetic phenomena [
14], especially with high concentration molten-salt as the heat-carrier from the solar micro-collector. Bazant
et al. [
14] proposed mean-field electro-hydrodynamic models, based on the Poisson-Nernst-Planck and Navier-Stokes equations, otherwise known as the modified Poisson-Boltzmann theories (MPB). These classical equations provide a useful first approximation for understanding micro-channel transport phenomena, such as charge selectivity [
15,
16], mechanical-to-electrical power conversion efficiency [
4], current-voltage characteristics [
17], and non-linear ion-profile dynamics [
18,
19]. However, many researchers have adopted diverse variants of the combined
mean-field and
local density approximations (MF-LDA) for continuum modelling of the MPB.
Among other efforts in developing the key concepts of the MPB approach, it appears that Bikerman [
20] was the first to complete the MPB model with steric effects in the electrolyte phase. The effects are captured within the diffuse (double) layer thickness or the Debye-Huckel screening length, λ
d, where:
That model corresponds to an excess chemical potential associated with the entropy of the fluid,
i.e.:
where
is the local volume fraction of solvated ions on the lattice [
21]. Assumming a symmetric binary electrolyte, where
=
,
, the ion profiles in the underlying lattice-gas model for excluded volume obey Fermi-Dirac statistics [
14],
i.e.:
where
is the bulk volume fraction of solvated ions. The equilibrium ion distribution expressed in Equation (10) is substituted into Poisson’s equation in order to obtain the Bikerman MPB equation, as follows:
3. Exergetic Analysis
The Second Law describes the irreversibility within the boundaries of energy and other systems. Due consideration of this law in addition to the First Law can provide better assessments of the quality of available thermal energy recoverable via the serving stream of conjugate micro devices. These two laws of thermodynamics can be written as [
22]:
and:
By eliminating
from Equations (12) and (13), the work rate output can be maximized as:
Since cannot be negative, the maximum possible work from the system is obtained at the minimum value of , which known as the lost available work via the Gouy-Stodola theorem. In order to understand the application of this theorem to conjugate heat transfer design, it is useful to comprehend the process of entropy generation via the interaction of the streams with the walls.
System optimization can be aided by exergy analysis for all energy systems where the power or refrigeration effect is operational. In this case and as it applies to heat transfer design, the First Law, which deals with the conservation of energy is not adequate, in order to capture the heat and work interaction through the conjugate system.
From the First Law (using the statements of the First and Second Laws for a one-dimentional heat transfer duct, as developed by Bejan [
23]):
Assuming steady state conditions with no work and heat interaction with the environment, the Second Law states that:
Here, the
sign denotes either the hot or cold stream of the heat exchanger. Now, the canonical entropy relationship states that:
Therefore, the entropy generation term, after linking Equations (15-17), can be expressed as:
where
, the dimensionless temperature difference. This equation reveals the two basic components of entropy generation: the temperature gradient term and the pressure gradient term. Since heat transfer is directly proportional to the temperature gradient, the entropy generation rate for the thermal component is proportional to the square of the dimensionless temperature difference. This term plays a vital role in the minimization of the generation of entropy within the energy system. The importance of entropy generation to the design of energy systems can be significant, even with micro devices, especially when incorporating the thermal-kinetic energy influence of slip at the near wall at the micro-scale.
3.1. CSP-Powered Bio-Digester Subsystems
There are different options for the design of heat exchanger for the transport of the heat of formation required for the thermo-chemical energy conversion in the bio-digester, including shell and tube, helical coil, and printed circuit heat exchangers [
24]. Amongst these options, the printed circuit heat exchanger is preferred because of its application of microchannels. Printed circuit heat exchanger and microchannel have been proposed for use in high temperature nuclear reactors using helium and molten salt as the heat transfer media [
25]. Printed circuit heat exchangers are based on chemically etching plate sheets and joining the sheets by diffusion bonding. Electro-kinetic pumping with slip-irreversibility effects is anticipated to provide an enhanced heat transfer efficiency of the entire system assemblies.
Figure 2 shows a schematic of the CSP-powered bio-digester as an assembly of subsystems, including solar micro-collector, downdraft bio-digester (gasifier), feedstock collector/ homogenizer, and methane synthetizer, for a university cafeteria (see
Figure 4). Unlike CSP-based thermochemical cycles, where the concentrated thermal energy is utilized directly for the thermochemical energy conversion process, heat is carried away from the solar micro-collector for use in other subsystems, like the downdraft bio-digester and the feedstock collector/homogenizer. While heat losses due to irreversible effects during transport are inevitable, a technical solution that offers energy conversion from bio-degradable waste would be preferable to the thermochemical system where a processed fuel like methane is required for operation.
Figure 4.
University cafeteria complex.
Figure 4.
University cafeteria complex.
Biomass gasification is the subprocess that utilizes the bulk of the heat from the solar micro-collector, mainly for thermochemical conversion. The conversion is achieved by reactions between a feed gas and a feedstock. The primary goal of biomass gasification is the optimal energy conversion of the solid biomass into a combustible gaseous product. In a gasifier, there are three main thermal conversion layers, namely the combustion zone, the pyrolysis zone and the reduction zone. In a downdraft fixed bed, the biomass undergoes combustion, pyrolysis and gasification in sequence. Wang and Kinoshita [
26] studied the char reduction reactions and observed that, being a surface phenomena, the overall biomass gasification rate can be controlled by the char reduction zone. The reaction temperature, the residence time and thus the volume of the reaction zone decide the reaction rates and their direction and thus the calorific value of gas as well as the efficiency of conversion. In order to obtain the optimal energy conversion, it is important to understand the chemistry of heterogeneous and homogeneous reactions taking place in the downdraft biomass gasifier and specifically in the reduction zone. The heat carried from the solar micro-collector subsystem is exchanged at the wall of the gasifier chamber, through consideration of the irreversibility of the exchange between flow kinetic and thermal energy at the outer surface of the chamber.
The preconditioning of the organic feedstock or food waste enables control of the efficiency of the thermochemical energy conversion process in the gasifier. The food waste is fed into the gasifier as a moisture-rich liquid, known as a slurry. This process requires the design of a thermally controlled storage and homogenizing subsystem, where the time lag between food waste collection and its digestion is automated. The production of methane depends on the capacities of the methane synthesizer and the gasifier subsystems, which are designed based on the estimated supply of the food waste. Mansour [
27] estimated that 10 kg of kitchen waste produces 1.5 m
3 of biogas, which consists of 1 m
3 of methane. An energy audit of the university cafeteria and the energy input proposed for the integration of the CSP-powered bio-digester project was conducted by Ogedengbe
et al. [
28]. A multivariate energy consumption model was proposed as a significant design tool, based on an understanding of energy demand and the supply.
Figure 5 shows the daily production of methane, based on the system efficiency of Mansour’s system. It implies that 319.77 kg of the food waste daily will produce 31.97 m
3 of methane daily from Monday to Saturday, while on Sunday 150.48 kg of food waste will produce 15.48 m
3 of methane, resulting in an estimated monthly methane production of 200 m
3.
Figure 5.
Estimated volume of methane production.
Figure 5.
Estimated volume of methane production.
3.2. Entropy-Based Finite Volume Approach
The balance of entropy for a control volume can be written as [
5]:
where
is the entropy production rate (per unit volume). When this entropy production rate is multiplied by the reference-environment temperature, it represents the local rate of exergy destruction,
, per unit volume. Using the Gibbs equation, it can be shown that the rate of exergy destruction for micro-channel flows can be written directly in terms of both the velocity and temperature gradients as follows:
Thus, wall slip in Equation (5) affects the velocity and temperature profiles, yielding the volumetric exergy destruction rate expressed in Equation (20). This frictional dissipation of kinetic energy leads to pressure losses in micro-channels, which depend on thermal convection and streamwise temperature gradients, as outlined in Equation (5).
A finite volume method was developed based on the conjugate conduction of thermal energy across the wall boundary separating the two fluid streams. By integrating each conservation equation over the discrete control volume, algebraic equations are obtained in terms of nodal variables. An iterative solver was used to solve these resulting algebraic equations.
Using the resulting velocity field solutions, exergy losses are calculated based on Equation (20). Performing spatial differencing of Equation (20), the exergy destruction rate per unit volume at node P becomes:
where Δ
x and Δ
y refer to the grid spacing in the
x and
y directions, respectively; and N, S, E and W denote the north, south, east and west faces of each finite volume. All terms in Equation (21) remain positive since they are sums of squared terms. Physically, mechanical energy is irreversibly dissipated to internal energy through fluid friction, which produces entropy and requires additional input power to overcome pressure losses through the micro-channel. Reducing entropy production from thermo-fluid irreversibilities in micro-fluidic devices can provide useful benefits like improving the efficiency of energy utilization within the overall system and pinpointing the locations, causes and types of thermodynamic losses. In the next section, numerical results from micro-channel flow simulations will be presented and discussed.
4. Numerical Analysis and Results
Numerical predictions of gas flows in micro-channels having thermo-physical properties as shown in
Table 1 are presented in this section. The simulations for the stream are studied with various grid configurations and with grid independence verified.
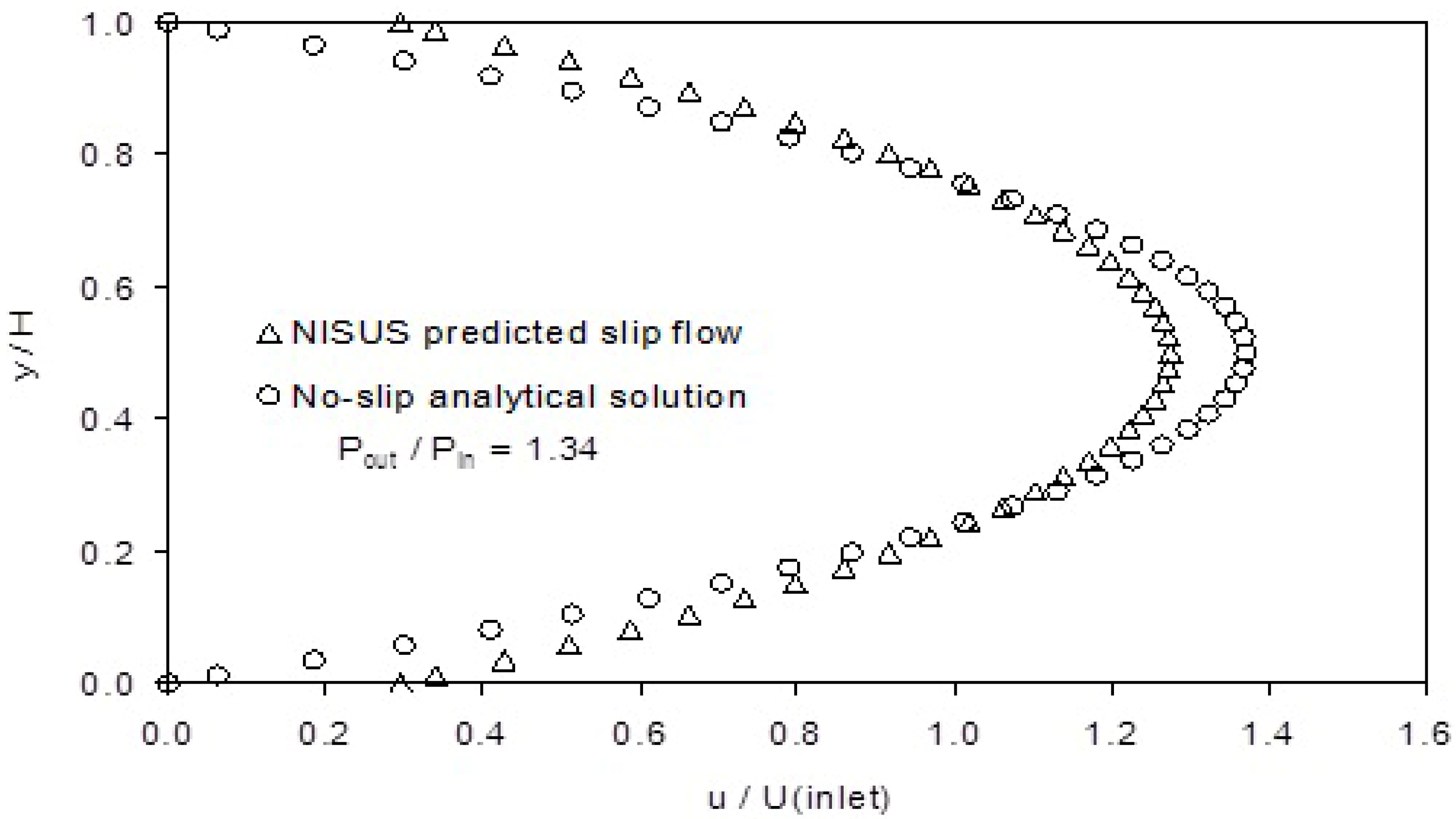
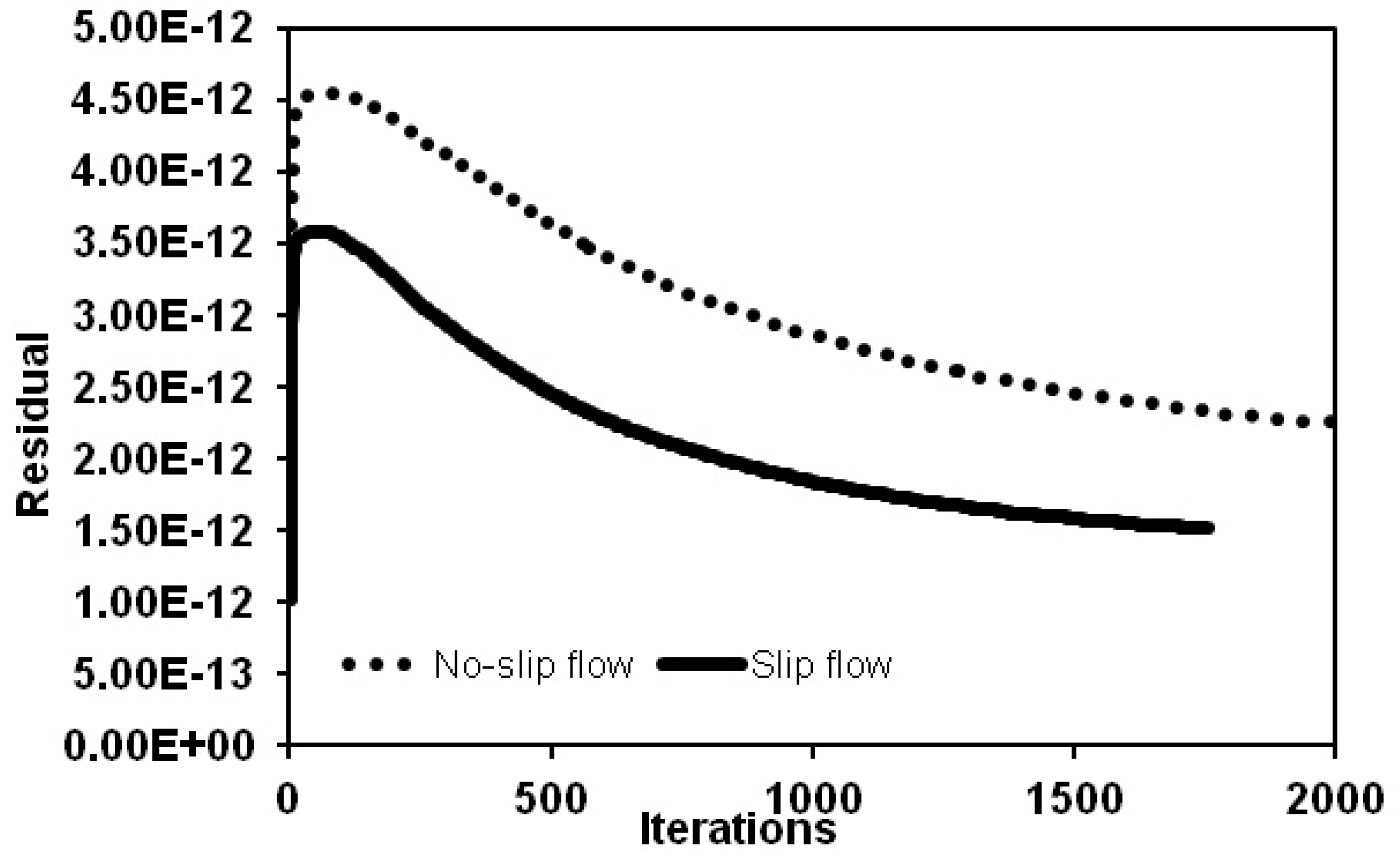
Figure 6 validates the predicted velocity profile within a channel by comparing results with analytical results. A slip scale of about 0.3 is observed at a pressure ratio of 1.34 and the profile agrees with analytical results, exhibiting errors of about 1% at the near-wall of the channel. The reduction of the maximum velocity for the slip profile appears to be due to the thermal-kinetic energy exchange at the boundary of the micro-channels. Slip irreversibility effects also increase the need for computational resources at the region of the flow where the greatest gradients of flow variables are experienced, as shown in
Figure 7.
Table 1.
Model thermo-physical properties.
Table 1.
Model thermo-physical properties.
| Flow parameter | Value |
|---|
| Length of micro-channels (μm) | 2560 |
| Square size of micro-channels (μm) | 1.0 |
| Dynamic viscosity of gas (Ns/m2) | 0.0000164 |
| Density of gas (kg/m3) | 1.2498 |
| Density of solid (kg/m3) | 998.2 |
| Specific gas constant of gas (J/kg K) | 296.8 |
| Specific gas constant of solid (J/kg K) | 390 + 0.9T |
| Outlet pressure (Pa) | 100800.0 |
| Pressure ratio, Pin/Pout | 1.34 – 3.34 |
Figure 6.
Velocity profile validation with slip boundary conditions (using a Non-Inverted Skew Upwind Scheme [NISUS]-based advection code [
29]).
Figure 6.
Velocity profile validation with slip boundary conditions (using a Non-Inverted Skew Upwind Scheme [NISUS]-based advection code [
29]).
The axial conduction temperature gradient has an influence on the slip boundary condition. However, it can be shown that entropy production from fluid friction depends on both velocity and temperature gradients within the flow field.
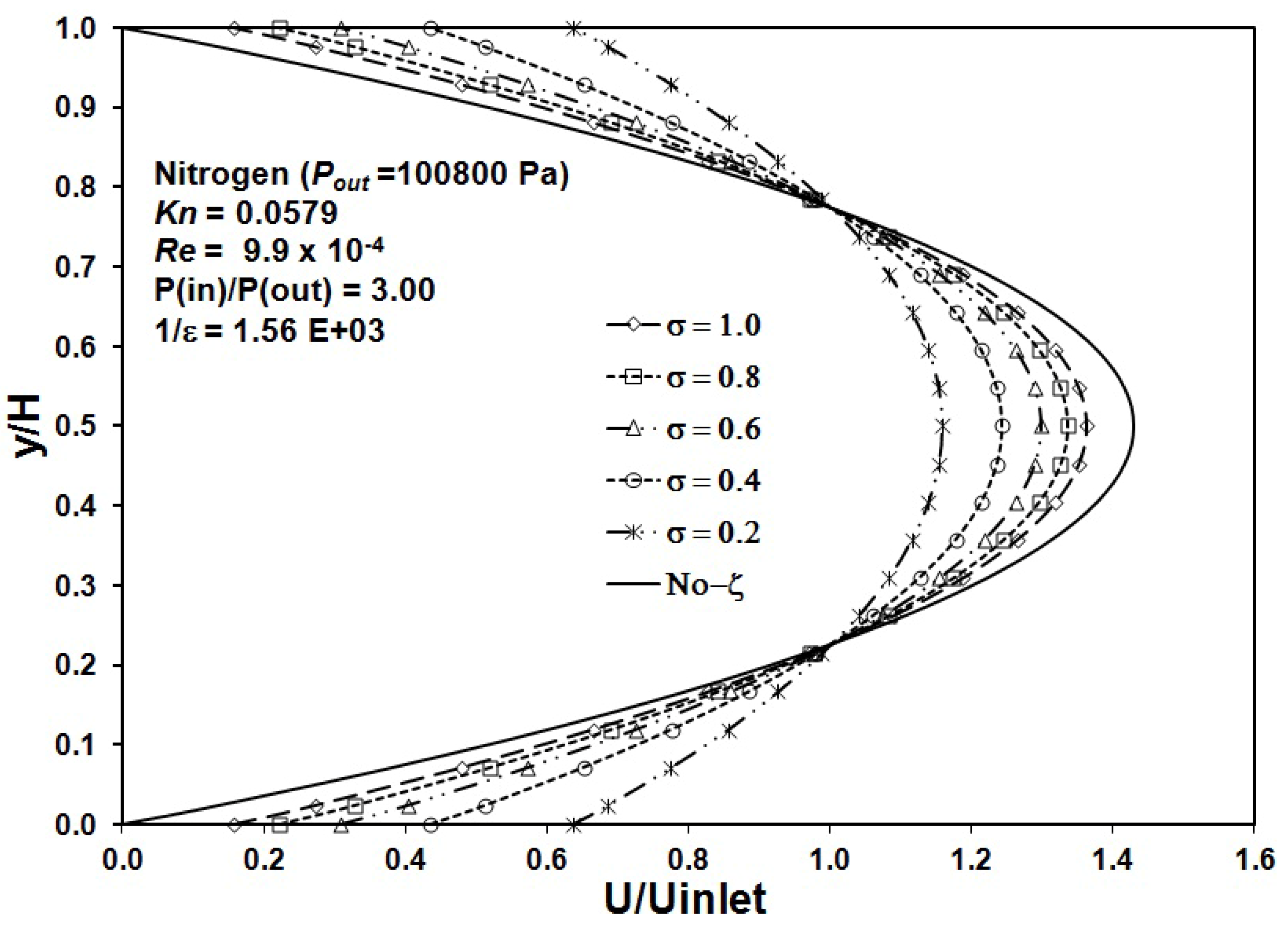
Figure 8 shows predictions of the effect of axial conduction of the thermal variable and the momentum accommodation coefficient along the length of the micro device. According to Equation (5), the wall slip velocity is dependent on both the momentum accommodation coefficient and the axial temperature gradient. This dependence directly impacts friction with an unusual thermal mechanism of entropy production in micro- and nano-scale channels.
Figure 7.
Computational effects of slip irreversibility.
Figure 7.
Computational effects of slip irreversibility.
Figure 8.
Effect of axial conduction and momentum accommodation coefficient.
Figure 8.
Effect of axial conduction and momentum accommodation coefficient.
This phenomenon may relate to previous studies by Wang
et al. [
13], which indicate that thermal energy may be temporarily converted to kinetic motion in a cohesive manner within very small-scale systems. It therefore implies that wall temperature gradients affect entropy production in the fluid stream. Efforts to fully comprehend this mechanism physically require a statistically based balance of momentum and energy equations for intermolecular motion near the wall. As channel sizes diminishes to micro- and nano-scales, the number of molecule interactions within the channel decreases.
Interactions between gas and solid phase molecules can influence the extent of energy transfer and accommodation in gas-surface collisions at micro- or nano-scales. The likelihood of random molecular motions within the wall (in the form of internal energy) being aligned in the direction of reflected motion of impacting fluid molecules rises when the channel size diminishes. In other words, when fewer wall molecules are considered in smaller channels, their alignment towards the gas velocity vector may contribute an effective temporary rise of kinetic energy. In this way, local temperature gradients affect the wall slip in Equation (5) and subsequently entropy production in the fluid stream, when formulating the Second Law. Thermal energy exchange affects the wall slip, thereby potentially reducing frictional entropy production. This observation has important implications for operation and efficiency of microfluidic devices.
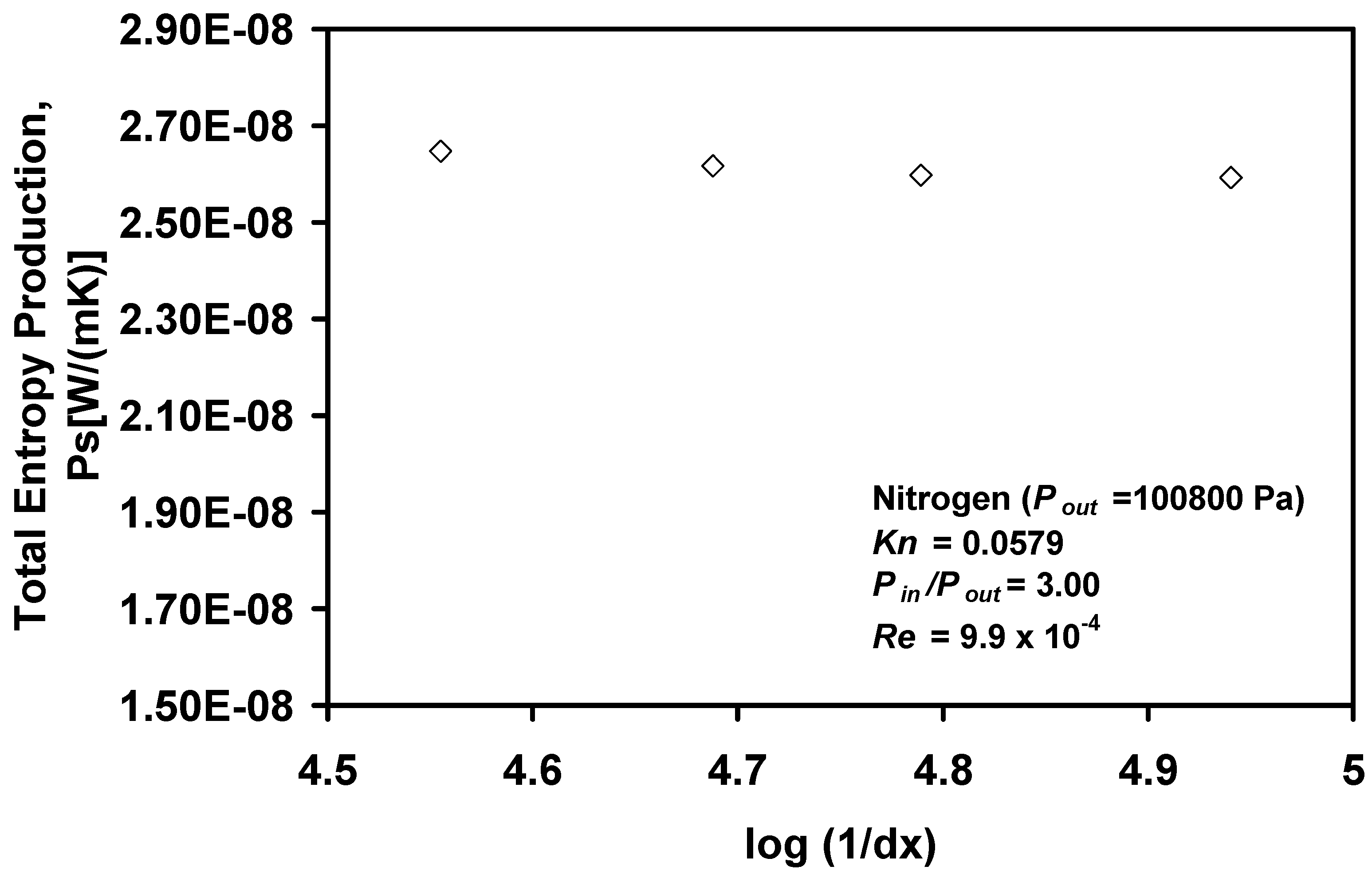
Figure 9 shows the effects of grid refinement on the predicted entropy production. The entropy production remains nearly constant over a range of grid spacings, which suggests that the results are essentially grid independent. However,
Figure 10 indicates a reduction in the level of entropy production with an increase in the magnitude of the pressure ratio at constant Reynolds number, while the expected increase in entropy production with Reynolds number is validated.
Figure 9.
Grid independence based on entropy production.
Figure 9.
Grid independence based on entropy production.
Figure 10.
Entropy distribution with Reynolds number and size pertubation of the micro-channel at pressure ratio of (a) 2.701; (b) 3.00; and (c) 3.34.
Figure 10.
Entropy distribution with Reynolds number and size pertubation of the micro-channel at pressure ratio of (a) 2.701; (b) 3.00; and (c) 3.34.
5. Conclusions
Possible configurations of CSP-powered bio-digester assemblies are presented, including a solar micro-collector, a downdraft bio-digester (gasifier), a feedstock collector/homogenizer, and a methane synthethizer. The fundamental application of slip-irreversibility within micro-channels of the constituent subsystems is studied. The possibility of enhancing the pumping performance of the heat carrier between a CSP-based micro-collector and a bio-digester is reviewed. Special consideration is given to the model of Bikerman to the modelling of continuum effects of the excess chemical potential associated with the entropy of the solvated ions at the diffuse layer of an applied large voltage across the micro-channel. Using a finite-volume formulation, the velocity profile with slip boundary conditions is presented. The variation of the momentum accommodation coefficient along the axial direction of the flow indicates a potential enhancement of flow pumping with induced electro-kinetic pumping. The development of a unique excess chemical potential model for the concentrated molten salt as the heat carrier, between the solar micro-collector and the bio-digester, is a useful factor in the exergy-based design of the proposed energy system.