A Free Energy Principle for Biological Systems
Abstract
:1. Introduction
| Domain | Process or paradigm |
|---|---|
| Perception | |
| Sensory learning |
|
| Attention | |
| Motor control | |
| Sensorimotor integration |
|
| Behaviour | |
| Action observation |
|
2. Entropy and Random Dynamical Attractors
2.1. Setup and Preliminaries
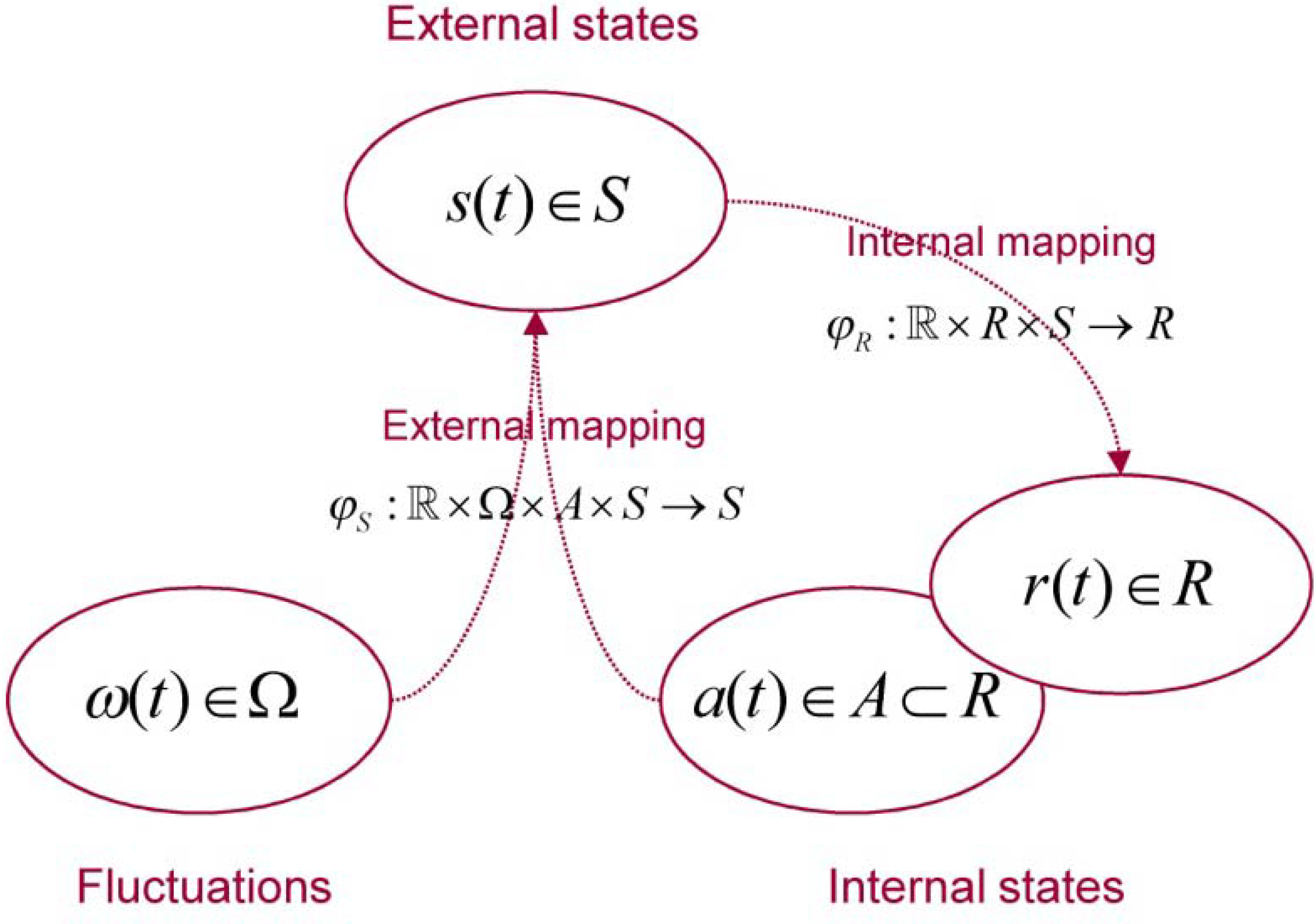
| Variable | Description |
|---|---|
| Physical state space a random dynamical system | |
| Base flow of a random dynamical system | |
| Flow or mapping to physical states | |
| Fluctuations generated by the base flow | |
| Internal state space | |
| External state space | |
| Active states | |
| Mapping to external states | |
| Mapping to internal states |
2.2. Ergodic Behaviour and Random Dynamical Attractors
2.3. Circular Causality and Active Systems
3. Active Inference and the Free Energy Principle
4. Perception, Free Energy and the Information Bottleneck
4.1. The Information Bottleneck
4.2. Free Energy Minimisation and the Information Bottleneck
5. Perception in the Brain
5.1. Predictive Coding and Free Energy Minimization
| Domain | Predictions |
|---|---|
| Anatomy: Explains the hierarchical deployment of cortical areas, recurrent architectures with functionally asymmetric forward and backward connections |
|
| Physiology: Explains both (short-term) neuromodulatory gain-control and the nature of evoked responses |
|

6. Conclusions
Acknowledgements
References
- Bialek, W.; Nemenman, I.; Tishby, N. Predictability, complexity, and learning. Neural Computat. 2001, 13, 2409–2463. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. The free-energy principle: a unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. A theory of cortical responses. Philos. Trans. R. Soc. Lond B Biol. Sci. 2005, 360, 815–836. [Google Scholar] [CrossRef] [PubMed]
- Helmholtz, H. Concerning the perceptions in general. In Treatise on Physiological Optics, 3rd ed.; Dover Publications: New York, NY, USA, 1962. [Google Scholar]
- Gregory, R.L. Perceptual illusions and brain models. Proc. R. Soc. Lond. B 1968, 171, 179–196. [Google Scholar] [CrossRef]
- Dayan, P.; Hinton, G.E.; Neal, R. The Helmholtz machine. Neural Comput. 1995, 7, 889–904. [Google Scholar] [CrossRef]
- Knill, D.C.; Pouget, A. The Bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci. 2004, 27, 712–719. [Google Scholar] [CrossRef] [PubMed]
- Yuille, A.; Kersten, D. Vision as Bayesian inference: analysis by synthesis? Trends Cogn. Sci. 2006, 10, 301–308. [Google Scholar] [CrossRef] [PubMed]
- Beal, M.J. Variational Algorithms for Approximate Bayesian Inference. Ph.D. Thesis, University College London, London, UK, 2003. [Google Scholar]
- Feynman, R.P. Statistical Mechanics; Reading MA: Benjamin, TX, USA, 1972. [Google Scholar]
- Hinton, G.E.; van Camp, D. Keeping neural networks simple by minimizing the description length of weights. In Proceedings of the Sixth Annual Conference on Computational Learning Theory, Santa Cruz, NY, USA, July 1993; pp. 5–13.
- MacKay, D.J. Free-energy minimisation algorithm for decoding and cryptoanalysis. Electron. Lett. 1995, 31, 445–447. [Google Scholar] [CrossRef]
- Friston, K.; Mattout, J.; Trujillo-Barreto, N.; Ashburner, J.; Penny, W. Variational free energy and the Laplace approximation. Neuroimage 2007, 34, 220–234. [Google Scholar] [CrossRef] [PubMed]
- Rao, R.P.; Ballard, D.H. Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 1999, 2, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Ortega, P.A.; Braun, D.A. A Minimum Relative Entropy Principle for Learning and Acting. J. Artif. Intell. Res. 2010, 38, 475–511. [Google Scholar]
- Friston, K.; Kilner, J.; Harrison, L. A free energy principle for the brain. J. Physiol. Paris. 2006, 100, 70–87. [Google Scholar] [CrossRef] [PubMed]
- Ashby, W.R. Principles of the self-organizing dynamic system. J. Gen. Psychol. 1947, 37, 125–128. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; Kiebel, S. Cortical circuits for perceptual inference. Neural. Netw. 2009, 22, 1093–1104. [Google Scholar] [CrossRef] [PubMed]
- Kiebel, S.J.; Daunizeau, J.; Friston, K.J. Perception and hierarchical dynamics. Front. Neuroinform. 2009, 3, 20. [Google Scholar] [CrossRef] [PubMed]
- Feldman, H.; Friston, K.J. Attention, uncertainty, and free-energy. Front. Hum. Neurosci. 2010, 4, 215. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J.; Daunizeau, J.; Kilner, J.; Kiebel, S.J. Action and behavior: a free-energy formulation. Biol. Cybern. 2010, 102, 227–260. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; Mattout, J.; Kilner, J. Action understanding and active inference. Biol. Cybern. 2011, 104, 137–160. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; Ao, P. Free-energy, value and attractors. Comput. Math. Methods Med. 2012, 937860. [Google Scholar] [CrossRef] [PubMed]
- Ortega, P.A.; Braun, D.A. Thermodynamics as a theory of decision-making with information processing costs. 2012. ArXiv:1204.6481v1. [Google Scholar] [CrossRef]
- Bernard, C. Lectures on the Phenomena Common to Animals and Plants; Charles, C., Ed.; Thomas Pub Ltd.: Springfield, IL, USA, 1974. [Google Scholar]
- Kauffman, S. The Origins of Order: Self-Organization and Selection in Evolution; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Maturana, H.R.; Varela, F. Autopoiesis: the organization of the living. In Autopoiesis and Cognition; Maturana, H.R., Reidel, V.F., Eds.; Springer: Dordrecht, The Netherlands, 1980. [Google Scholar]
- Nicolis, G.; Prigogine, I. Self-Organization in Non-Equilibrium Systems; John Wiley: New York, NY, USA, 1977. [Google Scholar]
- Qian, H.; Beard, D.A. Thermodynamics of stoichiometric biochemical networks in living systems far from equilibrium. Biophys. Chem. 2005, 114, 213–220. [Google Scholar] [CrossRef] [PubMed]
- Tschacher, W.; Haken, H. Intentionality in non-equilibrium systems? The functional aspects of self-organised pattern formation. New Ideas Psychol. 2007, 25, 1–15. [Google Scholar] [CrossRef]
- Conant, R.C.; Ashby, R.W. Every Good Regulator of a system must be a model of that system. Int. J. Systems Sci. 1970, 1, 89–97. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Crauel, H.; Flandoli, F. Attractors for random dynamical systems. Probab. Theory Rel. 1994, 100, 365–393. [Google Scholar] [CrossRef]
- Crauel, H.; Debussche, A.; Flandoli, F. Random attractors. J. Dyn. Differ. Equ. 1997, 9, 307–341. [Google Scholar] [CrossRef]
- Arnold, L. Random Dynamical Systems (Springer Monographs in Mathematics); Springer-Verlag: Berlin, Germany, 2003. [Google Scholar]
- Rabinovich, M.; Huerta, R.; Laurent, G. Neuroscience. Transient dynamics for neural processing. Science 2008, 321, 48–50. [Google Scholar] [CrossRef] [PubMed]
- Qian, H. Entropy demystified: the "thermo"-dynamics of stochastically fluctuating systems. Methods Enzymol. 2009, 467, 111–134. [Google Scholar] [PubMed]
- Davis, M.J. Low-dimensional manifolds in reaction-diffusion equations. 1. Fundamental aspects. J. Phys. Chem. A. 2006, 110, 5235–5256. [Google Scholar] [CrossRef] [PubMed]
- Ao, P. Emerging of Stochastic Dynamical Equalities and Steady State Thermodynamics. Commun. Theor. Phys. 2008, 49, 1073–1090. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, S.J.; Benaïm, M.; Atchadé, K.A.S. Persistence in fluctuating environments. J. Math. Biol. 2011, 62, 655–668. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Jirsa, V.K.; Friedrich, R.; Haken, H.; Kelso, J.A. A theoretical model of phase transitions in the human brain. Biol. Cybern. 1994, 71, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Tsuda, I. Toward an interpretation of dynamic neural activity in terms of chaotic dynamical systems. Behav. Brain Sci. 2001, 24, 793–810. [Google Scholar] [CrossRef] [PubMed]
- Hu, A.; Xu, Z.; Guo, L. The existence of generalized synchronization of chaotic systems in complex networks. Chaos 2010, 013112. [Google Scholar] [CrossRef] [PubMed]
- Ginzburg, V.L.; Landau, L.D. On the theory of superconductivity. Zh. Eksp. Teor. Fiz. 1950, 20, 1064. [Google Scholar]
- Haken, H. Synergetics: An introduction. Nonequilibrium Phase Transition and Self-Organisation in Physics, Chemistry and Biology, 3rd ed.; Springer Verlag: Berlin, Germany, 1983. [Google Scholar]
- Frank, T.D. Nonlinear Fokker-Planck Equations: Fundamentals and Applications (Springer Series in Synergetics), 1st ed.; Springer: Berlin, Germany, 2005. [Google Scholar]
- Breakspear, M.; Heitmann, S.; Daffertshofer, A. Generative models of cortical oscillations: neurobiological implications of the Kuramoto model. Front. Hum. Neurosci. 2010, 4, 190. [Google Scholar] [CrossRef] [PubMed]
- Auletta, G. A Paradigm Shift in Biology? Information 2010, 1, 28–59. [Google Scholar] [CrossRef]
- Kiebel, S.J.; Friston, K.J. Free energy and dendritic self-organization. Front. Syst. Neurosci. 2011, 5, 80. [Google Scholar] [CrossRef] [PubMed]
- Crauel, H. Global random attractors are uniquely determined by attracting deterministic compact sets. Ann. Mat. Pura Appl. 1999, 4, 57–72. [Google Scholar] [CrossRef]
- Birkhoff, G.D. Proof of the ergodic theorem. Proc. Natl. Acad. Sci. USA. 1931, 17, 656–660. [Google Scholar] [CrossRef] [PubMed]
- Banavar, J.R.; Maritan, A.; Volkov, I. Applications of the principle of maximum entropy: from physics to ecology. J. Phys. Condens. Matter 2010, 22, 063101. [Google Scholar] [CrossRef] [PubMed]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Zeki, S.; Shipp, S. The functional logic of cortical connections. Nature 1988, 335, 311–317. [Google Scholar] [CrossRef] [PubMed]
- Zemel, R.; Dayan, P.; Pouget, A. Probabilistic interpretation of population code. Neural Computat. 1998, 10, 403–430. [Google Scholar] [CrossRef]
- Tishby, N.; Pereira, F.C.; Bialek, W. The Information Bottleneck method. In Proceedings of The 37th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, September 1999; pp. 368–377.
- Friston, K.; Stephan, K.; Li, B.; Daunizeau, J. Generalised Filtering. Math. Probl. Eng. 2010, 621670. [Google Scholar] [CrossRef]
- Mumford, D. On the computational architecture of the neocortex. II. Biol. Cybern. 1992, 66, 241–251. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J.; Kiebel, S.J. Predictive coding under the free-energy principle. Phil. Trans. R. Soc. B 2009, 364, 1211–1221. [Google Scholar] [CrossRef] [PubMed]
- Sella, G.; Hirsh, A.E. The application of statistical physics to evolutionary biology. Proc. Natl. Acad. Sci. USA 2005, 102, 9541–9546. [Google Scholar] [CrossRef] [PubMed]
- Accord de différentes lois de la nature qui avaient jusqu'ici paru incompatibles. Avaiable online: https://fr.wikisource.org/wiki/Accord_de_diff%C3%A9rentes_loix_de_la_nature_qui_avoient_jusqu%E2%80%99ici_paru_incompatibles/ (accessed on 25 October 2012).
- Le lois de mouvement et du repos, déduites d'un principe de métaphysique. Avaiable online: http://fr.wikisource.org/wiki/Les_Loix_du_mouvement_et_du_repos_d%C3%A9duites_d%E2%80%99un_principe_metaphysique/ (accessed on 25 October 2012).
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Karl, F. A Free Energy Principle for Biological Systems. Entropy 2012, 14, 2100-2121. https://doi.org/10.3390/e14112100
Karl F. A Free Energy Principle for Biological Systems. Entropy. 2012; 14(11):2100-2121. https://doi.org/10.3390/e14112100
Chicago/Turabian StyleKarl, Friston. 2012. "A Free Energy Principle for Biological Systems" Entropy 14, no. 11: 2100-2121. https://doi.org/10.3390/e14112100
APA StyleKarl, F. (2012). A Free Energy Principle for Biological Systems. Entropy, 14(11), 2100-2121. https://doi.org/10.3390/e14112100





