Thermodynamic Modeling for Open Combined Regenerative Brayton and Inverse Brayton Cycles with Regeneration before the Inverse Cycle
Abstract
:1. Introduction
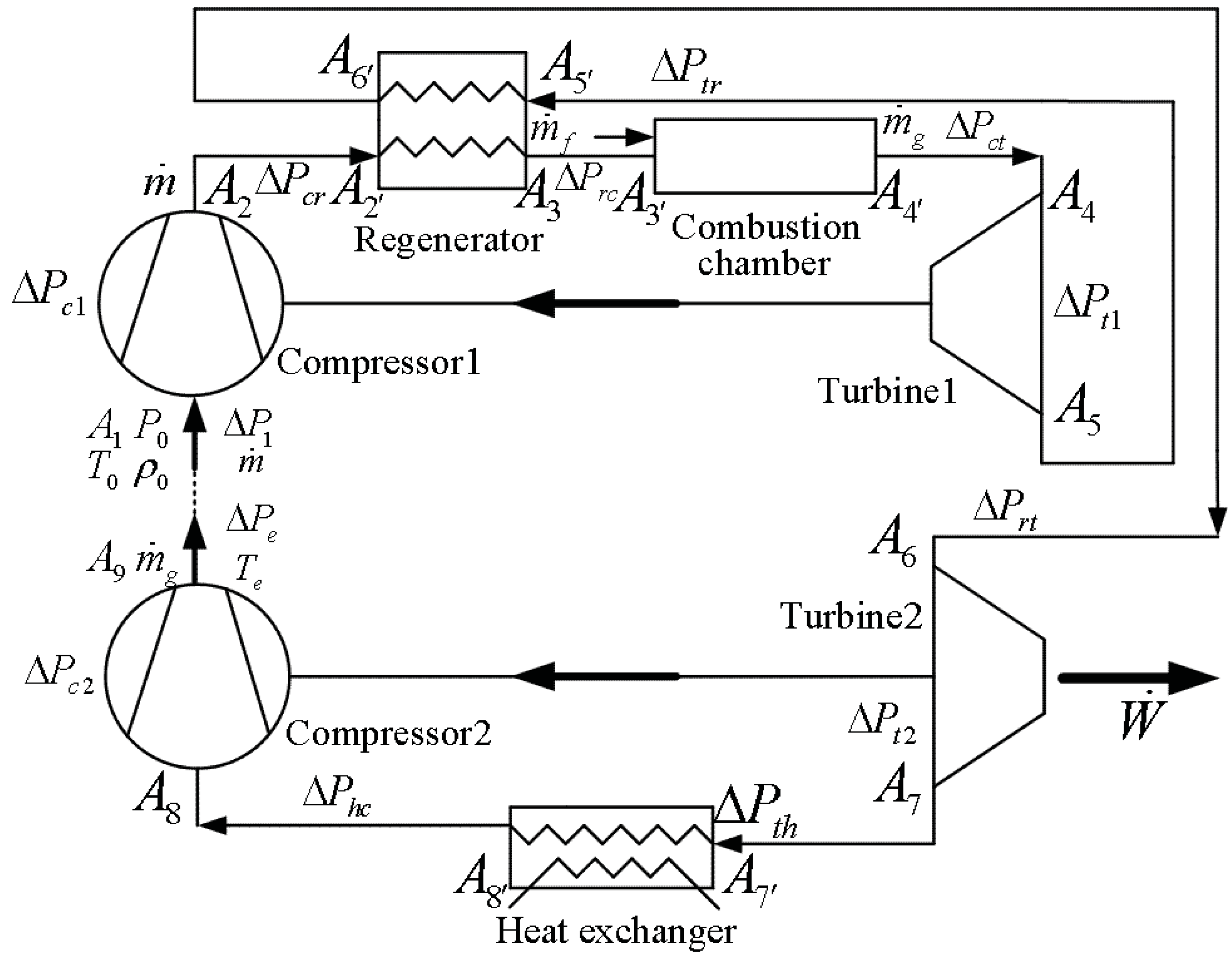
2. Physical Model
- (1)
- The working fluid (air, gas) is an ideal gas with a specific heat that depends on temperature and composition.
- (2)
- The air flows into the compressor of the top cycle (process 0 − 1) irreversibly and accompanied by the pressure drop and the entropy increase at the ambient temperature [26]. In the following analysis, represents overall pressure.
- (3)
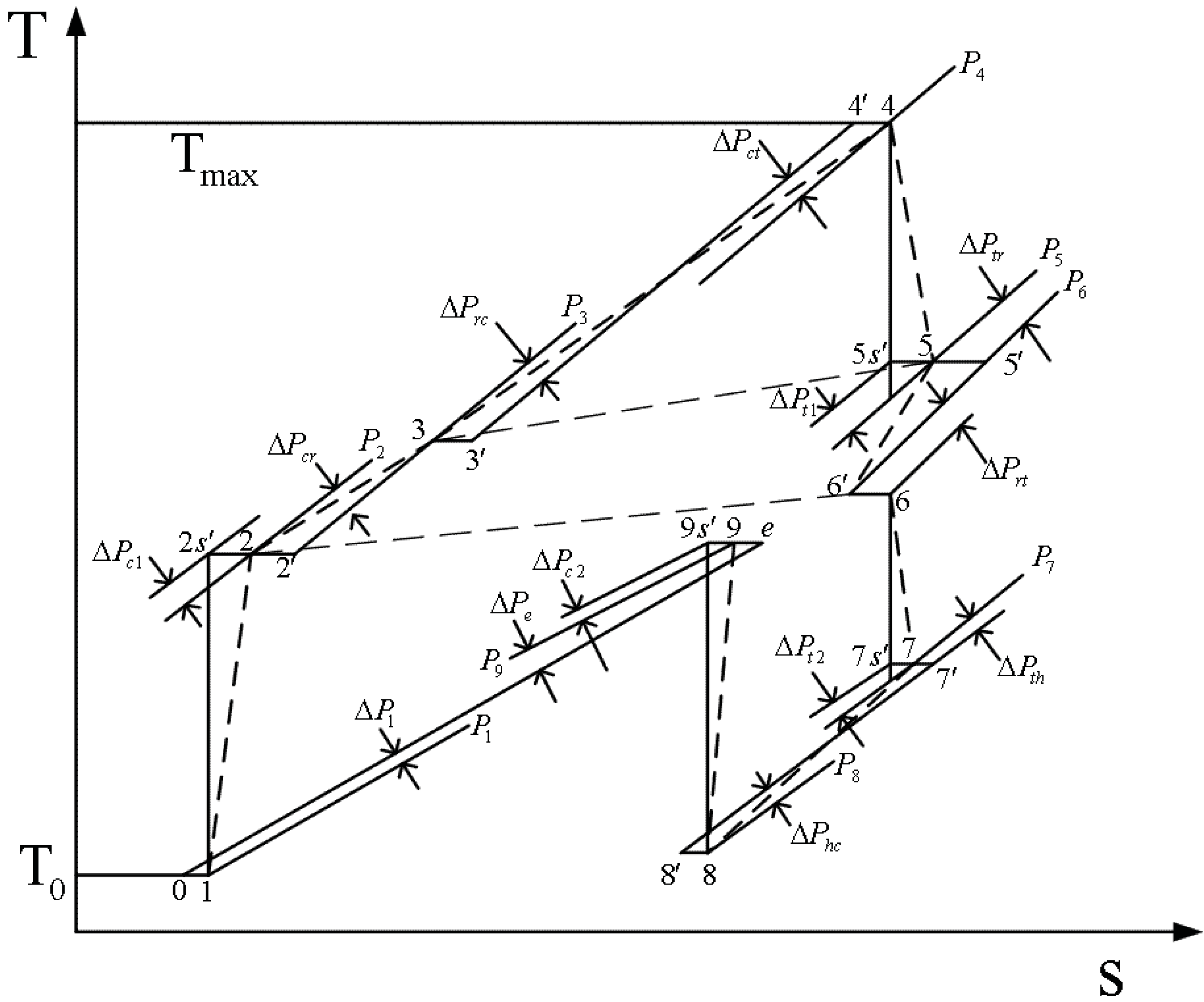
- The air compression process 1 − 2 of the top cycle is adiabatic and irreversible, leading to the entropy increase . In Figure 2 this process is represented schematically by the isentropic compression followed by the throttling process , which accounts for the pressure drop associated with fluid friction through the compressor stages of the top cycle.
- (4)
- The air flows into the cold-side of the regenerator (process 2 − 3) irreversibly and accompanied by the pressure drop . In Figure 2 this process is represented schematically by the throttling process (entropy increase is ) followed by the isobaric absorbed heat process (pressure is ).
- (5)
- The combustion process (process ) and flow through the combustion chamber are characterized by the pressure drop . In Figure 2 this process is represented schematically by the throttling process (entropy increase ) followed by the isobaric absorbed heat process (pressure is ). A fraction () of the heating rate produced by the burning fuel () leaks directly into the ambient through the walls of the combustion chamber [25,26,28].
- (6)
- The pressure drop associated with the flow out of the combustion chamber and into the turbine 1 (process ) is . The process is a accompanied by the entropy increase .
- (7)
- The turbine 1 expansion process 4 − 5 of the top cycle is modeled as adiabatic and irreversible with the entropy increase . In Figure 2 this process is represented schematically by the isentropic expansion from to , followed by the adiabatic throttling process accounting for the pressure drop through the blades and vanes of the turbine of the top cycle.
- (8)
- The air flows into the hot-side of the regenerator (process ) irreversibly and accompanied by the pressure drop . In Figure 2 this process is represented schematically by the throttling process (entropy increase is ) followed by the isobaric evolved heat process (pressure is ).
- (9)
- The pressure drop associated with the flow out of the hot-side of the regenerator and into the turbine 2 (process ) is . The process is a accompanied by the entropy increase .
- (10)
- The turbine expansion process of the top cycle is modeled as adiabatic and irreversible with the entropy increase . In Figure 2 this process is equivalent to the isentropic expansion from to , followed by the throttling process accounting for the pressure drop through the blades and vanes of the turbine of the top cycle.
- (11)
- The flow through the heat exchanger (process ) is characterized by the overall pressure drop . In Figure 2 this process is represented schematically by the throttling process followed by the isobaric evolved heat process at pressure , which accounts for the pressure drop associated with fluid friction through the heat exchanger. The effectiveness of the heat exchanger is defined as .
- (12)
- The flow into the compressor (process ) of the bottom cycle is irreversible and accompanied by the pressure drop and the entropy increase at the ambient temperature .
- (13)
- The flow compression process of the bottom cycle is adiabatic and irreversible, leading to the entropy increase . In Figure 2 this process is represented schematically by the isentropic compression followed by the throttling process , which accounts for the pressure drop associated with fluid friction through the compressor stages of the bottom cycle.
- (14)
- The discharge of the gas stream from the compressor of the bottom cycle (process ) causes another pressure drop and entropy increase at temperature .
3. Cycle Analysis
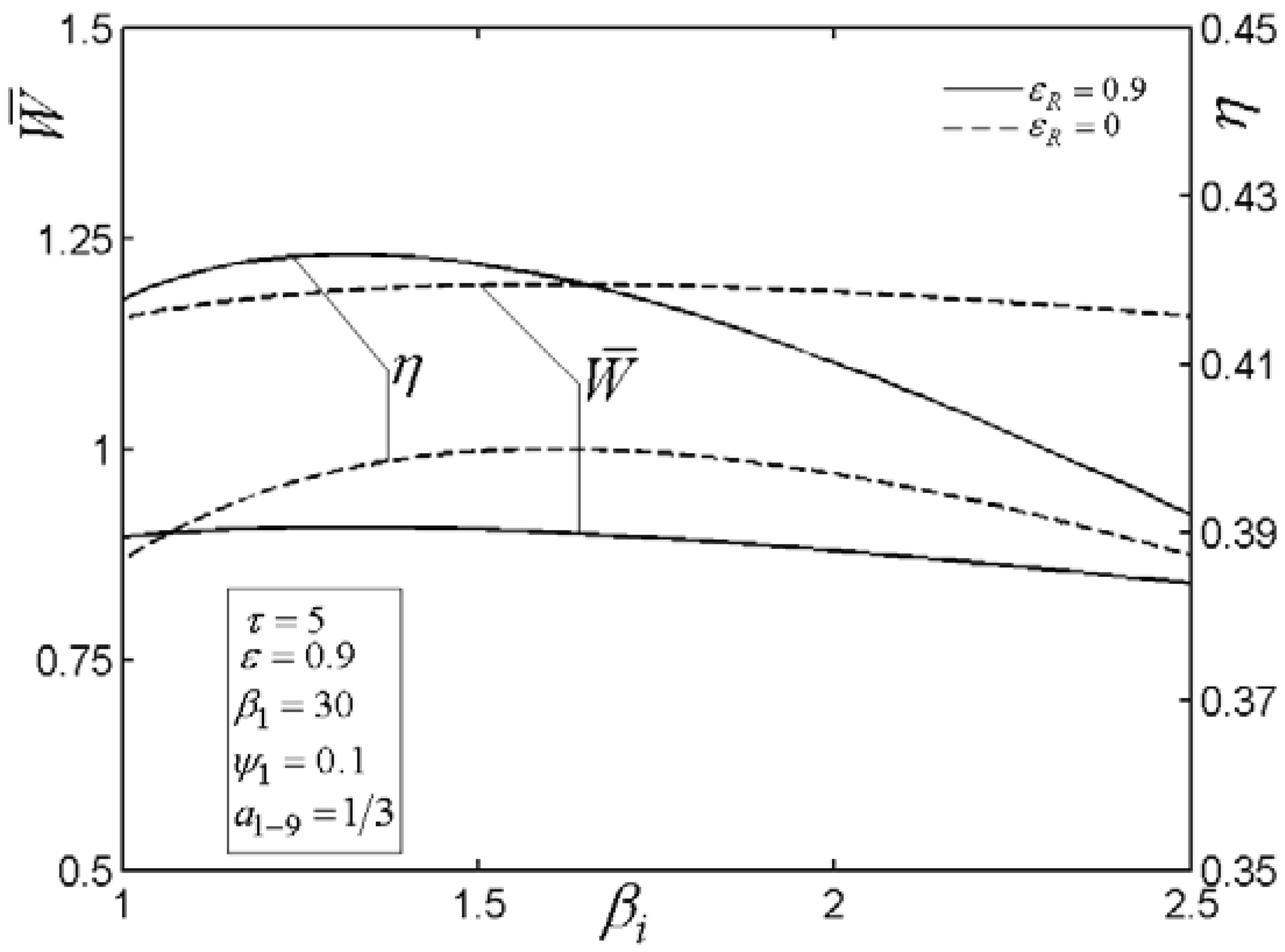
4. Numerical Examples
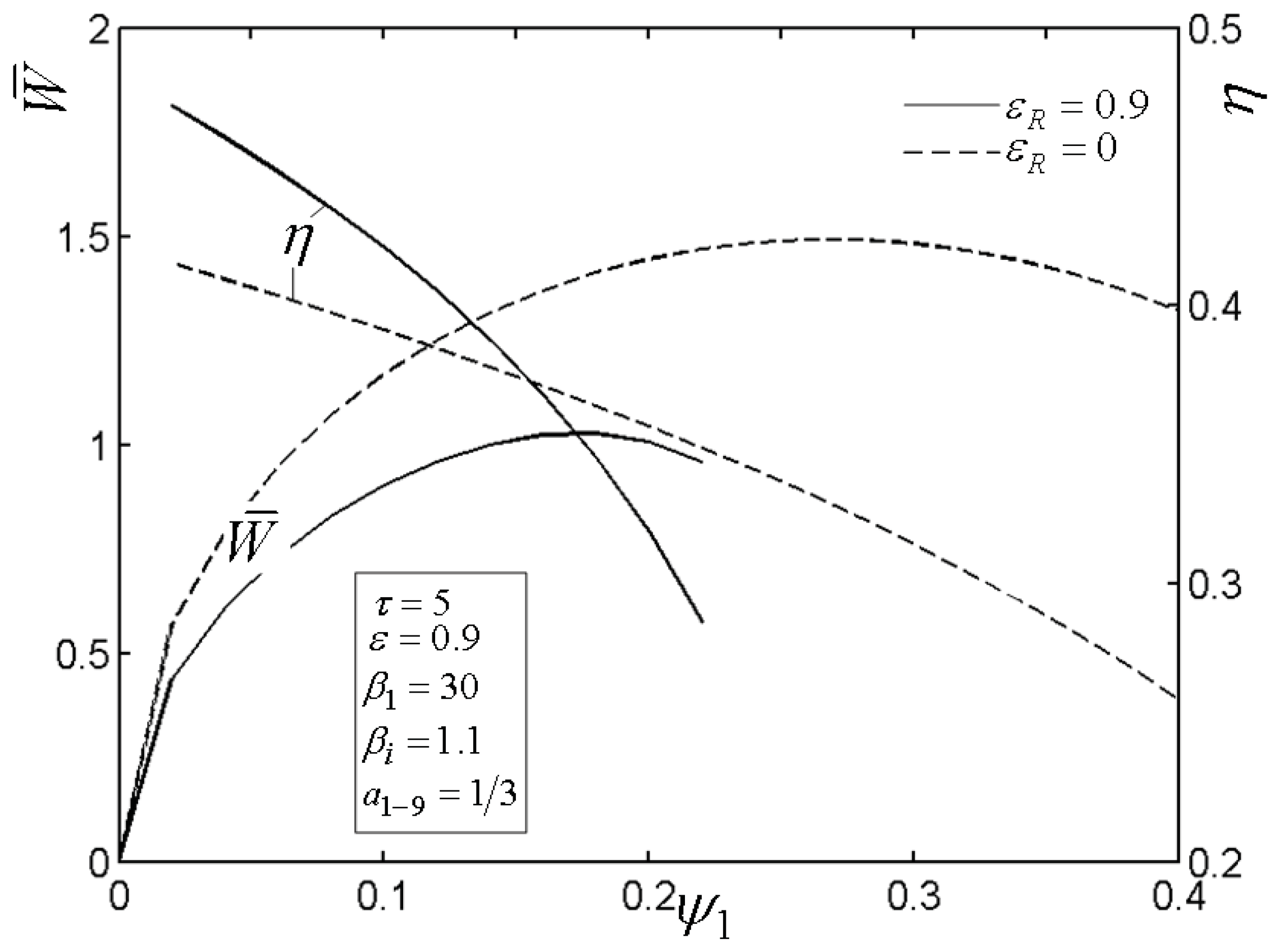
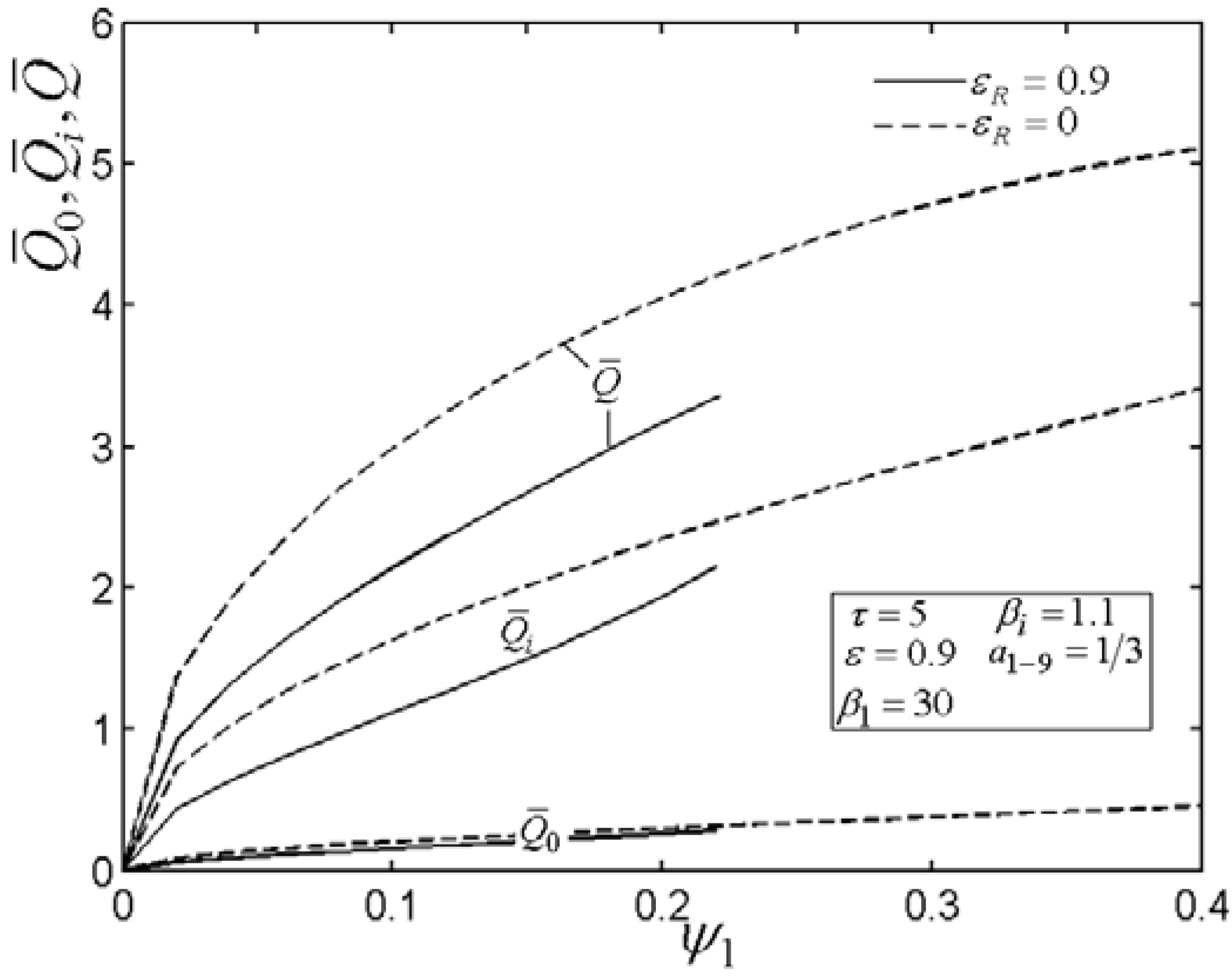

5. Conclusion
Acknowledgments
References
- Andresen, B. Finite-Time Thermodynamics; Physics Laboratory II, University of Copenhagen: Copenhagen, Denmark, 1983. [Google Scholar]
- Andresen, B.; Salamon, P.; Berry, R.S. Thermodynamics in finite time. Phys. Today 1984, September, 62–70. [Google Scholar] [CrossRef]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Chen, L.; Wu, C.; Sun, F. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J. Non-Equilib. Thermodyn. 1999, 24, 327–359. [Google Scholar] [CrossRef]
- Salamon, P.; Nulton, J.D.; Siragusa, G.; Andresen, T.R.; Limon, A. Principles of control thermodynamics. Energy 2001, 26, 307–319. [Google Scholar] [CrossRef]
- Bejan, A. Fundamentals of exergy analysis, entropy generation minimization, and the generation of flow architecture. Int. J. Energy Res. 2002, 26, 545–565. [Google Scholar] [CrossRef]
- Wu, F.; Wu, C.; Guo, F.; Li, Q.; Chen, L. Optimization of a thermoacoustic engine with a complex heat transfer exponent. Entropy 2003, 5, 444–451. [Google Scholar] [CrossRef]
- Zheng, T.; Chen, L.; Sun, F.; Wu, C. Effect of heat leak and finite thermal capacity on the optimal configuration of a two-heat-reservoir heat engine for another linear heat transfer law. Entropy 2003, 5, 519–530. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, T.; Sun, F.; Wu, C. Optimal cooling load and COP relationship of a four-heat-reservoir endoreversible absorption refrigerator cycle. Entropy 2004, 6, 316–326. [Google Scholar] [CrossRef]
- Durmayaz, A.; Sogut, O.S.; Sahin, B.; Yavuz, H. Optimization of thermal systems based on finite-time thermodynamics and thermoeconomics. Prog. Energy Combust. Sci. 2004, 30, 175–217. [Google Scholar] [CrossRef]
- Chen, L.; Sun, F. Advances in Finite Time Thermodynamics: Analysis and Optimization; Nova Science Publishers: New York, NY, USA, 2004. [Google Scholar]
- Chen, L. Finite-Time Thermodynamic Analysis of Irreversible Processes and Cycles; Higher Education Press: Beijing, China, 2005. [Google Scholar]
- Ladino-Luna, D. On optimization of a non-endoreversible Curzon-Ahlborn cycle. Entropy 2007, 9, 186–197. [Google Scholar] [CrossRef]
- Sieniutycz, S.; Jezowski, J. Energy Optimization in Process Systems; Elsevier: Oxford, UK, 2009. [Google Scholar]
- Barranco-Jimenez, M.A.; Sanchez-Salas, N.; Rosales, M.A. Thermoeconomic optimum operation conditions of a solar-driven heat engine model. Entropy 2009, 11, 443–453. [Google Scholar] [CrossRef]
- Feidt, M. Optimal thermodynamics-New upperbounds. Entropy 2009, 11, 529–547. [Google Scholar] [CrossRef]
- Feidt, M. Reconsideration of criterious and modeling in order to optimize efficiency of irreversible thermomechanical heat engines. Entropy 2010, 12, 2470–2484. [Google Scholar] [CrossRef]
- Xia, S.; Chen, L.; Sun, F. Power-optimization of non-ideal energy converters under generalized convective heat transfer law via Hamilton-Jacobi-Bellman theory. Energy 2011, 36, 633–646. [Google Scholar] [CrossRef]
- Meng, F.; Chen, L.; Sun, F. A numerical model and comparative investigation of a thermoelectric generator with multi-irreversibilities. Energy 2011, 36, 3513–3522. [Google Scholar] [CrossRef]
- Chen, L.; Ding, Z.; Sun, F. Model of a total momentum filtered energy selective electron heat pump affected by heat leakage and its performance characteristics. Energy 2011, 26, 4011–4018. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, G.; Chen, J. The performance analysis and multi-objective optimization of a typical alkaline fuel cell. Energy 2011, 36, 4327–4332. [Google Scholar] [CrossRef]
- Chen, Y. Maximum profit configuration of commercial engines. Entropy 2011, 13, 1137–1151. [Google Scholar] [CrossRef]
- Barranco-Jiménez, M.A.; Páez-Hernández, R.T.; Reyes-Ramírez, I.; Guzmán-Vargas, L. Local stability analysis of a thermo-economic model of a Chambadal-Novikov-Curzon-Ahlborn heat engine. Entropy 2011, 13, 1584–1594. [Google Scholar] [CrossRef]
- Andresen, B. Current trends in finite-time thermodynamics. Angew. Chem. Int. Ed. 2011, 50, 2690–2704. [Google Scholar] [CrossRef] [PubMed]
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Radcenco, V. Generalized Thermodynamics; Editura Techica: Bucharest, Romania, 1994. [Google Scholar]
- Bejan, A. Maximum power from fluid flow. Int. J. Heat Mass Transfer 1996, 39, 1175–1181. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Chen, L.; Wu, C.; Sun, F.; Yu, J. Performance characteristic of fluid flow converters. J. Inst. Energy 1998, 71, 209–215. [Google Scholar]
- Chen, L.; Bi, Y.; Wu, C. Influence of nonlinear flow resistance relation on the power and efficiency from fluid flow. J. Phys. D. Appl. Phys. 1999, 32, 1346–1349. [Google Scholar] [CrossRef]
- Hu, W.; Chen, J. General performance characteristics and optimum criteria of an irreversible fluid flow system. J. Phys. D. Appl. Phys. 2006, 39, 993–997. [Google Scholar] [CrossRef]
- Radcenco, V.; Vargas, J.V.C.; Bejan, A. Thermodynamics optimization of a gas turbine power plant with pressure drop irreversibilities. J. Energy Resour. Technol. 1998, 120, 233–240. [Google Scholar] [CrossRef]
- Chen, L.; Li, Y.; Sun, F.; Wu, C. Power optimization of open-cycle regenerator gas-turbine power-plants. Appl. Energy 2004, 78, 199–218. [Google Scholar] [CrossRef]
- Wang, W.; Chen, L.; Sun, F.; Wu, C. Performance optimization of an open-cycle intercooled gas turbine power plant with pressure drop irreversibilities. J. Energy Inst. 2008, 81, 31–37. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, W.; Sun, F. Performance optimization for an open cycle gas turbine power plant with a refrigeration cycle for compressor inlet air cooling. Part 1: Thermodynamic modeling. Proc. IMechE Part A: J. Power Energy 2009, 223, 505–513. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, L.; Sun, F. Performance optimization for an open cycle gas turbine power plant with a refrigeration cycle for compressor inlet air cooling. Part 2: Power and efficiency optimization. Proc. IMechE Part A: J. Power Energy 2009, 223, 515–522. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, W.; Sun, F. Thermodynamic optimization for an open cycle of externally fired micro gas turbine (EFmGT). Part 1: Thermodynamic modeling. Int. J. Sustain. Energy 2011, 30, 246–256. [Google Scholar] [CrossRef]
- Agnew, B.; Anderson, A.; Potts, I.; Frost, T.H.; Alabdoadaim, M.A. Simulation of combined Brayton and inverse Brayton cycles. Appl. Therm. Eng. 2003, 23, 953–963. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, L.; Sun, F.; Wu, C. Second-law analysis and optimization for combined Brayton and inverse Brayton cycles. Int. J. Ambient Energy 2007, 28, 15–26. [Google Scholar] [CrossRef]
- Alabdoadaim, M.A.; Agnew, B.; Alaktiwi, A. Examination of the performance envelope of combined Rankine, Brayton and two parallel inverse Brayton cycles. Proc. IMechE Part A: J. Power Energy 2004, 218, 377–386. [Google Scholar] [CrossRef]
- Alabdoadaim, M.A.; Agnew, B.; Potts, I. Examination of the performance of an unconventional combination of Rankine, Brayton and inverse Brayton cycles. Proc. IMechE Part A: J. Power Energy 2006, 220, 305–313. [Google Scholar] [CrossRef]
- Alabdoadaim, M.A.; Agnew, B.; Potts, I. Performance analysis of combined Brayton and inverse Brayton cycles and developed configurations. Appl. Therm. Eng. 2006, 26, 1448–1454. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, L.; Sun, F.; Wu, C. Second law analysis and parametric study for combined Brayton and two parallel inverse Brayton cycles. Int. J. Ambient Energy 2009, 30, 179–192. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, L.; Sun, F. Power and efficiency optimization for combined Brayton and inverse Brayton cycles. Appl. Therm. Eng. 2009, 29, 2885–2894. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, W.; Sun, F. Power and efficiency optimization for combined Brayton and two parallel inverse Brayton cycles, Part 1: Description and modeling. Proc. IMechE Part C: J. Mech. Eng. Sci. 2008, 222, 393–403. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, L.; Sun, F. Power and efficiency optimization for combined Brayton and two parallel inverse Brayton cycles, Part 2: Performance optimization. Proc. IMechE Part C: J. Mech. Eng. Sci. 2008, 222, 405–414. [Google Scholar] [CrossRef]
- Bejan, A. Heat Transfer; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Gordon, C.O. Aerodynamics of Aircraft Engine Components; AIAA: New York, NY, USA, 1985. [Google Scholar]
- Radcenco, V. Optimzation Criteria for Irreversible Thermal Processes; Editura Tehnica: Bucharest, Romania, 1979. [Google Scholar]
- Brown, A.; Jubran, B.A.; Martin, B.W. Coolant optimization of a gas-turbine engine. Proc. IMechE Part A: J. Power Energy 1993, 207, 31–47. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, L.; Zhang, Z.; Sun, F. Thermodynamic Modeling for Open Combined Regenerative Brayton and Inverse Brayton Cycles with Regeneration before the Inverse Cycle. Entropy 2012, 14, 58-73. https://doi.org/10.3390/e14010058
Chen L, Zhang Z, Sun F. Thermodynamic Modeling for Open Combined Regenerative Brayton and Inverse Brayton Cycles with Regeneration before the Inverse Cycle. Entropy. 2012; 14(1):58-73. https://doi.org/10.3390/e14010058
Chicago/Turabian StyleChen, Lingen, Zelong Zhang, and Fengrui Sun. 2012. "Thermodynamic Modeling for Open Combined Regenerative Brayton and Inverse Brayton Cycles with Regeneration before the Inverse Cycle" Entropy 14, no. 1: 58-73. https://doi.org/10.3390/e14010058
APA StyleChen, L., Zhang, Z., & Sun, F. (2012). Thermodynamic Modeling for Open Combined Regenerative Brayton and Inverse Brayton Cycles with Regeneration before the Inverse Cycle. Entropy, 14(1), 58-73. https://doi.org/10.3390/e14010058




