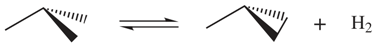2.1. Indistinguishable Particles and Third Law Entropies
Nowadays, 3
rd law entropies of small molecules in the gas-phase can be computed easily and with remarkable precision by feeding thermodynamic statistical formulae with molecular properties computed with quantum chemical methods [
18]. For example,
Table 1 shows both theoretical and experimental entropy values reported in the literature for small alkanes [
19]. For simplicity, the examples in
Table 1 are selected so that the
ω possible conformers for each molecule, if any, are not only isoenergetic, but also chemically identical. Thus, the conformational entropy would be zero, depending whether or not we are considering indistinguishability or distinguishability among identical conformers.
Table 1.
B3LYP/cc-pVTZ theoretical and experimental entropies in
[
19].
Table 1.
B3LYP/cc-pVTZ theoretical and experimental entropies in [19].
| Molecule | | Theory | Experiment | Abs. Error |
|---|
| methane | 12 | 186.20 | 186.37 | 0.17 |
| ethane | 6 | 228.50 | 229.16 | 0.66 |
| propane | 2 | 270.20 | 270.31 | 0.11 |
| methylpropane | 3 | 295.50 | 295.70 | 0.20 |
| dimethylpropane | 12 | 306.74 | 306.00 | 0.74 |
| 2,2-dimethylbutane | 1 | 358.70 | 358.40 | 0.30 |
Since molar entropies are being dealing with, the number of particles is chosen to be the Avogadro Number (
), expressing the entropy corrections preferably in terms of the gas constant
. The theoretical values in
Table 1 are Rigid-Rotor Harmonic-Oscillator (RRHO) entropies obtained from standard statistical thermodynamic formulae at the B3LYP/cc-pVTZ level of theory, where B3LYP is a hybrid density functional and cc-pVTZ denotes the correlation consistent basis set used [
20]. Standard formulae refers to the fact that in all cases the reported theoretical entropies are reduced due to the symmetry including the permutation symmetry (
i.e., reduced by the terms
and
) [
12]. In principle, we should also correct the entropy due to the internal symmetry number
by adding
. However, it is well known that RRHO entropies do not capture all the intramolecular entropy, as they lack the purely conformational part of the entropy [
21,
22,
23], which is in our case exactly
and, therefore, the last correction is automatically done due to the deficiencies of the RRHO method. As can be seen in
Table 1, the theoretical results are, without any doubt, in good agreement with the experimental values.
2.2. Distinguishable Particles and Third Law Entropies
If the particles are distinguishable, the entropy correction is not justified and there are new entropy terms that should be taken into account. The conformational entropy, for instance, is now not canceled and consequently the corresponding term
, as well as the one due to the external symmetry
, must be added to each of the theoretical values in
Table 1. By doing so, the agreement of the theoretical data with the experimental values
apparently worsens. However, we realise that standard experimental calorimetric entropies are ultimately an entropy change from
to
. This change is equal to the absolute entropy if the 3
rd law holds,
i.e.,
To interpret the experimental results assuming distinguishable particles, it can be noted first that, in the examples, any
formal conformational change of a single molecule near
, as well as any rotational symmetry operation, will lead to a different microscopic complexion compatible with the macroscopic state [
13]. Therefore, a residual entropy should be considered for these molecules having a value of
. This quantity must be added to the original experimental values and the resulting entropy values, which assume particle distinguishability, maintain the agreement between theory and experiment (see
Table 2).
Table 2.
Theoretical (B3LYP/cc-pVTZ) and experimental entropy values in augmented by due to the distinguishability.
Table 2.
Theoretical (B3LYP/cc-pVTZ) and experimental entropy values in augmented by due to the distinguishability.
| Molecule | ω | | Theory | Experiment | Abs. Error |
|---|
| methane | 1 | 12 | 206.86 | 207.03 | 0.17 |
| ethane | 3 | 6 | 252.53 | 253.19 | 0.66 |
| propane | | 2 | 294.23 | 294.34 | 0.11 |
| methylpropane | | 3 | 332.03 | 332.23 | 0.20 |
| dimethylpropane | | 12 | 363.93 | 363.19 | 0.74 |
| 2,2-dimethylbutane | | 1 | 404.37 | 404.07 | 0.30 |
At this point the reader might wonder why, if all particles are taken as distinguishable, the uncertainty due to the permutation symmetry in the solid state at
has not been considered. After all, any permutation would give a new
different microstate. In fact, it could have been done, but it would have changed nothing, because in such a case the term
needs to also be added to the theoretical value because the translational part of the entropy is computed in its corrected form
, where
is the translational partition function [
1]. Note that the corrected form is conceptually equivalent to the “reduced” entropy used by Cheng [
17]. In general any other intra- or extra-molecular permutation between identical but distinguishable atoms can both be considered in the gas phase and in the solid state nearby
, and the agreement between theory and experiment would be unaffected.
2.3. Entropy Changes in Chemical Reactions: Is There Any Difference?
The statement that the absolute entropy of a system depends on a subjective decision, to consider or not that identical atoms or particles are indistinguishable, most likely seems awkward. It is no less subjective, however, than setting an arbitrary reference in order to transform a relative magnitude into an absolute one. There are an infinite number of possible functions that would give the correct experimental entropy change, and therefore they all meet the original Clausius thermodynamic definition. The entropy change is the magnitude that must be invariant regardless of any considerations. Through two simple examples, both points of view discussed above (considering identical particles distinguishable or not) will be shown as totally equivalent.
Let us first consider the following equilibrium reactions in the gas phase:
If a quantum chemical program is used to optimize the molecular geometries, carry out the corresponding frequency calculations and compute the RRHO entropies without considering any symmetry operation except the identity, the entropy values, say,
,
,
, and
would be obtained. For convenience the required entropy corrections are introduced explicitly, then the estimated entropy change in (R-1) is
where
. In principle,
would reproduce the experimental entropy change provided that the level of theory in the calculations is adequate.
Considering distinguishability in the same reaction (R-1), it is now obvious that the
molecule can be formed by any of the 3 distinguishable
atoms involved, furthermore, the three numerable H atoms can be reordered in two different forms not superimposable by rotations, being the atoms in
completely determined by our first selection. Hence, the reactants would have an additional uncertainty that contributes to the entropy in
. On the other hand, the
molecule can be formed by any two of the three
and any two of the three H atoms, and once selected, there are two possible arrangements to be chosen between. Note that the atoms are numerable and we could obtain two enantiomeric configurations. The atoms in
will be determined once again by the previous selection and finally the entropy estimation under this new formalism is
which is exactly the same result obtained above.
Let us consider a more complex example where the conformational entropy is also involved. In (R-2), the symmetry number is three for the methylpropane, one in the methylcyclopropane and two for the H, being
.
Considering identical atoms as indistinguishable, there is no conformational entropy either in the methylpropane or in the methylcyclopropane molecules. The entropy change involved is .
If, on the contrary, identical atoms are distinguishable, the H atoms can be arranged in multiple different ways and the entropy value is not lower due to symmetry, but higher. Additionally, the conformational entropy must be taken into account since any conformational change in any methyl group would give a new different conformer. The uncertainty due to the arrangements of the carbon atoms (excluding the connectivity) is the same in reactant and products and will not be considered.
In order to build the reactant molecule (methylpropane), 10 H atoms need to be distributed into 4 “boxes” of capacities 3, 3, 3 and 1, where, in the boxes of capacity 3 (methyl groups), there are two possible enantiomeric arrangements. Also, each methyl group will contribute to the conformational entropy with 3 conformers, being the total number of complexions
For the products (methylcyclopropane and
) the carbon atoms which will close the cycle are selected first (there are
possibilities), then we have 10 H atoms for 5 boxes of capacities 3, 2, 2, 1 and 2, where we included the
molecule as the last box. Once again the methyl groups as well as the
groups have two possible arrangements and each methyl group generates three different conformers. As a consequence, the total number of complexions is
and therefore the computed entropy is
obtaining again the same result under both formalisms.
However, two examples do not equate to a formal proof, the idea needs to be extended to any chemical reaction. To this end, notice that for distinguishable particles, those permutations that lead to a different arrangement, i.e., not superimposable with the original one by rigid rotations are being considered. For a given system, a systematic way to compute the required number of permutations would be to consider all the possible permutations and then reduce this value taking into account the total symmetry number. For example, it is known that there are only two possible arrangements of the distinguishable atoms in the molecule, this quantity is equal to the number of permutations of the H atoms () divided by the symmetry number of a tetrahedral molecule ().
In general, the number of permutations not superimposable by rotations (internal or external) of a system that have
atoms of type 1,
atoms of type 2, and so on, is equal to
where the denominator is the product of all the symmetry numbers of the system (reactants or products). If, for instance, the last expression in the reaction (R-1) is applied, it results in
and
complexions for the reactants and products respectively, the same results obtained above (see Equation (
3)).
For a general reaction , since the number and type of atoms is conserved, the numerator in (5) always cancels out in the difference , where and are respectively the symmetry number of reactants and products. Consequently, the effect is equivalent to correcting the entropy change by , being the total symmetry number on each side of the chemical reaction. Note that the correction is the same as that for indistinguishable particles except for one point; in the above two examples when indistinguishable particles were considered, only external symmetry numbers were used, not because the internal symmetry was not present, but simply because of the flaws of the RRHO approach taken as “reference”. In other words, considering whether identical atoms are distinguishable or not has no effect on the entropy change in chemical reactions.