Thermodynamics of Thermoelectric Phenomena and Applications
Abstract
:1. Introduction
1.1. Historical Notes
1.2. The Thermoelectric Engine
2. Forces & Fluxes
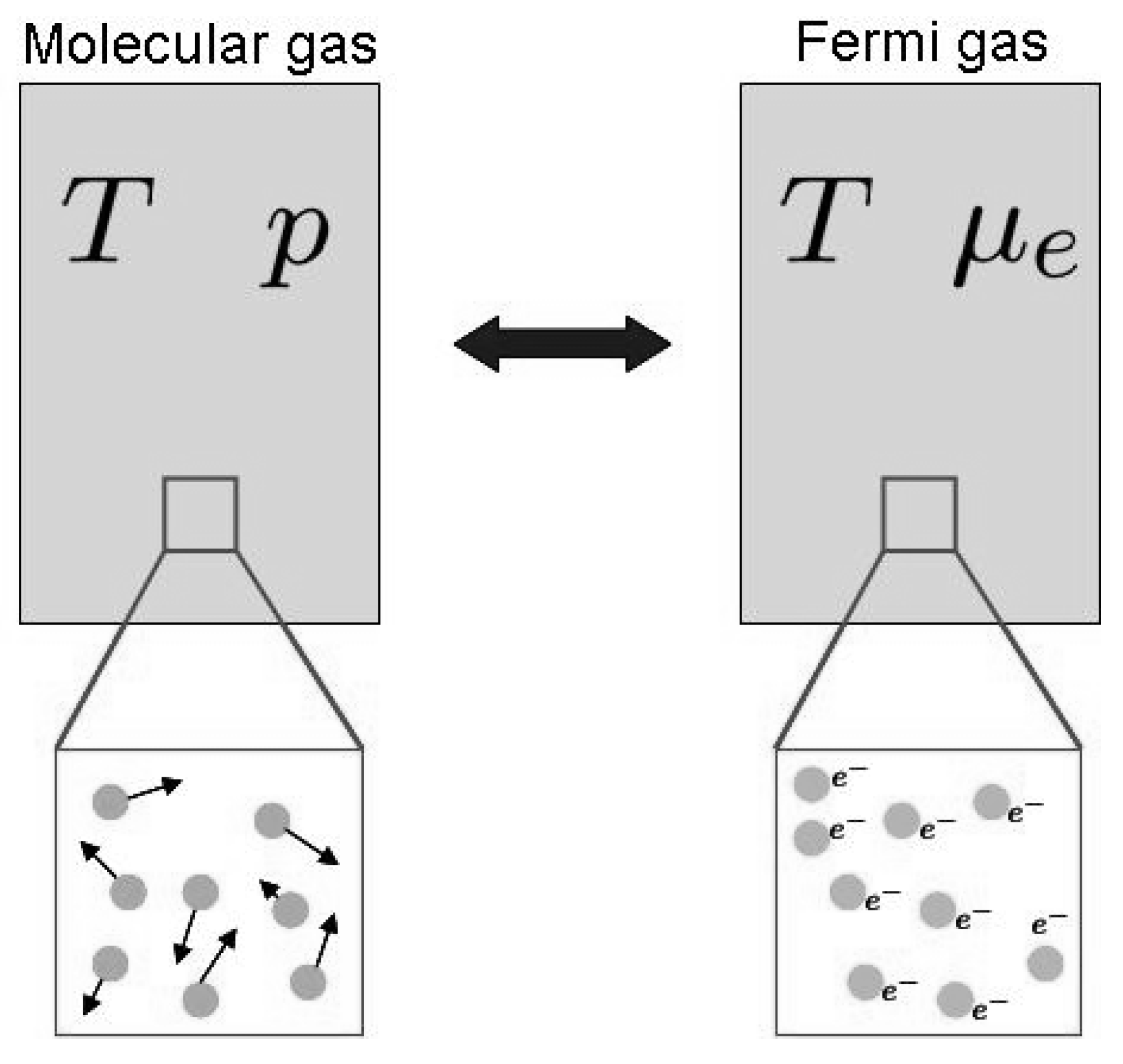
2.1. Irreversible Thermodynamics and the Onsager–de Groot–Callen Model
2.2. Forces and Fluxes
2.3. Energy Flux and Heat Flux
2.4. Thermoelectric Coefficients
2.4.1. Decoupled Processes
2.4.2. Coupled Processes
2.5. The Entropy per Carrier
2.6. Kinetic Coefficients and Transport Parameters
2.7. The Dimensionless Figure of Merit z T
3. Heat & Entropy
3.1. Volumetric Heat Production
3.2. Entropy Production Density
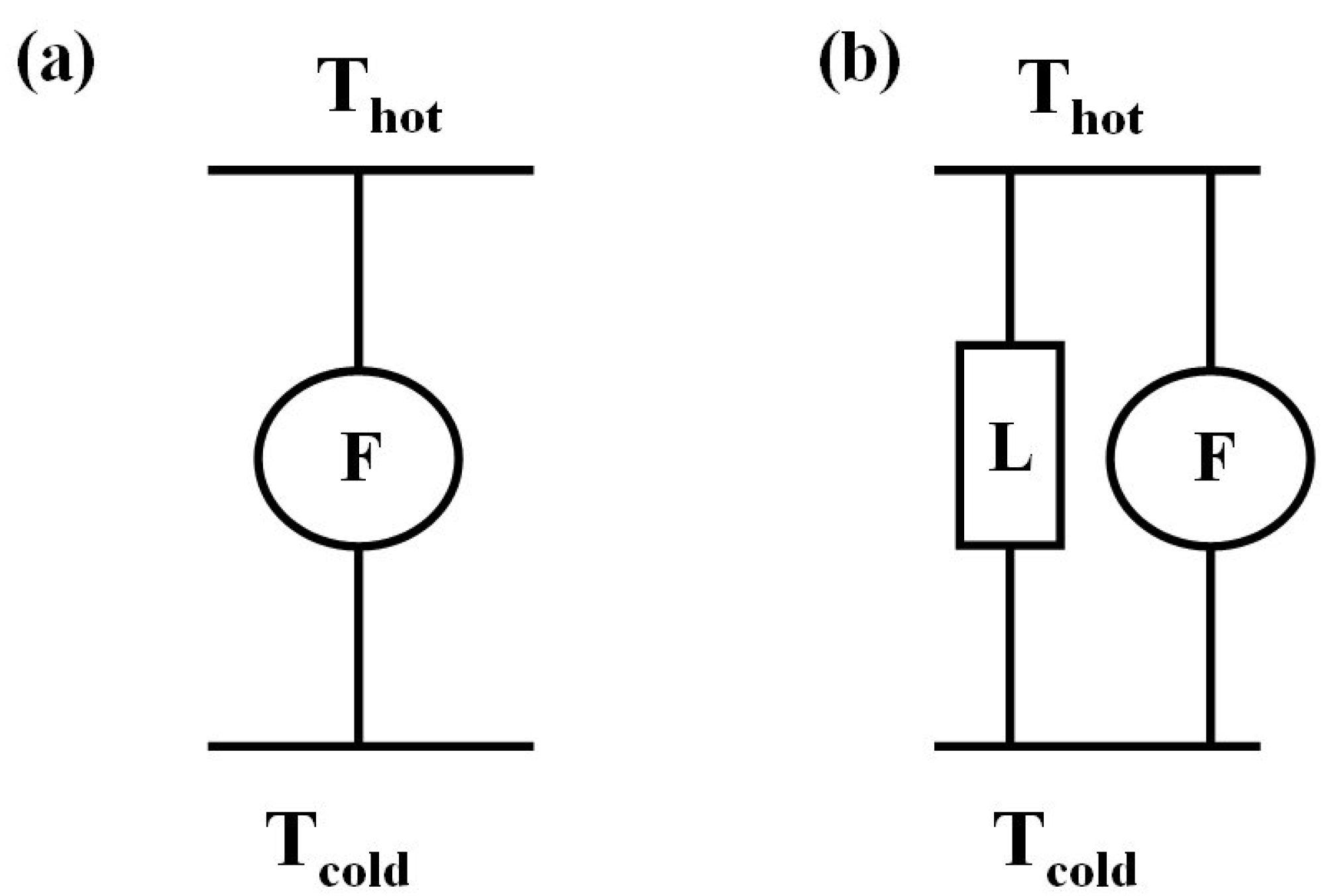
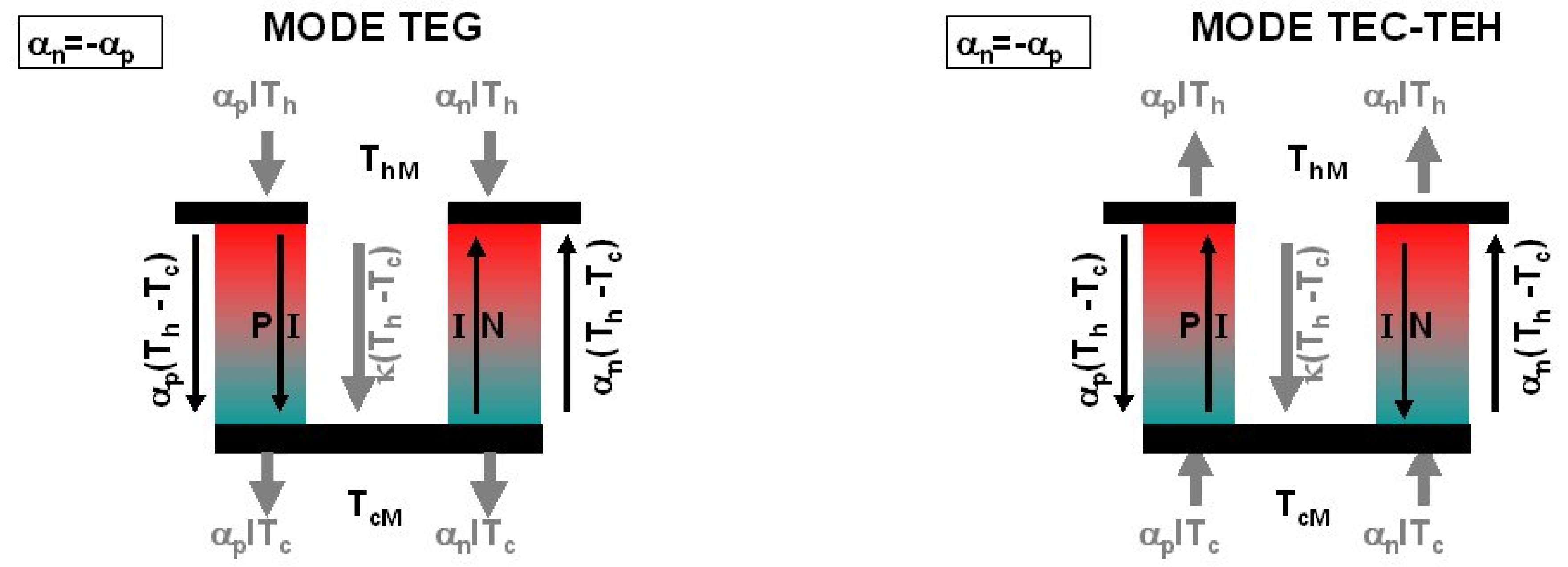
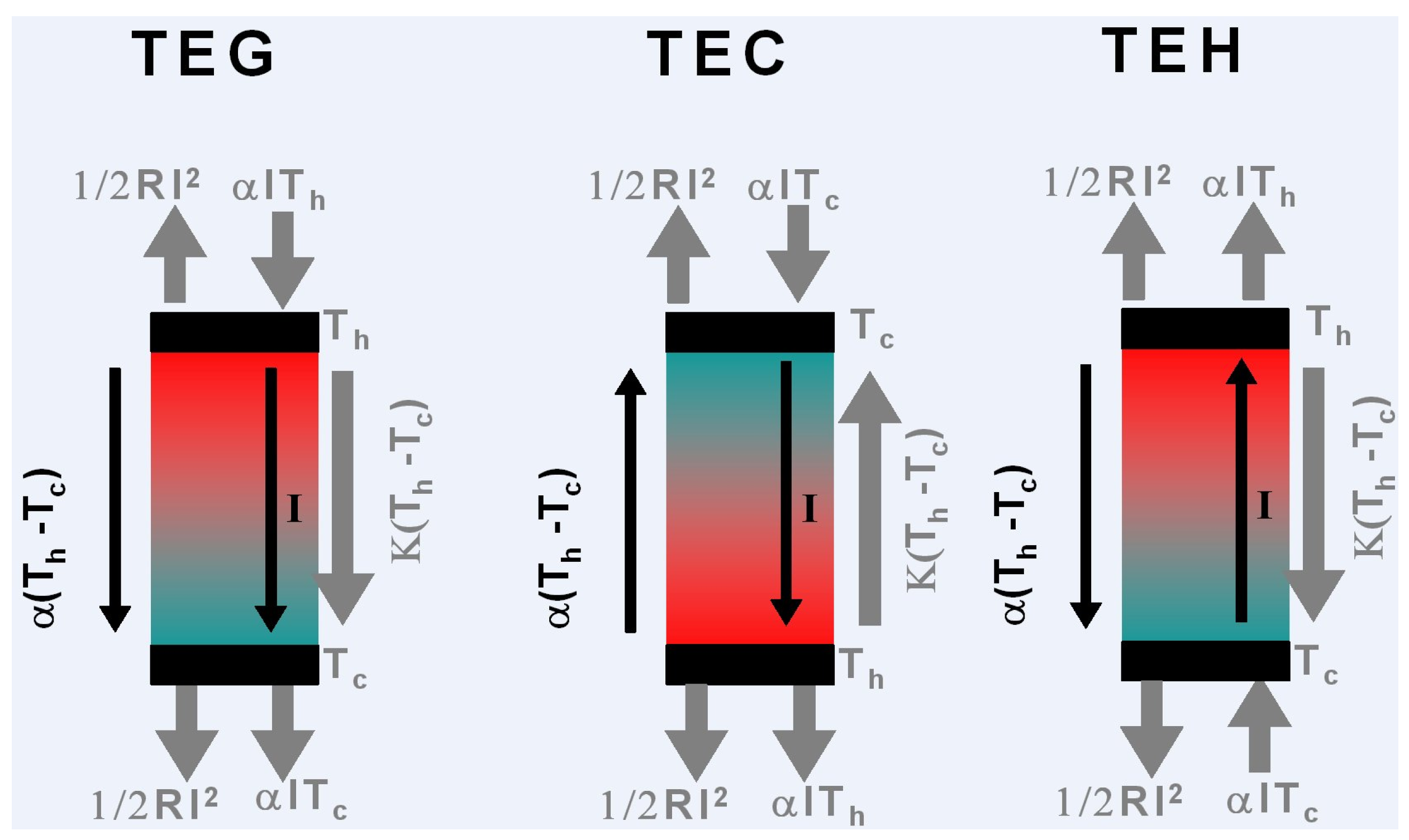
4. Thermoelectric Generator, Cooler, and Heater
- Thermoelectric heater: TEH.
- Thermoelectric cooler: TEC.
- Thermoelectric generator: TEG.
- Seebeck voltage,
- temperature difference,
- Peltier heat flow.
- conductive heat flow [113].
4.1. Thermoelectric Generator
- Incoming thermal power:
- Outgoing thermal power:
- Electrical power produced:
- Open voltage:
- Efficiency:As we can notice the efficiency is the product of the reversible Carnot efficiency with the irreversible factor
- Maximal efficiency:From the derivation , we get after a few algebra stepswith where .
- Maximal electrical power output:The last equation tells us that the maximal power output is obtained when the electrical load resistance is equal to the internal resistance of the TEG. Then the maximal output power is obtained for . The maximal power expression reduces toOne can notice that the condition for maximal efficiency () and maximal output power () are different. This means that given a fabricated TE device where the geometric lengths and areas are fixed, more power will be produced if additional heat is supplied and higher current drawn than in the maximum efficiency configuration. However, when designing an optimal device for a particular application, the optimum design will have the geometry and current for maximum efficiency because this will provide more power with the same designed heat input.
4.2. Thermoelectric Cooler
- Incoming thermal power:
- Outgoing thermal power:
- Consumed electrical power:
- Maximal cooling power:One can notice that the maximal cooling power is directly driven by the figure of merit of the material and of the device, respectively.
- Coefficient of performance [120]:
- Maximalis open voltage, a specific value of . The Carnot factor is the reversible term of . The second term contains the irreversible contributions,It should be noticed that Equation (56) is similar to the expression obtained for the TEG configuration, see Equation (49). Both formulae are well-known and often written as [27,119,121,122]andmaking a convenient definition of the device figure of merit (the exact value of which will depend on which equation is used and the temperature range). Moreover, maximum efficiency or ϕ are only obtained under specific working conditions, and practical applications usually do not exactly fulfill these conditions!
- Maximum coolingThe maximum temperature difference is achieved for and hence for . In this case we get from Equation (54)
4.3. Thermoelectric Heater
- Incoming thermal power:
- Outgoing thermal power:
- Consumed electrical power:
- Coefficient of performance:
- MaximalThe Carnot factor for ϕ is here , whereas the irreversible contribution is given by the second term.
5. The General Conductivity Matrix
5.1. Derivation of the Conductivity Matrix
5.2. The Peltier-Thomson Coefficient
- : equals zero due to particle conservation,
- : “Peltier-Thomson” term,
- electrical work production and dissipation,
- : change in thermal conduction due to heat produced or absorbed.
5.3. The Peltier–Thomson Term
- Pure Peltier, isothermal junction between two materials:
- Thomson, homogeneous material under temperature gradient:withand the heat flux divergence takes the formIf we consider a configuration κ=const, then Equation (71) reduces to
5.4. Local Energy Balance
6. Relative Current and Thermoelectric Potential
6.1. Relative Current and Thermoelectric Potential
6.2. Thermoelectric Potential and Local Reduced Efficiency for a Thermogenerator
6.3. Compatibility Approach
7. Optimum Device Design and FGM
8. Conclusions
Acknowledgements
References
- Seebeck, T.J. Ueber den Magnetismus der galvenischen Kette. Technical report for the Royal Prussian Academy of Science: Berlin, Germany, 1821. [Google Scholar]
- Seebeck, T.J. Magnetische Polarisation der Metalle und Erze durch Temperatur-Differenz. Technical report for the Royal Prussian Academy of Science: Berlin, Germay, 1823. [Google Scholar]
- Seebeck, T.J. Ueber die magnetische Polarisation der Metalle und Erze durch Temperatur-Differenz. Annalen der Physik 1826, 82, 1–20. [Google Scholar] [CrossRef]
- Seebeck actually misinterpreted the observed effect as a thermomagnetic coupling. The correct interpretation of the effect was given later by Oersted. Nevertheless, some authors consider Alessandro Volta to be at the origin of the discovery of this thermoelectric effect [172,173]. The introduction of additional effects due to a magnetic field into the Onsager relations is possible, see e.g. the Nernst effect and Ettinghausen effect [21,22,35,117].
- Peltier, J.C.A. Nouvelles expériences sur la caloricité des courants électrique. Annales de Chimie et de Physique 1834, 56, 371–386. [Google Scholar]
- Thomson, W. On the Mechanical Theory of Thermo-electric Currents. Trans. R. Soc. Edinburgh: Earth Sci. 1851, 3, 91–98. [Google Scholar]
- Kohlrausch, F. Ueber den stationären Temperaturzustand eines elektrisch geheizten Leiters. Annalen der Physik 1900, 306, 132–158. [Google Scholar] [CrossRef]
- Diesselhorst, H. Ueber das Problem eines elektrisch erwärmten Leiters. Annalen der Physik 1900, 306, 312–325. [Google Scholar] [CrossRef]
- Lord Rayleigh. On the thermodynamic efficiency of the thermopile. Philosophical Magazine Series 5 1885, 20, 361–363. [Google Scholar]
- Altenkirch, E. Über den Nutzeffekt der Thermosäulen. Physikalische Zeitschrift 1909, 10, 560–580. [Google Scholar]
- Altenkirch, E. Elektrothermische Kälteerzeugung und reversible elektrische Heizung. Physikalische Zeitschrift 1911, 12, 920–924. [Google Scholar]
- The transport parameters are often used without subscripts: σ ≡ σT is the isothermal conductivity and κ ≡ κJ the thermal conductivity under zero current.
- Telkes, M. Technical Report for Westinghouse: Pittsburgh, PA, USA, 1938; R-94264-8.
- Wood, C. Materials for thermoelectric energy conversion. Rep. Prog. Phys. 1988, 51, 459–539. [Google Scholar] [CrossRef]
- Telkes, M. The Efficiency of Thermoelectric Generators. I. J. Appl. Phys. 1947, 18, 1116–1127. [Google Scholar] [CrossRef]
- Telkes, M. Solar Thermoelectric Generators. J. Appl. Phys. 1954, 25, 765–777. [Google Scholar] [CrossRef]
- Telkes, M. Power Output of Thermoelectric Generators. J. Appl. Phys. 1954, 25, 1058–1059. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. II. Phys. Rev. 1931, 38, 2265–2279. [Google Scholar] [CrossRef]
- Onsager, L. Theories and Problems of Liquid Diffusion. Ann. N.Y. Acad. Sci. 1945, 46, 241–265. [Google Scholar] [CrossRef] [PubMed]
- Callen, H.B. The Application of Onsager’s Reciprocal Relations to Thermoelectric, Thermomagnetic, and Galvanomagnetic Effects. Phys. Rev. 1948, 73, 1349–1358. [Google Scholar] [CrossRef]
- Callen, H.B. On the theory of irreversible processes. PhD thesis, Massachusetts Institute of Technology - (M.I.T.), Cambridge, MA, USA, 1947. [Google Scholar]
- de Groot, S.R. Thermodynamics of Irreversible Processes; North-Holland Publishing Company: Amstedam, The Netherlands, 1963. [Google Scholar]
- Domenicali, C.A. Stationary Temperature Distribution in an Electrically Heated Conductor. J. Appl. Phys. 1954, 25, 1310–1311. [Google Scholar] [CrossRef]
- Joffe, A.F. The Revival of Thermoelectricity. Sci. Am. 1958, 199, 31–37. [Google Scholar] [CrossRef]
- Goldsmid, H.J.; Douglas, R.W. The use of semiconductors in thermoelectric refrigeration. Br. J. Appl. Phys. 1954, 5, 386. [Google Scholar] [CrossRef]
- Ioffe, A. Semiconductor Thermoelements and Thermoelectric Cooling; Infosearch, ltd.: London, UK, 1957. [Google Scholar]
- Joffe, A. Heat transfer in semiconductors. Can. J. Phys. 1956, 34, 1342–1355. [Google Scholar] [CrossRef]
- Joffe, A.F.; Stil’bans, L.S. Physical problems of thermoelectricity. Rep. Prog. Phys. 1959, 22, 167. [Google Scholar] [CrossRef]
- Tolman, R.C.; Fine, P.C. On the Irreversible Production of Entropy. Rev. Mod. Phys. 1948, 20, 51–77. [Google Scholar] [CrossRef]
- Bridgman, P.W. A Critical Thermodynamic Discussion of the Volta, Thermo-electric and Thermionic Effects. Phys. Rev. 1919, 14, 306–347. [Google Scholar] [CrossRef]
- Bridgman, P. On the nature of the transverse thermo-magnetic effect and the transverse thermo-electric effect in crystals. Proc. Natl. Acad. Sci. USA 1929, 15, 768–773. [Google Scholar] [CrossRef] [PubMed]
- Bridgman, P. Comments on the Note by E. H. Kennard on ”Entropy, Reversible Processes and Thermo-Couples”. Proc. Natl. Acad. Sci. USA 1932, 18, 242–245. [Google Scholar] [CrossRef] [PubMed]
- Bridgman, P.W. The Second Law of Thermodynamics and Irreversible Processes. Phys. Rev. 1940, 58, 845. [Google Scholar] [CrossRef]
- Sommerfeld, A.; Frank, N.H. The Statistical theory of thermoelectric, galvano- and thermomagnetic phenomena in metals. Rev. Mod. Phys. 1931, 3, 1–42. [Google Scholar] [CrossRef]
- Darrow, K.K. Statistical Theories of Matter, Radiation and Electricity. Rev. Mod. Phys. 1929, 1, 90. [Google Scholar] [CrossRef]
- Haase, R. Thermodynamisch-phänomenologische Theorie der irreversiblen Prozesse. In Ergebnisse der Exakten Naturwissenschaften; Springer: Berlin, Germany, 1952; Volume 26, pp. 56–164. [Google Scholar]
- Domenicali, C.A. Irreversible Thermodynamics of Thermoelectric Effects in Inhomogeneous, Anisotropic Media. Phys. Rev. 1953, 92, 877–881. [Google Scholar] [CrossRef]
- Domenicali, C.A. Irreversible Thermodynamics of Thermoelectricity. Rev. Mod. Phys. 1954, 26, 237–275. [Google Scholar] [CrossRef]
- Fieschi, R.; Groot, S.D.; Mazur, P.; Vlieger, J. Thermodynamical theory of galvanomagnetic and thermomagnetic phenomena II: Reciprocal relations for moving anisotropic mixtures. Physica 1954, 20, 245–258. [Google Scholar] [CrossRef]
- Fieschi, R.; Groot, S.D.; Mazur, P. Thermodynamical theory of galvanomagnetic and thermomagnetic phenomena. I: Reciprocal relations in anisotropic metals. Physica 1954, 20, 67–76. [Google Scholar] [CrossRef]
- Fieschi, R.; Groot, S.D.; Mazur, P. Thermodynamical theory of galvanomagnetic and thermomagnetic phenomena III: Explicit expressions for the measurable effects in isotropic metals. Physica 1954, 20, 259–273. [Google Scholar] [CrossRef]
- de Groot, S.; van Kampen, N. On the derivation of reciprocal relations between irreversible processes. Physica 1954, 21, 39–47. [Google Scholar] [CrossRef]
- Bernard, W.; Callen, H.B. Irreversible Thermodynamics of Nonlinear Processes and Noise in Driven Systems. Rev. Mod. Phys. 1959, 31, 1017–1044. [Google Scholar] [CrossRef]
- Tykodi, R.J. Thermodynamics, Stationary States, and Steady-Rate Processes. III. The Thermocouple Revisited. J. Chem. Phys. 1959, 31, 1517–1521. [Google Scholar] [CrossRef]
- Miller, D.G. Thermodynamics of Irreversible Processes. The Experimental Verification of the Onsager Reciprocal Relations. Chem. Rev. 1960, 60, 15–37. [Google Scholar] [CrossRef]
- Sherman, B.; Heikes, R.; R.W. Ure, J. Calculation of efficiency of thermoelectric devices. J. Appl. Phys. 1960, 31, 1–16. [Google Scholar] [CrossRef]
- Littman, H.; Davidson, B. Theoretical Bound on the Thermoelectric Figure of Merit from Irreversible Thermodynamics. J. Appl. Phys. 1961, 32, 217–219. [Google Scholar] [CrossRef]
- Clingman, W. Entropy production and optimum device design. Adv. Energy Convers. 1961, 1, 61–79. [Google Scholar] [CrossRef]
- Clingman, W. New Concepts in Thermoelectric Device Design. Proc. IRE 1961, 49, 1155–1160. [Google Scholar] [CrossRef]
- Littman, H. A Clarification of the Theoretical Upper Bound on the Thermoelectric “Figure of Merit” Derived from Irreversible Thermodynamics. J. Appl. Phys. 1962, 33, 2655–2656. [Google Scholar] [CrossRef]
- El-Saden, M.R. Irreversible Thermodynamics and the Theoretical Bound on the Thermomagnetic Figure of Merit. J. Appl. Phys. 1962, 33, 3145–3146. [Google Scholar] [CrossRef]
- Nourbehecht, B. Irreversible thermodynamic effects in inhomogeneous media and their applications in certain geoelectric problems. Technical report for Geophysics Laboratory - Massachusetts Institute of Technology: Cambridge, MA, USA, 1963. [Google Scholar]
- Borrego, J. Zener’s maximum efficiency derived from irreversible thermodynamics. Proc. IEEE 1964, 52, 95. [Google Scholar] [CrossRef]
- Osterle, J. A unified treatment of the thermodynamics of steady-state energy conversion. Appl. Sci. Res. 1964, 12, 425–434. [Google Scholar]
- Curzon, F.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Andresen, B.; Salamon, P.; Berry, R.S. Thermodynamics in finite time: Extremals for imperfect heat engines. J. Chem. Phys. 1977, 66, 1571–1577. [Google Scholar] [CrossRef]
- Hatsopoulos, G.N.; Keenan, J.H. Thermoelectricity. In Principles of General Thermodynamics; John Wiley & Sons: New York, NY, USA, 1981; pp. 675–683. [Google Scholar]
- Salamon, P.; Nitzan, A. Finite time optimizations of a Newton’s law Carnot cycle. J. Chem. Phys. 1981, 74, 3546–3560. [Google Scholar] [CrossRef]
- Ondrechen, M.J.; Rubin, M.H.; Band, Y.B. The generalized Carnot cycle: A working fluid operating in finite time between finite heat sources and sinks. J. Chem. Phys. 1983, 78, 4721–4727. [Google Scholar] [CrossRef]
- Gupta, V.K.; Shanker, G.; Saraf, B.; Sharma, N.K. Experiment to verify the second law of thermodynamics using a thermoelectric device. Am. J. Phys. 1984, 52, 625–628. [Google Scholar] [CrossRef]
- Rockwood, A.L. Relationship of thermoelectricity to electronic entropy. Phys. Rev. A 1984, 30, 2843–2844. [Google Scholar] [CrossRef]
- Vos, A.D. Thermodynamics of radiation energy conversion in one and in three physical dimensions. J. Phys. Chem. Solids 1988, 49, 725–730. [Google Scholar] [CrossRef]
- Mackey, M.C. The dynamic origin of increasing entropy. Rev. Mod. Phys. 1989, 61, 981. [Google Scholar] [CrossRef]
- Rowe, D.M. (Ed.) CRC Handbook of Thermoelectrics; RC: Boca Raton, FL, USA, 1995.
- Rowe, D.M. (Ed.) CRC Handbook of Thermoelectrics: Macro to Nano; RC: Boca Raton, FL, USA, 2006.
- Snyder, G.J. Thermoelectric Power Generation: Efficiency and Compatibility. In CRC Handbook of Thermoelectrics: Macro to Nano; Rowe, D.M., Ed.; Taylor and Francis: Boca Raton, FL, USA, 2006; Chapter 9. [Google Scholar]
- Riffat, S.; Ma, X. Thermoelectrics: a review of present and potential applications. Appl. Therm. Eng. 2003, 23, 913–935. [Google Scholar] [CrossRef]
- Gordon, J.M. Generalized power versus efficiency characteristics of heat engines: The thermoelectric generator as an instructive illustration. Am. J. Phys. 1991, 59, 551–555. [Google Scholar] [CrossRef]
- Lampinen, M.J. Thermodynamic analysis of thermoelectric generator. J. Appl. Phys. 1991, 69, 4318–4323. [Google Scholar] [CrossRef]
- Wu, C. Heat transfer effect on the specific power availability of heat engines. Energy Convers. Manage. 1993, 34, 1239–1247. [Google Scholar] [CrossRef]
- Özkaynak, S.; Gökun, S.; Yavuz, H. Finite-time thermodynamic analysis of a radiative heat engine with internal irreversibility. J. Phys. D: Appl. Phys. 1994, 27, 1139. [Google Scholar] [CrossRef]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Bejan, A. Method of entropy generation minimization, or modeling and optimization based on combined heat transfer and thermodynamics. Revue Gnrale de Thermique 1996, 35, 637–646. [Google Scholar] [CrossRef]
- Parrott, J.E. Thermodynamic Theory of Transport Processes in Semiconductors. IEEE Trans. Electron Devices 1996, 43, 809–826. [Google Scholar] [CrossRef]
- Agrawal, D.C.; Menon, V.J. The thermoelectric generator as an endoreversible Carnot engine. J. Phys. D: Appl. Phys. 1997, 30, 357. [Google Scholar] [CrossRef]
- Chen, J.; Yan, Z.; Wu, L. Nonequilibrium thermodynamic analysis of a thermoelectric device. Energy 1997, 22, 979–985. [Google Scholar] [CrossRef]
- Hoffmann, K.H.; Burzler, J.M.; Schubert, S. Endoreversible Thermodynamics. J. Non-Equilib. Thermodyn. 1997, 22, 311–355. [Google Scholar]
- Chen, L.; Wu, C.; Sun, F. Finite Time Thermodynamic Optimization or Entropy Generation Minimization of Energy Systems. J. Non-Equilib. Thermodyn. 1999, 24, 327–359. [Google Scholar] [CrossRef]
- Arenas, A.; Vázquez, J.; Sanz-Bobi, M.A.; Palacios, R. Performance of a Thermoelectric Module Using the Thermodynamic Relationship Temperature-Entropy (T-S). In Proceedings of XIX International Conference on Thermoelectrics, Cardiff, UK, 2000.
- Nuwayhid, R.Y.; Moukalled, F.; Noueihed, N. On entropy generation in thermoelectric devices. Energy Convers. Manage. 2000, 41, 891–914. [Google Scholar] [CrossRef]
- Chua, H.T.; Ng, K.C.; Xuan, X.C.; Yap, C.; Gordon, J.M. Temperature-entropy formulation of thermoelectric thermodynamic cycles. Phys. Rev. E 2002, 65, 056111. [Google Scholar] [CrossRef] [PubMed]
- Garrido, J. Observable Variables in Thermoelectric Phenomena. J. Phys. Chem. B 2002, 106, 10722–10724. [Google Scholar] [CrossRef]
- Xuan, X.C. Optimum design of a thermoelectric device. Semicond. Sci. Technol. 2002, 17, 114. [Google Scholar] [CrossRef]
- Bell, L. Alternate thermoelectric thermodynamic cycles with improved power generation efficiencies. In Proceedings of Thermoelectrics, 2003 Twenty-Second International Conference on - ICT, La Grande-Motte, France, 2003.
- Chakraborty, A. Thermoelectric cooling devices - thermodynamic modelling and their application in adsorption. PhD thesis, Department of Mechanical Engineering - National University of Singapore, Singapore, 2005. [Google Scholar]
- Chakraborty, A.; Saha, B.; Koyama, S.; Ng, K. Thermodynamic modelling of a solid state thermoelectric cooling device: Temperature-entropy analysis. Int. J. Heat Mass Transfer 2006, 49, 3547–3554. [Google Scholar] [CrossRef]
- Chakraborty, A.; Ng, K.C. Thermodynamic formulation of temperature-entropy diagram for the transient operation of a pulsed thermoelectric cooler. Int. J. Heat Mass Transfer 2006, 49, 1845–1850. [Google Scholar] [CrossRef]
- Pramanick, A.; Das, P. Constructal design of a thermoelectric device. Int. J. Heat Mass Transfer 2006, 49, 1420–1429. [Google Scholar] [CrossRef]
- Xuan, X.; Li, D. Thermodynamic analysis of electrokinetic energy conversion. J. Power Sources 2006, 156, 677–684. [Google Scholar] [CrossRef]
- Chen, M.; Rosendahl, L.; Bach, I.; Condra, T.; Pedersen, J. Irreversible transfer processes of thermoelectric generators. Am. J. Phys. 2007, 75, 815–820. [Google Scholar] [CrossRef]
- Fronczak, A.; Fronczak, P.; Hołyst, J.A. Thermodynamic forces, flows, and Onsager coefficients in complex networks. Phys. Rev. E 2007, 76, 061106. [Google Scholar] [CrossRef] [PubMed]
- Izumida, Y.; Okuda, K. Onsager coefficients of a finite-time Carnot cycle. Phys. Rev. E 2009, 80, 021121. [Google Scholar] [CrossRef] [PubMed]
- Goddard, J. On the Thermoelectricity of W. Thomson: Towards a Theory of Thermoelastic Conductors. J. Elast. 2011, 104, 267–280. [Google Scholar] [CrossRef]
- Vining, C.B. The thermoelectric process. In Materials Research Society Symposium Proceedings: Thermoelectric Materials - New Directions and Approaches; Tritt, T., Kanatzidis, M., Lyon, H.B., Jr., Mahan, G., Eds.; Materials Research Society: Warrendale, PA, USA, 1997; pp. 3–13. [Google Scholar]
- Strictly speaking, a small interaction level is needed in order to reach thermalization of the gas.
- The chemical potential is defined as the mean Gibbs free energy per particle. In TE materials, this holds for the electrochemical potential.
- Normally e is the elementary charge. Here e is negative for electrons, but positive if holes are considered.
- Agrawal, M. Basics of Irreversible Thermodynamics; Stanford University: Stanford, CA, USA, 2008. [Google Scholar]
- Tschoegl, N. Fundamentals of Equilibrium and Steady-state Thermodynamics; Elsevier Science Ltd: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Rocard, Y. Thermodynamique, 2nd ed.; Masson: Paris, France, 1967. [Google Scholar]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1968. [Google Scholar]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; Wiley-Interscience: New York, NY, USA, 1971. [Google Scholar]
- Pottier, N. Physique statisitique hors équilibre, processus irréversibles linéaires; Savoirs Actuels EDP Sciences/CNRS Editions: Paris, France, 2007. [Google Scholar]
- Callen, H.B.; Welton, T.A. Irreversibility and Generalized Noise. Phys. Rev. 1951, 83, 34–40. [Google Scholar] [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 1966, 29, 255. [Google Scholar] [CrossRef]
- Chandler, D. Introduction to Modern Statistical Mechanics; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- The off-diagonal terms of the kinetic matrix are symmetric, only if the correct thermodynamic potentials of the system has been chosen. In the case of a Fermi gas the correct potentials are μe/T and 1/T, see Section 2.2 for an example and 5.1 for a counter-example.
- This time reversal symmetry is broken under the application of Coriolis or magnetic force.
- Callen, H.B.; Greene, R.F. On a Theorem of Irreversible Thermodynamics. Phys. Rev. 1952, 86, 702–710. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics; John Wiley & Sons, Inc.: New York, NY, USA, 1960. [Google Scholar]
- Zener, C. Putting Electrons to work. Trans. the Am. Soc. Met. 1961, 53, 1052–1068. [Google Scholar]
- The reader will take note of the naming conventions with respect to fluxes and flows: is the heat transfer rate or heat flow in units of 1 W. For the sake of simplicity the dot is sometimes omitted. Often used is the heat flux which is the heat transfer rate per cross-sectional area in units of 1 W/m2.
- With the restriction to one type of semiconductor (p-type, the index can be omitted from the material coefficients in the following calculations, i.e., αp = α or Kp = K.
- Seifert, W.; Ueltzen, M.; Müller, E. One-dimensional Modelling of Thermoelectric Cooling. Physica Status Solidi (a) 2002, 1, 277–290. [Google Scholar] [CrossRef]
- Seifert, W.; Müller, E.; Walczak, S. Generalized analytic description of onedimensional non-homogeneous TE cooler and generator elements based on the compatibility approach. In Proceedings of 25th International Conference on Thermoelectrics, Vienna, Austria, 6–10 August 2006.
- Harman, T.C.; Honig, J.M. Thermoelectric and Thermomagnetic Effects and Applications; McGraw-Hill Book Company: New York, NY, USA, 1967. [Google Scholar]
- The Joule effect induced by the circulation of the electrical current has been often considered to be spread over the hot and cold source in equal contributions . Obviously, this is valid only under CPM condition, see Equations (43), but sufficient for most design.
- Goldsmid, H.J. Electronic Refrigeration; Pion: London, UK, 1986. [Google Scholar]
- We follow here Sherman’s notation and use ϕ instead of C.O.P. in appropriate formulae.
- Heikes, R.R.; Roland W. Ure, J. Thermoelectricity: Science and Engineering; Interscience Publishers, Inc.: New York, NY, USA, 1961. [Google Scholar]
- Egli, P.H. Thermoelectricity; John Wiley & Sons, Inc.: New York, NY, USA, 1960. [Google Scholar]
- Greene, R.F.; Callen, H.B. On a Theorem of Irreversible Thermodynamics. II. Phys. Rev. 1952, 88, 1387–1391. [Google Scholar] [CrossRef]
- Gascoin, F.; Goupil, C.; de Vaulx, C.; Papavero, A. Non-homogeneous thermoelectric material study using the linear reponse approach. In Proceedings of The 29th International Conference on Thermoelectrics, Shanghai, China, 30 May–3 June 2010.
- Ball, C.; Jesser, W.; Maddux, J. The distributed Peltier effect and its influence on cooling devices. In Proceedings of The 14th International Conference on Thermoelectrics, St. Petersburg, Russia, 27–30 June 1995.
- Buist, R.J. The extrinsic Thomson effect. In Proceedings of The 14th International Conference on Thermoelectrics, St. Petersburg, Russia, 27–30 June 1995.
- Belov, I.; Volkov, V.; Manyakin, O. Optimization of Peltier thermocouple using distributed Peltier effect. In Proceedings of Eighteenth International Conference on Thermoelectrics, 1999, Piscataway, NI, USA, 29 August–2 September 1999.
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media, 2nd ed.; Butterworth Heinemann: Oxford, UK, 1984. [Google Scholar]
- Snyder, G.J.; Fleurial, J.P.; Caillat, T.; Yang, R.; Chen, G. Supercooling of Peltier cooler using a current pulse. J. Appl. Phys. 2002, 92, 1564–1569. [Google Scholar] [CrossRef]
- Stil’bans, L.; Fedorovitch, N. Cooling of thermoelectric cells under nonstationary conditions. Sov. Phys. Tech. Phys. 1958, 3, 460–463. [Google Scholar]
- Parrott, J.E. The interpretation of the stationary and transient behaviour of refrigerating thermocouples. Solid-State Electron. 1960, 1, 135–143. [Google Scholar] [CrossRef]
- Gray, P.E. The Dynamic Behavior of Thermoelectric Devices; John Wiley & Sons, Inc.: Cambridge, MA, USA, 1960. [Google Scholar]
- Reich, A.D.; Madigan, J.R. Transient Response of a Thermocouple Circuit Under Steady Currents. J. Appl. Phys. 1961, 32, 294–301. [Google Scholar] [CrossRef]
- Landecker, K.; Findlay, A. Study of the fast transient behaviour of Peltier junctions. Solid-State Electron. 1961, 3, 239–260. [Google Scholar] [CrossRef]
- Parrott, J. The stationary and transient characteristics of refrigerating thermocouples. Adv. Energy Convers. 1962, 2, 141–152. [Google Scholar] [CrossRef]
- Naer, V. Transient regimes of thermoelectric cooling and heating units. J. Eng. Phys. Thermophys. 1965, 8, 340–344. [Google Scholar] [CrossRef]
- Iordanishvili, E.K.; Malkovich, B.E.S. Experimental study of transient thermoelectric cooling. J. Eng. Phys. Thermophys. 1972, 23, 1158–1163. [Google Scholar] [CrossRef]
- Miner, A.; Majumdar, A.; Ghoshal, U. Thermoelectromechanical refrigeration based on transient thermoelectric effects. Appl. Phys. Lett. 1999, 75, 1176–1178. [Google Scholar] [CrossRef]
- Thonhauser, T.; Mahan, G.D.; Zikatanov, L.; Roe, J. Improved supercooling in transient thermoelectrics. Appl. Phys. Lett. 2004, 85, 3247–3249. [Google Scholar] [CrossRef]
- Bechtold, T.; Rudnyi, E.B.; Korvink, J.G. Dynamic electro-thermal simulation of microsystems - a review. J. Micromech. Microeng. 2005, 15, R17–R31. [Google Scholar] [CrossRef]
- Hussein, M.; Hanim, S.; Zamri, Y.M. The transient response for different types of erodable surface thermocouples using finite element analysis. Therm. Sci. 2007, 11, 49–64. [Google Scholar]
- Zhou, Q.; Bian, Z.; Shakouri, A. Pulsed cooling of inhomogeneous thermoelectric materials. J. Phys. D: Appl. Phys. 2007, 40, 4376–4381. [Google Scholar] [CrossRef]
- Ursell, T.; Snyder, G. Compatibility of segmented thermoelectric generators. In Proceedings of Twenty-First International Conference on Thermoelectrics, Long Beach, CA, USA, 25 August–29 August 2002.
- Snyder, G.J.; Ursell, T.S. Thermoelectric Efficiency and Compatibility. Phys. Rev. Lett. 2003, 91, 148301. [Google Scholar] [CrossRef] [PubMed]
- A more general definition of u seems possible when writing the relative current density in terms of fluctuating currents which are indeed 3D. In this context, particle and heat flow should be considered in an anisotropic medium where the material parameters are tensors, see e.g., [174].
- Goupil, C. Thermodynamics of the thermoelectric potential. J. Appl. Phys. 2009, 106, 104907. [Google Scholar] [CrossRef]
- Power output is defined here according to thermodynamic rules: quantities input to the system are positive.
- Seifert, W.; Zabrocki, K.; Müller, E.; Snyder, G. Power-related compatibility and maximum electrical power output of a thermogenerator. Phys. Stat. Sol. A 2010, 207, 2399–2406. [Google Scholar] [CrossRef]
- The Carnot engine exchanges energy in a reversible form, that means after an infinite time. Therefore, the Carnot engine transforms energy efficiently but with zero power.
- Replace in [116] Equation (9), right hand side, the ± sign by a minus sign valid for both the pump up and the pump down situation.
- Seifert, W.; Müller, E.; Snyder, G.; Walczak, S. Compatibility factor for the power output of a thermogenerator. Phys. Stat. Sol. (RRL) 2007, 1, 250–252. [Google Scholar] [CrossRef]
- Seifert, W.; Müller, E.; Walczak, S. Local optimization strategy based on first principles of thermoelectrics. Phys. Stat. Sol. A 2008, 205, 2908–2918. [Google Scholar] [CrossRef]
- Seifert, W.; Zabrocki, K.; Snyder, G.; Müller, E. The compatibility approach in the classical theory of thermoelectricity seen from the perspective of variational calculus. Phys. Stat. Sol. A 2010, 207, 760–765. [Google Scholar] [CrossRef]
- In [116] and [153] reduced efficiencies , are introduced for both TEG and TEC, respectively.
- Seifert, W.; Pluschke, V.; Goupil, C.; Zabrocki, K.; Müller, E.; Snyder, G. Maximum performance in self-compatible thermoelectric elements. J. Mater. Res. 2011, in press. [Google Scholar]
- The relative current density is defined by Equation (75); the 1D variants are espectively , whereby the temperature gradient decides the sign of u. Note that T(x) peaks in the interior of the TE element only far above the optimum current for maximum efficiency and maximum coefficient of performance. Then u has a pole.
- Note that Sherman et al. used the function ϵ(T) instead of optimal reduced efficiency.
- Cadoff, I.B.; Miller, E. The thermoelectric circuit. In Thermoelectric Materials and Devices; Cadoff, I.B., Miller, E., Eds.; Materials Technology Series; Reinhold Publishing Cooperation: New York, NY, USA, 1960; Chapter 2; pp. 18–32. [Google Scholar]
- Kerr, D.L. Design calculations for thermoelectric generators. In Thermoelectric Materials and Devices; Cadoff, I.B., Miller, E., Eds.; Materials Technology Series. Reinhold Publishing Cooperation: New York, NY, USA, 1960; Chapter 16; pp. 227–249. [Google Scholar]
- Vought, R.H. Design calculations for Peltier cooling. In Thermoelectric Materials and Devices; Cadoff, I.B., Miller, E., Eds.; Materials Technology Series; Reinhold Publishing Cooperation: New York, 1960; chapter 17; pp. 250–274. [Google Scholar]
- Sickert, R. A Thermoelectric Refrigerating System for Submarines. Electr. Eng. 1960, 79, 364–371. [Google Scholar] [CrossRef]
- Ure, R.W., Jr.; Heikes, R.R. Theoretical Calculation of Device Performance. In Thermoelectricity: Science and Engineering; Heikes, R.R., Ure, R.W., Jr., Eds.; Interscience Publishers, Inc.: New York, NY, USA, 1961; Chapter 15; pp. 458–517. [Google Scholar]
- Min, G.; Rowe, D.M. Peltier Devices as Generators. In CRC Handbook of Thermoelectrics; Rowe, D.M., Ed.; CRC Press: RC, Boca Raton, FL, USA, 1995; Chapter 38; pp. 479–488. [Google Scholar]
- Min, G. Thermoelectric Module Design Theories. In CRC Handbook of Thermoelectrics: Macro to Nano; Rowe, D.M., Ed.; Taylor and Francis: Boca Raton, FL, USA, 2006; Chapter 11. [Google Scholar]
- Shiota, I.; Miyamoto, Y. (Eds.) Functionally Graded Material 1996; AIST Tsukuba Research Center: Tsukuba, Japan, 1996.
- Helmers, L.; Müller, E.; Schilz, J.; Kaysser, W. Graded and stacked thermoelectric generators - numerical description and maximisation of output power. Mater. Sci. Eng., B 1998, 56, 60–68. [Google Scholar] [CrossRef]
- Müller, E.; Drašar, Č.; Schilz, J.; Kaysser, W.A. Functionally graded materials for sensor and energy applications. Mater. Sci. Eng. A 2003, 362, 17–39. [Google Scholar] [CrossRef]
- Kuznetsov, V.L. Functionally Graded Materials for Thermoelectric Applications. In CRC Handbook of Thermoelectrics: Macro to Nano; Taylor and Francis: Boca Raton, FL, USA, 2006; Chapter 38. [Google Scholar]
- Müller, E.; Zabrocki, K.; Goupil, C.; Snyder, G.; Seifert, W. Functionally graded thermoelectric generator and cooler elements. In CRC Handbook of Thermoelectrics: Thermoelectrics and Its Energy Harvesting; Rowe, D.M., Ed.; RC: Boca Raton, FL, USA, 2012; Chapter 4. [Google Scholar]
- Zabrocki, K.; Müller, E.; Seifert, W.; Trimper, S. Performance optimization of a thermoelectric generator element with linear material profiles in a 1D setup. J. Mater. Res. 2011, in press. [Google Scholar]
- Müller, E.; Walczak, S.; Seifert, W. Optimization strategies for segmented Peltier coolers. Phys. Stat. Sol. A 2006, 203, 2128–2141. [Google Scholar] [CrossRef]
- Anatychuk, L. Seebeck or Volta? J. Thermoelectricity 1994, 1994, 9–10. [Google Scholar]
- Anatychuk, L. On the discovery of thermoelectricity by Volta. J. Thermoelectricity 2004, 2004, 5–10. [Google Scholar]
- Buda, I.S.; Lutsyak, V.S.; Khamets, U.M.; Shcherbina, L.A. Thermodynamic definition of the thermoelectric figure of merit of an anisotropic medium. Phys. Stat. Sol. A 1991, 123, K139–K143. [Google Scholar] [CrossRef]

© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Goupil, C.; Seifert, W.; Zabrocki, K.; Müller, E.; Snyder, G.J. Thermodynamics of Thermoelectric Phenomena and Applications. Entropy 2011, 13, 1481-1517. https://doi.org/10.3390/e13081481
Goupil C, Seifert W, Zabrocki K, Müller E, Snyder GJ. Thermodynamics of Thermoelectric Phenomena and Applications. Entropy. 2011; 13(8):1481-1517. https://doi.org/10.3390/e13081481
Chicago/Turabian StyleGoupil, Christophe, Wolfgang Seifert, Knud Zabrocki, Eckhart Müller, and G. Jeffrey Snyder. 2011. "Thermodynamics of Thermoelectric Phenomena and Applications" Entropy 13, no. 8: 1481-1517. https://doi.org/10.3390/e13081481
APA StyleGoupil, C., Seifert, W., Zabrocki, K., Müller, E., & Snyder, G. J. (2011). Thermodynamics of Thermoelectric Phenomena and Applications. Entropy, 13(8), 1481-1517. https://doi.org/10.3390/e13081481



