1. Introduction
In recent years, Estimation of Distribution Algorithms (EDAs) have received numerous attention [
2,
3,
4,
5,
6]. In the procedures of research, explicitly learning and building a probabilistic model from the parental distribution, and then sampling new solutions according to the probabilistic model [
7] has been a key focus of researchers. In addition, building the probabilistic model is a statistical learning problem which is a probability estimation in terms of a generalized relative entropy [
8]. Sampling from probabilistic models avoids the disturbance of some of the salient genes represented by the model, which is contrary to what could occur when genetic operators such as crossover and mutation are applied [
9]. The most important characteristic to distinguish between EDAs and Standard Genetic Algorithms (SGA) is the use of probability learning and sampling from the probabilistic model.
As claimed by Zhang and Muhlenbein [
10], EDAs might be a promising method capable of capturing and manipulating the building blocks of chromosomes and hence have become efficient tools for solving hard optimization problems. Some well-known EDAs include cGA [
3], UMDA [
4], GA-EDA [
11], Guided Mutation (EA/G) [
6], Model-Based Evolutionary Algorithm (EA) [
12], Artificial Chromosomes with Genetic Algorithms (ACGA) [
13], Self-Guided GA [
14], and VNS·EDAs [
9],
etc. For the detailed review, please refer to [
7].
If we lack the prior knowledge of concepts necessary to address problems, EDAs would be regarded as good techniques at solving hard problems. EDAs also can be used to characterize the search space of the changing environment [
15]. According to Santana
et al. [
9], however, EDAs may have the overfitting problem in the search space and the probabilistic models can no longer represent the general information. In addition, due to premature convergence of EDAs, the probabilistic models can not provide diversified solutions, which has also resulted in poor performance [
1,
16]. To conquer the aforementioned difficulties facing EDAs, our previous paper [
1] proposed some important guidelines for designing effective EDAs. These proposed guidelines are:
Gradually increasing diversity among the populations.
Using other meta-heuristics algorithms as alternatives to EDAs.
Replacing the procedures of sampling new solutions.
Incorporating EDAs with other heuristics.
The first guideline proposes to use a diversification technique in EDAs. Since EA/G can converge to local optimal solutions quickly or diverge altogether, we added this concept to EA/G by using the adaptive strategy and named the new version EA/G “Adaptive EA/G”. In order to evaluate the performance of Adaptive EA/G, we compared the original EA/G and the ACGA on the NP-Hard single machine scheduling problems considering both the earliness and tardiness costs. When three different stopping criteria were applied (CPU time was divided into short-term, medium-term and long-term scheduling), the result indicated that the Adaptive EA/G statistically significantly outperformed the EA/G and ACGA [
1]. It is interesting to see the Adaptive EA/G under different CPU usages has consistent performances.
In this paper, we illustrate that the second guideline is much more effective in designing EDAs. The well-known EDA, EA/G, was selected again to work with other meta-heuristic methods. Because genetic algorithms (GAs) are widely used in the engineering applications, we blended the concept of GAs with the EA/G for the second guideline. The proposed algorithm is named the “EA/G-GA”, which is used to solve the NP-Hard single machine scheduling problems concerning the weighted earliness and tardiness costs.
The rest of the paper is organized as follows. In
Section 2, we review the single machine scheduling problems, related works of alternating EDAs with GAs, and the problem statements. After that,
Section 3 discusses how implementation of EA/G alternates with GAs.
Section 4 reveals the experimental results whereas the EA/G, Adaptive EA/G, EA/G-GA, and ACGA are evaluated by using the single machine scheduling problems. Finally, the conclusions of this paper are drawn in
Section 5.
2. Literature Review
We review the single machine scheduling problems in the first sub-section, particularly the objective of minimizing the earliness/tardiness cost. Since some similar works related to this paper have been done by other researchers, the relevant results are presented in
Section 2.2. Last but not least, we give the problem definition of the NP-Hard scheduling problems in
Section 2.3.
2.1. Surveys of the Earliness/Tardiness Single Machine Scheduling Problems
As a generalization, the single-machine scheduling problem to minimize the total weighted earliness and tardiness costs is strongly NP-hard [
17]. The earlier works on this problem were due to [
18,
19,
20]. Belouadah
et al. [
21] dealt with a similar problem with the objective of minimizing the total weighted completion time. Later on, Alves and Almeida [
22] developed various dominance rules to solve the problem. In [
23,
24], they presented branch-and-bound algorithms by decomposing the problem into weighted earliness and weighted tardiness sub-problems. Two lower bound procedures were used for each sub-problem. The lower bound for the original problem was the sum of the lower bounds for the two sub-problems. Valente and Alves [
24] analyzed the performance of various heuristic procedures, including dispatching rules, a greedy procedure, and a theory-based decision heuristic.
Several authors have mentioned the earliness/tardiness scheduling problem with equal release dates and no idle time and proposed both exact and heuristic approaches in their literature to solve the problem. They presented branch-and-bound algorithms for the exact approaches [
25,
26,
27]. The lower bounding procedure of Abdul-Razaq and Potts [
25] applied sub-gradient optimization and the dynamic programming state-space relaxation technique, whereas [
26] and [
27] used Lagrangian relaxation and the multiplier adjustment method. Among these heuristics, Morton [
28] developed several dispatching rules and a filtered beam search procedure to solve the problem. Valente and Alves [
23] presented an additional dispatching rule and a greedy procedure. They also considered the use of dominance rules to further improve the schedule obtained through the heuristic method. Li [
26] presented a neighborhood search algorithm.
In [
29], they developed a new algorithm called the “Electromagnetism-like algorithm” to deal with the single-machine scheduling problem concerning earliness/tardiness penalties. The electromagnetism-like algorithm was originally devised by Birbil
et al. [
30], which can solve continuous problems but need to utilize the random key method in solving discrete problems like the scheduling problems. Therefore, the electromagnetism-like algorithm increases the diversity of inferior solutions, whereas the genetic algorithm operator,
i.e., the crossover operator, recombines solutions to construct better performing algorithms. Experimental results show that the performance of hybrid algorithms is far superior to using the electromagnetism-like algorithm alone.
2.2. Relative Works of Alternating EDAs with GAs
Since the EDAs may not generate diversified solutions in the long run and cause the problem of premature convergency, hybridizing with other metaheuristics, the genetic algorithm in particular, is possibly a good approach to increase diversity among populations. Some researchers have conducted similar studies in their publications [
11,
12,
13]. Their key idea is to use the EDA as an alternative to the genetic algorithms so as to further enhance the quality of the solution by implementing the searching strategy of intensification using the EDAs and diversification via GAs.
In addition to generating a population of chromosomes by probabilistic models or genetic operators in a single generation, there are other possible ways that include sampling from a probabilistic model to obtain a proportional solution and using crossover and mutation operators to generate the rest of solutions. MGSPGA [
31] samples 20% solutions from a probability matrix and the remaining chromosomes are generated by the genetic operators. Consequently, the goal to create a balance between intensification and diversification has been achieved. For the future research project, both approaches mentioned above should be examined because it is still unknown about which approach is better (samples new solutions entirely or partially).
Finally, choosing not to take a sample of the solution from probabilistic models can be advantageous. When we look for solutions to sequential problems, the time complexity of the proportional algorithm is . It is particularly time-consuming when we handle larger size problems. As a result, it is an efficient approach when the EDAs alternate with other metaheuristics.
2.3. Problem Statements
In this paper, we tackle a deterministic single machine scheduling problem without release dates in an attempt to minimize the total sum of earliness and tardiness penalties. A detailed formulation of the problem is described as follows: A set of n independent jobs has to be scheduled without preemptions on a single machine that can handle at most one job at a time. It is assumed that the machine will be continuously available from time zero onwards and unforced machine idle time is not allowed. Job becomes available for the processing at the beginning, requires a processing time and should be completed on its due date . For any given schedule, the earliness and tardiness of can be defined as and respectively, where is the completion time of .
The objective is then to find a schedule that minimizes the sum of the earliness and tardiness penalties of all jobs
where
and
are the earliness and tardiness penalties of job
. Considering the inclusion of both earliness and tardiness costs in the objective function is compatible with the philosophy of just-in-time production, which emphasizes producing goods only when they are needed. The early costs may represent the cost of completing a job early, the deterioration cost of perishable goods or a holding (stock) cost for finished goods. The tardy costs can represent the cost of rush shipping, lost sales and loss of goodwill. We assume that no unforced machine idle time is allowed and let the machine idle only when no job is available for processing. This assumption reflects that the cost of machine idleness is higher than the early cost stemming from completing any job before its due date in a production setting or the capacity of the machine is limited as compared with its demand so that the machine must remain in operation all the time. In [
20] and [
28], they provided some specific examples of production arrangements with these characteristics. A characteristic of the deterministic problem is an assumption that the set of jobs is ready to process jobs in the beginning.
3. EA/G-GA: The Framework of the EDAs with Meta-Heuristic
According to our prior research [
1], EDAs converge faster whereas GAs evolves slowly because meta-heuristics can perform global search in the evolutionary progress. However, meta-heuristics might provide better diversity among populations. Based on these characteristics, we could take advantages on both sides. We employ the EDAs to characterize the parental solutions and then search around the current solution space. After that, meta-heuristics might introduce new solutions into the population to maintain the diversity, which can avoid the premature convergency of EDAs. As an example, we proposed a hybrid framework combining the well-known EDAs, EA/G and Standard Genetic Algorithm (SGA). The proposed algorithm is named “EA/G-GA”.
Alternating the EA/G and GAs in the evolutionary progress is a main characteristic of the EA/G-GA. Once the current generation is done by EA/G, GAs carries out the evolution progress in the next generation. Through the alternation of the EA/G and GAs, the researchers would expect to reduce the computing efforts and avoid the premature convergency of EA/G because the diversity has been improved. The pseudo code of the EA/G-GA is shown as the following.
Algorithm 1: EA/G-GA Main Procedure
: The whole population.
: the set of parent solutions selected from the current population.
t: Current Generation
: Probabilistic matrix at generation
t.
- 1:
- 2:
Initialize and
- 3:
Evaluate()
- 4:
while do
- 5:
Select()
- 6:
if then
- 7:
modelUpdate(, )
- 8:
EAGP(t+1))
- 9:
else
- 10:
GAOperators().
- 11:
end if
- 12:
Evaluate()
- 13:
- 14:
end while
In Step 2, we initialize the population and the probabilistic model
before the evolutionary progress begins. The detailed definition and the initialization method of the probabilistic model are discussed in
Section 3.1. When the evolutionary progress starts, we select good solutions from the current population. In principle, any selection method such as proportional selection and tournament selection can be used for this purpose. For the sake of simplicity, the 2-tournament selection is adopted in our experiments. It randomly draws two members from
and selects the fitter one to become a member in
.
After the selection procedure is done, the while-loop controls the stopping criterion determined by the maximum number of generations. Step 6 decides what kinds of algorithm can be used in the current generation
t. This research conducted some experiments to obtain this parameter setting in
Section 4.1. In this research, when
t can be divided by 2, this generation updates the probabilistic model first (Step 7) and then executes the EA/G (Step 8). The details of the two steps are shown in
Section 3.1 and
Section 3.2 respectively. On the other hand, the GAs is run at the next generation of EA/G. The two algorithms are implemented alternatively. Within this scheme, EA/G-GA keeps the simplicity for the researchers to solve their own specific problems. The following sub-sections explain the details of the proposed algorithm.
3.1. Updating the Probabilistic Model
The probability estimation is a generalized relative entropy [
8], which measures the strength of the variable in EDAs. Probability
is of the form:
where is the probability of job i in position j in a promising solution in the generation t. summarizes the global statistical information about promising solutions obtained from the previous search.
In Step 2 of the EA/G-GA main procedure, each
is initialized to be
, where
n is the number of jobs. This initialization means that all the solutions have the same likelihood to be an optimal solution. The reason for such an initialization is that we have no information about the location of promising solutions. A better initialization procedure can be refer to [
5].
Let
be the number of the solutions in
in which job
i is in position
j and
be the size of
.
in Line 7 is updated as follows:
As in PBIL [
32], we update
in an incremental learning way.
is the learning rate. The larger
λ is, the more
contributes to
. In the above equation, we use the Laplace correction
, instead of
. The Laplace correction [
33,
34,
35] can prevent
from becoming too small.
As soon as the probabilistic matrix is built, jobs are assigned onto each position. The approach of how to utilize the probabilistic model to generate a sequence is illustrated in the next section.
3.2. The Detailed Procedures of EA/G
We use the proportional selection to assign jobs onto each position. Through this proportional selection [
10], it is demonstrated that if the distribution of the new elements matches that of the parent set, a global optimal solution will be found and a factorized distribution algorithm converges globally. The assignment sequence for each position is assigned in random order. A specific parameter of EA/G is
β, which determines the proportion of elite genes copied from elite solution directly. The assignment procedure is determined as follows:
Notation:
S: A set of shuffled sequence determining the sequence of each position to be assigned a job.
Ω: The set of un-arranged jobs.
J: The set of arranged jobs. J is empty in the beginning.
θ: A random probability is drawn from .
i: A selected job by proportional selection
k: The element index of the set S
β: The EA/G parameter controls the proportion of elite genes copied to offspring
Algorithm 2: EA/G Operator- 1:
shuffled the job number []
- 2:
- 3:
EA/G Operator .
- 4:
Output: .
- 5:
while do
- 6:
while do
- 7:
Flip a coin with head probability β;
- 8:
if The head turns up then
- 9:
Select a job i satisfies
- 10:
- 11:
else
- 12:
.
- 13:
end if
- 14:
- 15:
- 16:
end while
- 17:
end while
From the above EA/G operator, is directly copied from the parent or randomly sampled from the probability vector p. The larger β is, the more elements of y are sampled from the probability vector p. In other words, β, similar to the mutation rate in conventional mutation, controls the similarity between offspring and the parent, while the parent can be chosen from the best solutions found so far. After the generation runs the EA/G, the next generation executes the genetic operators which is shown in the next sub-section.
3.3. GAs Operators
When GAs receive the
, genetic operators including the crossover and mutation will deal with it. Two chromosomes are randomly selected to mate in the crossover procedure. There are several crossover methods available for solving the combinatorial problem. The two-point center crossover [
36] is employed in this study with below procedures:
Select two chromosomes and name them as parent 1 and parent 2.
Determine the two cut points, suppose they are at position i and j, copy the genes which are outside the range from i to j to the offspring in the same position.
Copy the remaining genes which are inside the range of parent 1 in the order of relative gene position of parent 2.
The pictorial representation of this crossover operator is shown in
Figure 1:
Figure 1.
Two-point center crossover.
Figure 1.
Two-point center crossover.
Finally, the purpose of the mutation operator is to generate a new chromosome with a better fitness by changing the gene position of the current chromosome. We adopt the swap mutation here because it is easy to implement by setting two positions and exchanging the two values of these positions.
Summary: In the proposed framework, EA/G and GAs are employed in turn. This approach may combine the benefits of providing better convergency brought by the EA/G while maintaining better population diversity by applying the genetic operators. Although EA/G and GAs are used in this framework, it is not limited to these two algorithms. Other EDAs may have the problem of premature convergency, which can be improved when they alternate with other meta-heuristics. This section illustrates the potential implications of the same class of EDAs as well as the meta-heuristic.
In order to validate the performance of the EA/G-GA, we compare it with other algorithms and show the experimental result for solving the single machine scheduling problems under different stopping criteria in
Section 4.
4. Experiment Results of EA/G-GA for Single Machine Scheduling Problems
We first explain the environment settings and then demonstrate the experiment results including the problem instances, parameter configurations, and analysis methods. In order to show the performance of the EA/G-GA, we compare the proposed algorithm with the original version of EA/G [
6], ACGA [
13], and Adaptive EA/G [
1].
4.1. Settings of the Experiments and the Background of Design-of-Experiment
We analyze all the algorithms by running the instances of single machine scheduling problems with minimized earliness/tardiness costs and take the just-in-time production environment into consideration. There are numerous data sets published in the literature [
37] for the single machine scheduling problems, including 20, 30, 40, 50, 60, and 90 jobs. Each data set of 20 jobs up to 50 jobs contains 49 instances (problems) whereas there are 9 instances in the data set of 60 jobs and 90 jobs. We carry out our experiments on these total 214 instances. Each algorithm will replicate every instance 30 times.
In order to show the robustness of the algorithms, we set the stopping criteria based on the number of examined solutions, which are 50,000, 75,000, 100,000, and 125,000 solutions, identical to our previous research [
1]. The four solutions stand for the different implementation environments allowing lower, medium, high, and higher level of CPU time with the same default parameter settings: the population size is 100, the crossover rate is 0.9, and mutation rate is 0.5 across all experiments. Moreover, using 50,000 solutions means the algorithms stop at generation 500.
An important parameter in the proposed algorithm determines when to use the EDA operator. To set this parameter, we validate this setting for EDA and GA combination in the following experiment. Different combinations for EDA and GA are shown in the following table.
The above experiments are conducted with a different number of generations respectively,
i.e., 500, 750, 1000, and 1250. The experimental results are shown in
Figure 2, which have clearly indicated that 1:1 is the best among the five combinations. The 1:1 combination consistently performs better than the others by a different number of generations. In addition, “the higher the ratio of EDA operator, the lower the solution quality” is another interesting aspect we want to point out.
This result is very consistent with our previous research in [
1] where we advocated that the EDA operator may cause the dramatic loss of diversity and lead to poor solution quality. A rule of thumb in the problem solving process is to balance the combination of EDA and GA. The combination could be problem-dependent and this parameter has to be revalidated for other applications. The detailed experiment results for this parameter is available at our website (
http://peterchenweb.appspot.com/publications/sourceCodes/Entropy2011/index.htm).
Table 1.
The combinations of EDA and GA.
Table 1.
The combinations of EDA and GA.
| EDA:GA |
|---|
| 1:1 | The original setting (t % 2) |
| 1:2 | GA operator is used for 2/3 occasions and EDA runs for the 1/3 occasions in the total generations. |
| 1:3 | GA operator is employed for 75% of total generations and EDA runs in the remaining 25% of the entire generations. |
| 2:1 | EDA operator is run in 2/3 of the number of total generations and GA runs for the 1/3 occasions in the whole period. |
| 3:1 | EDA operator is applied for 3/4 occasions and GA is executed in the remaining 1/4 generations. |
Figure 2.
Performance evaluation for different combinations of EDA and GA.
Figure 2.
Performance evaluation for different combinations of EDA and GA.
We first explain the parameter used in the proposed algorithm and then introduce the Design-of-Experiment because the analysis is primarily done by Design-of-Experiment to distinguish the differences of these algorithms. ANOVA is adopted as the comparison method where the source indicates factors and combinations of factors in the ANOVA table. In our case,
Instance and
Method are factors,
DF represents the degree of freedom and
SS is the sum of squares. The mean square is equal to
SS divided by
DF. If the
-value of a factor (source) is less than 0.05, it means that there is a significant difference in this factor [
38]. Because the ANOVA table does not provide the comparisons between/among the levels, we further conduct the Duncan grouping test to differentiate the performances of these algorithms.
Duncan Grouping test is used to further distinguish the performance of the levels belonged to the factor. In Duncan Group test, when the algorithms share the same alphabet, it means they are in the same group so that there is no difference between/among these algorithms. On the other hand, as soon as they are not in the same group (or to share the same alphabet), there is significant difference between/among them. The detailed explanations of statistics terms are available in [
38]. Finally, the following subsections are the empirical results of solving the single machine scheduling problems.
4.2. The Empirical Results
We compare the proposed algorithms with the EA/G, ACGA, and Adaptive EA/G discussed in other literature. These algorithms are tested under various stopping criteria where 50000, 75000, 100000, and 125000 solutions are evaluated respectively. The ANOVA
Table 2 to
Table 5 implies that these compared algorithms have strong significance because the P-Value is less than 0.0001. The ANOVA results show there is difference among the compared algorithms. To distinguish the differences among the algorithms, a famous statistic method Duncan grouping analysis is used to compare the significance of these algorithms.
Table 2.
ANOVA results at the stopping criterion of 50,000 examined solutions.
Table 2.
ANOVA results at the stopping criterion of 50,000 examined solutions.
| Source | DF | SS | Mean Square | F Value | P Value |
|---|
| instances | 213 | 5.32E+12 | 24966564338 | 1.41E+07 | <.0001 |
| method | 3 | 990458.8414 | 330152.9471 | 186.73 | <.0001 |
| instances*method | 639 | 21834746.74 | 34170.1827 | 19.33 | <.0001 |
| Error | 24824 | 43891753.69 | 1768.117696 | | |
| Corrected Total | 25679 | 5.32E+12 | | | |
Table 3.
ANOVA results at the stopping criterion of 75,000 examined solutions.
Table 3.
ANOVA results at the stopping criterion of 75,000 examined solutions.
| Source | DF | SS | Mean Square | F Value | P Value |
|---|
| instances | 213 | 5.31E+12 | 24941096330 | 1.64E+07 | <.0001 |
| method | 3 | 107158.5288 | 35719.50961 | 23.43 | <.0001 |
| instances*method | 639 | 2569676.571 | 4021.403085 | 2.64 | <.0001 |
| Error | 24824 | 37840343.96 | 1524.345148 | | |
| Corrected Total | 25679 | 5.31E+12 | | | |
Table 4.
ANOVA results at the stopping criterion of 100,000 examined solutions.
Table 4.
ANOVA results at the stopping criterion of 100,000 examined solutions.
| Source | DF | SS | Mean Square | F Value | P Value |
|---|
| instances | 213 | 5.31E+12 | 24936063497 | 1.74E+07 | <.0001 |
| method | 3 | 92494.17975 | 30831.39325 | 21.5 | <.0001 |
| instances*method | 639 | 1350141.22 | 2112.897058 | 1.47 | <.0001 |
| Error | 24824 | 35594800.28 | 1433.886573 | | |
| Corrected Total | 25679 | 5.31E+12 | | | |
Table 5.
ANOVA results at the stopping criterion of 125,000 examined solutions.
Table 5.
ANOVA results at the stopping criterion of 125,000 examined solutions.
| Source | DF | SS | Mean Square | F Value | P Value |
|---|
| instances | 213 | 5.31E+12 | 24931260598 | 1.93E+07 | <.0001 |
| method | 3 | 63931.9233 | 21310.6411 | 16.5 | <.0001 |
| instances*method | 639 | 1460446.674 | 2285.519051 | 1.77 | <.0001 |
| Error | 24824 | 32070591.19 | 1291.918756 | | |
| Corrected Total | 25679 | 5.31E+12 | | | |
Table 6,
Table 7,
Table 8 and
Table 9 present the results of the Duncan post-hoc comparisons. As we have mentioned earlier in this paper, when the algorithms share the same alphabet, there is no difference between/among the algorithms in Duncan analysis. On the other hand, if the algorithms do not share the same alphabet, they are different to each other. Take
Table 6 for instance, the four algorithms have different alphabets. We have known the objective is to minimize the earliness and tardiness cost. The lower the mean value, the better the algorithm. EA/G-GA is thus the best algorithm when the stopping criterion is set as 50000 examined solutions.
Across all the different stopping criteria (
i.e.,
Table 6,
Table 7,
Table 8 and
Table 9), EA/G-GA consistently outperforms others when we solve the single machine scheduling problems. EA/G-GA is not only the best algorithm but also the most robust one under different stopping criteria.
Table 6.
Duncan grouping at the stopping criterion of 50000 examined solutions.
Table 6.
Duncan grouping at the stopping criterion of 50000 examined solutions.
| Duncan Grouping | Mean | N | Methods |
|---|
| A | 12826.724 | 6420 | ACGA |
| B | 12814.85 | 6420 | EA/G |
| C | 12812.509 | 6420 | Adaptive EA/G |
| D | 12810.899 | 6420 | EA/G-GA |
Table 7.
Duncan grouping at the stopping criterion of 75000 examined solutions.
Table 7.
Duncan grouping at the stopping criterion of 75000 examined solutions.
| Duncan Grouping | Mean | N | Methods |
|---|
| A | 12814.902 | 6420 | ACGA |
| B | 12813.531 | 6420 | EA/G |
| C | 12812.059 | 6420 | Adaptive EA/G |
| D | 12809.391 | 6420 | EA/G-GA |
Table 8.
Duncan grouping at the stopping criterion of 100000 examined solutions.
Table 8.
Duncan grouping at the stopping criterion of 100000 examined solutions.
| Duncan Grouping | Mean | N | Methods |
|---|
| A | 12813.66 | 6420 | EA/G |
| A | | | |
| A | 12813.276 | 6420 | ACGA |
| B | 12811.168 | 6420 | Adaptive EA/G |
| C | 12808.906 | 6420 | EA/G-GA |
Table 9.
Duncan grouping at the stopping criterion of 125000 examined solutions.
Table 9.
Duncan grouping at the stopping criterion of 125000 examined solutions.
| Duncan Grouping | Mean | N | Methods |
|---|
| A | 12812.898 | 6420 | EA/G |
| B | 12810.827 | 6420 | Adaptive EA/G |
| B | | | |
| B | 12810.149 | 6420 | ACGA |
| C | 12808.48 | 6420 | EA/G-GA |
Except using 125000 solutions, Adaptive EA/G is better than ACGA through 50000 to 100000 examined solutions (because they share the same alphabet). Adaptive EA/G and ACGA works equally well when 125000 solutions are used. The reason why the Adaptive EA/G does not outperform ACGA is that the ACGA keeps better population diversity so that this algorithm has a better chance to find out a better solution in the longer computational time.
Finally,
Table 10 lists the basic statistic results of Adaptive EA/G and EA/G-SGA under different solution evaluations.
Table 10.
Selected results of Adaptive EA/G and EA/G-SGA employ different examined solutions in single machine scheduling problems.
Table 10.
Selected results of Adaptive EA/G and EA/G-SGA employ different examined solutions in single machine scheduling problems.
| | Examined Solutions: 50000 | |
| | Adaptive EA/G | EA/G-SGA |
| Instance | Min | Avg. | Max | Min | Avg. | Max |
| sks422a | 25656 | 25662.8 | 25712 | 25656 | 25662.1 | 25704 |
| sks455a | 6405 | 6420.1 | 6545 | 6405 | 6424.8 | 6545 |
| sks488a | 16862 | 16865.5 | 16888 | 16862 | 16862.9 | 16888 |
| sks522a | 29309 | 29326.2 | 29398 | 29309 | 29315.5 | 29396 |
| sks555a | 10187 | 10213.9 | 10256 | 10187 | 10210.7 | 10299 |
| sks588a | 24844 | 24847.9 | 24861 | 24844 | 24844.3 | 24853 |
| sks622a | 43048 | 43100.5 | 43371 | 43048 | 43079.9 | 43244 |
| sks655a | 16158 | 16163.2 | 16180 | 16158 | 16235.2 | 16721 |
| sks688a | 33551 | 33592 | 33686 | 33551 | 33608.4 | 33665 |
| sks922a | 88842 | 88872.1 | 88994 | 88842 | 88876.4 | 89017 |
| sks955a | 30582 | 30647 | 30804 | 30582 | 30649.9 | 30795 |
| sks988a | 81984 | 81986.4 | 81991 | 81984 | 81989.4 | 82034 |
| | Examined Solutions: 75000 | |
| | Adaptive EA/G | EA/G-SGA |
| Instance | Min | Avg. | Max | Min | Avg. | Max |
| sks422a | 25656 | 25659.7 | 25697 | 25656 | 25661.9 | 25704 |
| sks455a | 6405 | 6425.4 | 6545 | 6405 | 6424.8 | 6545 |
| sks488a | 16862 | 16862.9 | 16888 | 16862 | 16862.9 | 16888 |
| sks522a | 29309 | 29323.1 | 29398 | 29309 | 29312.6 | 29396 |
| sks555a | 10187 | 10224.2 | 10299 | 10187 | 10210.5 | 10299 |
| sks588a | 24844 | 24847.9 | 24861 | 24844 | 24844 | 24844 |
| sks622a | 43048 | 43078.7 | 43380 | 43048 | 43079.9 | 43244 |
| sks655a | 16158 | 16192.8 | 16616 | 16158 | 16234 | 16721 |
| sks688a | 33551 | 33624.4 | 33686 | 33551 | 33608.4 | 33665 |
| sks922a | 88841 | 88878.5 | 89100 | 88842 | 88869.4 | 89005 |
| sks955a | 30582 | 30674.8 | 31394 | 30582 | 30642.7 | 30785 |
| sks988a | 81984 | 81985.3 | 81989 | 81984 | 81985.7 | 82033 |
| | Examined Solutions: 100000 | |
| | Adaptive EA/G | EA/G-SGA |
| Instance | Min | Avg. | Max | Min | Avg. | Max |
| sks422a | 25656 | 25665.1 | 25697 | 25656 | 25661.9 | 25704 |
| sks455a | 6405 | 6428.4 | 6545 | 6405 | 6424.8 | 6545 |
| sks488a | 16862 | 16863.7 | 16888 | 16862 | 16862.9 | 16888 |
| sks522a | 29309 | 29326.7 | 29398 | 29309 | 29312.5 | 29396 |
| sks555a | 10187 | 10219.4 | 10301 | 10187 | 10210.5 | 10299 |
| sks588a | 24844 | 24845.8 | 24853 | 24844 | 24844 | 24844 |
| sks622a | 43048 | 43081 | 43273 | 43048 | 43079.9 | 43244 |
| sks655a | 16158 | 16208.1 | 16640 | 16158 | 16234 | 16721 |
| sks688a | 33551 | 33610 | 33686 | 33551 | 33608.4 | 33665 |
| sks922a | 88842 | 88871.6 | 89005 | 88842 | 88869.4 | 89005 |
| sks955a | 30582 | 30639.8 | 30800 | 30582 | 30642.4 | 30785 |
| sks988a | 81984 | 81985.2 | 81989 | 81984 | 81985.6 | 82033 |
4.3. Discussions
The result indicates that both the performances of EA/G-GA and Adaptive EA/G are better than those of ACGA and EA/G on a majority of stopping criteria because the former algorithms maintain better population diversity than the latter ones. Therefore, all algorithms outperform the original EA/G at the end of generations. In addition, the research outcome also demonstrates that EA/G-GA is significantly better than Adaptive EA/G because the genetic operators might produce more diversified chromosomes than the algorithms that merely change the parameters. The implication shows the greater the diversity of an algorithm, the better it can achieve performance, which is an important direction for researchers to conduct further studies.
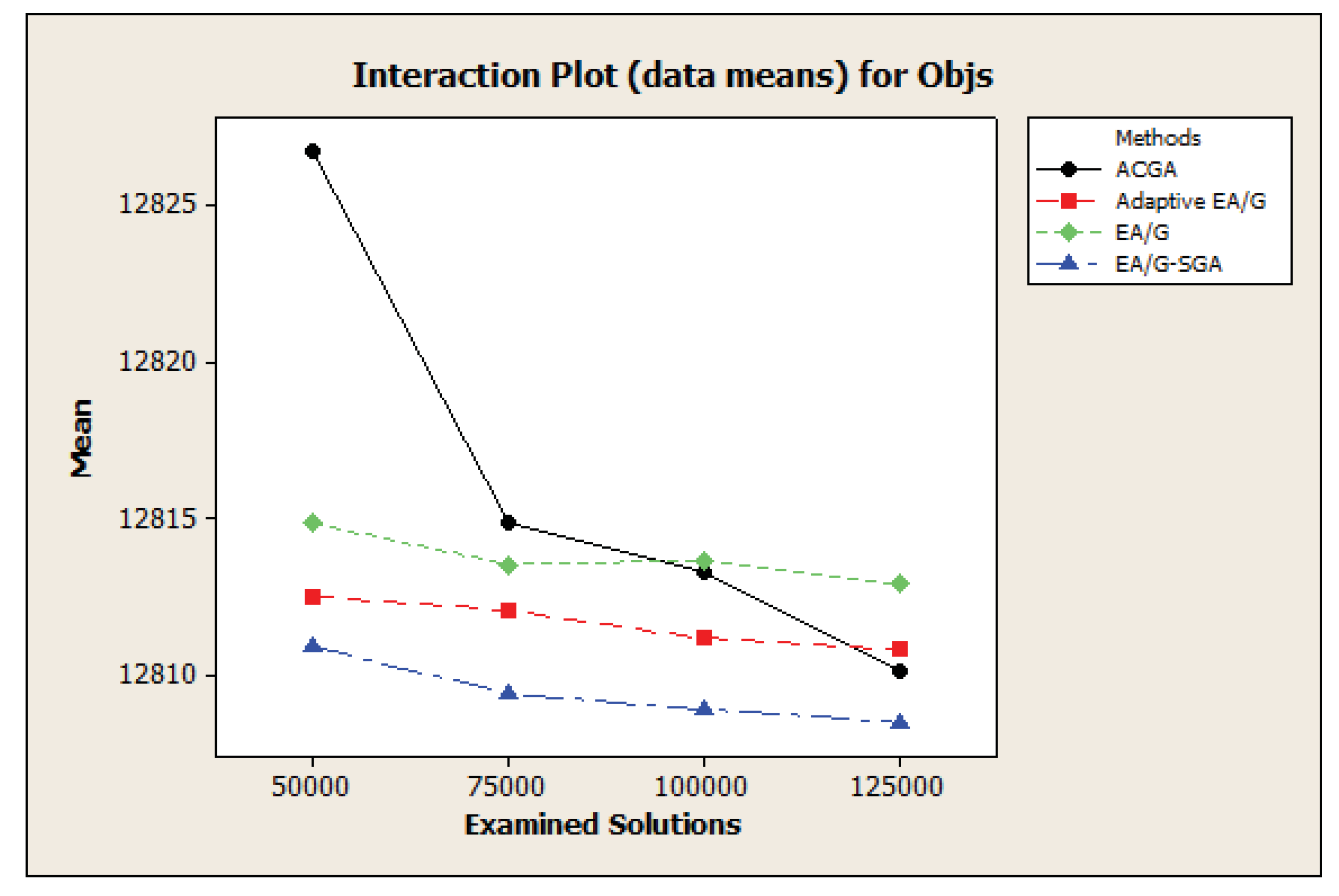
Figure 3.
Average Objective values under different stopping criteria.
Figure 3.
Average Objective values under different stopping criteria.
Two figures provided below support the evidence of the performance representation and they can display performance changes graphically. For example, in terms of the average objective value plot (See
Figure 3), EA/G-GA performs well by all stopping criteria while the ACGA is greatly improved when we employ more examined solutions. The convergence plot (See
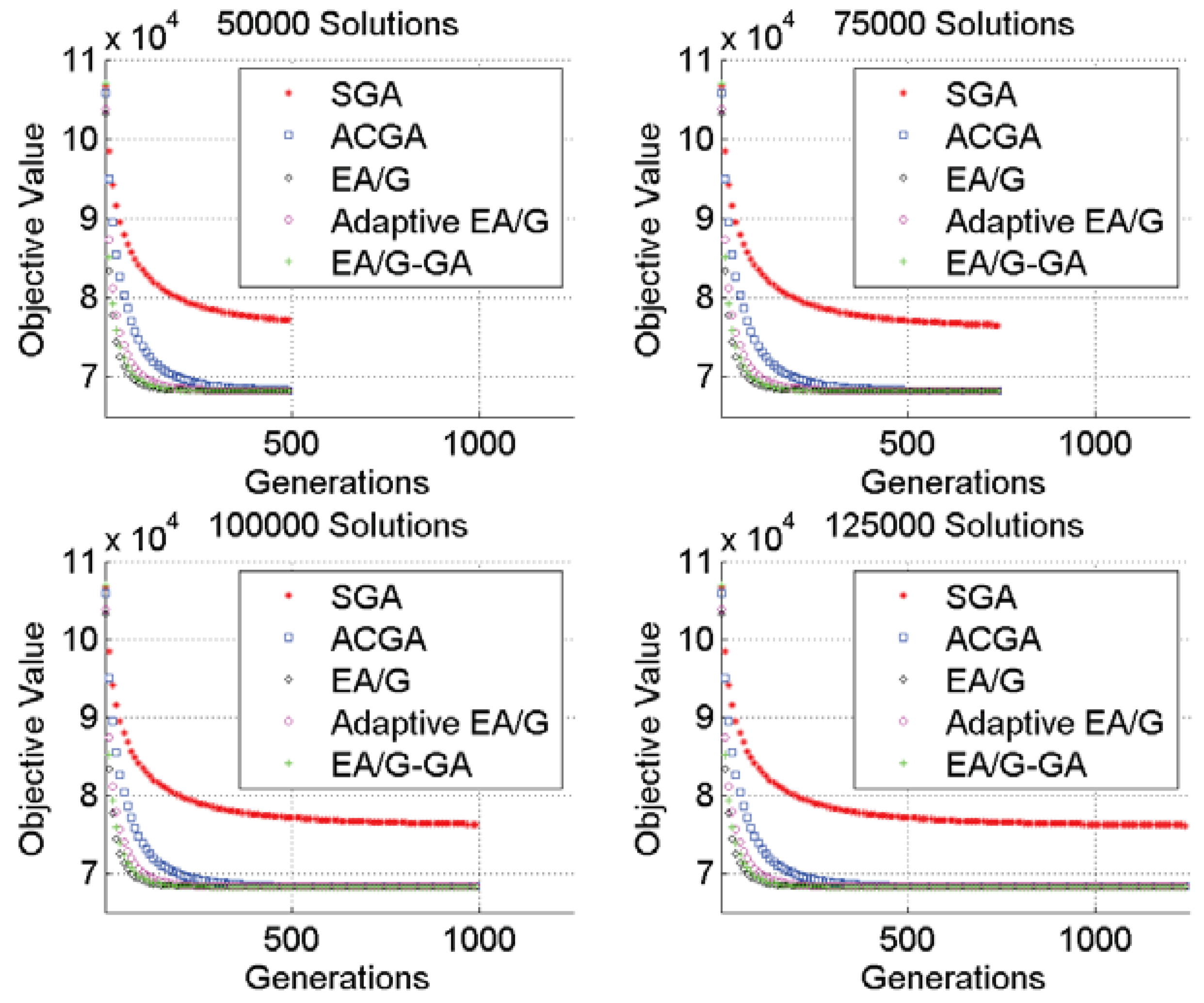
Figure 4) depicts that EA/G converges very fast before 150 generations. Other algorithms, nonetheless, gradually enhance the solution quality through the evolutionary progress. Thus, EA/G does not outperform either the EA/G-GA or Adaptive EA/G.
Figure 4.
Compare the convergency of Adaptive EA/G and EA/G-SGA with other algorithms.
Figure 4.
Compare the convergency of Adaptive EA/G and EA/G-SGA with other algorithms.
5. Conclusions
The feature of EDAs is to characterize the search space and then to sample new solutions from the probabilistic models. This feature has the benefit of not disrupting good gene structures; however, it causes the premature convergency of EDAs so that EDAs no longer generate diversified solutions. Even when we spend more computational efforts, EDAs can not improve the solution quality as indicated by our prior research [
1]. Consequently, this paper utilizes an important guideline in [
1], which hybridizes the EDAs with other meta-heuristics techniques. The advantage of the hybrid framework is to let EDAs gain more population diversity via the meta-heuristic. We use one of the famous EDAs, EA/G, to cooperate with GAs. The proposed algorithm is named “EA/G-GA”, which is used to solve the NP-Hard single machine scheduling problems.
Through the extensive experiments, we have compared EA/G-GA with some algorithms such as the ACGA, Adaptive EA/G, and EA/G described in other literature. In terms of statistical significance, EA/G-GA is found to have better performance than other algorithms by different stopping criteria. The results indicate that the EA/G-GA is not only superior to other algorithms but also proves to be a robust algorithm when different stopping criteria are applied (i.e., various CPU times). When we compare the differences between the EA/G-GA and Adaptive EA/G, the former algorithm is much more powerful than the latter one. It is meaningful that meta-heuristics provide more diversified solutions than we just change the parameters of an algorithm, which is a very important implication for EDAs researchers. Consequently, researchers could incorporate EDAs with other meta-heuristics in solving hard problems if they want to increase the population diversity to obtain better solution quality.
Finally, although we decide to alternate the EA/G with GAs in this research, there is no limitation on the selection of algorithms. For the future research, researchers may test different EDAs and meta-heuristics to solve various problems.