Static Isolated Horizons: SU(2) Invariant Phase Space, Quantization, and Black Hole Entropy
Abstract
:1. Introduction
2. Definition of Isolated Horizons
- (i)
- Manifold conditions:Δ is topologically , foliated by a (preferred) family of 2-spheres equipped with an equivalence class of transversal future pointing null vector fields whose flow preserves the foliation, where is equivalent to if for some positive real number c.
- (ii)
- Dynamical conditions: All field equations hold at Δ.
- (iii)
- Matter conditions: On Δ the stress-energy tensor of matter is such that is causal and future directed.
- (iv)
- Conditions on the metric g determined by e, and on its levi-Civita derivative operator ∇: (iv.a) The expansion of within Δ is zero. This, together with the energy condition (iii) and the Raychaudhuri equation at Δ, ensures that is additionally shear-free. This in turn implies that the Levi-Civita derivative operator ∇ naturally determines a derivative operator intrinsic to Δ via , tangent to Δ. We then impose (iv.b) .
- (v)
- Restriction to ‘good cuts.’ One can show furthermore that for some intrinsic to Δ. A 2-sphere cross-section H of Δ is called a ‘good cut’ if the pull-back of to H is divergence free with respect to the pull-back of to H. As shown in [32,33], every horizon satisfying (i)–(iv) above possesses at least one foliation into ‘good cuts’; this foliation is furthermore generically unique. We require that the fixed foliation coincide with a foliation into ‘good cuts.’
2.1. Isolated Horizon Classification According to Their Symmetry Groups
- (a)
- Type I: the isolated horizon geometry is spherical; in this case, is four dimensional ( rotations plus rescaling-translations along ℓ, which, in a coordinate system where , corresponds to the affine map with constants);
- (b)
- Type II: the isolated horizon geometry is axi-symmetric; in this case, is two dimensional (rotations round symmetry axis plus rescaling-translations along ℓ);
- (c)
- Type III: the diffeomorphisms generated by are the only symmetries; is one dimensional.
2.2. Isolated Horizons Classification According to the Reality of
- (a)
- Static: In the Newman-Penrose formalism (in the null tetrads adapted to the IH geometry introduced in the following section) static isolated horizons are characterized by the conditionon the Weyl tensor component . One can then show that for this class of isolated horizons (see next section) the pull-back to H (the preferred family of sections) of vanishes for all . This corresponds to having the horizon locally “at rest”. In the axisymmetric case, according to the definition of multiple moments of Type II horizons constructed in [34, static isolated horizons are non-rotating isolated horizons, i.e., those for which all angular momentum multiple moments vanish. Static black holes (e.g., those in the Reissner-Nordtrom family) have static isolated horizons. There are Type I, II and III static isolated horizons.
- (b)
- Non-Static: In the Newman-Penrose formalism (in the null tetrads adapted to the IH geometry introduced in the following section) non-static isolated horizons are characterized by the conditionThe pull-back to H (the preferred family of sections) of does not vanish for all . The horizon is locally “in motion”. The Kerr black hole is an example of this type.
3. Some Key Equations
4. The Conserved Symplectic Structure
4.1. The Action Principle
4.2. The Conserved Symplectic Structure in Terms of Vector Variables
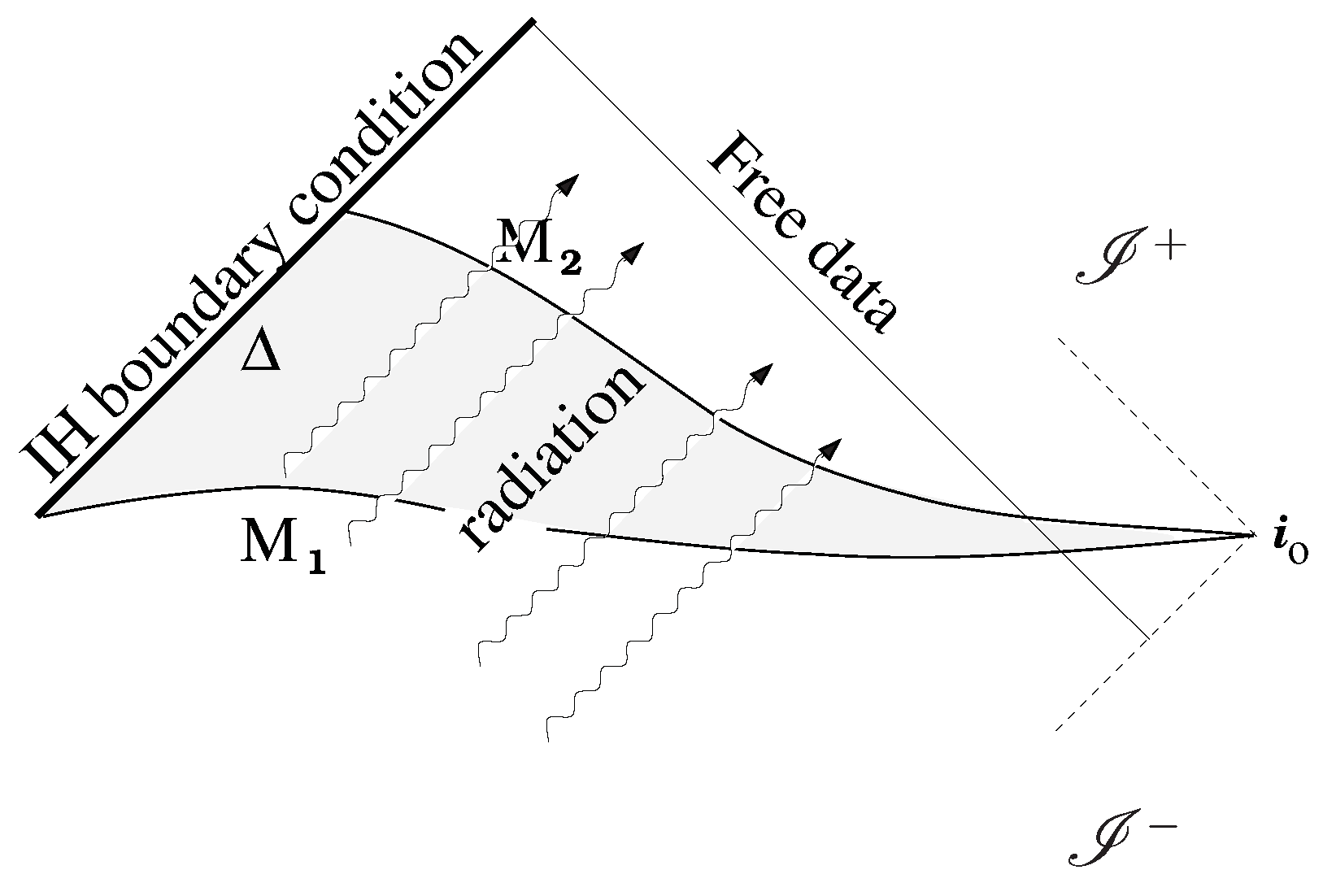
4.3. Gauge Symmetries
4.4. The Conserved Symplectic Structure for Non-Static Isolated Horizons
- To declare that diffeomorphism are not gauge symmetries in the non-static case and modify the definition of the phase space allowing variations of fields at the horizon which are only pure gauge transformations (i.e., what would correspond to in (29)).
- To restore diffeomorphism invariance at the horizon by the inclusion of new field degrees of freedom.
4.5. The Conserved Symplectic Structure in Terms of Real Connection Variables
4.6. Equivalence between the Triad and Connection Parametrizations of the Boundary Symplectic Structure
5. Quantization
Learning from the Restriction to Type I Isolated Horizons
6. Entropy Calculation
6.1. The Usual Paradigm
6.2. A Paradigm Shift: An -Independent Effective Theory
7. Conclusions
Acknowledgements
References and Notes
- Reid, M.J. Is there a supermassive black hole at the center of the milky way? Int. J. Mod. Phys. D 2009, 18, 889–910. [Google Scholar] [CrossRef]
- Mueller, A. Experimental evidence of black holes. PoS 2006, P2GC, 017. [Google Scholar]
- Broderick, A.E.; Loeb, A.; Narayan, R. The event horizon of Sagittarius A*. Astrophys. J. 2009, 701, 1357–1366. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Thiemann, T. Modern Canonical Quantum GR; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ashtekar, A.; Lewandowski, J. Background independent quantum gravity: A status report. Class. Quant. Grav. 2004, 21, R53. [Google Scholar] [CrossRef]
- Perez, A. Introduction to loop quantum gravity and spin foams. In Proceedings of the International Conference on Fundamental Interactions, Domingos Martins, Brazil, 6–12 June 2004.
- Ashtekar, A.; Taveras, V.; Varadarajan, M. Information is not lost in the evaporation of 2-dimensional black holes. Phys. Rev. Lett. 2008, 100, 211302. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Corichi, A.; Krasnov, K. Isolated horizons: The classical phase space. Adv. Theor. Math. Phys. 1999, 3, 419–478. [Google Scholar]
- Ashtekar, A.; Baez, J.; Krasnov, K. Quantum geometry of isolated horizons and black hole entropy. Adv. Theor. Math. Phys. 2000, 4, 1–94. [Google Scholar]
- Meissner, K.A. Black hole entropy in loop quantum gravity. Class. Quant. Grav. 2004, 21, 5245–5252. [Google Scholar] [CrossRef]
- Domagala, M.; Lewandowski, J. Black hole entropy from quantum geometry. Class. Quant. Grav. 2004, 21, 5233–5244. [Google Scholar] [CrossRef]
- Ghosh, A.; Mitra, P. A bound on the log correction to the black hole area law. Phys. Rev. D 2005, 71, 027502. [Google Scholar] [CrossRef]
- Gour, G. Algebraic approach to quantum black holes: Logarithmic corrections to black hole entropy. Phys. Rev. D 2002, 66, 104022. [Google Scholar] [CrossRef]
- Agullo, I.; Barbero, J.F.; Diaz-Polo, J.; Fernandez-Borja, E.; Villasenor, E.J.S. Black hole state counting in LQG: A number theoretical approach. Phys. Rev. Lett. 2008, 100, 211301. [Google Scholar] [CrossRef] [PubMed]
- Barbero, J.F.; Villasenor, E.J.S. Generating functions for black hole entropy in loop quantum gravity. Phys. Rev. D 2008, 77, 121502. [Google Scholar] [CrossRef]
- Barbero, J.F.; Villasenor, E.J.S. On the computation of black hole entropy in loop quantum gravity. Class. Quant. Grav. 2009, 26, 035017. [Google Scholar]
- Agullo, I.; Barbero, J.F.; Borja, E.F.; Diaz-Polo, J.; Villasenor, E.J.S. The combinatorics of the SU(2) black hole entropy in loop quantum gravity. Phys. Rev. D 2009, 80, 084006. [Google Scholar] [CrossRef]
- Agullo, I.; Barbero, J.F.; Borja, E.F.; Diaz-Polo, J.; Villasenor, E.J.S. Detailed black hole state counting in loop quantum gravity. Phys. Rev. D 2010, 82, 084029. [Google Scholar] [CrossRef]
- Engle, J.; Perez, A.; Noui, K. Black hole entropy and SU(2) Chern-Simons theory. Phys. Rev. Lett. 2010, 105, 031302. [Google Scholar] [CrossRef] [PubMed]
- Engle, J.; Perez, A.; Noui, K.; Pranzetti, D. Black hole entropy from an SU(2)-invariant formulation of type I isolated horizons. Phys. Rev. D 2010, 82, 044050. [Google Scholar] [CrossRef]
- Basu, R.; Kaul, R.K.; Majumdar, P. Entropy of isolated horizons revisited. Phys. Rev. D 2010, 82, 024007. [Google Scholar] [CrossRef]
- Kaul, R.K.; Majumdar, P. Quantum black hole entropy. Phys. Lett. B 1998, 439, 267. [Google Scholar] [CrossRef]
- Kaul, R.K.; Majumdar, P. Logarithmic correction to the Bekenstein-Hawking entropy. Phys. Rev. Lett. 2000, 84, 5255. [Google Scholar] [PubMed]
- Carlip, S. Black hole thermodynamics and statistical mechanics. Lect. Notes Phys. 2009, 769, 89. [Google Scholar]
- Carlip, S. Entropy from conformal field theory at Killing horizons. Class. Quant. Grav. 1999, 16, 3327. [Google Scholar] [CrossRef]
- Carlip, S. Black hole entropy from conformal field theory in any dimension. Phys. Rev. Lett. 1999, 82, 2828. [Google Scholar] [CrossRef]
- Carlip, S. Logarithmic corrections to black hole entropy from the Cardy formula. Class. Quant. Grav. 2000, 17, 4175. [Google Scholar] [CrossRef]
- Livine, E.R.; Terno, D.R. Quantum black holes: Entropy and entanglement on the horizon. Nucl. Phys. B 2006, 741, 131. [Google Scholar] [CrossRef]
- Ashtekar, A.; Beetle, C.; Lewandowski, J. Geometry of generic isolated horizons. Class. Quant. Grav. 2002, 19, 1195. [Google Scholar] [CrossRef]
- Ashtekar, A.; Beetle, C.; Dreyer, O.; Fairhurst, S.; Krishnan, B.; Lewandowski, J.; Wisniewski, J. Generic isolated horizons and their applications. Phys. Rev. Lett. 2000, 85, 3564–3567. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Engle, J.; Van Den Broeck, C. Quantum horizons and black hole entropy: Inclusion of distortion and rotation. Class. Quant. Grav. 2005, 22, L27. [Google Scholar] [CrossRef]
- Beetle, C.; Engle, J. Generic isolated horizons in loop quantum gravity. Class. Quant. Grav. 2010, 27, 235024. [Google Scholar] [CrossRef]
- Ashtekar, A.; Fairhurst, S.; Krishnan, B. Isolated horizons: Hamiltonian evolution and the first law. Phys. Rev. D 2000, 62, 104025. [Google Scholar] [CrossRef]
- Ashtekar, A.; Beetle, C.; Lewandowski, J. Mechanics of rotating isolated horizons. Phys. Rev. D 2001, 64, 044016. [Google Scholar] [CrossRef]
- Ashtekar, A.; Engle, J.; Van Den Broeck, C. Quantum horizons and black hole entropy: Inclusion of distortion and rotation. Class. Quant. Grav. 2005, 22, L27. [Google Scholar] [CrossRef]
- Geroch, R.P.; Held, A.; Penrose, R. A space-time calculus based on pairs of null directions. J. Math. Phys. 1973, 14, 874. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Clarendon: Oxford, UK, 1992. [Google Scholar]
- Crnkovic, C.; Witten, E. Covariant description of canonical formalism in geometrical theories. In Three Hundred Years of Gravitation; Print-86-1309 (PRINCETON); Hawking, S.W., Israel, W., Eds.; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Lee, J.; Wald, R.M. Local symmetries and constraints. J. Math. Phys. 1990, 31, 725. [Google Scholar] [CrossRef]
- Corichi, A.; Wilson-Ewing, E. Surface terms, asymptotics and thermodynamics of the holst action. Class. Quant. Grav. 2010, 27, 205015. [Google Scholar] [CrossRef]
- Lewandowski, J.; Okolow, A.; Sahlmann, H.; Thiemann, T. Uniqueness of the diffeomorphism invariant state on the quantum holonomy-flux algebra. Commun. Math. Phys. 2006, 267, 703–733. [Google Scholar] [CrossRef]
- Fleischhack, C. Representations of the Weyl algebra in quantum geometry. Commun. Math. Phys. 2009, 285, 67. [Google Scholar] [CrossRef]
- Freidel, L.; Perez, A. PI, Waterloo, Canada; CPT, Marseille, France. Unpublished work. 2011. [Google Scholar]
- Witten, E. Quantum field theory and the Jones polynomial. Commun. Math. Phys. 1989, 121, 351. [Google Scholar] [CrossRef]
- Ashtekar, A. Lectures on Nonperturbative Canonical Gravity; World Scientific: Singapore, 1991. [Google Scholar]
- Ghosh, A.; Mitra, P. Counting black hole microscopic states in loop quantum gravity. Phys. Rev. D 2006, 74, 064026. [Google Scholar] [CrossRef]
- Ooguri, H.; Sasakura, N. Discrete and continuum approaches to three-dimensional quantum gravity. Mod. Phys. Lett. A 1991, 6, 3591. [Google Scholar] [CrossRef]
- Archer, F.; Williams, R.M. The Turaev-Viro state sum model and three-dimensional quantum gravity. Phys. Lett. B 1991, 273, 438. [Google Scholar] [CrossRef]
- Thiemann, T. Quantum spin dynamics. VIII: The master constraint. Class. Quant. Grav. 2006, 23, 2249. [Google Scholar]
- Thiemann, T. The Phoenix project: Master constraint programme for loop quantum gravity. Class. Quant. Grav. 2006, 23, 2211. [Google Scholar]
- Major, S.A. Shape in an Atom of Space: Exploring quantum geometry phenomenology. Class. Quant. Grav. 2010, 27, 225012. [Google Scholar]
- Engle, J.; Livine, E.; Pereira, R.; Rovelli, C. LQG vertex with finite Immirzi parameter. Nucl. Phys. B 2008, 799, 136. [Google Scholar] [CrossRef]
- Freidel, L.; Krasnov, K. A new spin foam model for 4d gravity. Class. Quant. Grav. 2008, 25, 125018. [Google Scholar] [CrossRef]
- Ding, Y.; Han, M.; Rovelli, C. Generalized spinfoams. arXiv 2010. arXiv:gr-qc/10112149. [Google Scholar] [CrossRef]
- Rezende, D.J.; Perez, A. 4d Lorentzian Holst action with topological terms. Phys. Rev. D 2009, 79, 064026. [Google Scholar] [CrossRef]
- Engle, J.; Perez, A.; Noui, K.; Pranzetti, D. The SU(2) black hole entropy revisited. arXiv 2011. arXiv:gr-qc/1103.2723. [Google Scholar] [CrossRef]
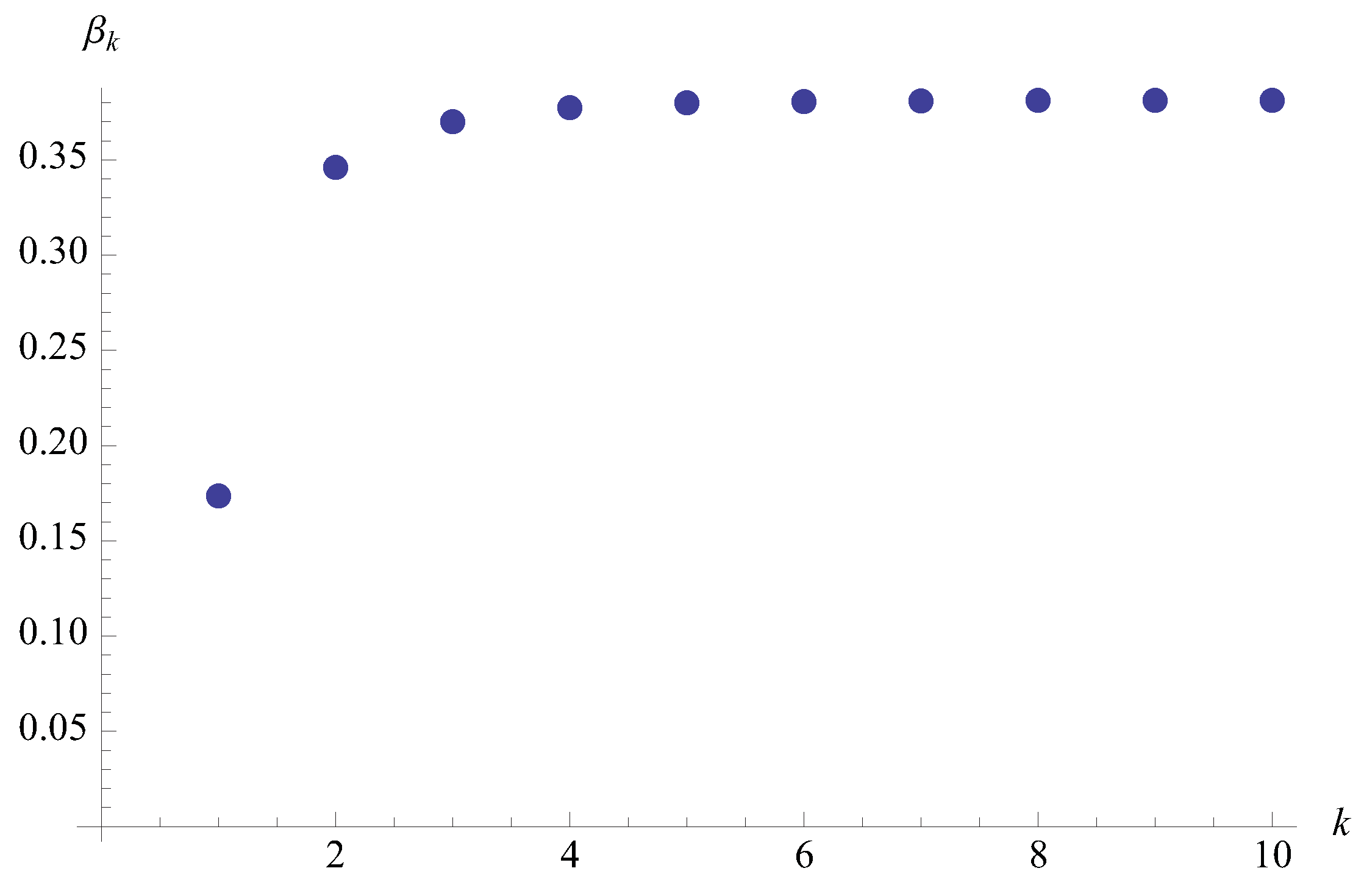
- Notice, that the family of descriptions here presented are labelled by an integer k ∈ ℕ and a correlated real number. This seem to be the structure that one would wish in order to establish a link between LQG and some interesting speculative ideas explored recently [62].
- It interesting to speculate a possible understanding of our result from the point of view of renormalization, as emphasized by Jacobson in [63].
- Sahlmann, H. Newton’s constant from a minimal length: Additional models. Class. Quant. Grav. 2011, 28, 015006. [Google Scholar] [CrossRef]
- Jacobson, T. Renormalization and black hole entropy in loop quantum gravity. Class. Quant. Grav. 2007, 24, 4875. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Perez, A.; Pranzetti, D. Static Isolated Horizons: SU(2) Invariant Phase Space, Quantization, and Black Hole Entropy. Entropy 2011, 13, 744-777. https://doi.org/10.3390/e13040744
Perez A, Pranzetti D. Static Isolated Horizons: SU(2) Invariant Phase Space, Quantization, and Black Hole Entropy. Entropy. 2011; 13(4):744-777. https://doi.org/10.3390/e13040744
Chicago/Turabian StylePerez, Alejandro, and Daniele Pranzetti. 2011. "Static Isolated Horizons: SU(2) Invariant Phase Space, Quantization, and Black Hole Entropy" Entropy 13, no. 4: 744-777. https://doi.org/10.3390/e13040744
APA StylePerez, A., & Pranzetti, D. (2011). Static Isolated Horizons: SU(2) Invariant Phase Space, Quantization, and Black Hole Entropy. Entropy, 13(4), 744-777. https://doi.org/10.3390/e13040744




