2. Kinetic Stability vs. Thermodynamic Stability
The second law of thermodynamics teaches us that closed systems tend to converge towards their equilibrium state and that the irreversible processes that lead to the equilibrium state result in an increase in global entropy. In chemistry, this is often expressed in terms of the minimization of the system’s Gibbs energy, G. When the equilibrium state is reached, the closed system ceases to undergo further change, and at that point the system is termed thermodynamically stable [
1].
The second law, however, does not predict how rapidly a closed system will reach its equilibrium state. For example, a H2-O2 mixture, under appropriate conditions, can be extremely persistent and maintained almost indefinitely, despite its non-equilibrium state. In order for reaction to take place, some form of activation, provided by a spark or appropriate catalyst, is necessary. Thus, we term aH2-O2 mixture (under appropriate conditions) to be kinetically stable due to the high kinetic barrier separating reactants from products.
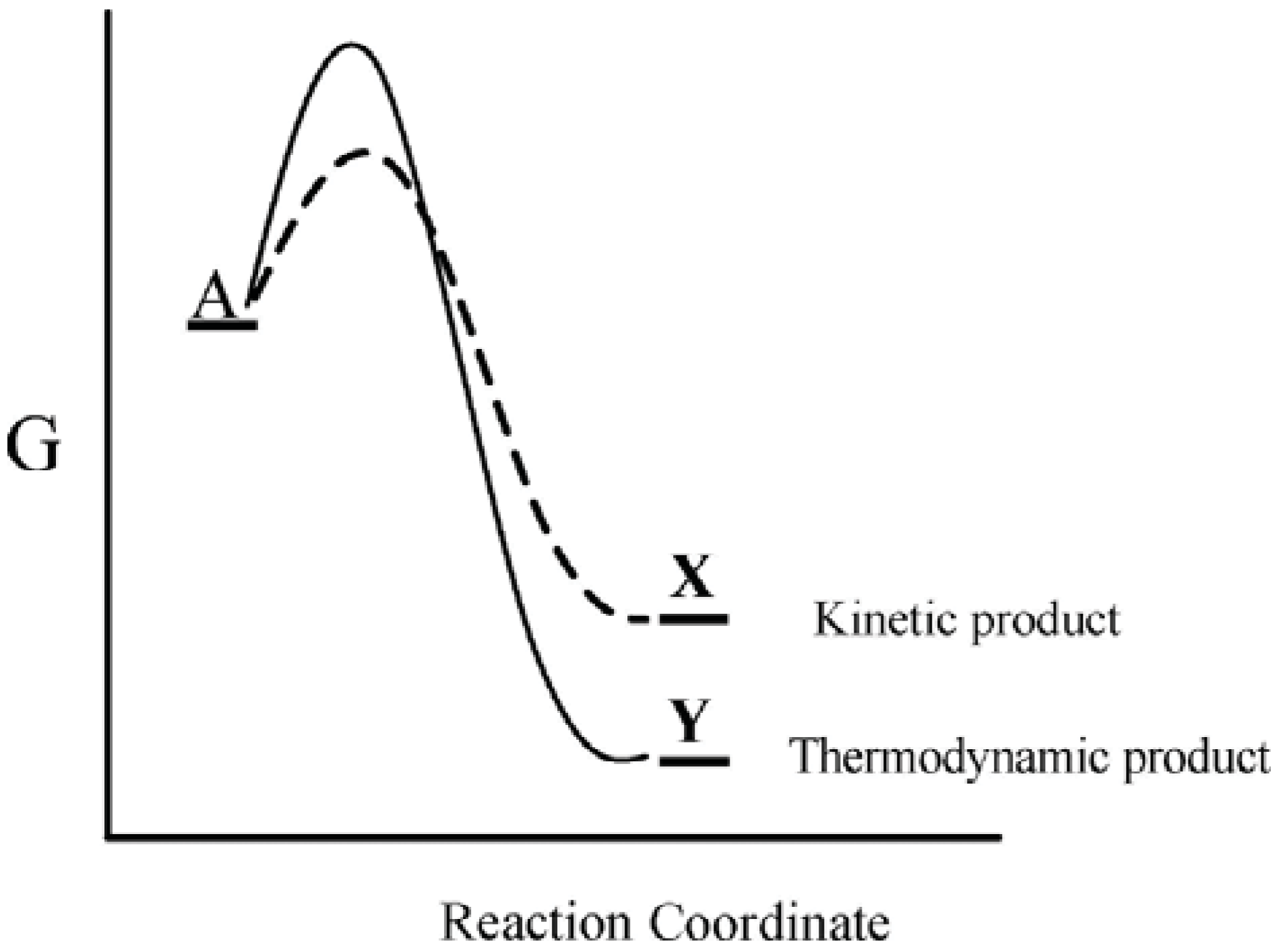
This well-known kinetic-thermodynamic dichotomy leads to the concepts of kinetic and thermodynamic control, whereby a substance A can react by two competing pathways—a kinetically preferred lower free energy pathway that leads to a thermodynamically less stable product, X, or a higher free energy pathway that leads to a thermodynamically more stable product, Y (
Figure 1). For such a system the preferred product will depend on the particular reaction conditions. Thus when the system is maintained under conditions of kinetic control, the kinetically preferred product X will be favored, while under conditions where the reaction barrier is readily overcome, the thermodynamically preferred product Y is favored. Accordingly, actual product formation is governed by a combination of thermodynamic and kinetic factors.
Figure 1.
Gibbs energy as a function of the reaction coordinate of A. Under conditions of kinetic control, product X will be favored, while under conditions of thermodynamic control, product Y will be favored.
Figure 1.
Gibbs energy as a function of the reaction coordinate of A. Under conditions of kinetic control, product X will be favored, while under conditions of thermodynamic control, product Y will be favored.
The kinetic stability associated with the H2-O2 mixture mentioned above is a static one, i.e., no change takes place within that system over time. However, within the category of kinetic stability there is a distinct class of systems whose stability is of a dynamic type, rather than of the more familiar static type. As its name implies, dynamic kinetically stable systems are dynamic, constantly in motion. A river or fountain provides a physical example of the dynamic aspect. A river’s stability is of a dynamic type in that the water that constitutes the river is continually changing—the rate of water flow into the river from its sources equaling the rate of flow out into the sea. Yet the river’s appearance remains constant over time, thereby manifesting stability. As long as the water supply is unimpeded, the river (or fountain) as an entity remains stable. Thus that river exemplifies a physical non-equilibrium steady state. Its stability, a dynamic stability, is based on change, as opposed to lack of change.
3. Dynamic Kinetic Stability of Replicating Systems
A stable population of replicating entities, whether molecular in nature or composed from a complex assembly, constitutes a chemical example of a non-equilibrium steady state, so its stability is also of a dynamic type. The kinetics of the replication reaction, a form of autocatalysis, which can result in exponential growth, was appreciated by Lotka [
6] almost a century ago. Since exponential growth is inherently unsustainable, a replicating system can only maintain a stable population if a balance between the rates of replicator formation and replicator decay has been established. This can be expressed by a simple differential kinetic equation, such as Equation (1), where
X is the replicator concentration,
M is the concentration of building blocks from which
X is composed, and
k and
g are rate constants for replicator formation and decay, respectively. A steady state population, a state that is effectively ‘stable’, is achieved and maintained as long as dX/dt remains close to zero. Accordingly the stability type is a dynamic one—it is the
population of replicators that is stable even though the individual members are being constantly turned over. It is this type of stability, one that is solely associated with persistent replicating systems, that we term
dynamic kinetic stability. The term ‘dynamic’ reflects the continual turnover of the population members, the term ‘kinetic’ reflects the fact that the stability of the replicating system is based on kinetic parameters, such as
k and
g of Equation (1),
i.e., on reaction rate constants, rather than on thermodynamic parameters:
Let us now specify some characteristics that distinguish these two types of stability—dynamic kinetic and thermodynamic, and demonstrate how the classification can be useful.
(i)
Circumstantial vs.
Inherent. Kinetic stability (static or dynamic), in contrast to thermodynamic stability, is not an intrinsic function of the system alone, but also depends on its surroundings. So, whereas thermodynamic stability is
inherent, kinetic stability is
circumstantial. A hydrogen-oxygen mixture in a glass container is kinetically stable, although that same mixture in the presence of a platinum catalyst becomes kinetically unstable. Dynamic kinetic stability, as manifest in replicating systems, follows the same pattern. A particular bacterial population in a pool of water might be kinetically stable, whereas that same population in a chlorinated pool would be unstable. Clearly, the dynamic kinetic stability of physical, chemical and biological systems may be dramatically affected by changing circumstances. In contrast, thermodynamic stability, being a state function, is independent of factors extraneous to the system. This difference is significant—it enables thermodynamic stability to be quantified and, accordingly, state functions such as G, H and S are applicable. In comparison, dynamic kinetic stability, being circumstantial, cannot be formally quantified and can only be assessed in some qualitative way. Two parameters that can give some indication of the dynamic kinetic stability of some replicating system are its size—the larger the population the more stable it is likely to be, and the length of time the replicating system has been able to maintain itself. Clearly, long-lived replicating populations are stable by definition, having proved stable by virtue of their persistence [
4,
5].
(ii)
Replicator Space vs.
‘Regular’ Chemical Space. A direct consequence of the division of stability into two discrete types is that chemical systems, when undergoing transformations, can be classified as belonging to two discrete chemical spaces—‘regular’ chemical space and replicator space. Replicator space is the all-encompassing grouping of persistent replicating systems, simple or complex. Thus molecular replicators, bacterial cells, birds, bees and camels all exemplify entities within replicator space. ‘Regular’ chemical space effectively incorporates all other chemical entities, non-replicating in their character. The utility of this classification is that entities within each of the two spaces follow different selection rules because of the different type of stability in operation. For ‘regular’ chemical systems the selection rule is the well-known thermodynamic one. However, it turns out that within replicator space the selection rule is primarily kinetic [
4,
5]. In order to understand the basis for that kinetic selection rule, consider the
in vitro molecular replication reaction such as the one described by Spiegelman in the late 1960s [
7]. In that study Spiegelman took an RNA strand (isolated from the Qβ virus), activated nucleotides (the building blocks that make up an RNA oligomer) and the Qβ replicating enzyme, and demonstrated that
in vitro replication of the RNA strand took place. However, since the replication reaction on occasion occurred imperfectly, mutated replicators were formed as well. Such transformations can be viewed as transitions in replicator space, from one replicating system to another. What was striking, however, was the fact that successful transitions in replicator space would only be those that lead to the formation of replicators of
higher kinetic stability (faster replicators). As pointed out by Lifson [
8] some years ago, a mutation leading to the formation of a kinetically
less stable replicator would likely be driven to extinction,
i.e., it would simply decay and disappear with time. Thus the transition between two connected elements in replicator space would effectively take place in just
one direction—the direction based on kinetic selection, one that leads to the formation of kinetically
more stable replicators. Indeed, Spiegelman observed that the initially extended and slow replicating RNA oligonucleotide ended up evolving into a much shorter and rapidly replicating entity [
7].
(iii)
Complexification vs.
Thermodynamic Aggregation. The different selection rules in replicator and ‘regular’ chemical spaces discussed above is of considerable significance since they induce different chemical behavior. When transformations within the two spaces lead to a process of aggregation, it turns out that the aggregation patterns within the two spaces are different. Within ‘regular’ space, aggregation is primarily thermodynamically-driven as exemplified by solid and liquid thermodynamic states of matter. However, within replicator space, aggregation is not primarily thermodynamic in character. In fact, within replicator space the process is better termed complexification since the aggregation process is highly organized, rather than ordered [
9]. The aggregation process is kinetically-driven, leading to complex assemblies that are kinetically stable, though thermodynamically unstable. Indeed, the idea of a kinetically-driven hypercyclic network–a form of complexification–obtained through cooperative molecular behavior, was theoretically predicted by Eigen and Schuster in the late 1970s [
10]. But it was only some 15 years later that the newly emergent area of Systems Chemistry [
11] provided striking empirical evidence for these ideas. Studies by von Kiedrowski
et al. [
12,
13], Ghadiri
et al. [
14], Chmielewski
et al. [
15], and Kassianidis and Philp [
16] all suggest that small replicating networks, based on the cross-catalysis of the network components, are feasible. Joyce’s studies on RNA enzymes, in particular, have demonstrated the importance of complexification on the efficacy of the replication process. Whereas a single RNA autocatalyst was a relatively ineffective replicator, incapable of more than two successive doublings, conversion of that RNA ribozyme into a small cross-catalytic network based on
two RNA ribozymes resulted in the formation of a rapidly replicating system which could be sustained indefinitely [
17].
Thus the on-going process of complexification appears to be not only a biological (evolutionary) property, but a kinetically-driven chemical property. The simple fact that complex (biological) replicators are kinetically more stable than simpler ones reaffirms the idea that there is a kinetic driving force that tends to transform less stable replicators, replicators that are
simpler, into more stable ones that are
complex. (However, that not all transformations in replicator space necessarily involve complexification. If a specific process of simplification were to lead to an increase in kinetic stability, then clearly that process would be kinetically selected for. Our point is that, in general, enhanced dynamic kinetic stability is achieved through complexification, not simplification.) The importance of network formation in replicating systems has recently been discussed byAshkenasy
et al. [
18], Ludlow and Otto [
19] and, in a more general context, by Kauffman [
20].
(iv) Chiral Stability in Regular Space vs. Replicative Space. The stability of chiral systems in ‘regular’ and replicator space is strikingly different. In regular chemical space a racemic mixture is clearly the more stable one. Chiral excess is inherently thermodynamically unstable, and with time all homochiral systems will tend to become transformed into the more stable racemic system(if aggregation effects are ignored). Within the replicative world, however, the reverse pattern is observed. Chiral recognition is crucial in biological processes, particularly in the process of replication, so that in a replicative context homochirality is the preferred stereochemical outcome. Thus the tendency of regular chemical systems toward racemization, and replicating systems toward homochirality, becomes understandable in terms of the stability types in the two chemical spaces–homochiral systems exhibit greater dynamic kinetic stability than racemic ones.
Interestingly, the importance of autocatalysis is not just manifest in maintaining that homochiral dynamic kinetic state, but is also considered instrumental in
generating that state. The symmetry breaking Soai reaction [
21,
22], in which a chiral product is formed and maintained in almost 100% enantiomeric excess from an achiral substrate, also derives from the predominant influence of
kinetic, as opposed to
thermodynamic, forces.
(v)
Convergence vs.
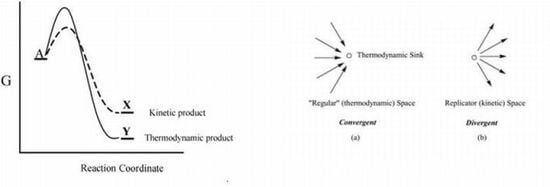
Divergence in Chemical Space. We have discussed replicating and ‘regular’ chemical systems as occupying different spaces based on their differing selection rules. Interestingly, those two spaces also exhibit different topologies [
5]. ‘Regular’ space is
convergent while replicator space is
divergent. Transitions within ‘regular’ space are convergent as all isomeric systems are directed toward their common thermodynamic sink. That convergent pattern is represented schematically in
Figure 2a. In contrast, transitions in replicator space, being kinetically directed, are
divergent in character as illustrated in
Figure 2b. For transformations in replicator space there is no specific target of maximal kinetic stability because kinetic stability is not a state function. Kinetic stability depends on factors external to the system, and, accordingly, there is no single unique pathway to higher values. Accordingly, each system within replicator space becomes a potential branching point for other kinetically stable systems, with the result being that within replicator space we observe a pattern of
diverging pathways, as opposed to the pattern of
converging pathways associated with transformations in “regular” chemical space [
5].
Figure 2.
Schematic representation of branching patterns within (a) ‘regular’ (thermodynamic) space (convergent); and within (b) replicator (kinetic) space (divergent).
Figure 2.
Schematic representation of branching patterns within (a) ‘regular’ (thermodynamic) space (convergent); and within (b) replicator (kinetic) space (divergent).
This different topology of the two spaces has interesting consequences. The patterns of convergence in ‘regular’ chemical space, as well as the patterns of divergence in replicator space, manifest themselves through the progress of time. This means that if we trace reaction pathways back in time, the patterns of convergence and divergence become reversed; a path that is convergent in the forward direction is necessarily divergent in the backward direction, and vice versa. This topological characteristic impacts on our ability to make both predictive and historical statements regarding systems in the two spaces. In replicator space, the convergence going back in time means it is easier to access historical information regarding precursor replicating systems, because a converging path by definition is directed toward a limited number of primal points. Indeed given the fossil and genetic record, the current evidence supports the view that all living systems on earth descended from just one such primal system. In other words, inspection of the fossil and genetic record has enabled us to explore our evolutionary history with considerable success, but this success has depended crucially on the convergent nature of replicator space as we go back in time. However, when we attempt to make predictive statements about replicator space the situation is reversed. The question as to where the future exploration of replicator space is likely to lead us is one which we cannot even begin to address; a diverging path, by definition, does not go anywhere in particular. The evolutionary future of replicating systems is effectively unknowable.
Applying the same thinking to the consideration of transformations in ‘regular’ space leads to the opposite pattern. We can make reasonable predictive statements as to where a regular chemical system is directed (i.e., in a convergent direction toward its thermodynamic sink). However, making reliable statements regarding the identity of historical precursor systems in regular space is much more problematic, since in a backward direction the space is divergent. In sum, the different patterns of the two spaces-replicator and ‘regular’ suggest that our ability to make either predictive statements regarding future transformations or historical statements regarding the nature of past transformations is greatly influenced by the topology of the two spaces. A convergent topology facilitates prediction, a divergent one does not.
4. Interplay between Dynamic Kinetic Stability and Thermodynamic Stability
Life’s far-from-equilibrium state, one that is maintained over time, has troubled physicists for over a century. Thus Niels Bohr, one of the fathers of atomic theory, in a well-known “Light and Life” lecture in 1933, proposed “that life is consistent with, but
undecidable or
unknowable by, human reasoning from physics and chemistry” [
23] and justified that conclusion with the following reasoning: “The existence of life must be considered as an elementary fact that can not be explained, but must be taken as a starting point in biology, in a similar way as the quantum of action, which appears as an irrational element from the point of view of classical mechanical physics, taken together with the existence of elementary particles, forms the foundation of atomic physics. The asserted impossibility of a physical or chemical explanation of the function peculiar to life would in this sense be analogous to the insufficiency of the mechanical analysis for the understanding of the stability of atoms.”
Simply put, Bohr believed that the animate-inanimate dichotomy was unbridgeable and could be compared to the classical physics-quantum physics divide! And Erwin Schrödinger, following that general line of reasoning, enigmatically concluded some years later in his classic “What is life?” book, that living matter, while not eluding the established laws of physics, was likely to involve “other laws of physics” hitherto unknown [
24]. Even after major discoveries in molecular biology during the 1950s and 1960s, the belief that the origin of life problem was unresolvable continued to be expressed by leading scientists and philosophers of science. Thus in 1974, twenty years after the discovery of DNA, Karl Popper, the iconic philosopher of science, supported the physicist position noted above with his assertion that the origin of life problem was “an impenetrable barrier to science and a residue to all attempts to reduce biology to chemistry and physics” [
25].
Clearly life’s far-from-equilibrium state is central to the dilemma of how biology and physics inter-relate. How can living systems be stable, in the sense of persistent, yet maintain a far-from-equilibrium state? The more recent development of non-equilibrium thermodynamics [
26], though throwing light on “dissipative structures” such as whirlpool, heated liquids, etc, has done little to resolve the puzzle of biological systems [
9]. Of course, from a purely thermodynamic perspective there is no contradiction—living systems undergo continual material and energy exchange with their environment. So just as a refrigerator can transfer heat from cold to hot, in the reverse direction to the natural one, and can do so through the consumption of energy, a living system can maintain itsfar-from-equilibrium state (like the refrigerator) through the continual utilization of energy. But how could such a highly organized energy-gathering entity have come about? That, in essence, was the issue that troubled those great physicists. So within the context of this thermodynamic overview of living systems, the issue that needs to be resolved is how do dynamic kinetic stability and thermodynamic stability relate to one another? In what manner do they coexist?
Even though we are claiming that dynamic kinetic stability governs the stability of replicating systems, it is clear that the drive toward greater dynamic kinetic stability must be consistent with the requirements of the second law. Initially that may not pose a problem, as the constraints of the second law permit many kinetically-allowed pathways. However, it is also clear that certain pathways leading to enhanced dynamic kinetic stability may not be allowed. In fact, one can presume that the greater complexity associated with the drive toward enhanced dynamic kinetic stability is likely to be thermodynamically unfavorable, so that such pathways will be at some point become effectively blocked. Simply, highly complex systems that exhibit high dynamic kinetic stability are likely to be thermodynamically unstable. However, a way to resolve the apparent conflict between these two types of stability is possible through the emergence of a metabolic (in the energy-gathering sense) capability. Let us consider this point in some detail.
In a theoretical simulation of molecular replication, we have recently demonstrated that a metabolic capability, given sufficient time, is likely to become incorporated into a replicating system [
27]. If through some chance mutation a replicating molecule acquires, for example, a photoactive site, a kinetic analysis of the competing replication reactions of the original non-metabolic replicator and the mutated metabolic replicator indicates that the metabolic replicator, the one with the energy-gathering photoactive site, will drive the non-metabolic replicator into extinction. In other words, the metabolic replicator exhibits greater dynamic kinetic stability than the non-metabolic replicator and as a result the
less stable non-metabolic replicator is transformed into the
more stable metabolic replicator. The significant point here is that once a replicator has acquired a metabolic capability it is now in some sense “freed” from the thermodynamic constraints associated with the directives of the second law. From that moment on, kinetic considerations, rather than thermodynamic ones, govern the continued evolution of that replicating system. Thus the theoretical simulation demonstrates that the incorporation of an energy-gathering metabolic capability into a non-metabolic system, once acquired through a chance mutation, will, through a process of kinetic selection, lead to a more effective metabolic replicator,
i.e., a replicator of greater dynamic kinetic stability. In fact the point at which a down-hill (thermodynamic) replicator acquired a metabolic capability can be viewed as a critical one in the emergence of life. One might even say that at that point life began. That was the moment that an objective (to use the Monod terminology [
28]) replicator was transformed into a projective (teleonomic) replicator, and (to a degree) cut loose from its thermodynamic chains. That was the moment that the system began to follow its kinetic “agenda” [
29], the moment, as Kauffman put it, it began “to act on its own behalf” [
20].