Fluctuation, Dissipation and the Arrow of Time
Abstract
:1. Introduction
- Equilibrium Principle
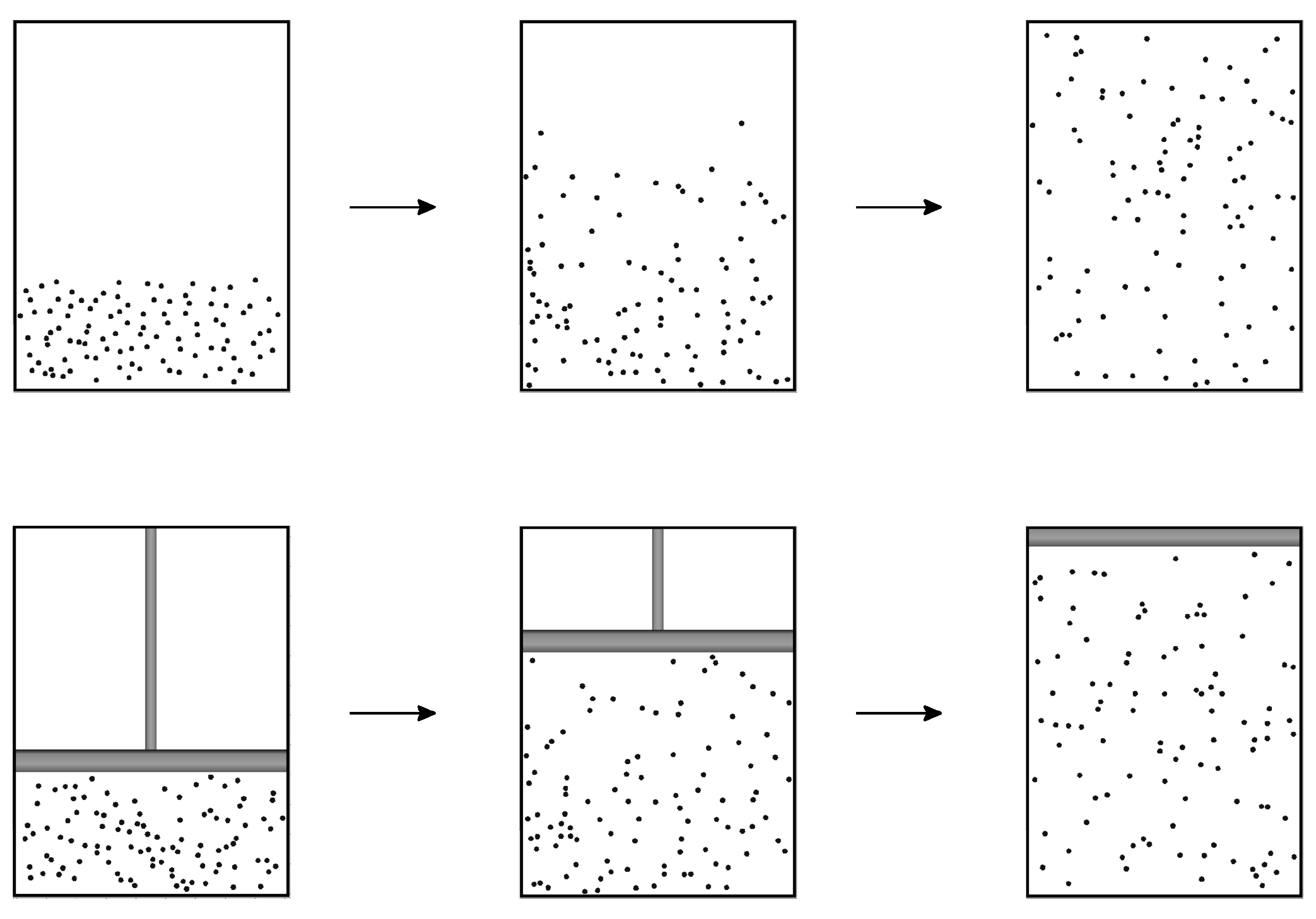
- An isolated, macroscopic system which is placed in an arbitrary initial state within a finite fixed volume will attain a unique state of equilibrium.
- Second Law (Clausius)
- For a non-quasi-static process occurring in a thermally isolated system, the entropy change between two equilibrium states is non-negative.
- Second Law (Kelvin)
- No work can be extracted from a closed equilibrium system during a cyclic variation of a parameter by an external source.
2. The Fluctuation Theorem
2.1. Autonomous Dynamics
2.2. Nonautonomous Dynamics
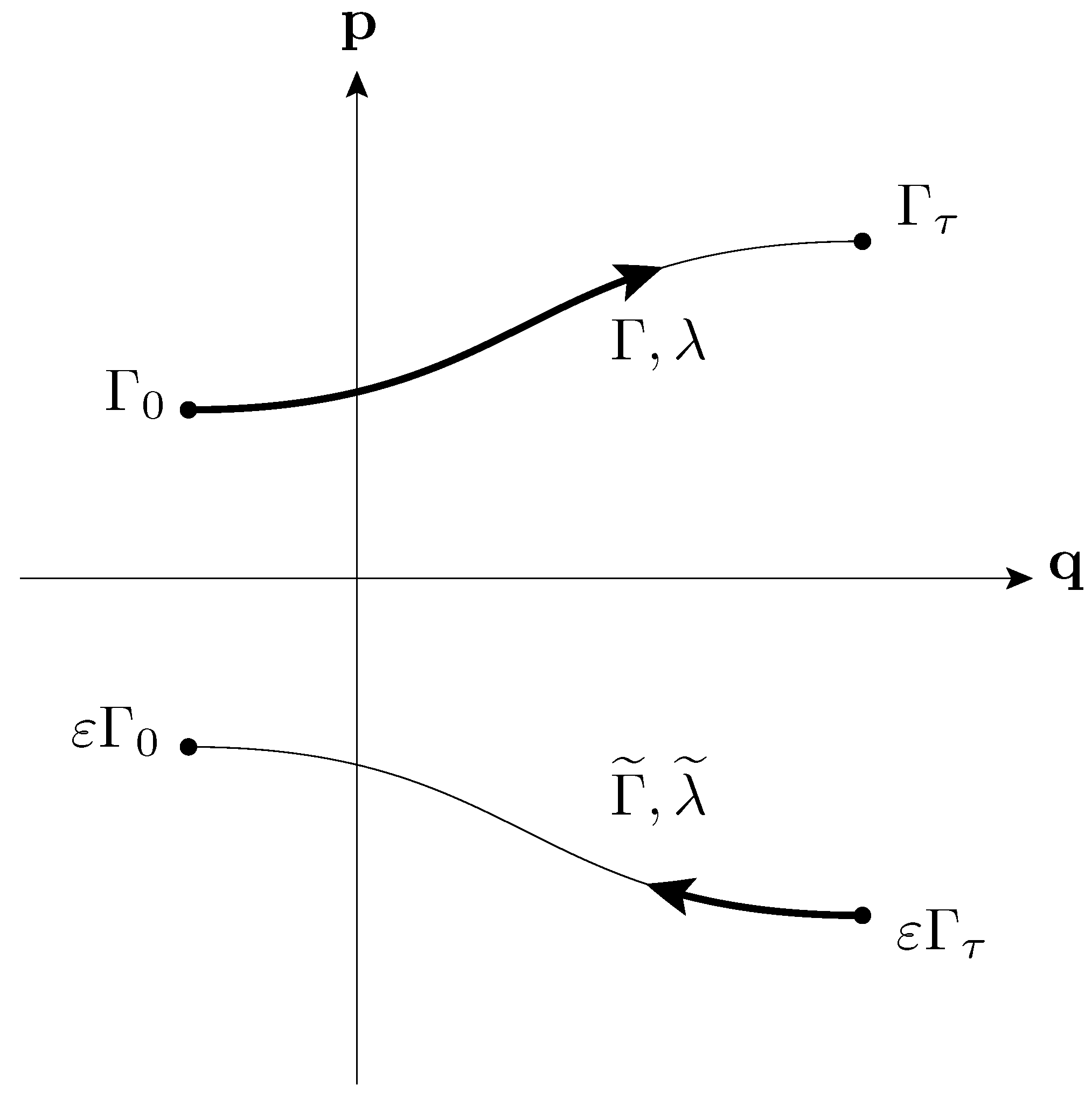
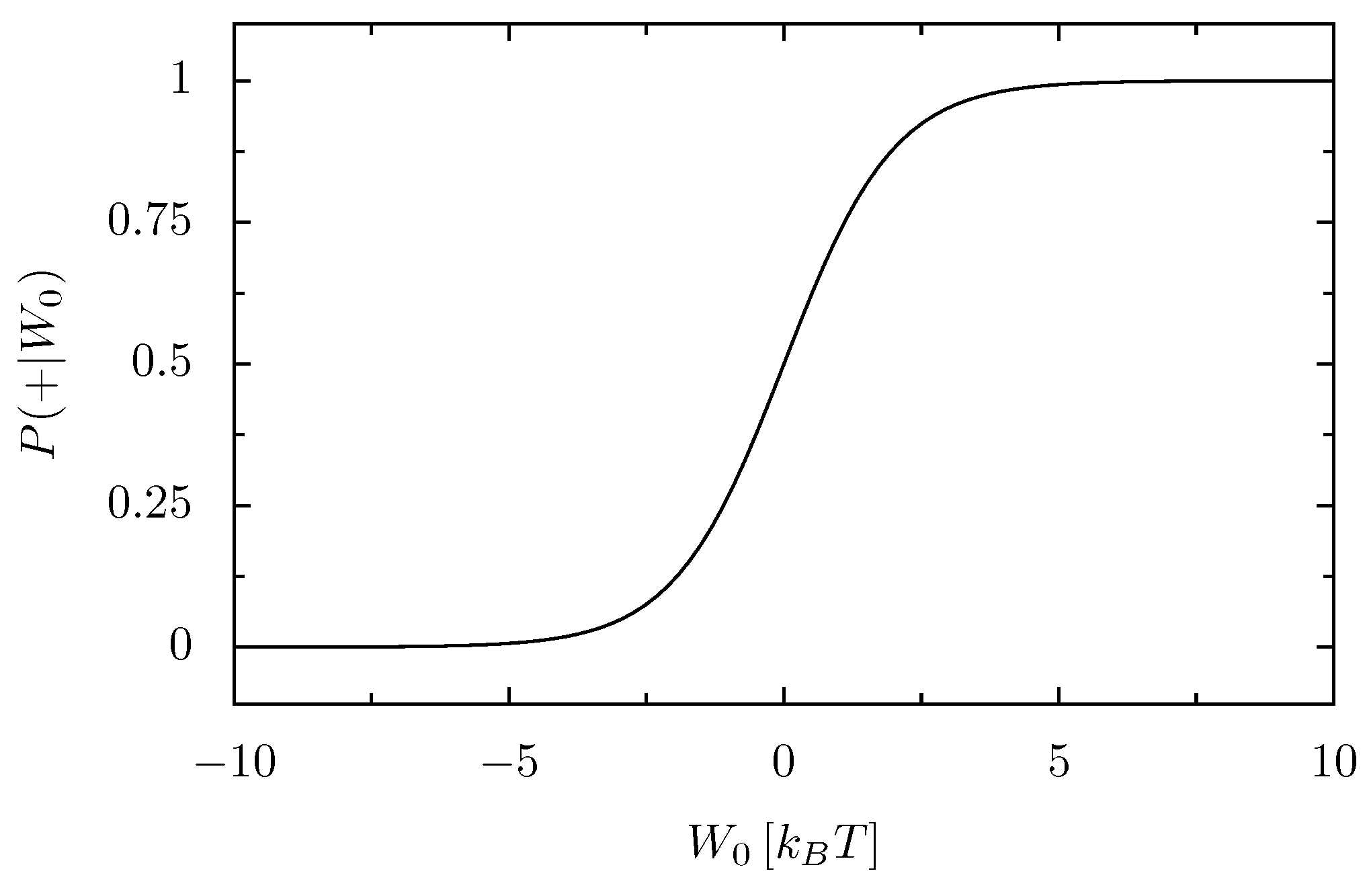
- Second Law (Fluctuation Theorem)
- Injecting some amount of energy into a thermally insulated system at equilibrium at temperature T by the cyclic variation of a parameter, is exponentially (i.e., by a factor ) more probable than withdrawing the same amount of energy from it by the reversed parameter variation.
3. Dissipation: Kubo’s Formula
4. Implications for the Arrow of Time Question
5. Remarks
Acknowledgments
References and Notes
- Brown, H.R.; Uffink, J. The origins of time-asymmetry in thermodynamics: The minus first law. Stud. Hist. Phil. Mod. Phys. 2001, 32, 525–538. [Google Scholar] [CrossRef]
- Campisi, M. On the mechanical foundations of thermodynamics: The generalized Helmholtz theorem. Stud. Hist. Phil. Mod. Phys. 2005, 36, 275–290. [Google Scholar] [CrossRef]
- Campisi, M.; Kobe, D.H. Derivation of the Boltzmann principle. Am. J. Phys. 2010, 78, 608–615. [Google Scholar] [CrossRef]
- That such final equilibrium state exists is dictated by the Minus-First Law. Here we see clearly the reason for assigning a higher rank to the Equilibrium Principle.
- Callen, H.B. Thermodynamics: An Introduction to the Physical Theories of Equilibrium Thermostatics and Irreversible Thermodynamics; Wiley: New York, NY, USA, 1960. [Google Scholar]
- Campisi, M.; Hänggi, P.; Talkner, P. Colloquium: Quantum fluctuation relations: Foundations and applications. Rev. Mod. Phys. 2011, 83, 771–791. [Google Scholar] [CrossRef]
- Jarzynski, C. Equalities and inequalities: Irreversibility and the second law of thermodynamics at the nanoscale. Annu. Rev. Condens. Matter. Phys. 2011, 2, 329–351. [Google Scholar] [CrossRef]
- Allahverdyan, A.; Nieuwenhuizen, T. A mathematical theorem as the basis for the second law: Thomson’s formulation applied to equilibrium. Physica A 2002, 305, 542–552. [Google Scholar] [CrossRef]
- Campisi, M.; Talkner, P.; Hänggi, P. Finite bath fluctuation theorem. Phys. Rev. E 2009, 80, 031145. [Google Scholar] [CrossRef]
- Esposito, M.; Harbola, U.; Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 2009, 81, 1665–1702. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics: Principles and perspectives. Eur. Phys. J. B 2008, 64, 423–431. [Google Scholar] [CrossRef]
- Bochkov, G.N.; Kuzovlev, Y.E. General theory of thermal fluctuations in nonlinear systems. Sov. Phys. JETP 1977, 45, 125–130. [Google Scholar]
- Messiah, A. Quantum Mechanics; North Holland: Amsterdam, The Netherlands, 1962. [Google Scholar]
- To be more precise, the probability density functional (PDFL).
- To be more precise P[Γ]Γ=ϱ(Γ0)dΓ0 where Γ is the measure on the Γ-trajectory space, and dΓ0 is the measure in phase space.
- Kubo, R. Statistical-mechanical theory of irreversible processes. I. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- For the sake of clarity we remark that the Hamiltonian describing the expansion of a gas, as depicted in Figure 1, bottom, is not of this form. Our arguments however can be generalized to nonlinear couplings [12].
- Stratonovich, R.L. Nonlinear nonequilibrium thermodynamics II: Advanced theory. In Springer Series in Synergetics; Springer-Verlag: Berlin, Germany, 1994; Volume 59. [Google Scholar]
- Andrieux, D.; Gaspard, P. Quantum work relations and response theory. Phys. Rev. Lett. 2008, 100, 230404. [Google Scholar] [CrossRef] [PubMed]
- Jarzynski, C. Comparison of far-from-equilibrium work relations. C. R. Phys. 2007, 8, 495–506. [Google Scholar] [CrossRef]
- Horowitz, J.; Jarzynski, C. Comparison of work fluctuation relations. J. Stat. Mech. Theor. Exp. 2007, 2007, P11002. [Google Scholar] [CrossRef]
- Campisi, M.; Talkner, P.; Hänggi, P. Quantum Bochkov-Kuzovlev work fluctuation theorems. Phil. Trans. R. Soc. A 2011, 369, 291–306. [Google Scholar] [CrossRef] [PubMed]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721–2726. [Google Scholar] [CrossRef]
- For a detailed discussion on the differences between the two work expressions we refer the readers to Section III. A in the colloquium [6].
- The nonequilibrium average 〈·〉λ can be understood as an average over the work probability density function p[W0; λ], that is the probability that the energy W0 is injected in the system during one realization of the driving protocol. It formally reads [6]: p[W0; λ] = ∫ dq0dp0ρ0(q0, p0)δ[W0 − λt(qt, pt)], where δ denotes Dirac’s delta function, and (qt, pt) is the evolved of its initial (q0, p0) under the driving protocol λ.
- Callen, H.B.; Welton, T.A. Irreversibility and generalized noise. Phys. Rev. 1951, 83, 34–40. [Google Scholar] [CrossRef]
- Einstein, A. Investigations on the Theory of Brownian Movement; Methuen: London, UK , 1926; Dover, NY, USA, 1956; reprinted. [Google Scholar]
- Johnson, J.B. Thermal agitation of electricity in conductors. Phys. Rev. 1928, 32, 97–109. [Google Scholar] [CrossRef]
- Nyquist, H. Thermal agitation of electric charge in conductors. Phys. Rev. 1928, 32, 110–113. [Google Scholar] [CrossRef]
- Collin, D.; Ritort, F.; Jarzynski, C.; Smith, S.B.; Tinoco, I.; Bustamante, C. Verification of the Crooks fluctuation theorem and recovery of RNA folding free energies. Nature 2005, 437, 231–234. [Google Scholar] [CrossRef] [PubMed]
- Liphardt, J.; Dumont, S.; Smith, S.B.; Tinoco, I.; Bustamante, C. Equilibrium information from nonequilibrium measurements in an experimental test of Jarzynski’s equality (article). Science 2002, 296, 1832–1836. [Google Scholar] [CrossRef] [PubMed]
- Douarche, F.; Ciliberto, S.; Petrosyan, A.; Rabbiosi, I. An experimental test of the Jarzynski equality in a mechanical experiment. Europhys. Lett. 2005, 70, 593–599. [Google Scholar] [CrossRef]
- Wu, T.-Y. On the nature of theories of irreversible processes. Int. J. Theor. Phys. 1969, 2, 325–343. [Google Scholar] [CrossRef]
- Hänggi, P.; Thomas, H. Stochastic processes: Time-evolution, symmetries and linear response. Phys. Rep. 1982, 88, 207–319. [Google Scholar] [CrossRef]
- Campisi, M. Statistical mechanical proof of the second law of thermodynamics based on volume entropy. Stud. Hist. Phil. Mod. Phys. 2008, 39, 181–194. [Google Scholar] [CrossRef]
- Campisi, M. Increase of Boltzmann entropy in a quantum forced harmonic oscillator. Phys. Rev. E 2008, 78, 051123. [Google Scholar] [CrossRef]
- In principle, one should treat the external parameter itself as a dynamical coordinate, and consider the autonomous evolution of the extended system.
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Campisi, M.; Hänggi, P. Fluctuation, Dissipation and the Arrow of Time. Entropy 2011, 13, 2024-2035. https://doi.org/10.3390/e13122024
Campisi M, Hänggi P. Fluctuation, Dissipation and the Arrow of Time. Entropy. 2011; 13(12):2024-2035. https://doi.org/10.3390/e13122024
Chicago/Turabian StyleCampisi, Michele, and Peter Hänggi. 2011. "Fluctuation, Dissipation and the Arrow of Time" Entropy 13, no. 12: 2024-2035. https://doi.org/10.3390/e13122024
APA StyleCampisi, M., & Hänggi, P. (2011). Fluctuation, Dissipation and the Arrow of Time. Entropy, 13(12), 2024-2035. https://doi.org/10.3390/e13122024



