1. Introduction
In 1973 Four laws of black hole mechanics were formulated [
1], and Bekenstein introduced a black hole entropy [
2]. A year later Hawking found a quantum evaporation of a black hole [
3,
4] which gave the birth to thermodynamics of black holes [
5,
6,
7] (for a review see [
8]). In 1976 Gibbons and Hawking found that also cosmological horizon can radiate [
9], and this gave rise to thermodynamics of horizons [
10,
11,
12,
13,
14,
15,
16,
17,
18].
Astronomical observations testify that our universe is dominated at above 73 % of its density by a dark energy responsible for its accelerated expansion due to negative pressure,
,
[
19,
20,
21,
22,
23,
24,
25], with the best fit
[
26,
27,
28,
29,
30,
31] corresponding to a cosmological constant
λ ([
32] and references therein). This motivates study of cosmological black holes.
Studies of black hole thermodynamics in the de Sitter space are also important in the context of the quantum theory of gravity and of dark matter physics. Theoretical developments suggest the existence of a holographic duality between quantum gravity on de Sitter space and a certain Euclidean conformal field theory on its spacelike boundary, dS/CFT correspondence [
33,
34]. Black hole remnants are considered as a source of dark matter for more than two decades [
35,
36,
37,
38,
39] (for a review see [
40,
41]), and are under search at the CERN LHC [
42,
43].
The basic problem concerning black hole remnants is which remnants (if any) leave from the Hawking evaporation. Generalized uncertainty principle requires the existence of a remnant of the Planck mass [
38]. On the other hand, an evident symmetry or quantum number preventing complete evaporation is not found [
44]. Another problem concerning the Planck mass remnant is that its entropy seems to be zero [
38], although the second law of black hole thermodynamics requires
[
5], and for a remnant the horizon radius
. This question and its relation to the third law of thermodynamics will be discussed in
Section 5.
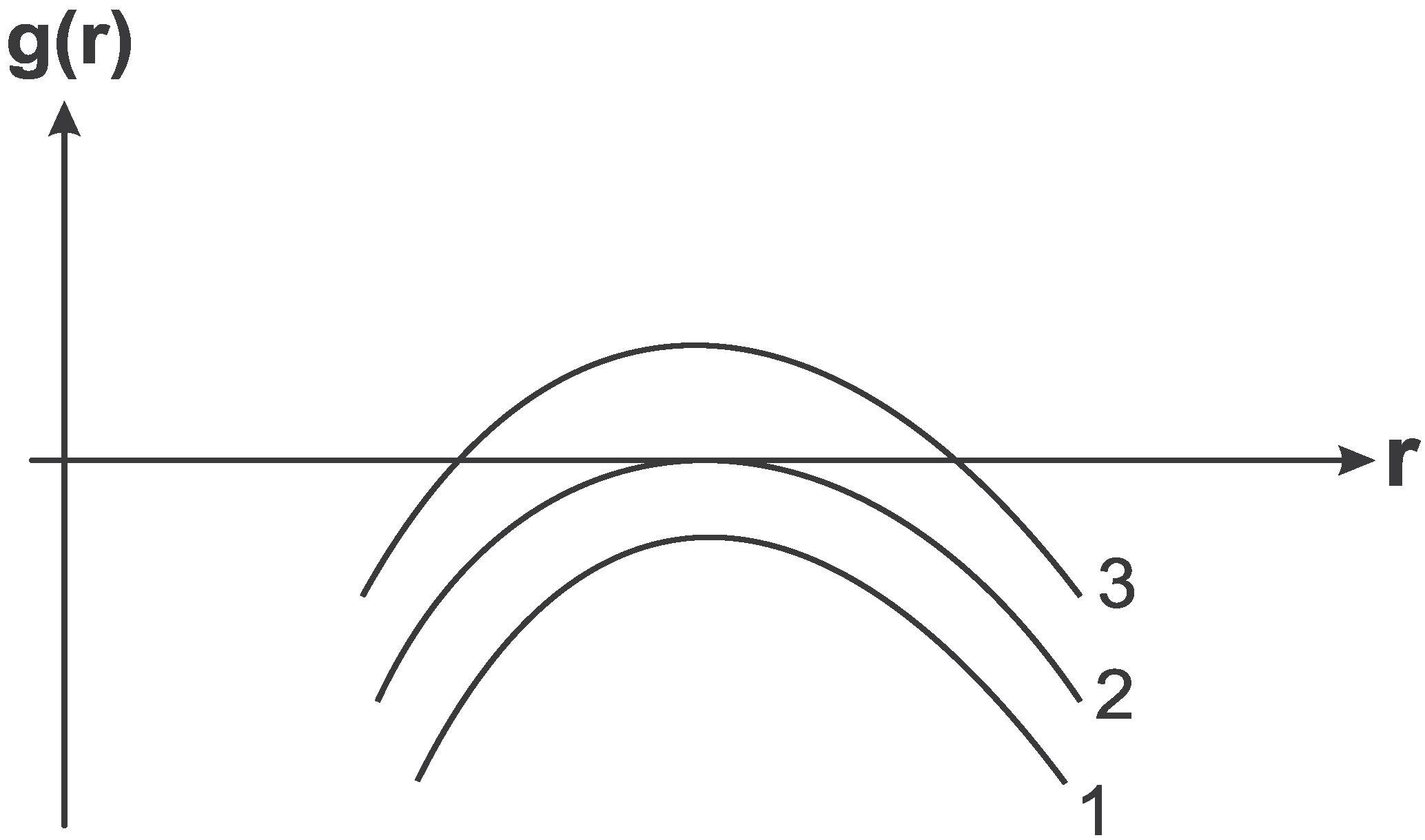
Thermodynamics of black holes in the de Sitter space is in essence thermodynamics in a multi-horizon space-time. The Schwarzschild-de Sitter metric belongs to the class of space-time metrics
The metric function is given by
where
M is the mass parameter and
l is related to the background cosmological constant
λ by
. Basic features of a space-time described by (2) depend on the value of the quantity
. For
it describes a Schwarzschild-de Sitter black hole with two horizons (curve 3 in
Figure 1). The case of double horizon
corresponds to the Nariai solution (curve 2 in
Figure 1), and for
the metric (4) is the Kantowski-Sachs metric describing an anisotropic homogeneous universe (curve 1 in
Figure 1).
Figure 1.
Metric function for the Schwarzschild-de Sitter space-time.
Figure 1.
Metric function for the Schwarzschild-de Sitter space-time.
The Schwarzschild-de Sitter black hole emits the Hawking radiation from both horizons [
9], but in general they are not in thermal equilibrium. The Gibbons-Hawking temperature on a horizon
with a surface gravity
corresponds to the periodicity of the Euclidean quantum field theory in the Euclidean time
. In the Kruskal coordinates introduced to avoid a singularity at the horizon, the Kruskal time
is the periodic function of
with the period
related directly to the inverse quantum temperature of a horizon. In the case of two horizons it is impossible to obtain, by one transformation, regularity on both horizons, so that an observer would detect the mixture of radiations from horizons [
9]. A common (global) temperature can be defined only in the case when the relation of surface gravities on horizons is the rational number [
45,
46]. The Kruskal extension of the metric (1) needs a separate coordinate patch for each horizon. For each patch the Kruskal extension takes the form
. The new and old time coordinates are related by
. In the Euclidean time
a minimal period appears as the lowest common multiple of
when the ratio
is a rational number (
,
are prime integers) [
45,
46]
From the minimal period
, one obtains a global temperature [
45,
46]
Dynamical evolution of the Schwarzschild-de Sitter black hole is typically studied for two horizons separately. Teitelboim considered the Euclidean Schwarzschild-de Sitter geometry as an extremum of two different action principles. He analyzed evolution of a cosmological horizon with a black hole as a boundary, and evolution of a black hole with a cosmological horizon as a boundary, identifying a black hole mass
M as a thermodynamical energy [
16]. He found the tendency of growing the mass parameter
M in the course of evaporation so that a black hole would evolve to the Nariai state. On the other hand, applying the second law of thermodynamics for a manifold between the horizons, Aros found an opposite tendency—complete evaporation of a black hole [
18], which agrees with the results obtained in [
47,
48].
Complete evaporation creates the problem clearly formulated by Aros [
18]: In the Schwarzschild-de Sitter space-time the cosmological horizon is not observer-dependent as in the de Sitter space, but real horizon—due to presence of the black hole which breaks the global symmetries involving the radial direction. A serious doubt concerns a causal structure of space-time: the fate of energy radiated once a black hole disappears “leaving behind the de Sitter space with nothing beyond the cosmological horizon but the de Sitter space itself, so energy can not be hidden there" [
18]. Complete evaporation would create one more serious problem—how to evaporate a singularity? [
49].
The uncertainties concerning endpoint of evaporation are related to the problem of a unique definition of thermodynamical parameters for the case of two horizons. A general approach for defining thermodynamical variables was proposed by Padmanabhan [
12,
13,
14]. He considered the spherically symmetric Einstein equations as the thermodynamical identity for the class of solutions described by the line element (1) which leads to the results confirmed by consideration of a canonical ensemble of space-time metrics from the class (1) at the constant temperature of the horizon determined by the periodicity of the Euclidean time in the Euclidean continuation of the Einstein action; the partition function for this ensemble calculated as the path integral sum [
12], can be written as
which leads to the identification
where
S is the entropy,
E is the thermodynamical energy,
g is value of the metric function on a horizon,
is its derivative on a horizon, and
is the horizon area.
In this paper we apply the Padmanabhan approach to study thermodynamics of a regular cosmological black hole with three horizons, which differs from the Schwarzschild-de Sitter black hole in that a central singularity is replaced with a de Sitter vacuum core.
The idea of replacing a Schwarzschild singularity with a de Sitter vacuum goes back to 1965 papers by Sakharov [
50] who considered
as the equation of state for superhigh density, and by Gliner who interpreted
as corresponding to a vacuum with a non-zero density and suggested that it could be a final state in a gravitational collapse [
51]. In 1988 Poisson and Israel proposed to introduce a transitional layer of an uncertain depth where geometry can be self-regulatory and describable semiclassically by the Einstein equations with a source term representing vacuum polarization effects [
52]. The regular black hole with the de Sitter vacuum interior was proposed first in 1990 [
53] but was lucky to be published only in 1992 after awarding by the Gravity Research Foundation in 1991 [
54].
Now situation looks as follows: A loop quantum gravity provides arguments in favor of a regular black hole [
55,
56]. Analyzing a Schwarzschild interior in frame of a minisuperspace model, Modesto found that the curvature invariant and the inverse volume operator have a finite spectrum inside a horizon [
57]. The “renormalization group improving" approach based on the running Newton constant (
,
in the spherically symmetric case) applied to the Scwarzschild space-time predicts an appearance of a smooth de Sitter core replacing a singularity [
58]. The noncommutative geometry approach (for a review see [
60], see also [
61]) applied to the Schwarzschild black hole, leads to a regular de Sitter core at short distances from the origin [
62]. Appearance of de Sitter core was found also for a cosmological noncommutative black hole of positive mass with the Gaussian density profile [
63].
On the other hand, the Einstein equations admit the class of regular spherically symmetric solutions asymptotically de Sitter at both the origin and infinity [
64,
65,
66]. It was found by investigation of typical features of spherically symmetric solutions to the Einstein equations. Such an approach is in essence model-independent; questions are addressed to equations (“what know equations").
For this class of spherically symmetric solutions a source term connects smoothly two de Sitter vacua with different values of cosmological constant (
as
,
as
with
), and corresponds to anisotropic vacuum dark fluid [
67] defined by symmetry of its stress-energy tensor. In a certain range of the mass parameter,
, a solution of this class describes a regular cosmological black hole with the de Sitter interior [
68,
69].
A smooth de Sitter-Schwarzschild transition has been described by the spherically symmetric Einstein equations with a source term satisfying [
54]
The equation of state, following from
, is
where
is the energy density,
is the radial pressure, and
is the tangential pressure for anisotropic perfect fluid.
A stress-energy tensor specified by (9) and satisfying the weak energy condition (non-zero density for any observer on a time-like curve) represents a spherically symmetric anisotropic (see (10)) vacuum fluid [
54,
64,
65,
66,
67,
70,
71] whose symmetry is reduced as compared with the maximally symmetric de Sitter vacuum [
72]. Vacuum with a reduced symmetry (for a review see [
73,
74,
75,
76,
77,
78,
79]) provides a unified description of dark ingredients in the Universe by a vacuum dark fluid [
67,
71], which represents distributed vacuum dark energy by a time evolving and spatially inhomogeneous cosmological term [
64], and compact objects with de Sitter vacuum interior: regular black holes and gravitational vacuum solitons G-lumps [
65,
67] which are regular gravitationally bound vacuum structures without horizons (dark particles or dark stars, dependently on a mass) [
65,
80,
81]. Mass of a compact object is generically related to interior de Sitter vacuum and to breaking of space-time symmetry from the de Sitter group in the origin [
65,
77,
79].
A regular spherically symmetric black hole with the de Sitter center is described by the metric (1). In the asymptotically flat case, the metric is asymptotically de Sitter for
and asymptotically Schwarzschild for large
r. It has two horizons which coincide for a certain mass
corresponding to an extreme black hole [
65,
80]. Typical behavior of the metric function is shown in
Figure 2. The parameter
m refers to the mass
M normalized to
(
corresponds to G-lump).
Figure 2.
Metric function for de Sitter-Schwarzschild space-time.
Figure 2.
Metric function for de Sitter-Schwarzschild space-time.
It evaporates from both horizons, and generic asymptotic behavior of the metric function
defines dynamics of evaporation. It involves a phase transition where a specific heat is broken and changes its sign. At the final stage a temperature vanishes on a double horizon [
65,
80,
82]. A regular black hole leaves behind a thermodynamically stable remnant with the positive specific heat [
84] (free of the existential problems).
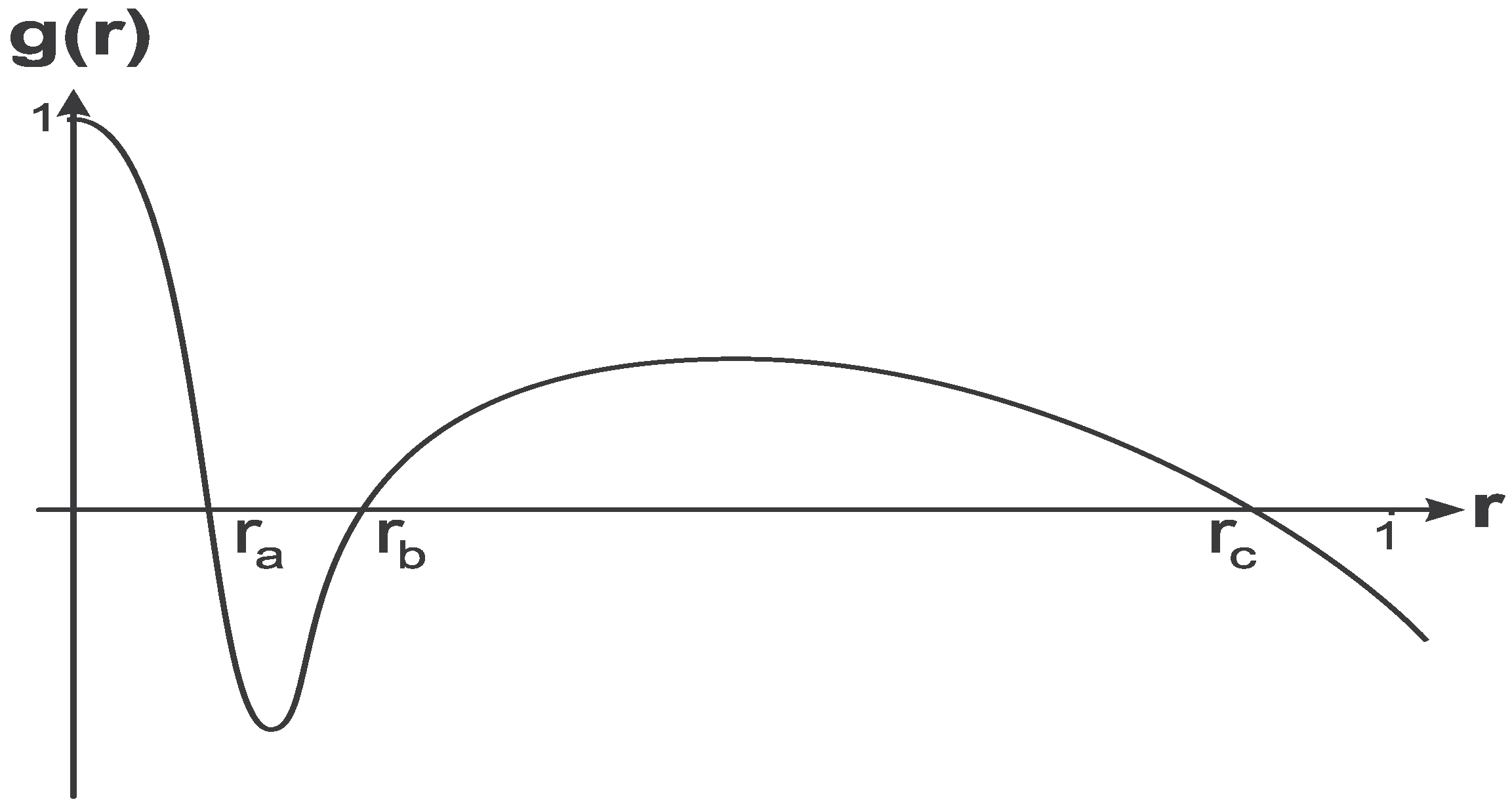
A regular cosmological black hole with the de Sitter center in place of a singularity (
as
) is described by the metric function [
68]
whose asymptotics are the de Sitter metrics with
λ as
and with
as
.
For two scales of vacuum density the geometry can have not more than two horizons [
85], a black hole horizon
, a cosmological horizon
, and an internal horizon
which are shown in
Figure 3.
Figure 3.
Metric function for a regular cosmological black hole with the de Sitter center.
Figure 3.
Metric function for a regular cosmological black hole with the de Sitter center.
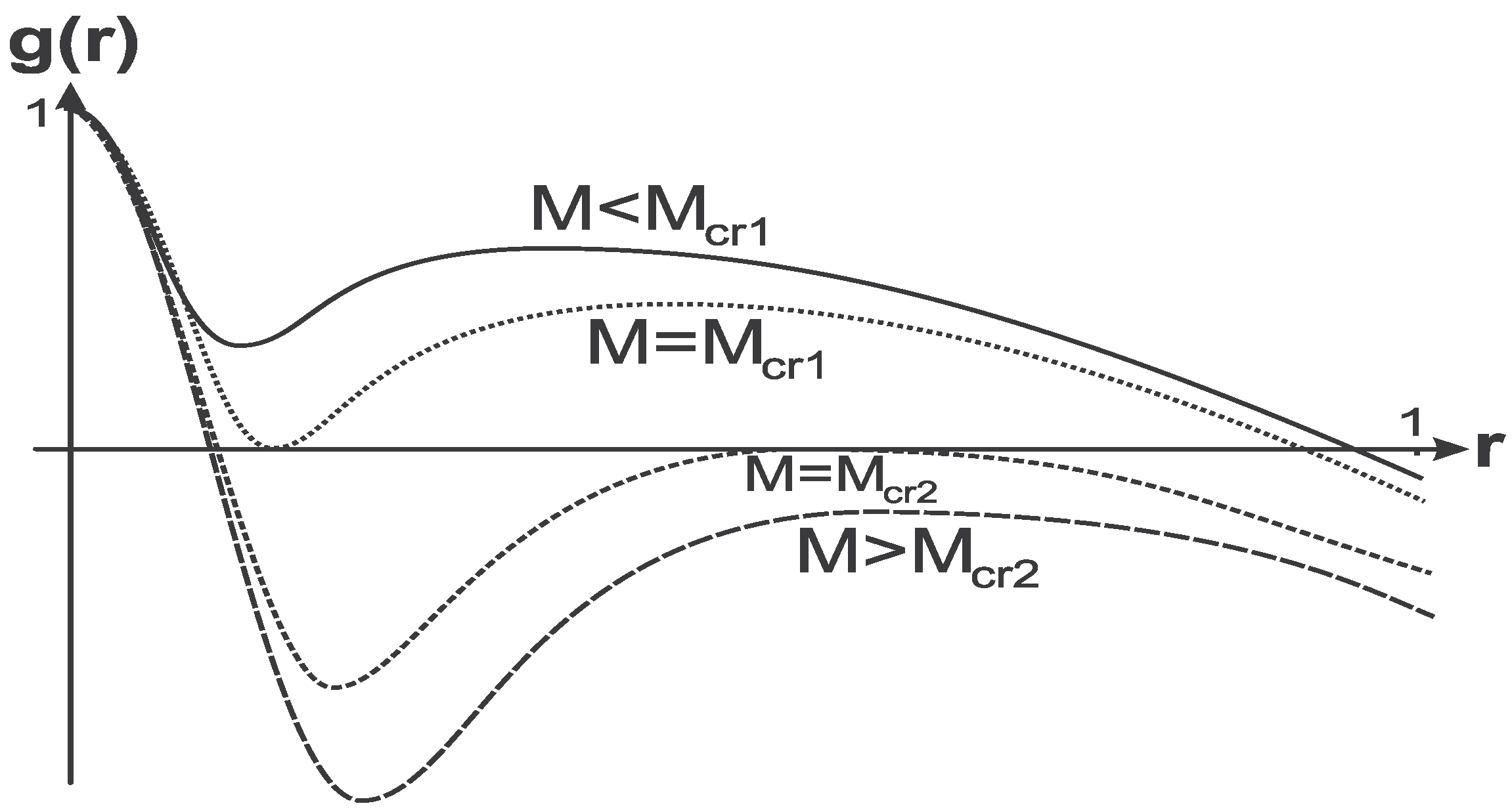
Two horizons
and
coincide at a certain value of a mass parameter
. The mass
puts a lower limit on a black hole mass [
68]. The extreme state
puts an upper limit on a mass of a black hole
. Four configurations including two extreme states and two one-horizon configurations are shown in
Figure 4.
Figure 4.
Metric function for space-time with the de Sitter center asymptotically de Sitter for .
Figure 4.
Metric function for space-time with the de Sitter center asymptotically de Sitter for .
Thermodynamics of a regular black hole with de Sitter interior is dictated by the typical behavior of the metric function , generic for the considered class of space-times specified by symmetry (9) of a stress-energy tensor satisfying the weak energy condition. A particular form of the density profile affects only numerical values of thermodynamical parameters but not their dynamical behavior.
This paper is organized as follows. In
Section 2 we present the basic features of space-time with de Sitter center in asymptotically de Sitter space. In
Section 3 we analyze thermodynamics of horizons. In
Section 4 we study evolution of a regular cosmological black hole during evaporation. In
Section 5 we summarize the results.
We keep fixed an internal Λ (as corresponding to a certain fundamental symmetry scale [
64,
81]). We keep also fixed (following [
16,
18]) a background
λ, so that the results are applicable to the case when a time scale of evaporation is less than a time scale of eventual changing
λ.
2. Basic Features of Space-Time
The stress-energy tensor responsible for geometry (10) connects two de Sitter vacua:
, and
at infinity. Its density component is given by
and includes a background vacuum density
and the dynamical density
ρ which should vanish at
quickly enough to ensure the finiteness of the mass
Space-time described by the metric function (10) has three characteristic length scales
where
l is related to the background vacuum density,
, and
to the de Sitter vacuum density in the origin,
. Normalizing
r to
or to
l we get the characteristic parameter relating two vacuum scales, Λ and
λ For
where
is the characteristic scale of space-times with the de Sitter interior [
52,
54], the metrics (10) are asymptotically Schwarzschild-de Sitter, Equation (2), or asymptotically Schwarzschild in the case
.
For the metric function is asymptotically de Sitter with .
A mass (12) for a regular cosmological black hole is confined within a certain range
which depends on the parameter
q [
68].
For numerical calculations we adopt the density profile [
54]
which describes the de Sitter-Schwarzschild transition in a simple semiclassical model for vacuum polarization in the spherically symmetric gravitational field [
80]. Relevant physical mechanism can be self-regulation of geometry noted by Poisson and Israel [
52]: An asymptotically flat space-time generated during spherically symmetric gravitational collapse can be described by the Schwarzschild vacuum solution down to the quantum barrier. Below this barrier there may exist a layer of an uncertain depth in which geometry could be self-regulatory and describable semiclassically by the Einstein field equations with a source term representing vacuum polarization effects [
52]. In a gravitational collapse all fields contribute to vacuum polarization. Complexity of such a task is evident. However one can use the advantage of involving all of the fields in a collapse: all of them contribute, via Einstein equations, to gravitational field; a limiting density in a collapse could be achieved at the Planck or perhaps at the GUT scale and thus would depend on some unified coupling and would not depend on specific parameters of particular fields (the Schwarzschild black hole which represents the result of a collapse, depends only on mass parameter
M). Therefore one can expect that the resulting effect would be vacuum polarization in a resulting gravitational field [
54]. It can be evaluated qualitatively applying an intuitive semiclassical approach as descried, e.g., by Novikov and Frolov [
86]: in accordance with the uncertainty relation, the lifetime of a virtual pair of particles with energy
is
. In a time
τ particles can move apart from each other at the distance
. The probability
w to find particles separated by a distance
l is proportional to
. To create real particles with a charge
g, a field
F should produce work
. As a result a vacuum polarization and particle creation effects in a field
F are described by the Schwinger formula [
86]
, where
α depends on detailed properties of a field
F. In the case
this qualitative formula agrees with the results of detailed calculations for particular fields [
86]. Gravitational field tension in the spherically symmetric case is characterized by the curvature component
, and the critical value for the case of self-regulation to a de Sitter core is related to the de Sitter curvature,
. As a result of this consideration [
80] we get the density profile (16). It depends, via
, on a limiting density
which is related to a certain unification scale (
).
For the case of the density profile (16) the mass function is given by [
54]
In all pictures below we use the normalization
so that the mass parameter is normalized to
.
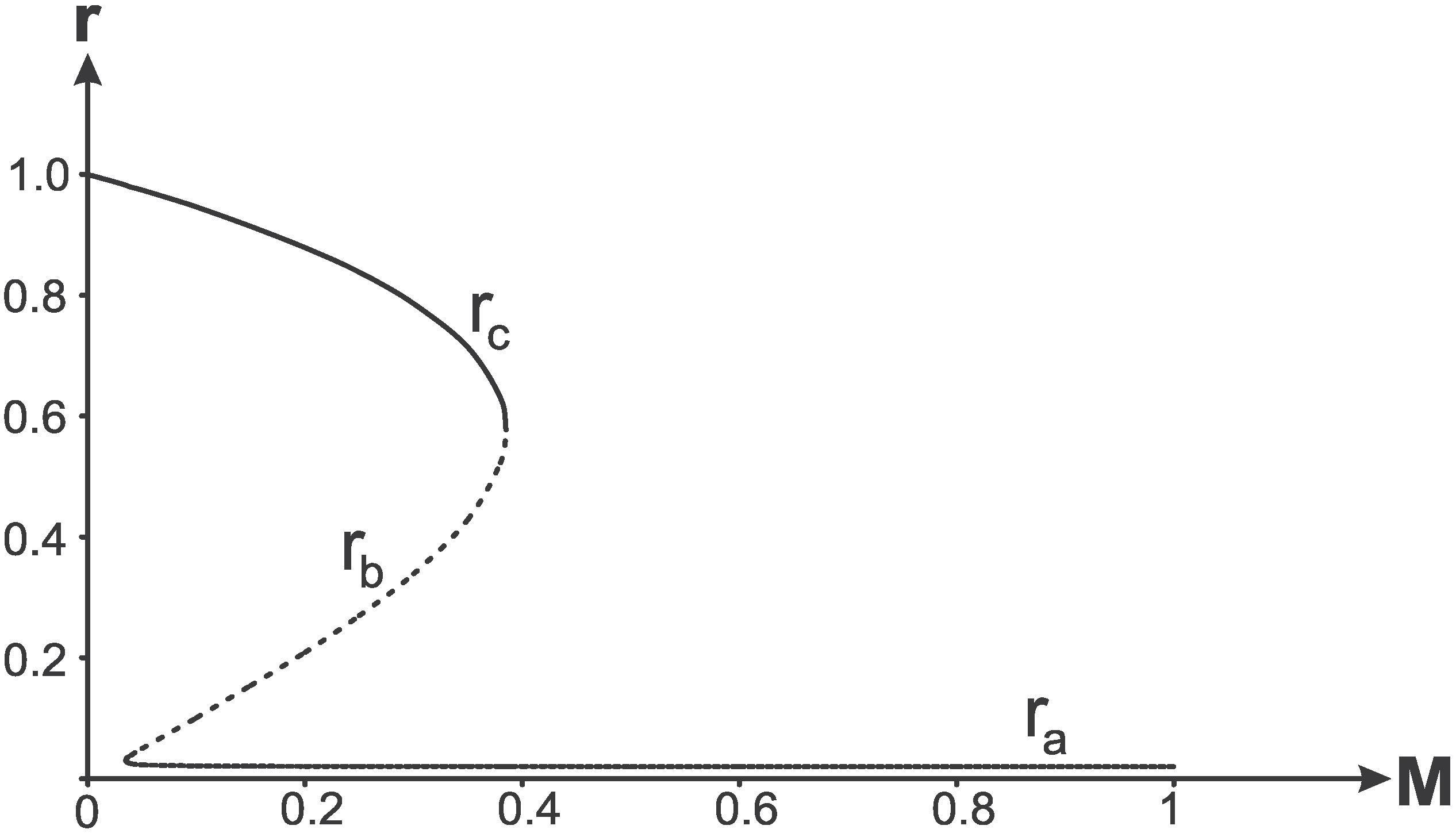
Horizon-mass diagram is plotted in
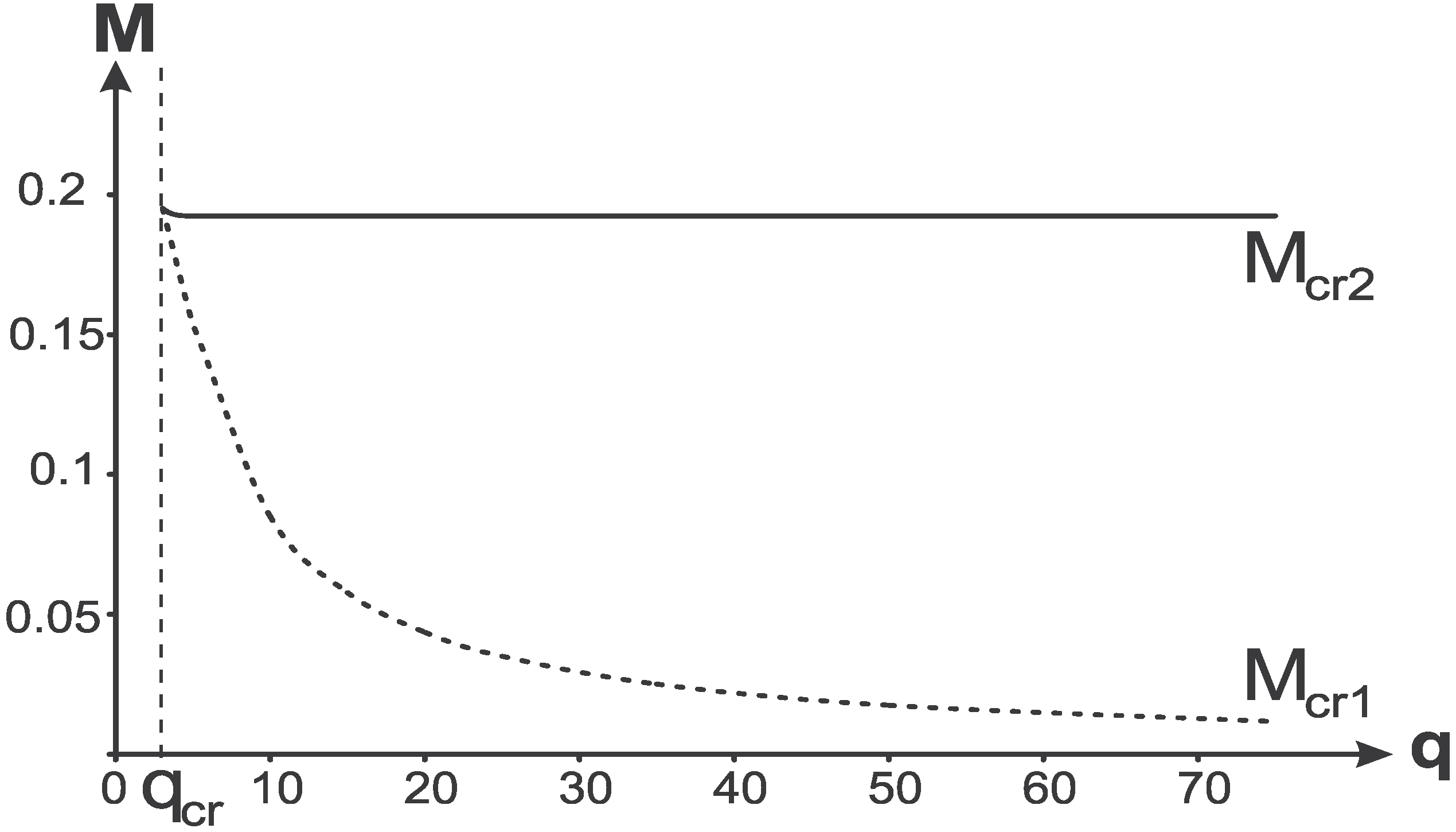
Figure 5 with the the density profile (16). Dependence of boundary masses
and
on
q is shown in
Figure 6.
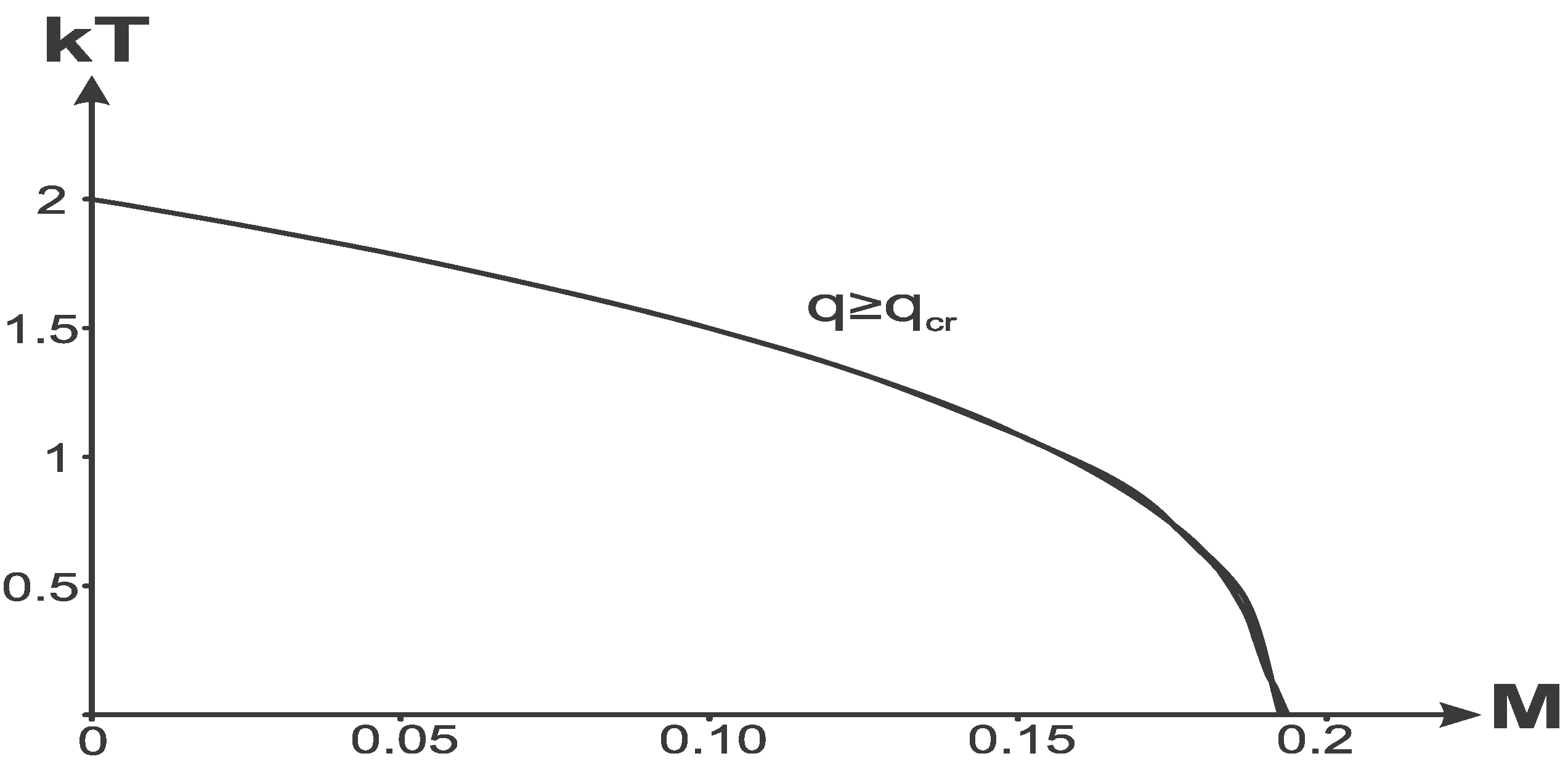
Figure 5.
Horizons-mass diagram for .
Figure 5.
Horizons-mass diagram for .
Figure 6.
Critical masses dependently on q.
Figure 6.
Critical masses dependently on q.
The point where two critical masses coincide, , corresponds to a triple horizon.
For any geometry with the de Sitter center there exist zero gravity surfaces defined by
[
64,
80], beyond which the strong energy condition (
) is violated and gravitational attraction becomes gravitational repulsion.
For geometries satisfying the weak energy condition, there exist also surfaces of zero 4- and 3-scalar curvatures [
80] which can be essential for details of evaporation dynamics [
65,
81]. In the case of two vacuum scales the 4-curvature scalar
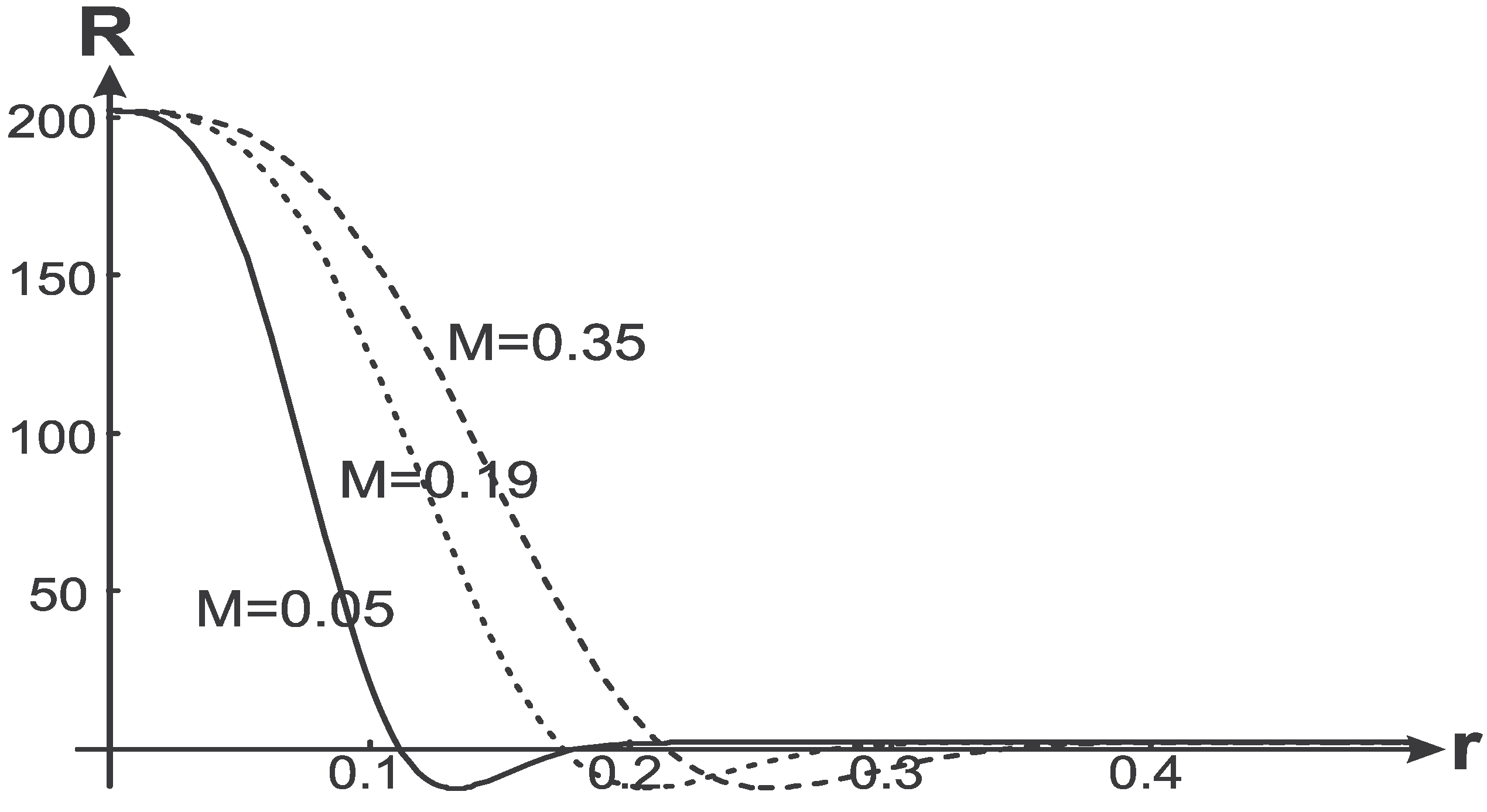
can have two zero points (see
Figure 7 where
R is normalized to
), because
as
and
as
.
Figure 7.
4-curvature scalar for .
Figure 7.
4-curvature scalar for .
There exists a certain value of the parameter q, such that . For , 4-curvature scalar is positive throughout the whole manifold. In the case of the density profile (16) .
Zero-gravity surfaces
and surfaces of zero 4-curvature
are plotted in
Figure 8 together with the horizons for the case
.
Figure 8.
Horizons, zero gravity and zero 4-curvature surfaces for .
Figure 8.
Horizons, zero gravity and zero 4-curvature surfaces for .
We see that there are two surfaces of zero curvature
(
), and two surfaces of zero gravity
(
). In the case of two vacuum scales, the pressure
is negative near
where
, and near
where
. All four characteristic surfaces fit between the internal horizon
and the black hole horizon
. During evaporation they change their mutual location [
81], and this process can provide information about details of evaporation dynamics.
3. Thermodynamics of Horizons
Applying the Padmanabhan approach [
12] we get on the horizons
A specific heat,
is calculated from
which gives
It is easy to check that
can be written as
On a double horizon
a specific heat takes the value [
84]
This simple formula is quite powerful since it tells us unambiguously that an extreme state with a double horizon is thermodynamically stable when it appears in a minimum of the metric function
, and thermodynamically unstable when it appears in its maximum.
An observer in the R-region can detect radiation from the black hole horizon and from the cosmological horizon . An observer in the R-region can detect radiation from the internal horizon which is his cosmological horizon.
The question of stability of an internal horizon
can be essential, especially in the asymptotically flat case. In singular black hole space-times the internal Cauchy horizons suffer from blue shift instabilities. In the case of a black hole with de Sitter vacuum core one can expect stability of an internal horizon. General arguments are given in [
87]: in a singular black hole an infinite blue shift of inward directed signals combined with infalling radiation leads to divergence of stress-energy tensor
near the Cauchy horizon and thus to its instability. In the regular case there exist a limiting density and limiting curvature, and the back reaction of matter does not allow unlimited growth of the curvature and an effective
. Achieving a limiting density is directly related to formation of the de Sitter core, and one may expect stability of the internal horizon [
87]. Detailed investigation for the case of renormalization group improved black hole (without a de Sitter core) has shown that quantum gravity effects weaken the strength of the Cauchy singularity and suggest that presence of some self-regulation mechanism could prevent the local curvature from divergence on the Cauchy horizon [
88].
Derivative of the metric function
is negative on the cosmological horizons and positive on a black hole horizon. As a results on the horizons
and on a black hole horizon
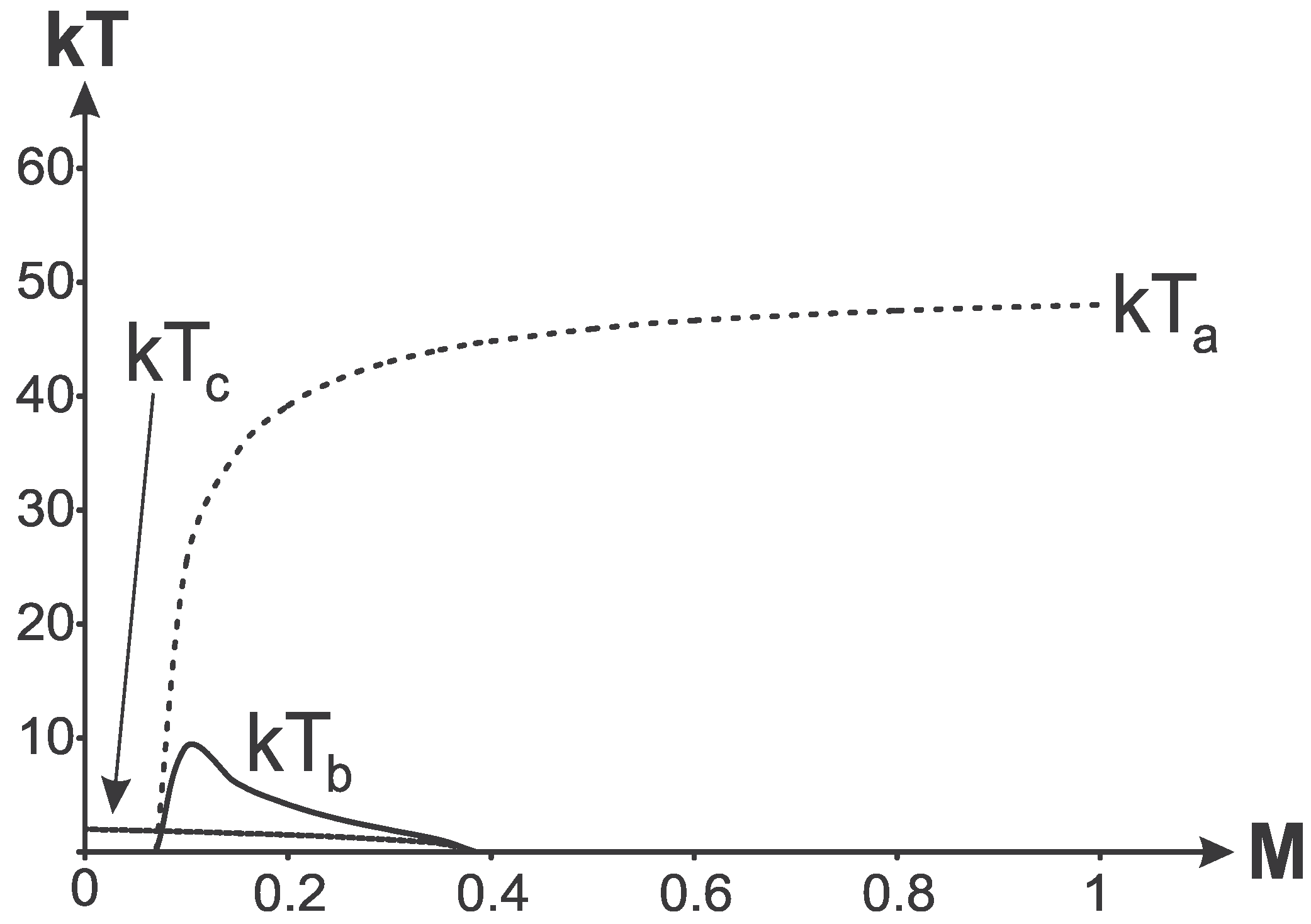
Temperature-mass diagrams for all three horizons are shown in
Figure 9. Numerical analysis shows that dependence of the temperature of the cosmological horizon on the mass
M and on the horizon
is very similar for all
.
In all the pictures below the temperature is normalized in such a way that and .
Figure 9.
Temperatures in the case .
Figure 9.
Temperatures in the case .
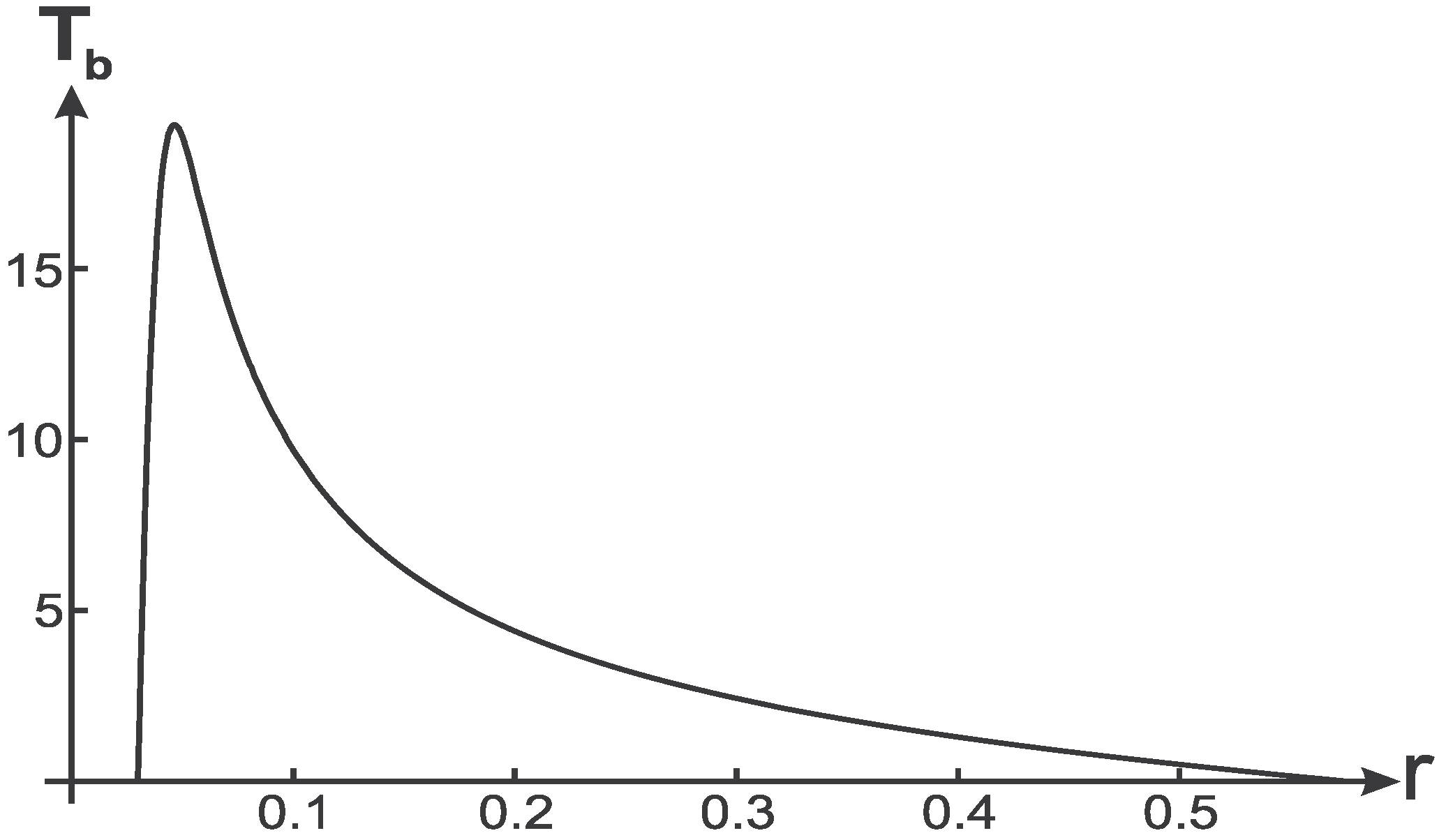
3.1. Thermodynamics of the Black Hole Horizon
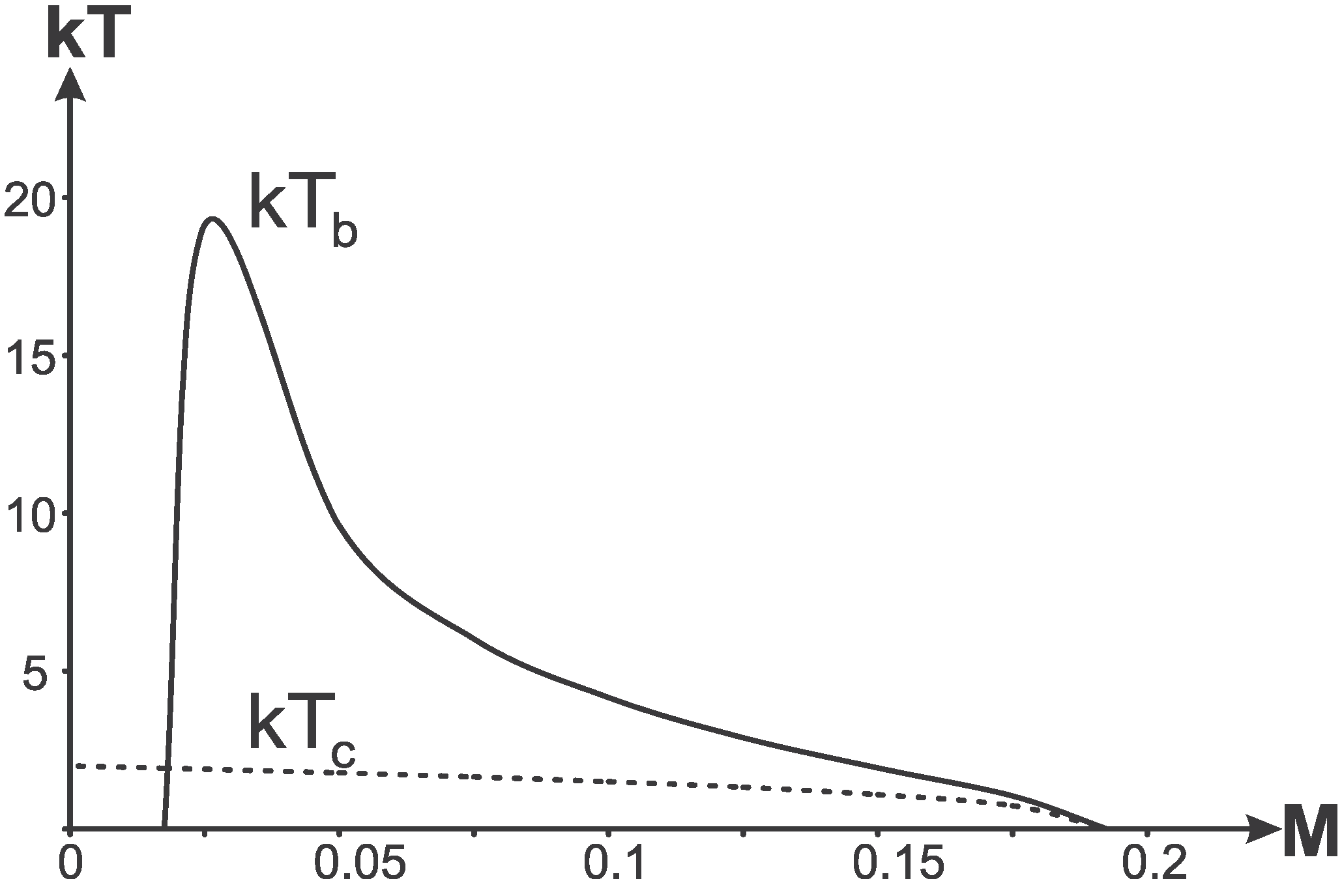
Temperature on a black hole horizon is shown in
Figure 10.
Figure 10.
Dependence of on for the case .
Figure 10.
Dependence of on for the case .
This curve is generic and defined actually by the asymptotic behavior of the metric function [84]. as (zero surface gravity, )
as (zero surface gravity, )
Hence it should exist a maximum in between. At the maximum a specific heat is broken and changes sign (
), hence a second order phase transition occurs during evaporation [
80,
84]. At this point the temperature
acquires its maximal value.
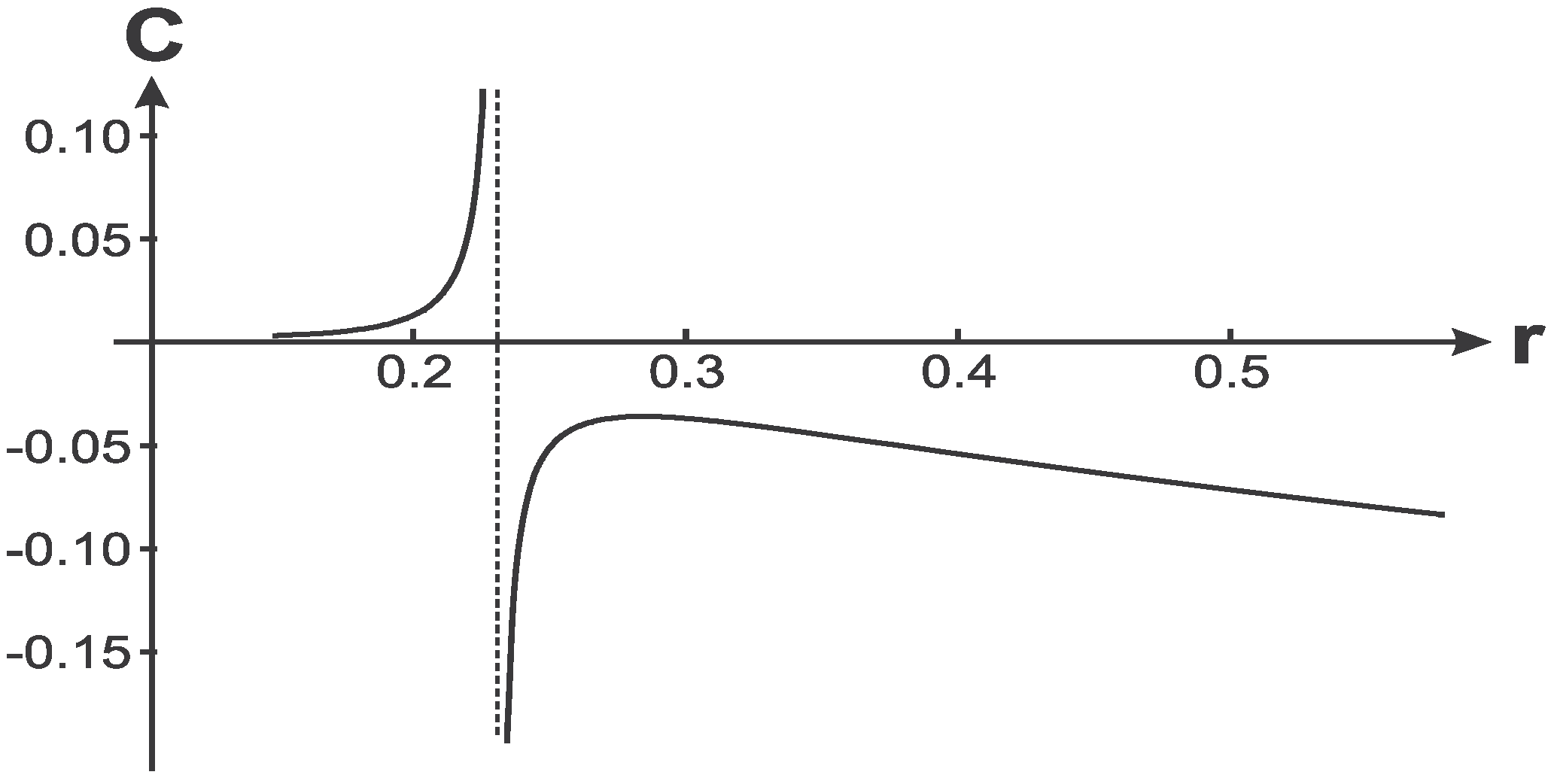
Behavior of a specific heat on the black hole horizon dependently on
is shown in
Figure 11.
Figure 11.
Dependence of on for the case .
Figure 11.
Dependence of on for the case .
Numerical analysis of specific heat did not reveal an essential differences in dependence of
on mass
M and on the horizon radius
. Vanishing of temperature on a double horizon
occurs at a certain value of the parameter
, as we see in
Figure 12.
Figure 12.
Temperature on the black hole horizon.
Figure 12.
Temperature on the black hole horizon.
Maximal temperature—temperature at the phase transition—is given by
For the case of the density profile (16)
For
and
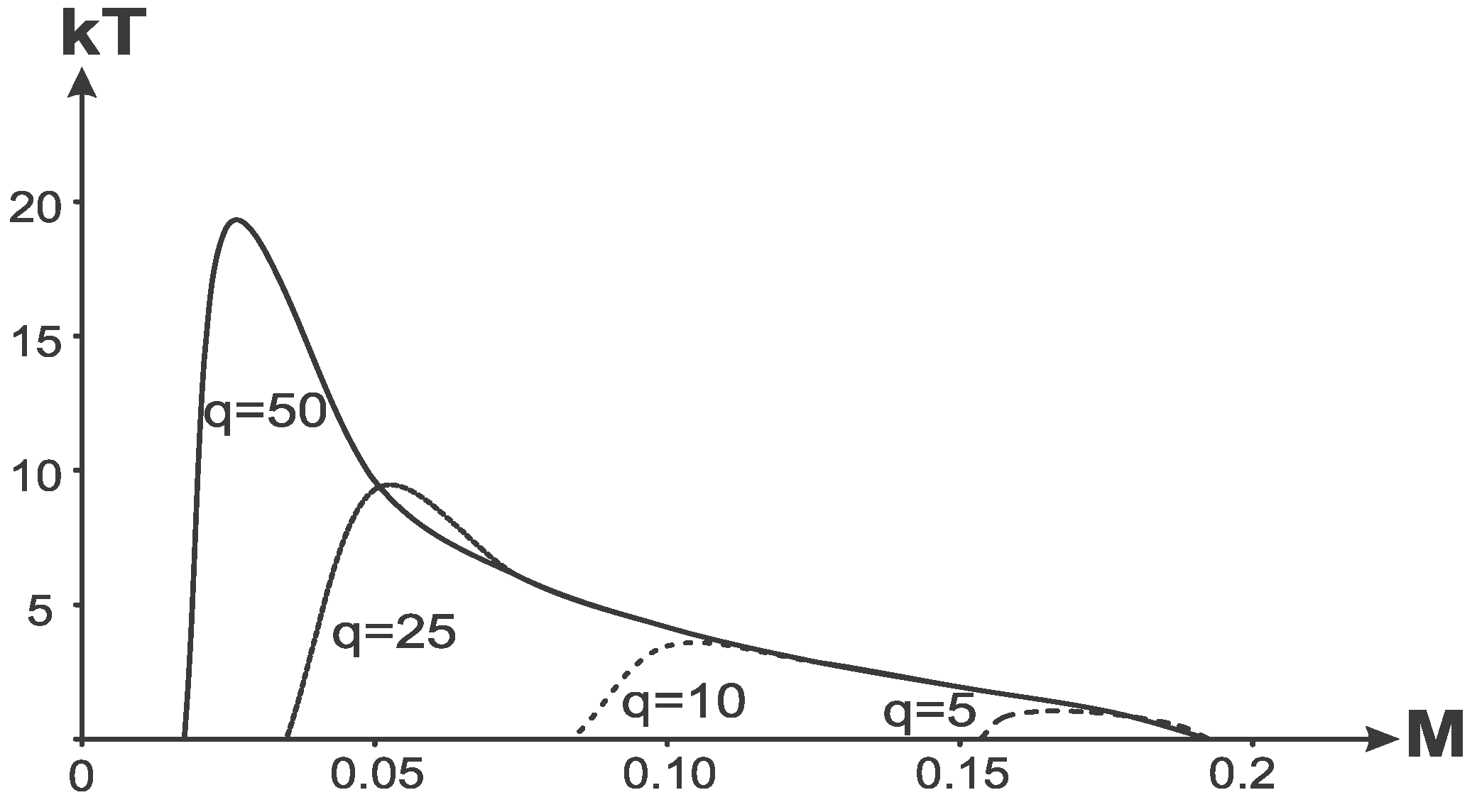
3.2. The Case of Global Temperature for an Observer between and
Let us now compare temperatures from a black hole and cosmological horizon because they can be measured by the same observer (pictured in
Figure 13).
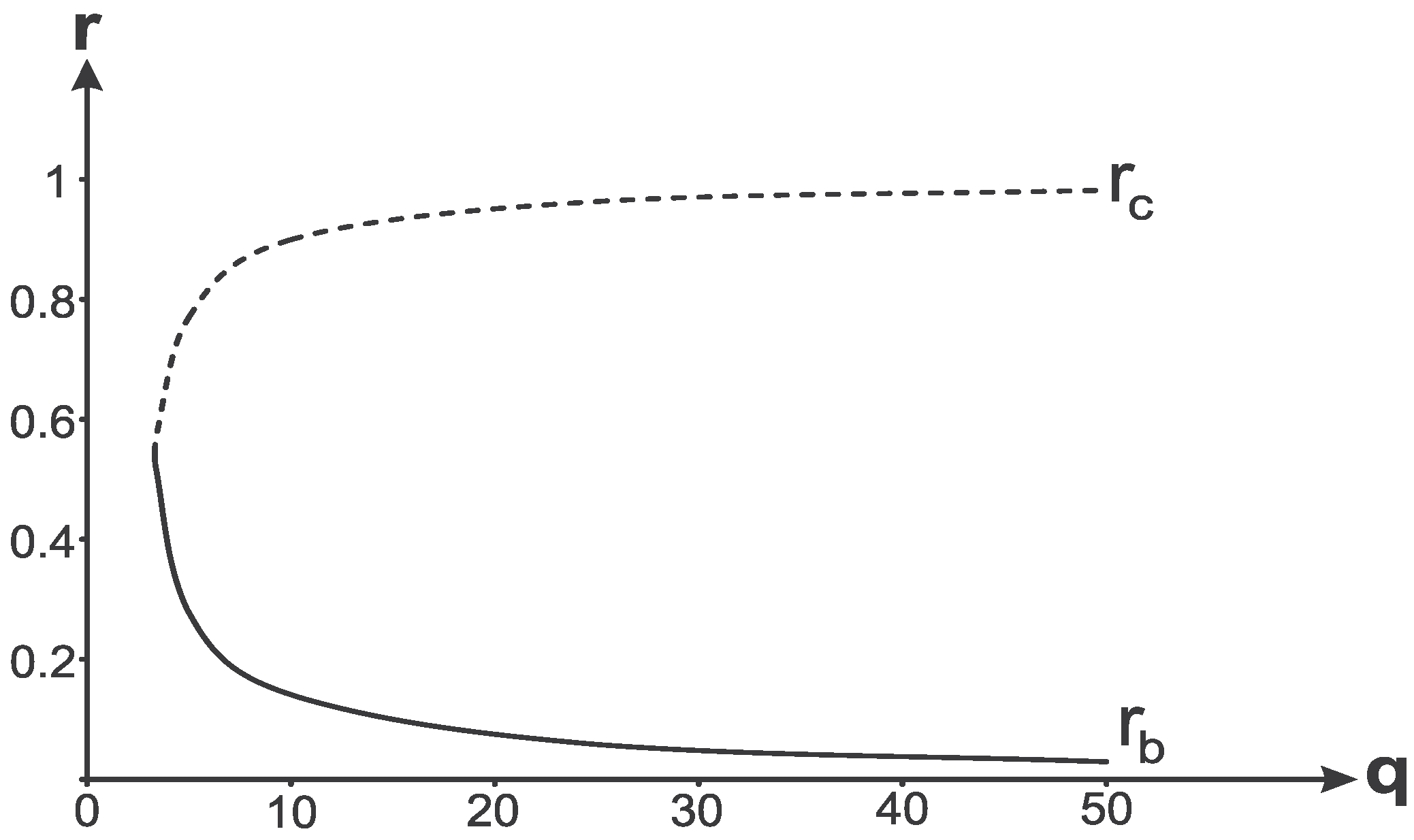
We compare these two temperatures in
Figure 14. In general an observer in R-region
would detect the mixture of radiations from his horizons. Their temperatures are shown in
Figure 14.
Figure 13.
R-region between the horizons and .
Figure 13.
R-region between the horizons and .
Figure 14.
and for the case .
Figure 14.
and for the case .
The most interesting possibility arising here is the existence of a certain range of masses for which temperatures on the black hole and cosmological horizons are equal,
i.e., the case when one can speak about a common (global) temperature for an observer in the R-region between the black hole horizon
and the cosmological horizon
. Dependence of the global temperature on the parameter
q is shown in
Figure 15, where we show also dependence of the mass
M on
q. It tells us that for each value of the mass parameter
M there exists such a value of the parameter
q that the relation of surface gravities on the black hole and cosmological horizons is a rational number.
Figure 15.
Dependence of the global temperature and on q.
Figure 15.
Dependence of the global temperature and on q.
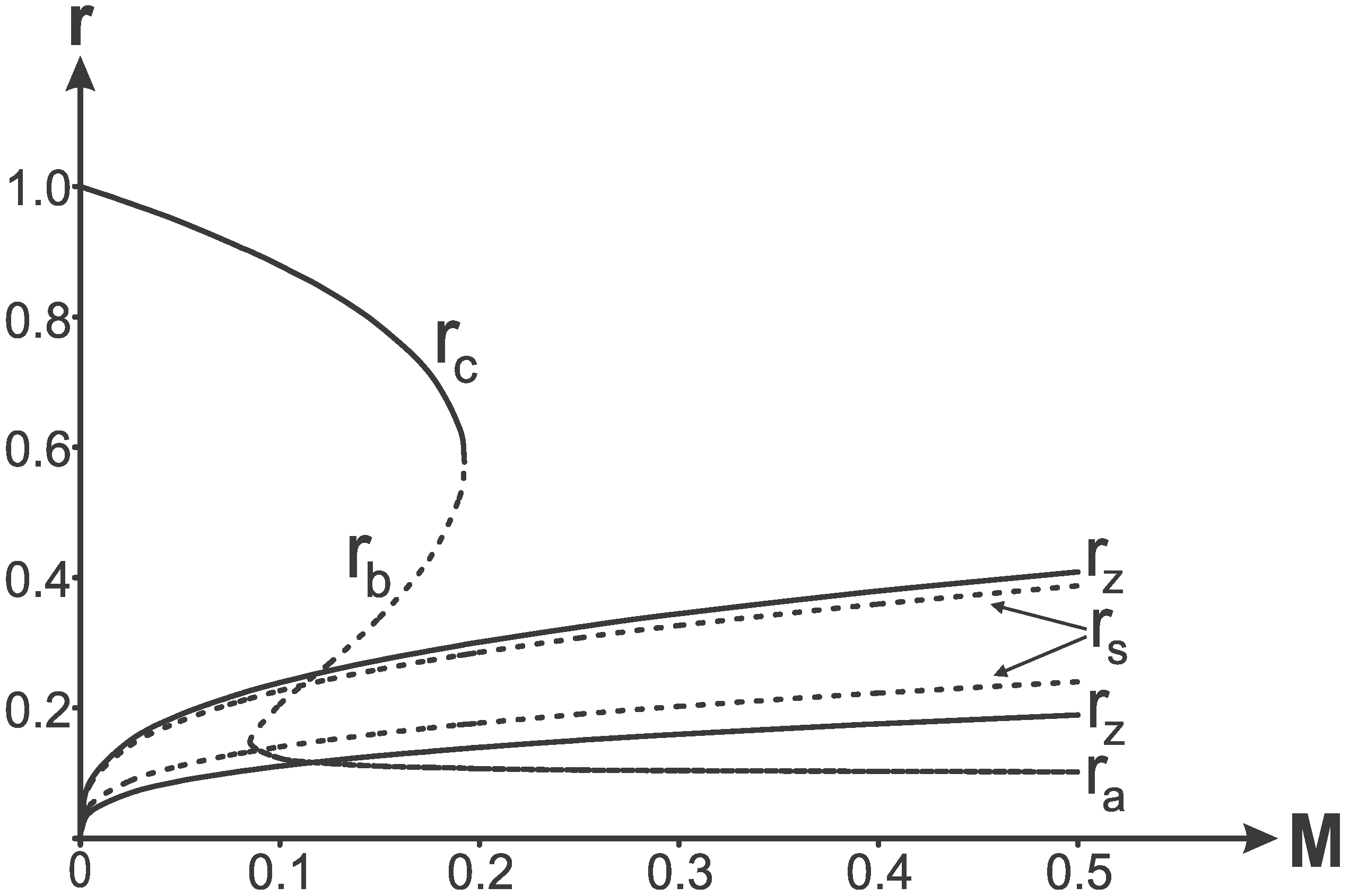
Dependence of horizons on the parameter
q in this case is shown in
Figure 16.
Figure 16.
Dependence of horizons on q in the case of existence of the global temperature.
Figure 16.
Dependence of horizons on q in the case of existence of the global temperature.
Horizons coincides at , which corresponds to a triple horizon.
For a regular spherically symmetric space-time with
there exists a certain value
at which, for a certain value
, the metric function
, its first and second derivative (and hence tangential pressure) vanish; as a result the temperature and the specific heat vanish, so the triple-horizon configuration is thermodynamically stable [
84]. Near
a metric function has only one zero and a plateau distinguished by two conditions:
,
. These two equations give two dependencies,
and
. Imposing the third condition defining a horizon,
, we define uniquely a triple-horizon configuration for any density profile [
84].
For the case of the density profile (16)
. As we shall see below, the triple horizon is not involved in a black hole evolution during evaporation (see also [
84]).
4. Evolution of a Black Hole During Evaporation
The main question is where move horizons?
For an observer in the R-region , the internal (for a black hole) horizon is his cosmological horizon, which is the boundary of his manifold, so that the second law of thermodynamics reads . As a result, the evolution of as governed by the second law gives .
Looking at the horizon-mass diagram
Figure 5 plotted for the density profile (16) we see that on the black hole horizon
while on both cosmological horizons
:
It follows then that when
increases, mass
M decreases by (29), hence black hole horizon shrinks,
, and cosmological horizon moves outward,
.
How general is the relation (29) and how it can be justified?
Following Teitelboim we can take derivative of the relation
keeping
λ constant [
16]. In our case we keep constant also central Λ. It gives on the horizons
With taking into account behavior of
on the horizons, we should have
on each horizon in order to get (29).
Let us show that (31) holds everywhere (not only on the horizons) for the wide class of density profiles whose dependence on the coordinate
r involves
where
is the characteristic scale in a geometry with the de Sitter interior [
52]. For the density profile
the mass function can be written as
where
.
The metric function takes the form
It follows from (34) that in the considered case (31) holds everywhere. On the horizons we get
As a result, evolution goes towards a formation of the double horizon
.
Near the double horizon the specific heat is negative by (24). The same relation requires be positive near the double horizon . Therefore it should occur the phase transition during evaporation where is broken and changes sign and acquires its maximal value (27).
Before the transition,
, hence
, when
decreases,
decreases too, temperature increases to a maximum (27) where
changes sign, so that after transition we have
, and thus further decreasing
leads to decreasing
until it vanishes at the double horizon. At this point the specific heat
is positive and takes the value (24), free energy is positive and equal
, and energy
achieves its minimum, so that the configuration with the double horizon
can be the thermodynamically stable endpoint of evolution during evaporation. Let us study now the evolution on the internal horizon. Its thermodynamical energy
By (29),
and
M decreases when
grows. Since
on the internal horizon, we have
Specific heat
is positive near
, so that
and
when
approaches the double horizon. Hence
decreases with increasing
, the mass
M decreases too,
and
, so the growth in
leads to monotonic decreasing of the mass
M and of the temperature
until it vanishes at the double horizon where the energy
achieves its minimum.
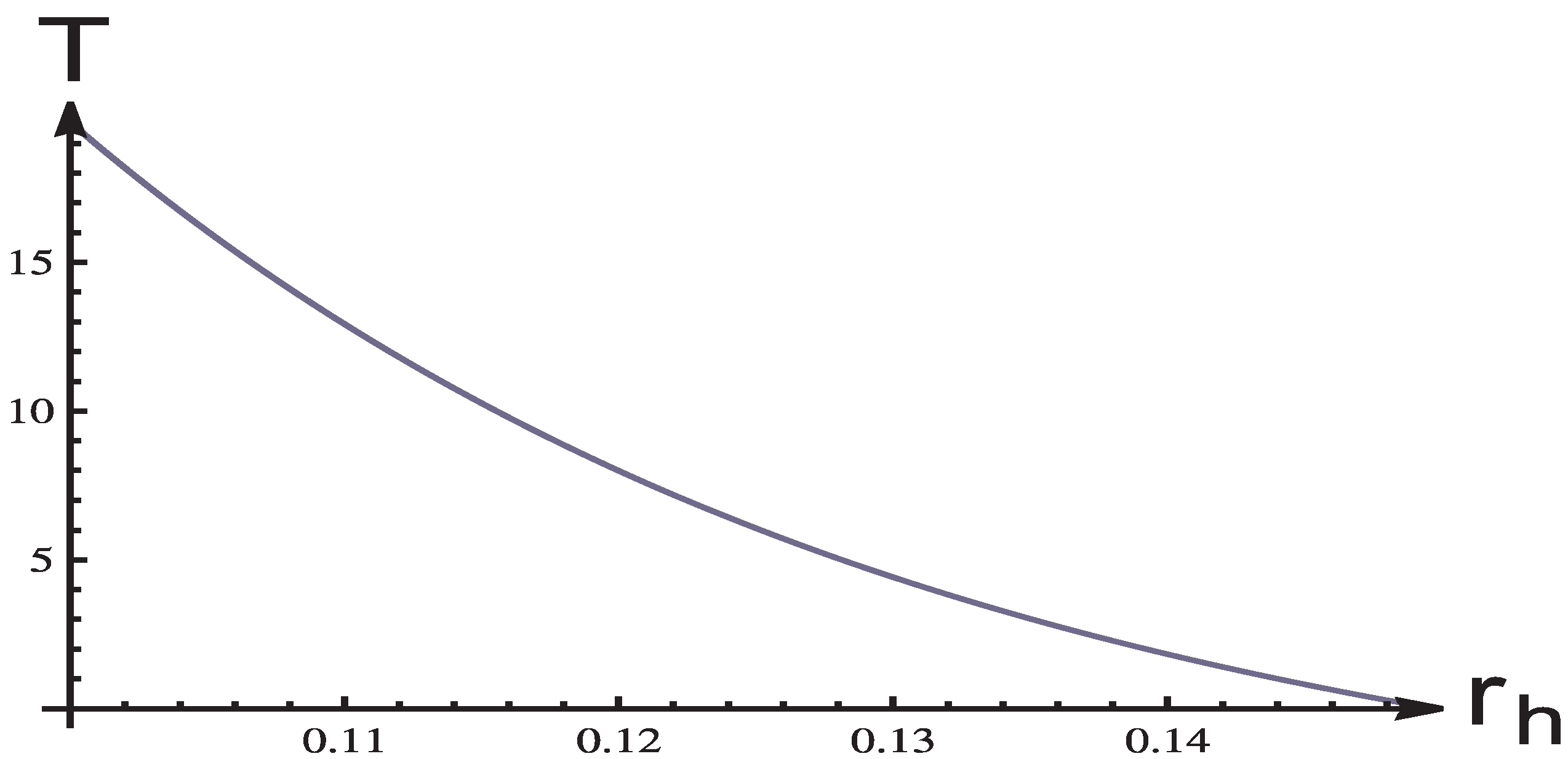
Temperature of the internal horizon is shown in
Figure 17 for
. It decreases monotonically with increasing
, and vanishes for
when
.
Figure 17.
Temperature on the internal horizon .
Figure 17.
Temperature on the internal horizon .
The cosmological horizon
moves outwards during evaporation. The reasoning is similar to the case of
but the essential difference is that the specific heat is negative near the double horizon
. Hence
and
; because the mass decreases by virtue of (29),
which we see in
Figure 18. Starting from the double horizon
evolution must thus occur as follows:
M decreases and
increases by (29), hence
decreases, according to (25), and specific heat remains negative. Numerical analysis shows that for
the temperature on the cosmological horizon
is almost insensitive to the parameter
q as we see in
Figure 18.
Figure 18.
Temperature on the cosmological horizon .
Figure 18.
Temperature on the cosmological horizon .
We conclude that a regular cosmological black hole leaves behind the thermodynamically stable double-horizon remnant with zero temperature and positive specific heat.
Let us note that this conclusion follows unambiguously from thermodynamics of horizons, so that a regular cosmological black hole, like the asymptotically flat regular black hole [
65,
80], leaves behind the remnant free of the existential problems.
For the case of the density profile (16) mass of the remnant
For
and
5. Summary and Discussion
We have studied thermodynamics of regular spherically symmetric cosmological black holes with two vacuum scales, Λ as as a certain fundamental symmetry scale, and the background . We applied the Padmanabhan approach relevant for the multi-horizon space-time with non-zero pressure. We present the basic thermodynamical formulae valid for any density profile satisfying the weak energy condition (needed for replacing a Schwarzschild singularity with a de Sitter vacuum interior).
Let us first discuss the question of entropy. The Padmanabhan obtains the same non-zero value for entropy of any horizon [
12] as dictated by the Bekenstein formula for a black hole entropy [
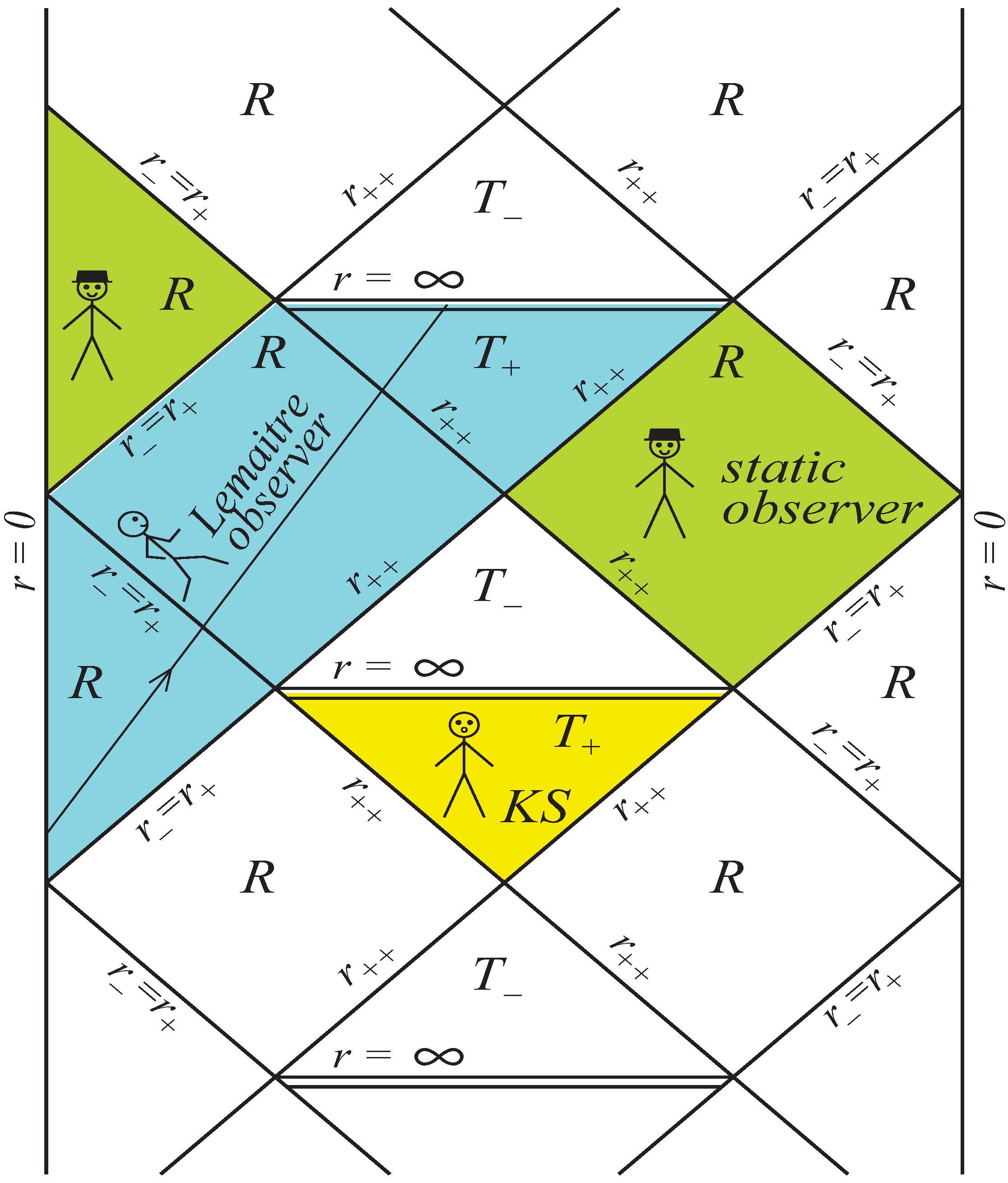
2]. Generalized uncertainty principle predicts zero entropy of the Planckian remnant in agreement with the third law of thermodynamics for a zero temperature thermodynamical system. The key point is that the entropy related to a horizon is the measure of a lack of information about a system surrounded by this horizon for an observer in a relevant R-region. The causal structure of space-time for a regular double-horizon remnant asymptotically de Sitter at both origin and infinity, is shown in
Figure 19 [
85,
89].
Figure 19.
Global structure of space-time for a double-horizon remnant in de Sitter space.
Figure 19.
Global structure of space-time for a double-horizon remnant in de Sitter space.
This picture shows how the manifold of events is seen by different observers. Here
is the internal horizon,
is the black (white) hole horizon, and
is the cosmological horizon. Thermodynamics of horizons is considered from the point of view of static observers in R-regions (observers in hats). Static observers are those who move on world lines of constant
r,
θ and
ϕ which coincide with orbits of the static Killing vector
[
9]. T-regions correspond to homogeneous anisotropic cosmological models of Kantowski-Sachs type [
85,
90]. Lemaitre observers (using coordinates, e.g., related to radial timelike geodesics) see two R-regions and one T-region.
The internal horizon is the cosmological horizon for an observer in the R-region . For a static observer in this region boundaries of his manifold are horizons in his absolute past and future (his time coordinate changes from to ). Such an observer has no access to information beyond the horizons . A static observer in the R-region has no access to information beyond the horizon and cosmological horizon . In accordance with the causal structure of space-time, static observers feel the lack of information from regions beyond their horizons, and it seems evident that measure of this information cannot rather be zero, suggesting in particular a non-zero entropy for the remnants. It follows that the question of the remnant entropy, as well as the question of consensus between non-zero remnant entropy and third law of thermodynamics, needs further investigation.
We studied in details dynamics of all three horizons and found that dynamics of evaporation is dictated in essence by generic behavior of the regular metric with the de Sitter interior.
We found that in the case of a regular cosmological black hole there exists a certain range of parameters M and , for which an observer in the region between the black hole horizon and the cosmological horizon would detect the global temperature.
During evaporation a second-order phase transition occurs where the specific heat on the black hole horizon is broken and changes its sign, and the black hole temperature achieves its maximum. At the final stage temperature drops to zero and a black hole evolves to soliton-like double-horizon remnant.
Soliton-like character of remnants was noted in [
58,
63,
65,
80]. The existence of gravitational solitons with the de Sitter interior was found first in [
80] including those without a black hole horizon. They can arise not only as final products of evaporation but also in a way similar to primordial black hole formation from quantum fluctuations emerging in a quantum tunnelling process [
67]. Cosmological production of positive mass noncommutative black holes and solitons was studied in [
63] where it was shown that they would have plentifully been produced during inflationary epoch [
63].
Let us emphasize that the basic features of evaporation dynamics of a regular black hole with the de Sitter interior are generic and dictated by generic behavior of a metric function
[
80,
84]. A particular form of the density profile
affects only numerical values of thermodynamical parameters but not their dynamical behavior [
84]. The Hawking temperature drops to zero when an internal and black hole horizons coalesce just because the surface gravity
vanishes at an extremum of a metric function
[
80]. In the asymptotically flat case it vanishes as
in the Schwarzschild limit, hence a temperature-mass function must have a maximum (defined by
) where the specific heat its broken and changes its sign which testifies for a second-order phase transition in the course of evaporation [
80]. Similar behavior was found in [
58,
59] for the renormalization group improved black hole [
88], in [
62] for a noncommutative black hole, and in [
82] for a minimal black hole model [
83]—even though in [
58,
82] thermodynamical energy was identified with the black hole mass
M which is true for the Schwarzschild black hole with one horizon but not true for a multihorizon spacetime with non-zero pressure [
12]. This mistake leads only to vanishing specific heat of the remnant but not affect the typical behavior—zero temperature of the remnant and the existence of the maximal temperature [
58,
62,
80,
82]. The proper choice of thermodynamical energy leads to the remnant with the positive specific heat [
84]. For a cosmological regular black hole temperature drops to zero when black hole horizon coalesce with the cosmological horizon (
vanishes in the maximum of
), so that temperature vanishes on both boundaries of the R-region
, hence it achieves a certain maximum value (proportional to
) [
84]. The same behavior was found recently for a noncommutative black hole with positive mass and the gaussian density profile [
63].
We conclude that a regular spherically symmetric black hole in de Sitter space leaves behind a thermodynamically stable double-horizon remnant with the positive specific heat and zero temperature [
49,
84]. Its stability to small perturbations is now under investigation, preliminary results suggest stability in a wide range of density profiles. We can thus expect that regular black holes and their remnants can contribute to dark matter black holes ([
41,
91] and references therein).